2. 中国海洋大学海洋地球科学学院,山东 青岛 266100;
3. 太原理工大学大数据学院,山西 太原 030100
良导体海水在地磁场中运动,产生运动感应电磁场[1],这种运动感应电磁场对海洋电磁数据的处理和解释具有重要意义[2]。当台风发生时,海况变得更加复杂。台风过程中,大气和海洋之间的相互作用强烈,台风向海洋内部注入大量机械能,强迫海洋在局地产生强烈混合[3-4],改变海洋上层的温盐流结构分布[5-6]。强风驱动导电海水在地球磁场中运动,产生感应电流,海洋作为天然源激发感应电磁场,这种与海水电导率和流速密切相关的海洋感应电磁场可在台风条件下表现出明显的时空变化特征。
海水电导率与温度、盐度和压力有关[7-8],这意味着台风能引起海水电导率发生变化。海水电导率和流速的变化对海水运动感应电磁场产生重要影响[9-10]。关于海水电导率和流速的处理大体有3种方式:(1)凭经验给定,例如通常将电导率设为常数[11-12],速度场由一个随深度指数衰减变化的函数给出或者设为常数[13]; (2)直接观测数据得到[14-16]; (3)利用数值模式输出参数计算得到[17-19]。第1种方式对海水物理性质的描述过于简单直接; 第2种方式比较真实可靠,但极易受到天气、海况、仪器甚至人为因素的影响,数据量受限; 第3种方式能够很好的描述海洋的动力过程,得到三维连续的网格化电导率和流速数据,但对数值模式的分辨率和精度具有很大的依赖性。
精确估计海水电导率和流速的分布变化是提高台风条件下海洋电磁场数值模拟精度的基础。目前运动感应电磁场数值模拟研究工作取得了较大进展。Bhatt等[9]利用格林函数法计算了一维和二维海水运动感应电磁场,探讨了水深、电导率、海水速度等对运动感应电场和磁场的影响; Velímsky等[20]采用时间域球谐有限元方法求解三维电导率模型的电磁感应方程,模拟环型模式和极型模式的感应磁场,最近又模拟了全球大尺度环流引起的感应磁场,研究了感应磁场与横向电导率的变化关系[21]; Šachl等[22]在海洋环流和潮汐模式框架下采用不同的数值方法(ElmgTD,X3DG和UTSM法)模拟全球环流感应磁场,通过数值模拟试验结果评估了这些方法的模拟效果。
综上所述,近年来在海水运动感应电磁场研究方面取得了丰硕的成果,但这些研究大多基于平静海况,而对于台风影响下极端海况引起的感应电磁场研究比较少见。目前,随着海气耦合模式不断发展和完善,台风个例的模拟能力不断提升[23-25],这为台风条件下获取大量网格化的海水电导率和流速等数据提供了支持条件,便于开展极端海况下海水运动感应电磁场研究。本文结合台风数值模拟试验结果,定量估算海水运动感应磁场对台风的响应,探讨台风条件下海水运动感应磁场的时空分布特征。
1 海水运动感应电磁场的估算海水流动切割地磁场产生感应电流,进而产生感应磁场。这种变化的电场和磁场在海洋中再次相互感应,产生多次感应场。本文估算台风影响下海水电导率和流速变化产生的感应磁场变化。
假设海水运动为多个带电粒子定向运动的宏观表现,地磁场中带电运动粒子在洛伦兹力作用下产生累积电荷,形成恒定电流,其电流密度可以近似表示成为J=σ(V×Bearth)。式中:σ为海水电导率; V=(vx, vy, vz),为流速(假设x轴指向地磁北极; y轴指向东; z轴取垂直海面向下); Bearth=(Bex, Bey, Bez),为地磁场。在海水中产生的感应电流分量为:
| $ \begin{aligned} J_x=\sigma\left(v_z B_{e y}-v_y B_{e z}\right), \end{aligned} $ | (1) |
| $J_y=\sigma\left(v_x B_{e z}-v_z B_{e x}\right), $ | (2) |
| $ J_z=\sigma\left(v_y B_{e x}-v_x B_{e y}\right) 。$ | (3) |
该感应电流激发的磁场其实是由运动电荷所激发的,在任意一点处运动电荷激发的磁感应强度可由毕奥萨伐尔定律
对目标海域求积分可得到任意一点的海水运动感应磁场。为简化计算,将海水假设为分层海水模型,海水水平尺度远大于垂直深度尺度,积分区域V可近似表示为(-∞≤x≤+∞,-∞≤y≤+∞,0≤z≤h),在海面上方,水平磁场强度近似表示为[26]:
| $\begin{aligned} B_x=\frac{\mu_0 \sigma\left(v_x B_{e z}-v_z B_{e x}\right) h}{2}, \end{aligned} $ | (4) |
| $ B_y=\frac{\mu_0 \sigma\left(v_z B_{e y}-v_y B_{e z}\right) h}{2} 。$ | (5) |
式中h为薄层厚度。地磁场由世界地磁模型WMM2015计算得到。根据海水电导率和流速,可利用(1)~(5)式估算海水运动感应磁场。流速可通过耦合模式模拟台风个例直接得到,海水电导率通过以下方法计算。
2 海水电导率的计算电导率是海水重要基本电学参数之一,早期常被用于盐度测量。海水电导率可通过海洋水文要素(温度、盐度和压力)计算得到[7],其计算公式为:
| $ C(S, T, P)=R \cdot C $ | (6) |
式中:参考电导率C(35, 15 ℃, 0 dbar)表示标准大气压下温度15 ℃、实用盐度35时测得的电导率,取值4.291 4 S/m[27]; R为相对电导率,其计算式为:
| $ \begin{gathered} R=\frac{1}{2 A} \times \\ {\left[\sqrt{\left(B-A r_t R_t\right)^2+4 r_t R_t A(B+C)}-\left(B-A r_t R_t\right)\right]}。\end{gathered} $ | (7) |
式中A,B和C表达式分别为:
| $ \begin{gathered} A=a_1+a_2 T_{68}, \end{gathered} $ | (8) |
| $ B=1+b_1 T_{68}+b_2 T_{68}^2, $ | (9) |
| $ C=P\left(c_1+c_2 P+c_3 P^2\right) 。$ | (10) |
式中:T68=1.000 24T; 常数a1=0.421 5;a2=-3.107×10-3; b1=3.426×10-2; b2=4.464×10-4; c1=2.07×10-4; c2=-6.37×10-10; c3=3.989×10-15。(7)式中rt与温度T有关:
| $ r_t=d_0+d_1 T+d_2 T^2+d_3 T^3+d_4 T^4 。$ | (11) |
式中:常数d0=0.676 609 7;d1=2.005 64×10-2; d2=1.104 259×10-4; d3=-6.969 8×10-7; d4=1.003 1×10-9。Rt和盐度S、温度T满足以下关系式:
| $ \begin{aligned} &S=e_0+e_1 R_t^{1 / 2}+e_2 R_t+e_3 R_t^{3 / 2}+e_4 R_t^2+e_5 R_t^{5 / 2}+ \\ &\frac{T-15}{1+k(T-15)} \times \\ &\left(m_0+m_1 R_t^{1 / 2}+m_2 R_t+m_3 R_t^{3 / 2}+m_4 R_t^2+m_5 R_t^{5 / 2}\right) 。\end{aligned} $ | (12) |
式中:常数e0=0.008;e1=-0.169 2;e2=25.385 1;e3=14.094 1;e4=-7.026 1;e5=2.708 1;m0=0.000 5;m1=-0.005 6;m2=-0.006 6;m3=-0.037 5;m4=0.063 6;m5=-0.014 4;k=0.016 2。
根据(6)~(12)式,代入温度、盐度和压力,计算可得海水电导率。
3 台风模拟试验本文以台风“格美”(201220)为例,利用区域耦合模式COAWST进行台风模拟试验(COAWST模式详见文献[23]),获取台风影响下的模式网格化海洋水文数据,研究台风对海水运动感应磁场的影响。
台风“格美”(201220)发生于2012年9月29日—10月7日,位于中国南海海域。在10月2日0时(UTC,下同),台风风速为18 m/s,逐渐加强,向东南移动,在18时风速增大到23 m/s; 3日6—18时风速维持在25 m/s,为强热带风暴,之后逐渐减弱为热带风暴; 至6日12时,减弱为热带低压,逐渐消失。
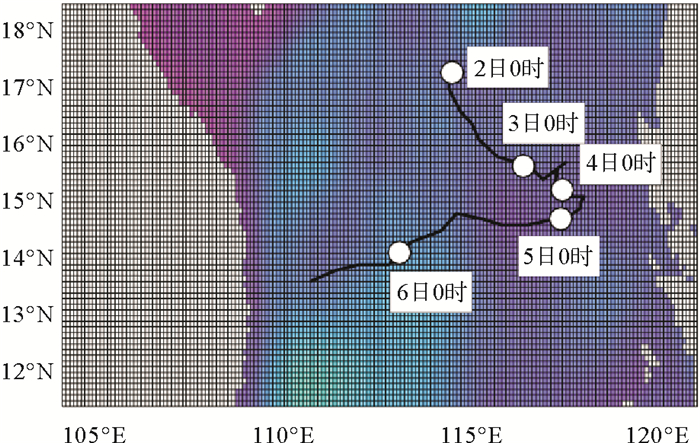
本文模拟台风个例“格美”,设置模拟区域(108°E—120°E,12°N—18°N),模拟时间从2012年10月2日00:00(UTC)—6日12:00(UTC),模拟时长为108 h,每6 h输出一次结果。海洋模式水平分辨率为9 km,对应网格个数183×74,垂向分层10层,模拟深度由海表至1 000 m深度。图 1为模拟区域和台风路径。
|
(台风信息参考http://typhoon.nmc.cn/web.html。Please refer http://typhoon.nmc.cn/web.html for more detail. ) 图 1 模拟区域和台风路径 Fig. 1 Model domain and typhoon |
本文讨论的海水温度范围0~40 ℃,盐度范围2~42,深度在1 000 m以内压力随深度近似线性变化。本文根据COAWST模式的海洋模式网格信息,经过插值和转换,重构海水电性模型; 然后提取模式1 000 m海水深度内的温度、盐度和深度数据(深度转换为压力),计算台风影响下的海水电导率; 最后结合模式输出的流速数据,计算海水运动感应磁场。
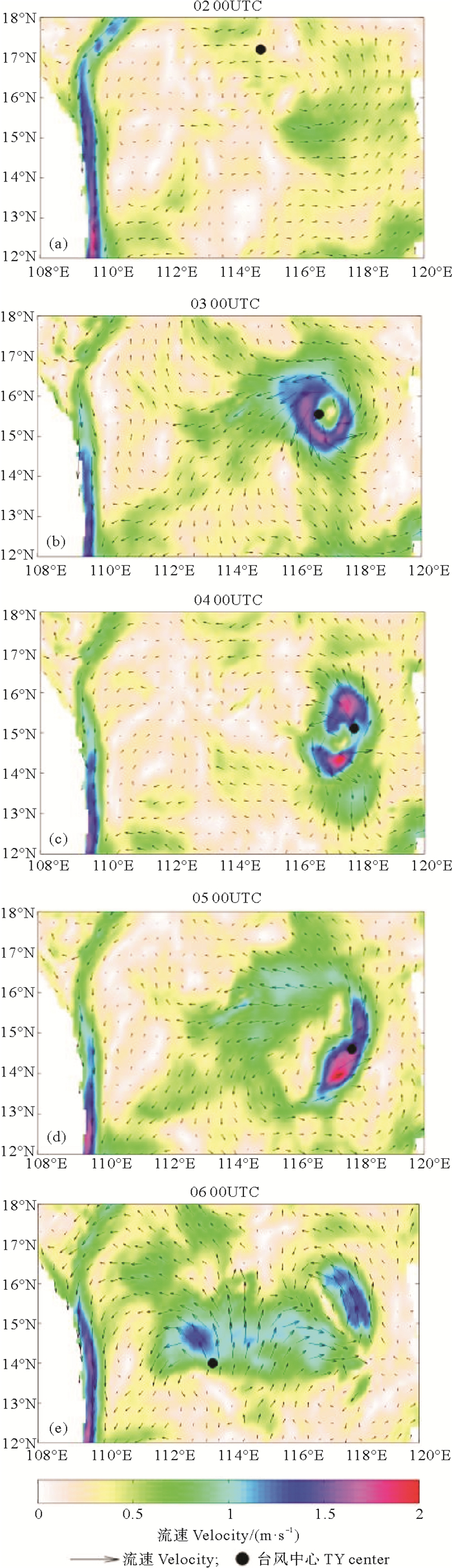
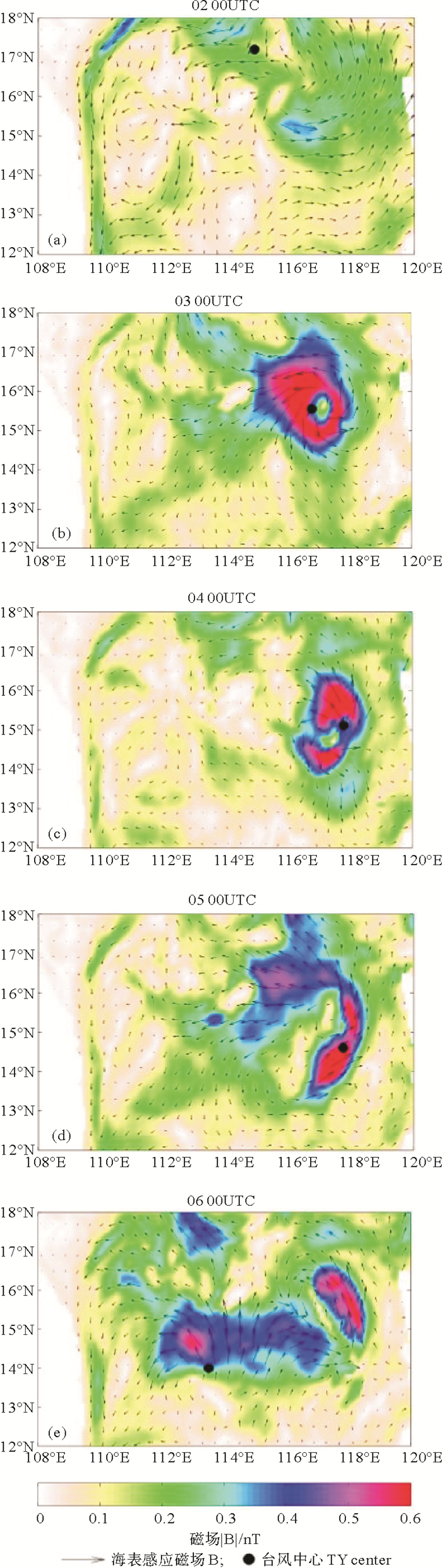
4 结果分析 4.1 流速对海水运动感应磁场的影响台风条件下,流速发生异变,海水运动感应磁场的变化与流速具有密切关系。图 2和3分别为台风发展过程中海表流场和海表感应磁场分布。2日0时,台风风力较弱,对海洋的影响较小,西边界流区流速较大,在流速较大区域感应磁场较大(见图 2(a)和3(a)所示(黑点为该时刻台风中心位置,下同))。随着台风的发展,台风中心移动,风力加强,对海洋的影响逐渐增大,可以看到西边界流区流速发生变化(相对于2日0时,见图 2(a)),以及台风中心附近的流场形成了明显的气旋式分布强流区,强流区中心出现一个不与台风中心重合的流场低速中心(见图 2(b),(c)),最大流速达2 m/s; 西边界流区感应磁场发生变化(相比于2日0时,见图 3(a)),在台风中心附近感应磁场亦呈气旋式分布(见图 3(b),(c)),幅值变大,且出现一个不与台风中心重合的感应磁场低值中心,台风影响下最大感应磁场达0.8 nT。当风力逐渐减弱,台风注入的能量在海洋中逐渐扩散,台风中心附近区域流场和感应磁场呈辐射状分布,能量向外传递,逐渐耗散。由图 2(d)和3(d)可见,台风对感应磁场的影响范围进一步扩大了。到6日0时(见图 2(e),3(e)),台风所过移动路径附近,台风对流场和感应磁场的影响仍然存在,台风又对该时刻台风中心附近流场和感应磁场产生了新的影响,使得该位置处流速和感应磁场增大,但由于风力减弱,没有形成明显的气旋式分布特征。
|
图 2 10月2—6日00时海表流场分布 Fig. 2 Sea surface flow velocity at the time of 00:00 UTC on 2 to 6 Oct. |
|
图 3 10月2—6日00时海表感应磁场分布 Fig. 3 Sea surface magnetic field at the time of 00:00 UTC on 2 to 6 Oct. |
对图 2和3进行定量分析,2日0时在西边界流区最大流速达1.82 m/s,最大感应磁场约0.37 nT。随着台风对海洋影响的增大,西边界流区流速变化幅度在-0.85~0.72 m/s范围内(相对于2日0时),感应磁场最大降幅约0.15 nT。在强流区,流速的最大增幅约1.57 m/s,感应磁场最大增幅约0.56 nT。由以上讨论可知,海水运动感应磁场的大小和方向变化与流速具有高度的一致性。
4.2 台风对海水运动感应磁场的时空影响分析台风条件下,海水运动感应磁场在时间和空间上发生明显变化。根据图 2和3可知,在空间上,台风对海洋的强迫使得台风中心附近感应磁场呈明显不对称的气旋式分布,且存在一个不与台风中心重合的低值中心; 当台风风力减弱,感应磁场气旋式分布逐渐消失,但在新的台风中心附近区域感应磁场值较大,这表明当台风风力达到一定强度时,才能使得感应磁场出现和维持气旋式分布。在时间上,感应磁场随台风演变而变化,与海洋其他水文要素(如温度等)对台风的反馈类似[6]。海表感应磁场对台风的响应可能具有滞后性和持续性,即台风路过时,海表感应磁场不能立即响应台风的影响,具有一定时间的延迟,当台风中心离开后,台风对海表感应磁场的影响没有消失,将延续一段时间。
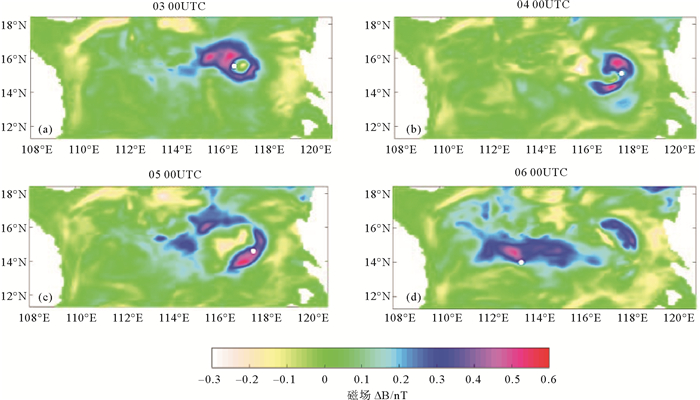
为进一步探讨该台风对感应磁场的影响范围和影响时间,将3—6日0时的感应磁场分别与2日0时进行对比,感应磁场差异如图 4所示。由图 4(a)可见,3日0时台风中心外围附近区域,感应磁场为正差异值,靠近台风中心区域感应磁场变化不大,影响范围约为200~300 km。到4日0时,风力加强,但从图 4(b)上看,台风的影响范围减小,这可能与台风路径变化有关。5日0时,台风的影响范围扩大到约400 km以上,到6日0时进一步增大到约500 km。从整个变化过程来看,当该台风路过后,对该位置感应磁场的影响可能能够持续1~2 d时间,比如,在6日0时(见图 4(d))仍然可以看到4日0时(见图 4(b))台风中心附近位置的感应磁场差异。
|
图 4 10月3—6日台风影响下海表感应磁场差异 Fig. 4 Sea surface magnetic field difference under the influence of typhoon on 3 to 6 Oct |
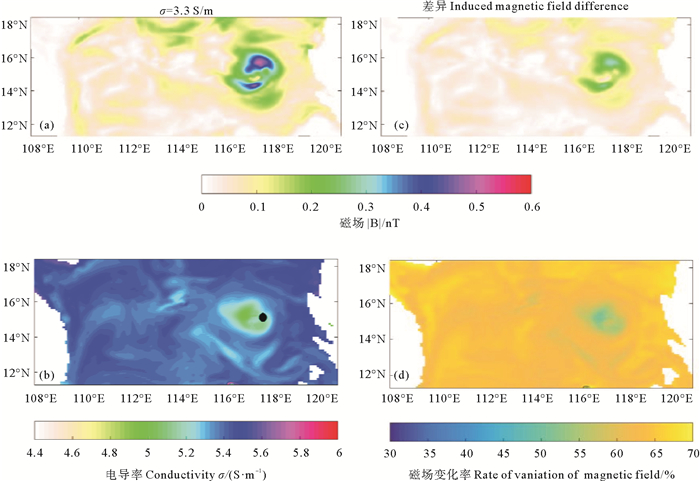
以4日0时刻为例,讨论台风影响下海表电导率变化对海表感应磁场的影响。将海表电导率设为常数3.3 S/m,其他参数如前所述,感应磁场分布如图 5(a)所示。由图 5(a)可知,不考虑电导率变化,将其设为常数估计的感应磁场也能反映台风的影响,在流速增大的区域海水运动感应磁场增大。
|
((a)海表电导率设为常数3.3 S/m感应磁场,(b)模式海表电导率,(c)感应磁场差异分布,(d)海表感应磁场变化率。(a) Sea surface conductivity 3.3 S/m. (b) Sea surface conductivity given by coupled model. (c) Induced magnetic field difference. (d) Rate of variation of sea surface induced magnetic field. ) 图 5 10月4日海表电导率变化对感应磁场的影响 Fig. 5 Influence of sea surface conductivity on induced magnetic field on 4 Oct |
图 5(b)给出了模式4日0时刻海表电导率分布,可见其水平分布不均匀,在台风影响下台风中心(黑点位置)附近出现明显的电导率低值区域,最低值约4.9 S/m,其他区域海表电导率约5.5 S/m左右。相应地根据模式输出参数计算的结果如图 3(c)所示,与电导率设为常数3.3 S/m时估算的感应磁场(见图 5(a))进行比较,两者感应磁场差异如图 5(c)所示(图 3(c)与图 5(a)感应磁场之差),均为正差异,最大的差异值达0.29 nT。这表明当电导率设为常数3.3 S/m时,估算的感应磁场值偏小,尤其在强流区位置处感应磁场差异明显。
图 5(d)给出了4日0时刻模式电导率对应的感应磁场(见图 3(c))相对于设为常数电导率对应的感应磁场(见图 5(a))的变化率,台风中心附近感应磁场相对变化了约55%,而其他区域则达65%左右。
以上分析表明,在台风条件下,海表电导率呈现明显的不均匀性,如果在应用中将电导率设为常数,可能会错误的估计台风对感应磁场的实际影响强度。
5 结论本文以台风“格美”为例,基于区域耦合模式COAWST模拟台风个例的海洋水文参数,估算了海水运动感应磁场,并探讨了台风条件下海水运动感应磁场的时空变化特征。研究表明:
(1) 流速和海水电导率与海水运动感应磁场具有密切关系。台风影响下感应磁场与流速的变化具有一致性; 台风引起的海水电导率不均匀性对感应磁场具有重要影响。
(2) 在空间分布上,海水运动感应磁场在台风中心附近区域出现不对称气旋式分布,且存在一个低值中心,台风影响水平范围约200~500 km,海表感应磁场最大可达0.8 nT; 在时间上,台风对海表感应磁场的影响具有滞后性和持续性,持续时间约为1~2 d。
本文研究旨在为极端条件下海洋电磁场的模拟、电磁数据的处理和解释提供理论参考。限于台风个例模拟试验的可靠性和准确性,收集更多数据来源并对多个台风个例样本进行统计分析将是我们下一步要开展的工作。
| [1] |
Sanford T B. Motionally induced electric and magnetic fields in the sea[J]. Journal of Geophysical Research, 1971, 76: 3476-3492. DOI:10.1029/JC076i015p03476 (  0) 0) |
| [2] |
Chen K, Zhao Q, Deng M, et al. Seawater motion-induced electromagnetic noise reduction in marine magnetotelluric data using current meters[J]. Earth Planets and Space, 2020, 72(1): 1-11. DOI:10.1186/s40623-019-1127-2 (  0) 0) |
| [3] |
Sriver R L, Huber M. Observational evidence for an ocean heat pump induced by tropical cyclones[J]. Nature, 2007, 447(7144): 577-580. DOI:10.1038/nature05785 (  0) 0) |
| [4] |
Liu L L, Wang W, Huang R X. The mechanical energy input to the ocean induced by tropical cyclones[J]. Journal of Physical Oceanography, 2008, 38(6): 1253-1266. DOI:10.1175/2007JPO3786.1 (  0) 0) |
| [5] |
Chiang T L, Wu C. Typhoon Kai-Tak: An ocean's perfect storm[J]. Journal of Physical Oceanography, 2011, 41(1): 221-233. DOI:10.1175/2010JPO4518.1 (  0) 0) |
| [6] |
陈大可, 雷小途, 王伟, 等. 上层海洋对台风的响应和调制机理[J]. 地球科学进展, 2013, 28(10): 1077-1086. Chen Dake, Lei Xiaotu, Wang Wei, et al. Upper ocean response and feedback mechanisms to typhoon[J]. Advances in Earth Science, 2013, 28(10): 1077-1086. DOI:10.11867/j.issn.1001-8166.2013.10.1077 (  0) 0) |
| [7] |
Fofonoff N P, Millard R C. Algorithms for computation of fundamental properties of seawater[J]. Unesco Technical Papers in Marine Science, 1983, 44(4): 203-209. (  0) 0) |
| [8] |
Fofonoff N P. Physical properties of seawater: A new salinity scale and equation of state for seawater[J]. Journal of Geophysical Research Atmospheres, 1985, 90(C2): 3332-3342. DOI:10.1029/JC090iC02p03332 (  0) 0) |
| [9] |
Bhatt K M, Hördt A, Weidelt P, et al. Motionally Induced Electromagnetic Field Within the Ocean[C]. [s. l. ]: 23th Schmucker-Weidelt-Kolloquium für Elektromag-Netische Tiefenforschung. Heimvolkshochschule am Seddiner See, 2009.
(  0) 0) |
| [10] |
林智恒, 李予国. 海水运动感应磁场的数值计算方法[J]. 中国海洋大学学报(自然科学版), 2019, 49(2): 74-78. LIN Zhi-heng, LI Yu-guo. Calculations of magnetic variations induced by ocean waves[J]. Periodical of Ocean University of China, 2019, 49(2): 74-78. (  0) 0) |
| [11] |
Kuvshinov A, Junge A, Utada H. 3-D modelling the electric field due to ocean tidal flow and comparison with observations[J]. Geophysical Research Letters, 2006, 33(6): 239-241. (  0) 0) |
| [12] |
Schnepf N R, Manoj C, Kuvshinov A, et al. Tidal signals in ocean-bottom magnetic measurements of the Northwestern Pacific: Observation versus prediction[J]. Geophysical Journal International, 2014, 198(2): 1096-1110. DOI:10.1093/gji/ggu190 (  0) 0) |
| [13] |
周春, 李予国, 张宝强. 变速海水运动感应电磁场数值模拟及特征分析[J]. 海洋与湖沼, 2019, 50(2): 261-268. ZHOU Chun, LI Yu-guo, ZHANG Bao-qiang. Numerical simulation and characteristic analysis of electromagnetic field induced by variable velocity seawater movement[J]. Oceanologia et Limnologia Sinica, 2019, 50(2): 261-268. (  0) 0) |
| [14] |
Sabaka T J, Tyler R H, Olsen N. Extracting ocean-generated tidal magnetic signals from Swarm data through satellite gradiometry[J]. Geophysical Research Letters, 2016, 43(7): 3237-3245. DOI:10.1002/2016GL068180 (  0) 0) |
| [15] |
Zheng Z Y, Fu Y, Liu K Z, et al. Three-stage vertical distribution of seawater conductivity[J]. Scientific Reports, 2018, 8(1): 9916. DOI:10.1038/s41598-018-27931-y (  0) 0) |
| [16] |
Szuts Z B, Bower A S, Donohue K A, et al. The scientific and societal uses of global measurements of subsurface velocity[J]. Frontiers in Marine Science, 2019, 6: 1-8. DOI:10.3389/fmars.2019.00001 (  0) 0) |
| [17] |
Vivier F, Maier-Reimer E, Tyler H R. Simulations of magnetic fields generated by the Antarctic Circumpolar Current at satellite altitude: Can geomagnetic measurements be used to monitor the flow[J]. Geophysical Research Letters, 2004, 31(10): L10306. (  0) 0) |
| [18] |
Manoj C, Kuvshinov A, Maus S, et al. Ocean circulation generated magnetic signals[J]. Earth Planets and Space, 2006, 58(4): 429-437. DOI:10.1186/BF03351939 (  0) 0) |
| [19] |
Irrgang C, Saynisch J, Thomas M. Impact of variable seawater conductivity on motional induction simulated with an ocean general circulation model[J]. Ocean Science, 2016, 12(1): 129-136. DOI:10.5194/os-12-129-2016 (  0) 0) |
| [20] |
Velímsky J, Martinec Z. Time-domain, spherical harmonic-finite element approach to transient three-dimensional geomagnetic induction in a spherical heter-ogeneous Earth[J]. Geophysical Journal International, 2005, 161(1): 81-101. DOI:10.1111/j.1365-246X.2005.02546.x (  0) 0) |
| [21] |
Velímský J, šachl L, Martinec Z. The global toroidal magnetic field generated in the Earth's oceans[J]. Earth and Planetary Science Letters, 2019, 509: 47-54. DOI:10.1016/j.epsl.2018.12.026 (  0) 0) |
| [22] |
Šachl L, Martinec Z, Velímsky J, et al. Modelling of electromagnetic signatures of global ocean circulation: physical approximations and numerical issues[J]. Earth Planets and Space, 2019, 71(1): 1-13. DOI:10.1186/s40623-018-0980-8 (  0) 0) |
| [23] |
Warner J C, Armstrong B, He R, et al. Development of a coupled Ocean-Atmosphere-Wave-Sediment Transport (COASWST) modeling system[J]. Ocean Modelling, 2010, 35(3): 230-244. DOI:10.1016/j.ocemod.2010.07.010 (  0) 0) |
| [24] |
Liu N, Ling T, Wang H, et al. Numerical simulation of typhoon Muifa (2011) using a coupled Ocean-Atmosphere-Wave-Sediment Transport (COAWST) modeling system[J]. Journal of Ocean University of China, 2015, 14(2): 199-209. DOI:10.1007/s11802-015-2415-5 (  0) 0) |
| [25] |
雷小途. 中国台风科研业务百年发展历程概述[J]. 中国科学: 地球科学, 2020, 50(3): 321-338. LEI Xiao-tu. Overview of the development history of China's typhoon research and operational work in the past century[J]. Scientia Sinica(Terrae), 2020, 50(3): 321-338. (  0) 0) |
| [26] |
李庚伟. 海洋感应电磁场理论研究[D]. 北京: 中国地质大学, 2012. LI Geng-wei. The Theory Research on Ocean Induction Electromagnetic Field[D]. Beijing: China University of Geosciences, 2012. (  0) 0) |
| [27] |
Culkin F, Smith N. Determination of the concentration of potassium chloride solution having the same electrical conductivity, at 15℃and infinite frequency, as standard seawater of salinity 35.000 0(Chlorinity 19.373 94)[J]. IEEE Journal of Oceanic Engineering, 1980, 5: 22-23. DOI:10.1109/JOE.1980.1145443 (  0) 0) |
2. College of Marine Geosciences, Ocean University of China, Qingdao 266100, China;
3. College of Data Science, Taiyuan University of Technology, Taiyuan 030100, China
 2022, Vol. 52
2022, Vol. 52


