2. 中国海洋大学工程训练中心,山东 青岛 266100;
3. 中国海洋大学 山东省海洋工程重点实验室,山东 青岛 266100
叶片是潮流能水轮机的主要获能部件,其性能的优劣直接影响水轮机的发电效率和使用寿命。近年来改善水轮机叶片水动力学性能,提高其发电效率成为潮流能领域的研究热点之一[1]。设计研发一种高效率的水轮机叶片周期长、造价高,而通过在已有叶片上安装合适的被动流动装置,来提高其性能则更为实用。作为一种简单有效的被动流动控制技术,格尼襟翼(Gurney flap, GF)的结构简单、增升效果显著,因而受到了广泛关注[2]。
格尼襟翼是位于叶片尾缘压力侧,垂直于弦线且高度厚度均较小的一种有效增升装置[4-7]。格尼襟翼最早应用于赛车后翼板,用来增大赛车的抓地力;后来被成功应用于改善风机叶片的气动性能[3]。目前格尼襟翼的研究和应用主要集中在风电领域。Chakroun Yosra等[8]研究了格尼襟翼对NACA 4412翼型性能的影响,结果表明:随着格尼襟翼高度的不断增加,翼型的升力系数会逐渐增大,但同时阻力系数也会略有增加。Xi等[9]研究了格尼襟翼对流动分离现象的影响,结果表明:当攻角较小(α≤2°)时,格尼襟翼会抑制翼型表面的流动分离现象;格尼襟翼的存在会增大翼型失速前的升力,并可提高特定攻角下的升阻比。Chen等[10]对有无格尼襟翼的翼型气动性能进行了分析,结果表明格尼襟翼可以使翼型的最大升力系数提高15.33%,翼型升力的增量同格尼襟翼高度的平方根成正比。
虽然潮流能水轮机同风力机有一定相似之处,但水轮机所处海水的密度大,故不能忽视海水所受重力的影响,且水轮机的工作环境较风力机更为复杂恶劣。目前潮流能水轮机领域主要是通过改变叶片形状来提高其性能,如袁鹏等[11]基于遗传算法,利用儒可夫斯基保角变换法对翼型进行参数化建模,从而改善原有翼型的升力系数和升阻比。Shi等[12]结合座头鲸鳍的前缘结节来改善水轮机叶片的翼型结构,结果表明:前缘结节可使得翼型在失速条件下保持较高的升力系数,并使最大升阻比提高5.8%,但同时还会降低最大升力系数。上述方法虽然可在一定程度上提高叶片性能,但使叶片的设计变得更加复杂。
该文在不改变原始叶片翼型的前提下,于翼型段上安装格尼襟翼这种附加件,并由此开展格尼襟翼对水轮机叶片水动力学特性的影响规律的研究,以NACA4418翼型为研究对象,研究了不同格尼襟翼参数对水轮机叶片翼型水动力性能的影响规律,通过水槽试验和数值模拟相结合的方法,验证了该文研究方法的正确性,所得结论可为格尼襟翼安装于潮流能水轮机的后续研究提供一定参考。
1 几何模型 1.1 翼型段选取NACA4418翼型段为研究对象,该翼型具有较高的升力系数以及较低的阻力系数,因而在潮流能水轮机领域应用比较广泛[13]。该文采用NACA4418翼型的直翼段,其弦长为300 mm,展向长度为260 mm,基础翼型段和加装格尼襟翼后的翼型段分别如图 1(a)、(b)所示。

|
( (a) 基础翼型段Basic hydrofoil; (b)带GF翼型Hydrofoil with GF. ) 图 1 基础翼型段和加装GF翼型段的几何参数 Fig. 1 Geometry of basic hydrofoil and hydrofoil with GF |
格尼襟翼通过增加翼型尾缘的曲率,增大翼型绕流环量,来改善翼型的水动力学性能并提高翼型升力,其具体实现效果同格尼襟翼的几何参数直接相关[14-19]。格尼襟翼的几何参数如图 1(b)所示,取襟翼厚度为1 mm,高度、弦向位置(即尾缘长度)以及偏转角度分别用H、L和Φ表示。
为了验证格尼襟翼不同几何参数对翼型水动力学性能的影响,该文共设计了8组模型,分别改变格尼襟翼的高度、弦向位置以及偏转角度来模拟其性能,8组格尼襟翼模型的数据如表 1所示,其中C为叶片翼型弦长。
|
|
表 1 不同格尼襟翼及其几何参数 Table 1 Different GFs and their geometric parameters |
该文采用STAR CCM+商业软件进行数值模拟计算,该软件的优点是在网格适应性、计算稳定性和收敛性等方面均具有较好性能[19]。该文将翼型绕流问题看作是不可压缩流动问题,控制方程选用三维不可压缩Navier-Stokes方程和三维连续性方程,进行稳态流场计算。湍流模型选择SST k-ω湍流模型,该模型具有k-ω模型在近壁区计算和k-ε模型在远场计算的两方面优点[22]。
三维连续性方程:
| $\frac{\partial(\rho \boldsymbol{u})}{\partial x}+\frac{\partial(\rho \boldsymbol{v})}{\partial y}+\frac{\partial(\rho \boldsymbol{w})}{\partial z}=0 \text { 。}$ | (1) |
三维不可压缩Navier-Stokes方程:
| $\begin{gathered} \frac{\partial(\rho \boldsymbol{u})}{\partial t}+u \frac{\partial(\rho \boldsymbol{u})}{\partial x}+v \frac{\partial(\rho \boldsymbol{u})}{\partial y}+w \frac{\partial(\rho \boldsymbol{u})}{\partial z}= \\ -\frac{\partial p}{\partial x}+\mu\left(\frac{\partial \boldsymbol{u}}{\partial x^2}+\frac{\partial \boldsymbol{u}}{\partial y^2}+\frac{\partial \boldsymbol{u}}{\partial z^2}\right) 。\end{gathered}$ | (2) |
| $\begin{gathered} \frac{\partial(\rho \boldsymbol{v})}{\partial t}+u \frac{\partial(\rho \boldsymbol{v})}{\partial x}+v \frac{\partial(\rho \boldsymbol{v})}{\partial y}+w \frac{\partial(\rho \boldsymbol{v})}{\partial z}= \\ -\frac{\partial \boldsymbol{p}}{\partial y}+\mu\left(\frac{\partial \boldsymbol{v}}{\partial x^2}+\frac{\partial \boldsymbol{v}}{\partial y^2}+\frac{\partial \boldsymbol{v}}{\partial z^2}\right) 。\end{gathered}$ | (3) |
| $\begin{gathered} \frac{\partial(\rho \boldsymbol{w})}{\partial t}+u \frac{\partial(\rho \boldsymbol{w})}{\partial x}+v \frac{\partial(\rho \boldsymbol{w})}{\partial y}+w \frac{\partial(\rho \boldsymbol{v})}{\partial z}= \\ -\frac{\partial \boldsymbol{p}}{\partial z}+\mu\left(\frac{\partial \boldsymbol{w}}{\partial x^2}+\frac{\partial \boldsymbol{w}}{\partial y^2}+\frac{\partial \boldsymbol{w}}{\partial z^2}\right) 。\end{gathered}$ | (4) |
式中:ρ为流体密度(kg/m3 );u、v、w分别为x、y、z方向上的速度分量(m/s);t为时间(s);p为压力(Pa)。
假设叶片翼型的水动力性能参数主要由升力系数Cl、阻力系数Cd以及升阻比Cl/Cd表示,则升力系数Cl的计算公式为:
| $C_1=\frac{F_1}{0.5 \rho V^2 A} {\rm{。}}$ | (5) |
阻力系数Cd的计算式为:
| $C_{\mathrm{d}}=\frac{F_{\mathrm{d}}}{0.5 \rho V^2 A} \text { 。}$ | (6) |
式中:ρ为流体密度(kg/m3);V为来流方向上的速度值(m/s);A为翼型参考面积(m2);Fl为翼型升力(N);Fd为翼型阻力(N);
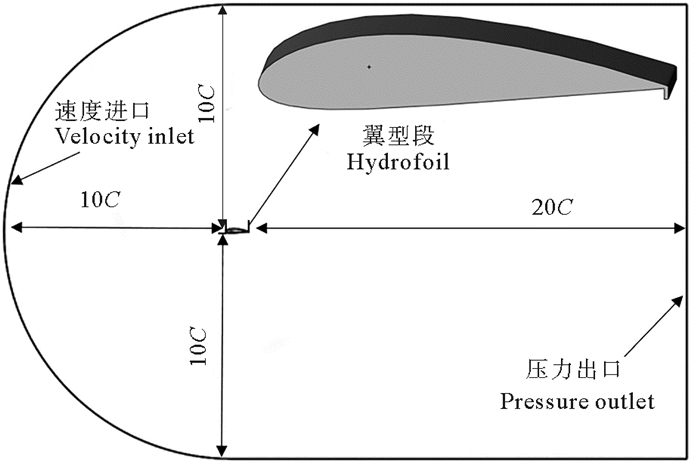
2.2 计算域和边界条件该文采用的计算域如图 2所示,为降低边界对计算结果的影响,设置计算域入口距离翼型前缘为10倍弦长,计算域出口距离翼型尾缘为20倍弦长,上、下边界距离翼型均为10倍弦长。计算域左侧设置为速度入流边界,入口速度取1.0 m/s,右侧为压力出口边界,前、后面为对称面边界条件,上、下面和翼型表面为无滑移壁面边界条件。
|
图 2 整体计算域 Fig. 2 Overall computational domain |
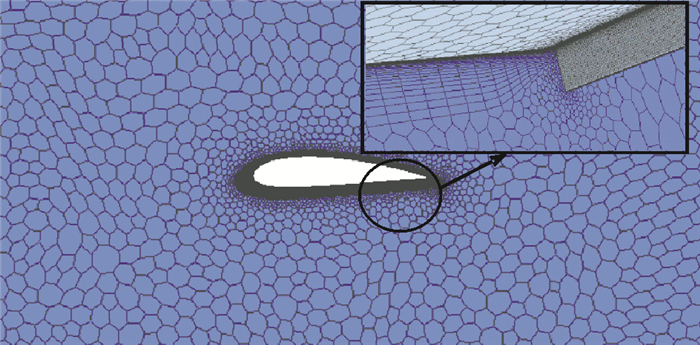
该文采用STAR CCM+软件特有的多面体网格,其优点是同时具有六面体网格的精确性和四面体网格的易生成性。基础翼型段和带格尼襟翼的水轮机叶片翼型段采用相同的网格设置参数,在翼型段表面设置第一层边界层厚度为0.01 mm,边界总层数为30,网格增长率取1.3,以保证边界层y+≤1。为提高仿真结果的准确性,对翼型表面、格尼襟翼及其附近流场的网格进行加密处理(见图 3)。
|
图 3 带GF翼型段表面附近的多面体网格 Fig. 3 Polyhedral mesh generated around the surface of hydrofoil with GF |
采用SST k-ω湍流模型,对基础翼型和加装不同参数格尼襟翼的翼型进行数值模拟。为验证数值模拟结果的正确性,本研究通过水槽试验[20]来加以验证。试验在山东省海洋工程重点实验室进行,实验水槽长60 m,宽1.2 m,高1 m,最大设计流速可达1.5 m/s,满足试验要求。水槽试验装置及模型如图 4所示。试验模型与数值模型一致,均采用弦长300 mm,展长为260 mm的翼型段。当水槽来流速度为1.0 m/s时,对不同攻角下基础翼型段进行试验,通过三向力测量仪测量基础翼型段的升力和阻力。

|
图 4 实验场地及翼型段模型 Fig. 4 Testing site and model of hydrofoil |
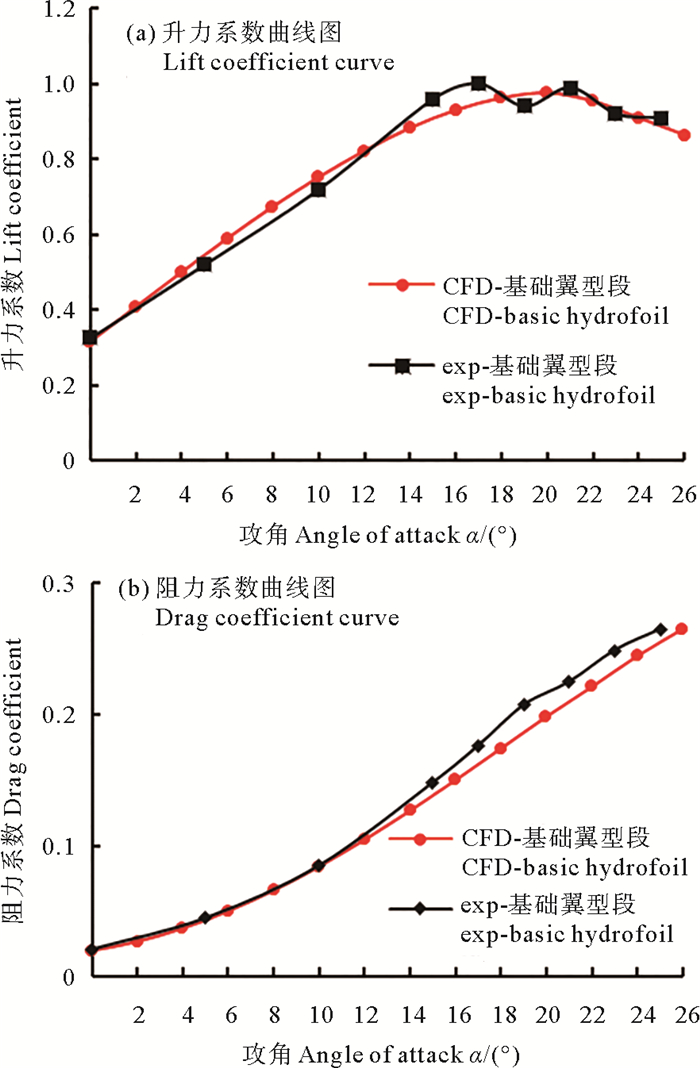
图 5所示为水槽试验结果与数值模拟结果的水动力学性能对比,可以看出,试验结果与模拟结果吻合良好。
|
图 5 翼型段性能试验数据和数值模拟对比 Fig. 5 Comparison of hydrofoil's performance of numerical simulation with testing value |
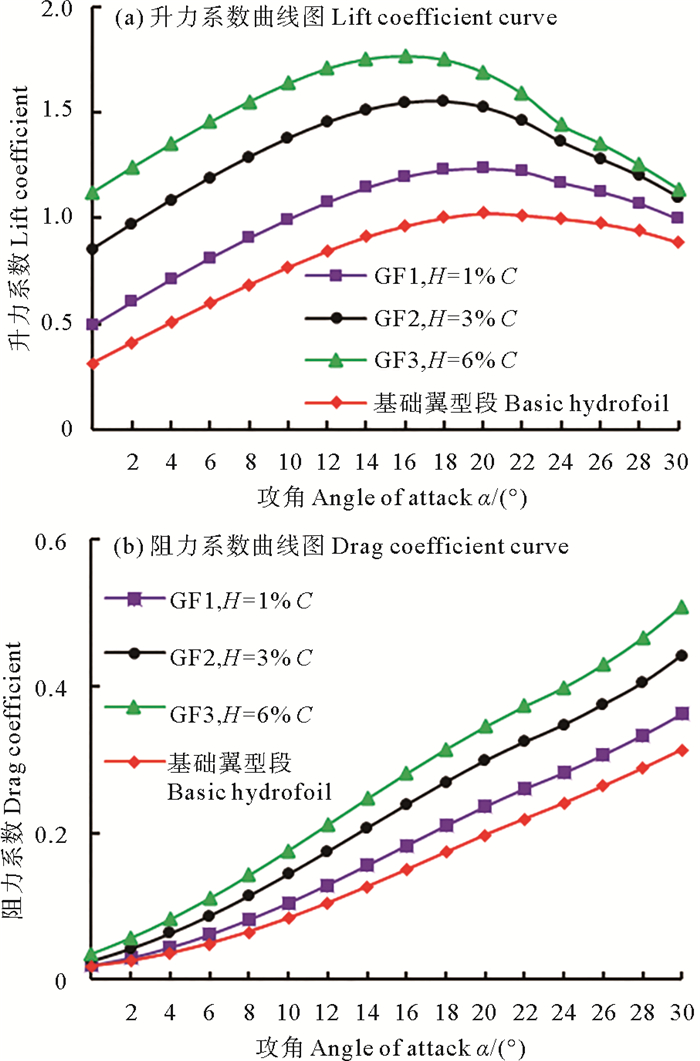
对加装GF1、GF2、GF3的三种翼型段进行水动力学性能分析,其结果如图 6所示。GF1(H=1%C)、GF2(H=3%C)和GF3(H=6%C)是除了高度不同其他参数相同的3个模型,取襟翼厚度为1 mm,尾缘长度L为0%C,偏转角度Φ为90°。
|
图 6 襟翼高度对翼型水动力学性能的影响 Fig. 6 Effect of GF height on hydrofoil performance |
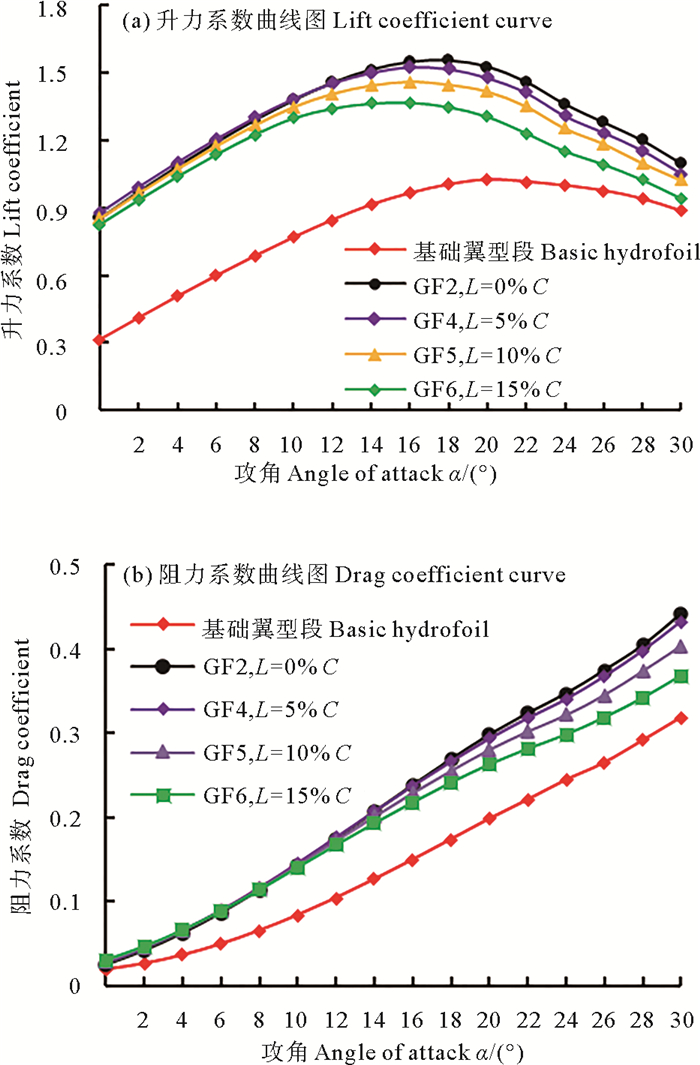
由图 6(a)可以看出,同基础翼型段相比,加装格尼襟翼会明显提高翼型的升力系数,且随着襟翼高度的增加,翼型升力系数呈非线性增大。对于分别加装GF1、GF2和GF3的三种翼型段,它们的最大升力系数分别增加了24.08%、60.51%和83.51%;翼型失速后,GF3的升力系数相比于GF2会急剧降低,整体增升效果变差。同时还可以看出,襟翼高度的增加会使翼型失速角降低,而翼型的零升力攻角也有变负的趋势,这是由于襟翼的存在,增大翼型的有效外倾角和弯度[24]。
由图 6(b)可以看出,襟翼的存在还会增大翼型段的阻力系数,且襟翼高度越高,阻力系数越大。对于分别加装GF1、GF2和GF3的三种翼型段,它们的最大阻力系数分别增加了15.53%、41.03%和72.08%,且阻力增加的幅度会随着高度的增加而增大。综合分析可知,存在一个最佳襟翼高度可使得翼型段获得最佳的水动力学性能,针对此模型,GF2对翼型段的性能提升最明显。
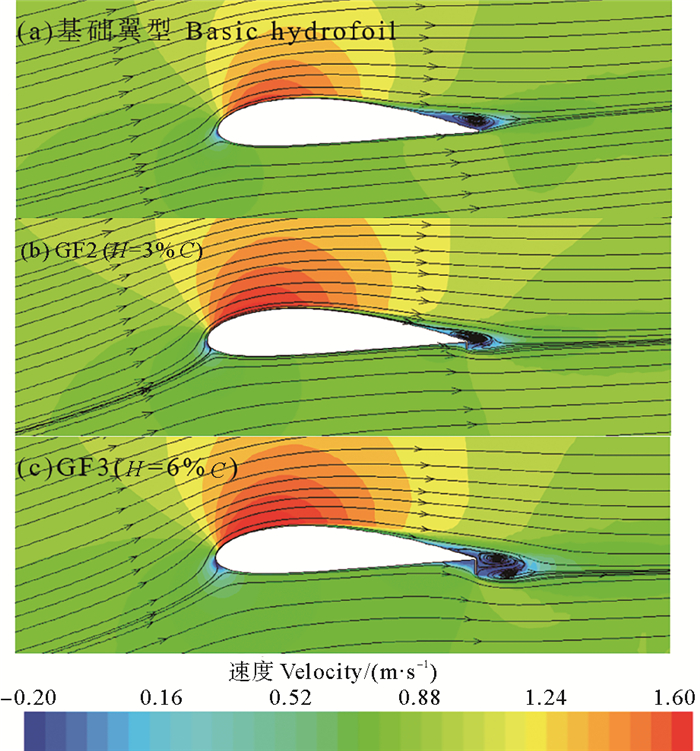
为进一步揭示格尼襟翼对水轮机叶片翼型水动力学性能的作用机理,图 7给出了最大升力系数(α=16°)下,不带襟翼和带不同高度格尼襟翼模型的流线图。由图 7可看出,加装襟翼使得翼型上表面流线更贴合吸力面。一方面,这是由于在襟翼后方生出一对反向涡,其内上方顺时针转动的涡,会诱导翼型段上表面流体在尾缘处向下偏转,从而增大上表面的绕流环量和边界层抵抗逆压梯度的能力;另一方面,襟翼下方逆时针转动的涡则会抵消压力面绕流的部分能量,从而降低流速。通过伯努利定理中流速和压强的关系可知,襟翼高度的增加会增大翼型上下表面的压差和升力,但是当格尼襟翼高度增大到一定程度即GF3(H=6%C)时,其高度已远大于此翼型的边界层厚度,此时尾流区内反向涡的尺寸和尾流区面积都急剧增加(见图 7c),导致翼型的阻力随之增大[5],襟翼的增升效果变差。
|
图 7 α=16°时,不同襟翼高度对翼型流场的影响 Fig. 7 Comparison of hydrofoil flow fields about different GF height at α=16° |
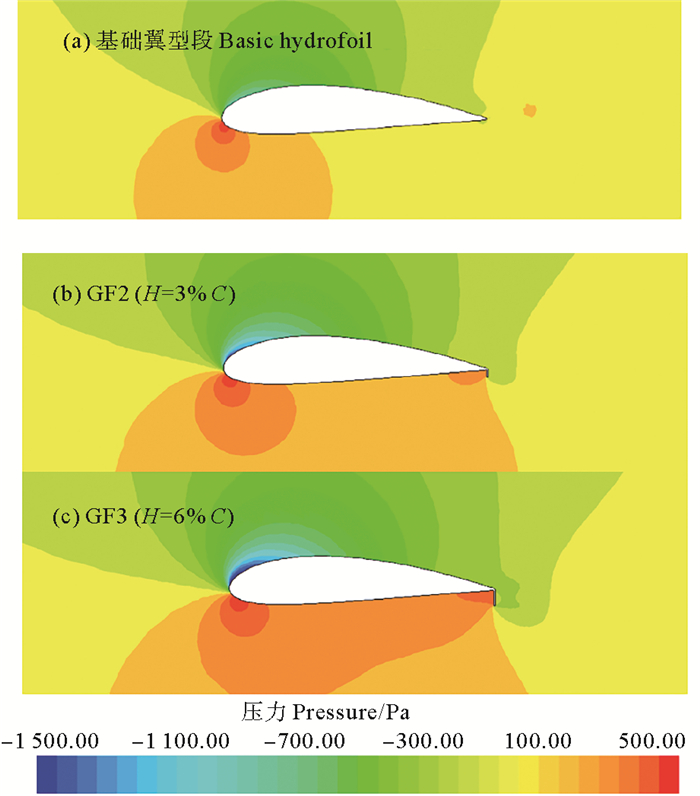
如图 8所示,分别为基础翼型段和加装高度分别为3%C和6%C襟翼的翼型段压力云图。可以看出,在加装GF后,压力面的尾缘襟翼前方会出现高压区域,并显著增大下表面的压力,而襟翼后方则出现低压区域;吸力面的前缘附近产生更小的负压区,且上表面的整体压力变小。这是由于襟翼高度的增加相当于尾缘的延伸,从而提高翼型的有效弯度,导致翼型吸力面的压力增大和压力面压力减小,即翼型的升力随襟翼高度的增加而增大。
|
图 8 α=16°时,襟翼高度对翼型表面静压力的影响 Fig. 8 Effect of GF height on static pressure distribution of hydrofoil at α=16° |
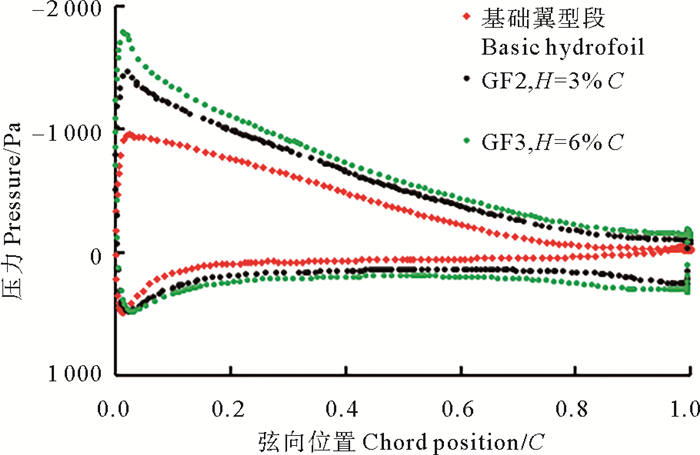
图 9为16°攻角时不同高度下,沿弦长方向翼型表面的压力散点图。可以看出,随着襟翼高度的增加,翼型上表面负压明显降低,上表面前缘的吸力增大;下表面的压力逐渐增大,而在翼型表面压力分布图中,曲线所围面积可表示翼型的升力大小[25],即翼型段的升力逐渐增大。但当高度超过一定值(H=3%C)时,曲线所围面积的增加幅度会变小,此时再增加高度会降低襟翼的增升效果。
|
图 9 α=16°时,襟翼高度对翼型表面压力影响 Fig. 9 Effect of GF height on pressure distribution of hydrofoil at α=16° |
对加装GF2、GF4、GF5、GF6的四种翼型段进行水动力学性能对比分析,其中GF2 (L=0%C)、GF4 (L=15%C)、GF5(L=10%C)、GF6 (L=15%C)是除弦向位置不同其余参数相同的4个模型,取厚度为1 mm,高度H为3%C,偏转角度Φ为90°,所得升阻力系数变化如图 10所示。
|
图 10 襟翼弦向位置对翼型水动力学性能的影响 Fig. 10 Effect of GF chord position on hydrofoil performance |
由图 10(a)可知,随着襟翼远离尾缘位置,翼型的失速角略有降低,而在翼型失速前,襟翼位置对升力系数的影响较小;失速后,随着襟翼远离尾缘位置,其升力系数会显著降低。同时,对于分别加装GF2、GF4、GF5和GF6的4种翼型段,它们的最大升力系数分别增加了60.51%、58.27%、51.34%和41.73%。由图 10(b)可以看出:在翼型失速(α=16°)前,阻力系数几乎不发生变化;在翼型失速后,随着襟翼远离尾缘,阻力略有减小。此时加装GF2、GF4、GF5和GF6的翼型段的最大阻力系数分别增加了41.01%、38.03%、28.84%和17.46%。但是考虑到随着襟翼远离尾缘位置,升力系数会显著降低,且尾缘位置处的失速角降低的最少,故尾缘位置处的格尼襟翼最能改善翼型的水动力性能。
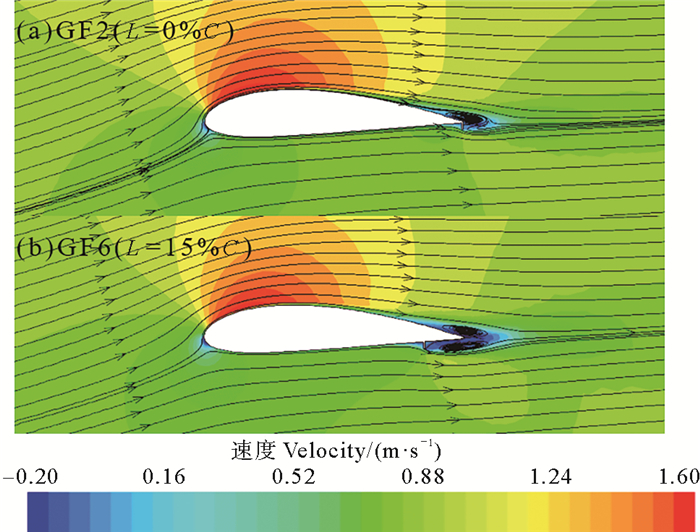
图 11为α=16°时,不同襟翼弦向位置下的翼型速度流场图。可以看出,随着襟翼远离尾缘位置(0~15%C),尾流区内上方的涡受襟翼的影响降低,上表面的流速略有下降,襟翼对上表面流体的引导作用减弱,绕流环量减小。而尾流区内下方的涡明显成型,湍流强度增大,下表面流速有所增加。据伯努利定理中速度和压力的关系可知,翼型上下表面的压差减小了,即襟翼的增升效果变差。
|
图 11 α=16°时,GF弦向位置对翼型流场的影响 Fig. 11 Comparison of hydrofoil flow fields about different chord position at α=16° |
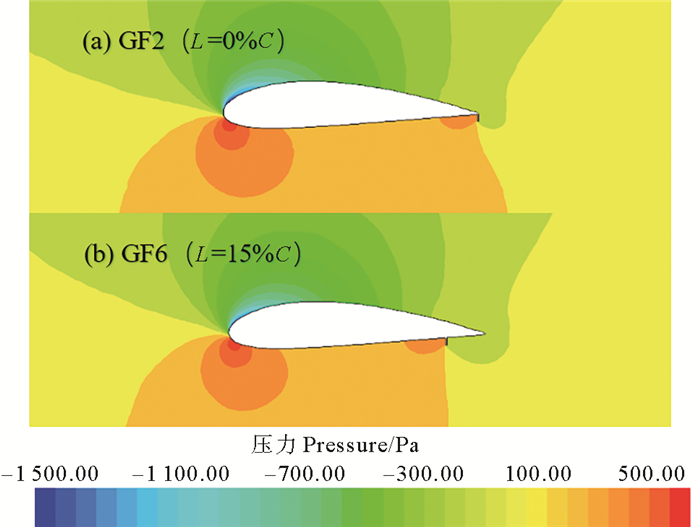
图 12为α=16°时,不同襟翼弦向位置处的翼型压力云图对比。可以看出,随着襟翼远离尾缘位置,翼型尾缘附近的高压区面积减小,压力降低,甚至在襟翼后方出现负压区域,导致翼型上下表面压差变小。同时襟翼的前移相当于降低翼型的有效弯度,使得襟翼的增升效果降低。
|
图 12 α=16°时,GF弦向位置对翼型表面压力影响 Fig. 12 Effect of GF chord position on static pressure distribution of hydrofoil at α=16° |
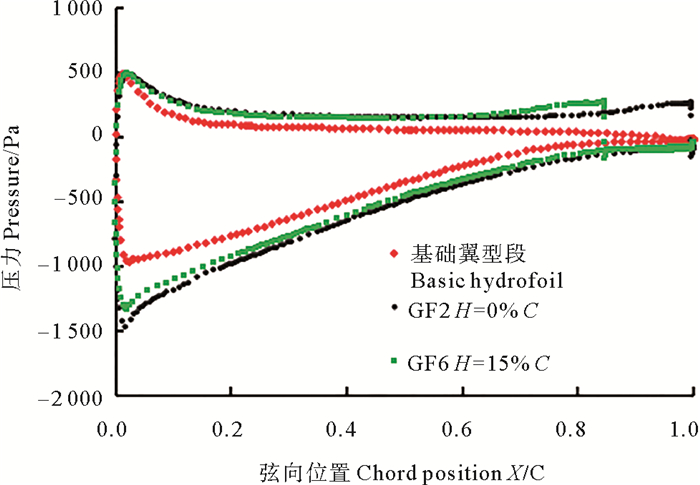
图 13为α=16°时,不同弦向位置下,沿弦长方向翼型表面的压力散点图。由图 13可知,随襟翼远离尾缘位置,上表面的压力略有降低,下表面前部分压力几乎不变,但在弦向0.6C~0.85C的范围内压力有所增加,同时襟翼后方的正压值则会急剧降低,直至为负。从整体上看,弦向位置的变化会使曲线所围面积减小,降低翼型的升力系数和增升效果。
|
图 13 α=16°时,弦向位置对翼型表面压力影响 Fig. 13 Effect of chord position on pressure distribution of hydrofoil at α=16° |
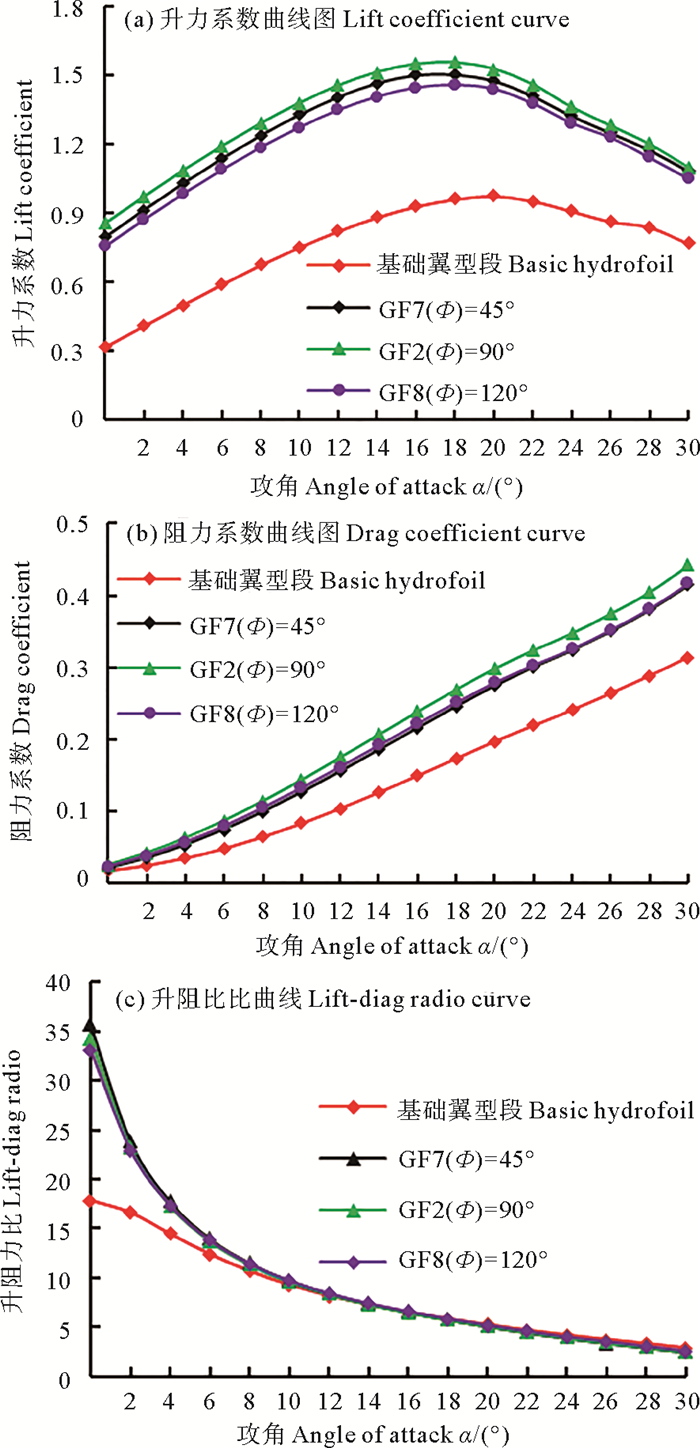
对分别加装GF2、GF7和GF8的3种翼型段进行水动力学性能分析,其中GF2(Φ=90°)、GF7(Φ=45°)和GF8(Φ=120°)是除偏转角度不同其余参数相同的3个模型,高度H为3%C,弦向位置L为0%C,其结果如图 14所示。由图 14(a)可以看出,随着偏转角度的赠加,升力系数先增大后减小,加装GF2的翼型段所获升力系数最大,且分别加装GF7、GF2和GF8的三种翼型段的最大升力系数分别增加了55.60%、60.51%和49.85%,其中加装GF2的翼型段所获升力系数最大。由图 14(b)和(c)可以看出,随着偏转角度的增加,阻力系数和升阻比变化不明显。
|
图 14 襟翼偏转角度对翼型水动力学性能的影响 Fig. 14 Effect of GF deflection degree on hydrofoil performance |
图 15为α=16°时不同偏转角度下,翼型的速度流线图。由图可知,随着偏转角度的增加,上表面的深色区域面积先增大后减小,即在GF2(Φ=90°)时上表面流速最大,而下表面的流速几乎不发生变化。综上所述,当襟翼偏转90°(即GF2)时翼型可获得最大的升力,即增升效果最佳。

|
图 15 α=16°时,偏转角度对翼型流场的影响 Fig. 15 Comparison of hydrofoil flow fields about different GF deflection degree at α=16° |
(1) 格尼襟翼可以有效地改善翼型段的水动力性能,提高翼型的最大升力系数,但翼型段的失速角会有所降低,同时阻力系数也略有增大。
(2) 在本次研究中,研究了不同格尼襟翼高度、弦向位置以及偏转角度对叶片翼型水动力学性能的影响,其中GF2(H=3%C, L=0%C, Φ=90°)的改善效果最佳,其最大升力系数增加了60.51%,这说明合理的格尼襟翼参数设置可有效地提高翼型的水动力学性能。
(3) 该文的研究结果能够为格尼襟翼应用于改善水轮机叶片翼型的水动力学性能提供理论指导,在上述基础上还需对加装格尼襟翼后翼型的失速角降低现象进行优化,并开展格尼襟翼对水轮机三维扭曲叶片水动力学特性的影响研究,这将是本研究团队下一步研究工作的重要内容。
| [1] |
孙浩伟, 谭俊哲, 刘永辉, 等. 涡流发生器对潮流能水轮机翼型水动力学特性影响的数值模拟[J]. 中国海洋大学学报(自然科学版), 2022, 52(2): 115-122. Sun H W, Tan J J, Liu Y H, et al. Numerical simulation of influence of vortex generator on hydrodynamic characteristics of tidal turbine hydrofoil[J]. Periodical of Ocean University of China, 2022, 52(2): 115-122. DOI:10.16441/j.cnki.hdxb.20200328 (  0) 0) |
| [2] |
吴柏慧, 李春, 朱海天, 等. 风力机叶片被动流动控制技术研究进展[J]. 热能动力工程, 2019, 34(9): 24-40. Wu B H, Li C, Zhu H T, et al. Research progress of passive flow control technology for wind turbine blade[J]. Journal of Engineering for Thermal Energy and Power, 2019, 34(9): 24-40. (  0) 0) |
| [3] |
崔钊, 高华, 韩东, 等. 格尼襟翼对低雷诺数翼型流场的影响研究[J]. 计算机仿真, 2018, 35(7): 15-21. Cui Z, Gao H, Han D, et al. Study on impact of Gurney flaps on low reynolds number airfoil flowfield[J]. Computer Simulation, 2018, 35(7): 15-21. (  0) 0) |
| [4] |
杨瑞, 郭瑞, 张康康, 等. 襟翼高度对风力机气动性能影响[J]. 太阳能学报, 2020, 41(11): 248-253. Yang R, Guo R, Zhang K K, et al. Effect of Gurney flap height on wind turbine aerodynamic performance[J]. Acta Energiae Solaris Sinica, 2020, 41(11): 248-253. (  0) 0) |
| [5] |
Liebeck R H. Design of subsonic airfoils for high lift[J]. Journal of Aircraft, 1978, 15(9): 547-561. DOI:10.2514/3.58406 (  0) 0) |
| [6] |
Amini Y, Emdad H, Farid M. Adjoint shape optimization of airfoils with attached Gurney flap[J]. Aerospace Science and Technology, 2015, 41(5): 216-228. (  0) 0) |
| [7] |
赵万里, 刘沛清, 朱建勇, 等. Gurney襟翼对风力机流动控制的数值研究[J]. 电网与清洁能源, 2011, 27(9): 85-92. Zhao W L, Liu P Q, Zhu J Y, et al. Numerical simulation of the flow control using Gurney flaps[J]. Power System and Clean Energy, 2011, 27(9): 85-92. DOI:10.3969/j.issn.1674-3814.2011.09.017 (  0) 0) |
| [8] |
Chakroun Y, Bangga G. Aerodynamic characteristics of airfoil and vertical axis wind turbine employed with Gurney flaps[J]. Sustainability, 2021, 13(8): 4284-4306. DOI:10.3390/su13084284 (  0) 0) |
| [9] |
He X, Wang J J, Yang M Q, et al. Numerical simulation of Gurney flaps lift-enhancement on a low reynolds number airfoil[J]. Science China Technological Sciences, 2017, 60(10): 1548-1559. DOI:10.1007/s11431-017-9085-4 (  0) 0) |
| [10] |
Chen H, Chen B, Andre C. Lift enhancement of tiltrotor wing using a Gurney flap[J]. International Journal of Aerospace Engineering, 2022(1): 1-9. (  0) 0) |
| [11] |
袁鹏, 王旭超, 王树杰, 等. 基于遗传算法的潮流能水轮机叶片翼型优化设计研究[J]. 中国海洋大学学报(自然科学版), 2018, 48(11): 125-131. Yuan P, Wang X C, Wang S J, et al. Study on optimization of hydrofoil of tidal turbine blade based on genetic algorithm[J]. Periodical of Ocean University of China, 2018, 48(11): 125-131. (  0) 0) |
| [12] |
Shi W, Atlar M, Norman R, et al. Biomimetic improvement for a tidal turbine blade[C]// Proceedings of the 11th European Wave and Tidal Energy Conference. Nantes, France: European Wave and Tidal Energy Conference, 2015, 110-119.
(  0) 0) |
| [13] |
黎作武, 陈江, 陈宝, 等. 风力机组叶片的先进翼型族设计[J]. 空气动力学学报, 2012, 30(1): 130-136. Li Z W, Chen J, Chen B, et al. Design of advanced airfoil families for wind turbines[J]. Acta Aerodynamica Sinica, 2012, 30(1): 130-136. (  0) 0) |
| [14] |
Yao Y, Ma D, Zhang L, et al. Aerodynamic optimization and analysis of low Reynolds number propeller with Gurney flap for ultra-high-altitude unmanned aerial vehicle[J]. Applied Sciences, 2022, 12(6): 3195-3224. DOI:10.3390/app12063195 (  0) 0) |
| [15] |
Maughmer M D, Bramesfeld G. Experimental investigation of Gurney flaps[J]. Journal of aircraft, 2008, 45(6): 2062-2067. (  0) 0) |
| [16] |
Wang J J, Li Y C, Choi K S. Gurney flap—Lift enhancement, mechanisms and applications[J]. Progress in Aerospace Sciences, 2007, 44(1): 22-47. (  0) 0) |
| [17] |
Zhang Y, Ramdoss V, Saleem Z, et al. Effects of root Gurney flaps on the aerodynamic performance of a horizontal axis wind turbine[J]. Energy, 2019, 187(1): 115955-115970. (  0) 0) |
| [18] |
Alber J, Soto-Valle R, Manolesos M, et al. Aerodynamic effects of Gurney flaps on the rotor blades of a research wind turbine[J]. Wind Energy Science, 2020, 5(4): 1645-1662. (  0) 0) |
| [19] |
Jain S, Sitaram N, Sriram K, et al. Computational investigations on the effects of Gurney flap on airfoil aerodynamics[J]. International Scholarly Research Notices, 2015, 2015(1): 1-11. (  0) 0) |
| [20] |
者浩楠, 刘永辉, 谭俊哲, 等. 不同涡流发生器参数对潮流能水轮机翼型水动力学特性影响研究[J]. 太阳能学报, 2022, 43(10): 350-356. Zhe H N, Liu Y H, Tan J Z, et al. Influence of different Vortex generator parameters on hydrodynamic characteristics of tidal current turbine hydrofoil[J]. Acta Energiae Solaris Sinica, 2022, 43(10): 350-356. (  0) 0) |
| [21] |
岳蛟. 船用舵设计系统开发及其水动力性能数值模拟研究[D]. 上海: 上海交通大学, 2020. Yue J. The Development of Ship Rudder Design System and Numerical Simulation of the Hydrodynamic Performance[D]. Shanghai: Shanghai Jiao Tong University, 2020. (  0) 0) |
| [22] |
Tseng C C, Cheng Y E. Numerical investigations of the vortex interactions for a flow over a pitching foil at different stages[J]. Journal of Fluids and Structures, 2015, 58(4): 291-318. (  0) 0) |
| [23] |
Masdari M, Mousavi M, Tahani M. Dynamic stall of an airfoil with different mounting angle of Gurney flap[J]. Aircraft Engineering and Aerospace Technology, 2020, 92(7): 1037-1048. (  0) 0) |
| [24] |
Wang J J, Li Y C, Choi K S. Gurney flap—Lift enhancement, mechanisms and applications[J]. Progress in Aerospace Sciences, 2008, 44(1): 22-47. (  0) 0) |
| [25] |
张红芬, 周云龙. 襟翼结构及安装位置对风力机翼型的流场影响[J]. 汽轮机技术, 2018, 60(4): 279-282. Zhang H F, Zhou Y L. The impact of flap structure and installation position on Flow Field of wind turbine airfoil[J]. Turbine Technology, 2018, 60(4): 279-282. (  0) 0) |
2. Engineering Training Center, Ocean University of China, Qingdao 266100, China;
3. Ocean Engineering Key Laboratory of Qingdao, Ocean University of China, Qingdao 266100, China
 2023, Vol. 53
2023, Vol. 53

