2. 浙江海洋大学船舶与海运学院,浙江 舟山 316022
由隔振的基本原理可知,减小隔振系统的刚度会使系统固有频率降低,从而拓宽隔振频带,提高整体的隔振效果,但对于传统的线性隔振系统而言,低刚度会造成承载能力下降,影响系统整体的稳定性。近年来,国内外学者尝试采用非线性系统解决上述问题[1-3]。其中,准零刚度隔振器作为一种隔振频带宽、承载能力好的非线性隔振器逐渐成为研究热点。Alabuzhev等[4]首先介绍了准零刚度隔振系统的基本理论和结构形式。Platus[5]对基于欧拉压杆负刚度特性的准零刚度隔振系统进行了研究。Carrella等[6-8]利用两根对称分布的倾斜线性弹簧与垂直弹簧并联构造出准零刚度系统,并对系统的幅频特性与传递特性进行了分析。吴文江等[9]基于三永磁体同极相对错开分布产生负刚度的特性设计了一种新型准零刚度系统,利用磁荷模型理论对系统的理论模型进行了数值分析,并通过实验证明了该系统可以有效降低整体的固有频率。刘兴天等[10-12]利用刀口支撑滑动梁以及对称倾斜分布欧拉梁的负刚度特性设计了一种新型准零刚度隔振系统,基于谐波平衡法分析了激振幅值、阻尼比值对系统力学特性的影响。研究结果显示,该系统适用于小幅值的振动环境,可以有效拓宽隔振频带,降低共振放大系数。在理论方面,Kovacic等[13]分析了分岔特性对准零刚度隔振系统动力学特性的影响,并根据分析结果对结构参数进行了优化。Sun等[14-15]研究了时滞控制对准零刚度隔振系统的影响,结果表明时滞控制可以有效改善隔振效果。
Asai等[16]利用恒力弹簧和椭圆规设计了一种准零刚度隔振器,通过理论推导和样机实验对隔振器开展了研究,结果表明该隔振器具有良好的滞回耗能能力,可以对简谐荷载与地震荷载实现良好的隔振效果。但该文未能针对此隔振器建立一套行之有效的有限元分析方法,针对一些复杂极端工况无法进行高效准确的研究。针对上述问题,本文建立了准零刚度隔振器的有限元模型,通过开展静压载实验和振动实验的有限元模拟,验证了该模型的准确性,研究了激振频率、幅值对隔振性能的影响,为该隔振器的实际应用效果提供科学的预测。
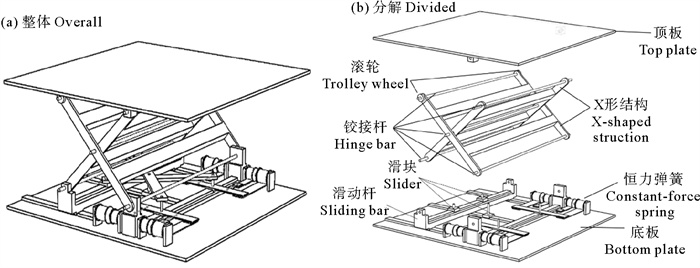
1 准零刚度隔振器工作原理 1.1 准零刚度隔振器的结构形式本文所研究的准零刚度隔振器结构形式如图 1所示,分为上中下三部分,其中上部组块由顶板构成,主要起到支撑上部重物的作用。中间组块的X形结构可以将荷载的作用方向由竖直方向转换为水平方向,以起到节省竖直方向空间的作用。下部组块主要包括椭圆规以及恒力弹簧等,主要承担提供准零刚度回复力的作用。
|
图 1 准零刚度隔振器示意图 Fig. 1 Schematic diagram of quasi-zero stiffness vibrationisolator |
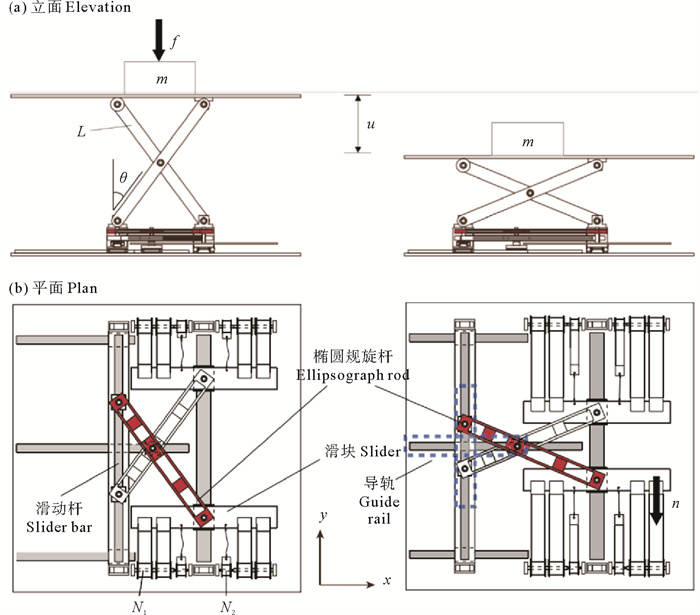
隔振器工作过程[16]如图 2所示,其中:N1为大恒力弹簧产生的回复力,N2为小恒力弹簧产生的回复力,隔振器在外部作用力f的作用下产生位移u,经过椭圆规和X形结构的传递,最终引起恒力弹簧组拉伸并产生回复力n。
|
( .f:外部作用力 External forces; u:位移 Displacement; m:质量块 Mass block;L:长度 Length;θ:角度 Angle ) 图 2 隔振器运行过程 Fig. 2 The operation process of the vibration isolator |
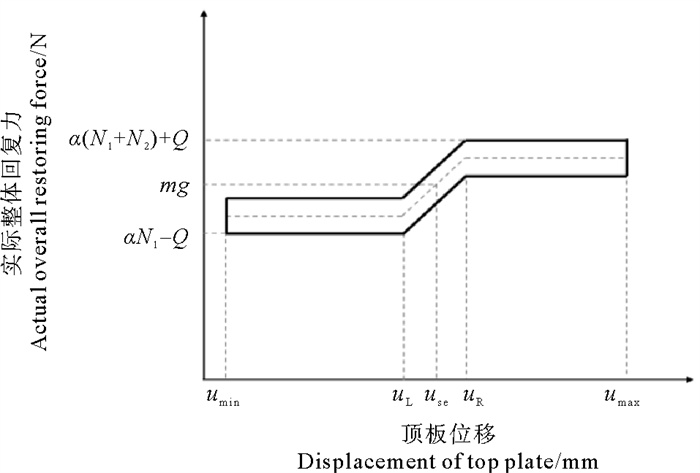
根据Asia[16]的理论推导,隔振器顶板位移u与实际整体回复力f的关系曲线如图 3所示,其中比例参数α为实际整体回复力f与恒力弹簧组产生的回复力n的比值,Q为隔振器在运行过程中产生的整体摩擦力。由图 3可知:
|
(mg: 顶板处承载物体的重量 The weight of the object at the top plate;umin:顶板与底板距离最小时顶板产生的位移 Displacement caused by the minimum distance between the top plate and the bottom plate;umax:顶板与底板距离最大时顶板产生的位移 Displacement of the top plate when the distance between the top plate and the bottom plate is the maximum;use:隔振器处于静平衡状态时顶板的位移 Displacement of top plate when the vibration isolator is in static equilibrium;uL:恒力弹簧2即将进入拉伸状态时顶板的位移 Displacement of the top plate when the constant force spring 2 is about to enter the tensile state;uR:恒力弹簧2线性拉伸阶段结束即将进入恒力拉伸阶段时顶板的位移 Displacement of top plate at the end of linear stretching stage of constant force spring 2 and about to enter constant force stretching stage ) 图 3 隔振器顶板位移-回复力曲线 Fig. 3 Displacement-restoring force curve of vibration isolator top plate |
(1) 当umin < u < uL或uR < u < umin时,隔振器整体刚度接近零,由隔振的基本原理可知,此时隔振器具备良好的隔振效果。
(2) 当uL < u < uR时,隔振器整体刚度较大,可以保证隔振器整体的稳定性以及外部荷载消失后的自复位能力。
(3) 隔振器位移-回复力曲线形成封闭的滞回环,这证明隔振器在运行过程中会有耗能,可以保证外部荷载消失后隔振器在较短时间里恢复到静平衡状态。
2 准零刚度隔振器有限元建模由图 1、2可知,准零刚度隔振器结构内部存在复杂的连接和接触关系,若按照实际的部件样式建模,会影响后续分析的收敛性,降低软件计算的效率。针对上述问题,本章根据结构内部的约束关系,通过在各部件之间设置连接器和质量点,在保证主要约束关系不变的基础上,利用ABAQUS软件的多体分析功能[17],建立准零刚度隔振器的有限元简化模型。
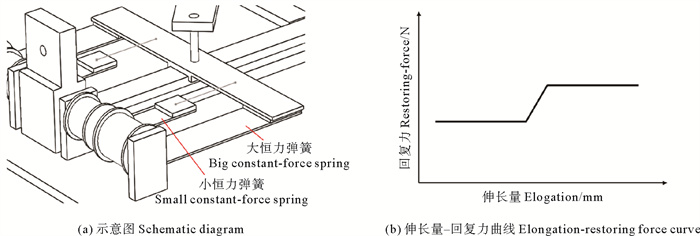
2.1 恒力弹簧和摩擦力的简化模拟恒力弹簧组是为隔振器提供回复力的核心部件,其构造形式如图 4(a)所示。恒力弹簧组所产生的伸长量-回复力关系曲线如图 4(b)所示。其中,两侧水平段的回复力曲线保证了隔振器具有准零刚度的特性,使隔振器具备良好的隔振效果;而中间倾斜线段部分保证了隔振器具有一定的承载能力,并使隔振器具备一定的自复位能力,避免隔振器因为残余位移的累积而逐渐失效。
|
图 4 恒力弹簧组合 Fig. 4 Constant-force spring combination |
该隔振器的阻尼主要由内部各接触对的摩擦力提供,可以起到耗能减振的作用,降低结构共振时的响应,然而若在有限元模型各接触对中设置摩擦力,会影响后续分析的收敛性,降低计算效率。针对上述问题,本文针对恒力弹簧部件和摩擦力均采用连接器进行简化建模。在弹簧部件连接点之间设置translator连接器,根据恒力弹簧组的弹性参数在连接单元属性中定义弹性特征,模拟弹簧变刚度的特性。同时将各接触对设为光滑接触,根据实验[16]得到的摩擦力数值,在模拟弹簧的translator连接器属性中定义摩擦力的大小,模拟隔振器的摩擦力。
2.2 铰接杆和导轨部件的简化模拟隔振器中存在数量较多的铰接杆和导轨部件,其作用是约束不同部件之间的位移和旋转自由度,但在有限元模拟中会增加接触对,同样造成数值分析不易收敛的问题。本文选用ABAQUS软件中的hinge连接器对铰接杆进行模拟,选用ABAQUS软件中的translator连接器对导轨部件进行模拟。一方面,铰接杆和导轨部件在隔振器中的约束关系保持不变;另一方面,减少了部件和接触对的数量,提高了后续分析计算过程的收敛性。
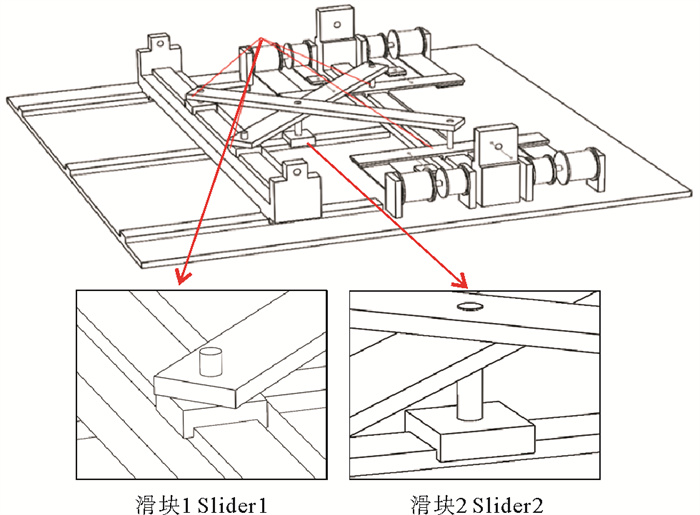
2.3 滑块的简化模拟滑块在隔振器中起着重要的连接作用,如图 5所示,滑块1位于椭圆轨旋杆末端,保证恒力弹簧与滑动杆之间作用力的传递。滑块2位于旋杆中间,起到铰接两个旋杆的作用,保证对称分布的两组恒力弹簧伸长量相同,使下部组块受力均衡。本文通过设置质量点和位移约束的方式对滑块进行模拟。
|
图 5 滑块 Fig. 5 Slider |
对于滑块1,通过设置质量点进行简化模拟。取消滑块部件,在原滑块位置处设置与滑块等质量的质量点,保证分析计算的准确性。同时在质量点与其他部件连接点之间建立连接器,保证滑块在隔振器中的连接作用。
对于滑块2,采用设置位移约束的方式进行简化。删除该滑块及下方导轨,在2个旋杆铰接位置处设置耦合约束,并在两个耦合约束点之间建立hinge连接器,保证2个旋杆可以绕铰接点旋转。同时对其中一个耦合约束点设置位移约束,限制该点只能沿原有导轨的方向移动,保证两侧恒力弹簧伸长量相同。
2.4 隔振器有限元模型的建立(1) 建立各部件的模型。在Part模块中,分别对隔振器各主要部件建立三维可变形实体模型。在Mesh模块中对各个部件划分网格,网格采用C3D8R单元。
(2) 设置材料属性。在Property模块中,对各部件赋予材料属性。材料密度设为7 800 kg/m3, 弹性模量为210 000 MPa, 泊松比为0.3。
(3) 设置接触、约束。在Interaction模块中将隔振器的接触类型设置为General contact,接触属性采用系统默认值。根据2.1~2.3节对部件的简化,在模型相应位置处设置连接器、质量点等,对导轨等部件进行模拟。
(4) 建立分析步。在Step模块中,针对静压载实验模拟和振动实验模拟,分别采用静态通用和动态显式分析步,输出顶板和底板参考点的反力和位移时程曲线,将step中的几何非线性参数Nlgeom设置为On。
(5) 施加荷载和边界条件。在Load模块中,将底板的耦合约束参考点设置全固定约束,根据模拟工况的不同,在顶板的耦合约束参考点上施加不同类型的载荷。
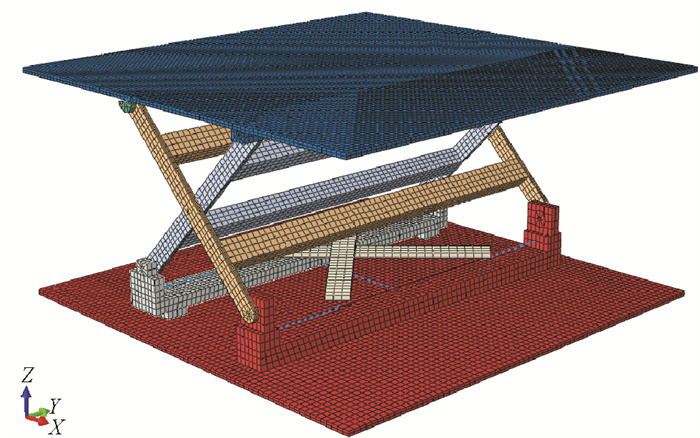
通过上述的简化建模,最终得到的模型如图 6所示。与图 1所示的实际模型相比,图 6中简化后的有限元模型主要的约束关系保持不变,结构中的部件和接触对数量减少,为提高后续分析的计算效率和收敛性奠定了基础。
|
图 6 简化后的隔振器有限元模型 Fig. 6 Simplified finite element model of vibration isolator |
本文作者针对该隔振器进行了两部分的数值研究,一是针对静压载实验进行模拟,从而得到该隔振器整体回复力的滞回曲线,进而验证有限元模型的准确性。二是针对振动实验进行模拟,研究激振频率、幅值这两者对隔振性能的影响。
3.1 隔振器滞回性能研究隔振系统在静压载实验中会产生滞回曲线,滞回曲线所围成的面积表示系统在加卸载过程中损耗的能量,同时有限元模拟所得滞回曲线中的参数可以反映有限元模型的准确性,基于以上因素对隔振器进行静压载实验模拟。
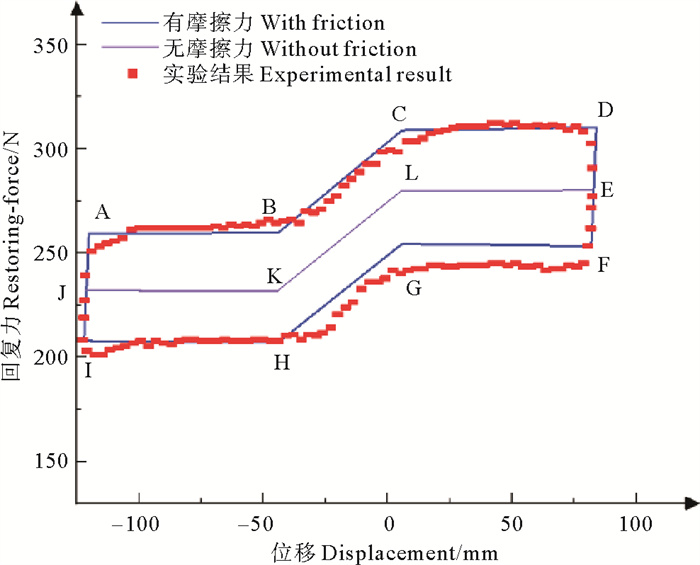
采用静态通用分析步,对顶板耦合约束参考点施加竖直方向的往复位移,输出该点的位移和反力。计算得到的隔振器滞回曲线如图 7中蓝色曲线所示。该曲线为较规整的闭合形状,所围面积即为隔振器在一个周期往复位移中损耗的能量。通过有限元模拟可以证明该隔振器具备良好的耗能能力。
|
图 7 滞回曲线 Fig. 7 Hysteresis curve |
将滞回曲线的有限元模拟结果与实验结果[16]进行比对,发现两者基本吻合,其中有限元模拟结果的左半部分与实验结果基本一致,但右半部分与实验结果相差较大,原因如下:有限元模型与样机模型在部件尺寸、材料参数等方面可能存在一些差异;样机模型自身存在一些缺陷,对实验结果造成干扰。对图 7进行统计分析,得到摩擦力和回复力两者的有限元模拟值与其理论值的相对误差大小(见表 1)。
|
|
表 1 有限元模拟值与理论值的相对误差 Table 1 Relative error between the finite element simulation value and the theoretical value |
如表 1所示,摩擦力和回复力两者的有限元模拟值与其理论值的相对误差大小均在5.2%以内,因此可以认为本文作者所建立的隔振器有限元模型能够对隔振器实际样机模型实现准确模拟。
3.2 隔振器隔振性能研究为了研究隔振器的隔振性能,本文对该隔振器的振动实验进行了模拟研究,通过对比激振力与响应力的大小,来考察隔振器在振动条件下的隔振性能。同时分析不同激振频率和幅值作用下的传递系数,研究该隔振器所适用的工作频率和幅值大小。
在step模块中采用显式动态分析步,输出顶板和底板参考点的反力时程曲线。在load模块中,在顶板的耦合约束参考点处施加简谐位移荷载,加载公式为
| $ y=A \sin 2 \pi f t。$ |
式中:y为施加的激振荷载大小,单位为mm;A为激振荷载的幅值;t为时间;f为激振荷载的频率。
为了降低显式算法特性导致的误差积累,采用双精度进行分析。
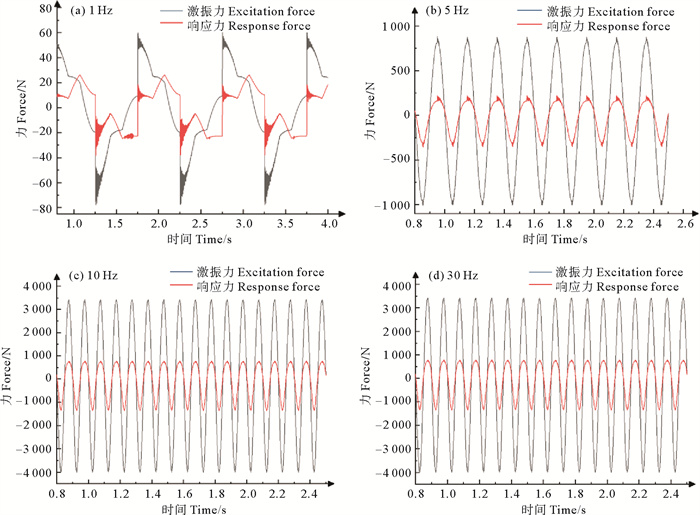
3.2.1 激振频率对隔振性能的影响为了研究激振频率对隔振性能的影响规律,确定该隔振器适用的工作频带范围,针对隔振器在不同频率荷载作用下的工作情况进行了研究。参考实验中荷载的设置情况[16],令激振幅值A=15 mm,激振频率f选取1~30 Hz之间的多个频率。为了避免初始时刻瞬态响应的影响,本文选取了0.8 s后稳态响应的曲线,得到的计算结果如图 8所示。
|
图 8 不同激振频率的响应曲线 Fig. 8 Response curves of different excitation frequencies |
对图 8中的响应曲线进行分析,发现对于各个激振频率隔振器均具有良好的隔振性能。随着激振频率的增加,激振力和响应力幅值大小也在增加,这是由于激振频率的提高导致构件加速度增大的结果。当激振频率较小时,各条曲线的极值点处均存在一个尖角,出现这种现象的原因是当顶板到达位移的最高点或最低点后,会继续朝反向运动,此时隔振器内部的摩擦力方向会在正向和反向之间发生切换。由于恒力弹簧组产生的拉力方向保持不变,摩擦力的突然转向会对隔振器的运动造成瞬态响应的干扰,因此在曲线的极值点处会出现一些“尖角形”的突变。隔振器运动速度越慢,系统整体由瞬态响应时的紊乱状态过渡到稳态响应时的稳定状态所耗费的时间越久,这种突变情况越明显。
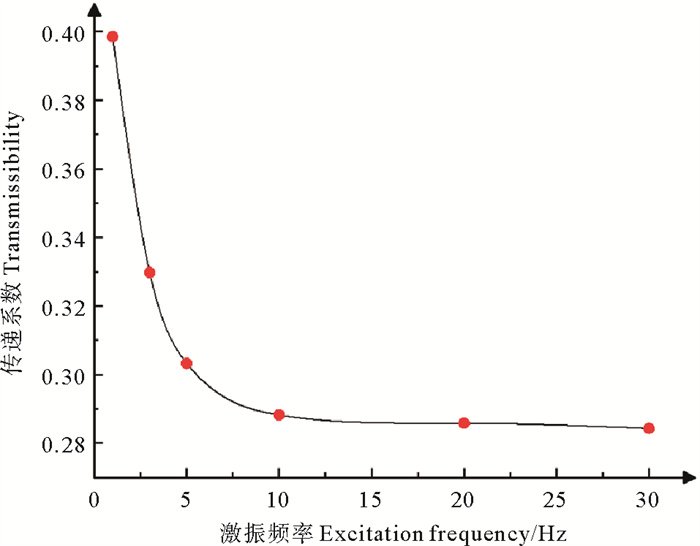
设隔振器的传递系数T为响应力幅值F0与激振力幅值Fint的比值,当T < 1时,证明隔振系统具备一定的隔振性能。对隔振器在不同频率激振荷载作用下的传递系数T利用样条曲线进行拟合统计,得到的激振频率-传递系数关系曲线如图 9所示。随着激振频率的增加,隔振器的传递系数不断下降,隔振性能不断提高。当激振频率大于10 Hz时,曲线形状接近水平直线,此时传递系数T下降幅度较小,因此可以证明该隔振器在激振频率为10 Hz以上的工作环境中隔振效果最好。
|
图 9 激振频率-传递系数关系曲线 Fig. 9 Curve of excitation frequency-transmissibility |
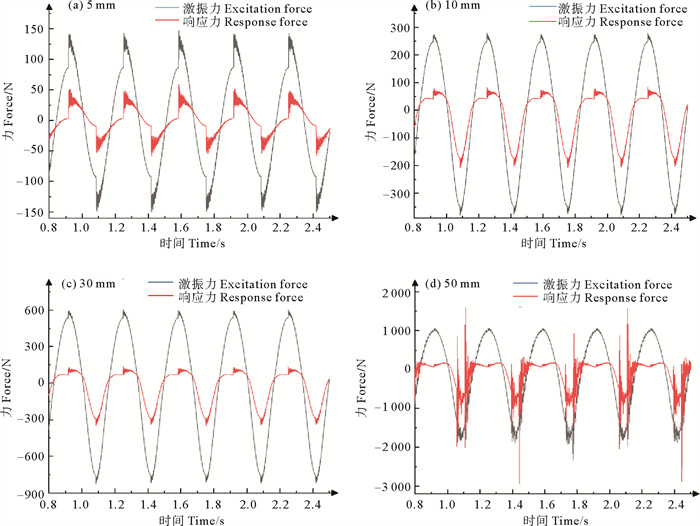
在实际工作中,激振荷载的幅值大小对隔振器的工作性能也会产生很大的影响。为了保证隔振器的安全可靠性,针对隔振器在不同频率荷载作用下的工作情况进行分析。设置激振频率f=3 Hz,激振幅值A取为5、10、30和50 mm。为了避免初始时刻瞬态响应的影响,选取0.8 s后隔振器稳态响应的曲线。计算的结果如图 10所示。
|
图 10 不同激振幅值的响应结果 Fig. 10 Response curves of different excitation amplitude |
对图 10进行分析,发现当激振幅值A < 50 mm时,隔振器均能够发挥较好的隔振效果。而当A=50 mm时响应力曲线较为紊乱,在一些时间点会出现响应力突变的情况,此时隔振器的稳定性较差,在这些时间点对于被隔振的目标物体来说该隔振器已经不够安全。出现这些突变的原因,一方面是由于摩擦力方向发生改变造成的瞬态响应的干扰,另一方面是由于隔振器在外部荷载的作用下位移的幅度过大,部分部件因应力过大而出现局部变形的原因。
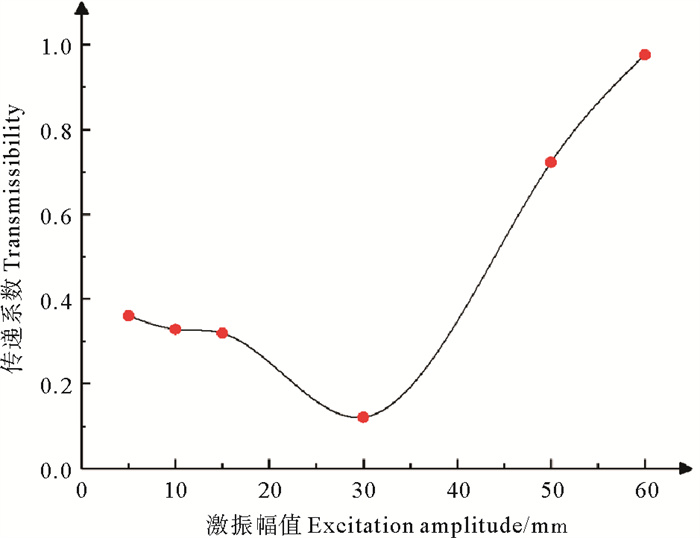
为了进一步研究激振荷载位移幅值大小对隔振性能的影响,对各激振幅值作用下的传递系数T进行整理,得到的结果如图 11所示。对图 11进行分析,发现随着激振幅值A的增大,传递系数T先减小后增大,在30 mm位置处达到最低值,而当A=60 mm时,T≈1。因此,在使用过程中应将激振位移荷载的幅值限制在60 mm以内,当激振位移荷载幅值在30 mm左右时隔振性能最好。
|
图 11 激振幅值-传递系数关系曲线 Fig. 11 Curve of excitation amplitude-transmissibility |
本文基于ABAQUS有限元软件的多体分析功能对一种准零刚度隔振器进行了研究。利用ABAQUS的translator、hinge连接属性,定义部件之间的约束和连接关系,对隔振器中的导轨、恒力弹簧等构件进行了简化建模,在保证关键部件约束条件与实际情况基本一致的前提下,减少了模型的部件和接触对数量,提高了计算的收敛性和效率。随后本文对该隔振器分别进行了静压载实验和振动实验的模拟,得到以下结论:
(1) 在隔振器滞回性能研究中,对隔振器的顶板施加循环往复的竖直位移荷载,得到隔振器的滞回曲线,其形式与实验中得到的滞回曲线基本吻合,根据该曲线得到的弹簧回复力以及摩擦力的模拟值与理论值的相对误差均在5.2%以内,证明该隔振器具备良好的滞回耗能能力,从而验证了本文有限元简化模型的可靠性。
(2) 在准零刚度隔振器隔振性能研究中,对隔振器的顶板施加竖直方向的简谐位移荷载,通过对比激振力的幅值大小和响应力的幅值大小,分别得到了激振频率对隔振性能的影响规律、激振幅值对隔振性能的影响规律,结果表明:当激振频率大于10 Hz、幅值约为30 mm时隔振器的隔振效果最佳。
以上结论对于准零刚度隔振器的性能优化与实际应用具有重要意义。
| [1] |
Ibrahim R. Recent advances in nonlinear passive vibration isolators[J]. Journal of Sound and Vibration, 2008, 314(3-5): 371-452. (  0) 0) |
| [2] |
Robertson W S, Kidner M, Cazzolato B S, et al. Theoretical design parameters for a quasi-zero stiffness magnetic spring for vibration isolation[J]. Journal of Sound and Vibration, 2009, 326(1-2): 88-103. DOI:10.1016/j.jsv.2009.04.015 (  0) 0) |
| [3] |
Winterflood J, Blair D, Slagmolen B. High performance vibration isolation using springs in Euler column buckling mode[J]. Physics Letters A, 2002, 300(2-3): 122-130. DOI:10.1016/S0375-9601(02)00258-X (  0) 0) |
| [4] |
Alabuzhev P, Gritchin A, Kim L, et al. Vibration Protecting and Measuring Systems with Quasi-Zero Stiffness[M]. USA: Hemisphere Publishing Corporation, 1989.
(  0) 0) |
| [5] |
Platus D L. Negative-stiffness-mechanism vibration isolation systems[J]. Proceedings of SPIE-The International Society for Optical Engineering, 1999, 3786: 98-105. (  0) 0) |
| [6] |
Carrella A, Brennan M J, Waters T P. Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic[J]. Journal of Sound and Vibration, 2007, 301(3-5): 678-689. DOI:10.1016/j.jsv.2006.10.011 (  0) 0) |
| [7] |
Carrella A, Brennan M J, Kovacic I, et al. On the force transmissibility of a vibration isolator with quasi-zero-stiffness[J]. Journal of Sound and Vibration, 2009, 322(45): 707-717. (  0) 0) |
| [8] |
Carrella A, Brennan M J, Waters T P, et al. Force and displacement transmissibility of a vibration isolator with high-static-low-dynamic-stiffness[J]. International Journal of Mechanical Sciences, 2012, 55(1): 22-29. DOI:10.1016/j.ijmecsci.2011.11.012 (  0) 0) |
| [9] |
Wu W J, Chen X D, Shan Y H. Analysis and experiment of a vibration isolator using a novel magnetic spring with negative stiffness[J]. Journal of Sound and Vibration, 2014, 333(13): 2958-2970. DOI:10.1016/j.jsv.2014.02.009 (  0) 0) |
| [10] |
刘兴天, 张志谊, 华宏星. 新型低频隔振器的特性研究[J]. 振动与冲击, 2012, 31(5): 161-164. Liu X T, Zhang Z Y, Hua H X. Characteristics of a novel low-frequency isolator[J]. Journal of Virbration and Shock, 2012, 31(5): 161-164. DOI:10.3969/j.issn.1000-3835.2012.05.033 (  0) 0) |
| [11] |
Liu X, Huang X, Hua H, et al. On the characteristics of a quasi-zero stiffness isolator using euler buckled beam as negative stiffness corrector[J]. Journal of Sound and Vibration, 2013, 332: 3359-3376. DOI:10.1016/j.jsv.2012.10.037 (  0) 0) |
| [12] |
刘兴天, 孙婧雅, 肖锋, 等. 准零刚度微振动隔振器的原理和性能研究[J]. 振动与冲击, 2013, 32(21): 69-73. Liu X T, Sun J T, Xiao F, et al. Principle and performance of a quasi-zero-stiffness isolator for micro-virbration isolation[J]. Journal of Sound and Vibration, 2013, 32(21): 69-73. DOI:10.3969/j.issn.1000-3835.2013.21.012 (  0) 0) |
| [13] |
Kovacic I, Brennanm M J, Waters T P. A study of a nonlinear vibration isolator with a quasi-zero stiffness characteristic[J]. Journal of Sound and Vibration, 2008, 315: 700-711. DOI:10.1016/j.jsv.2007.12.019 (  0) 0) |
| [14] |
Sun X T, Jing X J. Multi-direction vibration isolation with quasi-zero stiffness by employing geometrical nonlinearity[J]. Mechanical Systems and Signal Processing, 2015, 62-63: 149-163. DOI:10.1016/j.ymssp.2015.01.026 (  0) 0) |
| [15] |
Xu J, Sun X T. A multi-directional vibration isolator based on quasi-zero-stiffness structure and time-delayed active control[J]. International Journal of Mechanical Sciences, 2015, 100: 126-135. DOI:10.1016/j.ijmecsci.2015.06.015 (  0) 0) |
| [16] |
Asai T, Araki Y, Kimura K. Adjustable vertical vibration isolator with a variable ellipse curve mechanism[J]. Earthquake Engineering & Structural Dynamics, 2017, 46: 1345-1366. (  0) 0) |
| [17] |
石亦平, 周玉蓉. ABAQUS有限元分析实例详解[M]. 北京: 机械工业出版社, 2006. Shi Y P, Zhou Y R. Detailed Explanation of ABAQUS Finite Element Analysis Example[M]. Beijing: China Machine Press, 2006. (  0) 0) |
2. School of Naval Architecture and Ocean Engineering, Zhejiang Ocean University, Zhoushan 316022, China
 2022, Vol. 52
2022, Vol. 52


