2. 崂山实验室,山东 青岛 266237
海洋石油污染是海洋污染中的一个重要问题。海洋石油污染不仅对沿海经济和居民生活环境造成严重影响,而且还会造成资源的浪费。此外,溢油会阻碍海气交换,石油中含有有毒的芳香烃化合物,这些因素会造成海洋生物和海鸟的死亡,严重影响海洋生态环境[1-3]。随着经济全球化以及人类对石油能源的旺盛需求,海底石油密集开采且海上运输业快速发展,石油泄漏和被人为排放仍时有发生[4]。这就需要人们快速、准确地掌握溢油信息,以便指导应急响应行动,从而尽可能地减少溢油带来的危害和损失。
遥感具有动态、大范围的优势,已经被广泛应用于海上溢油监测。合成孔径雷达凭借其全天时、全天候的观测能力和较高的空间分辨率,已经被证明是海面溢油监测最有效的传感器之一[5-8]。海面溢油可分为原油和乳化油,前者通常是溢油事故刚发生后出现,后者在海面溢油中更为常见[9]。溢油发生后,在风力和湍流等外力作用下,海水和溢油容易混合,形成油包水或水包油乳化液[10]。油膜对海面电磁散射特征的影响体现在两个方面:其一是抑制海浪,尤其是对短波有强烈的抑制作用;其二是改变海表的介电性质[11-12]。
目前对溢油覆盖海面的微波散射问题的研究已经取得了一定的进展。2002年,Franceschetti等基于Alpers提出的抑制比模型,结合清洁海面的海浪谱模型,得到溢油覆盖海面的海浪谱模型,并仿真了单分子油膜覆盖海面的SAR图像,揭示了单分子油膜对SAR图像的影响,但Aleprs提出的抑制比模型只适用于单分子油膜,不能反映抑制比和油膜厚度的关系[13]。2005年,Migliaccio等人基于Ermakov提出的抑制模型,利用微扰法对溢油海面电磁散射进行建模,进而提出了一种通过SAR图像检测溢油的物理方法。然而,该抑制比模型也与厚度无关,且忽略了波-波相互作用,只适用于较低的风速条件[14]。2014年,Pinel利用Jenkins提出的有限厚度阻尼模型改进了Ermakov的抑制比模型,使之具有厚度依赖性,分别模拟了有限厚度油膜和单分子油膜覆盖海面的微波后向散射系数,并将双层介质散射问题简化为单层介质散射问题,用极化比研究了清洁海面和溢油海面的极化性质[15]。2015年,Zhang等人将Jenkins提出的有限厚度黏性流体抑制比模型运用到Alpers提出的局部平衡抑制比模型中,并分析了油膜物理参数和海洋环境对海面抑制比的影响[16]。
近年来,对乳化油散射特性和含水率估计的研究也越来越引起学者的重视。2012年,Minchew提出了一种油/水混合指数M,可以用来评估粗糙度减小和油水混合导致的信号衰减对后向散射功率影响的相对大小[11]。2018年,Angelliaume等基于L波段SAR图像提出了一种用极化比来估计乳化油含水率的方法[17]。2021年,Meng等人采用Zhang改进的局部平衡抑制比模型,结合高级积分方程法研究了乳化油覆盖海面的微波后向散射特性[18]。2022年,Zheng等人研究了溢油海面的非布拉格散射对总散射的影响,并提出了一种方法,通过消除非布拉格散射的影响来更准确地估计乳化油的含水率[19]。
溢油覆盖海面的太赫兹波散射特性方面的研究较少。2021年,Zhang等初步研究了小入射角下,油膜覆盖海面的太赫兹波后向散射系数,并揭示了散射系数随油膜厚度变化的振荡规律[20]。
本文首先介绍了改进的局部平衡抑制比模型,修正清洁海面的海浪谱以适用于油膜覆盖的海面;然后给出了简化的双层粗糙界面的反射系数公式和油膜覆盖海面斜率概率密度函数,利用几何光学近似法,研究了乳化油覆盖海面的后向散射特征,讨论了油厚、频率和含水率等参数对后向散射系数的影响,进一步研究了后向散射系数对含水率的敏感性。
1 基本理论 1.1 乳化油覆盖海面的海浪谱对乳化油覆盖海面的电磁散射进行合理建模,首先要研究乳化油对海浪谱的影响。Jenkins提出的有限厚度黏性流体的耗散公式能够反映不同厚度油膜抑制比的差异,然而其只能反映风速非常低时,油膜对波纹的影响。而Alpers提出的局部平衡抑制模型还考虑了非线性波波相互作用和风能输入的变化对油膜覆盖海面海浪谱的影响,适用于风速较高的情况。然而,该模型中黏性耗散项和油膜厚度无关,只适用于单分子油膜,而实际海面上的溢油存在一定厚度。因此,本文将Jenkins耗散公式和Alpers的局部平衡抑制模型进行结合以描述乳化油对海浪的抑制程度。海浪谱的演化可以通过作用量平衡方程来描述[21]:
| $ \frac{\mathrm{d} N^i(k)}{\mathrm{d} t}=0=Q_{\mathrm{in}}^i(k)+Q_{\mathrm{nl}}^i(k)-Q_{\mathrm{dis}}^i(k), $ | (1) |
| $ Q_{\mathrm{dis}}(k)=Q_{\mathrm{br}}(k)+Q_{\mathrm{vs}}(k) \text { 。} $ | (2) |
式中:i∈{s, w},s和w分别指油膜覆盖海面及清洁海面;N(k)=(ω/k)Sw(k)表示波数空间中每单位质量的波作用谱密度;Sw(k)是清洁海面海浪谱;ω和k分别表示海浪的角频率和波数;Qin是风输入项;Qnl是非线性波-波相互作用项;Qdis是耗散项,它由波破碎项Qbr和黏性耗散项Qvs贡献。然而,当风速不太高时(< 10 m/s),波破碎项可以忽略,即Sdis=Svs。风输入项、非线性项及黏性耗散项可以表示如下:
| $ Q_{\mathrm{in}}^i=Q_0^i+\beta^i\left(u_*^i, k\right) N^i(k), $ | (3) |
| $ Q_{\mathrm{nl}}^i=\alpha^i\left(u_*^i, k\right) N^i(k), $ | (4) |
| $ Q_{\mathrm{vs}}^i=2 c_{\mathrm{g}}(k) \Delta^i(k) N^i(k)。$ | (5) |
其中
| $ \beta^i=M \cos \varphi\left(\frac{u_*^i}{c_{\mathrm{p}}}\right)^2 \omega, $ | (6) |
| $ \alpha^w=-q \beta^w, $ | (7) |
| $ \alpha^s=\alpha^w+\delta \alpha \text {, } $ | (8) |
其中
| $ \delta \alpha=\alpha_M\left(\frac{k}{k_M}\right)^{3 / 2}\left(\frac{u_*^i}{u_*}\right)^2 。$ | (9) |
式中:Q0i是由大气压脉动引起的共振激发,即菲利普斯机制;u*表示摩擦风速,对于油膜覆盖海面,其摩擦风速通常比清洁海面低30%,即u*s=0.7u*w[22];风成长率β(u*, k)描述了风能输入到波浪系统的速率, α(u*, k)描述了非线性能量传输速率,它们的表达式在文献[13, 21]中给出;cp(k)是海浪的相速度,cg(k)是海浪的群速度;αM是黏性阻尼率;kM是黏性阻尼率的峰值波数;u*c是临界摩擦风速;M=0.04, q=1.15是无量纲常数。Δ(k)是黏性阻尼系数,油膜覆盖海面的黏性阻尼系数
| $ \Delta^s(k)=l(k, d) \Delta^w(k) \text { 。} $ | (10) |
其中,清洁海面的黏性阻尼系数Δw(k)由文献[13, 21]给出,l(k)表示相对阻尼系数,也称阻尼比。原油膜通常具有一定厚度,其阻尼比由下式表示[23]
| $ l(k, d)=\frac{\operatorname{Re}(\delta)}{2 v}, $ | (11) |
| $ \begin{gathered} \delta=\left\{2 v_{-}^*+\frac{1}{2} v_T+\mathrm{j} \Gamma^{-1 / 2}\left[\gamma\left(1-\rho_{+}\right)-\gamma_{-}^*\right] d+\right. \\ \frac{1}{2 v_{-}^{* 1 / 2} \mathrm{j}^{1 / 2}} \rho_{+} d \Gamma^{1 / 4} v_T+\frac{1}{2 v_{-}^{* 1 / 2}} \mathrm{j}^{1 / 2}\left(\rho_{+}^\rho d\right) 2 \Gamma^{3 / 4} \times \\ \left.\left(R^2-1\right)\right\} /\left\{1+\frac{1}{v_{-}^{* 1 / 2} \Gamma^{1 / 4}} \mathrm{j}^{1 / 2} v_T+\frac{1}{v_{-}^{* 1 / 2} \Gamma^{1 / 2}} \rho_{+} d \Gamma^{1 / 4}\right\}。\end{gathered} $ | (12) |
其中
| $ v_T=\frac{\chi_{+}^*+\chi_{-}^*}{n}+v_{s+}+v_{s-}+4 \rho_{+} v_{+}^* d+\frac{v_{E+} v_{E-} d}{\rho_{+} v_{+}^*}, $ | (13) |
| $ v_{ \pm}^*=g^{-1 / 2} k^{3 / 2} v_{ \pm}, $ | (14) |
| $ \left(\gamma_{ \pm}^*, \chi_{ \pm}^*\right)=k^2 \rho_{-}^{-1} g^{-1}\left(\gamma_{ \pm}, \chi_{ \pm}\right), $ | (15) |
| $ R=\frac{\rho_{+}+\gamma_{+}^*}{\rho_{+} \Gamma}, n=-\mathrm{j} \sqrt{\Gamma}, \Gamma=1+\gamma, \gamma=\gamma_{+}^*+\gamma_{-}^*, $ | (16) |
| $ v_{E \pm}=\chi_{ \pm}^* / n+v_{S \pm}, \mathrm{j}=\sqrt{-1} \text { 。} $ | (17) |
式中:τ是海水的表面张力;υ-是海水的运动学黏度,υ+是油的运动学黏度;ρ-是海水的密度,ρ+是油膜的密度;γ-是界面张力,γ+是表面张力;χ-是界面弹性,χ+是表面弹性;υS-是界面黏度,υS+是表面黏度。
油膜发生乳化后,其力学性质会发生改变,包括黏度、界面张力以及界面弹力等参数均与非乳化油膜存在差异,本文采用文献[24]中的实验值,列于表 1。
|
|
表 1 乳化油和海水的物理参数 Table 1 Physical parameters of oil emulsion and seawater |
将式(3)至(5)代入到式(1)中可得
| $ \begin{gathered} \frac{\left(\beta^w-2 c_{\mathrm{g}} \Delta^w+\alpha^w\right) N^w}{\left(\beta^s-2 c_{\mathrm{g}} \Delta^s+\alpha^s\right) N^s}= \\ \frac{\left(\beta^w-2 c_{\mathrm{g}} \Delta^w+\alpha^w\right) \frac{\omega S_w}{k}}{\left(\beta^s-2 c_{\mathrm{g}} \Delta^s+\alpha^s\right) \frac{\omega S_s}{k}}=\frac{Q_0^w}{Q_0^s}。\end{gathered} $ | (18) |
其中,参考文献[25]的研究表明,Q0w≈Q0s,因此,公式(18)表示为
| $ \frac{\left(\beta^w-2 c_{\mathrm{g}} \Delta^w+\alpha^w\right) \frac{\omega S_w}{k}}{\left(\beta^s-2 c_{\mathrm{g}} \Delta^s+\alpha^s\right) \frac{\omega S_s}{k}}=\frac{Q_0^w}{Q_0^s} \approx 1。$ | (19) |
于是得到中低风速时(2 m/s < U10 < 10 m/s)油膜对海面的抑制比
| $ y(k, d)=\frac{S_w(k)}{S_s(k)}=\frac{\beta^s-2 c_{\mathrm{g}} \Delta^s+\alpha^s}{\beta^w-2 c_{\mathrm{g}} \Delta^w+\alpha^w}。$ | (20) |
其中, Δs是用Jenkins耗散公式代替原Alpers抑制模型中Marangoni耗散公式,从而使抑制比与油膜厚度有关。Sw表示清洁海面的海浪谱,由于Elfouhaily谱对长波和短波均有比较较好的描述,因此本文中的清洁海面海浪谱采用Elfouhaily谱[26];Ss便是被油膜覆盖海面的海浪谱,其可以由抑制比和清洁海面海浪谱来表示
| $ S_s(k)=\frac{S_w(k)}{y(k, d)} 。$ | (21) |
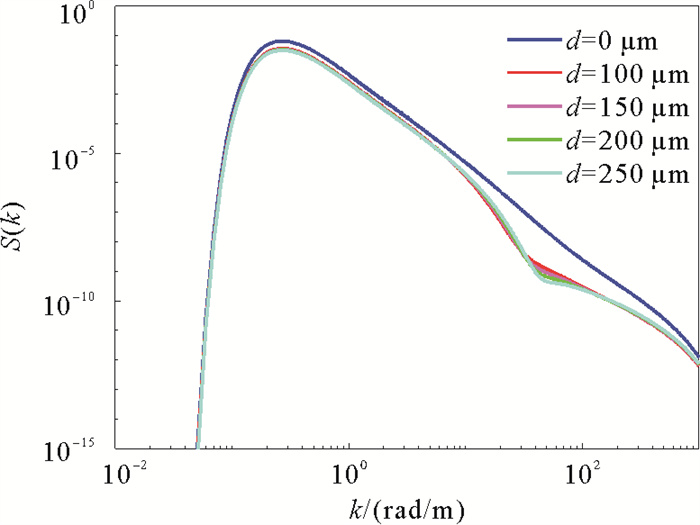
图 1展示了5m/s风速下,不同厚度乳化油覆盖海面的海浪谱。油膜对短波产生较为显著的抑制作用,又由于波-波相互作用,长波的能量部分地传递至被抑制的短波处,因而长波间接地被抑制,这和文献中的结果相一致。而不同厚度的乳化油覆盖海面的海浪谱之间差别较小,在50 rad/m左右差别最大。
|
图 1 不同厚度乳化油覆盖海面的海浪谱 Fig. 1 Wave spectra of emulsified oil-covered sea surface with different thicknesses |
小入射角下,海面的微波散射由镜面散射主导;而太赫兹波波长非常短,其Bragg散射本身非常弱,小入射角下则更弱。几何光学近似法能够较为准确地描述镜面散射,因此可以利用几何光学近似法求散射系数,其后向散射系数表达式为[27-28]
| $ \sigma_{p p}=\pi\left|R_{p p}\right|^2 \sec ^4 \theta_i P_{\mathrm{sl}}\left(z_x, z_y\right), $ | (22) |
| $ \sigma_{p q}=0 \text { 。} $ | (23) |
其中
| $ q_x=2 k_i \sin \theta_i \cos \varphi $ | (24) |
| $ q_y=2 k_i \sin \theta_i \sin \varphi, $ | (25) |
| $ q_z=2 k_i \cos \theta_i \text {, } $ | (26) |
| $ z_x=-\frac{q_x}{q_z}, z_y=-\frac{q_y}{q_z} 。$ | (27) |
式中:Rpp是海面的菲涅尔反射系数;σpp和σpq分别是同极化和交叉极化散射系数;k是入射波在真空中的波数;θi和θs分别表示入射角和散射角;φi和φs分别表示入射方位角和散射方位角。psl(zx, zy)表示海面沿坐标系x轴和y轴方向斜率的联合概率密度函数,zx和zy分别是x轴和y轴方向的海面斜率。
1.2.2 乳化油覆盖海面的介电特性在利用式(22)计算乳化油覆盖海面的后向散射系数时,海面的菲涅尔反射系数要用油膜-海水双层介质的复合反射系数来代替。而由于漂浮在海面上的油膜的厚度通常在微米到毫米量级,油膜上下表面是强相关的,两界面可近似看作平行的。基于该假设,油膜-海水双层介质的复合反射系数可以表示为[29]
| $ R_{p p}^c=\frac{R_{p p}^{a s}+R_{p p}^{s w} e^{-\mathrm{j} 2 k_{1 z^d} }}{1+R_{p p}^{a s} R_{p p}^{s w} e^{-\mathrm{j} 2 k_{1 z^d}}} 。$ | (28) |
式中:p∈{H, V}表示电磁波的极化状态;Rppas代表空气-油膜界面的菲涅尔反射系数;Rppsw代表油-海水界面的菲涅尔反射系数;d表示油膜的厚度;k1z=Re(ks)cosθt+Im(ks)·j;θt是电磁波在油膜中的透射角;ks=(εrsμrs)1/2ki是电磁波在油膜中的波数;ki是入射电磁波在空气中的波数;εrs和μrs分别是油的相对介电常数和相对磁导率。
要求式(28),首先要求空气-油膜界面和油膜-海水界面的菲涅尔反射系数,因此必须先得到乳化油和海水的介电常数。对于乳化油,本文以经典的Bruggeman公式计算其等效介电常数,乳化油的等效介电常数可以表示为[30-31]
| $ \begin{aligned} & \varepsilon_{\mathrm{BG}}=\frac{b+\sqrt{8 \varepsilon_1 \varepsilon_2+b^2}}{4} \\ & b=\left(2 f_1-f_2\right) \varepsilon_1+\left(2 f_2-f_1\right) \varepsilon_2 \end{aligned} $ | (29) |
Bruggeman公式是对称的,对水包油型和油包水型乳状液不作区分,水的体积分数设为fv(含水率),则油的体积分数可以表示为1-fv,式(29)中的b表示为
| $ b=\left(3 f_v-1\right) \varepsilon_{\text {water }}+\left(2-3 f_v\right) \varepsilon_{\text {oil }}。$ | (30) |
其中εoil和εwater分别为油和海水的介电常数。
油膜几乎是非色散介质,且其电磁损耗非常小,在本文中,频率低于100 GHz时的相对介电常数设置为2.2-0.01j,高于100 GHz时,其相对介电常数设置为1.96-0.03j[32]。海水是色散介质,其介电常数随频率变化比较显著,对于频率低于220 GHz的微波波段,采用Stogryn等人提出的模型[33],对于频率高于220 GHz的高频微波和太赫兹波段,采用Liebe等人的文献中提出的模型[34]。
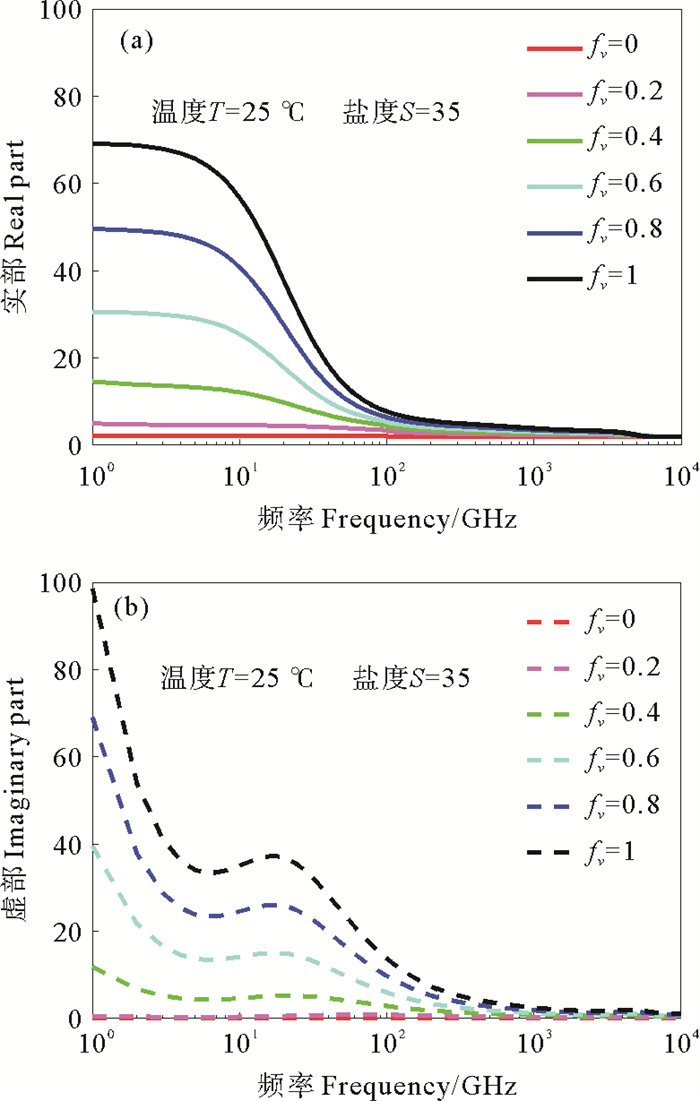
图 2展示了温度为25 ℃、盐度为35条件下,不同含水率的乳化油的介电常数。在相同频率下,乳化油介电常数的实部和虚部大小依赖于含水率,其值介于油的介电常数和海水的介电常数之间。对于固定的含水率,乳化油的介电常数的实部和虚部均随频率的增大而减小。
|
图 2 不同含水率乳化油相对介电常数实部(a)和虚部(b) Fig. 2 Real part (a)and imaginary part(b) of relative dielectric constant of oil emulsion with different water contents |
本文油膜覆盖海面的斜率分布采用Cox-Munk斜率分布,其联合概率密度函数表示为[35]
| $ \begin{gathered} p_{\mathrm{sl}}\left(z_u, z_c\right)=\frac{1}{2 \pi \sigma_u \sigma_c} \exp \left[-\frac{1}{2}\left(\frac{z_u^2}{\sigma_u^2}+\frac{z_c^2}{\sigma_c^2}\right)\right] \times \\ F\left(z_u, z_c\right)。\end{gathered} $ | (31) |
| $ \begin{aligned} &\begin{gathered} F\left(z_u, z_c\right)= \\ 1-\frac{1}{2} C_{21}\left(\frac{z_c^2}{\sigma_c^2}-1\right) \frac{z_u}{\sigma_u}-\frac{1}{6} C_{03}\left(\frac{z_u^3}{\sigma_u^3}-3 \frac{z_u}{\sigma_u}\right)+ \\ \frac{1}{24} C_{40}\left(\frac{z_u^4}{\sigma_u^4}-6 \frac{z_c^2}{\sigma_c^2}+3\right)+\frac{1}{4} C_{22}\left(\frac{z_c^2}{\sigma_c^2}-1\right)\left(\frac{z_u^2}{\sigma_u^2}-1\right)+ \\ \frac{1}{24} C_{04}\left(\frac{z_u^4}{\sigma_u^4}-6 \frac{z_u^2}{\sigma_u^2}+3\right)。\end{gathered}\\ &\text { } \end{aligned} $ | (32) |
| $ \begin{array}{ll} C_{21}=0.01-0.0088 U_{10} & C_{22}=0.12 \\ C_{03}=0.04-0.034 U_{10} & C_{04}=0.23 \\ C_{40}=0.40。& \end{array} $ | (33) |
其中,σu2、σc2分别是海面逆风和侧风向的均方根斜率。然而在应用(22)式求解镜面散射系数时,需要注意公式(22)中概率密度函数psl(zx, zy)为海面沿坐标系x轴和沿y轴方向斜率的联合概率密度函数。因此,应用式(31)计算式(22)时应基于下式先进行坐标变换。
| $ \left\{\begin{array}{l} z_u=-z_x \cos \varphi_w-z_y \sin \varphi_w \\ z_c=-z_y \cos \varphi_w+z_x \sin \varphi_w \end{array}\right.。$ | (34) |
其中φw为风向与坐标系x轴的夹角。可以利用转化关系psl(zx, zy)=psl(zu, zc)∂(su, sc)/∂(sx, sy)对式(31)进行坐标变换。
式(31)中海面逆风和侧风向的均方根斜率可以表示为
| $ \sigma_u^2=\int_0^{\infty} \int_0^{2 \pi}\left(k_w \cos \varphi_w\right)^2 S_{w / s}\left(k_w, \varphi_w\right) \mathrm{d} \varphi_w \mathrm{~d} k_w。$ | (35) |
| $ \sigma_c^2=\int_0^{\infty} \int_0^{2 \pi}\left(k_w \sin \varphi_w\right)^2 S_{w / s}\left(k_w, \varphi_w\right) \mathrm{d} \varphi_w \mathrm{~d} k_w。$ | (36) |
式中:Sw(kw, φ)和Ss(kw, φ)分别为清洁海面和溢油覆盖海面的海浪谱;kw表示海浪波数;φw=0表示逆风向;φw=±π/2表示侧风向。
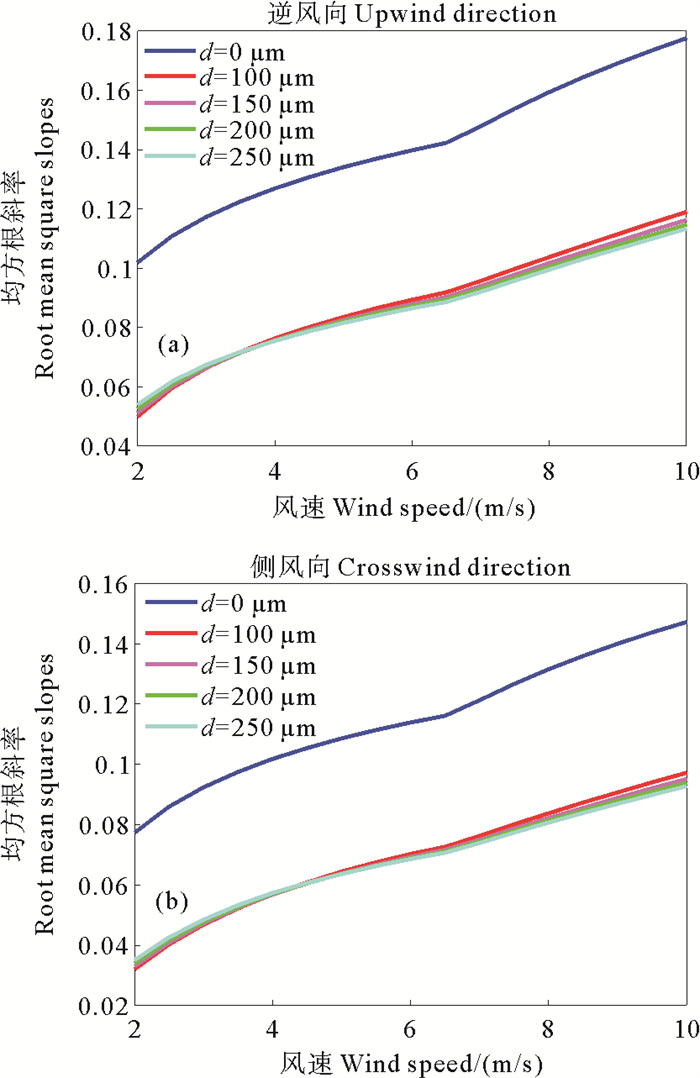
图 3给出了逆风向和侧风向清洁海面以及不同厚度乳化油覆盖海面的均方根斜率随风速的变化关系。在相同风速下,同一厚度乳化油覆盖海面的均方根斜率在逆风向大于侧风向。无论是逆风向还是侧风向,乳化油覆盖海面的均方根斜率均显著小于清洁海面的均方根斜率。无论是逆风向还是侧风向,清洁海面和乳化油覆盖海面的均方根斜率均随风速的增大而增大,乳化油覆盖海面的均方根斜率随风速增大而增大的速度和清洁海面接近。此外,不论是逆风向还是侧风向观测,油膜厚度对海面均方根斜率的影响均不大。
|
图 3 逆风向(a)和侧风向(b)不同厚度乳化油覆盖海面的均方根斜率 Fig. 3 Root mean square slopes of emulsified oil-covered sea surface with different thicknesses for upwind(a) and crosswind(b) direction |
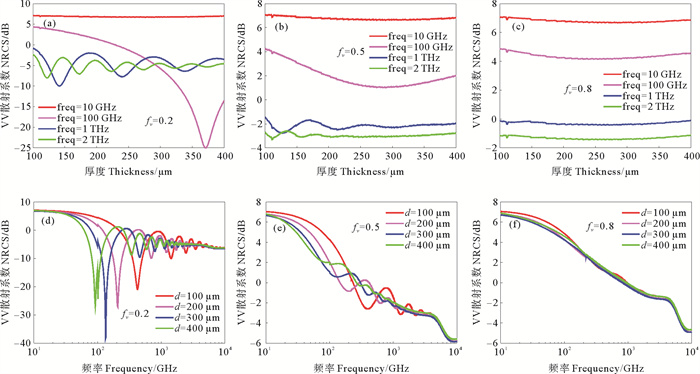
图 4展示了风速为5 m/s、入射角为10°条件下,不同厚度乳化油覆盖海面的VV极化后向散射系数随乳化油厚度和入射波频率的变化关系,各列分别给出不同含水率的结果,由于小入射角下HH极化的结果与VV极化的结果差别很小,故本文只给出VV极化的结果。10 GHz时,不同含水率下,散射系数几乎都不随乳化油厚度变化而变化,这是因为10 GHz时,海水的介电常数比乳化油大得多,海水-乳化油界面的散射波能量很低,干涉效应非常弱。而在100 GHz到1 THz范围内,当含水率较低时,散射系数随乳化油厚度的变化呈现较为显著的振荡变化的规律,这是由乳化油膜上下界面的散射波干涉所致,当油膜厚度变化时,两个界面的散射波之间的相位差也随之发生了变化。当含水率增大时,散射系数随乳化油厚度变化的振荡的不明显,这是因为,含水率增大时,乳化油的介电常数非常接近于海水的介电常数,乳化油-海水界面的散射波能量较低,干涉效应减弱,散射波能量主要由空气-乳化油界面的散射波贡献。而散射系数随入射波频率变化的关系也有类似的规律。此外,对于含水率较低的乳化油覆盖海面,散射系数随频率的增大而振荡的幅度减小,这是由于频率增大时,海水的介电常数实部和虚部减小到和乳化油相近,干涉效应减弱。
|
( (a)、(b)、(c)分别是含水率为20%、50%和80%时,乳化油覆盖海面的散射系数随油厚的变化关系;(d)、(e)、(f)分别是含水率为20%、50%和80%时,乳化油覆盖海面的散射系数随频率的变化关系。(a)、(b)and(c)are the backscattering coefficients vary with oil slick thickness at the water contents of 20%、50% and 80%, respectively. (d)、(e)and(f)are the backscattering coefficients vary with frequency at the water contents of 20%、50% and 80%, respectively. ) 图 4 后向散射系数随乳化油厚度和频率的变化关系 Fig. 4 The backscattering coefficient as a function of oil emulsion thickness and frequency |
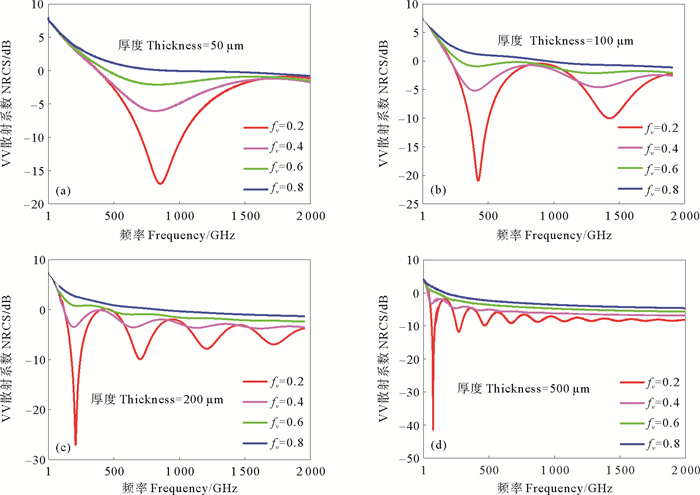
图 5展示了风速为5 m/s且入射角为10°条件下,1 GHz至2 THz范围内,不同厚度、不同含水率的乳化油覆盖海面的VV极化后向散射系数随频率的变化关系。和图 4(d)类似,同一个厚度下,散射系数随频率变化而振荡,且随频率增大其振荡幅度逐渐减小。对于同一厚度下,不同含水率的散射系数的极小值所对应的频率较为接近,在极小值处,不同含水率的散射系数差异较大,且在第一个极小值处其差异最大;而极大值处,则与之相反。
|
图 5 不同含水率的乳化油覆盖海面的后向散射系数 Fig. 5 The backscattering coefficients of emulsified oil-covered sea surfaces with different water contents |
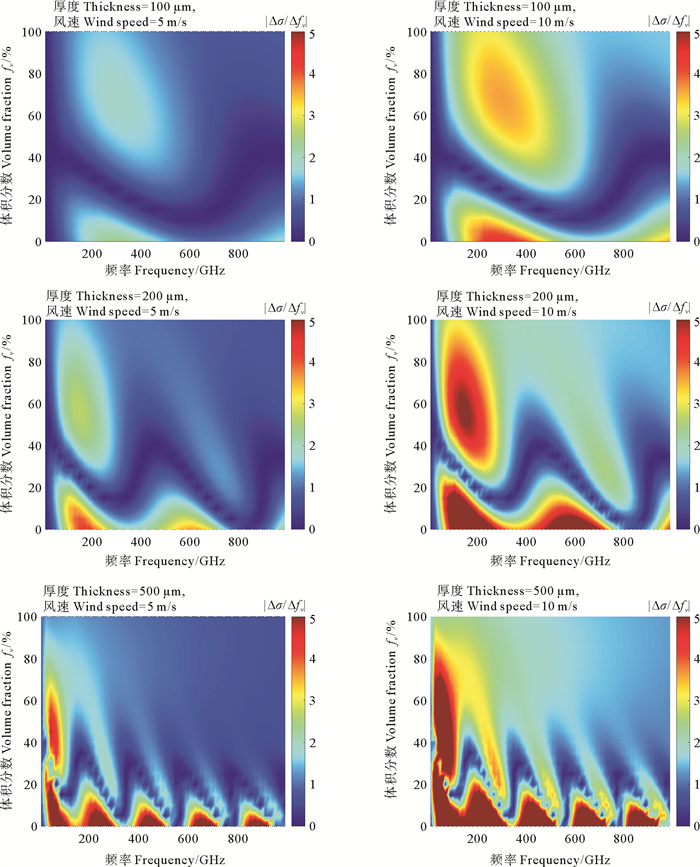
为了讨论后向散射系数对含水率变化的敏感性,以由含水率变化引起的后向散射系数变化的差值与含水率差值作商的绝对值作为后向散射系数对乳化油含水率敏感性的描述。图 6展示了VV极化、入射角为10°条件下,1 GHz至1 THz范围内,不同厚度乳化油覆盖海面的后向散射系数的含水率敏感性。左边一列风速为5 m/s,右边一列风速为10 m/s。从不同风速来看,在相同频率入射波和相同含水率的情况下,相比低风速,高风速下乳化油覆盖海面的后向散射系数也较高。相同的风速条件下,为了使散射系数的含水率敏感性在尽可能宽的含水率范围内有较高的值,其对应的频率随着厚度的增大逐渐向低频偏移。而相同厚度下,当频率增加时,后向散射系数仅在低含水率处有较高的敏感性。因此,对于100 μm以下稍薄的乳化油,需要用大约300 GHz以上的低频太赫兹波进行含水率的探测,对于几百微米的较厚的乳化油,需要用频率较低的几十GHz的微波对其含水率进行探测。
|
图 6 后向散射系数对含水率的敏感性 Fig. 6 Sensitivity of the backscattering coefficient to water contents |
本文利用几何光学近似法,结合局部平衡抑制模型,建立了小入射角下乳化油覆盖海面的微波和太赫兹波电磁散射模型。计算了不同油厚、不同频率及不同含水率下,乳化油覆盖海面的VV极化后向散射系数,并对其进行了讨论。乳化油覆盖海面的VV极化后向散射系数随油厚和频率振荡变化,且随着频率的增大振荡幅度逐渐减小;而较高的含水率下,散射系数随频率和厚度振荡幅度减小。此外,研究了散射系数对含水率的敏感性,结果表明:风速增大时,散射系数对含水率的敏感性增大;同一风速和油厚条件下,在微波波段和太赫兹波段范围内,对于高频的太赫兹波,后向散射系数只对含水率较低的乳化油具有较高的含水率敏感性;而对于相比太赫兹波而言频率较低的微波,散射系数对含水率较高的乳化油也具有较高的含水率敏感性。
| [1] |
Jackson J B, Cubit J D, Keller B D, et al. Ecological effects of a major oil spill on Panamanian coastal marine communities[J]. Science, 1989, 243(4887): 37-44. DOI:10.1126/science.243.4887.37 (  0) 0) |
| [2] |
Zhang B, Matchinski E J, Chen B, et al. Marine Oil Spills—Oil Pollution, Sources and Effects[M]. Elsevier: World seas: An Environmental Evaluation, 2019: 391-406.
(  0) 0) |
| [3] |
Langangen Ø, Olsen E, Stige L C, et al. The effects of oil spills on marine fish: Implications of spatial variation in natural mortality[J]. Marine Pollution Bulletin, 2017, 119(1): 102-109. DOI:10.1016/j.marpolbul.2017.03.037 (  0) 0) |
| [4] |
Li P, Cai Q, Lin W, et al. Offshore oil spill response practices and emerging challenges[J]. Marine Pollution Bulletin, 2016, 110(1): 6-27. DOI:10.1016/j.marpolbul.2016.06.020 (  0) 0) |
| [5] |
Brekke C, Solberg A H. Oil spill detection by satellite remote sensing[J]. Remote Sensing of Environment, 2005, 95(1): 1-13. DOI:10.1016/j.rse.2004.11.015 (  0) 0) |
| [6] |
Migliaccio M, Gambardella A, Tranfaglia M. SAR polarimetry to observe oil spills[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(2): 506-511. DOI:10.1109/TGRS.2006.888097 (  0) 0) |
| [7] |
Liu P, Li X, Qu J J, et al. Oil spill detection with fully polarimetric UAVSAR data[J]. Marine Pollution Bulletin, 2011, 62(12): 2611-2618. DOI:10.1016/j.marpolbul.2011.09.036 (  0) 0) |
| [8] |
Solberg A H, Brekke C, Husoy P O. Oil spill detection in Radarsat and Envisat SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(3): 746-755. DOI:10.1109/TGRS.2006.887019 (  0) 0) |
| [9] |
Quigley C, Brekke C, Eltoft T. Retrieval of marine surface slick dielectric properties from Radarsat-2 data via a polarimetric two-scale model[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(7): 5162-5178. DOI:10.1109/TGRS.2020.2973724 (  0) 0) |
| [10] |
Alpers W, Holt B, Zeng K. Oil spill detection by imaging radars: Challenges and pitfalls[J]. Remote Sensing of Environment, 2017, 201: 133-147. DOI:10.1016/j.rse.2017.09.002 (  0) 0) |
| [11] |
Minchew B. Determining the mixing of oil and sea water using polarimetric synthetic aperture radar[J]. Geophysical Research Letters, 2012, 39(16): 1-6. (  0) 0) |
| [12] |
Minchew B, Jones C E, Holt B. Polarimetric analysis of backscatter from the Deepwater Horizon oil spill using L-band synthetic aperture radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(10): 3812-3830. DOI:10.1109/TGRS.2012.2185804 (  0) 0) |
| [13] |
Franceschetti G, Iodice A, Riccio D, et al. SAR raw signal simulation of oil slicks in ocean environments[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(9): 1935-1949. DOI:10.1109/TGRS.2002.803798 (  0) 0) |
| [14] |
Migliaccio M, Tranfaglia M, Ermakov S A. A physical approach for the observation of oil spills in SAR images[J]. IEEE Journal of Oceanic Engineering, 2005, 30(3): 496-507. DOI:10.1109/JOE.2005.857518 (  0) 0) |
| [15] |
Pinel N, Bourlier C, Sergievskaya I. Two-dimensional radar backscattering modeling of oil slicks at sea based on the model of local balance: Validation of two asymptotic techniques for thick films[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(5): 2326-2338. DOI:10.1109/TGRS.2013.2259498 (  0) 0) |
| [16] |
Zhang Y, Zhang J, Wang Y, et al. The damping model for sea waves covered by oil films of a finite thickness[J]. Acta Oceanologica Sinica, 2015, 34: 71-77. (  0) 0) |
| [17] |
Angelliaume S, Boisot O, Guérin C-A. Dual-polarized L-band SAR imagery for temporal monitoring of marine oil slick concentration[J]. Remote Sensing, 2018, 10(7): 1012. DOI:10.3390/rs10071012 (  0) 0) |
| [18] |
Meng T, Yang X, Chen K-S, et al. Radar backscattering over sea surface oil emulsions: Simulation and observation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-14. (  0) 0) |
| [19] |
Zheng H, Gou C, Khenchaf A, et al. Retrieving oil-water mixture ratios of marine oil spills from L-Band SAR imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-11. (  0) 0) |
| [20] |
Zhang Y, Zheng H, Wang Y, et al. Investigation on THz EM wave scattering from oil-covered sea surface: Exploration for an approach to probe the thickness of oil film[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(3): 1827-1835. DOI:10.1109/TGRS.2020.3005019 (  0) 0) |
| [21] |
Alpers W, Hühnerfuss H. The damping of ocean waves by surface films: A new look at an old problem[J]. Journal of Geophysical Research: Oceans, 1989, 94(C5): 6251-6265. DOI:10.1029/JC094iC05p06251 (  0) 0) |
| [22] |
Gade M, Alpers W, Hühnerfuss H, et al. On the reduction of the radar backscatter by oceanic surface films: Scatterometer measurements and their theoretical interpretation[J]. Remote Sensing of Environment, 1998, 66(1): 52-70. DOI:10.1016/S0034-4257(98)00034-0 (  0) 0) |
| [23] |
Jenkins A D, Jacobs S J. Wave damping by a thin layer of viscous fluid[J]. Physics of Fluids, 1997, 9(5): 1256-1264. DOI:10.1063/1.869240 (  0) 0) |
| [24] |
Sergievskaya I, Ermakov S, Lazareva T, et al. Damping of surface waves due to crude oil/oil emulsion films on water[J]. Marine Pollution Bulletin, 2019, 146: 206-214. DOI:10.1016/j.marpolbul.2019.06.018 (  0) 0) |
| [25] |
Ermakov S, Zujkova A, Panchenko A, et al. Surface film effect on short wind waves[J]. Dynamics of Atmospheres and Oceans, 1986, 10(1): 31-50. DOI:10.1016/0377-0265(86)90008-4 (  0) 0) |
| [26] |
Elfouhaily T, Chapron B, Katsaros K, et al. A unified directional spectrum for long and short wind-driven waves[J]. Journal of Geophysical Research: Oceans, 1997, 102(C7): 15781-15796. DOI:10.1029/97JC00467 (  0) 0) |
| [27] |
Barrick D. Rough surface scattering based on the specular point theory[J]. IEEE Transactions on Antennas and Propagation, 1968, 16(4): 449-454. DOI:10.1109/TAP.1968.1139220 (  0) 0) |
| [28] |
Valenzuela G R. Theories for the interaction of electromagnetic and oceanic waves—A review[J]. Boundary-Layer Meteorology, 1978, 13(1-4): 61-85. DOI:10.1007/BF00913863 (  0) 0) |
| [29] |
Kong J A. Theory of Electromagnetic Waves[M]. Hpboken: John Wiley & Sons, Inc, 1975: 120-126.
(  0) 0) |
| [30] |
Ulaby F, Long D. Microwave Radar and Radiometric Remote Sensing[M]. Ann Arbor: University of Michigan Press, 2015: 129-133.
(  0) 0) |
| [31] |
Markel V A. Introduction to the maxwell garnett approximation: tutorial[J]. Journal of the Optical Society of America A, 2016, 33(7): 1244-1256. DOI:10.1364/JOSAA.33.001244 (  0) 0) |
| [32] |
李逸楠. 基于太赫兹时域光谱技术的成品油定量识别方法研究[D]. 天津: 天津大学, 2014. Li Y N. Study on the Quantifying of Refined Oil Mixtures by Terahertz Time-Domain Spectroscopy[D]. Tianjin: Tianjin University, 2014. (  0) 0) |
| [33] |
Wang J R. A Comparison of the MIR-estimated and model-calculated fresh water surface emissivities at 89150 and 220 GHz[J]. IEEE Transactions on Seascience and Remote Sensing, 2002, 90(6): 1356-1365. (  0) 0) |
| [34] |
Liebe H J, Hufford G A, Manabe T. A model for the complex permittivity of water at frequencies below 1 THz[J]. International Journal of Infrared and Millimeter Waves, 1991, 12: 659-675. DOI:10.1007/BF01008897 (  0) 0) |
| [35] |
Cox C, Munk W. Measurement of the roughness of the sea surface from photographs of the sun's glitter[J]. Journal of the Optical Society of America, 1954, 44(11): 838-850. DOI:10.1364/JOSA.44.000838 (  0) 0) |
2. Laoshan Laboratory, Qingdao 266237, China
 2024, Vol. 54
2024, Vol. 54


