2. 青岛海洋科学与技术试点国家实验室 海洋矿产资源评价与探测技术功能实验室,山东 青岛 266237;
3. 中国地质大学(武汉) 地质调查研究院,湖北 武汉 430074
大地电磁法(Magnetotelluric, MT)是利用天然交变电磁信号研究地球内部电性结构的一种地球物理方法,现已广泛应用于油气资源勘探和俯冲带、地壳与地幔电性结构研究中[1-3]。大地电磁反演是获得地下介质电阻率信息的重要方法。然而,MT反演存在多解性,如何减少MT反演的多解性一直是重要的研究方向。自从Karl Pearson提出卡方检验以来,在地球物理反演中便一直使用均方根拟合差(RMS misfit)衡量反演模型响应与实测数据的拟合程度[4]。
1980年代末以来,为了改善大地电磁反演问题的不适定性,吉洪诺夫(Tikhonov)正则化方法开始被应用于MT反演中,并取得了迅速发展[5-7]。目前,常用的大地电磁反演方法包括OCCAM反演方法、非线性共轭梯度法(NLCG)、拟牛顿法和高斯-牛顿法等[7-10]。这些反演方法关于反演模型响应与观测数据拟合程度的描述大都依赖于目标函数中的均方根拟合差,却没有考虑反演模型响应与观测数据之差(常称为残差)的统计特征,这可能导致反演模型响应形态与观测数据形态出现偏离较大的情况,尤其是当观测数据存在较大误差时,甚至可能得到错误的反演模型[11]。于是用于衡量实测数据与反演模型响应之间关系的其它统计量开始被应用于大地电磁反演中。Smith和Booker将斯皮尔曼(Spearman)相关系数应用于大地电磁(MT)反演结果评价中[12]。Jones利用DW统计量衡量观测数据与模型响应之间残差的自相关性[11],并将其应用于加拿大Great Slave Lake地区大地电磁测深数据反演中[13]。将统计学度量应用于MT反演中,一方面可以评价反演结果的合理性,另一方面可以为反演算法的改进提供依据,以便进一步优化反演方法。但是目前关于这方面的研究还不多见。本文将DW统计量应用于高斯-牛顿大地电磁一维反演中,通过修改目标函数,实现了基于DW统计量的大地电磁一维反演方法(以下简称为DW反演方法)。通过模型算例分析了该方法的有效性,并与传统的高斯-牛顿反演结果进行了对比。
1 反演方法 1.1 DW统计量杜宾-沃森(Durbin-Watson,简称DW)统计方法是用于检验回归分析中残差一阶自相关性的一种方法,该方法常用于检验计量经济学中的自相关问题[14-15]。一阶自相关DW统计量的定义式为[11, 16-17]:
| $ D W=\frac{\sum_{i=2}^n\left(\boldsymbol{e}_i-\boldsymbol{e}_{i-1}\right)^2}{\sum_{i=1}^n\left(\boldsymbol{e}_i-\overline{\boldsymbol{e}}\right)^2}。$ | (1) |
式中:ei(i=1, …, n)为观测数据与理论模型响应之间的差,常称为残差;n为数据个数;e为残差序列的平均值。DW统计量的值通常介于0~4之间。一般来说,DW统计量的值与序列自相关性之间的关系如图 1所示,图中dL和dU分别表示DW统计量的下临界值与上临界值。当DW统计量小于下临界值dL时,表明残差之间具有一阶正自相关,当DW大于4-dL时,表明残差具有一阶负自相关。而当DW统计量位于(dU, 4-dU)区间内时,残差序列之间不存在自相关性。通常,正自相关意味着多数残差都具有相同的符号,而负自相关意味着残差的符号在一段周期内不断变化。从图 1可以看出,DW统计量的期望值趋近于2。但实际上,在一定显著性水平的假设检验中,DW统计量的期望值与样本容量n和独立变量个数k有关。在本文中,由于反演模型参数为地层电阻率和厚度,故独立变量个数为2。Durbin和Watson给出了常见显著性水平下多种样本容量和独立变量的DW临界值[15],利用它们可以确定实际问题残差序列DW值的下临界值dL和上临界值dU,并依据图 1所述关系可以判断反演模型残差的自相关性。在统计学的假设检验中,显著性水平代表了原假设为真时拒绝原假设的概率,通常取5%或1%。表 1给出了显著性水平为5% 时部分DW统计量的临界值及其分布范围。在下一节中,将依据它们检验本文反演结果残差的自相关性。

|
图 1 序列自相关性与DW统计量的关系 Fig. 1 The relation between the sequence autocorrelation and the DW statistic |
|
|
表 1 部分DW统计量临界值分布表(k=2) Table 1 Distribution of critical values of DW statistic (The number of independent variables: k=2) |
通常地,DW统计量与自相关系数R具有如下关系[16, 18]:
| $ D W \approx 2(1-R)。$ | (2) |
式中,R为一阶自相关系数,其表达式为:
| $ R=\frac{\sum_{i=2}^n \boldsymbol{e}_i \boldsymbol{e}_{i-1}}{\sqrt{\sum_{i=2}^n \boldsymbol{e}_i^2} \sqrt{\sum_{i=2}^n \boldsymbol{e}_{i-1}^2}}。$ | (3) |
一阶自相关系数R的取值范围为(-1,1)。通常认为,当|R| < 0.2时,残差序列的自相关性极弱。
1.2 DW反演方法大地电磁反演问题实质上是目标函数的最优化问题。基于吉洪诺夫正则化反演思想,反演目标函数中通常包含数据拟合差项和正则化项[19]:
| $ \phi(\boldsymbol{m})=\phi_d(\boldsymbol{m})+\lambda_1 \phi_m(\boldsymbol{m})。$ | (4) |
式中:m=[m1, m2, ···, mM]T为模型参数向量,由反演模型中各地层的电阻率和厚度构成;ϕd(m)为观测数据与理论模型响应的拟合差,可表示为:
| $ \phi_d(\boldsymbol{m})=\left\|\boldsymbol{W}_d \boldsymbol{e}\right\|^2=\sum\limits_{i=1}^N\left(\frac{\boldsymbol{d}_i-\boldsymbol{F}_i(\boldsymbol{m})}{\sigma_i}\right)^2。$ | (5) |
式中:||·||表示L2范数;e=d-F(m)表示观测数据与理论模型正演响应之间的残差向量;d=[d1, d2, …,dN]T为观测数据向量;F(m)为模型m的正演响应;σi为第i个数据的标准差。ϕm(m)为模型约束项,可以表示为
| $ \phi_m(\boldsymbol{m})=\left\|\boldsymbol{W}_m\left(\boldsymbol{m}-\boldsymbol{m}^{\mathrm{ref}}\right)\right\|^2。$ | (6) |
式中:Wm为拉普拉斯算子的差分近似;mref为参考模型。
在传统的反演方法中,反演目标函数仅考虑了反演模型响应与观测数据的拟合差,但没有考虑其残差的统计学特征。本文将DW统计量加入反演目标函数中,通过反演倾向于寻找在拟合差和残差自相关性两个方面都可以接受的模型。经过修改后的反演目标函数具有如下形式[11]:
| $ \phi(\boldsymbol{m})=\phi_d(\boldsymbol{m})+\lambda_1 \phi_m(\boldsymbol{m})+\lambda_2(D W-2)^2 。$ | (7) |
上式中等号右端第三项是将DW统计量归一化为零。在反演中,正则化因子λ1从一个较大的初值开始,随迭代次数的增加逐渐减小;而与此相反,对于权重系数λ2,则先给定一个较小的初值,在迭代过程中缓慢递增。λ1递减和λ2递增的系数通常位于(1,2)之间。采用这种策略的基本思想是,在迭代反演的前期,注重数据拟合和模型约束,而在反演的后期通过增加DW项的权重,减少实测数据与反演模型响应之间残差的自相关性。
本文采用高斯-牛顿最优化方法求解目标函数式(7)的极小值。迭代反演过程中,模型更新量为:
| $ \Delta \boldsymbol{m}=-\boldsymbol{H}_k^{-1} \boldsymbol{g}_k。$ | (8) |
其中gk和Hk分别为第k次迭代时目标函数ϕ(m)的梯度向量和Hessian矩阵,其表达式为:
| $ \begin{gathered} \boldsymbol{g}_k=-2 \boldsymbol{J}_k^{\mathrm{T}} \boldsymbol{C}_d^{-1}\left[\boldsymbol{d}-\boldsymbol{F}\left(\boldsymbol{m}_k\right)\right]+2 \lambda_1 \boldsymbol{C}_m^{-1} \boldsymbol{m}_k+ \\ 2 \lambda_2(D W-2) \cdot \boldsymbol{g}_{d w}。\end{gathered} $ | (9) |
| $ \begin{gathered} \boldsymbol{H}_k=2 J_k^{\mathrm{T}} \boldsymbol{C}_d^{-1} \boldsymbol{J}_k+2 \lambda_1 \boldsymbol{C}_m^{-1}+ \\ 2 \lambda_2\left((D W-2) \boldsymbol{H}_{d w}+\boldsymbol{g}_{d w} \cdot \boldsymbol{g}_{d w}^{\mathrm{T}}\right) 。\end{gathered} $ | (10) |
在传统的高斯-牛顿反演方法中,gk和Hk分别仅由式(9)和式(10)右端的前两项构成,而除该两项以外的其它项反映了DW约束项对梯度向量和Hessian矩阵的贡献。其中:
| $ \boldsymbol{g}_{d w}=-2 Q \boldsymbol{J}^{\mathrm{T}} \boldsymbol{K}^{\mathrm{T}} \boldsymbol{K} e-2 P Q^2 \mathit{\boldsymbol{L}}(e-\bar{e} \boldsymbol{I})。$ | (11) |
| $ \begin{gathered} \boldsymbol{H}_{d w}=2 {Q} \boldsymbol{J}^{\mathrm{T}} \boldsymbol{K}^{\mathrm{T}} \boldsymbol{K} \boldsymbol{J}-2 P Q^2 \boldsymbol{L} \boldsymbol{L}^{\mathrm{T}}+8 {Q}^2 \boldsymbol{J}^{\mathrm{T}} \boldsymbol{K}^{\mathrm{T}} \boldsymbol{K} \boldsymbol{e}(\boldsymbol{L} \boldsymbol{E})^{\mathrm{T}}+ \\ 8 P Q^3 \boldsymbol{L} \boldsymbol{E}(\boldsymbol{L} \boldsymbol{E})^{\mathrm{T}}。\end{gathered} $ | (12) |
式中:J为雅可比矩阵;K为一阶差分算子;I为与观测数据向量同维度的元素均为1的列向量;P=eTKTKe;Q=(ETE)-1;L=
大地电磁阻抗Z可以写成下列指数形式
| $ Z=r\;e^{i \phi}。$ | (13) |
式中:r表示阻抗幅值;ϕ为相位;
由式(13)可以得到阻抗微小变化dZ的表达式
| $ \mathrm{d} Z=\mathrm{d} r e^{i \phi}+r e^{i_\phi} \cdot i \mathrm{~d} \phi。$ | (14) |
式(14)除以式(13),得
| $ \frac{\mathrm{d} Z}{Z}=\frac{\mathrm{d} r}{r}+i \mathrm{~d} \phi。$ | (15) |
上式表明,大地电磁阻抗Z的相对变化相当于其幅值的相对变化和相位的绝对变化。大多数时间序列分析表明,大地电磁阻抗的实部和虚部通常具有相等的误差。于是,有
| $ \mathrm{d} \phi=\frac{\mathrm{d} r}{r} \text { 弧度 }=\frac{\mathrm{d} r}{r} \cdot \frac{180}{\pi} \text { (度) }。$ | (16) |
这意味着,对于大地电磁阻抗Z,其相位的绝对误差与幅值的相对误差相对应。也就是说,如果给大地电磁阻抗幅值添加相对误差er, 则对应的应该给阻抗相位添加er弧度或er·180/π角度的绝对误差。
由于大地电磁视电阻率
| $ \frac{\mathrm{d} \rho_a}{\rho_a}=\frac{2|Z| \mathrm{d} Z \frac{1}{\omega u}}{\frac{|Z|^2}{\omega u}}=2 \frac{\mathrm{d} Z}{|Z|}。$ | (17) |
大地电磁理论模型合成数据反演中,通常会给正演合成数据加入一定的随机噪声,并将其结果作为反演数据。然而,若直接给视电阻率添加相对误差,可能会使得所添加的误差具有自相关性,以2.1节将要讨论的三层高阻薄层模型为例,对此进行说明。
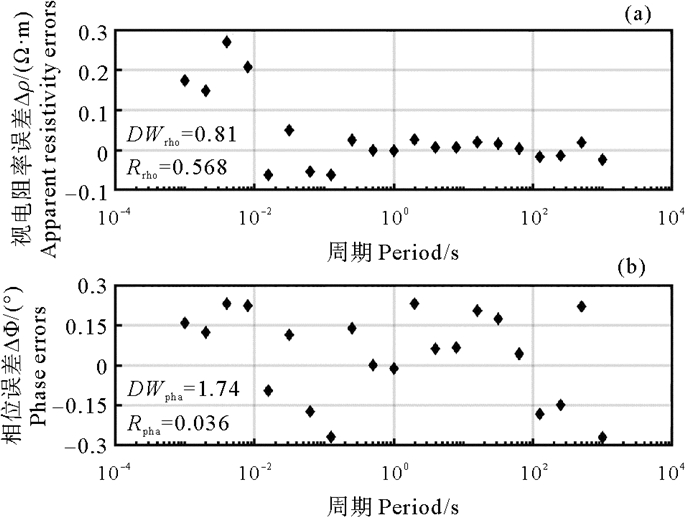
首先,在频率范围10-3~103Hz之间选取21个对数等间隔的频点,正演计算得到三层高阻薄层模型21个频点的视电阻率和阻抗相位。然后,在视电阻率数据中加入1%的随机相对误差噪声,相应地在阻抗相位数据中加入0.286 5°的随机绝对误差。用这样的方法得到的视电阻率误差和相位误差随周期的变化关系如图 2所示。
|
图 2 视电阻率误差(a)和阻抗相位误差(b)分布特征 Fig. 2 The distribution of Apparent resistivity errors (a) and impedance phase errors (b) |
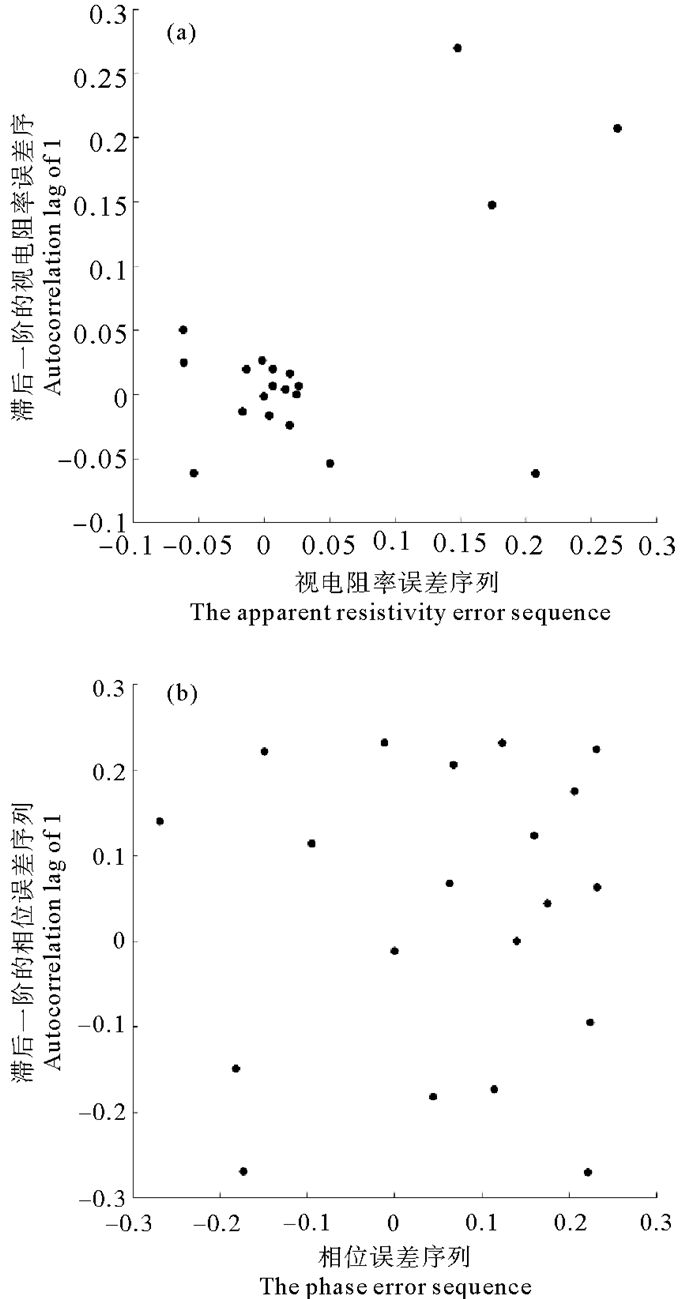
从图 2中可以看到,阻抗相位误差在周期范围(10-3~103 s)内是随机分布的。阻抗相位误差的DW统计量DWpha=1.74和自相关系数Rpha=0.036,这表明阻抗相位误差不具有自相关性。长周期视电阻率的误差是在零线附近上下随机分布的,而短周期视电阻率的误差并非是随机分布的。视电阻率误差的DW统计量DWrho为0.81,自相关系数Rrho为0.568,这表明视电阻率误差具有一定的自相关性。图 3分别绘出了视电阻率误差序列和相位误差序列与其滞后一阶误差序列的散点图,从图 3中也可以看到,视电阻率误差没有呈现出随机分布的状态,但相位误差呈现出了明显的随机分布特征。基于DW统计量的大地电磁反演方法需要满足噪声误差随机性的条件,因此需要对视电阻率进行转换。
|
图 3 视电阻率误差序列(a)和阻抗相位误差序列(b)与其滞后一阶误差序列散点图 Fig. 3 Scatter plot of (a) the apparent resistivity error sequence and (b) the impedance phase error sequence versus their lagging first-order error sequence |
在大地电磁反演中,通常会将视电阻率的对数值作为反演数据。若采用给视电阻率对数值添加绝对误差的方式,则所加误差便不具有自相关性。依据前面的讨论,如果给大地电磁阻抗添加相对误差er, 则应给视电阻率加入2er的相对误差,这相当于给视电阻率对数添加绝对误差log10(1+2er)。其原因解释如下。
假如给视电阻率ρa添加相对误差2er,则绝对误差Δρa=2ρa·er。若视电阻率取对数,y=log10ρa,则其绝对误差为:
| $ \begin{gathered} \Delta y=\log _{10}\left(\rho_a+\Delta \rho_a\right)-\log _{10} \rho_a= \\ \log _{10} \frac{\rho_a+2 \rho_a \cdot e_r}{\rho_a}= \\ \log _{10}\left(1+2 e_r\right) 。\end{gathered} $ | (18) |
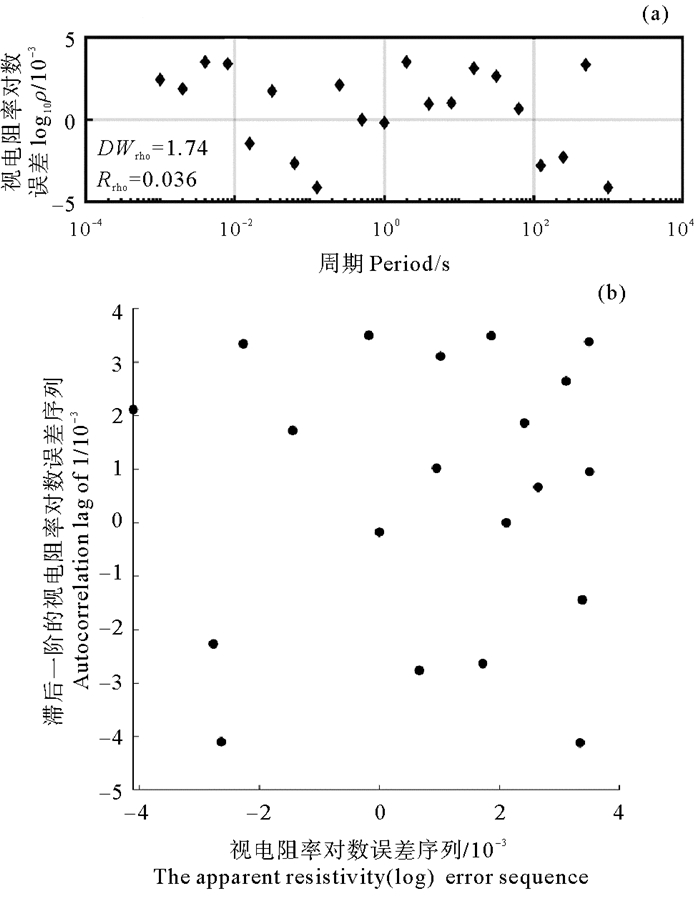
还是以高阻薄层模型为例,在视电阻率对数数据中加入log10(1+1%)的随机绝对误差。图 4给出了视电阻率对数的绝对误差随周期的变化关系以及散点图。由图 4可见,视电阻率对数的误差呈现出了随机分布状态。视电阻率对数误差的DW统计量DWrho = 1.74和自相关系数Rrho=0.036,这表明各个频点视电阻率对数的绝对误差之间不存在自相关性。
|
图 4 视电阻率对数值的绝对误差分布情况(a)和视电阻率对数值的误差与其滞后一阶误差序列散点图(b) Fig. 4 The distribution of the absolute errors in the apparent resistivity (logarithm) (a) and Scatter plot of the apparent resistivity error versus its lagging first-order error sequence (b) |
考虑到理想情况下,各个频点大地电磁数据的误差之间应各自独立,不存在自相关。因此,在大地电磁反演中应将视电阻率对数值和阻抗相位作为反演数据,在添加误差时应加入相应的绝对误差。
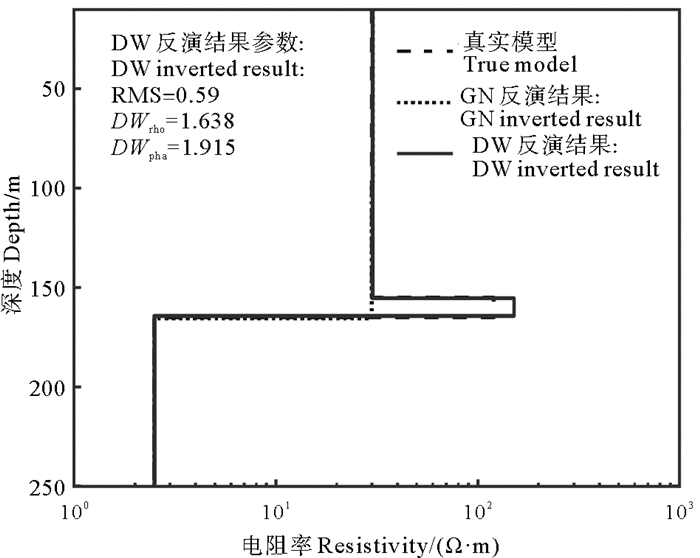
2 反演算例 2.1 高阻薄层模型首先考虑一个含有高阻薄层的三层模型(如图 5中黑色虚线)。该模型是根据文献[11, 20]建立的页岩油气高阻薄层模型。第一层的电阻率和厚度分别为30 Ω·m和120 m;中间层为高阻薄层,其电阻率和厚度分别为120 Ω·m和10 m,高阻层下方是电阻率为2.5 Ω·m的均匀半空间。假设21个频点对数等间隔地均匀分布在频率范围10-3~103 Hz之间。在各个频点的视电阻率对数和阻抗相位数据中,分别加入0.004 3(log10(1+0.01)=0.004 3,相当于给视电阻率添加1%的相对误差)和0.005弧度的随机噪声,从而构成反演数据。
|
图 5 反演结果对比 Fig. 5 Comparison of inversionresults |
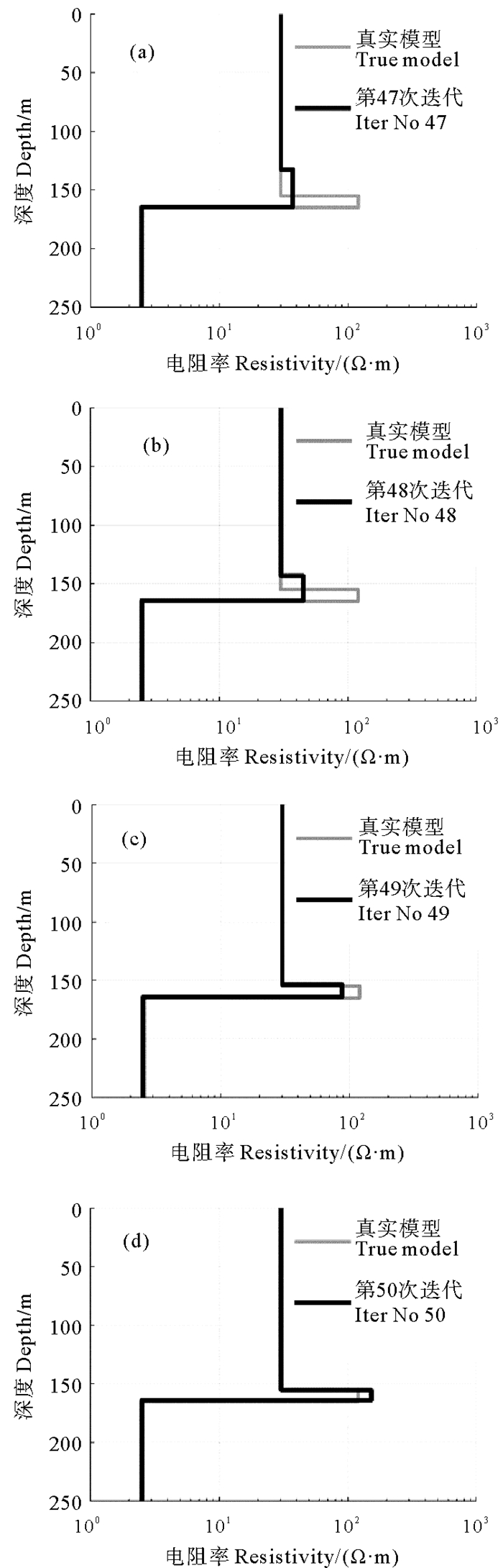
反演初始模型为100 Ω·m的均匀半空间。正则化因子和DW权重因子的初值分别为λ1=105和λ2=10-4。在迭代过程中,λ1逐渐减小,而λ2逐渐增大。在本例中,λ1的递减系数为1.23,λ2的递增系数为1.60。图 5展示了经过第50次迭代后获得的反演结果。从反演结果中可以看到,高阻薄层厚度及其电阻率均得到了很好的重构,其厚度非常接近真实值,其电阻率为151.30 Ω·m,比其真实值偏高。图 6展示了第47次至第50次迭代的反演结果。从图 6可以看出DW反演方法重构高阻薄层的过程。为了比较起见,图 5也给出了传统高斯-牛顿法反演结果。高斯-牛顿法反演方法很好地恢复了第一层和第三层的电阻率, 但是对高阻薄层几乎完全没有反映。
|
((a)第47次迭代,(b)第48次迭代,(c)第49次迭代,(d)第50次迭代。(a) The 47th iteration, (b) The 48th iteration, (c) The 49th iteration, (d) The 50th iteration.) 图 6 DW反演重构高阻薄层的迭代过程 Fig. 6 The iterative process of reconstructing a high-resistivity thin layer by DW inversion method |
由于大地电磁法存在等值性现象,含有高阻薄层的正演响应曲线与不含高阻薄层的正演响应曲线十分接近,使得大地电磁法对高阻薄层的分辨率极低。海洋大地电磁方法对高阻薄层分辨率低的特性制约了其在高阻薄层探测方面的发展,而本例则表明含DW项的反演方法可以通过减小反演拟合残差的自相关性,在一定程度上提高海洋大地电磁方法对高阻薄层的探测能力。
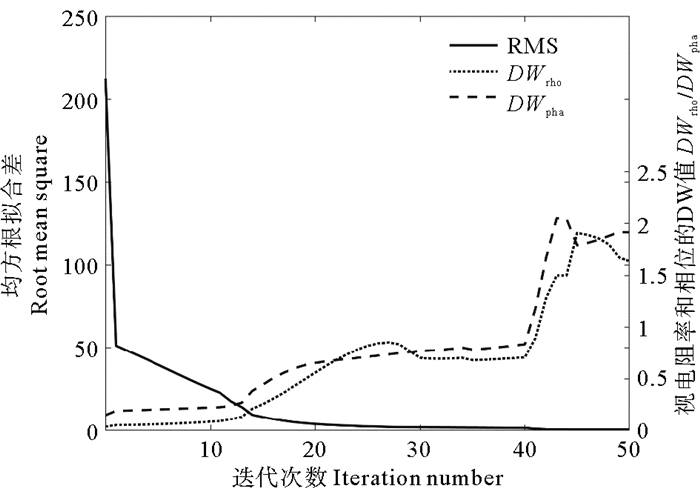
图 7给出了DW反演迭代过程中均方根RMS、视电阻率对数的DW统计量(DWrho)及相位DW统计量(DWpha)的变化情况。从图 7中可以看出,均方根RMS随着迭代次数的增加不断下降,而DWrho和DWpha随迭代次数逐渐增大,并逐渐趋近于它们的期望值。
|
图 7 DW反演迭代过程中RMS与DW值的变化 Fig. 7 Changes of RMS and DW values during the DW inversion iteration |
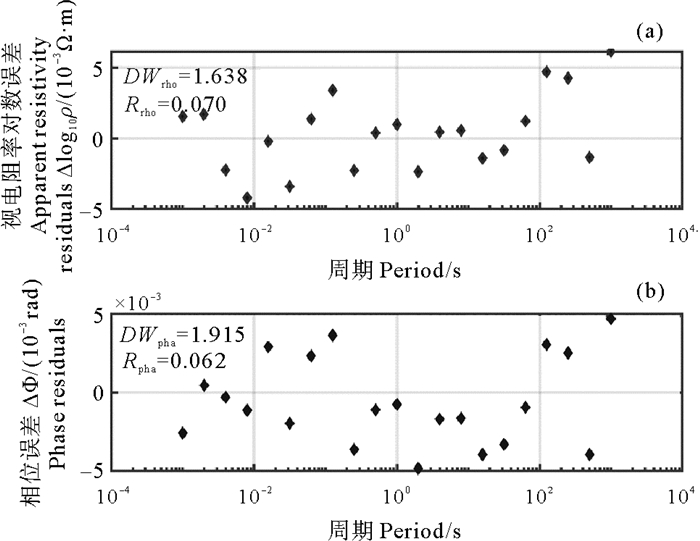
图 8绘出了DW方法第50次迭代反演模型与真实模型的视电阻率对数和相位之间的残差。从图 8可以看到,视电阻率对数残差和相位残差在各频段上基本呈现出随机波动的状态。由表 1可知,在数据个数为21的情形下,DW统计量位于(1.54, 2.46)内时,反演数据和反演模型响应之间的残差将不存在自相关性。图 5所示DW反演模型与真实模型视电阻率对数残差和相位残差的DW统计量,分别为DWrho = 1.638和DWpha = 1.915,它们均位于1.54~2.46之间,这表明DW反演模型的视电阻率对数残差和相位残差之间都不存在自相关性。
|
图 8 DW反演模型与真实模型的视电阻率残差(a)和相位残差(b) Fig. 8 The apparent resistivity (a) and phase residuals (b) between the DW inversion model response and the real model response |
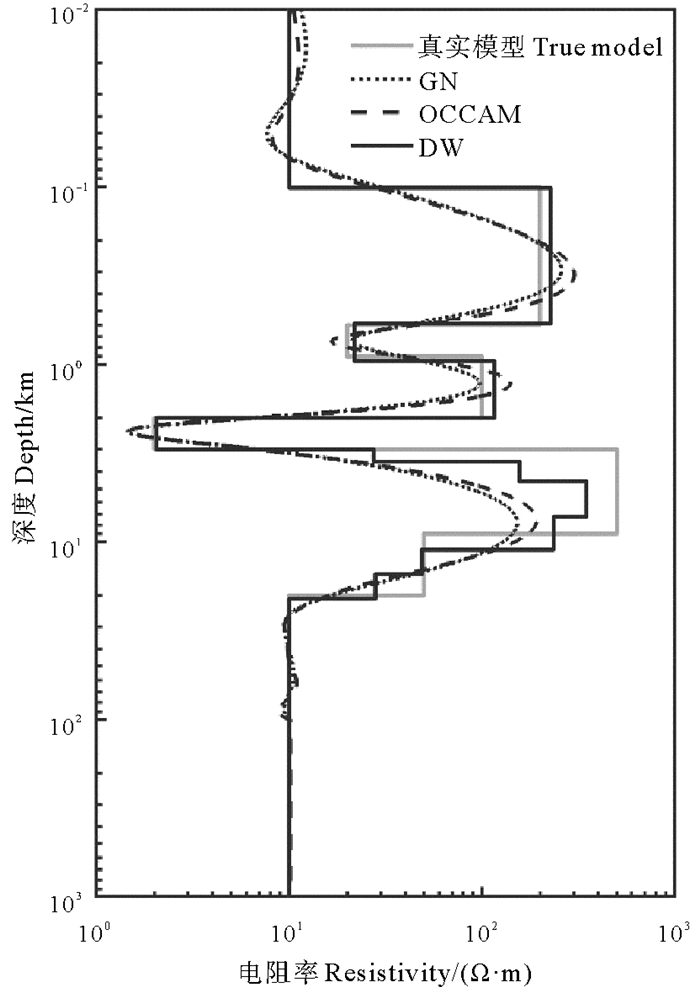
图 9中灰色实线所示一个八层地电模型。该模型常被用于验证大地电磁反演方法的效果[21-22]。先在0.000 1~1 000 Hz之间呈对数等间距选取40个频点,经正演计算得到40个频点的大地电磁响应,对视电阻率对数和相位分别添加0.004 3和0.005弧度的随机误差,将其作为反演数据。然后分别使用传统高斯-牛顿反演方法(GN)、OCCAM反演方法和DW反演方法进行反演计算。反演时,初始模型均为100 Ω·m均匀半空间。基于三种反演方法的反演结果如图 9所示。从反演结果中可以看出,相较于传统高斯-牛顿反演方法和OCCAM反演方法,DW方法反演结果更接近真实模型,对高阻层和低阻层的识别更加准确。DW反演模型视电阻率对数和相位的DW统计量分别为DWrho=1.208和DWpha= 1.978。由表 1可知,对于40个样本点,当DW统计量位于(1.60, 2.40)区间内时,反演数据和反演模型响应之间的残差将不存在自相关性。而当DW统计量小于1.39时,则认为残差具有正一阶自相关。据此认为,DW反演模型的视电阻率残差之间具有一定的正自相关性,而相位残差不具有自相关性。
|
图 9 DW反演结果与传统GN和OCCAM反演结果对比 Fig. 9 Comparison of the DW inversion result with the traditional GN, OCCAM inversion results |
|
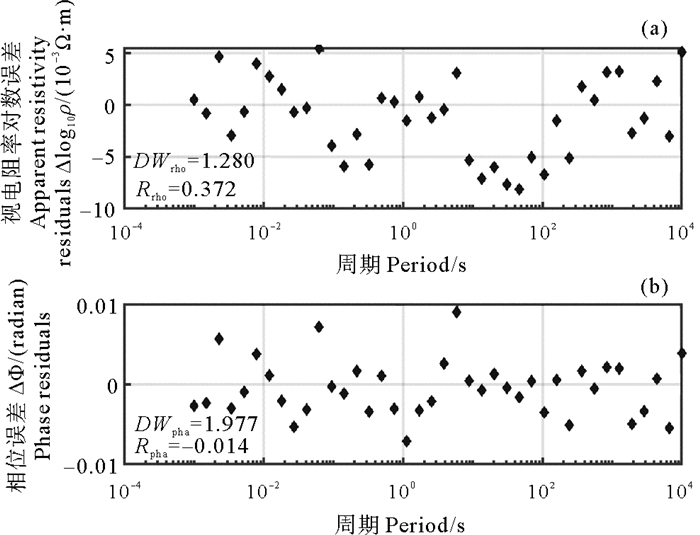
图 10 DW反演模型与真实模型的视电阻率残差(a)与相位残差(b) Fig. 10 The apparent resistivity residuals (a) and phase residuals (b) of the DW inversion model versus the real model |
在本节中,研究将DW反演方法应用于南黄海实测海洋大地电磁数据反演中。南黄海中部隆起区由于高速海相碳酸盐岩的屏蔽作用,导致地震勘探方法应用不理想,成为制约海相油气勘探的关键[23]。海洋大地电磁方法由于不受高阻层屏蔽、对低阻层敏感度高的特点,已应用于该海域,初步探明海相碳酸盐岩层的厚度[24]。由于研究区水深仅21 m,海水运动(如波浪,潮汐等)使得大地电磁视电阻率和相位在1~10 s周期受到较大干扰,一定程度降低了数据质量和分辨率,因此,在数据处理时需对受海水运动影响较大频点的大地电磁数据进行剔除。下面,给出利用S4站位27个频点的视电阻率数据和19个频点的相位数据的反演结果。
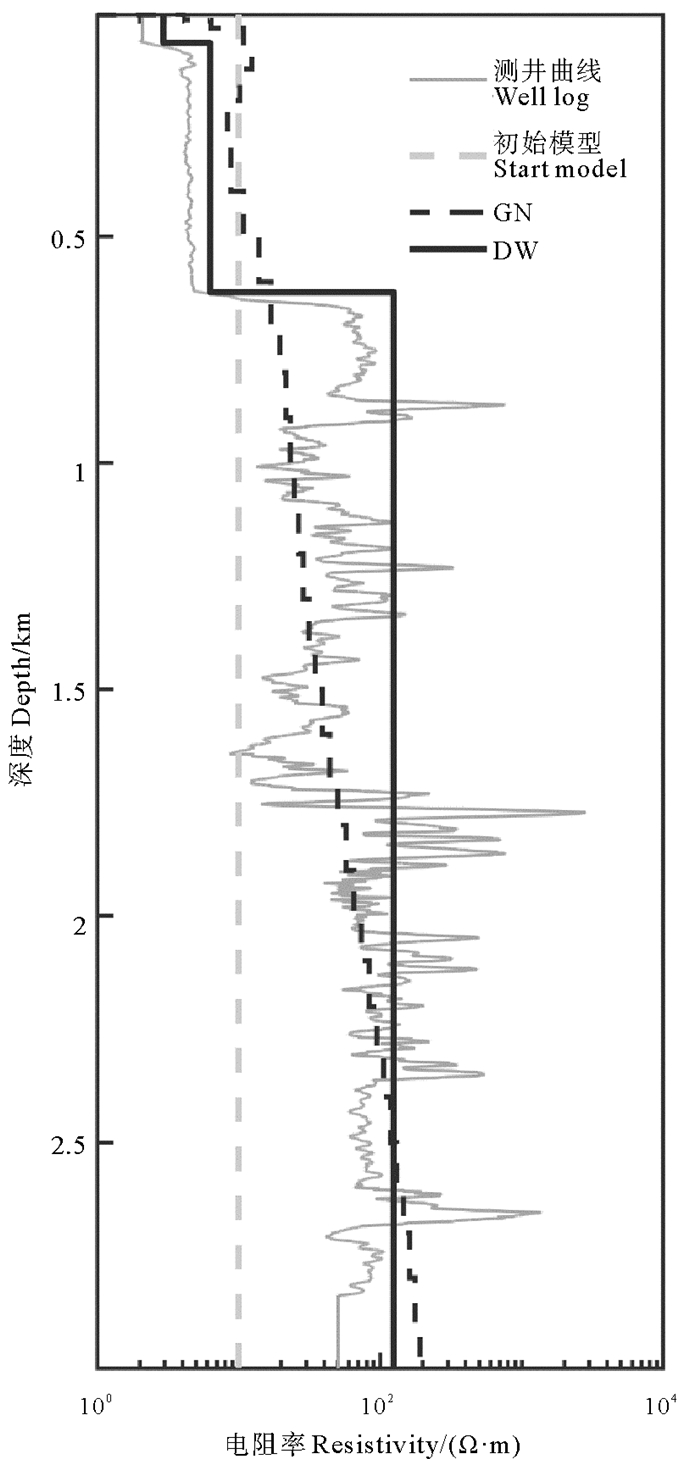
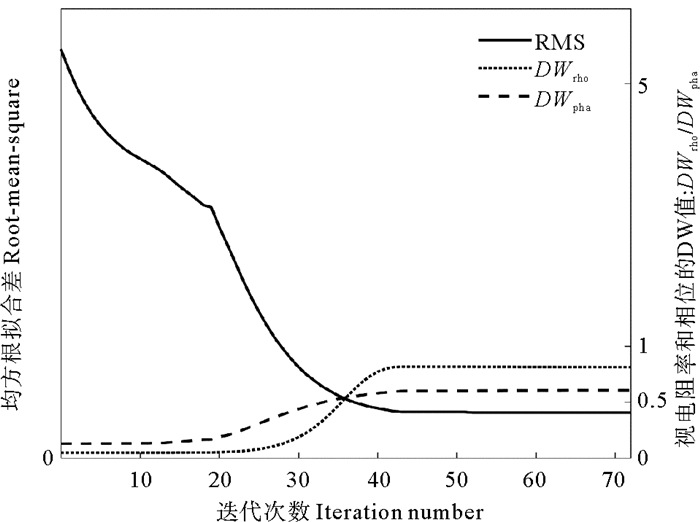
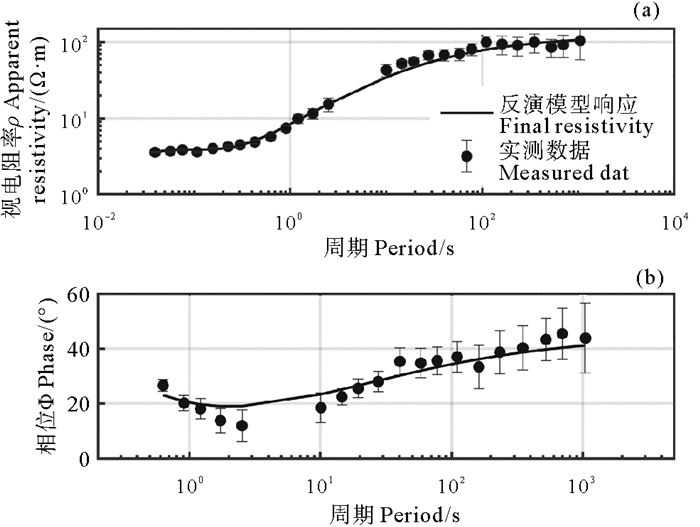
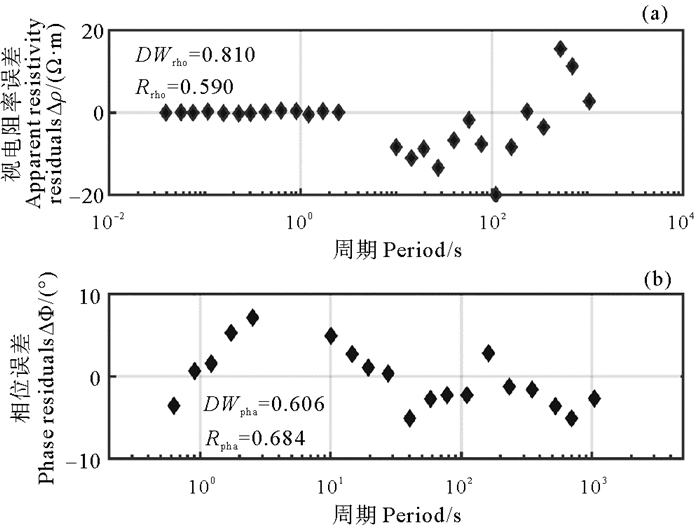
对S4站位实测MT数据进行了DW反演,并将反演结果与测点附近的测井电阻率数据进行对比(该站位位于CSDP-2井东南方向4 km处[25])。反演时,初始模型为10 Ω·m均匀半空间。图 11为该测点实测MT数据的反演结果。由图 11可以看出,DW反演结果与传统高斯-牛顿法反演结果[24]相比,对六百多米深处高阻界面的识别更为清晰。图 12为DW反演迭代过程中均方根RMS与DW统计量的变化情况。随着迭代次数的增加,均方根误差RMS逐渐下降,而视电阻率与相位的DW值逐渐增大,最后趋于稳定。图 13为反演模型的视电阻率和相位与实测数据的对比。图 14为它们之间的残差。由表 1可知,在样本数量分别为27与19时,如果DW统计量分别位于区间(1.56, 2.44)与(1.53,2.47)内,则反演数据和反演模型响应之间的残差不存在自相关性。通过对比分析DW值以及拟合曲线可以得到,DWrho = 0.81, 相位的DWpha = 0.61, 反演后残差具有正自相关性,这是因为实测数据经过处理后的误差无法满足随机性的特点,由于受海水运动、仪器噪声等影响,实测数据的误差具有较强的正自相关性。但是,较于传统的高斯-牛顿法反演,DW反演结果对浅层高阻层与620 m处的高阻层界面识别更清晰。
|
(测井和GN反演结果来自文献[24]。The GN inversion results are from reference[24].) 图 11 实测数据高斯-牛顿法和DW法反演结果与电阻率测井资料的对比 Fig. 11 Comparison of the GN and DW inversion results and resistivity logging data |
|
图 12 DW反演迭代过程中RMS与DW值的变化 Fig. 12 Changes of RMS and DW values during the DW inversion iteration |
|
图 13 反演模型响应(实线)与实测数据的视电阻率(a)和相位曲线(b)对比 Fig. 13 The comparison of the apparent resistivity (a) and phase curve (b) between the inversion response and measured data |
|
图 14 DW反演模型响应的视电阻率残差(a)和相位残差(b) Fig. 14 The apparent resistivity residuals (a) and phase residuals (b) between the data and the DW inversion model responses |
在MT反演的目标函数中加入Durbin-Watson(DW)统计量,可以降低反演模型响应与观测数据之间残差的自相关性,在一定程度上避免反演结果中出现的拟合差较小而反演模型响应偏离观测数据的情况,从而优化反演结果,降低反演的多解性。
本文通过两个层状模型模拟数据反演,验证了DW反演方法的有效性,并与传统高斯-牛顿法或OCCAM反演方法进行了对比,结果表明基于DW统计量的反演方法提高了对高阻薄层的反演分辨能力。南黄海实测大地电磁数据反演结果表明,该方法能够较准确地重构高阻层界面,具有良好的应用前景和效果。
针对目标函数中各项权重系数的选取策略以及如何将DW反演方法推广到二维和三维大地电磁反演中,有待下一步继续研究。
| [1] |
Chesley C, Naif S, Key K, et al. Fluid-rich subducting topography generates anomalous forearc porosity[J]. Nature, 2021, 595: 255-260. DOI:10.1038/s41586-021-03619-8 (  0) 0) |
| [2] |
Naif S, Key K, Constable S, et al. Water-rich bending faults at the middle america trench[J]. Geochemistry Geophysics Geosystems, 2015, 16(8): 2582-2597. DOI:10.1002/2015GC005927 (  0) 0) |
| [3] |
赵国泽, 陈小斌, 汤吉. 中国地球电磁法新进展和发展趋势[J]. 地球物理学进展, 2007, 22(4): 1171-1180. Zhao Guo-ze, Chen Xiao-bin, Tang Ji. Advanced geo-electromagnetic methods in China[J]. Progress in Geophysics, 2007, 22(4): 1171-1180. DOI:10.3969/j.issn.1004-2903.2007.04.024 (  0) 0) |
| [4] |
Pearson K. X.. On the criterion that a given system of deviationsfrom the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling[J]. The London, Edinburgh and Dublin Philosophical Magazine and Journal of Science, 1900, 50(305): 157-175. (  0) 0) |
| [5] |
Tikhonov A N. Regularization of incorrectly posed problems[J]. Soviet Mathematics Doklady, 1963, 4(6): 1624-1627. (  0) 0) |
| [6] |
Tikhonov A N, Arsenin V Y. Solutions of Ill-posed Problems[M]. Winston: Society for Industrial and Applied Mathematics, 1977.
(  0) 0) |
| [7] |
Constable S C, Parker R L, Constable C G. Occam's inversion: A practical algorithm for generating smooth models from electromagnetic sounding data[J]. Geophysics, 1987, 52(3): 289-300. DOI:10.1190/1.1442303 (  0) 0) |
| [8] |
Rodi W, Mackie R. Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion[J]. Geophysics, 2001, 66: 174-187. DOI:10.1190/1.1444893 (  0) 0) |
| [9] |
韩波. 大地电磁二维拟牛顿反演研究[D]. 武汉: 中国地质大学(武汉), 2012. HanBo. Quasi-Newton Method for Two-Dimensional Magnetotelluric Inversion[D]. Wuhan: China University of Geosciences, 2012. (  0) 0) |
| [10] |
Sasaki Y. Three-dimensional inversion of static-shifted magnetotelluric data[J]. Earth planets and Space, 2004, 56(2): 239-248. DOI:10.1186/BF03353406 (  0) 0) |
| [11] |
Jones A G. Beyond chi-squared: Additional measures of the closeness of a model to data[J]. ASEG Extended Abstracts, 2019, 2019(1): 1-6. (  0) 0) |
| [12] |
Smith J T, Booker J R. Magnetotelluric inversion for minimum structure[J]. Geophysics, 1988, 53(12): 1565-1576. DOI:10.1190/1.1442438 (  0) 0) |
| [13] |
Jones A G. Imaging and observing the electrical moho[J]. Tectonophysics, 2013, 609: 423-436. DOI:10.1016/j.tecto.2013.02.025 (  0) 0) |
| [14] |
Durbin J, Watson G S. Testing for serial correlation in least squares regression: Ⅰ[J]. Biometrika, 1950, 37(3/4): 409-428. DOI:10.2307/2332391 (  0) 0) |
| [15] |
Durbin J, Watson G S. Testing for serial correlation in least squares regression. Ⅱ[J]. Biometrika, 1951, 38(1/2): 159-177. DOI:10.2307/2332325 (  0) 0) |
| [16] |
Vinod. Generalization of the durbin-watson statistic for higher order autoregressive processes[J]. Communications in Statistics, 1973(2): 115-144. (  0) 0) |
| [17] |
Ali M M. Durbin-watson and generalized durbin-watson tests for autocorrelations and randomness[J]. Journal of Business & Economic Statistics, 1987, 5(2): 195-203. (  0) 0) |
| [18] |
刘明, 王永瑜. Durbin-Watson自相关检验应用问题探讨[J]. 数量经济技术经济研究, 2014, 31(6): 153-160. Liu Ming, Wang Yong-yu. Exploring in durbin-watson autocorrelation test[J]. The Journal of Quantitative & Technical Economics, 2014, 31(6): 153-160. (  0) 0) |
| [19] |
韩波, 胡祥云, 何展翔, 等. 大地电磁反演方法的数学分类[J]. 石油地球物理勘探, 2012, 47(1): 177-187. Han Bo, Hu Xiang-yun, He Zhan-xiang, et al. Mathematical classification of magnetotelluric inversion methods[J]. Oil Geophysical Prospecting, 2012, 47(1): 177-187. (  0) 0) |
| [20] |
Strack K M. Future directions of electromagnetic methods for hydrocarbon applications[J]. Surveys in Geophysics, 2014, 35(1): 157-177. DOI:10.1007/s10712-013-9237-z (  0) 0) |
| [21] |
陈小斌, 赵国泽, 汤吉, 等. 大地电磁自适应正则化反演算法[J]. 地球物理学报, 2005, 48(4): 937-946. Chen Xiao-bin, Zhao Guo-ze, Tang Ji, et al. An adaptive regularized inversion algorithm for magnetotelluric data[J]. Chinese Journal of Geophysics, 2005, 48(4): 937-946. (  0) 0) |
| [22] |
郭一豪, 陈晓, 杨海燕, 等. 大地电磁测深阶段式自适应正则化反演[J]. 石油地球物理勘探, 2020, 55(4): 906-914. Guo Yi-hao, Chen Xiao, Yang Hai-yan, et al. Staged adaptive regularized inversion of magnetotelluric data[J]. Oil Geophysical Prospecting, 2020, 55(4): 906-914. (  0) 0) |
| [23] |
张训华, 吴志强, 肖国林, 等. 南黄海前新生代油气地震勘探面临的问题与努力方向[J]. 海洋地质前沿, 2014, 30(10): 1-7. Zhang Xunhua, Wu Zhiqiang, Xiao Guolin, et al. A review and perspective of seismic survey for pre-cenozoic hydrocarbon in the Southern Yellow Sea[J]. Marine Geology Frontiers, 2014, 30(10): 1-7. (  0) 0) |
| [24] |
Duan S, Li Y, Pei J, et al. Carbonate imaging with magnetotellurics in a shallow-water environment, South Yellow Sea, China[J]. Journal of Applied Geophysics, 2020(178): 104076. (  0) 0) |
| [25] |
朱宇启, 裴建新, 段双敏, 等. 测井约束的海洋CSEM反演及其在南黄海中部隆起区勘探应用[J]. 中国海洋大学学报(自然科学版), 2021, 51(6): 70-77. Zhu Yu-qi, Pei Jian-xin, Duan Shuang-min, et al. Marine CSEM inversion with well logging constraints and its application in the central uplift of the South Yellow Sea[J]. Periodical of Ocean University of China, 2021, 51(6): 70-77. (  0) 0) |
2. Laboratory for Marine Mineral Resources, Pilot National Laboratory for Marine Science and Technology (Qingdao), Qingdao 266237, China;
3. Institute of Geological Survey, China University of Geosciences (Wuhan), Wuhan 430074, China
 2023, Vol. 53
2023, Vol. 53


