海洋混合对改变水团性质,维持海洋分层,驱动全球热盐环流有重要作用[1]。传统理论认为,维系混合的三大能量来源主要是内潮、近惯性内波及内背风波等不同尺度的内波[2]。南海是西北太平洋最大的边缘海之一,海底地形复杂,岛礁密布,有大量活跃的内潮和高频非线性内波[3-4],一直以来都是国内外学者关心的一个海域。目前对于南海混合的研究多集中于南海北部陆架陆坡、吕宋海峡、东沙岛附近。对于南海北部,20°N以北的耗散率是南部的两倍[5],混合在陆架上比在陆坡上大一个数量级[6]。在吕宋海峡的深水区,两脊之间的潮汐共振使内潮引起的混合增强[7-8]。将吕宋海峡两侧的混合强度进行对比,发现1 000 m以下南海一侧的混合比在太平洋一侧的混合大两个数量级,这里的混合增强可能与吕宋海峡处产生并传入南海的内潮能量通量[9],以及黑潮侵入造成的剪切不稳定[10]有关。在东沙岛东部[11]和东沙岛东北部的断层区[12]也观测到了强混合。在东沙岛附近,内孤立波经过时,局地的混合率和耗散率会提高三个数量级,内孤立波经过后,迅速恢复正常[13]。最近,越来越多的学者开始关注整个南海的混合情况。Sun等[14],Yang等[15]基于微观测结构和细尺度参数化方法,分别给出了南海上500 m和全水深的混合的三维分布。总体上,南海北部的混合要强于南海南部,而且南海混合呈现自东向西减弱的趋势,此外吕宋海峡和中沙岛岛链海域的底部是两个强混合区。
之前的研究主要是关注南海混合的时空分布、成因及其影响,目前还没有工作给出南海混合各个能量源的具体贡献。本文将利用公开的气候态温盐数据、风场数据、流场数据等,对整个南海混合的三个能量来源(近惯性内波、内潮、背风波)进行系统的计算和对比,给出各个能量源的具体贡献。
1 数据介绍本文使用的数据,时间范围选取2013年1月1日—12月31日,空间范围选取4°N~24°N,104°E~121°E。风场数据为NCEP/NCAR再分析数据集提供的海面10 m高度的风场数据,时间分辨率为6 h,空间分辨率为2.5°×2.5°,同一深度线性插值为0.5°×0.5°。月平均的温盐数据和流场数据来自Global Ocean Physics Reanalysis Cglors (1982—2013)数据集,空间分辨率为0.25°×0.25°,垂直方向共分50层。利用该温盐数据可以计算出层结、混合层深度及南海平均海水密度ρ=1 034 kg·m-3,其中在计算混合层深度时对温盐剖面进行了垂向线性插值。地形数据为Satellite Geodesy提供的srtm15_plus高分辨率地形数据,空间分辨率为0.25′×0.25′。利用该地形数据计算得出研究海域面积为2.92×1012 m2,全深度海水体积为4.14×1015m3,质量为4.26×1018 kg;上层500 m海水体积为0.87×1015 m3,质量为0.9×1018 kg;500 m以深海水体积为3.27×1015 m3,质量为3.38×1018 kg;近底层500 m海水体积为0.78×1015 m3,质量为0.8×1018 kg。下文涉及的计算会使用到这些数据。
2 近惯性内波能量基于海面10 m高度处的风速数据,根据公式
| $ \tau = {C_D}{\rho _a}U_{10}^2。$ | (1) |
计算风应力。其中:ρa为海表面空气密度,这里取值1.3 kg·m-3,为距离平均海面10 m处的风速;CD为拖曳系数。本论文采用Oey等[17]综合前人工作提出的计算拖曳系数的公式:
| $ {C_D} \times 1000 = \\\left\{ {\begin{array}{*{20}{c}} {1.2}&{{U_{10}} \le 11\;{\rm{m}} \cdot {{\rm{s}}^{-1}}}\\ {0.49 + 0.065{U_{10}}}&{11 < {U_{10}} \le 19~{\rm{m}} \cdot {{\rm{s}}^{-1}}}\\ {1.364 + 0.023\;4{U_{10}}-0.000\;231\;58}&{19 < {U_{10}} \le 100\;{\rm{m}} \cdot {{\rm{s}}^{ - 1}}} \end{array}} \right.。$ | (2) |
单位面积的功率或输入海面的能量通量可由下式给出:
| $ \prod = \tau \cdot \mu 。$ | (3) |
其中:τ代表风应力矢量;μ代表流速矢量。由于缺乏混合层流速数据,本文通过平板模型[18]来模拟由风引起的混合层内的运动。其控制方程为:
| $ \frac{{{\rm{d}}Z}}{{{\rm{d}}t}} + \left( {r + if} \right)Z = \frac{T}{H}。$ | (4) |
其中:
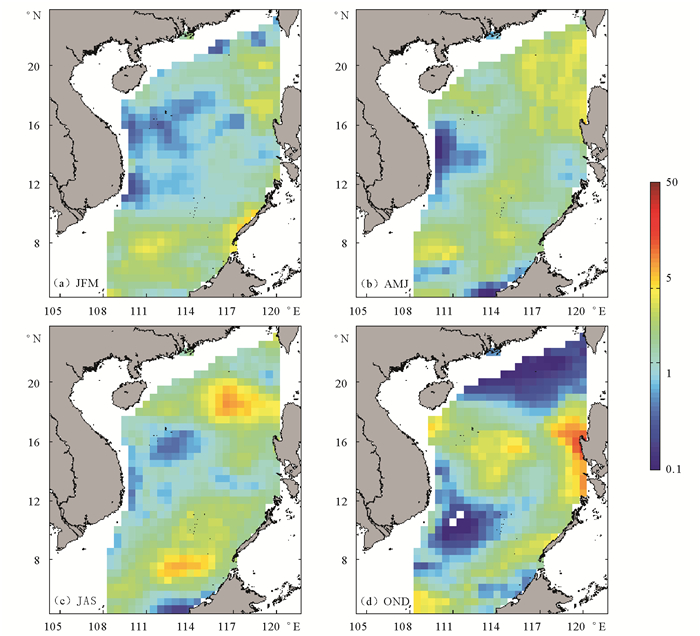
由于4和10月是南海季风的转换时期,所以本文以这2个月作为节点,将2013年划分为1—3月、4—6月、7—9月、10—12月4个时间区间进行分析。近惯性能量通量的3个月平均空间分布图(见图 1)。其中小部分区域(约为1%)的年平均值小于0(海洋向大气释放能量)。从图上可以看出冬半年近惯性内波能量通量明显增强。Sun等[14]发现南海北部存在冬季混合增强的现象,这与冬季海面风场加强导致的风输入海洋的近惯性能量增多有着密切的关系。这与本文近惯性内波能量通量冬季输入增强的结果相一致。
|
((a)1, 2, 3月平均;(b)4, 5, 6月平均;(c)7, 8, 9月平均;(d)10, 11, 12月平均。(a)~(d) are the mean wind-input near-inertial energy flux during Jan-Feb-Mar, Apr-May-Jun, Jul-Aug-Sep, Oct-Nov-Dec, respectively.) 图 1 2013年南海季节平均近惯性内波能量通量分布图(单位为mW·m-2) Fig. 1 Seasonal characteristics of near-inertial internal wave energy flux (unit: mW m-2) in the South China Sea in 2013 |
南海年平均近惯性内波能量通量约为1.7 mW·m-2,结合第2部分给出的南海海域面积,可得年平均近惯性内波能量总量约为5.1 GW。一般认为风生近惯性能量在海洋上层全部耗散,本文中假设这些能量全部在上层500 m耗散为混合提供能量[19],结合第2部分中给出的南海上层500 m海水质量,则平板模型给出的南海近惯性内波引起的平均湍动能耗散率约为5.7×10-9W·kg-1。
3 内潮能量南海是一个半封闭的海盆,海底多海山、岛屿,地形复杂,为内潮的产生提供了绝佳的地形扰动条件。本文利用二维高分辨率地形数据,基于适用于亚临界地形的线性内波理论来计算内潮的能量通量。一般来说,潮流分量可以表示为(U,V)=[u0cos(ωt), v0cos(ωt+v)],其中υ是U和V之间的相对时间相位。然而,对于给定的潮汐椭圆,长半轴和短半轴潮流分量可以表示为(Ue, Ve)=[uecos(ωt), vesin(ωt)]。这样一来,所有相位信息被包含进到潮汐椭圆参数中,使得长半轴和短半轴分量完全异相[20]。在这个坐标系中,垂向的底边界条件表示为:
| $ w\left( {-H} \right) = {u_e}\cos \left( {\omega t} \right)\frac{{\partial h}}{{\partial {x_e}}} + {v_e}\sin \left( {\omega t} \right)\frac{{\partial h}}{{\partial {y_e}}}。$ | (5) |
其中(xe, ye)是由长半轴和短半轴确定的坐标轴。使用压力p或垂向群速度cg和能量密度Ed的标准内波关系[21],垂向通量可以表示为:
| $ {E_f} = {\rho _0}\frac{{{{[(N_b^2-{\omega ^2})({\omega ^2}-{f^2})]}^{1/2}}}}{{\omega {{({k^2} + {l^2})}^{1/2}}}}\left\langle {{w^2}} \right\rangle。$ | (6) |
其中〈·〉是波相位的所有分量的平均值。则垂直能量通量进一步可以表示为:
| $ \begin{array}{l} {E_f} = \frac{1}{2}{\rho _0}\frac{{{{[(N_b^2-{\omega ^2})({\omega ^2}-{f^2})]}^{1/2}}}}{\omega }\int_0^{2\pi } {\int_{{K_1}}^\infty {(u_e^2{{\cos }^2}\theta + } } \\ v_e^2{\sin ^2}\theta ){K^2}\phi \left( {K, \theta } \right){\rm{d}}K{\rm{d}}\theta 。\end{array} $ | (7) |
这里(k, l)是对应于(xe, ye)坐标系的波数,是总波数。地形的功率谱需要进行归一化以满足。
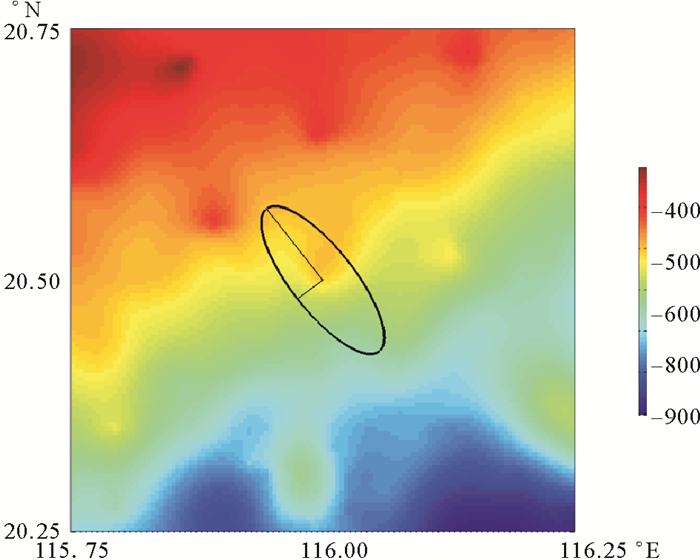
本文选取东沙群岛附近一处位置(约116°E,20.5°N附近)作为例子,基于(7)式进行内潮能量通量的估计。其周边地形及潮流椭圆(以M2分潮为例)(见图 2)。
|
(颜色代表水深。The contour represents water depth.) 图 2 东沙群岛附近(约116°E,20.5°N)M2潮流椭圆(黑色实线) Fig. 2 Topography near the Dongsha islands and an example for tidal ellipses of M2 currents |
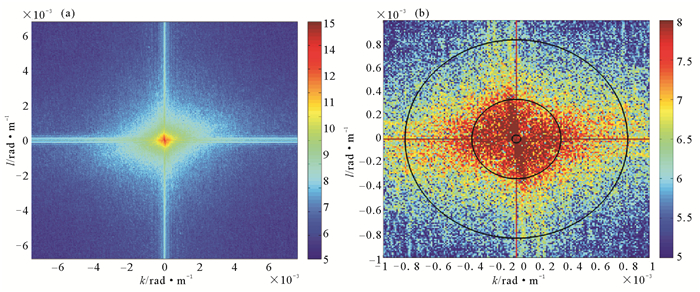
每个潮流椭圆的长半轴和短半轴用于定义局部坐标系,地形数据被重新定义到潮流椭圆坐标系中。使用潮流椭圆坐标系计算二维地形谱(见图 3(a)),并得到了一个平均能量谱Φ(k, l)(见图 3(b))。使用(7)式估计能量通量。
|
((a)为二维地形谱;(b)为平均能量谱,其中三个黑色实线圆圈分别表示第1模态、第10模态、第25模态。k、l为水平波数。(a) 2D power spectrum of topography near the Dongsha islands;(b) 2D spectrum of internal tide energy flux in a four-quadrant wavenumber space, with black circles corresponding to the equivalent modes 1, 10, and 25. k and l are horizontal wavenumbers.) 图 3 东沙群岛附近(约116°E,20.5°N)二维地形谱和平均能量谱 Fig. 3 2D power spectrum of topography and internal tide energy fluxnear the Dongsha islands (116°E, 20.5°N) |
通过气候态温盐数据计算得到该区域的平均层结约为Nb2=0.8×10-5 s-2。能量通量的平均谱如图 3(b)所示。这里积分前25个模态得到的能量通量为2.9 mW·m-2,并根据Laurent和Garrett[22]提出第1~25模态占总垂直能量通量的80%,计算得到总能量通量约为3.6 mW·m-2。乘以该区域的总面积2.9×109m2,得到该区域M2内潮的能量为107W。
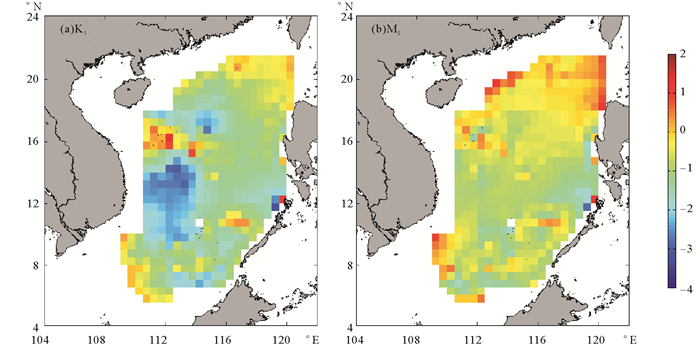
用上述方法对整个南海各个网格点分别进行计算,其中仅K1分潮、M2分潮贡献显著。南海内部年平均的内潮能量通量如图 4所示。
|
((a)为全日内潮K1产生的能量通量;(b)为半日内潮M2产生的能量通量。(a)和(b)中均为取对数后的结果,单位为mW·m-2。(a) and (b) are internal tide energy flux of K1 and M2internal tides, respectively. The logarithmic scale and the unit of mW·m-2 are used in both (a) and (b).) 图 4 2013年南海年平均内潮能量通量空间分布图 Fig. 4 Thedistribution of mean internal tide energy flux during 2013 in the South China Sea |
总体来看,复杂地形的海域,例如东沙群岛、西沙群岛和中沙群岛的海域,产生的内潮能量通量约为O(101) mW·m-2,而其他海底地形平缓的海域产生的内潮能量通量仅为O(10-3)~O(10-1) mW·m-2。并且整体上M2内潮对南海能量通量的贡献要比K1内潮大。经过计算,南海整体年平均的M2内潮产生的能量通量约为0.6 mW·m-2,K1内潮产生的能量通量约为0.3 mW·m-2,结合第2部分给出的南海海域面积,计算可得南海内部年平均内潮生成的能量通量总量约为2.6 GW。
由于吕宋海峡处的地形非常陡峭,不适用于此方法,所以本文在计算中没有考虑吕宋海峡附近海域的内潮能量。但吕宋海峡作为内潮的重要源地,会产生大量内潮并传入南海内部,最终在南海陆架陆坡处破并为混合提供能量。本文中,吕宋海峡处产生并传入南海的内潮能通量引用前人研究结果,现场实验[9]和数值模拟[4, 23]均认为,吕宋海峡进入南海的内潮能量通量约有10 GW参与南海混合。加上本文计算得到的南海内部产生的内潮能量通量2.6 GW,南海获得的内潮能量约为12.6 GW。假设这些能量全部在500 m以深海域耗散为混合提供能量[4],结合第2部分给出的500 m以深海水质量,则内潮引起的平均湍动能耗散率约为3.7×10-9 W·kg-1。
4 背风波能量虽然在全球深层海洋中,背风波与内潮相比生成量要少很多,但是内潮和背风波的空间分布明显不同。最近的研究结果表明,背风波驱动的混合对海洋状态有潜在的影响[24]。
在层化流体中,准定常流动流经小尺度地形时,产生内背风波。线性理论[25]表明,在亚临界地形中,背风波辐射的能量通量E为:
| $ \begin{array}{l} E = \frac{{{\rho _0}}}{{4{\pi ^2}}}\int_{-\infty }^{ + \infty } {\int_{-\infty }^{ + \infty } {P\left( {k, l} \right)\frac{{U \cdot k}}{{|k|}}\sqrt {{N^2}-{{\left( {U \cdot k} \right)}^2}} \cdot } } \\ \sqrt {{{\left( {U \cdot k} \right)}^2} - {f^2}} {\rm{d}}k{\rm{d}}l。\end{array} $ | (8) |
其中:k=(k, l)是波数矢量;P(k, l)是二维地形谱,是底部流速矢量;f是局地惯性频率;N是底部层结,是参考密度。基于线性理论计算各波数处的能量通量取决于地形谱的大小以及速度矢量和波数矢量的相对取向。以每个位置处速度矢量的方向为k轴建立新的局地坐标系,则E的表达式化简为:
| $ \begin{array}{l} E = \frac{{{\rho _0}|U|}}{{4\pi }}\int_{f/U}^{N/U} {{P_*}\left( k \right)\sqrt {{N^2}-{U^2}{k^2}} \cdot } \\ \sqrt {{U^2}{k^2}-{f^2}} {\rm{d}}k。\end{array} $ | (9) |
其中k =(k, l)为新坐标系中的波数;Pk(k)=
通过Nikurashin和Ferrari[26]的模拟表明,背风波辐射的特性由陡度参数ε控制,ε=Nh0/|u|,其中:h0是地形的振幅。根据线性理论,当ε≤εc时,其中εc= 0.7是临界陡度参数,能量通量随ε二次函数增长,当ε≥εc时,一部分背风波被地形阻塞,能量通量饱和不再随ε增加。为了得到能辐射背风波的临界地形,陡度参数可通过为
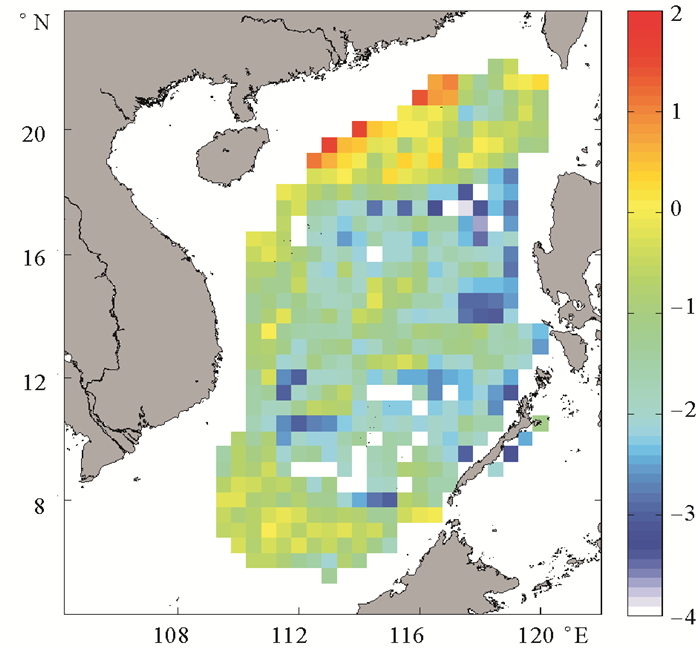
用上述方法对整个南海各个网格点计算背风波产生的能量通量,得到如图 5所示的2013年年平均南海背风波能量通量空间分布。可以看出在北部陆架陆坡处背风波生成的能量较多。
|
(图中为取对数后的结果,单位为mW·m-2。Both the logarithmic scale and the unit of mW·m-2 are used in this figure.) 图 5 2013年南海年平均背风波能量通量空间分布图 Fig. 5 The distribution of meaninternal lee wave energy flux during 2013 in the South China Sea |
对整个南海海域平均后,背风波输入能量通量约为0.5 mW·m-2,结合第2部分给出的南海海域面积,计算可得背风波输入的能量总量约为1.4 GW。假设这些能量全部在近底层500 m耗散为混合提供能量[8],结合第2部分给出的近底层500 m海水质量,则背风波引起的湍动能耗散率约为1.7×10-9 W·kg-1。
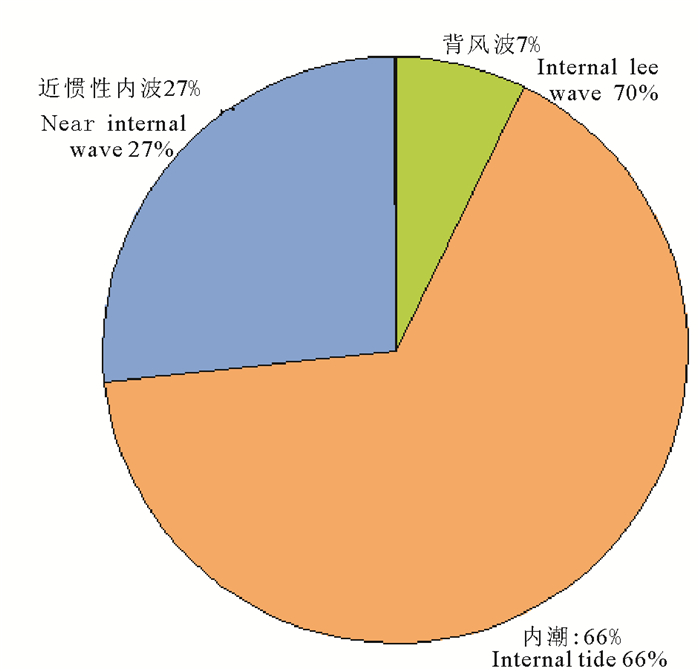
5 结论与讨论本文基于公开数据和前人研究结果,对近惯性内波、内潮、背风波输入南海的能量进行估计,分别给出了三种不同来源的能量在南海所占的比例。在南海中,各部分能量贡献所占比例如图 6所示。其中近惯性内波约贡献能量5.1 GW,占总能量的27%,引起南海上500 m水体的平均湍动能耗散率约为5.7×10-9W·kg-1;内潮贡献能量约为12.6 GW,占总能量的66%,引起南海500 m以深水体的平均湍动能耗散率约为3.7×10-9 W·kg-1;背风波贡献能量约为1.4 GW,占总能量的7%,引起近底500 m范围内水体的湍动能耗散率约为1.7×10-9 W·kg-1。
|
图 6 近惯性内波、内潮、背风波能量贡献比例图 Fig. 6 Energy contributions of near-inertial internal wave, internal tide and internal lee wave to mixing in the SCS |
近惯性内波、内潮、背风波三者输入的能量之和约为19 GW。假设这些能量全部在南海耗散为混合提供能量,则通过计算可知,南海的平均湍动能耗散率约为4.5×10-9 W·kg-1,混合率为2.8×10-3 m2·s-1。这一结果与Yang等[15]基于南海全海域全水深温盐流观测数据,利用参数化方法计算得到的结果基本一致。尽管如此,所选方法的理想假设条件使得计算结果可能存在一定偏差。
本文中使用温盐等数据为同化的再分析数据,数据集的空间或时间分辨率较低,作者对其进行了插值处理。由于混合层内流速是通过平板模型计算得到的,近惯性能量的计算结果可能存在偏差。显然,有力的现场观测是下一步努力的方向。
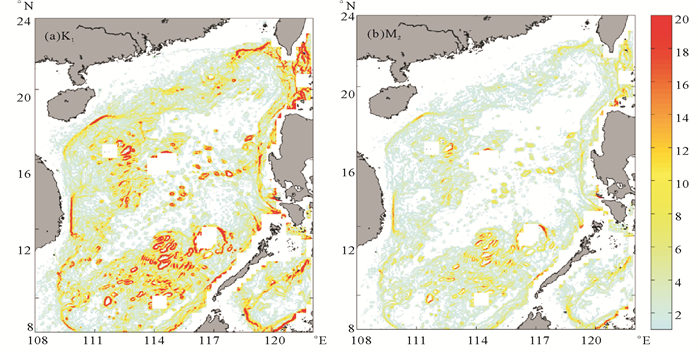
本文中计算内潮与背风波能量通量时使用的线性理论仅适用于亚临界地形,但南海地形复杂,岛礁密布,存在许多超临界地形。图 7为K1内潮、M2内潮对应的超临界地形。尽管半日潮的超临界区域比全日潮的超临界区域要少,但南海有许多地形对于全日潮和半日潮均为超临界的。这里,临界坡度(slope criticality)S/α定义为局部地形坡度与内波射线传播方向的比率。ω和f分别是内潮频率和科氏参数。当S/α>1,为超临界地形;当S/α < 1,为亚临界地形。这些陡峭地形正是内波的重要生成源地。本文根据Nikurashin和Ferrari [26]提出的矫正方法对背风波的计算过程进行了矫正,但对于内潮,还没有很好的矫正方法可以将线性理论应用于陡峭复杂的超临界地形,所以本文中给出的内潮能量通量可能偏小。此外,本文使用的地形数据为卫星数据,其对地形刻画的准确程度直接影响到计算内潮和背风波生成的能量。因此下一步计划利用多波束高分辨率地形观测数据的支持,进一步优化矫正方法,并对这些超临界地形产生的内潮、背风波能量通量进行探讨。
|
(图中仅对超临界地形区域填色。The colors indicate the slope criticality, with only the supercritical area shown.) 图 7 K1内潮(a),M2内潮(b)的超临界地形 Fig. 7 Area of supercritical bathymetry for internal tides (a) K1 and (b) M2 in the SCS |
| [1] |
Munk W, Wunsch C. Abyssal recipes Ⅱ: Energetics of tidal and wind mixing[J]. Deep Sea Research Part Ⅰ: Oceanographic Research Papers, 1998, 45(12): 1977-2010. DOI:10.1016/S0967-0637(98)00070-3
(  0) 0) |
| [2] |
Mac Kinnon J. Oceanography: Mountain waves in the deep ocean[J]. Nature, 2013, 501(7467): 321-322. DOI:10.1038/501321a
(  0) 0) |
| [3] |
Zhao Z, Klemas V, Zheng Q, et al. Remote sensing evidence for baroclinic tide origin of internal solitary waves in the northeastern South China Sea[J]. Geophysical Research Letters, 2004, 31(6): L06302.
(  0) 0) |
| [4] |
Jan S, Lien R C, Ting C H. Numerical study of baroclinic tides in Luzon Strait[J]. Journal of Oceanography, 2008, 64(5): 789-802. DOI:10.1007/s10872-008-0066-5
(  0) 0) |
| [5] |
Liu Z Y, Lozovatsky I. Upper pycnocline turbulence in the northern South China Sea[J]. Science Bulletin, 2012, 57(18): 2302-2306. DOI:10.1007/s11434-012-5137-8
(  0) 0) |
| [6] |
Yang Q, Tian J, Zhao W, et al. Observations of turbulence on the shelf and slope of northern South China Sea[J]. Deep Sea Research Part Ⅰ: Oceanographic Research Papers, 2014, 87: 43-52. DOI:10.1016/j.dsr.2014.02.006
(  0) 0) |
| [7] |
Alford M H, MacKinnon J A, Nash J D, et al. Energy flux and dissipation in Luzon Strait: Two tales of two ridges[J]. Journal of Physical Oceanography, 2011, 41(11): 2211-2222. DOI:10.1175/JPO-D-11-073.1
(  0) 0) |
| [8] |
Buijsman M C, Legg S, Klymak J. Double-ridge internal tide interference and its effect on dissipation in Luzon Strait[J]. Journal of Physical Oceanography, 2012, 42(8): 1337-1356. DOI:10.1175/JPO-D-11-0210.1
(  0) 0) |
| [9] |
Tian J, Yang Q, Zhao W. Enhanced diapycnal mixing in the South China Sea[J]. Journal of Physical Oceanography, 2009, 39(12): 3191-3203. DOI:10.1175/2009JPO3899.1
(  0) 0) |
| [10] |
Zhang S, Xie L, Cao R, et al. Observation of upper-ocean mixing in the region west of the Luzon Strait in Spring[J]. Journal of Coastal Research, 2012, 28(5): 1208-1213.
(  0) 0) |
| [11] |
Klymak J M, Alford M H, Pinkel R, et al. The breaking and scattering of the internal tide on a continental slope[J]. Journal of Physical Oceanography, 2011, 41(5): 926-945. DOI:10.1175/2010JPO4500.1
(  0) 0) |
| [12] |
Laurent L S. Turbulent dissipation on the margins of the South China Sea[J]. Geophysical Research Letters, 2008, 35(23): 399-406.
(  0) 0) |
| [13] |
Xu J, Xie J, Chen Z, et al. Enhanced mixing induced by internal solitary waves in the South China Sea[J]. Continental Shelf Research, 2012, 49: 34-43. DOI:10.1016/j.csr.2012.09.010
(  0) 0) |
| [14] |
Sun H, Wang Q. Microstructure observations in the upper layer of the South China Sea[J]. Journal of Oceanography, 2016, 72(5): 777-786. DOI:10.1007/s10872-016-0371-3
(  0) 0) |
| [15] |
Yang Q, Zhao W, Liang X, et al. Three-dimensional distribution of turbulent mixing in the South China Sea[J]. Journal of Physical Oceanography, 2016, 46(3): 769-788. DOI:10.1175/JPO-D-14-0220.1
(  0) 0) |
| [16] |
Wu J. Wind-stress coefficients over sea surface from breeze to hurricane[J]. Journal of Geophysical Research Atmospheres, 1982, 87(C12): 9704-9706. DOI:10.1029/JC087iC12p09704
(  0) 0) |
| [17] |
Oey L Y, Inoue M, Lai R, et al. Stalling of near-inertial waves in a cyclone[J]. Geophysical Research Letters, 2008, 35(12): 150-152.
(  0) 0) |
| [18] |
D'Asaro E A. The energy flux from the wind to near-inertial motions in the surface mixed layer[J]. Journal of Physical Oceanography, 1985, 15(8): 1043-1059. DOI:10.1175/1520-0485(1985)015<1043:TEFFTW>2.0.CO;2
(  0) 0) |
| [19] |
Alford M H. Internal swell generation: The spatial distribution of energy flux from the wind to mixed layer near-inertial motions[J]. Journal of Physical Oceanography, 2001, 31(8): 2359-2368. DOI:10.1175/1520-0485(2001)031<2359:ISGTSD>2.0.CO;2
(  0) 0) |
| [20] |
Godin G. The Analysis of Tides[M]. Toronto, Buffalo: University of Toronto Press, 1972, 1005-1012.
(  0) 0) |
| [21] |
Gill A E. International Geophysics, 30: Atmosphere-Ocean Dynamics[M]. Burlington: Elsevier, 1982, 258-267.
(  0) 0) |
| [22] |
St. Laurent L, Garrett C. The role of internal tides in mixing the deep ocean[J]. Journal of Physical Oceanography, 2002, 32(10): 2882-2899. DOI:10.1175/1520-0485(2002)032<2882:TROITI>2.0.CO;2
(  0) 0) |
| [23] |
Niwa Y, Hibiya T. Three-dimensional numerical simulation of M2 internal tides in the East China Sea[J]. Journal of Geophysical Research, 2004, 109(C4): 4027. DOI:10.1029/2003JC001923
(  0) 0) |
| [24] |
Melet A, Hallberg R, Legg S, et al. Sensitivity of the ocean state to lee wave-driven mixing[J]. Journal of Physical Oceanography, 2014, 44(3): 900-921. DOI:10.1175/JPO-D-13-072.1
(  0) 0) |
| [25] |
Bell T H. Topographically generated internal waves in the open ocean[J]. Journal of Geophysical Research, 1975, 80(3): 320-327. DOI:10.1029/JC080i003p00320
(  0) 0) |
| [26] |
Nikurashin M, Ferrari R. Radiation and dissipation of internal waves generated by geostrophic motions impinging on small-scale topography: Theory[J]. Journal of Physical Oceanography, 2010, 40(5): 1055-1074. DOI:10.1175/2009JPO4199.1
(  0) 0) |
 2018, Vol. 48
2018, Vol. 48


