内孤立波是发生在海洋密度跃层中的非线性波动,振幅可达上百米、流速最大可达2 m/s。内孤立波主要形式有单个孤立波、多个孤立波组成波包和多个波包组成波群,其产生需要稳定层化的海水、地形的扰动和动力源[1]。内孤立波经过时可引起强剪切流,对海洋结构物、潜体以及密度跃层附近的管道等造成严重威胁。内孤立波在世界各海洋分布广泛,尤其在我国南海频发,对南海开发利用有较大影响。随着计算机技术的发展,使用数值模拟研究内孤立波的方法得到了越来越广泛的应用。
目前学者们为分析内孤立波和海洋结构物的相互作用所构建的内孤立波数值水槽,通常忽略实际海洋中密度跃层的厚度,并将上下层流体简化为两层密度不同的均一流体。文献[2-4]中使用Fluent软件,采用速度入口法,以两层模型定态内孤立波理论解作为边界条件,在数值水槽入口输入上下层平均速度和波面位置以构造内孤立波数值水槽,黄文昊等[5]通过水槽实验分析了各理论的适用条件; 文献[6-7]中使用重力塌陷法,文献[8-9]中使用推板法,通过模拟内波实验室的造波过程构造内孤立波数值水槽; 尤云祥等[10]使用质量源法研究内孤立波生成机理、传播及流场特性。以上构造的内孤立波数值水槽均基于两层模型,李景远等[11]引入密度输运方程,模拟了密度连续分层流体中内孤立波的传播,指出忽略密度跃层的厚度会高估内孤立波的传播速度。两层模型上下层最大流速均出现在流体分界面处,与实测数据存在差异,进而可能误估其载荷,因此有必要建立密度连续变化内孤立波数值水槽。构建密度连化变化数值水槽的关键在于确定数值水槽的密度分布形式和与之相应的边界条件。
物理海洋中对于内波问题的研究十分广泛,积累了大量的观测资料和数值模拟方法,建立了大量可用于分析密度连续层化内孤立波的计算模型。麻省理工学院通用环流模式(MIT general circulation model,MITgcm)是大气海洋的通用数值计算模型,采用有限体积法离散N-S方程,可计算完全非静压项,在内孤立波研究中得到了广泛的应用。Legg等[12]使用MITgcm对潮流经过高斯地形后产生的内潮现象进行了研究,文献[13-18]中使用MITgcm对中国南海的内孤立波生成及传播演化规律进行了研究。蔡树群[19]将内孤立波计算模型的结果与莫里森公式结合计算了内孤立波对圆形桩柱的载荷。MITgcm模拟得到的内孤立波数据能够与观测数据趋势吻合,但MITgcm无直接分析内孤立波与海洋结构物相互作用的功能。
本文提出将MITgcm与Fluent相结合的方法构造密度连续变化内孤立波数值水槽。以潮流经过高斯地形产生的内孤立波为例,通过MITgcm构建二维数值模型,使用南海北部物理海洋数据,由潮地作用生成内孤立波,将Fluent数值水槽置于MITgcm计算域内,提取MITgcm对应位置处的结果数据,利用用户自定义函数(User defined function, UDF)对Fluent数值水槽进行初始化并将入口对应位置的结果数据作为边界条件,通过两侧的速度入口边界使内孤立波进入数值水槽中,在数值水槽与MITgcm计算域的相同位置处可以形成基本一致的内孤立波。本文提供了研究连续层化模型下内孤立波与海洋结构物相互作用的数值造波方法。
1 模拟方法 1.1 MITgcm设置及计算结果本文首先在MITgcm中生成内孤立波,建立二维模型,坐标系x轴放在海平面上。地形设置为高斯型海山模型,海底坐标形式为:
| $ z=-H_0+h_0 \cdot \exp \left(-x^2 /\left(2 L^2\right)\right) 。$ |
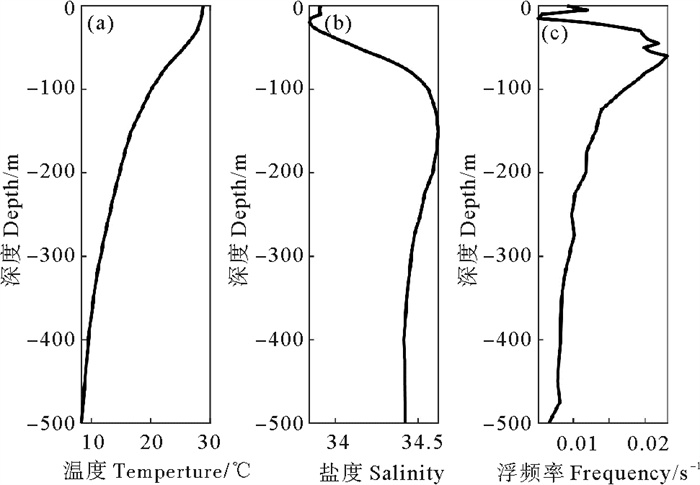
式中:总水深H0=500 m; 海山高h0=230 m; 设置山脊宽度L=15 km。模式水平计算域设置为500 km,水平长度足够大,使得生成的内孤立波不会到达边界。水平方向网格尺寸为250 m,垂向共分为50层,层厚10 m。将模式时间步长设为10 s以满足柯朗-弗里德里希斯-列维(Courant-Friedrichs-Lewy, CFL)条件,共模拟4个太阳主要半日分潮(M2潮)周期。模式初始条件为水平均匀,层化数据选自海洋世界地图(World Ocean Atlas 2018,WOA18)数据集,取南海北部夏季的平均温度和平均盐度(见图 1),将其平均值插值到垂向网格点上。本文取AH=KH=1×10-4 (单位:m2/s),AZ=KZ=0 (单位:m2/s),采用Pacanowski和Philander[20](PP81)混合方案作为参数化方案。开边界采用M2潮流驱动,设置潮流振幅U0分为0.55、0.65、0.75、0.85和1 m/s的五种工况。为了防止在开边界处发生反射,采用海绵边界进行消波,海绵层设置宽度为15 km。模式使用刚盖边界条件,忽略内孤立波与海表面的相互作用,在底部使用自由滑移边界条件。
|
图 1 模式初始温度(a)、盐度(b)及对应浮性频率(c)的垂向结构 Fig. 1 Vertical profiles of initial temperature(a), salinity(b) and corresponding buoyancy frequency(c) |
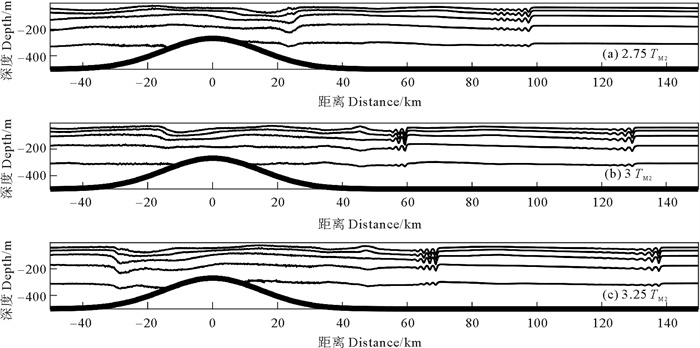
如图 2所示,以U0=0.65 m/s的工况为例,在2.75个M2潮周期时,潮流向右,在海山处等密线出现大幅凹陷; 在3个M2潮周期时,在50 km处出现大幅的内孤立波; 在3.25个M2潮周期时,潮流转为向左,内孤立波传播至70 km处,并进一步演化为内孤立波列。同时,可见上一潮周期生成的内孤立波列从100 km处传播至140 km处,相速度约为1.73 m/s,在传播过程中受到潮流影响,振幅先增大后减小,波包中各内孤立波的间距先增大后减小。在不同潮流振幅下,M2潮均与地形相互作用激起内孤立波,当潮流与内孤立波传播方向一致时内孤立波流速增大,方向相反时流速减小。潮流振幅越大,内孤立波振幅越大,背景潮流对内孤立波流速的影响也越大。
|
( (起始时刻Start time:U0=0.65 m/s; TM2: M2潮周期Period of M2.) ) 图 2 MITgcm运行至(a)2.75TM2、(b)3.0TM2、(c)3.25TM2时刻的等密度线变化 Fig. 2 The isodensity line change of MITgcm running up to (a)2.75 TM2、(b)3.0TM2、(c)3.25TM2 |
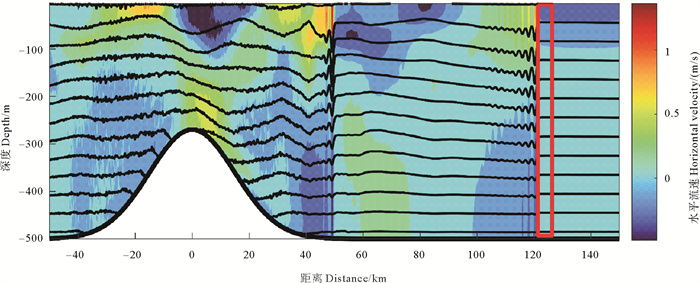
Fluent数值水槽的左侧边界设置在MITgcm计算域121 km处,右侧边界设置在计算域126 km处,内孤立波数值水槽总长5 000 m,如图 3红框所示。各工况基本设置一致,仅初始化条件不同,以U0=0.65 m/s工况的衔接初始时刻为例(见图 3)进行说明。在第3个M2潮周期时,由潮地作用生成的内孤立波波包的头波到达数值水槽左侧边界,以此刻作为Fluent数值水槽计算的起始时刻,以1 200 s作为终止时刻,以使得内孤立波可以完全进入数值水槽中。起始时刻数值水槽内部水平流速在靠近海表面处为正向,靠近海底处为反向,最大流速约0.2 m/s,等密线水平变化较小。各工况数值水槽起始时刻的流速场和密度场均受到背景潮流的影响,与两层模型静止稳定的初始条件明显不同。
|
( (起始时刻U0=0.65 m/s; 黑线表示等密度线; 红色方框表示Fluent数值水槽位置。Start time U0=0.65 m/s; Black lines mean density; Red box means the Fluent numerical water tank position.) ) 图 3 MITgcm与Fluent数值水槽位置示意图 Fig. 3 MITgcm and Fluent numerical tank position diagram |
在Fluent软件中建立水平向5 000 m,垂向500 m的数值水槽,坐标系放在海平面上,以左侧边界为X轴起点。水平网格尺寸取为内孤立波特征长度的十五分之一,垂向网格尺寸在浮力频率最大处做加密处理。
采用流体体积(Volume of fluid,VOF)法模拟密度连续变化的水体,通过求解每一相流体的体积分数来确定每一控制体的密度大小。设置第一相流体密度为1 020 kg/m3,第二相流体密度为1 030 kg/m3,两者动力黏度均为1.003×10-3 kg/(m·s)。由于内孤立波的流线曲率较大,本文选取RNG k-ε型湍流模型。
数值水槽的上、下边界条件均取为固壁边界条件,左、右两侧取为速度入口边界条件。提取MITgcm计算结果中对应数值水槽边界处的密度和速度时程数据,编写UDF文件,将时程数据导入到数值水槽两侧边界。
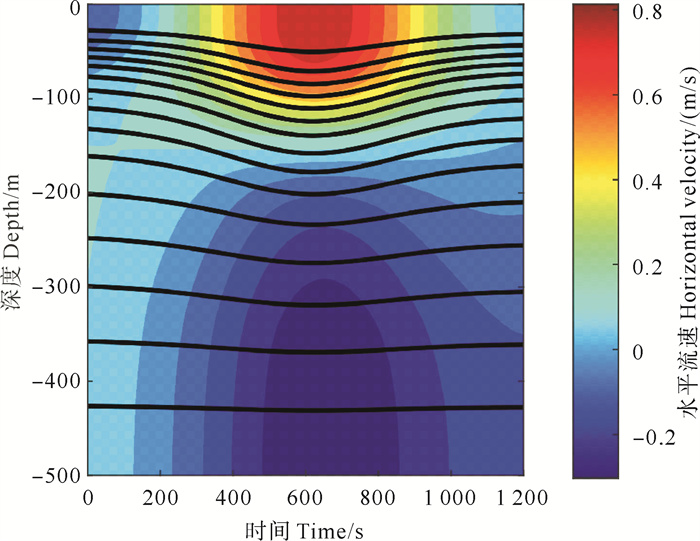
以U0=0.65 m/s工况的数值水槽左侧边界为例,在MITgcm计算结果对应位置处的密度和水平速度时程数据如图 4所示。在衔接620 s左右时,内孤立波波谷到达数值水槽左侧边界,内孤立波上层水平流速方向向右,与内孤立波传播方向一致,最大流速达0.8 m/s,下层流速方向向左,与内孤立波传播方向相反,达-0.25 m/s,等密线达到最大振幅约48.9 m。
|
( (黑线表示等密度线。Black lines mean density. U0=0. 65 m/s) ) 图 4 Fluent左侧入口边界条件随时间变化数据 Fig. 4 Fluent entry boundary conditions on the left side change with time |
在计算开始前,需将MITgcm计算域中的流场信息作为初始条件设置在Fluent中。选择基于压力的二阶隐式时间离散的瞬态求解器,压力速度耦合方式使用PISO,压力插值选择体积力加权法,对流项及输运方程采用一阶迎风格式进行离散。迭代时间步长取0.5 s,为保证计算精度,每个时间步内最大迭代次数30次。
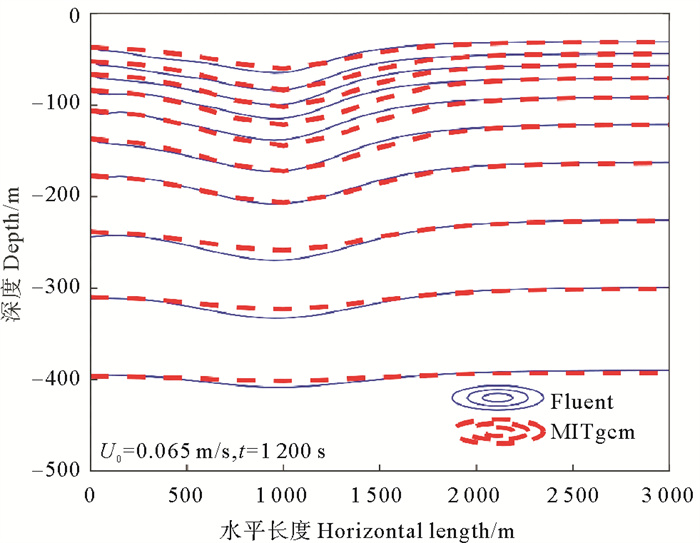
2 结果分析 2.1 等密度线振幅以U0=0.65 m/s的工况为例,衔接计算结束时等密度线对比如图 5所示。内孤立波传播至距左侧入口约1 000 m处,相速度约1.68 m/s,最大振幅50.21 m。等密度线在水深小于200 m时,Fluent计算结果与MITgcm计算结果吻合度高,水深大于200 m时,Fluent计算的振幅略大于而MITgcm计算的振幅。在各工况中均出现此现象,原因在于两者对密度的处理方法不同,MITgcm使用海水状态方程计算密度,考虑到密度受压强影响,而Fluent使用不可压缩假设,在深水中密度随水深变化缓慢,浮力频率小,两者差异明显。
|
图 5 密度模拟结果对比 Fig. 5 Contrast of density simulation results |
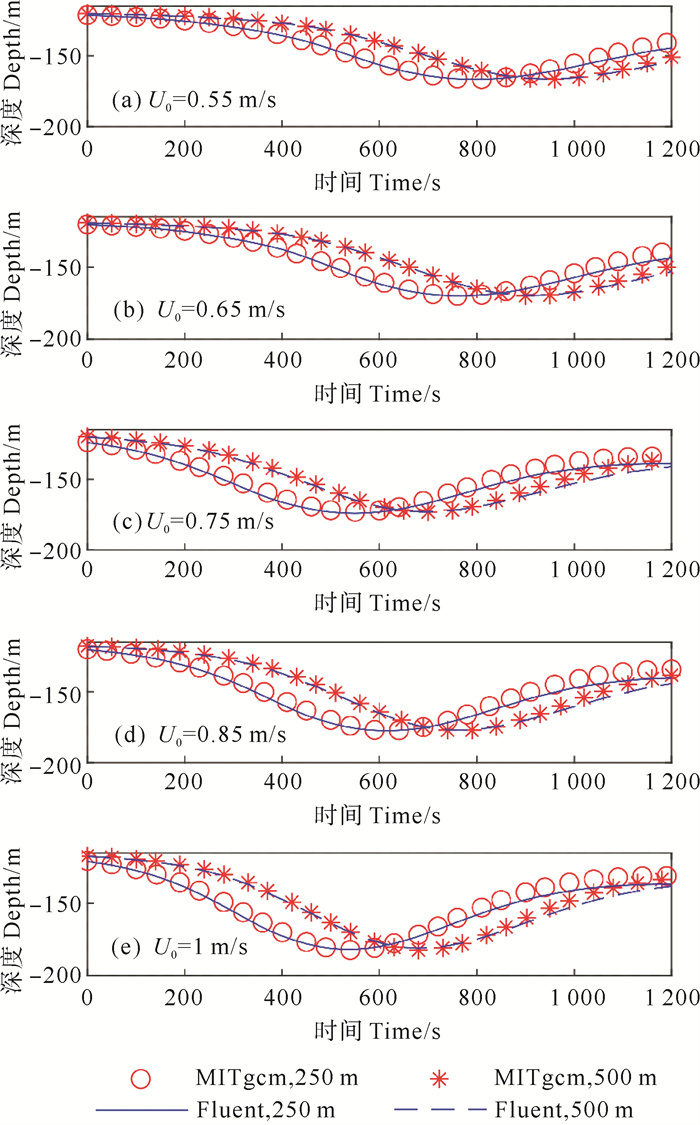
提取各工况1 025.5 kg/m3等密度线在距入口250和500 m处的时程数据,对比如图 6所示。各工况中波谷到达时间不同,这是由于不同工况下开始衔接时内孤立波距入口的位置有差异,并且各工况内孤立波传播速度也有差异导致的。在各工况中,Fluent计算结果均能同MITgcm计算结果吻合,总体偏差较小。
|
图 6 1 025.5 kg/m3等密线时程数据 Fig. 6 1 025.5 kg/m3 isodensity line time-history data |
将等密度线最低深度与初始深度之差作为振幅,统计各工况1 025.5 kg/m3等密度线振幅如表 1所示。可见随着潮流振幅增加,内孤立波振幅基本增大。在内孤立波由距入口250 m传播至距入口500 m的过程中,内孤立波振幅也在演变,呈增大趋势。在各工况中,数值水槽与MITgcm计算域的相同位置处的内孤立波振幅偏差小。
|
|
表 1 1 025.5 kg/m3等密线振幅数据 Table 1 1 025.5 kg/m3 isodensity line amplitude data |
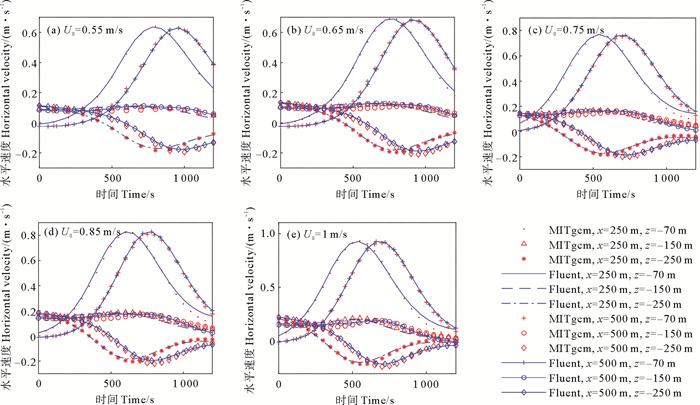
统计各工况在距入口250和500 m处, 水深70、150、250 m处水平速度时程计算结果(见图 7)。当内孤立波到达时各水深水平流速同时到达最值,水深70和150 m处流速相反,可形成较大的水平流速垂向剪切作用。在水深150 m附近的水平流速在全时程中始终变化不大。
|
图 7 水平速度时程数据 Fig. 7 Horizontal velocity time-history data |
以U0=0.75 m/s工况为例(见图 7(c))。在初始时刻,水深70 m处流速接近零,水深150和250 m处流速向右,最大不超过0.18 m/s。随着内孤立波到来,上层流速方向转为向右,最大达0.76 m/s,下层流速方向转为向左,达-0.18 m/s。Fluent计算结果能够较好地反映出MITgcm计算结果中水平流速的时程变化,仅水深70 m处在内孤立波经过后水平流速有最大0.05 m/s的偏差。
图 7(a)—(e)对比分析可知,随着潮流振幅U0的增加,在水深70 m附近的最大水平流速增加,但在水深250 m附近的最大水平流速基本不变。在各工况各水深中,Fluent计算结果与MITgcm计算结果吻合。
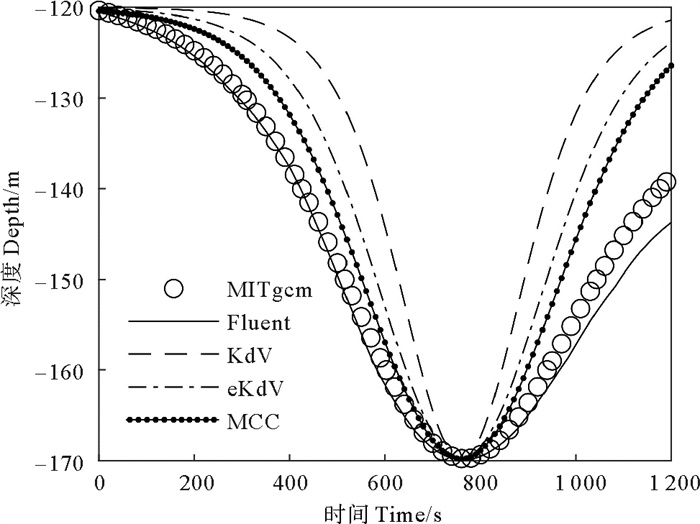
2.3 两层模型以U0=0.65 m/s工况为例对比两层模型理论结果。提取Fluent数值水槽的浮频率分布,以最大浮频率和最小浮频率的平均值所在深度为密度跃层的上、下位置,取密度跃层下层位置为两层模型的分界面,可得上层水深120 m,平均密度1 022.1 kg/m3,下层水深380 m,平均密度1 027.6 kg/m3。理论解振幅取对应深度处等密度线振幅为-49.8 m。
在距入口250 m处波面对比结果如图 8所示。内孤立波波谷在衔接至760 s时到达距入口250 m处,两层模型的各理论波面均与MITgcm的计算结果有偏差。Korteweg de Vries(KdV)理论波长最短,波形最为陡峭,拓展的KdV(Extended KdV, eKdV)理论和Miyata-Choi-Camassa(MCC)理论波长稍宽,波形也较为平缓。与两层模型结果对比,MITgcm计算结果所得的波形更为平缓,并且在内孤立波经过后出现波面下降的现象,两侧并不对称。在各理论中,MCC理论结果与MITgcm计算结果最为接近。Fluent计算结果在波谷到达前能够与MITgcm结果吻合,在波谷到达后出现偏差,波面下降更大。
|
( (U0=0.65m/s, x=250 m) ) 图 8 1 025.5 kg/m3等密线时程数据对比, Fig. 8 Comparison of 1 025.5 kg/m3 isodensity line time-history data |
水平流速在垂向分布对比结果如图 9所示。两层模型理论结果与MIT gcm计算结果存在较大偏差,其中MCC理论的偏差最小。在衔接至500 s时,由MCC理论得到的上层水平流速为0.33 m/s,在水深80 m以上均小于MITgcm结果,在水深350 m以下则同MITgcm结果接近。在750 s时,波谷到达距入口250 m附近,由MCC理论得到的上层水平流速达0.73 m/s,与MITgcm在表层处的水平流速相当。在衔接至1 000 s时,内孤立波已经通过距入口250 m处,由MCC理论得到的上层水平流速回落至0.34 m/s,下层水平流速回落至-0.14 m/s,均与MITgcm计算结果存在较大差异。MCC理论解在两层流体分界面处存在水平流速迅速变化的跃层,但MITgcm中水平流速不会在某个水深处出现强烈的垂向变化,与实际海洋中内孤立波流速分布规律接近。由MCC理论得到的水平流速同MITgcm计算得到的水平流速在靠近上、下边界处偏差小,在分界层附近偏差较大。
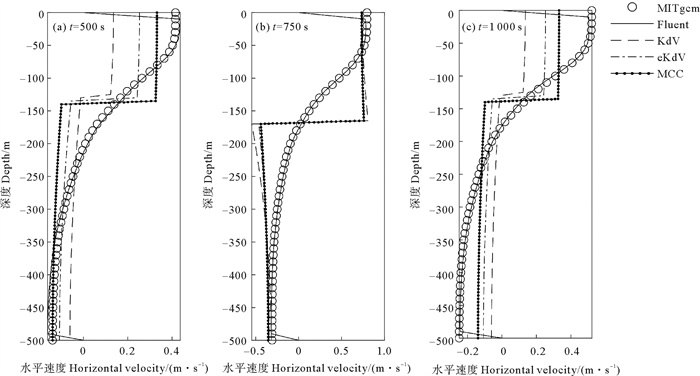
|
图 9 距入口250 m处不同时刻水平速度垂向分布(U0=0.65 m/s) Fig. 9 Vertical distribution of horizontal velocity at different time at 250 m from the entrance(U0=0.65 m/s) |
数值水槽对水平流速在垂向分布的计算结果可以同各时刻的MITgcm计算结果吻合,仅在上、下边界处会由于固壁条件差异而出现偏差。
各工况均发现模拟得到的水平流速分布与两层模型不同,上、下层流速极值并未出现在同一水深。这是由于两层模型将浮频率较大的密度跃层厚度忽略,密度在跃层附近迅速变化,导致水平流速在密度跃层处的垂向变化过于剧烈,并且MITgcm水平流速的计算结果受到了背景流影响。
3 结论(1) 本文使用MITgcm生成内孤立波,将Fluent数值水槽置于MITgcm计算域内,提取MITgcm的结果数据对Fluent数值水槽进行初始化并将入口对应MITgcm位置处的结果数据作为边界条件,实现了两者的衔接。使用这一模拟方法对给定海域不同潮流振幅下的算例进行计算得到的结果表明:数值水槽中的内孤立波同MITgcm相同位置处的内孤立波水平流速基本一致,且等密度线在密度跃层处偏差小,可以认为在数值水槽中形成了同MITgcm计算域相同位置处对应的内孤立波。本文为内孤立波数值水槽提供了一种确定密度分布形式和边界条件的模拟方法。
(2) 本文中使用MITgcm模拟结果作为边界条件,而MITgcm可以使用观测的密度分布形式、潮流和地形生成内孤立波,相较于在数值水槽入口直接使用两层模型定态内孤立波理论解作为边界条件,使用范围更加广泛。进一步可以借鉴物理海洋中对实际海域的三维数值模拟结果,统计海洋结构物布置地的内孤立波载荷,为分析海洋工程问题提供工具。
(3) 算例结果表明,随着潮流振幅增加,内孤立波振幅和最大水平流速均增大。本文模拟方法得到的内孤立波水平流速垂向分布较为连续,没有出现两层模型水平流速在分界面处突变的现象。
| [1] |
方欣华, 杜涛. 海洋内波基础和中国海内波[M]. 青岛: 中国海洋大学出版社, 2004: 1-281. Fang X H, Du T. Fundamental of Oceanic Internal Waves and Internal Waves in the China Seas[M]. Qingdao: China Ocean University Press, 2004: 1-281. (  0) 0) |
| [2] |
陈钰, 朱良生. 基于FLUENT的海洋内孤立波数值水槽模拟[J]. 海洋技术, 2009, 28(4): 72-75. Chen Y, Zhu L S. Numerical wave tank simulation of oceanic internal solitary waves based on FLUENT[J]. Ocean Technology, 2009, 28(4): 72-75. (  0) 0) |
| [3] |
刘碧涛, 李巍, 尤云祥, 等. 内孤立波与深海立管相互作用数值模拟[J]. 海洋工程, 2011, 29(4): 1-7. Liu B T, Li W, You Y X, et al. Numerical simulation of interaction of internal solitary waves with deep-sea risers[J]. The Ocean Engineering, 2011, 29(4): 1-7. (  0) 0) |
| [4] |
高原雪, 尤云祥, 王旭, 等. 基于MCC理论的内孤立波数值模拟[J]. 海洋工程, 2012, 30(4): 29-36. Gao Y X, You Y X, Wang X, et al. Numerical simulation for the internal solitary wave based on MCC theory[J]. The Ocean Engineering, 2012, 30(4): 29-36. (  0) 0) |
| [5] |
黄文昊, 尤云祥, 王旭, 等. 有限深两层流体中内孤立波造波实验及其理论模型[J]. 物理学报, 2013, 62(8): 354-367. Huang W H, You Y X, Wang X, et al. Wave-making experiments and theoretical models for internal solitary waves in a two-layer fluid of finite depth[J]. Acta Physica Sinica, 2013, 62(8): 354-367. (  0) 0) |
| [6] |
Terez D E, Knio O M. Numerical simulations of large-amplitude internal solitary waves[J]. Journal of Fluid Mechanics, 1998, 362: 53-82. DOI:10.1017/S0022112098008799 (  0) 0) |
| [7] |
叶潇潇, 游景皓, 宋金宝. 实验室造波条件对内孤立波发展影响的直接数值模拟[J]. 海洋与湖沼, 2021, 52(3): 573-583. Ye X X, You J H, Song J B. Direct numerical simulation of the effect of laboratory wave-making conditions on the development internal solitary waves[J]. Oceanologia et Limnologia Sinica, 2021, 52(3): 573-583. (  0) 0) |
| [8] |
付东明, 尤云祥, 李巍. 两层流体中内孤立波与潜体相互作用数值模拟[J]. 海洋工程, 2009, 27(3): 38-44. Fu D M, You Y X, Li W. Numerical simulation of internal solitary waves with a submerged body in a two-layer fluid[J]. The Ocean Engineering, 2009, 27(3): 38-44. (  0) 0) |
| [9] |
苗得胜, 郭海燕, 赵婧, 等. 内孤立波数值模拟方法研究[J]. 中国海洋大学学报(自然科学版), 2016, 46(10): 123-128. Miao D S, Guo H Y, Zhao J, et al. Study of numerical simulation method of internal solitary waves[J]. Periodical of Ocean University of China, 2016, 46(10): 123-128. (  0) 0) |
| [10] |
王旭, 林忠义, 尤云祥. 两层流体中内孤立波质量源数值造波方法[J]. 上海交通大学学报, 2014, 48(6): 850-855. Wang X, Lin Z Y, You Y X. A mass source method for numerically generating internal solitary waves in two-layer fluid[J]. Journal of Shanghai Jiao Tong University, 2014, 48(6): 850-855. (  0) 0) |
| [11] |
李景远, 张庆河, 陈同庆. 密度连续变化水体内孤立波数值模拟研究[J]. 天津大学学报(自然科学与工程技术版), 2021, 54(2): 161-170. Li J, Zhang Q H, Chen T Q. Numerical simulation of internal solitary wave incontinuously stratified fluid[J]. Journal of Tianjin University (Science and Technology), 2021, 54(2): 161-170. (  0) 0) |
| [12] |
Legg S, Klymak J. Internal hydraulic jumps and overturning generated by tidal flow over a tall steep ridge[J]. Journal of Physical Oceanography, 2008, 38(9): 1949-1964. (  0) 0) |
| [13] |
Vlasenko V, Stashchuk N, Guo C, et al. Multimodal structure of baroclinic tides in the South China Sea[J]. Nonlinear Processes in Geophysics, 2010, 17(5): 529-543. (  0) 0) |
| [14] |
Guo C, Chen X. Numerical investigation of large amplitude second mode internal solitary waves over a slope-shelf topography[J]. Ocean Modelling, 2012, 42: 80-91. (  0) 0) |
| [15] |
Li D, Chen X, Liu A. On the generation and evolution of internal solitary waves in the northwestern South China Sea[J]. Ocean Modelling, 2011, 40(2): 105-119. (  0) 0) |
| [16] |
李德磊. 南海西北部内孤立波的数值模拟研究[D]. 青岛: 中国海洋大学, 2012. Li D L. Numercal Simulations of Internal Solitary Waves in the Northwestern South China Sea[D]. Qingdao: Ocean University of China, 2012. (  0) 0) |
| [17] |
龚延昆, 陈学恩. 南海北部内孤立波绕东沙岛传播特性的数值研究[J]. 中国海洋大学学报(自然科学版), 2016, 46(12): 1-8. Gong Y K, Chen X E. Modelling of internal solitary waves propagating over Dongsha Atoll in the South China Sea[J]. Periodical of Ocean University of China, 2016, 46(12): 1-8. (  0) 0) |
| [18] |
张哲恩, 陈学恩. 南海北部内孤立波非线性陡斜的数值研究[J]. 中国海洋大学学报(自然科学版), 2017, 47(11): 1-8. Zhang Z E, Chen X E. Numerical modelling of internal solitary waves nonlinear steepen in the Northern South China Sea[J]. Periodical of Ocean University of China, 2017, 47(11): 1-8. (  0) 0) |
| [19] |
蔡树群. 内孤立波对南海石油平台圆形桩柱的载荷研究及其风险防范[M]. 北京: 科学出版社, 2021: 57-95. Cai S Q. Study on the Load Exerted by Internal Solitary Waves on Cylindrical Piles of Oil Platform in the South China Sea and Risk Prevention[M]. Beijing: Science Press, 2021: 57-95. (  0) 0) |
| [20] |
Pacanowski R C, Philander S G H. Parameterization of vertical mixing in numerical models of tropical oceans[J]. Journal of Physical Oceanography, 1981, 11(11): 1443-1451. (  0) 0) |
 2023, Vol. 53
2023, Vol. 53

