随着石油、天然气等自然资源开采向深海进发,锚泊线作为锚泊系统的重要组成部分,动力特性分析一直是个具有挑战性的研究课题。传统的悬链线式锚泊线具有自重大、水平刚度小的缺点,不适合深海油气平台的固定,因此串联浮筒多组分锚泊线凭借诸多优势得到了广泛应用。
深海环境复杂多变,诸如风暴潮和巨浪等,导致油气平台产生剧烈运动,在这个过程中,会造成串联浮筒多组分锚泊线出现局部张力为零的情况,即发生了松弛-张紧现象。松弛-张紧现象的发生会产生冲击张力,这种冲击张力比一般动态荷载大得多[1],对串联浮筒多组分锚泊线的结构造成很大破坏,容易造成锚泊线断裂,严重影响锚泊线的使用寿命,因此对串联浮筒多组分锚泊线的松弛-张紧特性研究就显得意义重大。
在对锚泊线动力特性分析方面,Huang等[2]基于质量-弹簧模型分析预测了锚泊线在松弛-张紧现象下的冲击载荷,并与实验进行了对比,验证数值模拟的可靠性。Plaut等[3]基于只抗拉不抗压无质量弹簧模型,对刚性锚泊圆柱体进行了分析,发现锚泊线发生松弛-张紧现象时会产生冲击张力。Pascoal等[4]研究发现锚泊线在松弛-张紧状态下,跨越了从几何构型到弹性变形的过程。唐友刚等[5]考虑了锚泊线具有黏-弹特性,对深海锚泊线由松弛-张紧现象引起的冲击荷载进行了分析。张素侠等[6-7]对锚泊线进行实验研究,研究发现在发生松弛-张紧现象时会产生冲击张力,并且分析了锚泊线顶端运动和锚泊线自身特性对冲击张力的影响。曹阳[8]对锚泊线进行了水下冲击载荷的实验研究,分析了不同条件下松弛-张紧现象发生的条件。Palm等[9]开发一种自适应非连续伽辽金法来模拟锚泊线的张力,通过控制该方法中的网格尺寸h和多项式阶数p的数值,可以非常准确的计算出因松弛-张紧而产生的冲击张力。
在对串联浮筒锚泊线的动力特性分析方面,Shin等[10]研究发现当初始预张力不变时,串联浮筒能够造成锚泊线顶部张力和恢复力明显增加。王道能[11]基于锚泊线动力控制方程和浮筒的受力分析,建立了串联浮筒锚泊系统的动力控制方程,通过对方程求解,分析了锚泊线上特殊点的受力情况。Mavrakos等[12]研究了顶端沿锚泊线切向正弦激励下,浮筒不同位置、数量、尺寸对锚泊线动张力的影响,发现浮筒在适当的位置能减小动张力。Yuan等[13]研究了在锚泊线上串联浮筒和重块下的力学性能,发现浮筒和重块的位置、大小对锚泊线张力影响很大。Yan等[14]研究了在百年一遇的海况下,浮筒对锚泊线动张力和平台运动的影响。乔东升等[15]在串联浮筒锚泊线顶端施加水平运动和竖向运动的力,分析并总结了锚泊系统的动张力和阻尼的规律。闫俊等[16]研究了在锚泊线上串联浮筒对锚泊线阻尼特性的影响。李效民等[17]通过运用向量式有限元方法对串联浮筒锚泊线静力位形和内力进行了研究,分析了在不同浮筒质量和位置下的形态、张力值和回复力等特性。王瑞华等[18]研究了不同浮筒参数对锚泊线松弛-张紧现象以及冲击放大系数的影响,但仅仅对浮筒浮重进行了分析。
由各种多段线、浮筒组合而成的多组分锚泊系统,具有比单组分锚泊系统更好的优越性[20],被认为是最适合应用于深海和恶劣环境的一种锚线形式[19]。它通过改变锚泊线的组成以及串联浮筒参数,可以减小锚泊线的张力。因此多组分锚泊线也被用来扩展到混合系泊系统之中[21]。串联浮筒对扩大悬链式多组分锚泊线在深水和超水深领域的应用具有重要意义,但是当前人们对串联浮筒多组分锚泊线的松弛-张紧特性还未进行深入研究。
因此,本文基于向量式有限元方法,建立底端锚固、顶端做正弦运动的串联浮筒多组分锚泊线动力分析模型,分析不同振幅和频率以及不同浮筒参数下的松弛-张紧现象,得出具有规律性的结论,为海洋浮式平台的稳定和安全提供借鉴和指导意义。
1 动力分析模型的建立与求解 1.1 模型建立向量式有限元方法是将向量力学理论和数值计算进行结合,以此对结构构件进行力学分析。该方法主要概念有点值描述、途径单元和虚拟的逆向运动[22-23]。点值描述是将结构构件离散为有限数量的质点,把空间质点的位置和作用在点上的载荷作为点值描述对象,空间点之间通过内插函数进行计算。途径单元是结构构件上任意空间点在某一时刻的对应位置。在经历一段时间以后到达另一位置所依据的标准化方程[22]。结构构件的运动采用质点运动方程进行描述,由于内力计算和纯变形有关,通过虚拟的逆向运动进行结构构件纯变形的计算,从而求得结构构件内力。
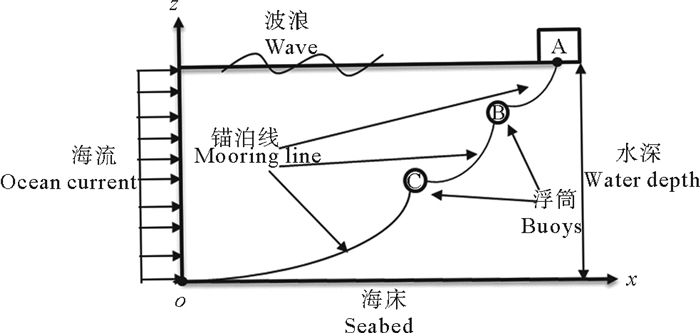
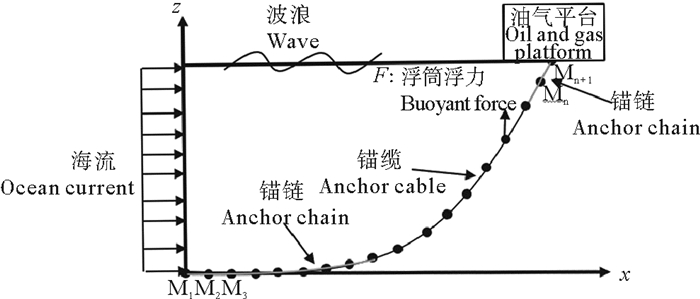
如图 1所示为串联浮筒多组分锚泊线系统示意图,周围受到波浪、海流等环境荷载作用。把串联浮筒多组分锚泊线离散为一组有限数量的质点,将这些质点从锚泊线的底端到顶端依次编号(见图 2),这些质点通过无质量的杆单元进行连接,并且外力施加到质点上,质点间的内力通过杆单元进行传递,把浮筒浮重假设为一个力F作用在点上。同时,以串联浮筒多组分锚泊线底端为原点,x轴位于锚泊线所在的平面内,z轴与海平面垂直并指向海平面,y轴通过右手法则确定为垂直x-z平面向内。在该模型中油气平台的运动可直接作为边界条件施加到锚泊线的顶端。
|
((A: 油气平台Oil and gas platform; B: 球形浮筒Spherical-buoy; C: 球形浮筒Spherical-buoy) ) 图 1 串联浮筒多组分锚泊系统示意图 Fig. 1 Schematic diagram of multi-component mooring system of series buoys |
|
图 2 串联浮筒多组分锚泊线向量式有限元模型 Fig. 2 Vector form intrinsic finite element model of multi-component mooring line of series buoys |
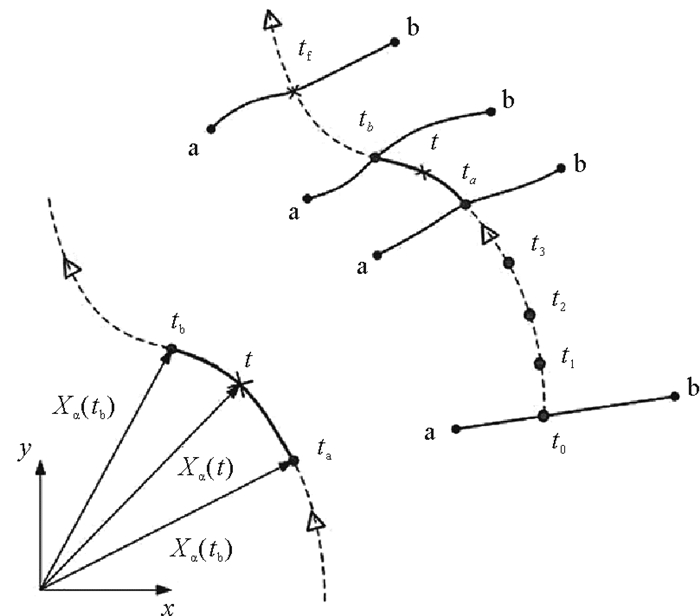
途径单元如图 3所示,即某一空间点i在t0到tf时间间隔内的运动轨迹和位置向量。其中:t0为初始时刻;tf为终结时刻;t1、t2、t3、t为t0~tf之间某一时刻;Xα为该空间质点在不同时刻对应的空间位置。取其中一组微段(ta为初始时间,tb为终结时间)。分析此空间质点在该时间段由Xα(ta)到Xα(tb)的变化过程。
|
图 3 途径单元 Fig. 3 Path element |
对空间问题,质点有3个平移自由度,考虑结构阻尼,各点遵循牛顿定律,质点的控制方程为:
| $ m_i \frac{\mathrm{d}^2}{\mathrm{~d} t^2}\left[\begin{array}{l} \boldsymbol{x}_i \\ \boldsymbol{y}_i \\ \boldsymbol{z}_i \end{array}\right]=\left[\begin{array}{l} \boldsymbol{P}_{i x} \\ \boldsymbol{P}_{i y} \\ \boldsymbol{P}_{i z} \end{array}\right]+\sum\limits_{\alpha=1}^n\left(\left[\begin{array}{l} \boldsymbol{P}_{\alpha x} \\ \boldsymbol{P}_{\alpha y} \\ \boldsymbol{P}_{\alpha z} \end{array}\right]+\left[\begin{array}{l} \boldsymbol{f}_{\alpha x} \\ \boldsymbol{f}_{\alpha y} \\ \boldsymbol{f}_{\alpha z} \end{array}\right]\right)_i。$ | (1) |
式中:mi是i质点和与之相连杆单元的等效质量之和;xi、yi、zi为i质点的位置向量;Pi是直接作用在质点i上的集中外力;Pαx、Pαy、Pαz是杆单元提供的x轴方向等效外力、y轴方向的等效外力、z轴方向的等效外力; fαx、fαy、fαz是杆单元提供的x轴方向等效内力、y轴方向的等效内力、z轴方向的等效内力;n是与质点相连接杆单元数目。
1.3 结构单元变形和内力计算途径单元将杆件的变形过程分解为一系列时间点的集合,单独对时间片段进行求解,每个结构单元都是相对独立的,这样便可以用小变位和小变形理论分析大变形问题。
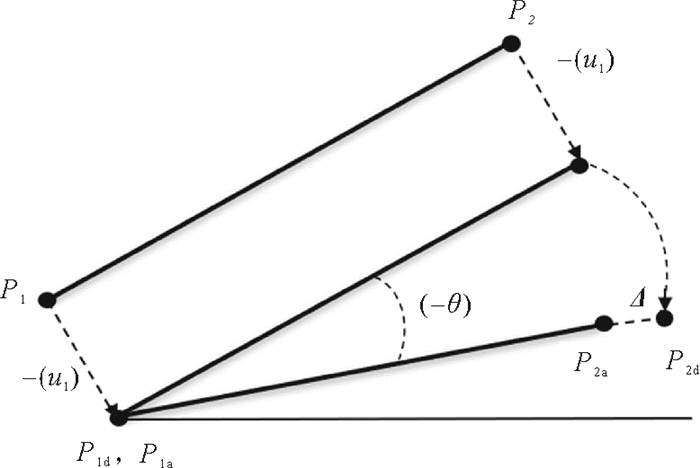
多组分锚泊线结构单元的内力求解与纯变形相关联,向量式有限元通过虚拟的逆向运动来处理纯变形,通过建立局部坐标系同时利用虚功原理计算内力的大小和方向,再经过正向运动让内力回到原来的位置。图 4为单元的逆向运动示意图,初始时刻ta的位置为P1-P2,以ta位置为基础构架,途径单元(ta-tb)内在任意时刻t的位置向量发生平移(-u1)和转动(-θ)内的逆向运动得到杆件的纯变形Δ。
|
图 4 单元的逆向运动示意图 Fig. 4 Schematic diagram of reverse movement of unit |
锚泊线作为柔性结构构件,杆件的轴力根据材料力学相关理论进行计算得到:
| $ \hat{\boldsymbol{f}}=\hat{\sigma} A=\frac{A E}{l_0} \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}。$ | (2) |
式中: E为弹性模量;l0为单元长度;Δ为单元变形;A为单元截面积;
将式(2)写成节点内力:
| $ \left\{\begin{array}{l} \hat{\boldsymbol{f}}_1=\hat{\boldsymbol{f}}_{1, 0}+\hat{f}\left(-\hat{\boldsymbol{e}}_x\right)=\left[-\left(\sigma^{(0)} A\right)-\frac{A E}{l_0} \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}\right] \hat{\boldsymbol{e}}_x \\ \hat{\boldsymbol{f}}_2=\hat{\boldsymbol{f}}_{2, 0}+\hat{f}\left(+\hat{\boldsymbol{e}}_x\right)=\left[+\left(\sigma^{(0)} A\right)+\frac{A E}{l_0} \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}\right] \hat{\boldsymbol{e}}_x \end{array}\right\}。$ | (3) |
式中:$\hat{\boldsymbol{f}}_1$和$\hat{\boldsymbol{f}}_2$分别是虚拟杆件的节点P1d、P2d在时刻t的内力向量;$\hat{\boldsymbol{f}}_{1, 0}$和$\hat{\boldsymbol{f}}_{2, 0}$分别为P1a和P2a的节点内力。最后通过正向运动回到初始位置,从而求得t时刻的节点内力:
| $ \left\{\begin{array}{l} -\boldsymbol{f}_1=\boldsymbol{f}_2=f(\boldsymbol{e}) \\ f=\left(\sigma_0 A\right)+\hat{f}=\left(\sigma_0 A\right)+\frac{A E}{l_0}(\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}) \end{array}\right.。$ | (4) |
式中f1和f2分别指质点提供的杆件元节点P1和P2的内力。
1.4 水动力荷载锚泊线的长度远大于自身直径,波浪和海流对锚泊线的作用力主要是黏滞效应引起的拖曳力和附加质量效应引起的惯性力组成,因此采用莫里森方程计算水动力[24-25],作用于锚泊线上的波浪和海流作用可以等效到锚泊线各质点上,对单位长度锚泊线所受到的水动力为:
| $ \begin{gathered} {\boldsymbol{f}}_{\text {sea }}=\rho_{\mathrm{sea}} A \dot{\boldsymbol{U}}_{\mathrm{n}}+C_a \rho_{\text {sea }}\left(\dot{\boldsymbol{U}}_{\mathrm{n}}-\ddot{r}\right)+ \\ 0.5 \rho_{\mathrm{sea}} C_{\mathrm{d}} D\left(\boldsymbol{U}_{\mathrm{n}}-\dot{r}\right)\left|\boldsymbol{U}_{\mathrm{n}}-\dot{r}\right| 。\end{gathered} $ | (5) |
式中:fsea是水动力;ρsea是海水密度;A是锚泊线横截面积A=πD2/4;D是锚泊线直径;Un、$\dot{\boldsymbol{U}}_{\mathrm{n}}$分别是倾斜锚泊线法线方向的水质点速度矢量和加速度矢量;$\mathit{\boldsymbol{\dot r}}、\mathit{\boldsymbol{\ddot r}}$分别是正交方向锚泊线速度矢量和加速度矢量;Ca、Cd分别是附加质量系数和拖曳力系数。
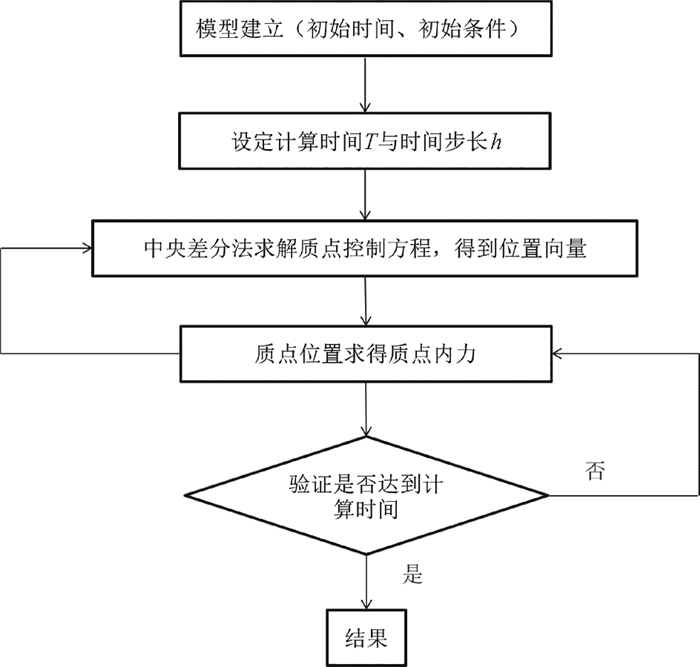
1.5 控制方程的求解为了避免隐式差分可能带来的迭代和收敛等问题,本文采用中央差分的显式时间积分法,对质点运动循环和内力循环进行计算。求解步骤分为三步:首先由i点第n-1步和第n步的位移向量Xn-1,i、Xn,i计算出第n+1步位移向量Xn+1,i;其次根据Xn-1,i计算该点空间点上作用的内力;然后用第n步代替第n-1步,用n+1步代替n步,更新位置向前,重复上述步骤,循环计算,直至完成分析,计算流程图如图 5所示。质点的速度和加速度为:
| $ \dot{\boldsymbol{X}}_i=\frac{\dot{\boldsymbol{X}}_{n+1, i}-\dot{\boldsymbol{X}}_{n-1, i}}{2 h}, \ddot{\boldsymbol{X}}_i=\frac{\boldsymbol{X}_{n+1, i}+\boldsymbol{X}_{n-1, i}-2 \boldsymbol{X}_{n, i}}{h^2} 。$ | (6) |
|
图 5 向量式有限元计算流程图 Fig. 5 Calculation process of vector form intrinsic finite element |
式中:Xn-1,i、Xn,i、Xn+1,i分别为i质点在第n-1步、n步、n+1步的位移;h为时间步长。将式(6)带入式(1)可得对应的拆分公式:
| $ \begin{aligned} & {\left[\begin{array}{l} \boldsymbol{x}_{n+1, i} \\ \boldsymbol{y}_{n+1, i} \\ \boldsymbol{z}_{n+1, i} \end{array}\right]=2 C_1\left[\begin{array}{l} \boldsymbol{x}_{n, i} \\ \boldsymbol{y}_{n, i} \\ \boldsymbol{z}_{n, i} \end{array}\right]-C_2\left[\begin{array}{l} \boldsymbol{x}_{n-1, i} \\ \boldsymbol{y}_{n-1, i} \\ \boldsymbol{z}_{n-1, i} \end{array}\right]+} \\ & C_1 h^2\left[\left[\begin{array}{l} \boldsymbol{f}_{\mathrm{ext}, i x} \\ \boldsymbol{f}_{\mathrm{ext}, i y} \\ \boldsymbol{f}_{\mathrm{ext}, i z} \end{array}\right]+\left[\begin{array}{l} \boldsymbol{f}_{\mathrm{int}, i x} \\ \boldsymbol{f}_{\mathrm{int}, i y} \\ \boldsymbol{f}_{\mathrm{int}, i z} \end{array}\right]\right) \times m_i^{-1} 。\end{aligned} $ | (7) |
式中:C1=1/(1+ξh/2);C2=C1/(1-ξh/2);ξ为阻尼系数;fext, i、fint, i分别为质点i所受到的外力和内力。
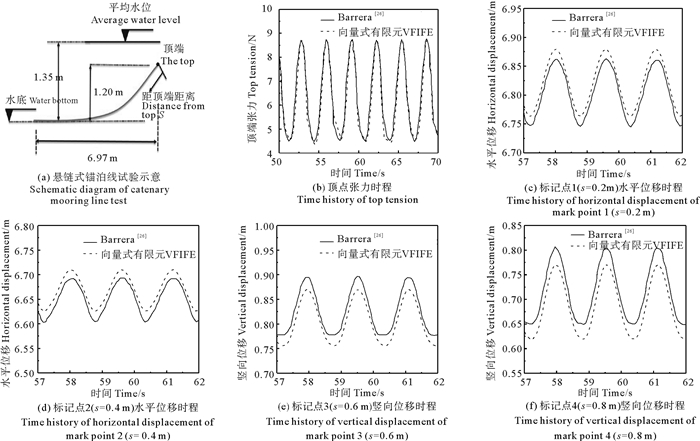
2 串联浮筒多组分锚泊线松弛-张紧特性分析 2.1 算例验证为了验证本文模型的有效性,首先进行算例对比分析。基于锚泊线的基本参数(见表 1),计算顶端纵荡激励下锚泊线的位移和张力。图 6(a)是悬链式锚泊线试验示意图,在试验中Barrera考虑了顶端纵荡激励,其中纵荡振幅为0.075 m,纵荡周期分别为1.58和3.16 s。图 6(b)展示的是周期为3.16 s时顶点张力时程图,图 6(c)~(f)分别展示的是周期为1.58 s时距顶端s=0.2 m处水平位移,s=0.4 m处水平位移s=0.6 m处竖向位移和s=0.8 m处竖向位移时程图,并且从表 2可以得知,位移最大误差范围未超过5%。因此可以得出,本文基于向量式有限元方法计算的锚泊线张力和位移数值模拟结果与Barrera的试验结果吻合度较高,验证了本文模型的准确性和有效性。
|
图 6 向量式有限元模拟和试验结果对比 Fig. 6 Comparison between vector form intrinsic finite element simulation and test results |
|
|
表 2 向量式有限元模拟和试验位移结果对比 Table 2 Comparison of displacement results between vector form intrinsic finite element simulation and test |
以某深海平台锚泊线为研究对象,该锚泊线由下部锚链、中部锚缆和上部锚链[27]以及浮筒组合而成,多组分锚泊线具体参数如表 3所示,浮筒参数如表 4所示。根据文献[12]确定浮筒浮重参数和位置。根据文献[28]设置波浪、波高为3 m;波周期为12 s;均匀海流速度为0.5 m/s,海流速度沿x轴方向。在锚泊线顶端施加正弦水平位移X(t)=Asin(ωt),方向沿x轴,分析不同振幅和频率以及不同浮筒参数下多组分锚泊线松弛-张紧特性。
|
|
表 3 多组分锚泊线的基本参数 Table 3 Basic parameters of multi-component mooring line |
|
|
表 4 浮筒参数 Table 4 Buoys parameters |
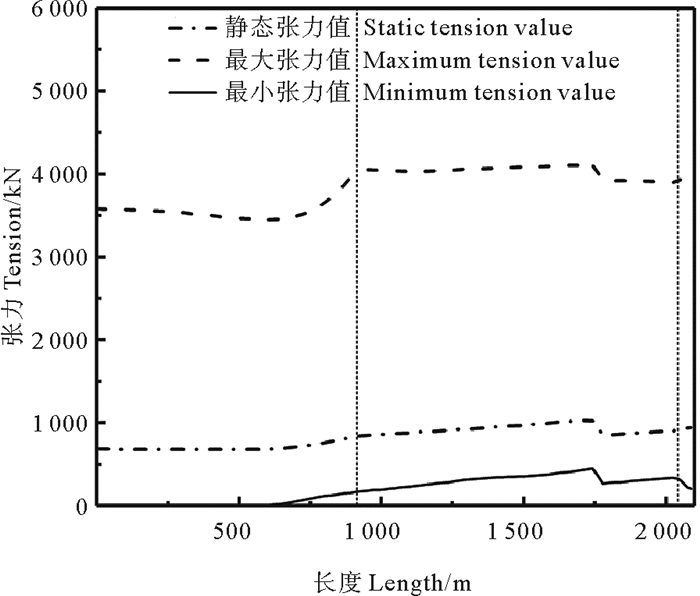
本文为了详细解释松弛-张紧现象,使串联浮筒多组分锚泊线顶端激励振幅A=12 m、激励频率ω=1.1 rad/s的运动,串联浮筒Ⅰ并且使其位于SⅠ处,计算得到锚泊线的最小张力值(见图 7)。从图 7可以发现串联浮筒多组分锚泊线底端区域出现了最小张力值0(即发生松弛-张紧现象),最大张力值同静态时张力值相比有了大幅度增加。进而计算出底端点静态与动态的张力和整条锚泊线的冲击放大系数(见图 8)。冲击放大系数α是锚泊线的最大动张力Tmax与锚泊线静张力Tc的比值[1],反映锚泊线的冲击强度:
| $ \alpha=\frac{T_{\max }}{T_{\mathrm{c}}} 。$ | (8) |
|
图 7 松弛-张紧现象 Fig. 7 Taut-slack phenomenon |
|
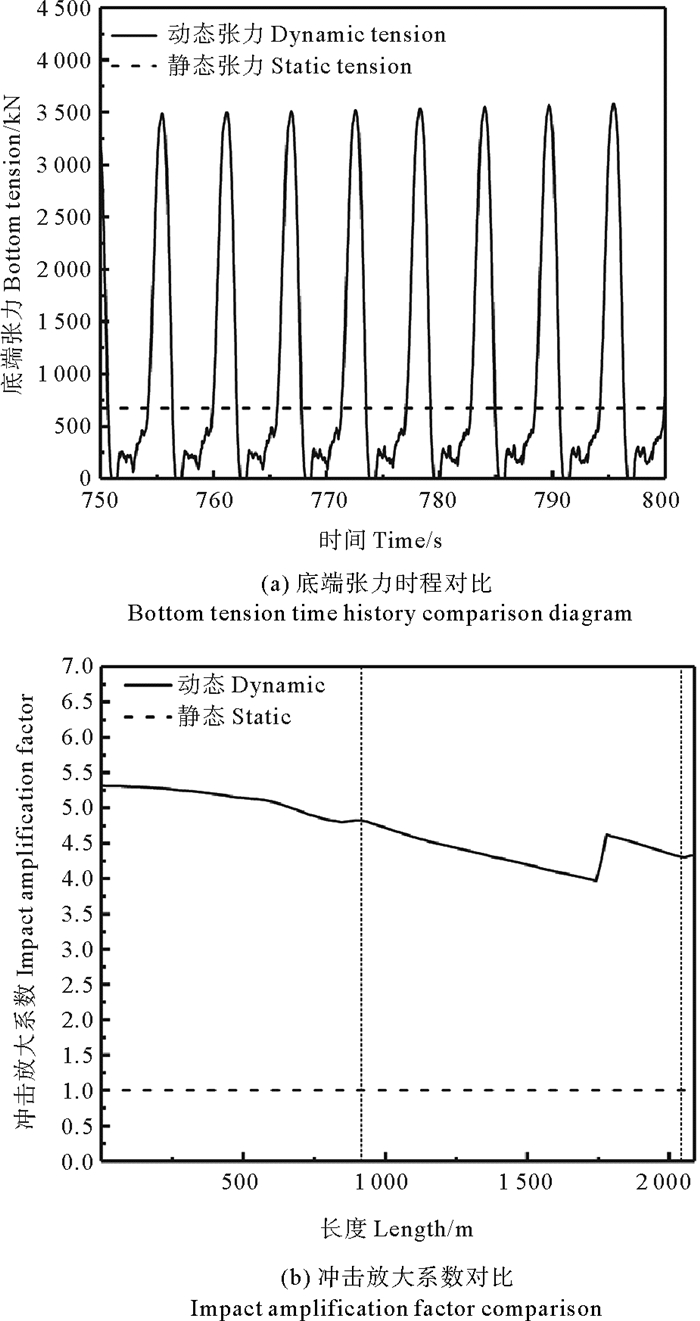
图 8 动态与静态对比 Fig. 8 Comparison of dynamic and static |
从图 8(a)可知,在顶端激励下底端张力出现周期性零张力,在零张力的位置附近有突变的尖峰,最大张力达到3 500 kN,可以判断多组分锚泊线底端部分单元发生了松弛-张紧现象。松弛-张紧现象的发生导致张力幅值变化增大,最大张力比静态张力大4.6倍左右。与此同时,从图 8(b)可知底端部分单元冲击张力系数是静态冲击张力系数的5倍左右,产生较大的冲击张力,由此可见松弛-张紧现象对串联浮筒锚泊线危害巨大。
2.2.1 浮体纵荡运动结果分析在多组分锚泊线顶端水平方向施加使其做正弦运动的力,由于浮式平台垂荡、横荡相比纵荡较小,故本文未考虑其对锚线松弛-张紧特性的影响。根据深海波浪的频率范围和浮式平台实际运动范围,串联浮筒多组分锚泊线顶端水平运动幅值A为5~15 m、频率ω为0.5~1.3 rad/s[18]。研究激励频率相同振幅不同以及振幅相同频率不同的工况。研究串联浮筒多组分锚泊线松弛-张紧现象随顶端激励振幅的变化时,使激励频率ω固定为1.1 rad/s,激励振幅A的取值为8~14 m,并以2 m的间隔增加,设置了4组工况;研究串联浮筒多组分锚泊线随顶端激励频率的变化时,使激励振幅固定A为12 m,激励频率取值ω为0.7~1.3 rad/s,并以0.2 rad/s的间隔增加,设置了4组工况。限于篇幅,仅给出串联浮筒Ⅰ位于SⅠ的计算结果进行说明,其他串联浮筒同此计算结果趋势基本一样。
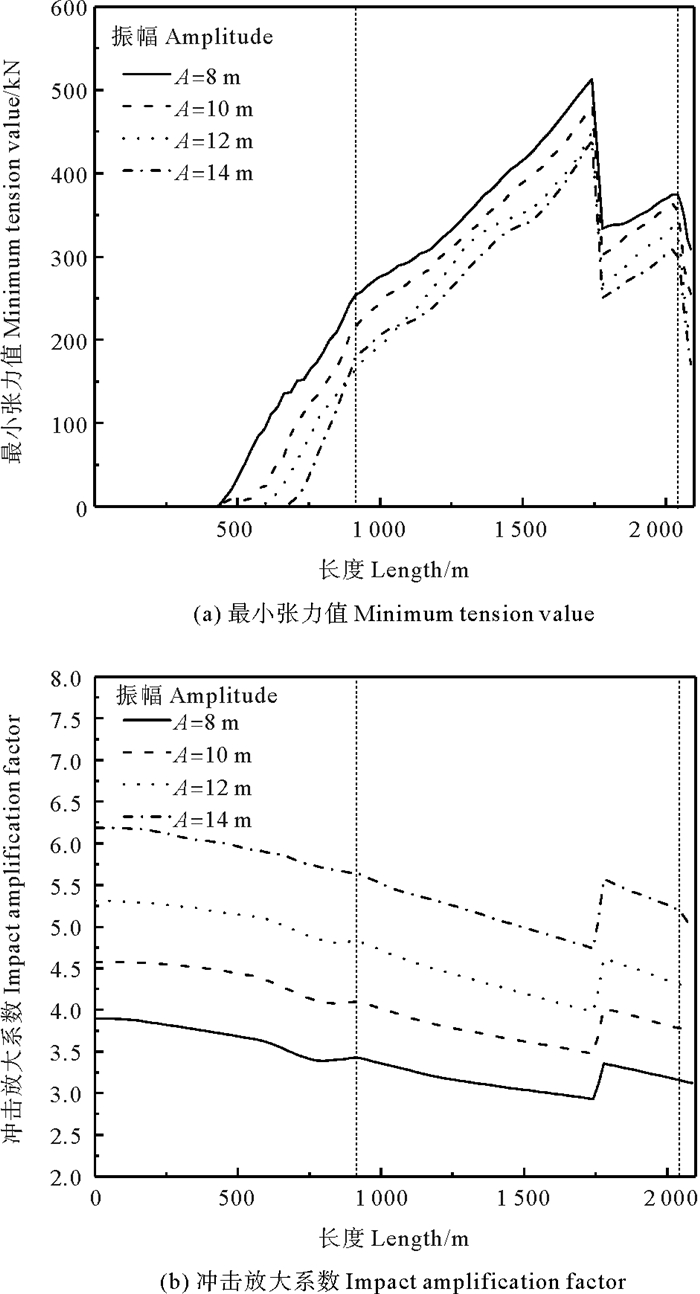
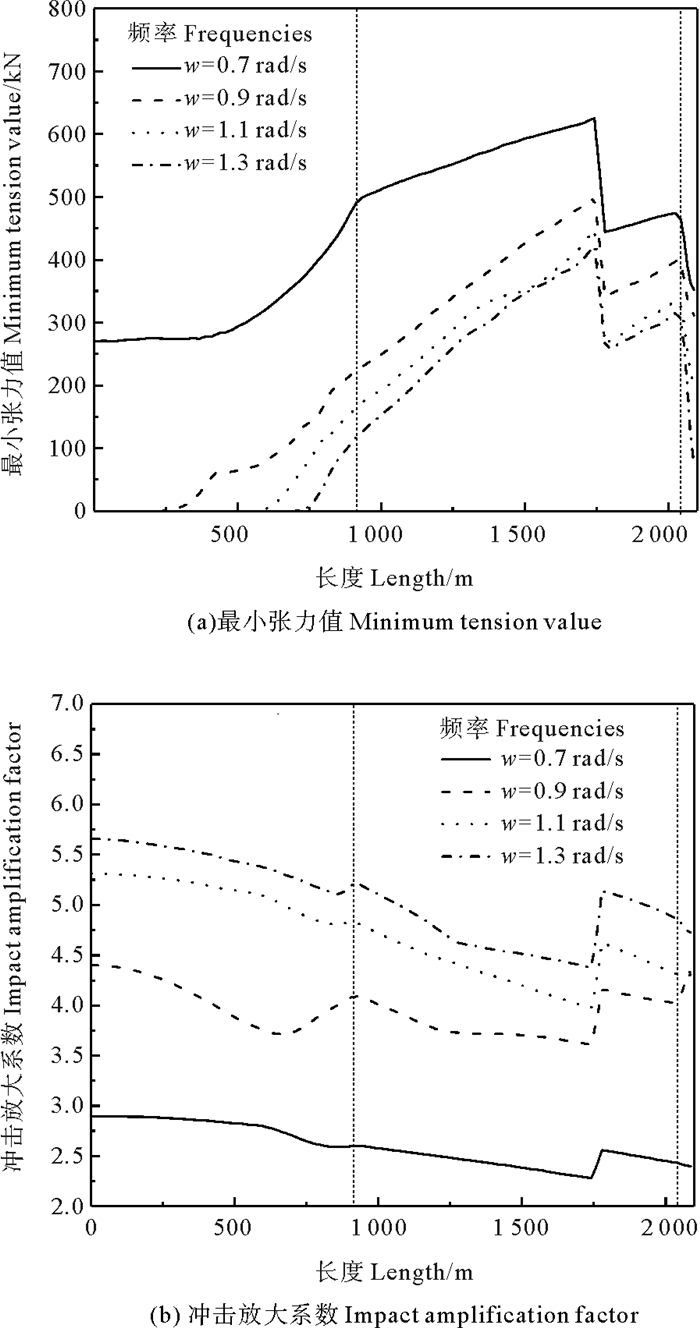
从图 9(a)、图 10(a)可知,最小张力值为0(即出现松弛-张紧现象)是先从底端位置开始出现的,主要原因是多组分锚泊线预张力从顶端到底端依次下降,预张力越小,发生松弛-张紧现象的概率越大。并且在不同成分锚泊线节点和串联浮筒位置处,可以明显观察到最小张力值降低,这说明多组分锚泊线比单组分锚泊线更能有效降低张力值,提高承载能力。从整体分析来看,随着激励频率和激励振幅的增加,松弛-张紧长度呈增加趋势。如图 10(a)所示,在激励振幅A=12 m,激励频率ω=0.7 rad/s时,可以发现串联浮筒多组分锚泊线最小张力值在0 kN以上,即未发生松弛-张紧现象。但是当激励频率ω=1.3 rad/s时,锚泊线从底端位置向上近750 m长度发生松弛-张紧现象,与此同时顶端最小张力值趋于0,如果激励频率继续增加,顶端部分单元将发生松弛-张紧现象,这比底端部分单元发生松弛-张紧现象危害更大。
|
图 9 不同振幅下多组分锚泊线特性 Fig. 9 Characteristics of multi-component mooring line under different amplitudes |
|
图 10 不同频率下多组分锚泊线特性 Fig. 10 Characteristics of multi-component mooring line at different frequencies |
从图 9(b)、10(b)可知,随着激励振幅和激励频率的增加,冲击放大系数呈上升趋势。从单一工况来看,从锚固点底端自下而上冲击放大系数呈下降趋势,导缆点顶端冲击放大系数小于锚固点冲击放大系数,原因分析为顶端区域预张力大于底端区域,顶端发生运动时,顶端区域的扰动大于底端区域,顶端区域处于高张力范围,底端区域处在低张力范围,底端在受到扰动带来的张力变化时反应更大。并且发生松弛-张紧现象的锚泊线位置冲击张力系数大于未发生区域。总而言之,顶端浮体运动越激烈(激励振幅和激励频率增加),发生松弛-张紧现象的概率越大。
2.2.2 浮筒浮重参数变化结果分析浮筒参数对串联浮筒多组分锚泊线松弛-张紧现象具有重要影响。保证顶端浮体激励振幅和激励频率不变,分析浮筒的浮重、位置和数量对多组分锚泊线松弛-张紧特性影响,并总结规律。
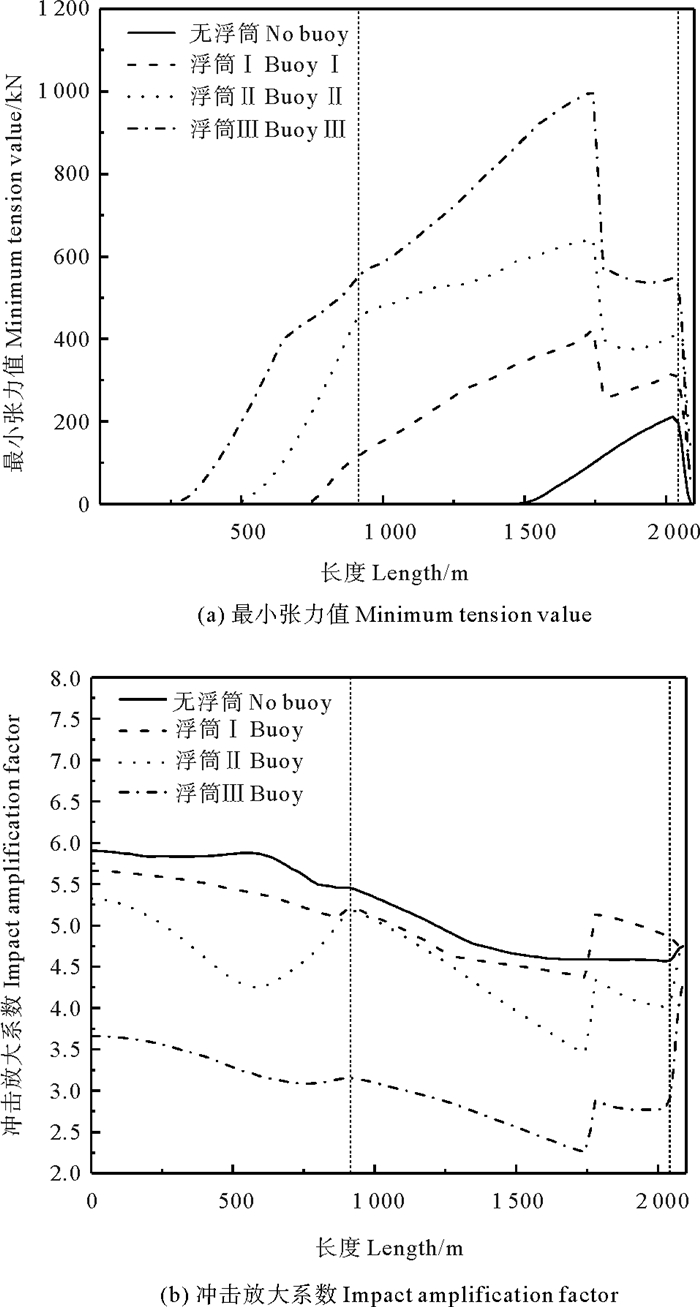
研究浮筒浮重对多组分锚泊线松弛-张紧特性影响时,由于频率ω=1.1 rad/s时,串联浮筒导致多组分锚泊线未发生松弛-张紧现象,为更方便研究此特性,将激励频率增加。设置浮体激励振幅A=12 m,频率ω=1.3 rad/s,在SⅠ处布置单个浮筒,分别对浮筒浮重进行改变(浮筒Ⅰ浮重281.8 kN、浮筒Ⅱ浮重469.7 kN、浮筒Ⅲ浮重845.5 kN),以此对串联浮筒多组分锚泊线松弛-张紧特性进行分析,计算结果如图 11所示。
|
( (浮筒Ⅰ、Ⅱ、Ⅲ位于SⅠ处。Buoy Ⅰ、Ⅱ、Ⅲ are located at SⅠ.) ) 图 11 不同浮筒浮重下多组分锚泊线特性 Fig. 11 Characteristics of multi-component mooring line under different buoys floating weight |
如图 11(a)可知,随着浮筒浮重(见表 4)的增加,串联浮筒多组分锚泊线松弛-张紧长度呈下降趋势。主要原因是由于浮筒浮重的增加,提高了多组分锚泊线的初始预张力,降低了发生松弛-张紧现象的概率。同无浮筒工况相比可知,串联浮筒对松弛-张紧现象具有很好的抑制作用。值得注意的是在无浮筒情况下,多组分锚泊线不仅在预张力较小的锚固点底端区域发生松弛-张紧现象,而且在预张力较大的导缆点顶端区域也出现了松弛-张紧现象。在实际工程中,导缆点顶点是浮式平台连接的关键部位,此部位的断裂会严重影响深海油气资源的开采,造成平台失稳。
如图 11(b)可知,随着浮筒浮重的增加,串联浮筒多组分锚泊线冲击放大系数呈下降趋势。在单一工况下值得注意的是,随着浮筒浮重的增加,造成了导缆点顶端冲击放大系数开始由原来小于锚固点底端变成大于锚固点底端,主要原因是串联浮筒降低了顶端导缆点区域的预张力,且顶端浮体扰动剧烈。同时还发现,串联浮筒虽然降低了整体的冲击放大系数,但是串联浮筒处的冲击放大系数发生突变,明显升高。随着浮筒浮重的增加,突变逐渐变小。因此在实际工程中,浮筒虽然能够降低张力值和松弛-张紧现象发生的概率,但是浮筒位置处的突变荷载需要注意选择合适的浮筒浮重,避免此处荷载突然变大。由此可见,串联浮筒虽然对底端区域提高了初始预张力,降低了整体冲击张力系数,减少了松弛-张紧长度,但是不可避免的影响了顶端区域的预张力,造成顶部冲击放大系数的增加,提高发生松弛-张紧现象的概率,因此浮筒浮重对多组分锚泊线松弛-张紧特性影响至关重要。
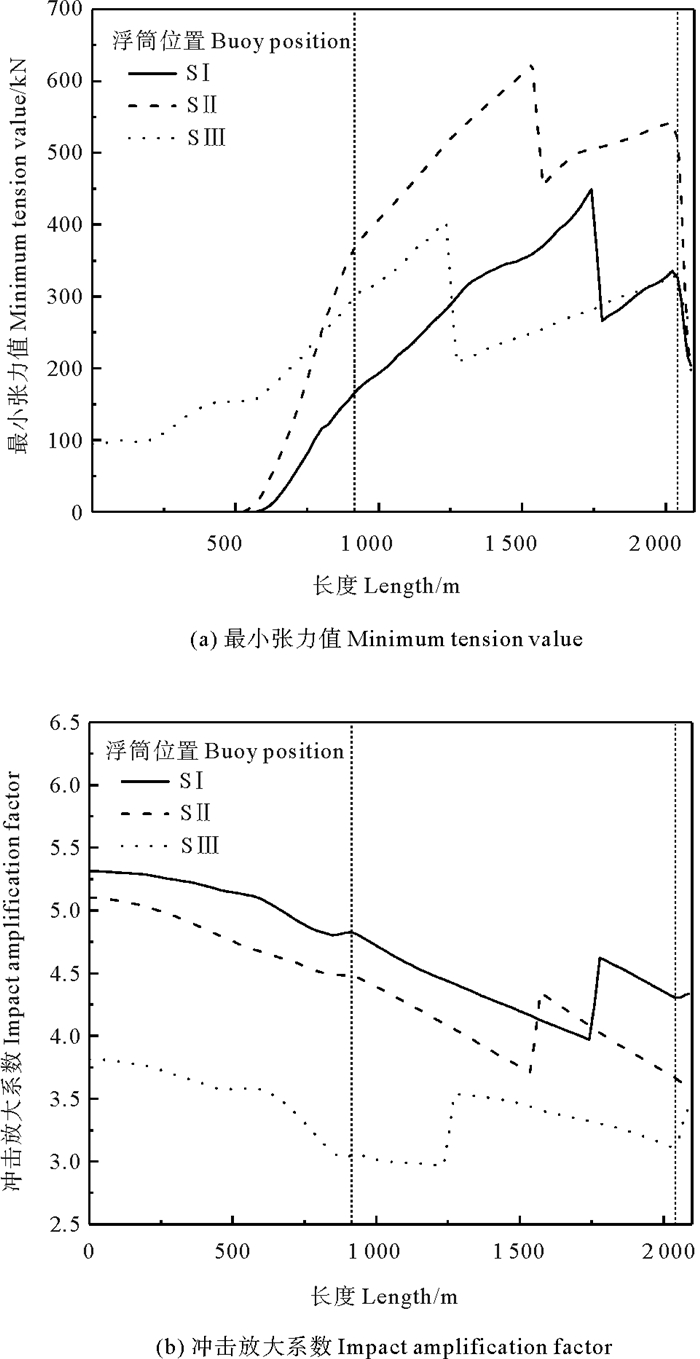
2.2.3 浮筒位置参数变化结果分析研究浮筒位置对多组分锚泊线松弛-张紧特性影响时,浮体激励设置振幅A=12 m,频率ω=1.1 rad/s,选择浮筒浮重Ⅰ为281.8 kN,并且对浮筒距顶端导缆点的位置(SⅠ=313.2 m、SⅡ=522.0 m、SⅢ=835.2 m)进行改变,以此对串联浮筒多组分锚泊线松弛-张紧特性进行分析,计算结果如图 12所示。
|
图 12 不同浮筒位置下多组分锚泊线特性 Fig. 12 Characteristics of multi-component mooring line at different buoys positions |
如图 12(a)可知,随着S(锚泊线上一点到锚泊线导缆点顶端的距离)增加,串联浮筒多组分锚泊线松弛-张紧长度呈下降趋势。主要原因是浮筒下移,提高了底端区域的初始预张力,进而提高了承载力。例如,在浮筒位于SⅠ时明显观察到发生松弛-张紧长度约为625 m,但是在浮筒位于SⅢ时,整条多组分锚泊线无松弛-张紧现象发生。
如图 12(b)可知,随着S的增加,串联浮筒多组分锚泊线冲击放大系数呈下降趋势。在单一工况下发现,随着S的增加,冲击放大系数开始由锚固点底端大于顶端导缆点变成小于顶端导缆点,原因分析是多组分锚泊线的初始位形随着浮筒下移改变,造成了以浮筒位置为界,顶端区域预张力小于底端区域预张力。这就需要在实际工程中把控好浮筒的位置,控制好浮筒两端的初始预张力,尽可能使多组分锚泊线不仅避免发生松弛-张紧现象,而且降低张力值,提高使用寿命。
2.2.4 浮筒数量参数变化结果分析研究浮筒数量对多组分锚泊线松弛-张紧特性影响时,浮体激励设置振幅A=12 m,频率ω=1.1 rad/s,选择浮筒浮重Ⅰ为281.8 kN,在这些位置(SⅠ=313.2 m、SⅡ=522.0 m、SⅢ=835.2 m) 分别串联单个浮筒、双浮筒、3个浮筒,其中串联双浮筒和三浮筒区分浮筒在不同的位置,且对浮筒超出水面的不予分析,以此对串联浮筒多组分锚泊线松弛-张紧特性进行分析,计算结果如图 13所示。
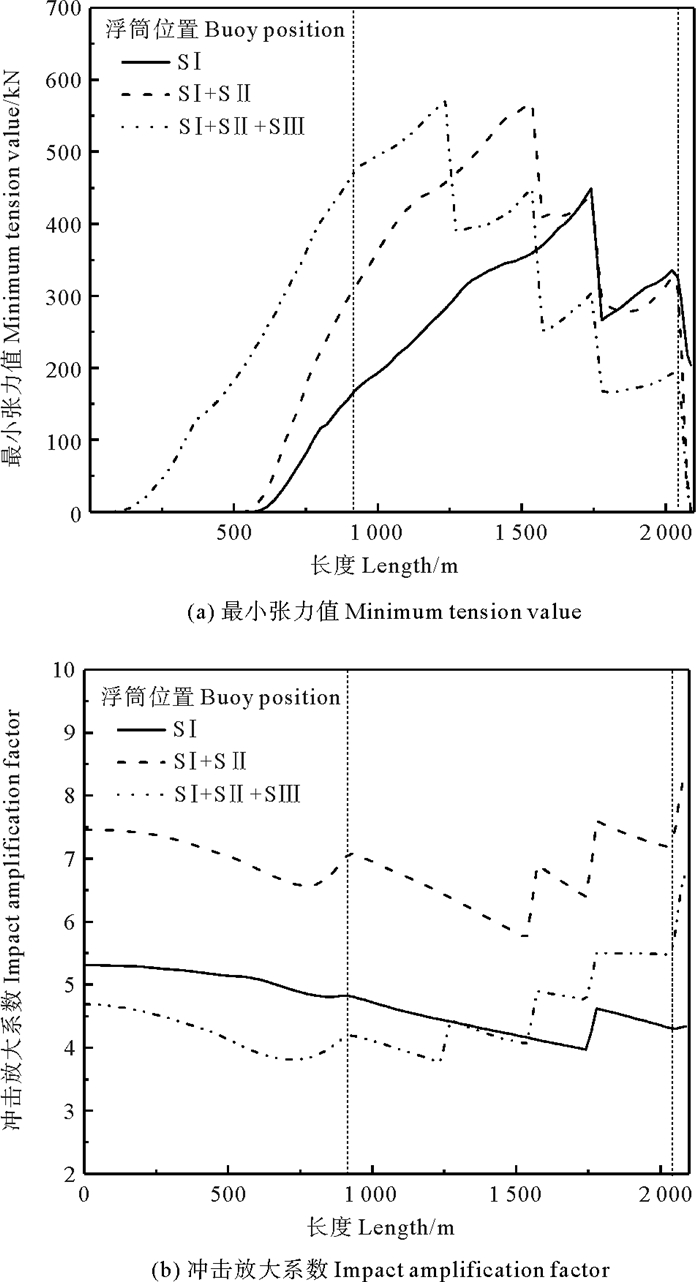
|
图 13 不同浮筒数量下多组分锚泊线特性 Fig. 13 Characteristics of multi-component mooring line under different number of buoys |
如图 13(a)可知,随着浮筒数量的增加,串联浮筒多组分锚泊线松弛-张紧长度呈下降趋势。主要原因是浮筒数量的增加,提高多组分锚泊线以浮筒为界的各个区域的初始预张力。值得注意的是在三浮筒(SⅠ+SⅡ+SⅢ)工况中,虽然底端区域的松弛-张紧长度有所减少,但是顶端导缆点发生了松弛-张紧现象。分析原因:浮筒只是合理串联在多组分锚泊线的中间区域,而对于首尾两端来说,初始预张力相对较小,并且靠近顶端的浮筒降低了底端区域的预张力。
如图 13(b)可知,随着浮筒数量的增加,冲击放大系数并没有呈增加趋势,而锚固点从原来自下而上呈下降趋势变为中间小两边大,这是由于浮筒串联在多组分锚泊线的中间区域,提高了初始预张力,降低了中间区域的冲击放大系数。并且随着浮筒数量的增加,顶端冲击放大系数开始大于其他部位的冲击放大系数。总之,浮筒数量的增加对多组分锚泊线松弛-张紧现象具有重要影响。
3 结论本文以串联浮筒多组分锚泊线为研究对象,基于向量式有限元方法建立了动力分析模型,将数值模拟结果与试验结果作对比,并进一步分析了不同参数对串联浮筒多组分锚泊线松弛-张紧特性影响。通过研究得出以下结论:
(1) 串联浮筒多组分锚泊线最先从底端开始发生松弛-张紧现象,随着激励振幅和激励频率的增加,松弛-张紧现象长度呈增加趋势,且松弛-张紧现象的发生造成冲击放大系数增加。
(2) 随着浮筒浮重的增加,松弛-张紧长度呈下降趋势。同无浮筒相比,串联浮筒确实可以降低松弛-张紧长度,进而降低多组分锚泊线断裂的风险;浮筒虽然降低了整体的冲击张力系数,但是浮筒位置附近冲击张力系数发生突变式增长。
(3) 随着距离的增加,发生松弛-张紧现象长度呈下降趋势。实际工程中需要合理串联浮筒位置,提高浮筒两边的初始预张力,避免顶端区域发生松弛-张紧现象。
(4) 随着浮筒数量的增加,发生松弛-张紧现象长度呈下降趋势;冲击放大系数从底端自下而上呈下降趋势变为出现两端大中间小,实际工程中应注意合理串联浮筒数量,多关注锚泊线首、尾两端初始预张力。
(5) 串联浮筒多组分锚泊线的松弛-张紧现象多数发生在锚泊线的底端部分单元,但当达到极端海况时,该现象在顶端部分单元也开始出现, 且在顶端部分单元出现比在底端出现更具危害性。
| [1] |
唐友刚, 张若瑜, 程楠, 等. 集中质量法计算深海系泊冲击张力[J]. 天津大学学报, 2009, 42(8): 695-701. Tang Y G, Zhang R Y, Cheng N, et al. Analysis of snap tension of deep water mooring with lumped mass method[J]. Journal of Tianjin University, 2009, 42(8): 695-701. DOI:10.3969/j.issn.0493-2137.2009.08.007 (  0) 0) |
| [2] |
Shan H, Vassalos D. A numerical method for predicting snap loading of marine cables[J]. Applied Ocean Research, 1993, 15(4): 235-242. DOI:10.1016/0141-1187(93)90012-M (  0) 0) |
| [3] |
Plaut R H, Archilla J C, Mays T W. Snap Loads in mooring lines during large three-dimensional motions of a Cylinder[J]. Nonlinear Dynamics, 2000, 23(3): 271-284. DOI:10.1023/A:1008368427878 (  0) 0) |
| [4] |
Pascoal R, Huang S, Barltrop N, et al. Assessment of the effect of mooring systems on the horizontal motions with an equivalent force to model[J]. Ocean Engineering, 2006, 33(11/12): 1644-1668. (  0) 0) |
| [5] |
唐友刚, 张素侠, 张海燕, 等. 系泊系统松弛一张紧引起的冲击张力研究[J]. 振动与冲击, 2008, 27(4): 70-73. Tang Y G, Zhang S X, Zhang H Y, et al. Snap tension induced by slack-taut in a mooring system[J]. Journal of Vibration and Shock, 2008, 27(4): 70-73. DOI:10.3969/j.issn.1000-3835.2008.04.019 (  0) 0) |
| [6] |
张素侠, 唐友刚, 林维学, 等. 水下缆绳松弛-张紧过程的冲击张力实验研究[J]. 中国造船, 2008, 49(S2): 385-390. Zhang S X, Tang Y G, Lin W X, et al. Experimental investigation of marine cable snap tension in taut-slack condition[J]. Shipbuilding of China, 2008, 49(S2): 385-390. (  0) 0) |
| [7] |
张素侠, 唐友刚, 张若瑜, 等. 水下缆绳松弛-张紧过程的冲击张力影响因素实验研究[J]. 哈尔滨工程大学学报, 2009, 30(10): 1102-1107. Zhang S X, Tang Y G, Zhang R Y, et al. Experimental investigation into factors affecting marine cable snap tension in taut-slack conditions[J]. Journal of Harbin Engineering University, 2009, 30(10): 1102-1107. (  0) 0) |
| [8] |
曹阳. 深水系泊缆绳冲击载荷实验研究[D]. 天津: 天津大学, 2009. Cao Y. Experimental Study for Snap Loading of Mooring Lines in Deep-Sea[D]. Tianjin: TianJin University, 2009. (  0) 0) |
| [9] |
Palm J, Eskilsson C, Bergdahl L. An hp-adaptive discontinuous Galerkin method for modelling snap loads in mooring cables[J]. Ocean Engineering, 2017, 144: 266-276. DOI:10.1016/j.oceaneng.2017.08.041 (  0) 0) |
| [10] |
Shin H. Dynamic Analysis of Cable with intermediate submerged buoys for offshore applications frequency domain analysis[J]. Journal of Comparative Neurology, 1989, 3(2): 26-34. (  0) 0) |
| [11] |
王道能. 浮筒锚泊系统受力分析及其仿真[D]. 哈尔滨: 哈尔滨工程大学, 2008. Wang D N. Force Analysis and Simulation of Mooring System with Buoys[D]. Harbin: Harbin Engineering University, 2008. (  0) 0) |
| [12] |
Mavrakos S A, Chatjigeorgiou J. Dynamic behaviour of deep water mooring lines with submerged buoys[J]. Computers & Structures, 1997, 64(1-4): 819-835. (  0) 0) |
| [13] |
Yuan Z M, Incecik A, Ji C. Numerical study on a hybrid mooring system with clump weights and buoys[J]. Ocean Engineering, 2014, 88: 1-11. DOI:10.1016/j.oceaneng.2014.06.002 (  0) 0) |
| [14] |
Yan J, Qiao D, Fan T, et al. Concept design of deep water catenary mooring lines with submerged buoy[C] // Proceedings of the Twelfth Pacific Asia Offshore Mechanics Symposium. Gold Coast, Australia: International Society of Offshore and Polar Engineers, 2016: 305-311.
(  0) 0) |
| [15] |
乔东生, 闫俊, 欧进萍. 深水锚泊线串联浮筒系统的动力特性分析[J]. 振动与冲击, 2013, 32(15): 54-58. Qiao D S, Yan J, Ou J P. Dynamic characteristics of deep water mooring lines with buoys system[J]. Journal of Vibration and Shock, 2013, 32(15): 54-58. (  0) 0) |
| [16] |
闫俊, 乔东生, 樊天慧, 等. 新型深水串联浮筒锚泊线阻尼特性分析[J]. 中国造船, 2017, 58(2): 145-155. Yan J, Qiao D S, Fan T H, et al. Damping characteristics of a new type of deep water mooring line with submerged buoy[J]. Shipbuilding of China, 2017, 58(2): 145-155. (  0) 0) |
| [17] |
李效民, 张宸鑫, 刘震, 等. 串联浮筒锚泊系统的静力位形及内力分析[J]. 船舶工程, 2020, 42(1): 128-134. Li X M, Zhang C X, Liu Z, et al. Static configuration and internal forces analysis of buoys mooring system[J]. Ship Engineering, 2020, 42(1): 128-134. (  0) 0) |
| [18] |
王瑞华, 张素侠, 刘习军. 浸没式浮筒对系泊缆松弛-张紧特性的影响研究[J]. 应用力学学报, 2020, 37(2): 543-550. Wang R H, Zhang S X, Liu X J. Study on the effect of submersed buoy on the taut-slack characteristics of the mooring line[J]. Chinese Journal of Applied Mechanics, 2020, 37(2): 543-550. (  0) 0) |
| [19] |
Qiao D S, Li B B, Ou J P. Comparative analysis on coupling effects between an innovative deep draft platform and different mooring models[J]. Brodogradnja, 2012, 63(4): 318-328. (  0) 0) |
| [20] |
Childers M A. Ultradeep water spread mooring system[J]. Petroleum Engineer International, 1974, 46(11): 108-110, 112, 116, 118. (  0) 0) |
| [21] |
Xu S, Ji C Y, Guedes Soares C. Experimental and numerical investigation a semi-submersible moored by hybrid mooring systems[J]. Ocean Engineering, 2018, 163: 641-678. (  0) 0) |
| [22] |
Ting E C, Shih C, Wang Y K. Fundamentals of a vector form intrinsic finite element: Part Ⅰ. Basic procedure and a plane frame element[J]. Journal of Mechanics, 2004, 20(2): 113-122. (  0) 0) |
| [23] |
Ting E C, Shih C, Wang Y K. Fundamentals of a vector form intrinsic finite element: Part Ⅱ. Plane solid elements[J]. Journal of Mechanics, 2004, 20(2): 123-132. (  0) 0) |
| [24] |
Chen X, Zhang J, Wei M. On dynamic coupling effects between a spar and its mooring lines[J]. Ocean Engineering, 2001, 28(7): 863-887. (  0) 0) |
| [25] |
Sarkar A, Taylor R E. Dynamics of mooring cables in random seas[J]. Journal of Fluids and Structures, 2002, 16(2): 193-212. (  0) 0) |
| [26] |
Barrera C, Guanche R, Losada I. Experimental modelling of mooring systems for floating marine energy concepts[J]. Marine Structures, 2019, 63: 153-180. (  0) 0) |
| [27] |
Low C M, Ng Y K, Narasimalu S, et al. Numerical modelling of seabed impact effects on chain and small diameter mooring cables[J]. Applied Ocean Research, 2018, 80: 248-277. (  0) 0) |
| [28] |
董艳秋. 深海采油平台波浪载荷及响应[M]. 天津: 天津大学出版社, 2005. Dong Y Q. Wave Loads and Response of the Oil-Extraction Platform in Deep Ocean[M]. Tianjin: TianJin University Press, 2005. (  0) 0) |
 2023, Vol. 53
2023, Vol. 53


