碰撞是引起船舶与海洋结构物损伤的重要因素,也是船舶工程上的热点问题。海洋平台一般在海况恶劣的深海海域工作,由于作业需要,附近常有穿梭油轮和供应船的航行或停靠,因此系泊状态下的平台被碰撞的机会较多。
对于复杂的碰撞问题,有限元分析方法和简化解析法具有高效、简便和精确的优点,因此应用最为广泛。
目前,非线性显式有限元软件能够精确地计算碰撞力和结构损伤,模拟船体的运动过程。学者们通过研究碰撞有限元法的关键技术,提高数值仿真结果的准确性。顾永宁等[1]阐述了材料本构和网格质量对计算结果精确程度的直接影响;Getter[2]等通过确定钢材断裂极限应变和应变率等材料参数,保证分析结果的正确性;Sören[3]得到失效应变与单元长度的关系曲线,为有限元建模和参数设置提供了依据。
在简化解析方面,学者们建立不同的力学模型,多角度解释了碰撞机理。Minorsky[4]根据完全非弹性碰撞理论,求解船舶舷侧撞击时的能量耗散,提出简化解析公式。Pedersen和Zhang[5]提出外部动力学的二维理论模型,利用动能定理和动量方程,求解碰撞系统的耗散能,与Minorsky[4]的计算结果相吻合。Stronge[6]针对多种碰撞形式,阐述了刚体的三维碰撞理论解法。Liu和Amdahl[7]基于Stronge[6]的理论发展了局部坐标系下的三维碰撞理论,验证结果的准确性。
本文研究的被撞平台主船体和系泊系统以一定的方式相连接,组成多体系统。多体系统的碰撞问题有两种解决思路:“分段”分析法将碰撞过程视为瞬时的,分别对碰撞前后进行动力分析。Wehage[8]首次通过求解平衡、动量和冲量方程,获得碰撞后的结果,并根据多体连接处的铰接形式,建立约束方程求解其运动状态。“连续”分析法将碰撞载荷视为持续作用力,把各时刻的碰撞力作为已知载荷加入系统方程求解。Khulief和Shabana[9]采用等效质量法简化多体系统,并验证曲轴连杆算例。Lankarani和Nikravesh[10]基于两球碰撞模型推导出碰撞力与撞深的函数关系,并应用于Khulief[9]的连杆系统。
本文采用ANSYS建立了单点系泊状态下的平台模型,其中系泊装置间连接部分的模拟是本文的难点。使用LS-DYNA计算了不考虑流体情况下,平台在碰撞载荷作用下的运动状态。基于外部动力学理论,对比了有、无系泊工况的结果,探究平台整体运动的普适性规律。
1 碰撞有限元分析方法本文采用显式有限元数值仿真方法分析碰撞过程,其基本原理是:将碰撞体模型离散化,定义合适的时间步长Δt,根据t时刻的位移计算碰撞力,建立t+Δt时刻的运动方程,采用中心差分法求解出该时刻的位移。由于中心差分法是条件稳定的,设定的时间步长Δt应满足以下关系:
| $ \Delta t \leqslant \alpha\left(\frac{L_{\min }}{c}\right)。$ | (1) |
式中:α为时步因子,根据经验取0.9;Lmin是模型最小单元长度;材料声速c通过式(2)计算。
| $ c=\sqrt{\frac{E}{\left(1-\nu^{2}\right) \rho}}。$ | (2) |
式中:E为材料的弹性模量;ν为泊松比;ρ为材料密度。
1.1 碰撞力计算在每个时间步上,应将载荷作为已知条件施加到结构上,需优先计算。通过罚函数法可计算平台和船之间的碰撞力:在两碰撞体的接触面上定义主、从节点,考察各时刻从节点是否穿透主面;若没有穿透,不做任何处理;若穿透,则在主、从面间引入法向接触力,其大小与穿透深度、主面的刚度成正比。
| $ f_{\mathrm{s}}=-\overrightarrow{l }k_{i} n_{i}。$ | (3) |
式中:fs为法向接触力;
| $ k_{i}=\frac{f K_{i} A_{i}}{L_{i}}。$ | (4) |
式中:f为接触刚度比例因子,取0.1;Ki为接触单元的体积模量;Ai为主面的单元面积;Li为接触单元的最大对角线长度。
将作用在主面上的接触力-fs(法向接触力的反作用力)等效分配到主单元(通常是是四节点单元)的节点上:
| $ f_{j m}=-\phi_{j} f_{\mathrm{s}}, j=1, 2, 3, 4。$ | (5) |
式中:fjm为主单元等效接触力;ϕj为主单元面上的二维形函数,下标j为节点号。
1.2 建立碰撞运动方程本文采用更新拉格朗日算法建立t时刻的运动方程。将平台和船的结构空间离散化,单元上任一质点X在t时刻的位移ui(X, t)为[12]:
| $ u_{i}(X, t)=N_{I} u_{i I}(t)。$ | (6) |
式中:NI为单元内的形函数;uiI(t)为单元上节点I的位移,下标i为坐标系方向。对ui(X, t)作变换可得:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot u}_i}(X, t) = {N_I}{{\dot u}_{iI}}(t)}\\ {{{\ddot u}_i}(X, t) = {N_I}{{\ddot u}_{iI}}(t)}\\ {{D_{ij}} = \frac{1}{2}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) = \frac{1}{2}\left( {{u_{iI}}\frac{{\partial {N_I}}}{{\partial {x_j}}} + {u_{jI}}\frac{{\partial {N_I}}}{{\partial {x_i}}}} \right) = {B_{iI}}{u_{iI}}}\\ {\partial {v_i} = {N_I}\delta {v_{iI}}} \end{array}} \right.。$ | (7) |
式中:
虚功率方程表示为:
| $ \int_V {\left[ {\frac{{\partial \left( {\delta {v_i}} \right)}}{{\partial {x_j}}}{\sigma _{ji}} - \delta {v_i}\rho {b_i} - \delta {v_j}\rho {{\ddot u}_j}(t)} \right]} {\rm{d}}V = \int_A \delta {v_i}{f_{jm}}{\rm{d}}A。$ | (8) |
式中:ρ为t时刻的密度;σji为应力张量;bi为作用在物体单位质量上的力。
将式(7)写成矩阵形式,代入虚功率方程(8)中,整理得到碰撞的运动方程:
| $ M \ddot{u}_{t}+f^{\mathrm{int}}=f^{e x t}。$ | (9) |
质量阵M为∫VρNTNdV,内力和外力分别为fint=∫VBTσdV,fext=∫VNTρbdV+∫ANfjmdA。
1.3 多体系统约束方程的建立由于平台是主船体和系泊装置所组成的多体系统,各部分的位移相互约束,系统的运动方程不同于单体,因此需要对式(9)进行补充。
对于N个质点组成的系统,一阶线性约束方程表示的限制条件为:
| $ \sum\limits_{i = 1}^{3N} {{A_{\alpha i}}} {\dot u_i} + {A_{a0}} = 0, \alpha = 1, 2, \cdots , m。$ | (10) |
式中:Aαi和Aα0均为各质点在t时刻的变换矩阵;α为约束方程数。
利用拉格朗日乘子法,在运动方程式(9)中加入广义约束力CqTλ,整理得:
| $ M \ddot{u}_{t}+C_{q}^{T} \lambda+f^{\mathrm{int}}=f^{e x t}。$ | (11) |
式中,λ为拉格朗日乘子向量,系数满足Cq(u, t)=0。
1.4 节点位移求解基于以上结果,假定0~(t-Δt)时刻的节点位移、速度和加速度均已求得,利用中心差分法求解t时刻的位移,迭代公式如下所示:
| $ \left\{\begin{array}{l}{\ddot{u}_{t-\Delta t}=\frac{1}{\Delta t^{2}}\left(u_{t-2 \Delta t}-2 u_{t-\Delta}+u_{t}\right)} \\ {\dot{u}_{t-\Delta t}=\frac{1}{2 \Delta t}\left(-u_{t-2 \Delta t}+u_{t}\right)}\end{array}\right.。$ | (12) |
将式(12)代入式(11)中,反复迭代求出t时刻的节点位移。
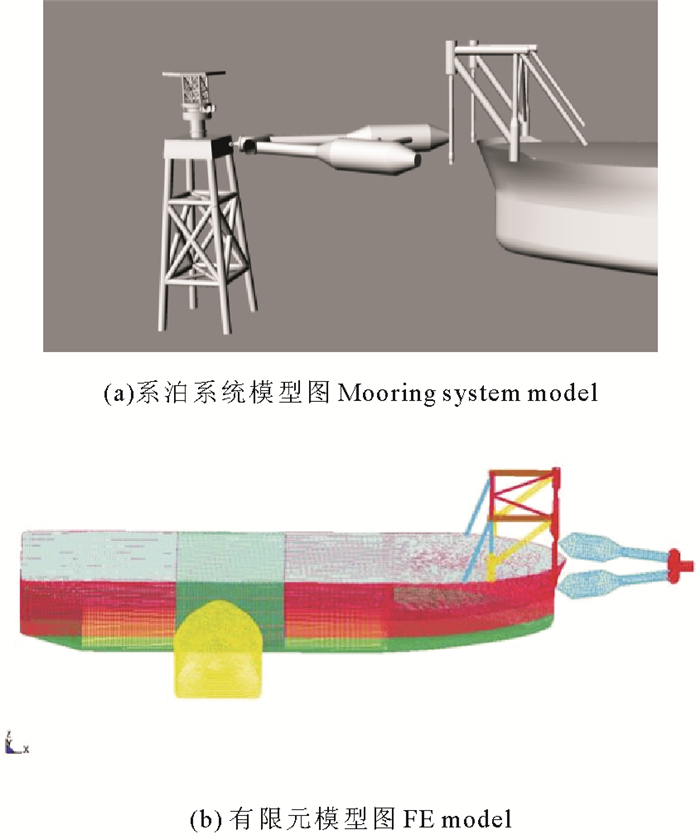
2 碰撞分析模型 2.1 碰撞仿真模型单点系泊FPSO平台和单点系泊系统如图 1(a)所示,主尺度如表 1所示,撞击船主尺度如表 2所示。采用ANSYS软件建立有限元模型,LS-DYNA软件进行碰撞计算和后处理。为降低计算时间,将撞击船模型简化为刚性船首。平台和撞击船模型均采用SHELL163单元模拟。平台重量为24 610 t,重心在纵向上位于船后部距船中3.5 m,垂向上距基线7.6 m。
|
图 1 带系泊系统碰撞船模型 Fig. 1 Ship collision model in mooring condition |
|
|
表 1 平台主尺度 Table 1 Principal dimension |
|
|
表 2 撞击船主尺度 Table 2 Principal dimension |
平台模型共有255 087个单元,撞击船模型有4 388个单元,如图 1(b)所示。
平台及撞击船所用钢材为船体235钢,材料本构采用线性强化的弹塑性模型,相关的参数为:材料密度为7 850 kg/m3,弹性模量为206 GPa,泊松比为0.3,硬化模量1.18 GPa。考虑到碰撞的应变率作用,钢材本构采用Cowper-Symonds模型,其本构方程为[13]:
| $ \frac{\sigma_{0}^{\prime}}{\sigma_{0}}=1+\left(\frac{\dot{\varepsilon}}{D}\right)^{\frac{1}{q}}。$ |
式中:σ0为材料的静屈服应力; σ′0为塑性应变率
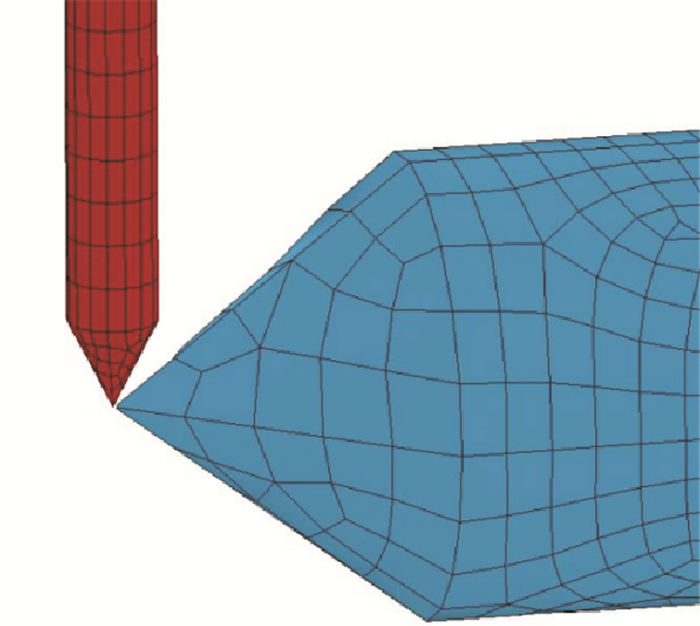
本文将平台主船体与系泊装置作为多体系统考虑,在YOKE端部采用铰支,比一般碰撞问题中铰支或固支的单一主船体模型更为真实,在数值模拟方法上也更为复杂。系泊系统包括MSS、连接臂和YOKE,各构件之间以球铰相连。为了模拟构件间的球铰连接,建立如图 2所示的模型,在构件端部增加圆锥面,使得两构件的连接集中于一点,采用Couple命令耦合两端点的平动自由度。这样,实现了构件端点处所有平动运动一致、转动不受限制,且其他部位互不影响的目的,简便地模拟了系泊装置的铰接。
|
图 2 连接臂和YOKE之间的连接 Fig. 2 The joint between pendant and YOKE |
根据DNV-OS-A101给出的碰撞分析要求,给定排水量为5 000 t的撞击船以2 m/s的速度垂直于平台舷侧碰撞,撞击位置为船体后侧距船中15.2 m的堆舱处。
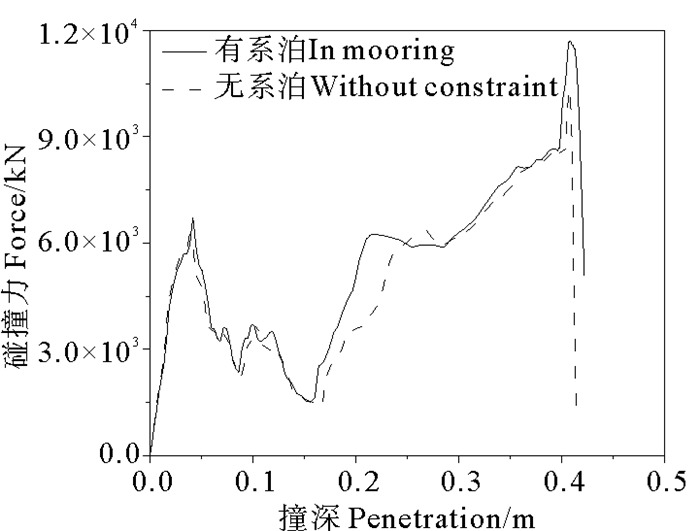
3 碰撞分析 3.1 碰撞力分析图 3对比了有、无系泊条件下碰撞力与撞深的关系曲线。由于系泊系统的约束作用,有系泊工况的最大碰撞力比无系泊大13.2%(1.4 kN),极限撞深大1.86%(0.007 7 m)。在曲线后半段(撞深0.3~0.45 m)上,两种工况的卸载路径均与相应的加载路径不同,说明碰撞力和撞深的关系具有路径相关性。
|
图 3 碰撞力-撞深曲线 Fig. 3 Curves of collision force against penetration |
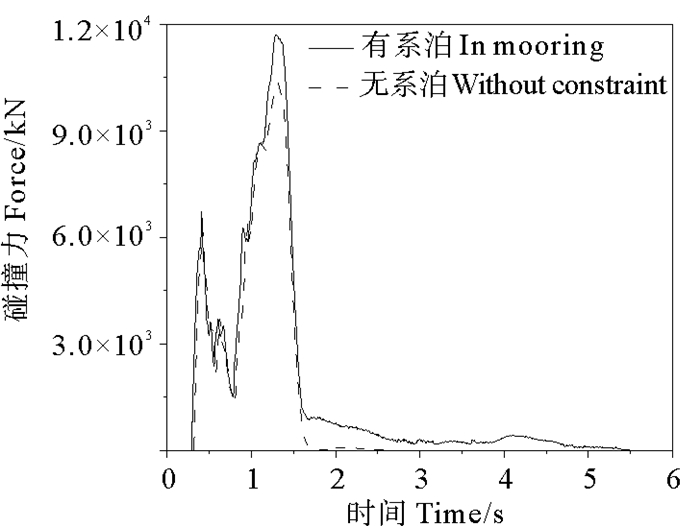
图 4展示了有、无系泊工况碰撞力随时间的变化趋势。由于碰撞中存在着大量的接触非线性,碰撞力经历多次加载和卸载过程,呈现反复波动的特征。碰撞力在0.36~0.76 s内显著下降,后又急剧上升。这是因为0.36 s之前,只有形状尖锐的撞击船上部与平台碰撞,接触单元的应力较大,碰撞力也因此较大;0.36~0.76 s内,撞击船上部因挤压发生形变,接触面积增大,应力也随之减小,碰撞力呈下降趋势;0.76 s后,撞击船下部球鼻艏也开始与舷侧接触,加速度急剧上升,使得碰撞力曲线呈上升趋势。1.3 s后,平台和船仍沿原方向运动,但彼此分离,碰撞力也随之降低。此外,对比两种工况的曲线情况,在0~1.3 s内,两种工况的曲线基本重合,说明此阶段系泊作用还未显现;在1.3 s后的碰撞力卸载阶段,无系泊工况的碰撞力直接降为0,而系泊工况降为0.25 kN(约为最大碰撞力的2%)左右并维持了约2.89 s,即有系泊工况的碰撞持续时间比无系泊长120%。
|
图 4 碰撞力时程曲线 Fig. 4 Time history curves of collision force |
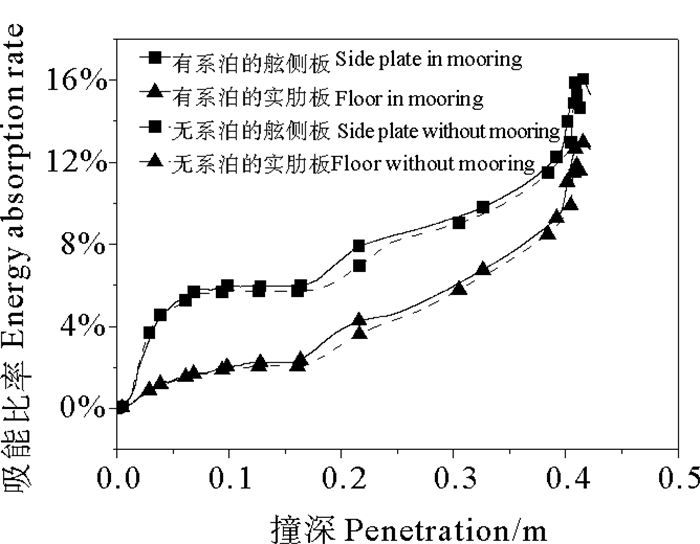
图 5比较了两种工况下平台舷侧外板和实肋板能量吸收的比率(结构变形吸收的能量与总能量的比值)。两种工况的同一舷侧结构在撞深0.1 m范围内吸能比率几乎相同;在0.1~0.4 m内,系泊工况比无系泊的吸能比大0.1%~0.9%;在最大撞深处,前者比后者大0.8%。撞击船的初始动能通过碰撞力做功,转化为平台的动能和舷侧构件的势能(即吸收的能量)。在系泊系统的约束作用下,碰撞强度和持续时间的增加导致碰撞力做功变大,因此舷侧构件的吸能比率也相应提高。对比同一工况的不同舷侧结构,舷侧外板的吸能比率比实肋板大2%~4%,在最大撞深处有、无系泊工况的舷侧外板吸能分别为15.3%和14.4%,实肋板吸能分别为12.6%和11.6%。舷侧板由于较大的膜拉伸变形,吸能较大,成为第一吸能构件,而实肋板因弯曲变形较小,吸能相对较少。
|
图 5 舷侧能量吸收时程曲线 Fig. 5 Time history curves of energy absorption |
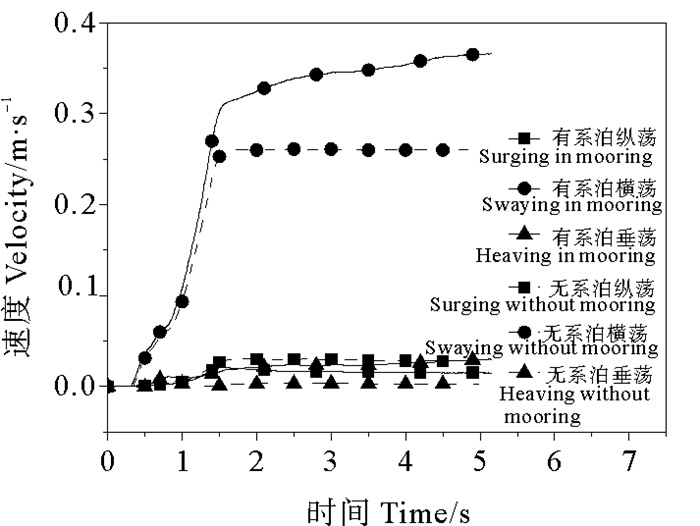
如图 6所示,碰撞结束时有系泊工况的横荡速度大于无系泊,分别为0.37和0.26 m/s,大约是撞击船初始速度2 m/s的18.5%和13%,而纵荡和垂荡速度均小于0.03 m/s,说明相当一部分初始动能转化为平台在Y方向的动能,X、Z方向的平动影响很小。
|
图 6 速度时程图 Fig. 6 Time history curve of velocities |
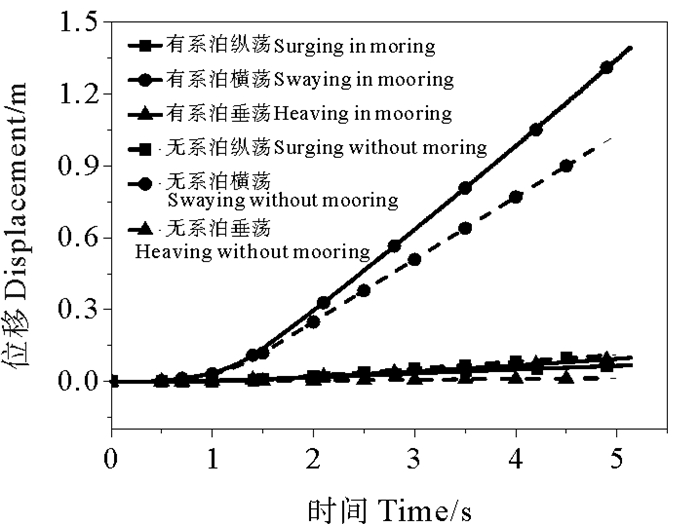
图 7中显示,在有、无系泊工况下横荡位移均最大,碰撞结束时达到1~1.5 m。而垂荡和纵荡位移在0.12 m以下,分别为横荡的7.19%和10.87%、4.77%和1.3%,说明在垂直舷侧碰撞中,平台最主要的运动是横荡,然而由于碰撞力的偏心作用,平台发生弯曲变形,产生了少量的垂荡和纵荡位移。
|
图 7 位移时程曲线 Fig. 7 Time history curve of displacements |
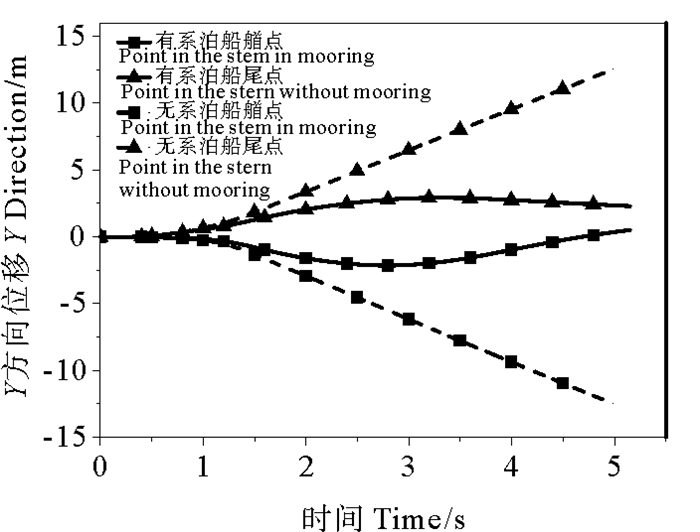
在Y方向上,一方面,有系泊状态的碰撞强度更大、持续时间更长,因此平台重心的横荡位移较大。在图 7中,1.5 s后有、无系泊工况的横荡位移近似线性地增加至1.53和1.03 m,前者始终大于后者,并比后者高48.50%。另一方面,系泊系统对平台的整体偏转有限制作用,平台艏、尾位移远小于无系泊状态。图 8显示,有系泊的艏、尾位移在3 m以下,仅为无系泊工况的25%。
|
图 8 Y方向位移时程曲线 Fig. 8 Time history curve of displacements in Y direction |
无系泊状态下的碰撞过程可近似看做二维碰撞,如图 7所示,垂荡位移只有0.0137 m,远小于X、Y方向的位移,可忽略不计。而在有系泊工况下,由于多体系统间的作用,平台在三个方向上的运动相互影响,因此纵荡和垂荡幅值分别降低和提高,导致碰撞扩展到三维空间。图中显示,在X方向,有系泊工况的纵荡位移始终小于无系泊工况,最大值为0.073 m,比后者低34.29%;在Z方向,垂荡位移则一直大于无系泊,在碰撞结束时上升到最大值0.11 m,是后者的8.1倍。
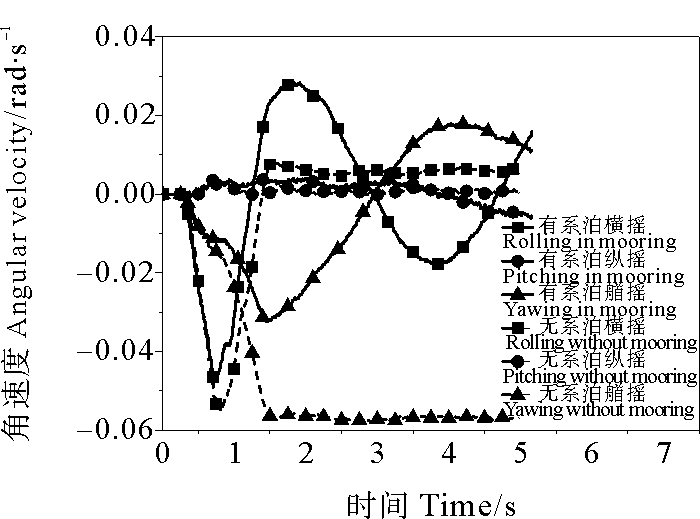
在图 9中,平台在横摇、纵摇和艏摇角速度幅值在0~0.06 rad/s,由此判断,仅有少部分初始动能转化为平台的转动动能。其中纵摇角速度在零值附近波动,并且幅值极小,可忽略不计。与无系泊工况不同,有系泊工况横摇和艏摇的变化趋势近似正弦曲线,有一定的周期性。
|
图 9 角速度时程图 Fig. 9 Time history curves of angular velocities |
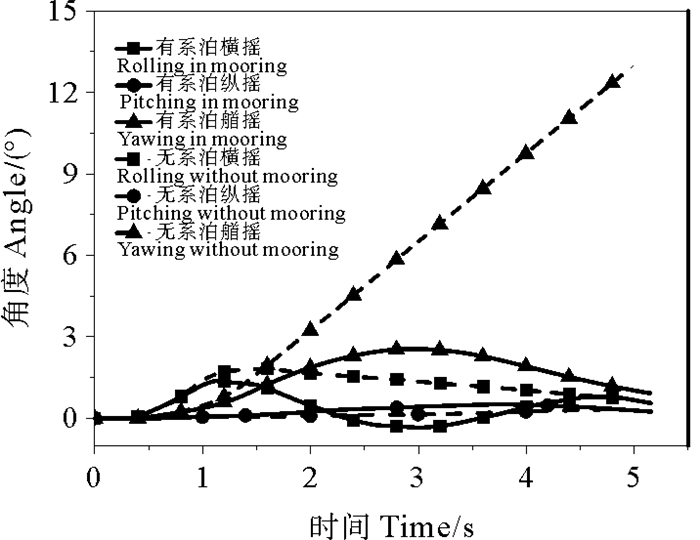
在图 10中,两种工况均是艏摇角度最大,横摇和纵摇角度幅值分别为艏摇的53.51%和14.11%、19.92%和2.78%,说明平台三个方向的旋转运动都比较明显,而艏摇最为剧烈。
|
图 10 角度时程图 Fig. 10 Time history curves of angles |
与平动位移类似,系泊系统极大地限制了平台的艏摇运动,同时平衡了纵摇和横摇运动。图 9中显示,有系泊工况的艏摇角度始终远小于无系泊,其艏摇角度在3s时刻达到最大值2.56°,比无系泊工况的12.91°小80.17%;横摇角度于1.12 s达到最大值1.37°,比无系泊工况小25.05%;有系泊工况的纵摇角度于3.75s上升至最大值0.51°,比无系泊大41.67%。
总体来看,两种工况平台的运动情况有所不同:无系泊工况下平台的运动集中在X-Y平面内,发生剧烈的横荡和小幅纵荡运动,产生明显的右倾,同时匀速地顺时针旋转;有系泊工况下平台也发生右倾,在六个自由度上的运动均有变化,其中横荡、垂荡和纵摇幅值较大,艏摇、横摇和纵荡位移明显减小。
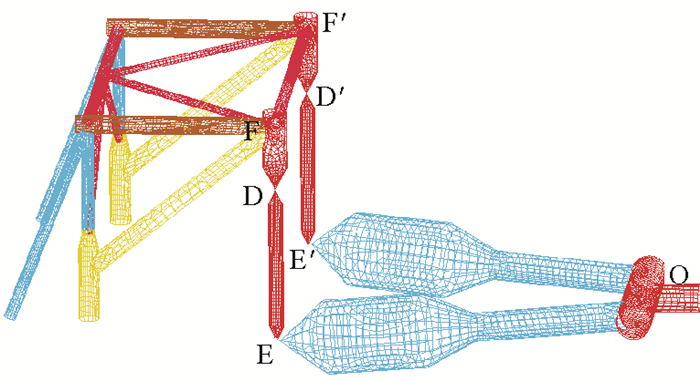
3.4 平台运行轨迹分析系泊条件下,平台的系泊装置是整个多体系统的重要部分,其运动状态也影响着主船体的运动。将MSS与连接臂、连接臂和YOKE的铰点定义为D和D’、E和E’,YOKE的铰支端点定义为O,如图 11所示。
|
图 11 系泊系统模型图 Fig. 11 the model of mooring system |
图 12和13展示了铰点E和E’、D和D’的运动轨迹在3个平面上的投影,分别反应了YOKE和连接臂的运动情况。

|
图 12 YOKE与连接臂铰点E、E’路径投影图 Fig. 12 The projected paths of points E and E' |

|
图 13 YOKE与连接臂铰点D、D’路径投影图 Fig. 13 The projected paths of points D and D' |
图 12(a)和(b)显示,E和E’在Y-Z和X-Z平面上的路径完全对称,并且X-Y平面内的轨迹近似于直线(拟合度高达99%),拟合后的关系式为y=1.04×10-3-2.40x和y=-9.84×10-4+2.49x,可推断YOKE在过这两条直线的竖直平面内做圆周运动。由于受撞击位置的影响,YOKE左右两侧的运动趋势不同,因此两铰点的轨迹形状差异很大。E、E’在Z方向的位移变化范围分别是-0.3~0.2 m和-0.35~0.15 m,是X、Y的变化范围的10~20倍,说明YOKE在Z方向的运动更剧烈。
D和D’与平台主船体焊接在一起,又与连接臂的端点相耦合,其运动轨迹是复杂的三维曲线,如图 12所示,其中Y方向的范围(-2~0.5 m)均为是X、Z的5倍。此外,D和D’点在X-Y平面内的轨迹关于Y轴(x=0)近似对称,即X方向位移反向,验证了3.3中的结论:连接臂对主船体的艏摇运动施加了回复力约束。
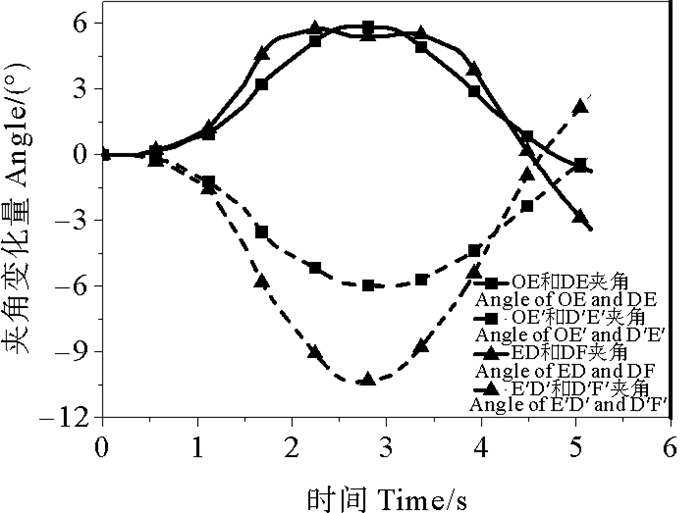
在图 14中,连接臂和YOKE(左侧OE和DE、右侧OE’和D’E’)、MSS和连接臂(左侧ED和DF、右侧E’D’和D’F’)的夹角随主船体平动和旋转运动而变化,其变化量的时程图线与正弦曲线近似。OE和DE、OE’和D’E’的曲线大致对称,变化范围分别是-1.35°~5.88°和-6.05°~0.86°;ED和DF、E’D’和D’F’在-4.98°~5.79°和-10.42°~4.23°变化,说明同侧的两个夹角同增减(变化量同号),异侧相反(变化量反号);两侧的连接臂和YOKE夹角变化量基本相同,而右侧的MSS和连接臂夹角约为左侧的2倍。
|
图 14 系泊系统各部分夹角变化量时程曲线 Fig. 14 Time history curves of angle in mooring system |
(1) 单点系泊状态下的平台在船舶侧向垂直撞击过程中,碰撞强度、作用时间及极限撞深均显著增加,舷侧结构的能量吸收比率也相应提高。
(2) 系泊系统的约束作用对平台的运动响应有较大影响:横荡速度和位移显著增加,但整体偏转幅度降低(即艏尾位移减小);出现垂荡位移,碰撞过程由二维扩展到了三维,并且在该方向上平台振动明显,速度波动较大;在系泊系统提供的回复力作用下,横摇和艏摇的角速度和角度幅值降低,沿近似正弦曲线变化。
(3) 系泊系统左右两侧的运动情况差异较大,应分开考虑。YOKE的两臂在不同的竖直平面内做圆周运动,在竖直方向运动最剧烈。连接臂在三维空间做复杂的曲线运动,其左右两侧沿船长方向交替错动,控制平台的艏摇角度。
| [1] |
顾永宁, 胡志强, 高震. 船舶碰撞与触底事故的数值仿真[J]. 上海交通大学学报, 2003, 37(8): 1176-1180. Gu Yongning, Hu Zhiqiang, Gao Zhen. Numerical simulation of ship collision and grounding accident[J]. Journal of Shanghai Jiaotong University, 2003, 37(8): 1176-1180. DOI:10.3321/j.issn:1006-2467.2003.08.009 (  0) 0) |
| [2] |
Getter D J, Kantrales G C, Consolazio G R, et al. Strain rate sensitive steel constitutive models for finite element analysis of vessel-structure impac[J]. Marine Structures, 2015, 44: 171-202. DOI:10.1016/j.marstruc.2015.09.001
(  0) 0) |
| [3] |
Ehlers Sören. The influence of the material relation on the accuracy of collision simulations[J]. Marine Structures, 2010, 23(4): 462-474. DOI:10.1016/j.marstruc.2010.12.002
(  0) 0) |
| [4] |
Minorsky V U. An analysis of ship collisions with reference to protection of nuclear power plants[J]. Journal of Ship Research, 1957, 3(2).
(  0) 0) |
| [5] |
Pedersen P T, Zhang S. On impact mechanics in ship collisions[J]. Marine Structures, 1998, 11(10): 429-449. DOI:10.1016/S0951-8339(99)00002-7
(  0) 0) |
| [6] |
Stronge W J. Impact mechanics[J]. Impact Mechanics, 2004, 100.
(  0) 0) |
| [7] |
Liu Z, Amdahl J. A new formulation of the impact mechanics of ship collisions and its application to a ship-iceberg collision[J]. Marine Structures, 2010, 23(3): 360-384. DOI:10.1016/j.marstruc.2010.05.003
(  0) 0) |
| [8] |
Wehage R A, Haug E J, Beck R R, et al. Generalized coordinate partitioning in dynamic analysis of mechanical systems[J]. ASME Journal of Mechanical Design, 1982, 104(1): 247-255. DOI:10.1115/1.3256318
(  0) 0) |
| [9] |
Khulief Y A, Shabana A A. Dynamic analysis of constrained system of rigid and flexible bodies with intermittent motion[J]. American Society of Mechanical Engineers, 1986, 10(1): 38-45.
(  0) 0) |
| [10] |
Pereira M S, Nikravesh P. Impact dynamics of multibody systems with frictional contact using joint coordinates and canonical equations of motion[J]. Nonlinear Dynamics, 1996(1-2): 53-71.
(  0) 0) |
| [11] |
白金泽. LS-DYNA3D理论基础与实例分析[M]. 北京: 科学出版社, 2005. Jinze Bai. Theoretical Basis and Case Analysis of LS-DYNA3D[M]. Beijing: Science Press, 2005. (  0) 0) |
| [12] |
陆佑方. 柔性多体系统动力学[M]. 北京: 高等教育出版社, 1996. Lu Y F. Flexible Multi-Body Dynamics[M]. Beijing: Higher Education Press, 1996. (  0) 0) |
| [13] |
胡志强, 高震, 顾永宁. Y型浮式生产储油轮船侧结构耐撞性[J]. 上海交通大学学报, 2005, 39(5): 706-710. Hu Zhiqiang, Gao Zhen, Gu Yongning. Research on the crashworthiness of a Y-shape side structure design for FPSO[J]. Journal of Shanghai Jiaotong University, 2005, 39(5): 706-710. DOI:10.3321/j.issn:1006-2467.2005.05.010 (  0) 0) |
 2019, Vol. 49
2019, Vol. 49

