在中国2030年“碳达峰”与2060年“碳中和”目标的推进过程中,清洁可再生能源的开发利用是核心问题。海上风电具有发电效率高、时间长、噪声影响弱、开发空间广阔等优势,是中国能源结构优化的重要组成部分。随着中国海上风电开发不断推进,固定式基础将难以满足环境以及大功率风机的结构支撑要求,海上风电走向深远海域已是必然趋势。而漂浮式风电基础在50 m以上水深环境中具有显著经济性优势,将成为未来海上风电的重点发展方向。
目前浮式基础的研究主要针对200 m以上的水深环境[1-3]。然而,中国海域地势大陆架宽阔,水深变化缓慢,适宜建造海上风电结构的海域主要在100 m以下的水深范围。水深对浮式风电基础结构的水动力特性和波浪荷载具有显著影响。因此,研究浅水环境下浮式风电结构分析方法及运动特征,形成符合中国国情的漂浮式风电基础结构设计的参考依据,对中国海上风能资源开发具有实际工程的意义。
目前,针对浅水浮式风电结构的相关研究较少。Choi等[4]应用基于不可压N-S方程的两相流模型和处理自由液面的流体体积法的三维数值模型研究了作用于浅海浮式风机基础的非线性波浪力。Pokhrel等[5]模拟作用于浅海风机的风浪荷载,并以易损性曲线的形式对其进行了易损性分析。Wang[6]发展了一种变换的线性仿真方法来等效模拟作用于浅海浮式风电的非线性波浪力。Yin等[7]对13.2-MW的大型浅海浮式风机在工作海况和极端海况下的动力响应进行了模拟分析。钟驰[8]针对50 m水深的浅海浮式风电系泊系统开展研究,通过等效水平截断设计使其满足运动特性等效并对截断结果进行了分析与验证。Xu等[9]针对5-MW半潜式风机分析了50 m水深下包括悬链线式和张紧式在内的七种系泊设计方案。
当浮式风电结构处于浅水环境时,波浪和结构水动力特性的非线性特征更为显著,导致其对结构动力响应的影响机理更加复杂。其一,在浅水条件下,应用线性波理论来描述波浪不够精确;其二,浅水浮式结构的固有周期、阻尼比等结构动力特性参数相较于深水,受海洋环境影响更为显著;其三,波浪荷载非线性特性增强,传统的基于势流理论的分析方法无法考虑二阶以上速度势,求解浅水波浪力将产生较大误差。因此,本研究采用基于黏性流理论的计算流体动力学(Computational Fluid Dynamics,CFD)方法,应用naoe-FOAM-SJTU求解器[10]建立波浪与OC4-DeepCwind半潜式风机基础相互作用的数值分析模型,根据结构固有周期、阻尼比和规则波下幅值响应算子RAO等水动力参数的计算结果,深入探讨浮式风机基础的水动力特性随水深的变化规律,并分析浅水条件下结构受到的波浪荷载特性,提供浅水浮式风电基础结构设计参考。
1 数值方法 1.1 求解器简介与求解流程naoe-FOAM-SJTU是基于OpenFOAM开发的船舶与海洋工程CFD求解器,包括数值波浪水池和六自由度运动模块,采用动网格技术处理结构运动,能够模拟空气-水两相流场以及流场与结构之间的相互作用,可用来对结构在风浪流作用下的动力响应进行实尺度上的数值模拟[11-13]。
应用求解器对流场和结构进行计算时可分为以下几个步骤:(1)读取计算域网格信息以及初始条件和边界条件,对流场进行初始化;(2)确定自由液面位置,求解控制方程,得到各网格的速度和压力,基于壁面网格的压力计算结构受力;(3)根据结构受力计算结构的速度、加速度和位移;(4)进入下一时间步,更新网格,重复步骤(2)和(3),直至完成全部计算。
1.2 控制方程本研究数值分析的控制方程为不可压黏流RANS方程[13]:
| $ \nabla \cdot U=0, $ | (1) |
| $ \begin{gathered} \frac{\partial \rho U}{\partial t}+\nabla \cdot\left[\rho\left(U-U_{\mathrm{g}}\right) U\right]= \\ -\nabla p_{\mathrm{d}}-g \cdot x \nabla \rho+\nabla \cdot\left(\mu_{\mathrm{eff}} \nabla U\right)+ \\ (\nabla U) \cdot \nabla \mu_{\mathrm{eff}}+f_\sigma+f_{\mathrm{s}} 。\end{gathered} $ | (2) |
式中:U为流场速度,Ug为网格节点运动速度;pd=p-ρg·x,表示流场动压力,其数值为总压力减静水压力;g为重力加速度;ρ为流体密度;μeff=ρ(ν+νt),表示流体有效动力黏性系数,其中ν为运动黏性系数,νt为湍流涡黏系数;fσ为表面张力源项,fs为用于消波的源项[14]。
为求解RANS方程,本研究选取在CFD中应用广泛的两方程k-ω SST(Shear stress transport)作为湍流模型,模型方程为:
| $ \frac{{D\rho k}}{{Dt}} = {\tau _{ij}}\frac{{\partial {u_i}}}{{\partial {x_j}}} + {\beta ^*}\rho \omega k + \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + {\sigma _k}{\mu _t}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right], $ | (3) |
| $ \begin{aligned} & \quad \frac{D \rho \omega}{D t}=\frac{\gamma}{\nu_t} \tau_{i j} \frac{\partial u_i}{\partial x_j}-\beta \rho \omega^2+\frac{\partial}{\partial x_j}\left[\left(\mu+\sigma_\omega \mu_t\right) \frac{\partial \omega}{\partial x_j}\right] \cdot \\ & 2 \rho\left(1-F_1\right) \sigma_\omega \frac{1}{\omega} \frac{\partial k}{\partial x_j} \frac{\partial \omega}{\partial x_j} 。\end{aligned} $ | (4) |
式中:F1为网格与结构表面距离的函数,当距离结构表面较近时,F1趋向于1,即采用标准k-ω模型;在远离结构壁面的区域F1趋向于0,即采用标准k-ε模型[14]。本研究中,初始时刻湍动能k=0.4 m2/s2,湍动耗散率ω=8.587 s-1。
1.3 数值造波与消波对波浪的数值模拟是否准确直接影响到波浪作用下基础结构运动响应和受力的计算结果。求解器包含数值波浪水池,本研究通过设置入口造波条件的方法来模拟Stokes二阶波[15],其波面方程为:
| $ \left\{\begin{array}{l} \eta=a_1 \cos (k x-\omega t)+a_2 \cos 2(k x-\omega t) \\ a_1=\frac{H}{2} \\ a_2=\frac{\pi H^2}{4 L}\left(1+\frac{3}{2 \sinh ^2 k d}\right) \operatorname{coth} k d \end{array}\right. $ | (5) |
式中:η为波面高程;H为波高;k为波数;ω为波浪圆频率;L为波长;d为水深。
为减轻来自计算域出口边界的波浪反射,在出口边界附近设置海绵层(Sponge layer)阻尼消波区,通过在动量方程中添加源项fs来实现消波功能[16]。
2 计算模型与网格 2.1 计算模型风机基础的试验模型和数值计算模型如图 1所示。

|
图 1 OC4-DeepCwind半潜式风机基础试验模型[17](a)及数值计算模型(b) Fig. 1 (a) Experimental[17] and (b) numerical models of the OC4-DeepCwind semi-submersible wind turbine foundation |
基础由一根主立柱、三根侧立柱(每根侧立柱均包括上部立柱和底部立柱)和多条横撑及斜撑组成,关键结构参数见表 1,几何参数见表 2。将风机基础的形心定为xOy平面的原点,初始时刻自由液面的高度为z=0,波浪传播方向为x轴正方向。波浪从计算域入口传播至风机基础位置处的距离为1个波长,计算域出口前的消波区为1.5个波长。
|
|
表 1 风机基础结构基本参数 Table 1 Structural parameters of the wind turbine foundation |
|
|
表 2 风机基础几何参数 Table 2 Geometric parameters of the wind turbine foundation |
为了验证基础结构数值模型网格划分的准确性,本研究通过基础的自由衰减运动进行网格收敛性验证。选取基础垂荡运动,给定-2 m/s的初始速度,对比在238×104、696×104以及908×104三种不同计算网格数量下基础自由衰减运动的时历曲线(见图 2), 可以看出,这三种网格数量对基础垂荡固有周期的模拟结果较为接近,但对阻尼的模拟存在差距。696×104和908×104这两种计算网格数量对基础垂荡自由衰减运动的模拟较为一致,因此选取696×104网格作为总计算网格数量以兼顾计算结果的准确性与计算效率。
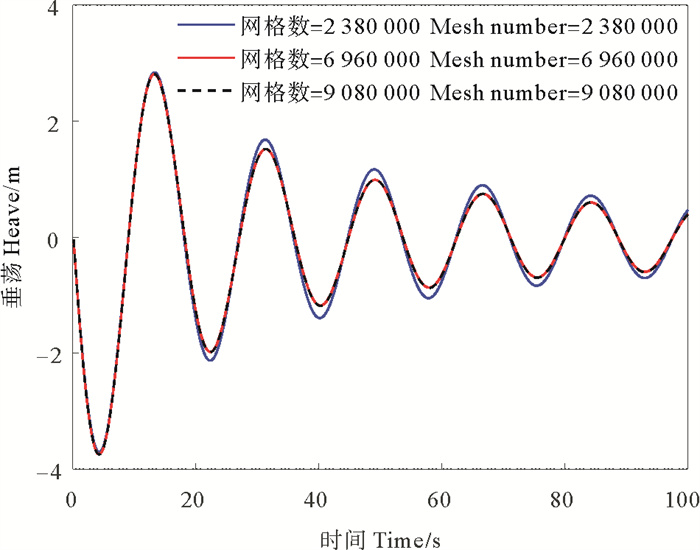
|
图 2 基础垂荡自由衰减运动网格收敛性验证 Fig. 2 Verification of grid convergence by free decay motion in heave |
图 3展示了经过网格收敛性验证的总体计算域网格。为提高计算精度,对自由液面附近的网格进行了加密处理(见图 4), 保证沿波浪传播方向每个波长的距离有至少80个网格,沿垂直于水平面方向每个波高的距离有至少10个网格。基础结构表面网格的加密原则为保证边或面的弯曲角度小于10°。
|
图 3 总体计算域网格示意图 Fig. 3 Sketch of overall computational domain |
|
图 4 自由液面附近区域网格示意图 Fig. 4 Sketch of grids near free surface |
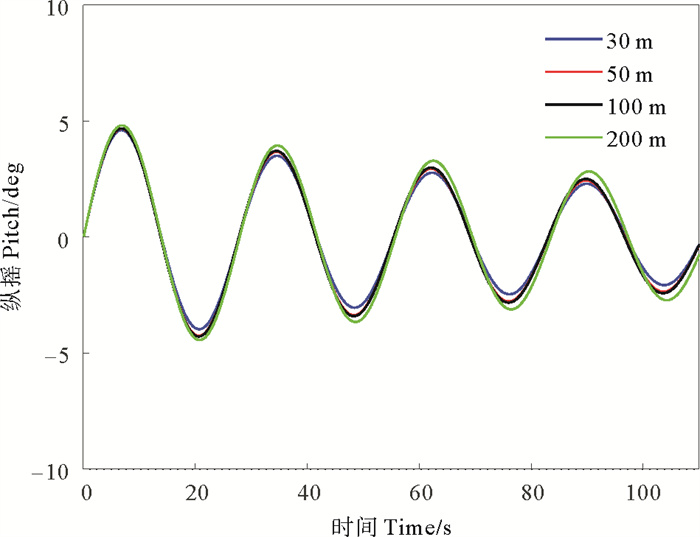
为探究水深对浮式基础结构动力特性的影响,本研究选取30、50、100和200m四种不同水深,进行基础结构自由衰减运动的模拟。为体现基础本身的水动力特性,排除不同水深下系泊系统造成的差别,本节的计算模型均去除基础的系泊系统,对除垂荡和纵摇外的自由度施加约束。在不同水深下给处于静水环境的基础施加相同的初始速度,使其分别在垂荡和纵摇方向作自由衰减运动,模拟结果如图 5和6所示。从图中可以看出,水深变化对于基础结构固有周期及阻尼比都会产生影响, 随着水深降低,基础垂荡固有周期略微增大,纵摇固有周期略微减小,而阻尼比则明显增大。
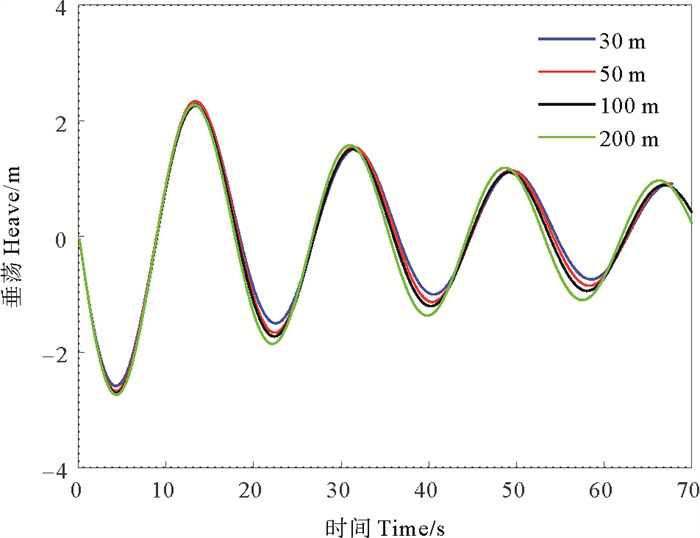
|
图 5 垂荡自由衰减运动时历曲线 Fig. 5 Time history of the free decay tests in heave |
|
图 6 纵摇自由衰减运动时历曲线 Fig. 6 Time history of the free decay tests in pitch |
按照式(6)计算得到基础在不同水深下垂荡和纵摇方向的固有周期和阻尼比:
| $ \left\{\begin{array}{l} y(t)=A e^{-\zeta \omega t} \sin \left(\sqrt{1-\zeta^2} \omega t+\nu\right) \\ A=\sqrt{y_0^2+\left(\frac{\dot{y}_0+\zeta \omega y_0}{\sqrt{1-\zeta^2 \omega}}\right)^2} \\ \nu=\tan ^{-1}\left(\frac{\sqrt{1-\zeta^2} \omega y_0}{\dot{y}_0+\zeta \omega y_0}。\right) \end{array}\right. $ | (6) |
式中:y为结构运动的线位移或角位移;t为时间; ζ为阻尼比; ω为固有频率; ν为结构运动的初相位; y0为初始位移。
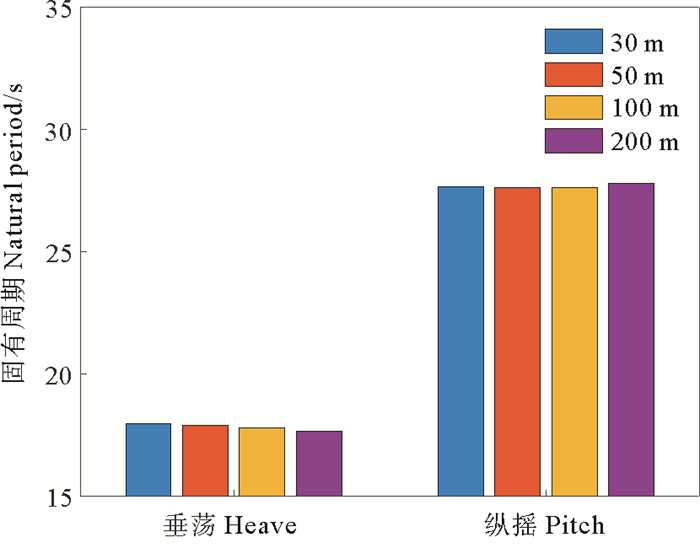
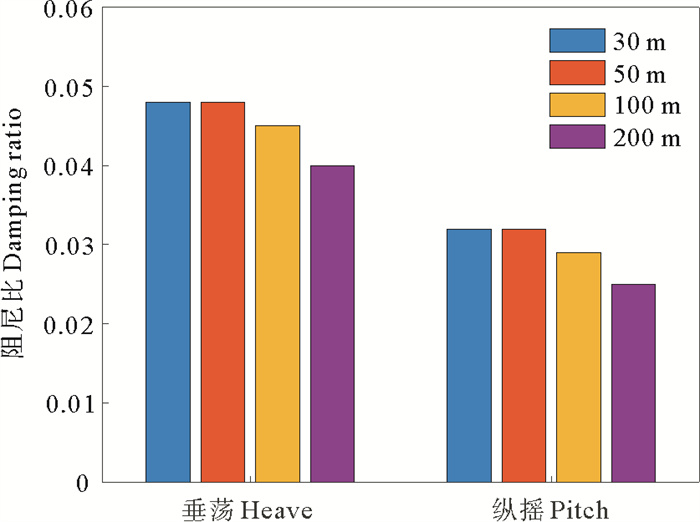
固有周期和阻尼比的具体结果如图 7和8所示。当水深从200 m逐渐减小到30 m时,风机基础结构垂荡方向的固有周期增加约1.8%,纵摇固有周期减小约0.5%。由于不同水深下基础质量和水线面面积不变,因此基础垂荡方向回复刚度相同。不同水深下基础水线面面积矩及重心与浮心高度差不变,因此基础纵摇方向回复刚度也相同。垂荡固有周期随水深的变化规律可能是由于水深减小时基础的附加质量略有增大,随着水深的减小基础阻尼比增加显著,其中30 m水深的垂荡阻尼比相比200 m水深增加约20%,纵摇阻尼比增加约28%。由此可见,对于该类结构在深、浅水环境下结构的固有周期基本不变,而阻尼比所引起的变化则较为显著。
|
图 7 垂荡和纵摇固有周期 Fig. 7 Natural periods in heave and pitch |
|
图 8 垂荡和纵摇阻尼比 Fig. 8 Damping ratios in heave and pitch |
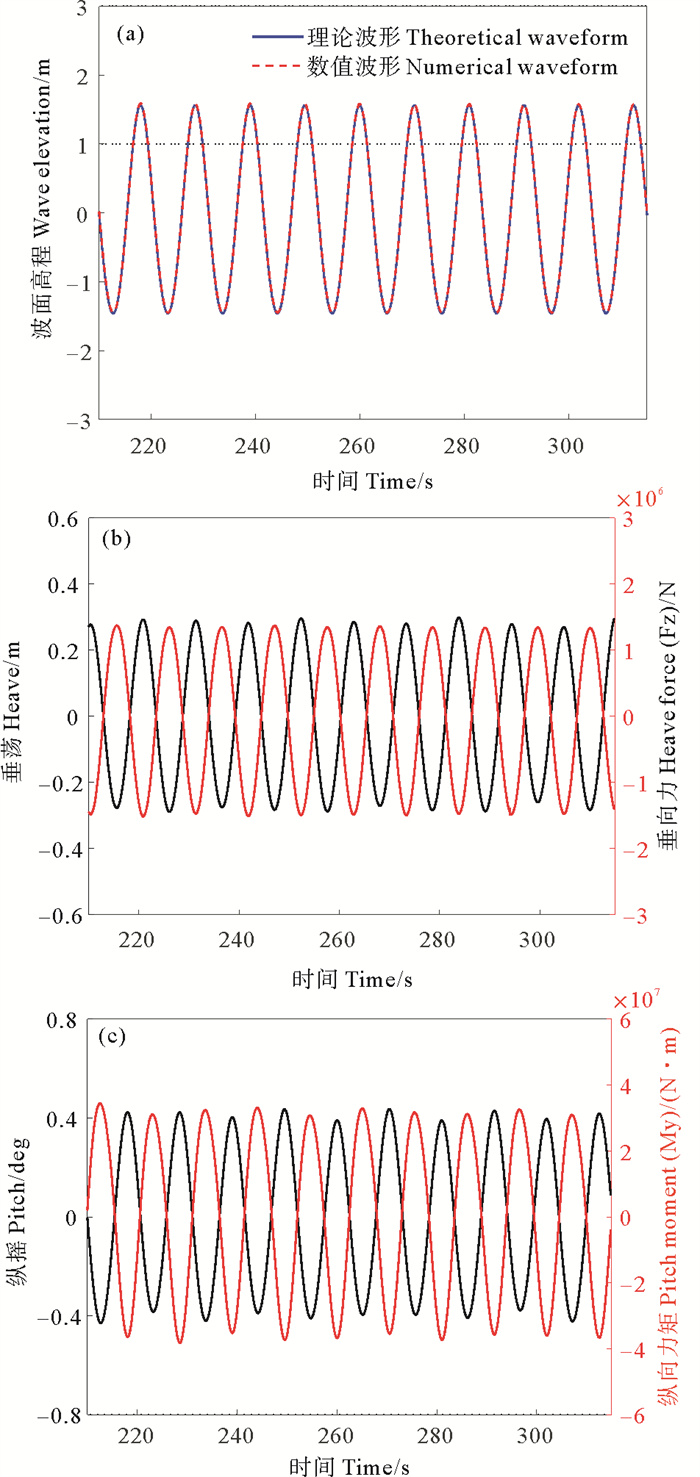
为探究水深对风机基础在波浪作用下的运动响应特性的影响,选取30、50和100 m三种不同水深条件进行波浪作用下的运动模拟。重点关注垂荡和纵摇两个自由度上的动力响应特性,因此将其他四个自由度固定,以水深d=50 m,波高H=3 m,波浪周期T=10.5 s的工况为例,选取稳定后的10个周期的时历曲线展示波浪及结构运动响应(见图 9)。
|
图 9 水深d=50 m,波高H=3 m,波浪周期T=10.5 s工况下基础前波面高程(a)、垂荡运动与垂向力(b)及纵摇运动与纵向力矩(c) Fig. 9 Wave elevation in front of the foundation (a), motion in heave and vertical force(b) and motion in pitch and longitudinal moment (c) when d=50 m, H=3 m and T=10.5 s |
从图中可以看出,经过20个波浪周期后,时历曲线已趋于稳定,且基础前波面高程与理论波形基本重合。此外,垂荡和纵摇响应与对应方向荷载的相位之差均接近π,这是由于垂荡和纵摇阻尼比较小,且波频与基础这两个自由度的固有频率之比较大。
为对比势流理论和黏性流理论对基础结构水动力特性的数值模拟结果,采用基于势流理论的SESAM软件建立半潜式风机基础的模型,并选择相同的波浪工况,分别计算出基础的RAO。基于时历曲线,按照式(7)计算得基础的垂荡和纵摇RAO:
| $ \left\{ {\begin{array}{*{20}{l}} {R{\rm{A}}{{\rm{O}}_3} = \frac{{{\chi _3}}}{\xi }}\\ {R{\rm{A}}{{\rm{O}}_5} = \frac{{{\chi _5}}}{\xi }} \end{array}{\rm{ }}} \right.。$ | (7) |
式中:RAO3和RAO5分别为垂荡和纵摇的RAO;χ3和χ5分别为垂荡和纵摇的幅值;ξ为波幅。
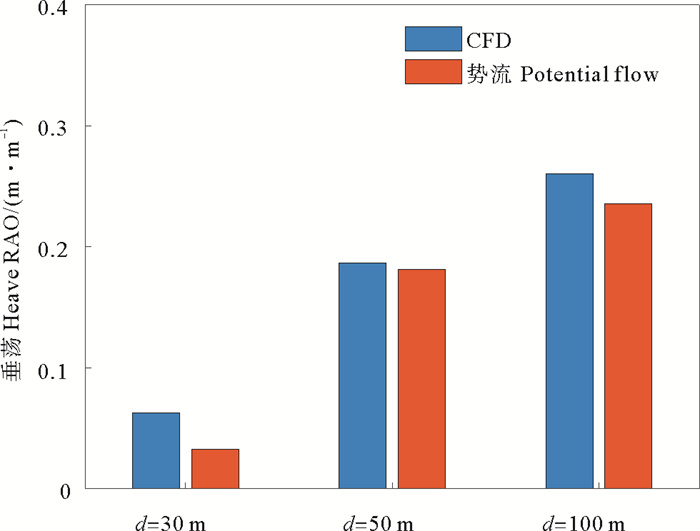
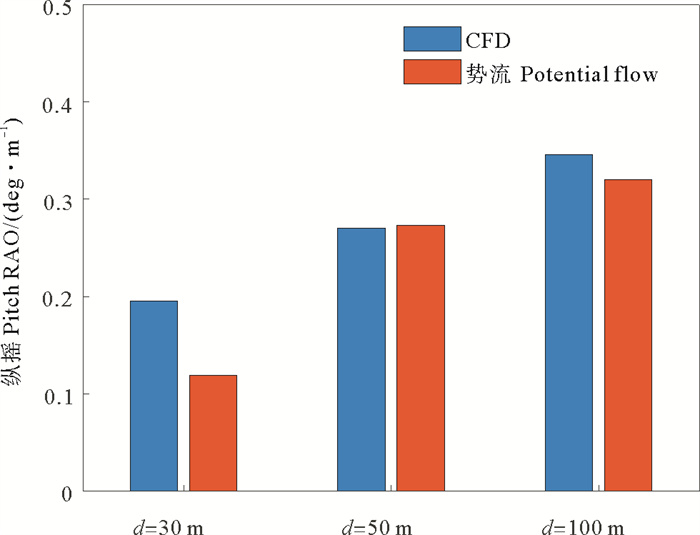
基于10个以上完整波浪周期的运动响应计算垂荡和纵摇RAO如图 10和11所示。从图中可以看出,势流理论和黏性流理论的计算结果随水深的变化规律相同,即RAO均随水深的降低而减小。在水深较大时,两种理论的计算结果吻合较好,但在浅水条件下,采用势流理论和黏性流理论计算得到的风机基础结构垂荡和纵摇RAO差距较大。水深为30 m时,采用势流理论计算得到的垂荡和纵摇RAO的数值仅分别为黏性流计算结果的52.63%和60.78%。由于势流理论无法考虑基础结构的运动与周围波浪场相互影响,因此该结果体现了浅水波浪的非线性和黏性对基础运动的显著影响。
|
图 10 波浪周期为10.5 s时的垂荡RAO Fig. 10 Heave RAO when T=10.5 s |
|
图 11 波浪周期为10.5 s时的纵摇RAO Fig. 11 Pitch RAO when T=10.5 s |
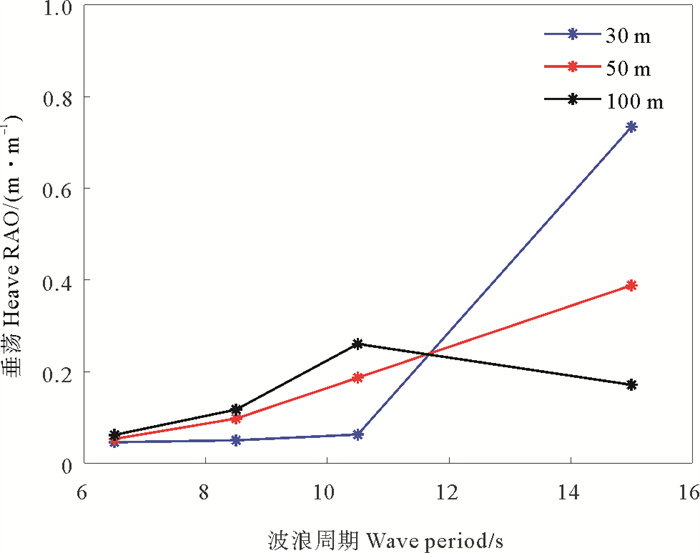
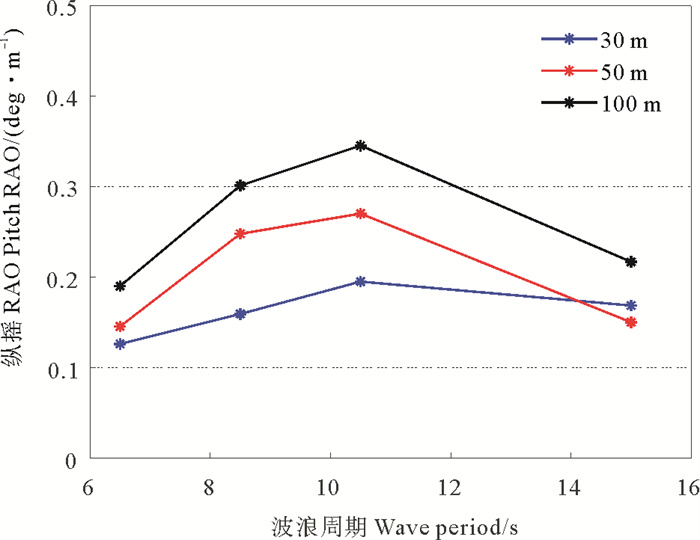
结构在不同波浪周期和水深下的RAO如图 12和13所示。由图可知,水深较小时垂荡RAO随周期增加而增加,这是由于基础垂荡固有周期约为17.5 s,波浪周期与之接近时共振程度提升,从而导致垂荡RAO增大。水深d=100 m条件下垂荡RAO随周期增加而先增加后减小,变化规律与水深较小时不同的原因在于d=100 m条件下垂荡固有周期和阻尼比相比于水深较小时均有所减小,这影响了基础运动响应与波浪周期之间的耦合程度。不同水深下纵摇RAO随周期增加而先增加后减小,其最大值均出现在周期T=10.5 s的工况下,造成这种现象的原因在于此工况下波长接近基础结构纵向长度的两倍,基础前后两端相对于波浪的相位接近π,导致所受纵向波浪力矩增大。周期较小时,垂荡和纵摇RAO随水深的降低而降低;周期较大时,垂荡RAO随水深的降低而增大,纵摇RAO呈现先减小后增大的趋势。
|
图 12 垂荡RAO随波浪周期变化 Fig. 12 Change of heave RAO with wave period |
|
图 13 纵摇RAO随波浪周期变化 Fig. 13 Change of pitch RAO with wave period |
计算不同水深下浮式风电基础结构的迎浪波浪力,通过快速Fourier变换(FFT)求得并绘制出频谱图(见图 14)。从图中可以看出,迎浪波浪力存在多个高阶频率成分,说明此时波浪荷载的非线性较强。由于在波浪作用下基础结构以波频运动且结构表面附近黏性较强,对周围流场产生了明显的干扰,从而影响波浪荷载的频率成分。
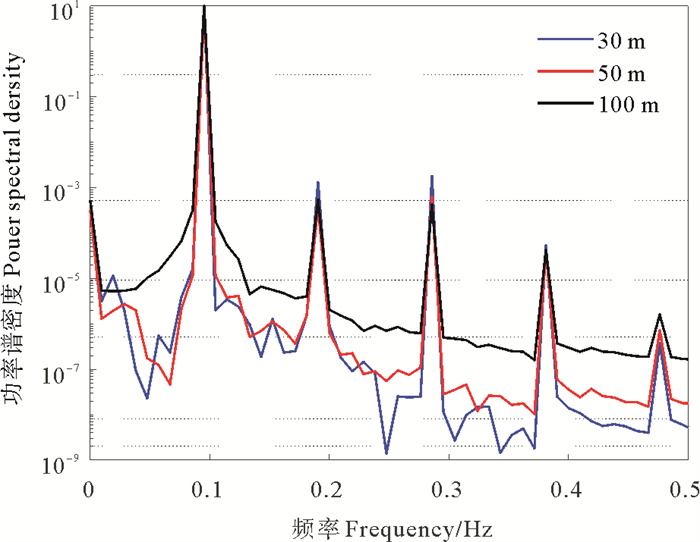
|
图 14 波浪周期T=10.5 s工况下迎浪波浪力频谱 Fig. 14 Spectrum of the wave load when T=10.5 s |
为对波浪荷载的非线性进行量化分析,采用傅里叶曲线拟合的方法将稳定后的波浪荷载时历曲线进行不同频率成分分解。波浪荷载经过傅里叶三阶曲线拟合后的结果可用下式表示:
| $ \begin{gathered} f(t)=a_0+a_1 \cos (\omega t)+b_1 \sin (\omega t)+ \\ a_2 \cos (2 \omega t)+b_2 \sin (2 \omega t)+ \\ a_3 \cos (3 \omega t)+b_3 \sin (3 \omega t) 。\end{gathered} $ | (8) |
式中:f(t)为波浪荷载;t为时间;ω为波浪频率;a0为平均漂移力;ancos(nωt)+bnsin(nωt)为n倍波频成分,其中n = 1, 2, 3。
为探究不同水深下波浪荷载的非线性特性,详细分析纵向力、垂向力和纵向力矩的三倍波频成分在波浪荷载中的占比(见图 15)。随着水深的减小,浮式风机基础结构所受波浪荷载三倍波频成分的占比逐渐增大。30 m水深的纵向力、垂向力和纵向力矩三倍波频成分占比相比于100 m水深在周期T=10.5 s时分别增长101%、642%和153%,周期T=15 s时分别增长120%、70%和123%。这说明在浅水波浪作用下,风机基础所受波浪荷载的非线性增强。因此,浮式风机基础结构在浅水波浪作用下的受力分析时应特别考虑高阶非线性波浪力的影响。
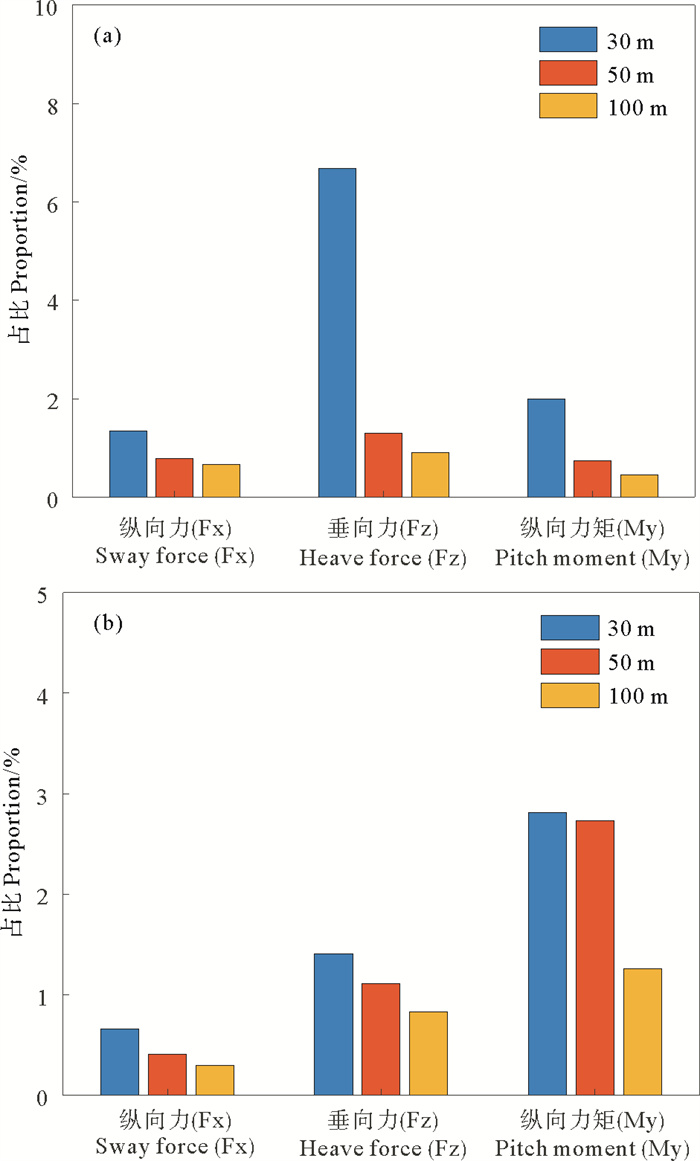
|
图 15 波浪周期(a) T=10.5 s及(b) T=15 s工况下波浪荷载三倍波频成分占比 Fig. 15 Proportion of the triple frequency wave load when (a) T=10.5 s and (b) T=15 s |
本研究采用CFD方法对OC4-DeepCwind半潜式风机基础在30~100 m水深下的水动力特性和非线性波浪荷载进行研究,得到如下结论:
(1) 水深变浅导致基础垂荡固有频率略微降低,但可引起基础阻尼比显著增加。
(2) 浅水条件下,势流计算结果会低估结构响应。
(3) 水深变浅导致波浪荷载中的高倍频成分显著增加,非线性效应明显,采用势流理论计算方法将低估波浪荷载与振动响应。
| [1] |
Jonkman J M. Dynamics Modeling and Loads Analysis of an Offshore Floating Wind Turbine[M]. Colorado: University of Colorado at Boulder, 2007.
(  0) 0) |
| [2] |
李嘉文. 新型海上风机浮式基础设计与风机系统耦合动力分析[D]. 天津: 天津大学, 2014. Li J W. A New Floating Platform Design and the Coupled Dynamic Analysis of the Offshore Wind Turbine System[D]. Tianjin: Tianjin University, 2014. (  0) 0) |
| [3] |
Robertson A, Jonkman J, Masciola M, et al. Definition of the Semisubmersible Floating System for Phase Ⅱ of OC4[R]. United States: National Renewable Energy Laboratory(NREL), Golden, CO, 2014.
(  0) 0) |
| [4] |
Choi S J, Lee K H, Hong K, et al. Nonlinear wave forces on an offshore wind turbine foundation in shallow waters[J]. International Journal of Ocean System Engineering, 2013, 3(2): 68-76. (  0) 0) |
| [5] |
Pokhrel J, Seo J. Natural hazard vulnerability quantification of offshore wind turbine in shallow water[J]. Engineering Structures, 2019, 192: 254-263. (  0) 0) |
| [6] |
Wang Y. Bottom effects on the tower base shear forces and bending moments of a shallow water offshore wind turbine[J]. Marine Structures, 2020, 70: 102705. (  0) 0) |
| [7] |
Yin L L, Lo K H, Wang S S. Structural Dynamics and Load Analysis of Large Offshore Wind Turbines in Western Gulf of Mexico Shallow Water[C]. America: International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2014, 45547: V09BT09A036.
(  0) 0) |
| [8] |
钟驰. 浅海浮式风机悬链系泊及水平截断模型的设计与分析[D]. 哈尔滨: 哈尔滨工业大学, 2019. Zhong C. Design and Analysis of Catenary Mooring for the Floating Offshore Wind Turbine in Shallow Water with its Horizontal Truncated Model[D]. Harbin: Harbin Institute of Technology, 2019. (  0) 0) |
| [9] |
Xu K, Larsen K, Shao Y, et al. Design and comparative analysis of alternative mooring systems for floating wind turbines in shallow water with emphasis on ultimate limit state design[J]. Ocean Engineering, 2021, 219: 108377. (  0) 0) |
| [10] |
李鹏飞. 海上浮式风机尾流场模拟及耦合动力分析[D]. 上海: 上海交通大学, 2016. Li P F. Numerical Simulation of Wake Flows and Coupled Aero-hydrodynamic Analysis of Floating Offshore Wind Turbines[D]. Shanghai: Shanghai Jiao Tong University, 2016. (  0) 0) |
| [11] |
Shen Z, Wan D. An irregular wave generating approach based on naoe-FOAM-SJTU solver[J]. China Ocean Engineering, 2016, 30(2): 177-192. (  0) 0) |
| [12] |
Wang J, Wan D. CFD investigations of ship maneuvering in waves using naoe-FOAM-SJTU solver[J]. Journal of Marine Science and Application, 2018, 17(3): 443-458. (  0) 0) |
| [13] |
Liu Y, Xiao Q, Incecik A, et al. Establishing a fully coupled CFD analysis tool for floating offshore wind turbines[J]. Renewable Energy, 2017, 112: 280-301. (  0) 0) |
| [14] |
程萍. 浮式风机气动-水动耦合复杂流场数值模拟[D]. 上海: 上海交通大学, 2019. Cheng P. Numerical Simulation of Complex Flows Around Floating Offshore Wind Turbine in Winds and Waves[D]. Shanghai: Shanghai Jiao Tong University, 2019. (  0) 0) |
| [15] |
曹洪建. 海洋工程粘性数值波浪水池开发及应用[D]. 上海: 上海交通大学, 2014. Cao H J. Development of Viscous Numerical Wave Tank and Its Application in Ocean Engineering[D]. Shanghai: Shanghai Jiao Tong University, 2014. (  0) 0) |
| [16] |
赵文超. 海上风机气动性能和浮式平台水动力计算分析[D]. 上海: 上海交通大学, 2015. Zhao W C. Numerical Simulation and Analysis on Aerodynamic Performance of Offshore Wind Turbine and Hydrodynamics of Floating Platform[D]. Shanghai: Shanghai Jiao Tong University, 2015. (  0) 0) |
| [17] |
Coulling A J, Goupee A J, Robertson A N, et al. Validation of a FAST semi-submersible floating wind turbine numerical model with DeepC wind test data[J]. Journal of Renewable and Sustainable Energy, 2013, 5(2): 023116. (  0) 0) |
 2023, Vol. 53
2023, Vol. 53


