成像声呐是一种主动声呐, 被广泛应用于海洋勘测、海底地形地貌构建以及失事沉船飞机打捞等场合, 在军事上也被应用在水雷探测等任务中[1]。目前市面上大多数成像声呐只能探测目标物体的距离和水平参数, 即二维成像声呐, 能够探测物体在水平、垂直以及距离3个方向参数的三维成像声呐实现难度较大, 研发成本较高, 因此只有少数国家进行了研究与设计[2-3]。
目前, 三维成像技术最为常见的实现方法是采用球面发射换能器进行球面波束的发射, 并通过二维平面接收阵列接收声呐回波信号, 系统进行实时计算生成上万个波束强度信号, 最终实现物体水平、垂直以及距离上的三维成像[3]。由英国Coda Octopus公司于2005年研发的世界上第一台商用水下三维成像声呐Echoscope Mark Ⅱ就是基于此种技术方案, 该系统使用48×48路规模的二维平面接收阵列, 形成128×128个波束强度信号, 其最大探测距离为200 m, 可视角度为50°×50°, 实时帧率最大为20帧/s[3-4]。在中国, 由浙江大学和中船重工715研究所在国家863计划海洋重大专项基金的支持下, 率先开展了三维声学成像技术的研究, 并于2010年成功研制了基于二维平面接收阵列的相控阵三维成像声呐, 填补了我国在水下三维成像领域的空白[3]。
但是, 基于二维面阵的水下成像系统有着以下不足之处:(1)硬件系统复杂。由于二维平面换能器数量较多, 导致与其相关的滤波、放大、信号采集、数字处理等电路规模庞大, 从而使声呐系统的体积较大、成本较高, 难以实现普及, 并且在浅滩水域的无法应用。(2)计算量庞大。由于需要实时生成的波束强度信号较多, 因此系统对波束形成的计算能力有着较高的需求。
为解决这些问题, 一种基于垂直线阵的水下三维成像技术逐渐发展并获得应用。垂直线阵作为一种优化的阵列配置方案, 有效解决了由于换能器数量多导致的系统硬件复杂度较高的问题。其原理是利用两个相互垂直的一维线阵分别进行发射和接收, 通过数据处理系统把扫描的结果进行三维图像合成。日本无线公司于1986年最先提出基于垂直线阵的水下成像技术, 并研制出了一种多波束海底测绘系统, 成功绘制了水下三维图[4]。丹麦Reson公司推出了一款基于垂直线阵的水下三维声呐系统, 其探测范围可达到120 m, 并具有120°的可视角度[5]。然而垂直线阵水下成像系统的实时性较差, 由于系统在成像过程中需要对整个观测场景进行逐一扫描, 过长的扫描时间导致系统成像帧率较低, 因此现阶段市面上的垂直线阵声呐只能应用于静止目标或无实时需求的场景。
在此背景下, 本文设计了一种基于垂直阵列的水下实时三维成像声呐系统, 该系统使用一种多频率发射波束形成算法(MFT), 通过优化垂直阵列的发射过程, 减少了波束发射的次数, 从而减少了阵列扫描时间, 提升了成像速度。同时系统在波束形成时使用并行子阵波束形成算法减小了波束形成的计算量, 提高了计算效率。本文设计的垂直线阵三维声呐在一定程度上解决了现阶段三维成像声呐系统硬件复杂、体积庞大、计算量庞大的问题, 满足了低功耗、小型化的三维声学成像需求。
1 系统原理 1.1 垂直线阵波束形成原理在二维平面阵三维声呐系统中, 发射阵一般只发射一组脉冲波束, 并由二维平面接收阵列独立完成所有波束形成的过程。垂直线阵由发射阵和接收阵共同形成整个系统的波束形成。
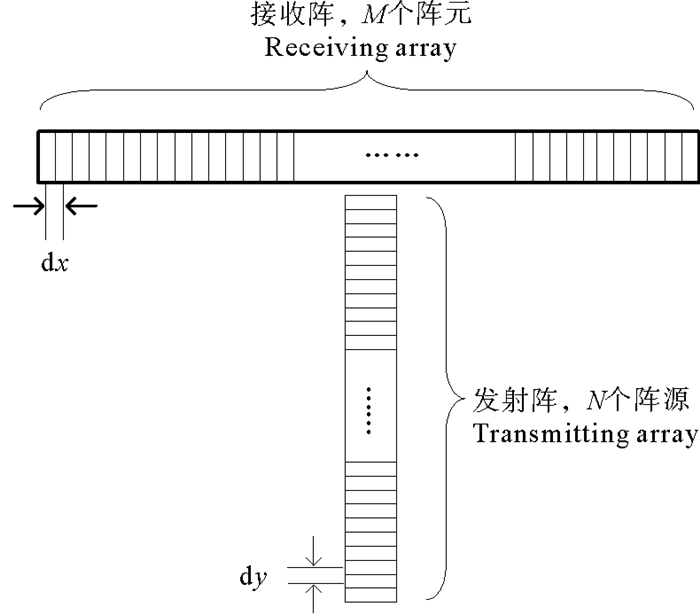
垂直线阵的阵列结构如图 1所示, 它由相互垂直的两条线阵构成。其中水平方向的阵列为接收阵列, 由M个接收阵元组成, 每个阵元之间的距离为dx。垂直方向的阵列为发射阵列, 由N个发射阵元组成, 每个阵元之间的距离为dy。
|
图 1 垂直线阵的阵列结构 Fig. 1 Structure of the vertical line array |
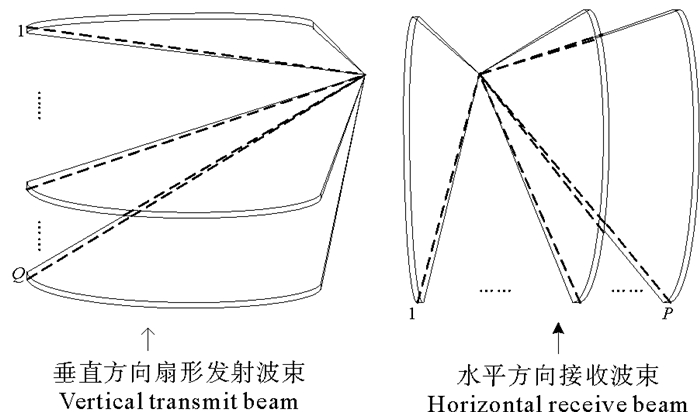
垂直线阵声呐系统工作时, 首先由垂直的发射阵列通过各个阵元之间的相位补偿, 向预设的垂直方向发射一条扇形窄带波束信号; 然后, 水平方向的接收阵列根据接收到的回波信号, 在发射波束的扇形窄带范围内进行水平方向的波束形成。当系统完成该截面的波束形成之后, 开始进行下一个垂直方向的波束发射, 重复此过程直到垂直方向上的波束发射完毕以及水平方向上波束形成完毕。垂直线阵的波束形成过程如图 2所示。
|
图 2 垂直线阵波束形成过程 Fig. 2 Beam-forming process of the vertical line array |
系统在垂直方向总共发射Q个扇形窄带波束, 在水平方向总共P个接收方向。因此整个波束形成过程中总共形成P×Q个波束结果。
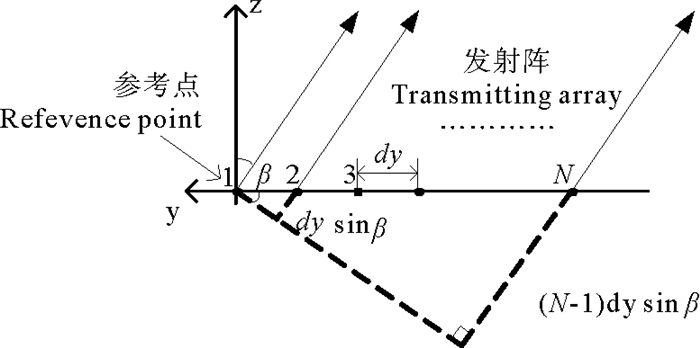
在远场条件下, 声呐的发射波束和接收波束均可看做平行波束进行处理。垂直线阵发射波束示意图如图 3所示。
|
图 3 垂直线阵发射波形示意图 Fig. 3 Beam transmitting figure of the array |
把发射阵与接收阵的交叉点作为参考点, 波束的发射角为β。则垂直线阵发射频域的波束强度可表示为:
| $ \left| {{B_T}} \right| = \left| {\sum\limits_{n = 1}^N {{S_n}\left( k \right)} \cdot{\rm{exp}}( - j(2{\rm{ \mathsf{ π} }}{f_0}\cdot\left( {n - 1} \right)dy\cdot{\rm{sin}}\beta /c))} \right|。$ | (1) |
其中:Sn(k)表示发射阵元的声纳信号经过L点DFT运算的结果; k为DFT变化的线谱号; c为声波在水下的传播速度, 约1 500 m/s; f0是声纳信号的中心频率。
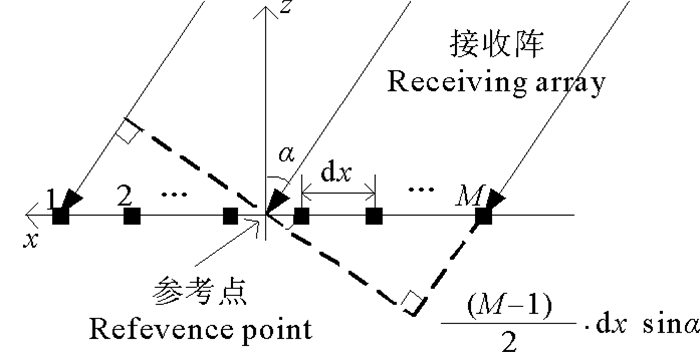
垂直线阵接收回波示意图如图 4所示。
|
图 4 垂直线阵接收波形示意图 Fig. 4 Beam receiving figure of the array |
波束的接收角为α。则垂直线阵接收频域波束强度可以表示为:
| $ \left| {{B_R}} \right| = \left| {\sum\limits_{m = 1}^M {{S_m}\left( k \right)} \cdot{\rm{exp}}( - j(2{\rm{ \mathsf{ π} }}{f_0}\cdot\left( {m - \frac{{M + 1}}{2}} \right){\rm{d}}x\cdot{\rm{sin}}\alpha /c))} \right|。$ | (2) |
其中:Sm(k)表示接收阵元的声纳信号经过L点DFT运算的结果; k为DFT变化的线谱号。
与二维平面接收阵列相比, 垂直线阵很大程度上减少了换能器的数量, 同时也有效降低了系统的计算量。在相同信号频率以及相同阵元间距的条件下, 垂直线阵可以使用M+N个阵元达到与二维平面接收阵列M×N个阵元近似的成像效果。但是, 垂直线阵相比于传统二维平面接收阵列有着固有的缺点, 垂直线阵成像帧率较低。若垂直线阵垂直方向发射波束数Q=60, 探测距离R=54 m, 则垂直线阵生成一帧图像的理论成像时间t0 = 2Rmax×Q/c=4.32 s, 由此可知垂直线阵的成像帧率太低, 完全无法满足水下实时成像的需求。
1.2 MFT算法根据垂直线阵波束形成过程可知, 在探测距离一定的情况下, 影响成像帧率的主要因素是波束发射次数, 因此减少发射次数是提高垂直线阵声呐系统成像速率的主要手段。在此背景下, 本文提出了一种多频率发射波束形成(MFT)算法。该算法将垂直方向的一系列扇形波束分成若干组, 发射时系统在每个组内依次发射不同频率的波束信号, 每个扇形波束对应一种特定的频率。接收时, 接收阵元收到回波信号后通过DFT运算抽取所有每个扇形波束对应的频率信息, 并在对应频域上完成波束形成的过程。
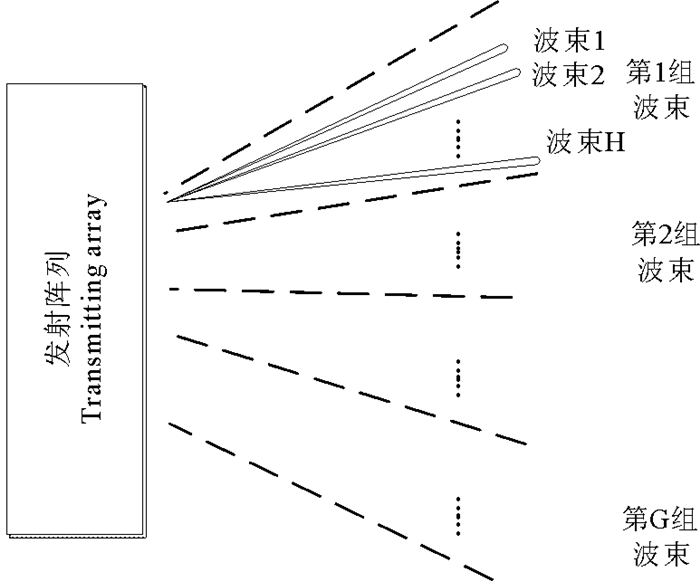
若系统垂直发射波束的方向数为Q个, 水平接收波束的方向数为P个, MFT算法具体实现过程是:首先, 将Q个方向顺次分为G组, 每组包含的方向数为H个, 即Q=G×H, 由发射阵列通过相位补偿依次往H个方向上发射不同频率的扇形波束, 每个扇形波束对应一个特定的频率; 然后, 当接收阵列接收到H个不同频率的回波之后通过DFT运算抽取所有波束对应的频率信息, 并在H个不同频域上进行波束形成计算, 获得P×H个波束强度结果; 最后, 系统对其余各组波束进行相同处理, 即可获得全部P×Q个结果。算法示意如图 5所示。
|
图 5 MFT算法示意图 Fig. 5 MFT algorithm map |
在MFT算法中, 发射角度为β, 则发射阵列的波束强度可表示为:
| $ \left| {{B_T}({f_h},\beta )} \right| = \left| {\sum\limits_{n = 1}^N {{S_n}({k_h})} \cdot{\rm{exp}}( - j{\theta _n}({f_h},\beta ))} \right|。$ | (3) |
其中θn(fh, β)为系统发射相位偏移参数, 表达方式如下:
| $ {\theta _n}({f_h},\beta ) = 2{\rm{ \mathsf{ π} }}{f_h}\cdot\left( {n - 1} \right){\rm{d}}y\cdot{\rm{sin}}\beta /c。$ | (4) |
Sn(kh)是声纳波束采样信号sn(l)经过L点DFT变换, 表达方式如下:
| $ {S_n}({k_h}) = \sum\limits_{l = 1}^L {{s_n}\left( l \right)} \cdot{\rm{exp}}( - j\frac{{2{\rm{ \mathsf{ π} }}}}{L}l\cdot{k_h})。$ | (5) |
fh为对应扇形波束的频率。
接收阵列的接收角度为α, 则接收阵列的波束强度可表示为:
| $ \left| {{B_R}({f_h},\alpha )} \right| = \left| {\sum\limits_{m = 1}^M {{S_m}({k_h})} \cdot{\rm{exp}}( - j{\theta _m}({f_h},\alpha ))} \right|。$ | (6) |
其中θm(fh, α)为系统接收相位偏移参数, 表达方式如下:
| $ {\theta _m}({f_h},\alpha ) = 2{\rm{ \mathsf{ π} }}{f_h}\cdot\left( {m - \frac{{M + 1}}{2}} \right)dx\cdot sin\alpha /c 。$ | (7) |
Sm(kh)是声纳波束采样信号sm(l)经过L点DFT变换, 表达方式如下:
| $ {S_m}({k_h}) = \sum\limits_{l = 1}^L {{s_m}\left( l \right)} \cdot{\rm{exp}}( - j\frac{{2\pi }}{L}l\cdot{k_h})。$ | (8) |
综上所述, MFT算法把垂直线阵的发射次数由垂直方向的波束个数Q变成了划分组数G, 也就是说, 若发射波分组数G=6时, 在54 m的范围内, 垂直波束个数Q=60的情况下, 成像时间由原来的t0 = 2Rmax×Q/c=4.32 s, 变成现在的t1 = 2Rmax×G/c=0.43 s, 大幅度缩短了系统成像时间, 从而使系统水下实时成像的需求成为可能。
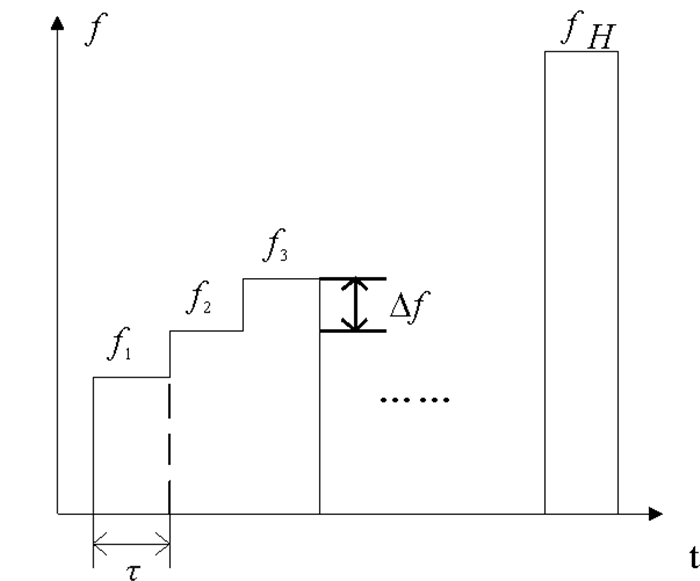
1.3 延时补偿为了保证系统在接收波束形成过程中, DFT变换能够完整抽取每个频率的信息, 从而避免多个频率的回波之间出现相互干扰, 发射波束时信号的脉冲宽度τ必须满足一定条件。
相邻波束的频率递增为Δf, 即:
| $ {f_{h + 1}} - {f_h} = \Delta f。$ | (9) |
则脉冲宽度的约束条件为:
| $ 1/\Delta f \le \tau 。$ | (10) |
每组发射波束的时域图见图 6。
|
图 6 发射波束时域图 Fig. 6 Time domain diagram of the transmit beam |
由于不同频率的信号按顺序先后发射, 因此相邻的信号之间存在宽度为τ的延时。信号的延时会导致空间上的距离误差, 因此需要对不同频率的信号进行延时补偿。为了避免增加系统资源开销, 由上位机根据不同频率信号的延时值进行相应的距离补偿。
各频率的延时值Th如下:
| $ {T_h} = \left( {h - 1} \right)\tau 。$ | (11) |
声信号在水中传播距离与时间的关系如下:
| $ z = \frac{{ct}}{2}。$ | (12) |
其中z为距离值, c为声波在水下传播速度。
因此不同频率信号补偿方式如下:
| $ z\prime = z - \frac{{c{T_h}}}{2} = z - \frac{{c\tau \left[ {h - 1} \right]}}{2}。$ | (13) |
使用该方法进行距离补偿之后就避免了由于信号延时产生的图像误差。图 7为水下现场实验中拍摄的一条笔直铁链, 从中可以看出经过延时补偿和未经过延时补偿在成像效果上的差别。

|
图 7 使用延时补偿 Fig. 7 Pictures of underwater imaging with |
为进一步分析基于MFT算法的垂直线阵三维成像声呐在简化系统复杂度方面的优势, 将该系统和传统二维面阵三维成像声呐分别进行计算量对比。
对于包含M×N个阵元的二维面阵, 首先要对M×N个通道进行L点的DFT变换, 每个通道进行一次DFT变换需要进行2L次实数乘法以及2(L-1)次实数加法, 则二维面阵DFT运算的计算量为:
| $ {O_M}\left( {DFT} \right) = \left[ {2L + 2\left( {L - 1} \right)} \right]\cdot M \cdot N = \left( {4L - 2} \right)\cdot M \cdot N $ | (14) |
其次, 波束形成过程中, 生成每个波束需要M×N次复数乘法以及M×N-1次复数加法, 由于M×N次复数乘法相当于4MN次实数乘法和2MN次实数加法, 则生成P×Q个波束需要的计算量为:
| $ {O_M}\left( B \right) = \left( {8MN - 2} \right)\cdot P \cdot Q 。$ | (15) |
因此, M×N个阵元的二维面阵生成P×Q个波束需要的总计算量为:
| $ {O_M} = {O_M}\left( {DFT} \right) + {O_M}\left( B \right) = \left( {4L - 2} \right)\cdot M\cdot N + \left( {8MN - 2} \right)\cdot P\cdot Q $ | (16) |
对于包含M+N个阵元的基于MFT算法的垂直线阵系统, N个发射通道所发射的波束信号被提前计算并存储在系统中, 因此不需要额外的计算量, 则分析计算量时只需分析M个接收阵元进行波束生成所需要的计算量即可。
若系统把Q个垂直方向分成G组, 每组波束数为H, 则MFT算法在进行波束形成时需要在H个频域上并发进行, 因此MFT算法生成P×Q个波束需要的计算量为:
| $ {O_C} = \left[ {\left( {4L - 2} \right)\cdot M + \left( {8M - 2} \right)\cdot P} \right]\cdot H = \\ \left[ {\left( {4L - 2} \right)\cdot M + \left( {8M - 2} \right)\cdot P} \right]\cdot Q/G。$ | (17) |
当DFT点数为150点时, 分别将阵元数量为M×N=100×100的二维面阵与阵元数量为M+N=100+100的垂直线阵进行计算量对比。其中垂直线阵垂直方向发射波束的分组数G=6。两种算法的具体计算量如表 1所示:
|
|
表 1 二维面阵与MFT垂直线阵计算量对比 Table 1 Comparison of the calculation of MFT vertical line array and planar array |
由表 1可知, 在上述的参数配置下, 基于MFT算法的垂直线阵比传统二维面阵可以降低3个数量级的计算量。虽然基于MFT算法的垂直线阵比传统单频率发射的垂直线阵在计算量上有所增加, 但是相比于二维面阵有着数量级上的提高。因此, 相比于二维面阵三维成像声呐, 基于MFT算法的垂直线阵可以有效简化系统复杂度, 同时提高系统计算效率, 降低系统计算需求。
2 系统实现针对传统三维成像声呐硬件系统复杂、计算量庞大, 以及传统垂直线阵三维声呐成像速率慢的问题, 本文设计了基于MFT算法的垂直线阵三维成像声呐系统。该系统有效解决了制约水下三维成像技术发展的这些难题, 实现了实时三维成像声呐低功耗、小型化的设计需求。
经过系统需求分析, 最终垂直线阵的发射阵元为80路, 阵元间距dy为2 mm, 垂直波束方向数为54;接收阵元为120路, 阵元间距dx为1.5 mm, 水平接收方向数为120。发射波束分为6组, 每组波束频率在480~660 kHz范围内以20 kHz的间距递增。系统最远探测距离为50 m, 探测角度范围是80°×50°。
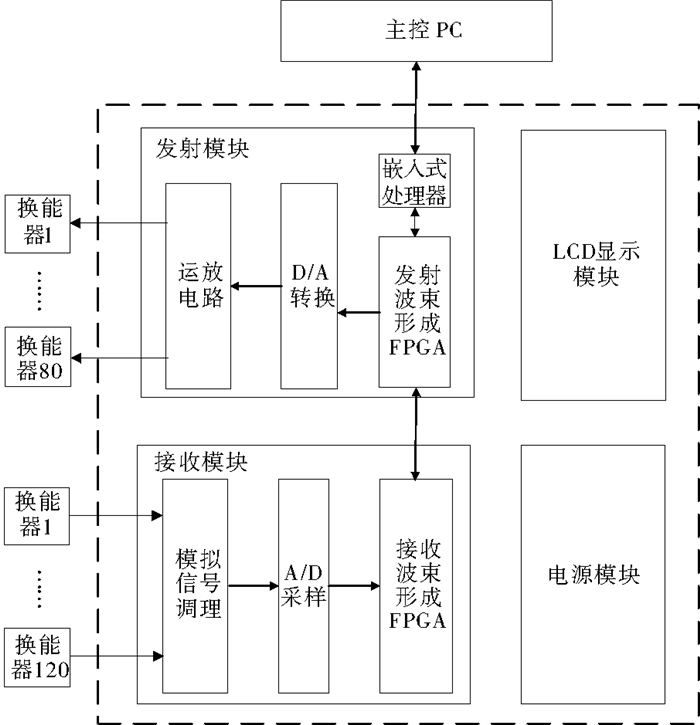
2.1 硬件结构系统硬件部分主要由发射模块、接收模块、电源模块以及显示模块四个部分组成。系统硬件结构如图 8所示。
|
图 8 系统硬件结构 Fig. 8 Hardware structure of the system |
系统工作时, 首先由上位机将发射的波束信息和发射指令传送到发射模块的嵌入式处理器中, 由嵌入式处理器控制发射模块的FPGA进行扇形波束的发射。FPGA传送的数字信号经过D/A转换和运算放大后传送至80路垂直方向的换能器完成波束发射。
120路水平方向的接收阵元接收到的回波信号经过滤波、放大等模拟调制后通过A/D采样芯片, 转换而成的数字信号进入接收模块的FPGA中进行波束形成计算, 计算结果发送给发射模块的FPGA。发射模块的FPGA通过PCIe接口把波束强度数据传送给嵌入式处理器, 并最终通过千兆以太网接口传送至上位机PC进行三维图像的合成。
由于水下环境复杂干扰较多, 而声呐回波信号相对较弱, 因此需要对模拟信号进行放大滤波。本设计选用ADA4841芯片对回波信号进行两级运放滤波, 带通滤波频率为480~660 kHz, 滤波放大的增益约为5 dB, 有效区间衰减小于3 dB。此外, 系统使用8片AFE5851芯片完成对120路模拟信号进行模拟调制以及A/D采样, 每片AFE5851内部集成有16个增益可变放大器以及A/D转换器。
发射模块以TI公司的TMS320DM8127处理器为核心, 外扩4片DDR3 SDRAM。处理器通过PCIe接口与FPGA进行通信, 用来向FPGA传送波形数据, 接收FPGA上传的波束强度结果, 并外扩千兆以太网接口把波形强度数据传给上位机。
系统FPGA选用Xilinx公司的高性能Spartan-6系列FPGA。发射模块使用1片FPGA并外扩2片DDR3 SDRAM, 工作时FPGA首先读取DDR3中存储的波形数据, 然后分配给相应的换能器完成发射。接收模块使用2片FPGA, 每片FPGA接收60路换能器采集的信号, 并进行波束形成计算, 计算结果通过发射模块的FPGA上传至上位机。
2.2 FPGA分级波束设计为进一步减少波束形成计算量、提高系统计算速率, 本文提出一种并行子阵分级波束形成算法, 该算法是对垂直线阵波束形成算法的一种优化。
分级波束形成算法将水平方向的接收阵列分成若干个子阵列, 每个子阵列包含若干个阵元。系统进行波束形成时, 先在各个子阵上并行进行一级波束形成, 然后在把每个子阵看做一个阵元进行二级波束的形成, 从而得到最终的波束强度结果。
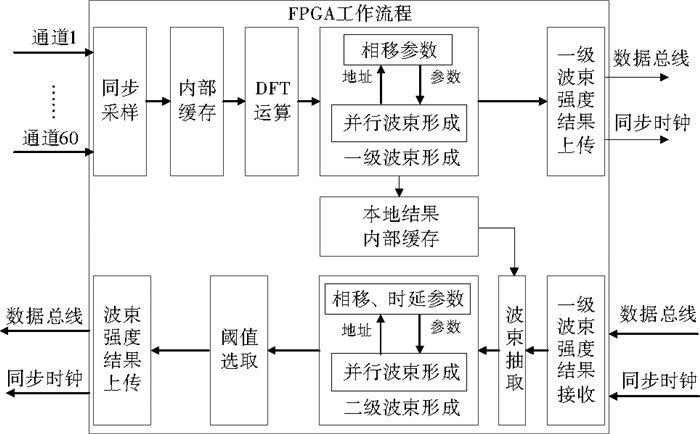
FPGA工作流程如图 9所示。分级波束形成工作由两片FPGA并发进行, 每片FPGA负责对60路声学信号进行同步采样, 采样结果在FPGA内部RAM中暂存。DFT模块从RAM中抽取采样结果并进行DFT运算, 把回波信号从时域转换到频域。每片FPGA对一半子阵进行一级波束形成, 得到的一级波束强度结果在本地缓存, 并传送给另一片FPGA。两片FPGA得到所有的一级波束强度结果后并发进行各一半发射频率的二级波束形成, 并将二级波束强度结果上传至发射模块及主控PC。
|
图 9 FPGA工作流程 Fig. 9 The procedures of FPGA |
本设计中, 120个接收阵元被划分为10个子阵, 每个子阵包含12个阵元。每片FPGA对9个发射频率对应的回波进行DFT运算, 并在5个子阵以及9个频域并发进行以及波束的形成。子阵中DFT运算变换公式如下:
| $ {S_{{m_F}}}({k_h}) = \sum\limits_{l = 1}^L {{s_{{m_F}}}} \left( l \right)\cdot{\rm{exp}}( - j\frac{{2{\rm{ \mathsf{ π} }}}}{L}l\cdot{k_h}) 。$ | (18) |
其中:mF表示子阵中阵元的序号(1≤mF≤12);smF(l)表示子阵中每个阵元的采样数据; L表示DFT运算点数, 本设计中L值为300;kh代表对应发射频率fh的线谱, 用fs表示系统采样频率, 则满足以下关系:
| $ {k_h} = \frac{{{f_h}}}{{{f_s}}}L(1 \le h \le 9)。$ | (19) |
一级波束形成在子阵上生成的波束的数量为P′, 在本设计中P′的值为26。则一级波束强度结果如下:
| $ \begin{array}{*{20}{l}} {\left| {{B_{{m_S}}}\left( {{f_h},{\alpha _{p\prime }}} \right)} \right| = }\\ {\left| {\sum\limits_{{m_F} = 1}^{12} {{S_{{m_F}}}\left( {{k_h}} \right)} \cdot{\rm{exp}}\left( { - j{\theta _{{m_F}}}\left( {{f_h},{\alpha _{p\prime }}} \right)} \right)} \right|} \end{array} 。$ | (20) |
其中:mS表示子阵序号(1≤mF≤10);αp′为接收波束方向角(1≤p’≤26);θm(fh, α)为相位偏移参数, 表达方式如下:
| $ {\theta _{{m_F}}}({f_h},{\alpha _{p\prime }}) = 2{\rm{ \mathsf{ π} }}{f_h}\cdot({m_F} - \frac{{{M_F} + 1}}{2}){\rm{d}}x\cdot{\rm{sin}}{\alpha _{p\prime }}/c 。$ | (21) |
其中MF表示子阵中阵元数量, 本设计中MF的值为12。
2.2.2 二级波束形成当两片FPGA完成各自的5个子阵的一级波束形成后, 总共产生10×P′×H个波束强度结果。二级波束形成将在两片FPGA中并发进行, 其中一片FPGA完成4个频率(580~660 kHz)的二级波束形成, 另一片FPGA完成剩下5个频率(480~560 kHz)的二级波束形成, 因此两片FPGA均需要对方的一级波束数据才可进行下一步计算。
二级波束形成计算之前, 每片FPGA把另一片FPGA所需要的数据通过LVDS接口传输给对方, 当两片FPGA均接收到所需要的一级波束强度数据后则开始二级波束形成的计算。
二级波束形成时, 以每个子阵作为基本阵元, 子阵间的间距变为12dx。二级波束在水平方向共形成P个波束, 本设计中P的值为120。FPGA在一级波束结果中抽取与二级波束角最为近似的一级波束进行波束形成计算。二级波束结果表达式如下:
| $ \left| {{B_R}\left( {{f_h},{\alpha _p}} \right)} \right| = \left| {\sum\limits_{{m_S} = 1}^{10} {} {B_{{m_S}}}({f_h},{\alpha _{p\prime }})\cdot{\rm{exp}}( - j{\theta _{{m_S}}}({f_h},{\alpha _p}))} \right| 。$ | (22) |
其中αp为接收波束方向角(1≤p≤120), 数θmS(fh, αp)为相位偏移参数, 其表达式如下:
| $ {\theta _{{m_S}}}({f_h},{\alpha _p}) = 2{\rm{ \mathsf{ π} }}{f_h}({m_S} - \frac{{{M_S} + 1}}{2})\cdot12{\rm{d}}x\cdot{\rm{sin}}{\alpha _p}/c 。$ | (23) |
MS表示子阵总数, 本设计中MS值为10。
当所有G组波束发射完毕, 经过两片FPGA二级波束形成计算, 最终可以得到P×G×H个波束强度结果。
3 系统仿真与测试为了验证本文设计的基于MFT算法的垂直线阵三维成像声呐系统的性能指标, 需要对系统进行测试。测试内容分为2个部分, 首先在matlab环境下对系统进行波束形成的仿真实验, 然后在实际水下环境中对系统进行成像效果测试。
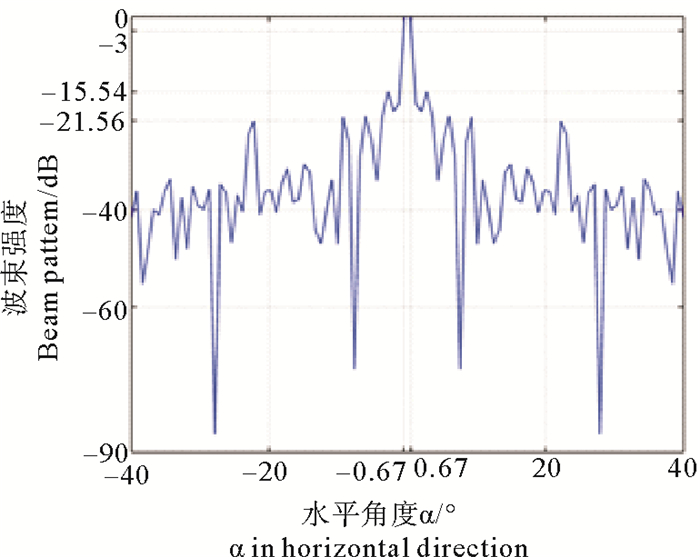
3.1 系统仿真首先, 为了验证垂直线阵的理论成像效果, 需要对垂直线阵的波束性能与同等级别的二维面阵成像声呐进行对比。本设计中垂直线阵的阵元规模为120+80, 对应的二维面阵成像声呐阵元规模为120×80。垂直线阵和二维面阵参数配置均相同, 探测范围均为80°×50°, 波束个数均为120×54。两者均对(0°, 0°)上的一个单点目标进行波束形成, 用matlab软件对两种声呐的水平、垂直方向上的波束方向进行仿真, 并对仿真结果中的主瓣宽度和旁瓣峰值两项指标进行对比。其中主瓣宽度越小声呐的角分辨率越高, 旁瓣峰值越低则声呐的成像精度越高。垂直线阵声呐和二维面阵声呐水平方向的波束仿真结果见图 10、11所示。
|
图 10 垂直线阵水平方向波束方向仿真结果 Fig. 10 Result of horizontal beam direction of the vertical line array |
|
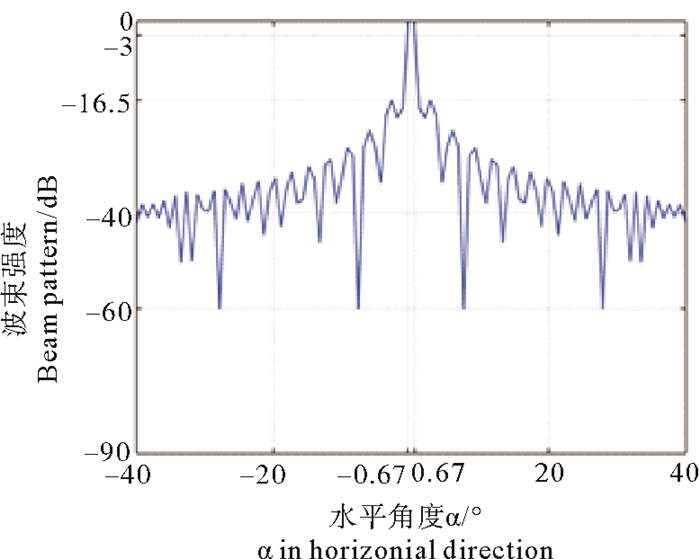
图 11 二维面阵水平方向波束方向仿真结果 Fig. 11 Result of horizontal beam direction of the two-dimensional array |
根据仿真结果, 垂直线阵和二维面阵声呐的主瓣宽度均为1.34°, 垂直线阵的旁瓣峰值为-15.54 dB, 而二维面阵旁瓣峰值为-16.5 dB, 若选择阀值为-15 dB的阀值过滤模块, 则二者在波束形成效果上没有区别。
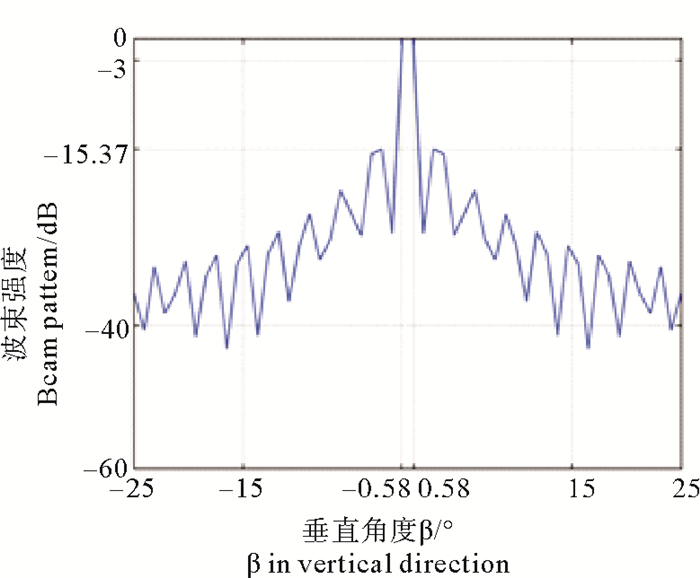
垂直线阵声呐和二维面阵声呐垂直方向的波束仿真结果如图 12、13所示。
|
图 12 垂直线阵垂直方向波束方向仿真结果 Fig. 12 Result of vertical beam direction of the vertical line array |
|
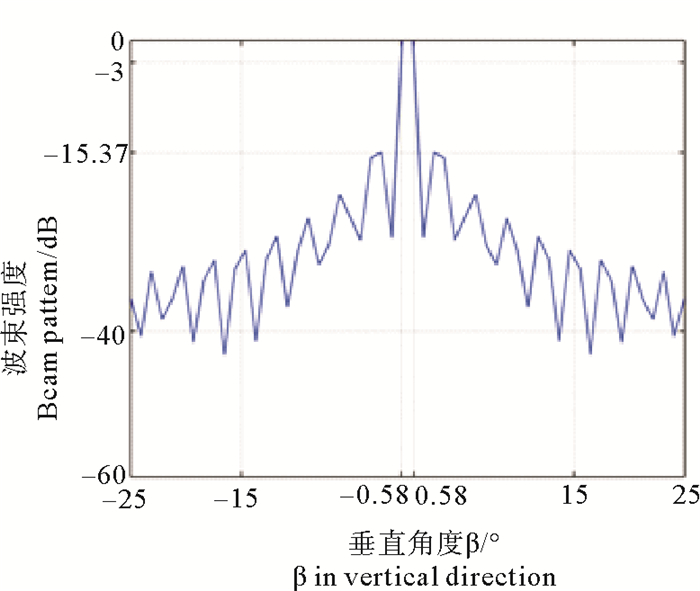
图 13 二维面阵垂直方向波束方向仿真结果 Fig. 13 Result of vertical beam direction of the two-dimensional array |
根据仿真结果, 垂直线阵和二维面阵在垂直方向上主瓣宽度均为1.16°, 旁瓣峰值均为-15.37 dB。因此可以看出垂直线阵可以达到和二维面阵几乎同等质量波束性能。
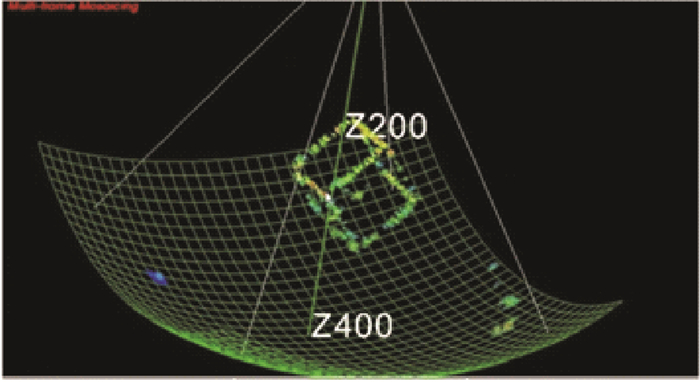
3.2 水下测试为测试系统实际成像性能, 需要对系统进行水下实际成像测试。图 14为本文设计的垂直线阵三维声呐水下实际拍摄效果, 拍摄目标为8 m外的一个边长1.5 m的立方体铁框。
|
图 14 垂直线阵三维声呐水下木框成像图 Fig. 14 The imaging of the underwater frame |
可见垂直线阵三维成像声呐拍摄的目标物体轮廓较为清晰, 分辨率较高。
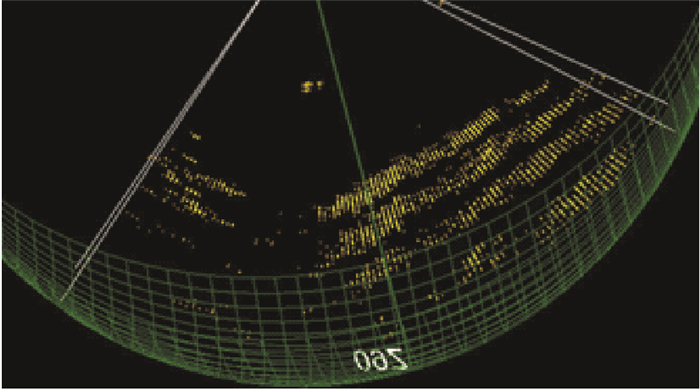
图 15为湖底地形成像图, 拍摄时声呐与湖底距离约50 m。
|
图 15 垂直线阵三维声呐湖底成像图 Fig. 15 The imaging of the bottom of the lake |
由图中成像结果可以分辨出湖底沉积物以及湖底地形结构。
测试中系统的成像帧率约为2.8帧/s, 可以满足水下实时成像的需求。
4 结语本文设计了基于垂直线阵的水下三维成像系统, 系统采用多频率发射波束形成算法, 有效解决了传统垂直线阵成像声呐扫描速率慢的问题。波束形成时采用并行子阵波束形成算法, 有效提高了系统的运算效率, 再次提高了系统的成像速率。经测试, 该系统实际成像效果可以接近同等配置的二维面阵三维声呐, 同时系统成像速率可以满足水下实时成像的需求。该系统解决了传统二维面阵成像声呐系统体积庞大、硬件复杂度较高的问题, 满足了三维声呐小型化、低功耗的需求, 具有较好的工程应用价值。
| [1] |
崔海英, 董琎琎, 夏伟杰, 等. 多波束成像声纳系统低功耗设计[J]. 海洋测绘, 2015, 35(3): 71-74. Cui Haiying, Dong Jinjin, Xia weijie, et al. Low-power Design of Multibeam Imaging Sonar System[J]. Hydrographic Surveying and Charting, 2015, 35(3): 71-74. (  0) 0) |
| [2] |
Han Y, Fu J, Zhou F, et al.Distributed and parallel subarray beamforming for near-field 3D sonar imaging[C]//Computer Science and Network Technology (ICCSNT), 2013 3rd International Conference on IEEE, 2013: 1021-1025.
(  0) 0) |
| [3] |
林贤洲, 陈耀武. 基于分级波束形成的三维声纳系统设计[J]. 传感器与微系统, 2014(8): 101-104, 108. Lin Xianzhou, Chen Yaowu. Design of 3 D sonar systen based on nultistage beanforning[J]. Transducer and Microsystem Technologies, 2014(8): 101-104, 108. (  0) 0) |
| [4] |
Okino M, Higashi Y. Measurement of seabed topography by multibeam sonar using CFFT[J]. Oceanic Engineering, IEEE Journal of, 1986, 11(4): 474-479. DOI:10.1109/JOE.1986.1145209
(  0) 0) |
| [5] |
Lear R. Data comparison of the Seabat 7125 and 8125 multi-beam sonars[J]. Hydro International, 2008, 12(5): 22.
(  0) 0) |
| [6] |
陈加洋, 陈耀武. 水下便携式三维声纳实时成像系统设计[J]. 传感器与微系统, 2015(2): 99-102. Chen Jiayang, Chen Yaowu. Design of portable 3 D underwater sonar real-time imaging system[J]. Transducer and Microsystem Technologies, 2015(2): 99-102. (  0) 0) |
| [7] |
Jinjin D, Jianjiang Z, Weijie X, et al. Imaging sonar dynamic focusing algorithm and FPGA realization[J]. Microcontrollers & Embedded Systems, 2015, 4: 010.
(  0) 0) |
| [8] |
刘天宝, 吴晓潭, 黄勇, 等. 三维成像声呐图像重建研究[J]. 声学技术, 2015(4): 358-361. Liu Tianbao, Wu Xiaotan, Huang Yong, et al. Image reconstruction for 3D acoustical imaging sonar[J]. Technical Acoustics, 2015(4): 358-361. (  0) 0) |
| [9] |
袁龙涛, 周凡, 陈耀武, 等. 相控阵三维摄像声纳系统的稀疏阵列优化设计[J]. 华南理工大学学报(自然科学版), 2013, 41(1): 29-37. Yuan Longtao, Zhou Fan, Chen Yaowu, et al. Optimization design of sparse arrays for Phased-Array 3D imaging sonar systems[J]. Journal of South China University of Technology(Natural Science Edition), 2013, 41(1): 29-37. DOI:10.3969/j.issn.1000-565X.2013.01.005 (  0) 0) |
| [10] |
LIN X, CHEN Y. Design of 3D sonar system based on multistage beamforming[J]. Transducer and Microsystem Technologies, 2014, 8: 29.
(  0) 0) |
| [11] |
Gu J H, Joe H G, Yu S C.Development of image sonar simulator for underwater object recognition[C]// Oceans-San Diego, 2013.IEEE, 2013: 1-6.
(  0) 0) |
| [12] |
王朋, 任宇飞, 黄勇, 等. 基于TMS320C6678三维成像声纳信号处理算法的设计与实现[J]. 海军工程大学学报, 2014(2): 85-90, 112. Wang Peng, Ren Yufei, Huang Yong, et al. Design and implementation of 3D acoustical imaging sonar signal processing method based on TMS 320C6678[J]. Journal of Naval University of Engineering, 2014(2): 85-90, 112. (  0) 0) |
| [13] |
袁龙涛, 田翔, 陈耀武, 等. 相控阵三维摄像声纳的自适应阈值选取[J]. 吉林大学学报(工学版), 2013, 43(3): 841-848. Yuan Longtao, Tian Xiang, Chen Yaowu, et al. Selection of adaptive threshold for phased array 3D sonar[J]. Journal of Jilin University(Engineering and Technology Edition), 2013, 43(3): 841-848. (  0) 0) |
| [14] |
徐亮. 一种低功耗三维成像声呐接收机设计[J]. 声学与电子工程, 2015(3): 29-30, 44. Xu Liang. Design of a low power 3D sonar[J]. Acoustics and Electronics Engineering, 2015(3): 29-30, 44. (  0) 0) |
| [15] |
CHEN P, CHEN Y. 3D sonar frequency-domain beamforming algorithm-optimization and implementation[J]. Journal of Jilin University (Engineering and Technology Edition), 2010, 3: 045.
(  0) 0) |
 2018, Vol. 48
2018, Vol. 48

