2. 自然资源部第一海洋研究所,山东 青岛 266061;
3. 青岛海洋科学与技术试点国家实验室 区域海洋动力学与数值模拟功能实验室,山东 青岛 266237
海浪作为海洋表面普遍存在的波动现象,与人类的海上活动和气候研究息息相关。合成孔径雷达(Synthetic Aperture Radar, SAR)具备全天时、全天候获取海面高分辨率微波后向散射图像的能力,是遥感观测海浪的有力工具。
海浪的SAR微波成像机制主要包括三种调制机制,即:流体力学调制、倾斜调制和速度聚束调制[1-3]。基于以上调制理论,Hasselmann等推导给出了SAR图像谱和海浪谱之间的非线性映射关系,建立了基于SAR图像的海浪谱迭代反演算法,即MPI反演法[4]。然而,由于MPI算法中的非线性映射关系无法直接求逆,因此,使用MPI方法反演海浪谱时依赖于初猜谱的输入。此外,基于MPI反演算法所得海浪谱存在原点对称的两个海浪谱谱峰,仅依靠MPI方法无法取舍两个海浪谱谱峰,因此,MPI SAR海浪谱反演算法存在海浪谱180°模糊问题。为了解决MPI方法中存在的海浪谱180°模糊问题,基于SAR子孔径图像的交叉谱方法被进一步应用于SAR海浪谱反演方法之中[5-7]。由于速度聚束效应存在显著非线性特征,这导致偏离SAR距离向传播的风浪在SAR图像中难以被成像,因此,为了进一步提升SAR海浪谱反演精度,研究者通过引入风场信息,提出了半参数化法海浪反演算法[8-10]。近年随着加拿大Radarsat-2和我国高分3号卫星在轨运行,为海浪谱和海浪参数提取提供了全极化数据。进而,诸多学者提出了基于极化SAR图像的海浪谱反演方法[11-16]。基于极化SAR图像的海浪谱反演算法可以消除流体力学调制效应的影响。近年来,有学者也提出了基于SAR图像参数的海浪有效波高经验反演算法[17-20],然而,这些海浪有效波高经验反演算法不能获得二维海浪谱。本质上基于单极化或多极化SAR图像的海浪谱反演算法都是在SAR图像纹理特征的基础上开展的,因此,这些反演算法的精确性必然会受到SAR图像中非海浪纹理的干扰。Li等[21]指出:SAR图像中的大尺度大气或海洋现象会导致SAR图像谱低波数域谱密度偏大。由SAR图像谱和海浪谱间的映射关系可知,低波数域的非海浪纹理信号谱密度在所反演的海浪谱中更容易被放大,从而影响海浪反演精度。此外,具有随机特征的相干斑噪声是海面SAR图像所固有的物理现象,然而这些随机相干斑噪声也会显著增大反演所得海浪谱的高波数域谱密度。
根据以上分析可见,当前基于SAR图像的海浪谱高精度反演算法依然存在挑战,其中,复杂的非线性映射关系依赖于初猜谱,而且计算过程较为困难;此外,SAR图像中的非海浪纹理和相干斑噪声也会影响反演所得海浪谱的精度。相对而言,准线性映射关系较为精简,本文分析了直接基于准线性映射关系从Sentinel-1 SAR波模式数据中反演海浪参数的可行性;同时,为了抑制SAR图像中大尺度非海浪纹理以及相干斑噪声的影响,根据大尺度非浪海洋现象的时间慢变特征和相干斑噪声的时间快变特征,基于SAR图像交叉谱提出了相应的抑制方案。
1 数据介绍 1.1 Sentinel-1卫星SAR数据Sentinel-1由A星和B星构成,在欧洲航天局哥白尼计划的支持下两颗星分别发射于2014和2016年。Sentinel-1搭载了可多模式成像的C波段SAR,其中,该SAR的波模式是专门针对海浪观测的成像模式。波模式图像的中心入射角为23°(WV1)或36°(WV2),WV1和WV2间隔100 km交替对海成像。Sentinel-1波模式图像的空间分辨率和图像大小分别为5 m×5 m和20 km×20 km,其极化方式为单极化(HH或VV)。本文海浪反演时所使用的SAR数据为2020年Sentinel-1获取的全球VV极化WV2波模式L2级产品,该产品中提供了SAR图像交叉谱、方位向截断波长等信息。其中,1月的数据用于误差校正模型的拟合,其余月份数据用于模型验证。需要说明的是:为了筛选出海浪纹理较清晰的SAR图像,同时避免海冰影响,在反演过程中,只保留了位于纬度(-60°N—+60°N) 之间且图像归一化方差(nv)介于1~1.4之间的SAR数据[19]。在此,归一化方差nv定义为:
| $ n v=\operatorname{var}\left(\frac{I-\langle I\rangle}{\langle I\rangle}\right) 。$ | (1) |
其中:I为SAR图像强度;var表示方差。
1.2 ECMWF再分析数据本文使用了ECMWF提供的第五代再分析风场数据和有效波高数据用于海浪有效波高校正模型的拟合和结果验证,其中,风场数据的时空分辨率为1 h和0.25°×0.25°;海浪有效波高的时空分辨率为1 h和0.5°×0.5°。本文在与Sentinel-1 SAR数据进行时空匹配时,选取了ECMWF数据中与SAR数据的时空间隔最近点。
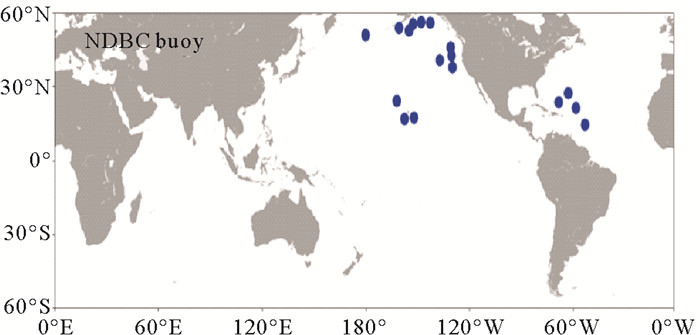
1.3 NDBC浮标数据为了进一步检验本文海浪反演结果的可靠性,NDBC提供的浮标数据也被用于最终的海浪有效波高结果检验。NDBC浮标每间隔1 h提供一个海浪有效波高数据,因此,本文选取浮标数据与SAR图像成像之间的时间间隔不超过30 min。同时,被选取的浮标位置与SAR图像中心位置不超过100 km。图 1中的蓝点标注了匹配成功的浮标位置。
|
图 1 匹配的NDBC浮标位置 Fig. 1 The position of the matched NDBC buoys |
SAR图像谱和海浪谱之间的非线性映射关系为[4]:
| $ \begin{gathered} P^S(\boldsymbol{k})=(2 \pi)^{-2} \exp \left(-k_y^2 \xi^2\right) \times \\ \int e^{-i k \cdot \boldsymbol{r}} \exp \left[k_y^2 \xi^2\left\langle v^2\right\rangle^{-1} f^v(\boldsymbol{r})\right] \times \\ \left\{1+f^R(\boldsymbol{r})+i k_y \beta\left[f^{R v}(\boldsymbol{r})-f^{R v}(-\boldsymbol{r})\right]+\right. \\ \left.\left(k_y \beta\right)^2\left[f^{R v}(\boldsymbol{r})-f^{R v}(0)\right]\left[f^{R v}(-\boldsymbol{r})-f^{R v}(0)\right]\right\} \mathrm{d} \boldsymbol{r} 。\end{gathered} $ | (2) |
式中:PS(k)为SAR图像谱;i为虚数单位;r为空间位置矢量;k为海浪波数向量;ky为方位向波数;ξ2=β2fv(0),ξ为目标成像位置沿方位向偏移量的均方根;v为散射单元的雷达视向运动速度;β=R/V,R为平台到目标的斜距,V为平台运动速度。
| $ T_k^v=-\omega\left(\sin \theta \frac{k_l}{|k|}+i \cos \theta\right) 。$ | (3) |
| $ f^v(\boldsymbol{r})=\int F(\boldsymbol{k})\left|T_k^v\right|^2 e^{i k \cdot \boldsymbol{r}} \mathrm{d} \boldsymbol{k} 。$ | (4) |
| $ f^R(\boldsymbol{r})=\frac{1}{2} \int\left\{F(\boldsymbol{k})\left|T_k^R\right|^2+F(-\boldsymbol{k})\left|T_{-k}^R\right|^2\right\} e^{i k \cdot \boldsymbol{r}} \mathrm{d} \boldsymbol{k} 。$ | (5) |
| $ f^{R v}(\boldsymbol{r})=\frac{1}{2} \int\left\{F(\boldsymbol{k}) T_k^R\left(T_k^v\right)^*+F(-\boldsymbol{k})\left(T_{-k}^R\right)^* T_{-k}^v\right\} e^{i k \cdot r} \mathrm{~d} \boldsymbol{k} 。$ | (6) |
式中:F(k)为海浪谱;θ为雷达入射角;ω为海浪角频率;kl是入射波数在雷达视向上的分量。在此,实孔径调制函数TkR可表示为[4]:
| $ T_k^R=T_k^t+T_k^h \text { 。} $ | (7) |
| $ T_k^h=4.5 k \omega \frac{\omega-i \mu}{\omega^2+\mu^2}\left(\frac{k_x^2}{k^2}+Y_r+i Y_i\right) 。$ | (8) |
式中:μ为阻尼系数;kx为海浪波数沿距离向分量;Yr+iYi为复反馈因子。在此,倾斜调制函数Tkt可使用基于Bragg散射理论推导的理论倾斜调制函数Tkt_t和基于CSAR模型推导的经验倾斜调制函数Tkt_e。Tkt_t及Tkt_e的具体形式详见文献[16]。
直接应用式(2)反演海浪谱是困难的,然而,如果忽略式(2)中的高阶非线性项后,则可得到SAR图像谱和海浪谱之间的准线性映射关系[4]:
| $ P_{\mathrm{ql}}^S(\boldsymbol{k})=\mathrm{e}^{-\left(k_y \xi\right)^2}\left[\left|T_k^S\right|^2 \frac{F(\boldsymbol{k})}{2}+\left|T_{-k}^S\right|^2 \frac{F(-\boldsymbol{k})}{2}\right] 。$ | (9) |
其中:
| $ T_k^S=T_k^R+T_k^{v b} 。$ | (10) |
| $ T_k^{v b}=-i \beta k_y T_k^v=-\beta k_y \omega\left(\cos \theta-i \sin \theta k_l / k\right) 。$ | (11) |
与式(2)相比,式(9)中的海浪谱F(k)与SAR图像谱PqlS(k)之间的关系较为简单,本文中我们将基于Sentinel-1 SAR图像数据分析应用式(9)反演海浪谱的可行性。式(9)中的指数因子e-(kyξ)2决定了SAR海浪图像谱的方位向截断效应,其中,参数ξ与散射单元的雷达视向运动速度的方差有关,在海浪谱未知时,可应用以下关系式估计参数ξ的大小[22-23]:
| $ \xi=\frac{\lambda_c}{\pi} \text { 。} $ | (12) |
其中,方位向截断波长λc可通过高斯函数对SAR图像沿方位向的自相关函数进行拟合得到[22]。然而,在实际反演过程中,为了更好地抑制方位向高波数域噪声,本文将指数因子e-(kyξ)2的值设置为:
| $ \mathrm{e}^{-\left(k_y \xi\right)^2}=\left\{\begin{array}{ll} \mathrm{e}^{-\left(k_y \xi\right)^2} & \left|k_y\right| \leqslant \frac{2 \pi}{\lambda_c} \\ 1 & \left|k_y\right|>\frac{2 \pi}{\lambda_c} \end{array} 。\right. $ | (13) |
SAR图像交叉谱和海浪谱之间的准线性映射关系为[7]:
| $ \operatorname{Re}\left[P_{\mathrm{ql}}^{S C}(\boldsymbol{k})\right]=\cos (\omega \tau) e^{-\left(k_y \xi^2\right)^2}\left[\left|T_k^S\right|^2 \frac{F(\boldsymbol{k})}{2}+\left|T_{-k}^S\right|^2 \frac{F(-\boldsymbol{k})}{2}\right] 。$ | (14) |
| $ \begin{gathered} \operatorname{Im}\left[P_{\mathrm{ql}}^{S C}(\boldsymbol{k})\right]=\sin (\omega \tau) e^{-\left(k_y \xi\right)^2}\left[\left|T_k^S\right|^2 \frac{F(\boldsymbol{k})}{2}-\right. \\ \left.\left|T_{-k}^S\right|^2 \frac{F(-\boldsymbol{k})}{2}\right] 。\end{gathered} $ | (15) |
式中:
由于海面上不同散射点的随机运动导致SAR不同时刻获取的子视图像上的相干斑噪声不相关,这一特征使得交叉谱受相干斑噪声的影响很小[6]。对比式(14)、式(15)和式(9)可见:
| $ \begin{gathered} P_{\mathrm{ql}}^S(\boldsymbol{k})=\sqrt{\operatorname{Re}\left[P_{\mathrm{ql}}^{S C}(\boldsymbol{k})\right]^2+\operatorname{Im}\left[P_{\mathrm{ql}}^{S C}(\boldsymbol{k})\right]^2} \approx \\ \sqrt{\operatorname{Re}\left[P^{s c}(\boldsymbol{k})\right]^2+\operatorname{Im}\left[P^{s c}(\boldsymbol{k})\right]^2}。\end{gathered} $ | (16) |
其中,
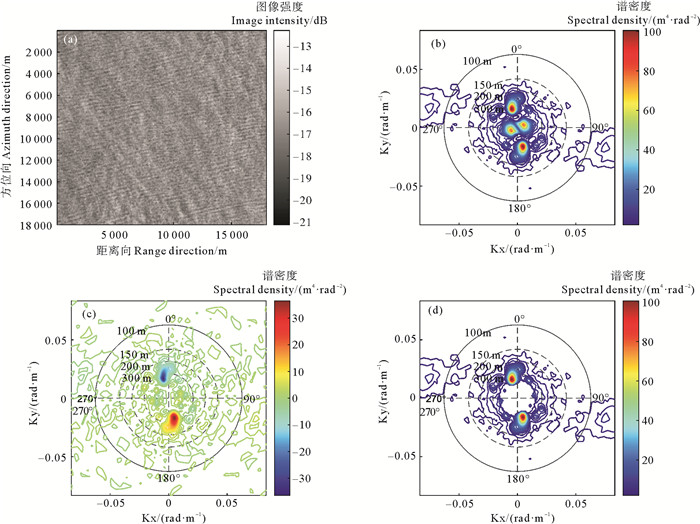
除相干斑噪声外,如图 2(a)所示,SAR海浪图像还常常呈现出大尺度大气或海洋现象的纹理,这些纹理会造成SAR图像谱密度在低波数域增大。由于SAR海浪成像调制函数在低波数域的幅值非常小,因此,在通过对式(9)求逆反演海浪谱的过程中,低波数域的非海浪特征谱密度更容易被放大,从而影响海浪反演结果。另一方面,由于大尺度大气或海洋现象具有慢时变特征,因此,基于实测SAR数据获得的交叉谱
|
图 2 Sentinel-1 VV极化图像(a),SAR图像谱(b),交叉谱虚部(c)和抑制低频噪声后的图像谱(d) Fig. 2 Sentinel-1 VV polarization image(a), SAR image spectrum(b), Imaginary part of the SAR cross spectrum(c) and SAR image spectrum after suppressing the low-frequency noise(d) |
首先定义交叉谱虚部的模与SAR图像谱的比值作为阈值,来判断是否去除该区域的能量,由于交叉谱虚部上存在噪声,在求比值前先减去一个与虚部能量成正比的平均噪声平面。定义该阈值参数Rk为:
| $ R_k=\frac{\left|\operatorname{Im}\left(P^{s c}(k)\right)\right|-\alpha \cdot \operatorname{mean}\left[\left|\operatorname{Im}\left(P^x(k)\right)\right|\right]}{P^S(k)} 。$ | (17) |
在此,mean(·)为求平均值。并通过下式对SAR图像谱进行滤波:
| $ P^s(\boldsymbol{k})=\left\{\begin{array}{lc} 0 & 650 \mathrm{~m}<\lambda \\ 0 & R_k<\beta_1 \& 500 \mathrm{~m}<\lambda<650 \mathrm{~m} \\ 0 & R_k<\beta_2 \& 400 \mathrm{~m}<\lambda<500 \mathrm{~m} \\ P^s(\boldsymbol{k}) & \text { else } \end{array}\right. \text { 。} $ | (18) |
其中λ为海浪波长。经过对大量数据的观察验证,本文中α设置为4。β1设置为0.12,β2设置为0.05。
图 2(d)为低波数域噪声去除后的图像谱,可以看到,噪声峰被去除而海浪图像谱的边缘被较好地保留。
3 仿真分析为了检验准线性近似法的反演能力,本节通过仿真实验对不同海况下的反演情况进行分析。仿真中使用的雷达和平台参数与Sentinel-1 WV2数据相同,入射角为36°,β为116 s,极化方式为VV。输入的海浪谱由风浪和涌浪两部分组成,其中风浪使用Elfouhaily谱,涌浪使用窄带谱。生成二维海浪谱后,使用SAR图像谱和海浪谱之间的非线性映射关系式(2)前向映射得到仿真图像谱。进而将仿真图像谱与准线近似法相结合,反演海浪谱,并将反演所得海浪谱有效波高参数与输入海浪参数进行对比,检验该方法的准确性。
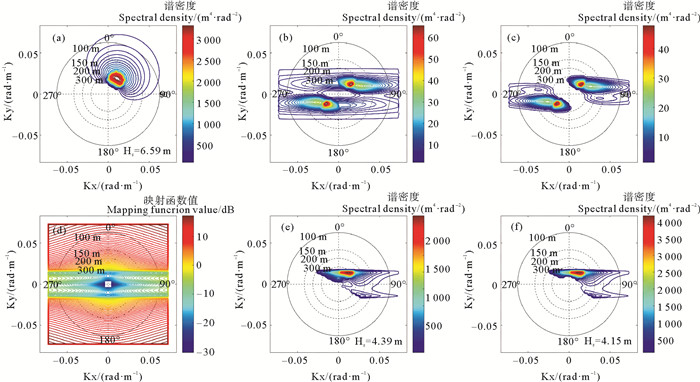
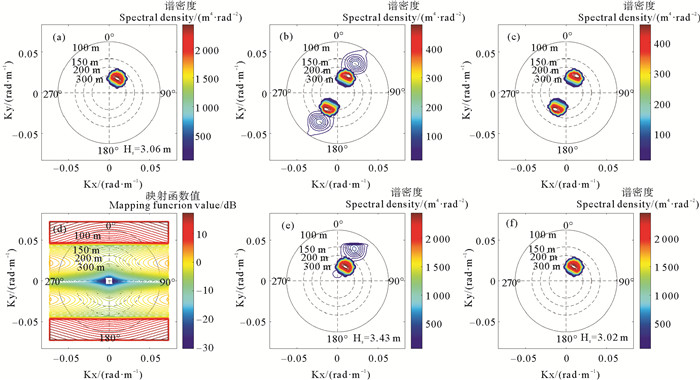
图 3展示了在海面10 m高处风速(U)为5 m/s,风向和涌浪主波波向与距离向夹角为60°,涌浪有效波高(Hswell)为3.00 m,主波波长(λswell)为250 m时的反演情况。此时,风浪和涌浪总有效波高为3.06 m,由于风速较低,风浪谱的值远小于涌浪谱的值,且风浪主波部分位于高波数域,故图 3(a)中未显示出风浪谱。对比图 3(b)和图 3(c)可以发现,使用非线性映射关系仿真得到的图像谱和使用准线性映射关系仿真得到的涌浪区域图像谱相似度很高,说明在该海况下,在进行准线性近似时舍弃的高阶项所占比重并不大,但从图 3(e)中可以看到,由于高阶项的存在,导致涌浪谱附近一些区域谱值偏大,在去除谱值小于输入海浪谱峰值千分之一的区域的能量之后得到图 3(f)所示的海浪谱,计算其有效波高为3.02 m,与输入的有效波高3.06 m差别不大,说明该方法成功地反演出了输入海浪谱的涌浪谱部分。图 4展示了其它参数不变,风速增加到15 m/s时的情况,此时,风浪谱的谱值增大,导致了方位向截断效应增强,SAR图像谱上峰值处的波向比海浪谱上的更靠近距离向,准线性映射图像谱(见图 4(c))与SAR图像谱图(见图 4(b))仍有一定的相似性,但相对于低风速时,相似度更低。从图 4(f)可以看到,最终反演的海浪谱发生了畸变,由于方位向高波数域海浪谱的缺失,反演有效波高也显著小于输入海浪有效波高。
|
(
(a)输入的海浪谱;(b)由式(2)仿真得到的SAR图像谱;(c)由式(9)仿真得到的准线性SAR图像谱;(d)准线性映射窗 |
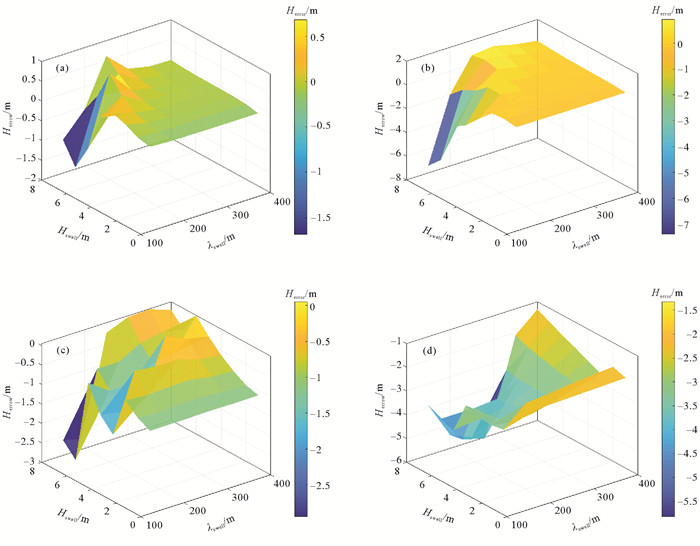
图 5展示了准线性近似法在不同海况下的反演情况,在此,反演有效波高误差Herror定义为:去除低谱值区后反演的有效波高与输入的有效波高之差。从图 5(a)和图 5(b)可看到,风速为5 m/s时,在涌浪波长较长,波高较小的情况下,有效波高反演精度高,在涌浪波高极高,波长又很短时,反演结果出现较大误差,而此类海况在现实中很少出现。而从图 5(c)和图 5(d)可看到,风速为15 m/s时,反演的有效波高通常偏低,浪向与距离向的夹角为90°时偏低得比30°时更多,这是因为海浪谱越靠近方位向,缺失的成分就越多。
|
( (a) 风速5 m/s,风向和涌浪主波波向与SAR距离向夹角为30°时,反演误差随涌浪有效波高从和涌浪主波波长的变化;(b) 同(a),但是风向和涌浪主波波向与距离向夹角为90°;(c) 同(a),但是风速为15 m/s;(d) 同(c),但是风向和涌浪主波波向与距离向夹角为90°。(a) When the wind speed is 5 m/s, the wind direction and the dominant wave direction of the swell are at an angle of 30° from the SAR range direction, the variation of the error with significant wave height and the wave wavelength of swell; (b) Same as (a), but the wind direction and the dominant wave direction of the swell are at an angle of 90° from the range direction; (c) Same as (a), but with a wind speed of 15 m/s; (d) Same as (c), but the wind direction and the dominant wave direction of the swell are at an angle of 90° from the range direction. ) 图 5 不同风速条件下有效波高反演误差 Fig. 5 The error of the retrieved significant wave height at different wind speed |
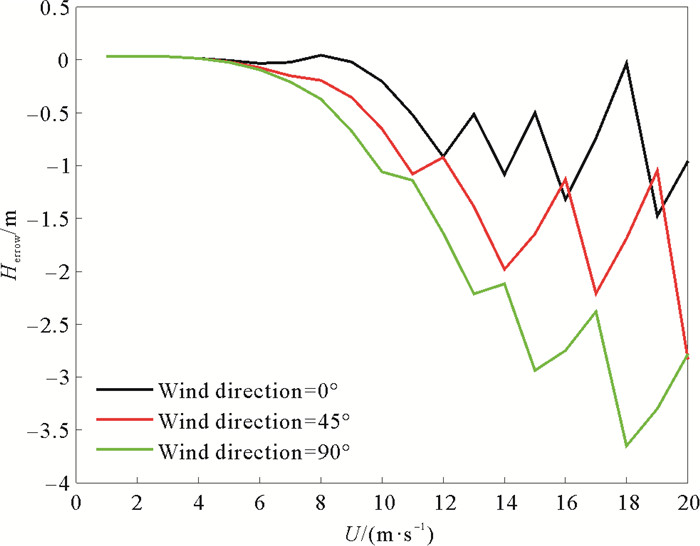
本文进一步分析了风场对准线性近似法反演效果的影响,图 6展示了输入的涌浪有效波高为3.00 m,主波波长为200 m,主波波向与距离向的夹角为45°时反演误差与风速和风向与距离向的夹角(Wind direction)的关系。随着风速的增加,反演的有效波高逐渐偏低,而风向与距离向的夹角越大,偏低得越多。
|
图 6 不同风向时有效波高反演误差随风速的变化 Fig. 6 The errors of the retrieved significant wave height versus wind speed for different wind directions |
通过对仿真图像谱的反演可以发现,该方法在涌浪主导情况下反演结果较好,但是在高风速情况下,由于方位向高波数域海浪信息缺失和准线性映射关系与非线性映射关系相似度降低,导致反演结果不理想。
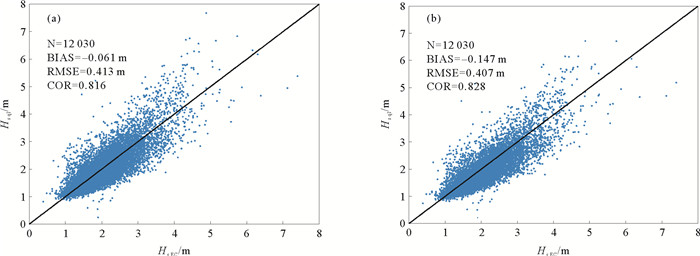
4 Sentinel-1波模式数据反演 4.1 准线性近似反演在完成噪声抑制后,首先筛选出风速小于7 m/s的数据用准线性近似法进行反演,并将反演的准线性近似有效波高(Hs ql)与ECMWF提供的有效波高(Hs EC)进行对比验证。本文中使用的风场数据为ECMWF提供的第五代再分析数据,对于Radarsat-2和高分3号等卫星获取的全极化数据,风场可直接从SAR图像反演[24]。图 7(a)和图 7(b)分别为对1月数据使用理论倾斜调制函数和经验倾斜调制函数的有效波高反演结果。本文用于评价反演结果的参数包括偏差(BIAS)、均方根误差(RMSE)和相关系数(COR)。对比发现,使用经验倾斜调制函数的反演结果虽然比使用理论倾斜调制的反演结果具有更大的负偏差,这与使用该方法反演的海浪谱缺失高波数域分量有关,但仍然具有更低的均方根误差和更高的相关性。
|
( (a)基于理论倾斜调制函数的反演结果; (b)基于经验倾斜调制函数的反演结果。(a) The retrieved result based on the theoretical tilt modulation function; (b) The retrieved result based on the empirical tilt modulation function. ) 图 7 1月风速小于7 m/s时基于准线性近似反演所得有效波高与ECMWF结果的比较 Fig. 7 The comparisons between the retrieved significant wave height by the quasi-linear approximation and the results of ECMWF at wind speed less than 7 m/s in January |
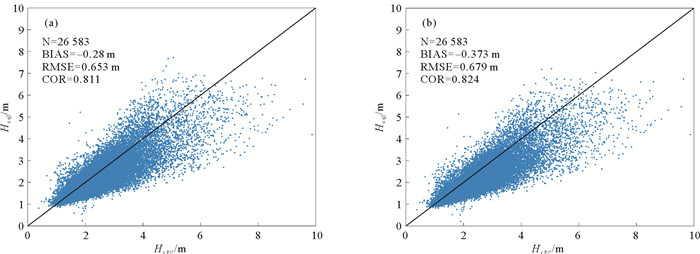
为了探索适用范围更广的有效波高反演方法,我们将反演范围扩展到风速小于20 m/s的数据,反演结果展示在图 8中,此时负偏差和均方根误差相对于低风速情况下都有明显的增大。
|
( (a)基于理论倾斜调制函数的反演结果;(b)基于经验倾斜调制函数的反演结果。(a) The retrieved result based on the theoretical tilt modulation function; (b) The retrieved result based on the empirical tilt modulation function. ) 图 8 1月风速小于20 m/s时基于准线性近似反演所得有效波高与ECMWF结果的比较 Fig. 8 The comparisons between the retrieved significant wave height by the quasi-linear approximation and the results of ECMWF at wind speed less than 20 m/s in January |
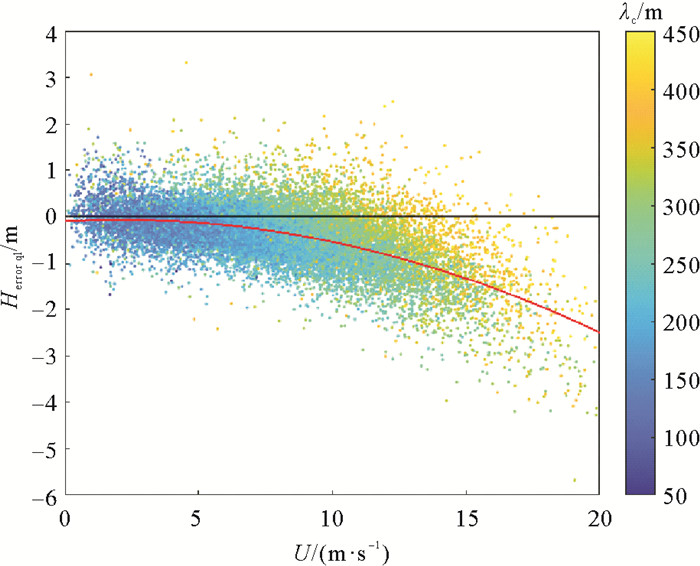
为了提升有效波高反演精度,分析了反演误差与环境参数以及图像参数之间的联系,图 9中展示了使用经验倾斜调制函数的有效波高反演误差与风速和截断波长的关系,图中颜色表示截断波长,随着风速的增大,反演的有效波高逐渐偏小,这与仿真实验中看到的现象相似。而在风速较高的情况下,截断波长较长的案例更多地位于散点图的上层。因此,我们将有效波高反演误差(Herror ql)与风速和截断波长进行多项式拟合,得到有效波高反演误差的经验关系,将反演的有效波高减去通过经验关系拟合的误差,从而提升有效波高反演精度。
|
( 红线为风速与有效波高误差的二次多项式拟合曲线。The red line is the quadratic polynomial fit line of the wind speed and the error of the retrieved significant wave height. ) 图 9 有效波高反演误差与风速和截断波长之间的关系 Fig. 9 The relationship between the error of the retrieved significant wave height and wind speed as well as cut off wavelength |
拟合的公式和具体参数为:
| $ \begin{gathered} H_{\text {error ql }}=\mathrm{p}_{00}+\mathrm{p}_{10} \mathrm{U}+\mathrm{p}_{01} \lambda_c+\mathrm{p}_{20} \mathrm{U}^2+\mathrm{p}_{11} \mathrm{U} \lambda_c+ \\ \mathrm{p}_{02} \lambda_c^2+\mathrm{p}_{30} \mathrm{U}^3+\mathrm{p}_{21} \mathrm{U}^2 \lambda_c+\mathrm{p}_{12} \mathrm{U}^2+ \\ \mathrm{p}_{03} \lambda_c^3+\mathrm{p}_{40} \mathrm{U}^4+\mathrm{p}_{31} \mathrm{U}^3 \lambda_c+\mathrm{p}_{22} \mathrm{U}^2 \lambda_c^2+ \\ \mathrm{p}_{13} \mathrm{U} \lambda_c^3+\mathrm{p}_{04} \lambda_c^4+\mathrm{p}_{50} \mathrm{U}^5+\mathrm{p}_{41} \mathrm{U}^4 \lambda_c+ \\ \mathrm{p}_{32} \mathrm{U}^3 \lambda_c^2+\mathrm{p}_{23} \mathrm{U}^2 \lambda_c^3+\mathrm{p}_{14} \mathrm{U} \lambda_c^4 。\end{gathered} $ | (19) |
其中,拟合系数为:
p00=-0.296 3;p10=-0.258 1;p01=0.022 08;
p20=0.051 62;p11=-1.905×10-5;
p02=-0.000 243;p30=-0.002 31;
p21=-0.000 430 9;p12=1.727×10-5;
p03=9.042×10-7; p40=0.000 561;
p31=-4.655×10-5; p22=2.865×10-6;
p13=-9.022×10-8; p04=-1.015×10-9;
p50=-6.942×10-6; p41=-4.343×10-7;
p32=7.412×10-8; p23=-3.819×10-9;
p14=1.099×10-10;
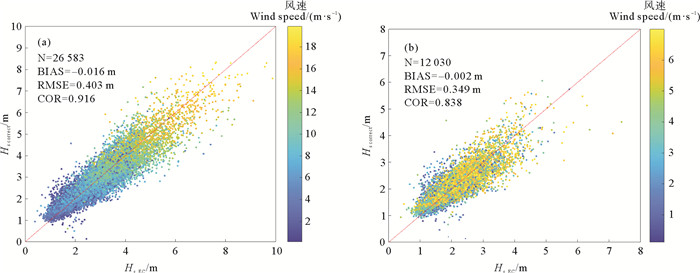
图 10中给出了校正后的有效波高结果(Hs correct)与ECMWF再分析数据的比较,由图可见:不论是高风速还是低风速的情况,校正后的有效波高精度明显提升。
|
( 色标代表风速, The color bar represents wind speed。(a)风速小于20 m/s时的结果; (b)风速小于7 m/s时的结果。(a) The results when wind speed is lower than 20 m/s; (b) The results when wind speed is lower than 7 m/s. ) 图 10 校正后的1月份SAR数据反演所得有效波高与ECMWF有效波高对比 Fig. 10 The comparison between the corrected significant wave height retrieved based on the SAR data in January and the results of ECMWF |
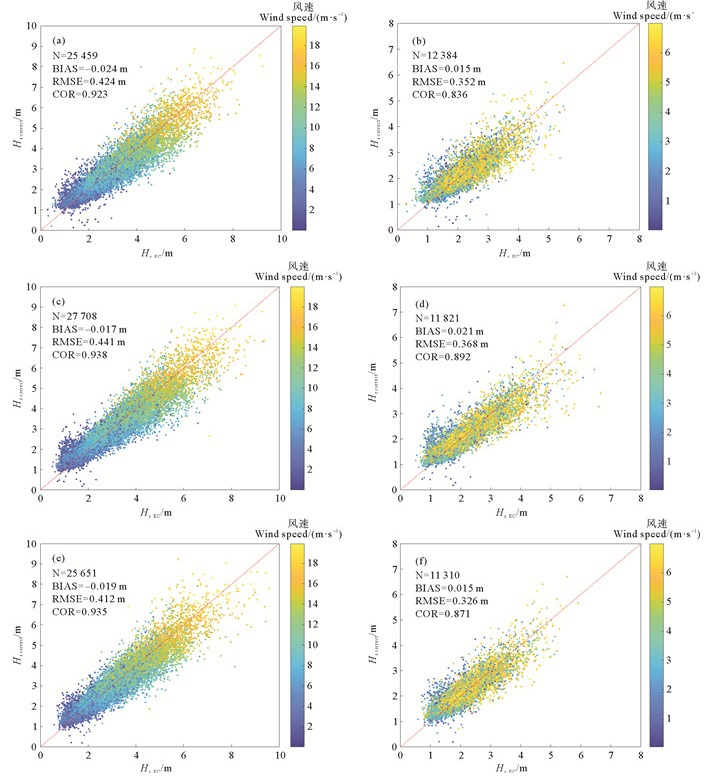
我们将误差校正模型应用到4、7、10月的数据中以检验其适用性。反演结果展示在图 11中展示,不同风速限制下校正前后的结果比较统计在表 1中。可以看到,由1月数据拟合出的经验校正模型在其它季度也是有效的,校正之后各统计参数都有明显的改善,尤其是在高风速情况下。对于低风速情况,四个月的数据均无需校正就可以得到比较准确的有效波高反演值,但是从图 11中可以看到,当风速极低时(小于2 m/s),出现了较多的偏离验证数据的样本。从7月的反演结果图 11(c)和图 11(d)中都能更明显地看到一团低风速的离群值,它们的反演结果高于验证数据,使得该月的RMSE相对于其它几个月稍大。
|
( (a)4月,风速小于20 m/s时的结果;(b)4月,风速小于7 m/s时的结果;(c)7月,风速小于20 m/s时的结果;(d)7月,风速小于7 m/s时的结果;(e)10月,风速小于20 m/s时的结果;(f)10月,风速小于7 m/s时的结果。(a) Results when Wind speed less than 20 m/s in April; (b) Results when Wind speed less than 7 m/s in April; (c) Results when Wind speed less than 20 m/s in July; (d) Results when wind speed less than 7 m/s in July; (e) Results when wind speed less than 20 m/s in October; (f)Results when wind speed less than 7 m/s in October. ) 图 11 4、7、10月等三个月SAR数据反演有效波高与ECMWF有效波高对比 Fig. 11 The comparison of the corrected significant wave height retrieved based on the SAR image in April、July and October and the results of ECMWF |
|
|
表 1 反演所得有效波高的统计结果 Table 1 Statistics result of the retrieved significant wave height |
Ren等[21]提出了截断波长和有效波高间的线性模型:
| $ H_{\mathrm{s empin}}=c_0 \frac{\lambda_c}{\beta}+c_1 \text { 。} $ | (20) |
并在Radarsat-2数据上验证了其有效性。本节使用ECMWF数据拟合了适用于Sentinel-1 WV2模式的经验参数:c0=1.511 5,c1=-0.356。
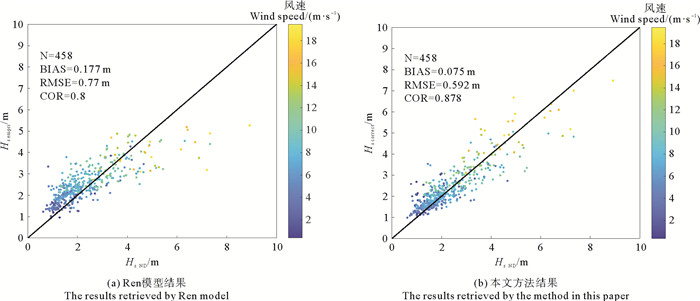
使用Ren模型(即式(20))反演得到的有效波高(Hs empri)与NDBC浮标测量得到的有效波高(Hs ND)对比结果展示在图 12(a)中,使用本文方法得到的校正有效波高(Hs correct)与浮标测量结果的对比展示在图 12(b)中,共有458景SAR数据与浮标数据满足匹配条件。可以看到,与浮标测量数据相比,两种方法均得到了较好的反演结果,且Hs correct精度高于Hs empri。
|
( (a) Ren模型结果;(b)本文方法结果。(a)The results retrieved by Ren model; (b) The results retrieved by the method in this paper. ) 图 12 反演的有效波高与浮标测量有效波高对比 Fig. 12 The comparison of the retrieved significant wave height with the buoy measurements |
本文先通过仿真实验分析了准线性近似法反演海浪参数的准确性和适用范围,仿真结果表明:排除一些实际不存在的一些极端情况,在海面风速较低时,不同波高波长波向的涌浪的海浪谱和有效波高都能得到较好的反演结果,但随着风速增加,海浪谱和有效波高的反演结果都不再可靠。这是由于在高风速下,经过准线性近似的映射关系与非线性映射关系产生了较大的偏差,以及方位向截断波长过长导致该方法反演的海浪谱大面积缺失造成的。然后对2020年的Sentinel-1卫星WV2数据进行反演,在反演过程中,利用交叉谱对相干斑噪声和图像谱中频繁出现的低波数域噪声进行了抑制,反演结果表明,在低风速下,反演的有效波高与ECMWF验证数据吻合较好,使用经验倾斜调制函数比使用理论倾斜调制函数反演结果与验证数据具有更高的相关性,而在高风速时,反演的有效波高逐渐偏低,这一现象与仿真结果相似。截断波长与有效波高反演误差也有一定的关联,但其相关性弱于风速,因此,将风速和截断波长同时用于误差校正将有更好的效果。本文通过1月数据拟合了有效波高反演误差与风速和截断波长之间的关系,建立了校正模型,并将4、7、10月数据的反演结果与ECMWF数据经行了比较,结果表明,在校正之后,有效波高反演精度得到明显的提升。最后将反演结果与NDBC浮标测量数据经行了对比,对于满足匹配条件的458个样本,反演有效波高的BIAS为0.075 m,RMSE为0.592 m, COR为0.878,统计参数优于直接使用截断波长拟合经验关系得到的结果。
| [1] |
Alpers W, Hasselmann K. The two-frequency microwave technique for measuring ocean-wave spectra from an airplane or satellite[J]. Boundary-Layer Meteorology, 1978, 13(1): 215-230. (  0) 0) |
| [2] |
Lyzenga D R. Numerical simulation of synthetic aperture radar image spectra for ocean waves[J]. IEEE Transactions on Geoscience and Remote Sensing, 1986(6): 863-872. (  0) 0) |
| [3] |
Alpers W, Rufenach C. The effect of orbital motions on synthetic aperture radar imagery of ocean waves[J]. IEEE Transactions on Antennas and Propagation, 1979, 27(5): 685-690. DOI:10.1109/TAP.1979.1142163 (  0) 0) |
| [4] |
Hasselmann K, Hasselmann S. On the nonlinear mapping of an ocean wave spectrum into a synthetic aperture radar image spectrum and its inversion[J]. Journal of Geophysical Research: Oceans, 1991, 96(C6): 10713-10729. DOI:10.1029/91JC00302 (  0) 0) |
| [5] |
Vachon P W, Raney R K. Resolution of the ocean wave propagation direction in SAR imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 1991, 29(1): 105-112. DOI:10.1109/36.103299 (  0) 0) |
| [6] |
Engen G, Johnsen H. SAR-ocean wave inversion using image cross spectra[J]. IEEE Transactions on Geoscience and Remote Sensing, 1995, 33(4): 1047-1056. DOI:10.1109/36.406690 (  0) 0) |
| [7] |
Bao M, Alpers W. On the cross spectrum between individual-look synthetic aperture radar images of ocean waves[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(3): 922-932. DOI:10.1109/36.673683 (  0) 0) |
| [8] |
Mastenbroek C D, De Valk C F. A semiparametric algorithm to retrieve ocean wave spectra from synthetic aperture radar[J]. Journal of Geophysical Research: Oceans, 2000, 105(C2): 3497-3516. DOI:10.1029/1999JC900282 (  0) 0) |
| [9] |
Zhang B, Li X, Perrie W, et al. Synergistic measurements of ocean winds and waves from SAR[J]. Journal of Geophysical Research: Oceans, 2015, 120(9): 6164-6184. DOI:10.1002/2015JC011052 (  0) 0) |
| [10] |
Sun J, Guan C L. Parameterized first-guess spectrum method for retrieving directional spectrum of swell-dominated waves and huge waves from SAR images[J]. Chinese Journal of Oceanology and Limnology, 2006, 24(1): 12-20. DOI:10.1007/BF02842769 (  0) 0) |
| [11] |
Tao X, Perrie W, Yijun H E, et al. Ocean surface wave measurements from fully polarimetric SAR imagery[J]. Science China Earth Sciences, 2015, 58(10): 1849-1861. DOI:10.1007/s11430-015-5078-6 (  0) 0) |
| [12] |
Schuler D, Lee J, Kasilingam D, et al. Measurement of ocean surface slopes and wave spectra using polarimetric SAR image data[J]. Remote sensing of environment, 2004, 91(2): 198-211. DOI:10.1016/j.rse.2004.03.008 (  0) 0) |
| [13] |
Zhang B, Perrie W, He Y. Validation of RADARSAT-2 fully polarimetric SAR measurements of ocean surface waves[J]. Journal of Geophysical Research: Oceans, 2010, 115(C06031): 1-11. (  0) 0) |
| [14] |
He Y, Perrie W, Xie T, et al. Ocean wave spectra from a linear polarimetric SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(11): 2623-2631. DOI:10.1109/TGRS.2004.836813 (  0) 0) |
| [15] |
He Y, Shen H, Perrie W. Remote sensing of ocean waves by polarimetric SAR[J]. Journal of Atmospheric and Oceanic Technology, 2006, 23(12): 1768-1773. DOI:10.1175/JTECH1948.1 (  0) 0) |
| [16] |
Zhang Y, Wang Y, Xu Q. On the nonlinear mapping of an ocean wave spectrum into a new polarimetric SAR image spectrum[J]. Journal of Physical Oceanography, 2020, 50(11): 3109-3122. DOI:10.1175/JPO-D-20-0045.1 (  0) 0) |
| [17] |
Schulz-Stellenfleth J, König T, Lehner S. An empirical approach for the retrieval of integral ocean wave parameters from synthetic aperture radar data[J]. Journal of Geophysical Research: Oceans, 2007, 112(C03019): 1-14. (  0) 0) |
| [18] |
Shao W, Zhang Z, Li X, et al. Ocean wave parameters retrieval from Sentinel-1 SAR imagery[J]. Remote Sensing, 2016, 8(9): 707. DOI:10.3390/rs8090707 (  0) 0) |
| [19] |
Stopa J E, Mouche A. Significant wave heights from Sentinel-1 SAR: Validation and applications[J]. Journal of Geophysical Research: Oceans, 2017, 122(3): 1827-1848. DOI:10.1002/2016JC012364 (  0) 0) |
| [20] |
Ren L, Yang J, Zheng G, et al. Significant wave height estimation using azimuth cutoff of C-band RADARSAT-2 single-polarization SAR images[J]. Acta Oceanologica Sinica, 2015, 34(12): 93-101. DOI:10.1007/s13131-015-0769-6 (  0) 0) |
| [21] |
Li H, Stopa J E, Mouche A, et al. Assessment of ocean wave spectrum using global Envisat/ASAR data and hindcast simulation[J]. Remote Sensing of Environment, 2021, 264: 112614. DOI:10.1016/j.rse.2021.112614 (  0) 0) |
| [22] |
Kerbaol V, Chapron B, Vachon P W. Analysis of ERS-1/2 synthetic aperture radar wave mode imagettes[J]. Journal of Geophysical Research: Oceans, 1998, 103(C4): 7833-7846. DOI:10.1029/97JC01579 (  0) 0) |
| [23] |
Ren L, Yang J, Chen P. A method for retrieving the directional ocean wave spectra from synthetic aperture radar image[C]. SPIE: Remote Sensing of the Ocean, Sea Ice, Coastal waters and Large Water Regions 2012, 2012, 8532: 240-248.
(  0) 0) |
| [24] |
Zhang B, Perrie W, He Y. Wind speed retrieval from RADARSAT-2 quad-polarization images using a new polarization ratio model[J]. Journal of Geophysical Research: Oceans, 2011, 116(C008008): 1-13. (  0) 0) |
2. The First Institute of Oceanography, Ministry of Natural Resources, Qingdao 266061, China;
3. Laboratory for Regional Oceanography and Numerical Modeling, Pilot National Laboratory for Marine Science and Technology(Qingdao), Qingdao 266237, China
 2024, Vol. 54
2024, Vol. 54