近年来，基于仿射变换下的低秩矩阵恢复问题在协同过滤^[1]、图像处理^[2]、量子成像^[3]等多个领域有重要应用，发展求解此问题的高效数值解法是当前数值最优化领域的研究热点之一。仿射秩最小化问题是指下述矩阵最优化问题

$ \mathop {\min }\limits_X {\mathop{\rm rank}\nolimits} (\mathit{\boldsymbol{X}}),s.t.\left\| {\mathscr{A}\mathit{\boldsymbol{X}} - b} \right\|_2^2 \le \varepsilon ; $

(1)

或者其拉格朗日形式

$ \mathop {\min }\limits_X \frac{1}{2}\left\| {\mathscr{A}\mathit{\boldsymbol{X}} - b} \right\|_2^2 + \lambda {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathop{\rm rank}\nolimits} (\mathit{\boldsymbol{X}})。$

(2)

式中：X∈R^m×n为要恢复的目标矩阵; b∈R^p为观测数据; $\mathscr{A}$：R^m×n→R^p为仿射变换; 参数ε≤0反映噪声水平；λ>0为正则化参数。当仿射变换$\mathscr{A}$为矩阵的取样算子时，仿射秩最小化问题就转化为矩阵填充问题^[4]。

由于矩阵秩函数非凸、非连续，秩最小化问题是一个NP问题^[5]，因此需要寻找近似函数来替代矩阵的秩函数。核范数是被广泛使用的一种替代函数^[1]，设d=min(m, n)，σ_i(X)为矩阵X按非增顺序排列的第i个奇异值，则核范数‖X‖_*=$\sum {_{i = 1}^d{\sigma _i}\left( \mathit{\boldsymbol{X}} \right)} $。虽然易于发展高效的数值解法，但是核范数只是秩函数的凸近似，因此其恢复能力仍有较大的提升空间^[6]。

Wen等^[7-9]提出了一种基于矩阵分解的建模方法，避免了对矩阵进行奇异值分解，但事先需要对矩阵的秩进行合理的预测。Mohan等^[10]利用矩阵的Schatten-p范数来代替秩函数，提高了模型的恢复能力。本文用下述新的松弛模型来求解秩最小化问题

$ \mathop {\min }\limits_X \frac{1}{2}\left\| {\mathscr{A}\mathit{\boldsymbol{X}} - b} \right\|_2^2 + \lambda \log {\kern 1pt} {\kern 1pt} {\kern 1pt} \det \left( {{{\left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}}} \right)}^{\frac{1}{2}}} + \gamma \mathit{\boldsymbol{I}}} \right)。$

(3)

其中γ≤1，并且发展了模型(3)的数值解法，证明了数值算法的收敛性，数值实验表明了模型(3)相较于核范数模型的优越性。

1 算法

下述引理用于得到模型(3)的等价形式。

引理 1  设X∈R^m×n，γ≤1，则

$ \log {\kern 1pt} {\kern 1pt} {\kern 1pt} \det \left( {{{\left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}}} \right)}^{\frac{1}{2}}} + \gamma \mathit{\boldsymbol{I}}} \right) = \sum\limits_{i = 1}^d {\log } \left( {{\sigma _i}(\mathit{\boldsymbol{X}}) + \gamma } \right)。$

(4)

证明  由矩阵行列式的性质可知

$ \begin{array}{*{20}{c}} {\log {\kern 1pt} {\kern 1pt} {\kern 1pt} \det \left( {{{\left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}}} \right)}^{\frac{1}{2}}} + \gamma \mathit{\boldsymbol{I}}} \right) = \log \left( {\prod\limits_{i = 1}^d {{\sigma _i}} (\mathit{\boldsymbol{X}}) + \gamma } \right) = }\\ {\sum\limits_{i = 1}^d {\log } \left( {{\sigma _i}(\mathit{\boldsymbol{X}}) + \gamma } \right)}。\end{array} $

由引理1，可得到模型(3)的如下等价形式

$ \mathop {\min }\limits_X \frac{1}{2}\left\| {\mathscr{A}\mathit{\boldsymbol{X}} - b} \right\|_2^2 + \sum\limits_{i = 1}^d {\log } \left( {{\sigma _i}(\mathit{\boldsymbol{X}}) + \gamma } \right)。$

(5)

定义 1  对于下半连续的正常函数g(x)：R→R及α>0，其邻近算子Prox_αg：R→R定义如下：

$ {\mathop{\rm Pro}\nolimits} {x_{\alpha g}}(y) = \arg \mathop {\min }\limits_{x \in {\bf{R}}} \left\{ {f(x) = \alpha g(x) + \frac{1}{2}{{(x - y)}^2}} \right\}。$

(6)

在本文中，我们讨论y为矩阵奇异值的情况，因此只需要对y≤0进行考虑。下面的三个定理给出了模型(5)中罚函数的邻近算子的相关性质及其显式表达式。

定理 1  设g(x)=log(x+γ)，γ≤1，α>0，g(x)的邻近算子满足如下性质：

① ∃c>0，∀y∈[0, c]，Prox_αg(y)=0。

② 当y→+∞时，对∀z∈Prox_αg(y)，有z→+∞且$\mathop {\lim }\limits_{y \to + \infty } (z - y) = 0$。

③ 当y₁ < y₂时，对∀z₁∈Prox_αg(y₁)，∀z₂∈Prox_αg(y₂)，有z₁ < z₂。

证明  ①令h(x)=$\frac{\alpha }{{x + \gamma }} + x$，则h(x)在x≤0上连续。设c为h(x)在[0, +∞)上的最小值，当y∈[0, c]时，f′(x)=$\frac{\alpha }{{x + \gamma }} + x - y \le 0$≤0，故f(x)在区间[0, +∞)上单调递增，故Prox_αg(y)=0。

② 当y→+∞时，对∀z∈Prox_αg(y)，z必为f(x)的一个驻点，即f′(z)=$\frac{\alpha }{{z + \gamma }} + z - y \le 0$。由于$\frac{\alpha }{{z + \gamma }} < \frac{\alpha }{\gamma }$，则$\mathop {\lim }\limits_{y \to + \infty } z = + \infty $，并且

$ \mathop {\lim }\limits_{y \to + \infty } (z - y) = \mathop {\lim }\limits_{y \to + \infty } \frac{{ - \alpha }}{{z + \gamma }} = 0。$

③ 当y₁ < y₂时，对∀z₁∈Prox_αg(y₁)，∀z₂∈Prox_αg(y₂)，由邻近算子的定义，则

$ \begin{array}{*{20}{l}} {\alpha g\left( {{z_1}} \right) + \frac{1}{2}{{\left( {{z_1} - {y_1}} \right)}^2} \le \alpha g\left( {{z_2}} \right) + \frac{1}{2}{{\left( {{z_2} - {y_1}} \right)}^2} \le }\\ {\alpha g\left( {{z_2}} \right) + \frac{1}{2}{{\left( {{z_2} - {y_2}} \right)}^2} + }\\ {\frac{1}{2}{{\left( {{y_2} - {y_1}} \right)}^2} + \left( {{z_2} - {y_2}} \right)\left( {{y_2} - {y_1}} \right) \le }\\ {\alpha g\left( {{z_1}} \right) + \frac{1}{2}{{\left( {{z_1} - {y_2}} \right)}^2} + \frac{1}{2}{{\left( {{y_2} - {y_1}} \right)}^2} + }\\ {\left( {{z_2} - {y_2}} \right)\left( {{y_2} - {y_1}} \right)} \end{array} $

对上述不等式化简可得z₁ < z₂。

定理 2  设g(x)=log(x+γ)，γ≤1，α>0，当$\frac{\alpha }{{{\gamma ^2}}}$≤1时，有

$ {\mathop{\rm Pro}\nolimits} {x_{\alpha g}}(y) = \left\{ {\begin{array}{*{20}{l}} {0,y \le \frac{\alpha }{\gamma }}\\ {\hat x,y > \frac{\alpha }{\gamma }} \end{array}} \right.。$

(7)

式中$\hat x = \frac{1}{2}\left( {y - \gamma + \sqrt {{{\left( {y + \gamma } \right)}^2} - 4\alpha } } \right)$，且Prox_αg(y)是关于y的连续函数。

证明  当$\frac{\alpha }{{{\gamma ^2}}}$≤1时，f″(x)=1-$\frac{\alpha }{{{{\left( {x + \gamma } \right)}^2}}}$≤0在x≤0上恒成立。当f′(0)≤0时，y≤$\frac{\alpha }{\gamma }$，f(x)在x≤0上单调递增，则Prox_αg(y)=0。当f′(0) < 0时，y>$\frac{\alpha }{\gamma }$，f(x)在x≤0上先减后增。由于f(x)是x≤0上的凸函数，Prox_αg(y)应在f(x)驻点处取得。令f′(0)=0，求得Prox_αg(y)=$，其中$\hat x = \frac{1}{2}\left( {y - \gamma + \sqrt {{{\left( {y + \gamma } \right)}^2} - 4\alpha } } \right)$，且$\mathop {\lim }\limits_{y \to \frac{\alpha }{\gamma }} \Pr {\rm{o}}{x_{\alpha g}}\left( y \right) = 0$=0，因此，Prox_αg(y) 是y≤0上的连续函数。

定理 3  设g(x)=log(x+γ)，γ≤1，α>0，当$\frac{\alpha }{{{\gamma ^2}}}$>1时，存在唯一的y^*∈($2\sqrt \alpha - \gamma $, $\frac{\alpha }{\gamma }$)使得

$ {\mathop{\rm Pro}\nolimits} {x_{ag}}(y) = \left\{ {\begin{array}{*{20}{c}} {0,}&{y < {y^*}}\\ {\{ 0,\hat x\} ,}&{y = {y^*}}\\ {\hat x,}&{y > {y^*}} \end{array}} \right.。$

(8)

式中$\hat x = \frac{1}{2}\left( {y - \gamma + \sqrt {{{\left( {y + \gamma } \right)}^2} - 4\alpha } } \right)$。

证明  可求$x + \frac{\alpha }{{x + \gamma }}$在x≤0上的最小值为2$\sqrt \alpha $-γ。当y≤2$\sqrt \alpha $-γ时，f′(x)=$\frac{\alpha }{{x + \gamma }} + x - y$≤0，因此f(x)在x≤0上单调递增，从而Prox_αg(y)=0。当y≤$\frac{\alpha }{\gamma }$时, f′(0)≤0，令f′(0)=0，求得驻点为$\hat x$，则f(x)在[0, $\hat x$]上单调递减，在[$\hat x$, +∞)上单调递增，因此Prox_αgy=$\hat x$。当2$\sqrt \alpha $-γ < y < $\frac{\alpha }{\gamma }$时，令f′(0)=0, 求得驻点${\tilde x} = \frac{1}{2}\left( {y - \gamma + \sqrt {{{\left( {y + \gamma } \right)}^2} - 4\alpha } } \right)$和$\hat x$。则f(x)在[0, ${\tilde x}$]上单调递增，在[${\tilde x}$, $\hat x$]上单调递减，然后在[$\hat x$, +∞)上单调递增，所以Prox_αg(y)应该等于0或$\hat x$。由于

$ \begin{array}{*{20}{c}} {f(0) = \frac{1}{2}{y^2} + \alpha \log \gamma ;}\\ {f(\hat x) = \frac{1}{2}{{\left( {\frac{{\sqrt {{{(y + \gamma )}^2} - 4\alpha } - (y + \gamma )}}{2}} \right)}^2} + }\\ {\alpha \log \frac{{\sqrt {{{(y + \gamma )}^2} - 4\alpha } + (y + \gamma )}}{2}}。\end{array} $

f(0)和f(${\hat x}$)在y∈(2$\sqrt \alpha $-γ, $\frac{\alpha }{\gamma }$)上单调递增，且当y=2$\sqrt \alpha $-γ时，f(0) < f(${\hat x}$)，当y=$\frac{\alpha }{\gamma }$时，f(0)>f(${\hat x}$)，因此必存在点y^*∈(2$\sqrt \alpha $-γ, $\frac{\alpha }{\gamma }$)，使得f(0)=f(${\hat x}$)。下证y^*的唯一性。

假设存在点${\tilde y}$∈(2$\sqrt \alpha $-γ, $\frac{\alpha }{\gamma }$)且${\tilde y}$≠y^*，使得f(0)=f(${\hat x}$)。不妨设${\tilde y}$ < y^*，则${\hat x}$∈Prox_αg(${\tilde y}$)，0∈Prox_αg(${\tilde y}$)。当$\frac{\alpha }{{{\gamma ^2}}}$>1时，${\hat x}$>0，又因为${\tilde y}$ < y^*，这与定理1结论③矛盾。因此存在唯一的点y^*∈(2$\sqrt \alpha $-γ, $\frac{\alpha }{\gamma }$)，使得f(0)=f(${\hat x}$)。

综上所述，当y < y^*时，Prox_αg(y)=0。当y=y^*时, Prox_αg(y)={0, ${\hat x}$}。当y>y^*时，Prox_αg(y)=0。

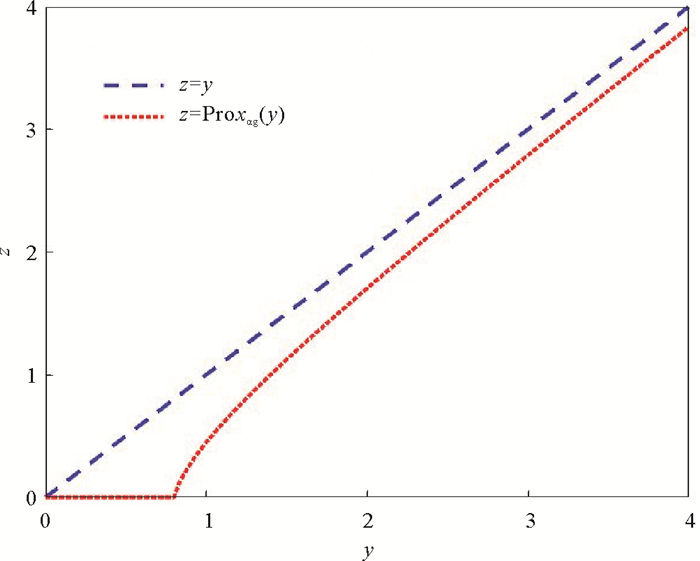
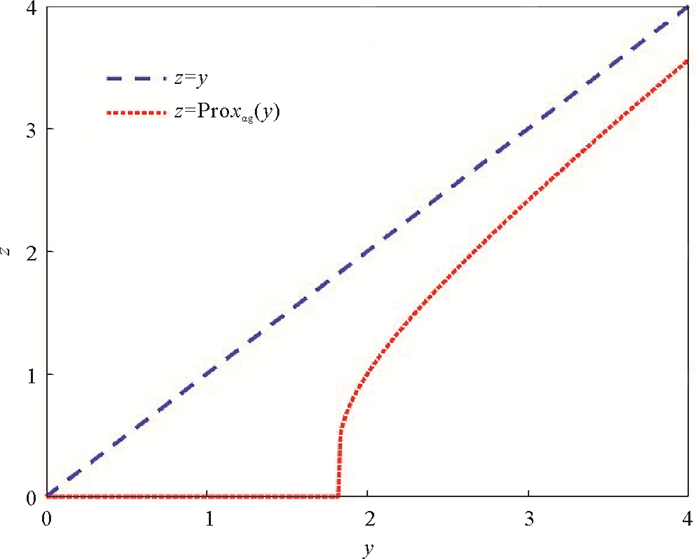
图 1和2分别画出了γ=1，α=0.8($\frac{\alpha }{{{\gamma ^2}}}$≤1)和γ=1，α=2($\frac{\alpha }{{{\gamma ^2}}}$>1)时，g(x)的邻近算子的图像，验证了定理1到定理3的结果。

下面将g(x)的邻近算子推广到矩阵情形。设α>0，G(X)=$\sum\limits_{i = 1}^d {\log \left( {{\sigma _i}\left( \mathit{\boldsymbol{X}} \right) + \gamma } \right)} $，σ_i(X)为矩阵X按非增顺序排列的第i个奇异值，定义

$ {\mathop{\rm Pro}\nolimits} {x_{\alpha G}}(\mathit{\boldsymbol{X}}) = \arg \mathop {\min }\limits_Y \frac{1}{2}\left\| {\mathit{\boldsymbol{Y}} - \mathit{\boldsymbol{X}}} \right\|_F^2 + \alpha G(\mathit{\boldsymbol{Y}})。$

设UDiag(σ)V^T为X的奇异值分解，由邻近算法^[11]中的结论可知有Prox_αG(X)的一个显式解为

$ {\mathop{\rm Pro}\nolimits} {x_{\alpha G}}(\mathit{\boldsymbol{X}}) = \mathit{\boldsymbol{U}}{\rm{Diag}}\left( {{\mathop{\rm Pro}\nolimits} {x_{\alpha g}}\left( {{\sigma _1}} \right), \cdots ,{\mathop{\rm Pro}\nolimits} {x_{\alpha g}}\left( {{\sigma _d}} \right)} \right){\mathit{\boldsymbol{V}}^{\rm{T}}}。$

(9)

我们接下来讨论模型(5)的数值解法，假设为第k步迭代中的解，在第k+1步迭代中，将$\frac{1}{2}{\left\| {{\mathscr{A}}\mathit{\boldsymbol{X}} - b} \right\|^2}$在X^k处用二次控制函数替代，得到如下更新准则

$ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{X}}^{k + 1}} \in \arg \mathop {\min }\limits_\mathit{\boldsymbol{X}} \frac{1}{2}\left\| {\mathscr{A}\mathit{\boldsymbol{X}} - b} \right\|_2^2 + < {\mathscr{A}^*}\left( {\mathscr{A}{\mathit{\boldsymbol{X}}^k} - b} \right),}\\ {\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{X}}^k} > + \frac{\mu }{2}\left\| {\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{X}}^k}} \right\|_F^2 + \sum\limits_{i = 1}^d \lambda {\kern 1pt} {\kern 1pt} {\kern 1pt} \log \left( {{\sigma _i}(\mathit{\boldsymbol{X}}) + \gamma } \right) = }\\ {\arg \mathop {\min }\limits_X \frac{\mu }{2}\left\| {\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{X}}^k} + \frac{1}{\mu }{\mathscr{A}^*}\left( {A{\mathit{\boldsymbol{X}}^k} - b} \right)} \right\|_F^2 + }\\ {\sum\limits_{i = 1}^d \lambda \log \left( {{\sigma _i}(\mathit{\boldsymbol{X}}) + \gamma }。\right)} \end{array} $

(10)

式中$\mathscr{A}$^*是$\mathscr{A}$的共轭算子，μ>λ_max($\mathscr{A}$^*  $\mathscr{A}$)/2，λ_max($\mathscr{A}$^*  $\mathscr{A}$)/2为$\mathscr{A}$^*  $\mathscr{A}$的最大特征值。

由(9)式我们得到迭代算法

$ {\mathit{\boldsymbol{X}}^{k + 1}} \in {\mathop{\rm Pro}\nolimits} {x_{\frac{\lambda }{\mu }G}}\left( {{\mathit{\boldsymbol{X}}^k} - \frac{1}{\mu }{\mathscr{A}^*}\left( {\mathscr{A}{\mathit{\boldsymbol{X}}^k} - b} \right)} \right)。$

(11)

记上述算法为PGA算法，Z^k=X^k-$\frac{1}{\mu }$$\mathscr{A}$^*·($\mathscr{A}$X^k-b)，奇异值分解Z^k=U^kΣ^k(V^k)^T，其中Σ^k=Diag(σ_i^k)，σ_i^k为矩阵Z^k按非增顺序排列的第i个奇异值，则X^k+1=U^k$\mathit{\boldsymbol{ \boldsymbol{\tilde \varSigma} }}$(V^k)^T，其中$\mathit{\tilde \Sigma }$=Diag(Prox_λμgσ_i^k)。

令

$ F\left( \boldsymbol{X} \right) = \frac{1}{2}\left\| {{\mathscr{A}}\boldsymbol{X} - b} \right\|_2^2 + \sum\limits_{i = 1}^d {\lambda \;\log \left( {{\sigma _i}\left( \boldsymbol{X} \right) + \gamma } \right)} $

下面的定理给出了上述算法的收敛性。

定理 4  设μ>λ_max($\mathscr{A}$^*  $\mathscr{A}$)/2，则由PGA算法得到的序列{X^k}具有如下性质：

①{F(X^k)}单调递减并收敛。

② $\mathop {\lim }\limits_{k \to + \infty } \left\| {{\mathit{\boldsymbol{X}}^{k + 1}} - {\mathit{\boldsymbol{X}}^k}} \right\|_F^2$=0。

证明  ①由(10)式可得

$ \begin{array}{*{20}{l}} {<{\mathscr{A}^*}\left( {A{\mathit{\boldsymbol{X}}^k} - b} \right),{\mathit{\boldsymbol{X}}^{k + 1}} - {\mathit{\boldsymbol{X}}^k} > + \frac{1}{2}\left\| {{\mathit{\boldsymbol{X}}^{k + 1}} - {\mathit{\boldsymbol{X}}^k}} \right\|_F^2 + }\\ {\sum\limits_{i = 1}^d \lambda \log \left( {{\sigma _i}\left( {{\mathit{\boldsymbol{X}}^{k + 1}}} \right) + \gamma } \right) \le \sum\limits_{i = 1}^d \lambda \log \left( {{\sigma _i}\left( {{\mathit{\boldsymbol{X}}^k}} \right) + \gamma } \right)}。\end{array} $

(12)

将$\frac{1}{2}\left\| {{\mathscr{A}}\mathit{\boldsymbol{X}} - b} \right\|_2^2$在X^k泰勒展开，得到

$ \begin{array}{*{20}{c}} {\frac{1}{2}\left\| {\mathscr{A}\mathit{\boldsymbol{X}} - b} \right\|_2^2 \le \frac{1}{2}\left\| {\mathscr{A}\mathit{\boldsymbol{X}} - b} \right\|_2^2 + < {\mathscr{A}^*}\left( {\mathscr{A}{\mathit{\boldsymbol{X}}^k} - b} \right),}\\ {\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{X}}^k} > + \frac{{{\lambda _{\max }}\left( {{\mathscr{A}^*}\mathscr{A}} \right)}}{2}\left\| {\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{X}}^k}} \right\|_F^2} \end{array} $

将X^k+1带入上式，则

$ \begin{array}{l} \frac{1}{2}\left\| {\mathscr{A}\mathit{\boldsymbol{X}} - b} \right\|\frac{2}{2} + \frac{{\mu - {\lambda _{\max }}\left( {{\mathscr{A}^*}\mathscr{A}} \right)}}{2}\left\| {{\mathit{\boldsymbol{X}}^{k + 1}} - {\mathit{\boldsymbol{X}}^k}} \right\|_F^2 \le \\ \frac{1}{2}\left\| {\mathscr{A}\mathit{\boldsymbol{X}} - b} \right\|_2^2 + < {\mathscr{A}^*}\left( {\mathscr{A}{\mathit{\boldsymbol{X}}^k} - b} \right),{\mathit{\boldsymbol{X}}^{k + 1}} - {\mathit{\boldsymbol{X}}^k} > + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{\mu }{2}\left\| {{\mathit{\boldsymbol{X}}^{k + 1}} - {\mathit{\boldsymbol{X}}^k}} \right\|_F^2。\end{array} $

(13)

由式(12)和(13)可得

$ F\left( {{\mathit{\boldsymbol{X}}^{k + 1}}} \right) + \frac{{\mu - {\lambda _{\max }}\left( {{\mathscr{A}^*}\mathscr{A}} \right)}}{2}\left\| {{\mathit{\boldsymbol{X}}^{k + 1}} - {\mathit{\boldsymbol{X}}^k}} \right\|_F^2 \le F\left( {{\mathit{\boldsymbol{X}}^k}} \right)。$

则

$ F\left( {{\mathit{\boldsymbol{X}}^k}} \right) - F\left( {{\mathit{\boldsymbol{X}}^{k + 1}}} \right) \le \frac{{\mu - {\lambda _{\max }}\left( {{\mathscr{A}^*}\mathscr{A}} \right)}}{2}\left\| {{\mathit{\boldsymbol{X}}^{k + 1}} - {\mathit{\boldsymbol{X}}^k}} \right\|_F^2。$

因为μ>λ_max($\mathscr{A}$^*  $\mathscr{A}$)/2，结论①得证。

② 设$C = \mathop {\lim }\limits_{k \to + \infty } F\left( {{\mathit{\boldsymbol{X}}^k}} \right)$，由上述证明可得

$ F\left( {{\mathit{\boldsymbol{X}}^1}} \right) - C \le \sum\limits_{i = 1}^\infty {\frac{{\mu - {\lambda _{\max }}\left( {{\mathscr{A}^*}\mathscr{A}} \right)}}{2}} \left\| {{\mathit{\boldsymbol{X}}^{k + 1}} - {\mathit{\boldsymbol{X}}^k}} \right\|_F^2, $

由于μ>λ_max($\mathscr{A}$^*  $\mathscr{A}$)/2，则$\mathop {\lim }\limits_{k \to + \infty } \left\| {{\mathit{\boldsymbol{X}}^{k + 1}} - {\mathit{\boldsymbol{X}}^k}} \right\|_F^2 = 0$。

2 数值实验

在本节中，我们通过矩阵填充问题来验证模型(3)的有效性和算法的可行性。算法中涉及到的奇异值分解利用PROPACK^[12]计算。

在无噪声的情况下，我们模拟模型和算法的恢复能力。假定采样率为50%，X=X₁X₂为目标矩阵，其中X₁∈R^200×r，X₂∈R^r×200为元素服从均值为0，方差为1的正态分布的随机矩阵，整数r为矩阵的秩，其变化范围为25~50。设X^*为算法得到的解，当相对误差满足

$ \frac{{{{\left\| {{\mathit{\boldsymbol{X}}^*} - \mathit{\boldsymbol{X}}} \right\|}_F}}}{{{{\left\| \mathit{\boldsymbol{X}} \right\|}_F}}} \le {10^{ - 3}}, $

则视为恢复成功。对每个r重复100次实验，设恢复成功的次数为S_r，则定义恢复概率为S_r/100。我们将PGA算法与采用核范数的IADM^[13]算法进行比较。由于侧重比较模型的恢复能力，我们希望算法能够得到充分迭代，因此设置停机准则为

$ \frac{{{{\left\| {{\mathit{\boldsymbol{X}}^{k + 1}} - {\mathit{\boldsymbol{X}}^k}} \right\|}_F}}}{{{{\left\| {{\mathit{\boldsymbol{X}}^k}} \right\|}_F}}} \le {10^{ - 6}}。$

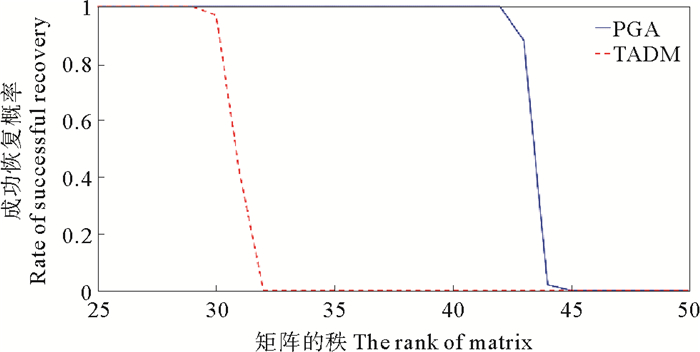
由图 3可以看出，当r≤29时，PGA和IADM算法都能够恢复成功；当r>32时，IADM算法恢复失败；而当r≤42时，PGA算法仍可恢复成功。

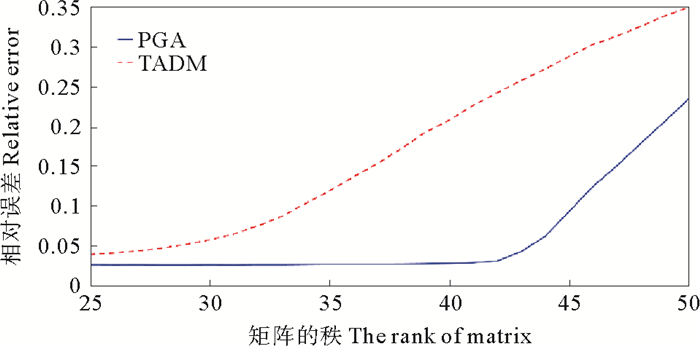
PGA算法亦适用于含噪声情况。假定采样率和目标矩阵X的构造与上述实验相同，令X_noise=X+0.1×E，其中E为元素服从均值为0，方差为1的正态分布的随机矩阵。然后对X_noise进行采样，矩阵的秩r变化范围为25~50。我们对每个r做20次实验得到其平均误差，并同IADM算法进行了对比。由图 4可以看出当r≤30时，IADM算法相对误差高于0.05，且相对误差逐渐增大，而PGA算法在r≤43时，相对误差仍在0.05以下。

3 结语

本文提出了一种矩阵秩最小化问题的松弛模型，并给出了邻近梯度下降算法，证明了算法的收敛性。通过实验表明，模型的恢复能力要高于核范数松弛，是求解原问题的一种好的模型，且在有噪声污染的情况下，算法的表现也优于核范数松弛，本研究为解决实际问题提供了一种新的途径。