2. 中国海洋大学工程学院,山东 青岛 266100
据世界气象组织估计,约有百分之九十的自然灾害是极端的气象灾害,如台风、飓风和热带风暴引发的灾害,其频次多、破坏力巨大、致灾方式多样,严重威胁着人类的生存和发展。在2005年8月,卡特丽娜飓风袭击了美国大西洋湾沿岸,最大风速为274 km/h,造成约1 200人死亡。经济损失总额约800亿美元。后来,飓风丽塔在美国和墨西哥登陆,造成了144亿美元的损失,在墨西哥湾摧毁了超过110个平台[1]。卡特丽娜飓风和丽塔袭击了美国沿海地区,给新奥尔良带来灾难性的伤害,也对墨西哥湾石油工业造成了很大的影响。
台风灾害是影响我国经济发展的重要因素之一。在我国,约有10个省、28个沿海地区和6个内陆省份都受到台风引发的灾害的影响。2006年,台风“桑美”导致3.76风暴增水和7 m高的巨浪,造成240人死亡,在沙埕港952艘船沉没,594人死亡[2]。如果台风桑美登陆晚2 h,当时的台风诱发的7 m巨浪恰逢天文大潮同时出现,会淹没浙江和福建省的大部分地区和几处核电站,这种小概率极端事件的发生是完全可能的。
随着化石燃料的大量使用,全球变暖,海平面上升,以及一系列其他气候变化,有研究表明:近几十年,台风和飓风引起的灾害的频率和强度会增加[3]。我国南部沿海地区人口密集,工业发达,随着经济的发展,海洋海岸工程越来越多,多个滨海核电站正在规划、设计或建造阶段。从卡特丽娜飓风和“桑美”台风灾害的教训表明,面对全球极端气候频发的趋势,现有的极值统计理论的观点不能满足台风灾害的预测,尤其是极端海洋工程环境的概率分析。
因此,本文将依据多维复合极值分布理论(MCEVD),分析台风诱发的巨浪、风暴潮及相应的天文潮等致灾因素的联合频率,同时引入整体不确定性理论(GUA),对各种统计理论,取样方法计算结果进行合理的不确定性评估,并结合实例分析,将联合概率法与传统方法做对比。
1 多维复合极值分布理论概率模型的建立对于每年台风自然灾害的发生频次λ,其符合泊松分布
| $ {P_i}=\frac{{{{\rm{e}}^{{\rm{ - }}\lambda }}{\lambda ^i}}}{{i!}}。$ | (1) |
多维复合极值分布可表示为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;{F_0}\left( {{x_1}, \Lambda , {x_n}} \right)={{\rm{e}}^{{\rm{ - }}\lambda }} + \\ \int_{ - \infty }^{{x_n}} {{\rm{K}}\int_{ - \infty }^{{x_1}} {\sum\limits_{m=0}^\infty {\frac{{{{\rm{e}}^{{\rm{ - }}\lambda }}{\lambda ^m}}}{{m!}}{G_1}{{\left( {{u_1}} \right)}^m}\lambda g\left( {{u_1}, {\rm{K, }}{u_n}} \right)} {\rm{d}}{u_1}{\rm{Kd}}{u_n}{\rm{=}}} } \\ {{\rm{e}}^{{\rm{ - }}\lambda }}\left( {1{\rm{ + }}\lambda \int_{ - \infty }^{{x_n}} {{\rm{K}}\int_{ - \infty }^{{x_1}} {{{\rm{e}}^{\lambda \cdot {G_{\rm{1}}}\left( {{u_1}} \right)}}g\left( {{u_1}, {\rm{K}}, {u_n}} \right)} {\rm{d}}{u_1}{\rm{Kd}}{u_n}} } \right)。\end{array} $ | (2) |
其相应的概率密度函数为:
| $ f\left( {{x_1}, {\rm{K}}, {x_n}} \right)=\lambda {{\rm{e}}^{{\rm{ - }}\lambda \left[ {1 - {G_1}\left( {{x_1}} \right)} \right]}}g\left( {{x_1}, {\rm{K}}, {x_n}} \right)。$ | (3) |
为解决多维复合极值分布的理论解法,本文将以三维复合极[4]值分布为例加以说明。
设三维连续型随机向量(ξ, η, γ), (ζ, Ψ, ν), 其联合概率分布函数为G(x, y, z)和Q(x, y, z)。g(x, y, z)为向量(ξ, η, γ)的联合概率密度函数;Gx(x)为ξ的边缘分布函数。令向量(ξ, η, γ)的第i次观测值是(ξi, ηi, γi),令n与向量(ξ, η, γ)和(ζ, Ψ, ν)皆独立,且n是取值非负整数的随机变量,其分布函数记作:
| $ P\left\{ {n=k} \right\}={P_K}, k=0, 1, \cdots , \Lambda , \sum {P_K}=1, $ |
定义随机向量(X, Y, Z)
| $ \left( {X, Y, Z} \right)=\left\{ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\left( {\zeta , \varphi , \nu } \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;n=0\\ \left( {{\xi _j}, {\eta _j}, {\gamma _j}} \right){\rm{|}}{\xi _j}{\rm{=}}\mathop {{\rm{Max}}\;{\xi _i}}\limits_{1 \le i \le n} \;\;\;\;\;n \ge 1 \end{array} \right\}。$ | (4) |
则(X, Y, Z)的联合分布函数为:
| $ \begin{array}{l} F\left( {x, y, z} \right)={P_0} \cdot Q\left( {z, y, z} \right) + \sum\limits_{K=1}^\infty {{P_K} \cdot k \cdot } \\ \int_{ - \infty }^y {\int_{ - \infty }^x {{{\int_{ - \infty }^z {{G_x}\left( u \right)} }^{k - 1}}g\left( {u, v, w} \right)} {\rm{d}}u{\rm{d}}v{\rm{d}}w, } \end{array} $ | (5) |
在实际问题中,我们主要考虑F(x, y, z)接近于1时的情况。当离散型随机变量是Poisson分布,g(x, y, z)为Nested-Logistic分布时,即构成Poisson-Nested-Logistic三维复合极值分布模型[5],其表达式为:
| $ \begin{array}{l} F\left( {{x_1}, {x_2}, {x_3}} \right)=\exp \left[ { - \left\{ {\left[ {{{\left( {1 + {\xi _1}\frac{{{x_1} - {\mu _1}}}{{{\sigma _1}}}} \right)}^{\frac{{ - 1}}{{\alpha \beta {\xi _1}}}}}{\rm{ + }}} \right.} \right.} \right.\\ \left. {{{\left. {{{\left. {{{\left( {1{\rm{ + }}{\xi _2}\frac{{{x_2} - {\mu _2}}}{{{\sigma _2}}}} \right)}^{\frac{{ - 1}}{{\alpha \beta {\xi _2}}}}}} \right]}^\beta } + {{\left( {1{\rm{ + }}{\xi _3}\frac{{{x_3} - {\mu _3}}}{{{\sigma _3}}}} \right)}^{\frac{{ - 1}}{{\alpha {\xi _3}}}}}} \right\}}^\alpha }} \right]。\end{array} $ | (6) |
这里α,β(0≤α,β≤1)为相关参数,它体现了变量之间相关的不对称性,当α,β均为0时,x1, x2, x3完全相关;β=1时,(3)式就变成了三维Logistic模型;α,β均为1时,x1, x2, x3相互独立。
式中,形状参数ξi位置参数μi尺度参数σi, 采用极大似然估计法即可得到。而通过矩估计法,史道济[5, 7]给出了相关参数α,β的显示表达式:
| $ \begin{array}{l} \alpha {\rm{=}}\frac{{\sqrt {1 - {r_{13}}} + \sqrt {1 - {r_{23}}} }}{2}, \\ \beta =\frac{{\sqrt {1 - {r_{12}}} }}{\alpha }。\end{array} $ | (7) |
式中γij为一般的线性相关系数,i<j,i=1,2,j=1,2,3。
2 2012年桑迪飓风及2013菲特台风灾害再次验证多维复合极值分布理论的合理性在1972年,台风丽塔袭击了中国北部渤海湾,重创大连港,给大连海域造成了空前的损失。鉴于国内惯用传统的年极值取样方式,常常会遗漏大量有效的实测资料,在估计尾部概率时常常有很大的偏差,为解决上述问题,1980年,国内海洋工程学者刘德辅、马逢时[8]首次提出了复合极值分布理论(CEVD)。
新理论自1980年在国外重要学术刊物公开发表后,在中国沿海、美国墨西哥湾及大西洋沿岸、挪威和韩国等多项海洋工程研究中都得到应用[9]。2005年,美国飓风卡特里娜飓风对新奥尔良的毁灭性破坏,进一步验证了复合极值分布(CEVD)模式25年前应用于飓风概率预测结果的正确性[10]。
近年来,复合极值分布理论(CEVD)完成了从一维拓宽到多维复合极值分布理论(MCEVD)[11-14]。2012年10月,桑迪飓风登陆美国,冲毁堤坝,对特拉华州,新泽西州以及纽约周边造成大面积淹没、大量人员伤亡和数百亿美元经济损失。桑迪飓风灾害再次验证了复合极值分布理论(CEVD)1982年风暴增水的预测结果和多维复合极值分布理论(MCEVD)2002年飓风最大风速的预测结果[15]。
台风菲特登陆中国,带来重大经济损失,浙江、上海多处防护工程倒塌,出现超警戒水位洪水。以上海的菲特台风灾害为例:2013年10月8日,受天文大潮、上游洪水下泄,本地大暴雨和台风暴潮的共同影响,黄浦江沿线水位迅速上涨,下午2时05分,吴淞口实测水位达5.15 m,超过警戒水位0.35 m,而该水位值仅为2006年使用多维复合极值分布理论(MCEVD)计算所得60年一遇预测值[16]。并且2006年多维复合极值分布理论(MCEVD)计算的百年一遇预测结果,已大大超过上海防护工程500年一遇超警戒水位设防标准。如表 1所示,传统的设计标准和工程结构是致灾的主要诱因,多维复合极值分布理论对灾害的强度的预测再次得到证实。
|
|
表 1 使用MCEVD和传统外延法预测结果比较 Table 1 Comparison between disaster prevention design criteria for Shanghai city |
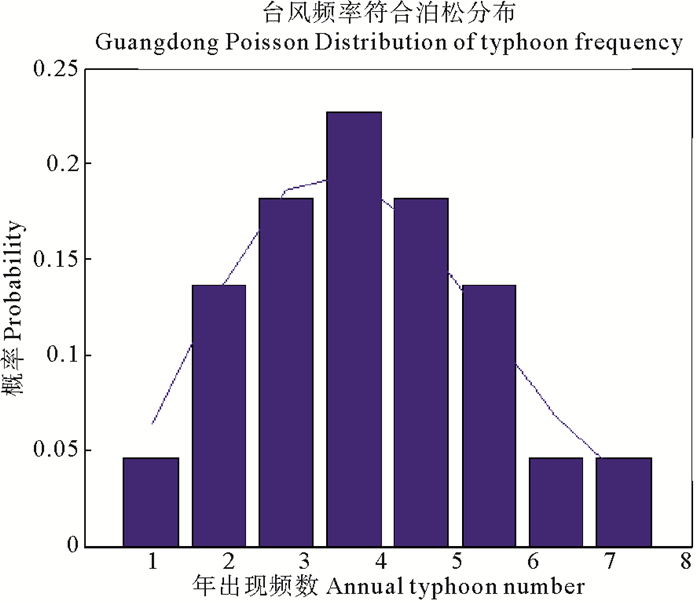
本文使用1984—2005年间中国南海海域的台风资料,将台风灾害影响区域的频次(λ)作为一种离散型随机量考虑。按照表 2对南海海岸带地区台风灾害频率的统计分析,研究海域的台风概率特征如图 1所示,经x2检验,台风出现频次符合Poisson分布,Poisson分布的均值为4.18。
|
|
表 2 南海海岸带台风影响频次统计(1984—2005) Table 2 Frequency of typhoons in South China Sea Coast(1984—2005) |
|
图 1 台风频次λ分布 Fig. 1 Typhoon occurring frequency λ |
台风诱发的暴潮是导致南海海岸带地区经济损失以及人员伤亡的主要方式之一,尤其是风暴潮与天文潮的联合作用,会使破坏力剧增,造成不可估量的灾害。因此,本文在多维复合极值分布概率模型中,考虑将台风诱发暴潮、巨浪及相应天文潮作为主要的致灾控制因素,对研究区域内的波高、潮汐和风暴增水的观测资料进行过程取样,并将其作为随机变量进行灾害预测。
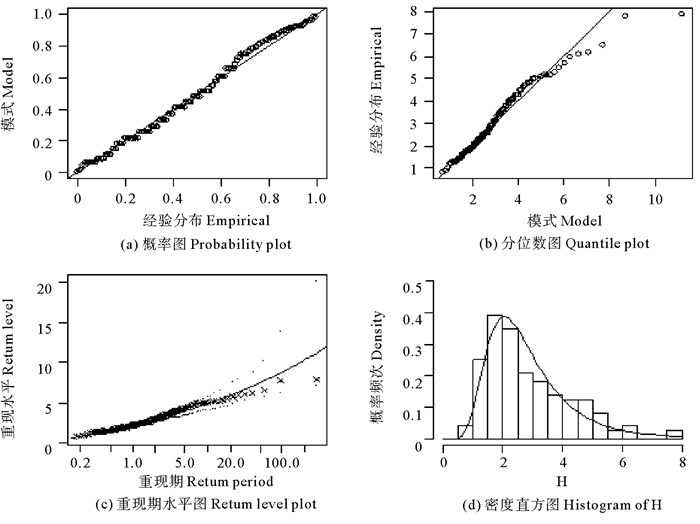
基于K-S诊断测试[17],三组样本点与广义极值分布拟合良好。以波高的统计分布诊断检验图为例(见图 2), 图中a为概率分布图;b为分位数图;c为重现水平图;d为密度直方图。图中圆点为实测资料点,实线为模型曲线;c图中外围2条曲线为模型95%置信区间,天文潮和风暴增水的诊断检验图类似。
|
图 2 波高诊断检验图 Fig. 2 Diagnostic checks of wave height |
通过对样本进行拟合检验,波高、风暴增水和天文潮的统计参数Dn变量分别是0.13,0.12,0.09,三组所选样本的置信水平全部在95%置信区间内(置信水平95%的样本置信区间内所有的分布的临界值是0.26,Dn=0.05[13]),可作为三维复合极值分布边缘分布的样本。
在其联合重现期的讨论中,这种多维复合极值分布可以用来求解析解。本文采用最大似然法[19]估计波高、风暴增水及天文潮的边缘分布参数,然后在经验法的基础上,引入多维联合分布理论和相应的公式,即可获得表 3所示不同重现期计算结果。
|
|
表 3 台风诱发暴潮增水、波高及天文大潮不同联合概率重现期计算结果 Table 3 Joint probability of typhoon induced storm surge, wave height and corresponding astronomical tide |
传统模式往往将风暴增水与天文潮看作独立过程,或者用组合概率法简单将二者叠加处理,往往不能客观、全面地反映二者的联合概率特征。根据多维复合极值分布概率模式,本研究给出了南海海岸带台风诱发暴潮、巨浪与伴生的天文大潮“三碰头”极端荷载组合的联合概率分析方法,与传统的分析法(如:年极值抽样法)[20]相比,联合概率法能全面反映灾害的整体特性。从而可以为沿海防护工程、海洋工程设计标准的制定校核与风险评估提供合理依据。
4 海洋平台甲板高程的设计标准分析关于海洋平台甲板高度的设计标准,在工程领域常常采用一种传统方法[21-22],即:“百年一遇风暴增水、百年一遇波高、平均大潮高潮位与1.5 m的不确定性安全裕量之和。”该设计标准基本上依据的是一种经验性的理论方法,虽然将重现期的概念引入规范,但仅仅是将几种要素的重现水平进行孤立的叠加,无法体现几种主要致灾要素联合出现的可能性。
2005年,美国发生的卡特里娜和丽塔飓风造成116座海洋平台倒塌,对墨西哥湾沿岸造成了巨大的经济损失。有研究表明[23],损毁的116座平台主要是由于波浪的上托力冲击甲板所造成的,传统规范所规定的标高过低是造成平台倒塌的主要原因。因此,本文采用联合概率的方法考虑各要素的影响,同时引出整体不确定性理论(GUA)[24]来评估不确定性的裕量,并将计算的结果与传统方法的计算结果进行对比。
(1) 极端波高的不确定性分析:
南海极端波浪的不确定因素主要有三种:
概率预测模式的不确定性,cov1=0.14;
数据抽样的不确定性,cov2=0.09;
统计方法的不确定性,cov3=0.18;
南海极端极端波高的总不确定度:整体不确定性=[(cov1)2 +(cov2)2 +(cov3)2] 1/2=0.245;
(2) 天文潮的不确定度分析:
调和常数不确定性:μ= 166.65;σ= 0.88;cov1=σ/μ= 0.005 3。
平均海平面不确定性:μ=4.80; σ=3.96;cov2=σ/μ=0.825 6。
天文大潮的总不确定度:整体不确定性=[(cov1)2+(cov2)2]1/2=0.825。
按照传统规范的设计标准,海洋平台甲板高程为:百年一遇波高(6.60 m)+百年一遇风暴增水(2.39 m)+平均大潮高潮位(2.40 m)+不确定性安全裕量(1.5 m)=12.89 m。
而使用多维复合极值理论与整体不确定性理论的计算结果如表 4所示。
|
|
表 4 多维复合极值理论与整体不确定性理论计算结果 Table 4 Calculated results by MCEVD and GUA method |
对比两种方法所到的设计标准,由多维复合极值理论所确定的百年一遇结果,其波高和风暴增水高于采用传统设计法所确定的值,而天文潮则相对较小。但计算取得的百年一遇联合出现的波高、风暴增水和天文大潮的组合要明显高于基于传统算法所得的结果。
同时,引入整体不确定性理论来定量分析该海域波高与天文潮的不确定性,与传统的1.5 m安全裕量相比,更具有科学性和可靠性,且在实际应用中可以根据不同海域的海况做具体分析。
5 结语实例计算表明:与多维复合极值理论相比较,传统的海洋工程平台设计标准中存在的缺陷和不足,传统方法采用单因素年极值采样方式来计算概率,其结果仅仅是几种因素的代数叠加,无法体现各变量之间的相关性和极端海况出现的频次。基于2005年卡特里娜飓风、2012年桑迪飓风及2013菲特台风等多场灾害的教训,近海的基础设施采用传统的安全法规受到台风灾害的可能性是有的。而本文所提供的联合概率设计法并将整体不确定性理论应用于设计标准的计算,能更科学地给出极端海况的预测,所得计算结果更具有合理性和安全性。
| [1] |
Army Corps of Engineers. History of Lake Pontchartrain and Vincinity Hurricane Protection Project[R]. Washington, DC: U S Government Accountability Office, 2005, No. GAO-06-244T: 1-4.
(  0) 0) |
| [2] |
Liu Defu, Jiang Yunpeng, Xie Botao, et al. Uncertainty analysis of breakwater wave overtopping volume, wave forces and structure stability[C]. //The Sixteenth International Offshore and Polar Engineering Conference. San Francisco, USA: International Society of Offshore and Polar Engineers, 2006. https://www.sciencedirect.com/science/article/pii/S0378383915000915
(  0) 0) |
| [3] |
周俊华.中国台风灾害综合风险评估研究[D].北京: 北京师范大学, 2004. Zhou Jun-Hua. Study on Comprehensive Risk Assessment of Typhoon Disaster in China[D]. Beijing: Beijing Normal University, 2004. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y680769 (  0) 0) |
| [4] |
Liu Defu, Wang Liping, Pang Liang. Theory of multivariate compound extreme value distribution and its application to extreme sea atae prediction[J]. Chinese Science Bulletin, 2006, 51(23): 2926-2930. DOI:10.1007/s11434-006-2186-x
(  0) 0) |
| [5] |
刘德辅, 庞亮, 谢波涛, 等. 中国台风灾害区划及设防标准研究——双层嵌套多目标联合概率模式及其应用[J]. 中国科学E辑, 2008, 38(5): 698-707. Liu D F, Pang L, Xie B T, et al. Typhoon disaster zoning and prevention criteria——A double layer nested multi-objective probability model and its application[J]. Science in China(E), 2008, 38(5): 698-707. DOI:10.3321/j.issn:1006-9275.2008.05.004 (  0) 0) |
| [6] |
史道济.实用极值统计方法[D].天津: 天津科学技术出版, 2006: 138-185. Shi Daoji. Practical Extreme Value Statistical Method[D]. Tianjin: Tianjin Science and Technology Press, 2006: 138-185. (  0) 0) |
| [7] |
Shi Daoji, Zhou Shengsheng. Moment estimation for multivariate extreme value distribution in a nested logistic model[J]. Ann Inst Statist Math, 1999, 51(2): 253-264. DOI:10.1023/A:1003854023902
(  0) 0) |
| [8] |
Liu T F, Ma F S. Prediction of extreme wave heights and wind velocities[J]. Journal of the Waterway Port Coastal & Ocean Division, 1980, 106: 469-479.
(  0) 0) |
| [9] |
Liu T F. Long Term distribution of hurricane characteristics[J]. Leej Transactions on Electrical & Electronic Engineering, 1982, 305-313.
(  0) 0) |
| [10] |
Liu Defu, Pang Liang, Fu Gang, et al. Joint probability analysis of hurricane katrina 2005[C]. //Proc Int Offsh Pol Eng Conf, San Francisco, USA: International Society of Offshore and Polar Engineers, 2006, 3: 74-80.
(  0) 0) |
| [11] |
Liu D F, Li H J. Prediction of extreme significant wave height from daily maxima[J]. China Ocean Engineering, 2001, 15(1): 97-106.
(  0) 0) |
| [12] |
刘德辅, 王莉萍, 宋艳, 等. 多维复合极值分布理论及其工程应用[J]. 中国海洋大学学报(自然科学版), 2004, 34(5): 893-902. Liu D F, Wang L P, Song Y, et al. Theory of multivariate compound extreme value distribution and its engineering application[J]. Periodical of Ocean University of China, 2004, 34(5): 893-902. (  0) 0) |
| [13] |
Liu Defu, Song Yan, Shi Hongda, et al. Poisson-logistic compound bivariate extreme distribution and its application for designing of platform deck clearance[J]. Asme International Conference on Offshore Mechanics & Arctic Engineering, 2003, 21(4): 409-414.
(  0) 0) |
| [14] |
Liu D F, Song Y, Wang S Q, et al. Combined environmental design loads criteria for marine structures[C]. //Houston, TX: Proc Offsh Tech Conf, 2002: 1749-1755. https://www.researchgate.net/publication/254518118_Combined_Environmental_Loads_Design_Criteria_for_Marine_Structures
(  0) 0) |
| [15] |
Liu Defu, Wang Liping, Pang Liang. Theory of multivariate compound extreme value distribution and its application to extreme sea atae prediction[J]. Chinese Science Bulletin, 2006, 51(23): 2926-2930. DOI:10.1007/s11434-006-2186-x
(  0) 0) |
| [16] |
Liu Defu, Ma Li, Jing Kun. Risk analysis of the disaster prevention design criteria for an estuarine city-Shanghai[C]. //Canada, OMAE: Proc Offsh Mech Arc Eng, 2004. http://proceedings.asmedigitalcollection.asme.org/proceeding.aspx?articleid=1630347
(  0) 0) |
| [17] |
Ochi M K. Stochastic analysis and probabilistic prediction of random seas[J]. Adv Hydro-Sci, 1982, 13: 217-315. DOI:10.1016/B978-0-12-021813-4.50010-X
(  0) 0) |
| [18] |
Xie Botao, Liu Defu, Li Huajun, Gong Chen. Design code calibration of offshore platform against typhoon_hurricane attacks[J]. China Ocean Engineering, 2010, 24(3): 431-442.
(  0) 0) |
| [19] |
Bourgund U, Ouypornprasert W, Prenninger P H W. Advanced simulation methods for the estimation of systems reliability[C]. //Univ Innsbr: Inst Eng Mech, 1986.
(  0) 0) |
| [20] |
Kirby W H, Moss M E. Summary of flood-frequency analysis in the united states[J]. J Hydrol, 1987, 96(1): 5-14.
(  0) 0) |
| [21] |
API RP2A-WSD. Planning, designing and constructing fixed offshore platforms-working stress design[C]. //Offshore Technology Conference. Washington, DC: API, 2000.
(  0) 0) |
| [22] |
DET Norske Veritas. Structural Design of Offshore Units (WSD Method). Offshore Standard DNV-OS-C201[S]. Oslo: DET Norske Veritas, 2002: 12-57.
(  0) 0) |
| [23] |
National Hurricane Center, Tropical Prediction Center. Tropiacl Weather Summary 2005[R]. Miami: National Hurricane Center, 2005.
(  0) 0) |
| [24] |
Tarantola S, Giglioli N, Jesinghaus N J, et al. Can global sensitivity analysis steer the implementation of models for environmental assessments and decision-making?[J]. Stochastic Environmental Research and Risk Assessment, 2002, 16: 63-76. DOI:10.1007/s00477-001-0085-x
(  0) 0) |
2. College of Engineering, Disaster Prevention Research Institute, Ocean University of China, Qingdao 266003, China
 2019, Vol. 49
2019, Vol. 49