2. 中国海洋大学海洋高等研究院,山东 青岛 266100;
3. 中国海洋大学信息科学与工程学部,山东 青岛 266100;
4. 山东国兴智能科技股份有限公司,山东 烟台 264001
海洋亚中尺度过程是大洋能量平衡的关键一环,对进一步探究海洋动力学具有重要意义,而对亚中尺度过程的现场立体观测具有十分重要的科学价值[1-2]。目前现场实时移动观测的主要手段为自沉浮式剖面探测(Argo)[3-4]和水下滑翔机[5-6],但是用Argo观测的入水点和出水点的位置通常相隔较远,而用水下滑翔机观测也存在同样的问题,影响了亚中尺度立体观测的空间一致性。本研究中研制了面向亚中尺度过程的精细化立体观测的亚中尺度观测器,使其具备了灵活的垂向的观测能力。
此外,海流对海洋移动观测平台的影响是一个不可忽视的因素[7],因此国内外许多学者在考虑海洋观测工程实用性的基础上开展了控制方法的研究。赵洪坛等[8]设计了一种含海流因素的模型预测与自适应滑模级联的控制方法,提高了水下机器人(UUV)在持续海流或突发海流扰动时跟踪控制效果;Shen等[9]开发了一种基于李雅普诺夫方法的模型预测框架(LMPC),在保证闭环稳定性的基础上,提高了跟踪控制在不同级别海流干扰下的鲁棒性。上述模型预测控制的方法能较好的解决海流干扰问题,但对于海流剖面对水下移动观测平台的影响问题,尚未提出有效的控制方法。
蒋亚丽等[10]将预测控制优化问题分解为多个单级优化问题,有效降低多速率分段线性系统的在线计算时间,在保证系统稳定性的同时,满足其对输入更新速度的要求;冷姚等[11]将动态干扰进行参数分区,求得最优转角控制量,降低车辆跟踪误差的同时提高了运行速度。上述研究表明对于复杂的干扰问题,分段处理的方法能够有效提高控制效果,对解决亚中尺度观测器剖面海流干扰问题具有重要的参考价值。
本文设计开发一种在满足亚中尺度观测需求的水下航行器的基础上采用分段模型预测控制的方法,解决亚中尺度过程垂向剖面海流干扰观测的问题。利用模型预测控制自身在滚动优化的过程中对模型具有很好模型预测能力的特点,并根据不同阶段海流剖面的特点进行分段化设计,同时对于亚中尺度观测器的垂向运动的模型也进行更新,有效降低了海流对亚中尺度观测器的垂向运动过程的影响,从而减少了观测器剖面运动的水平漂移量,使得观测的海洋数据能够满足亚中尺度过程观测的需求。
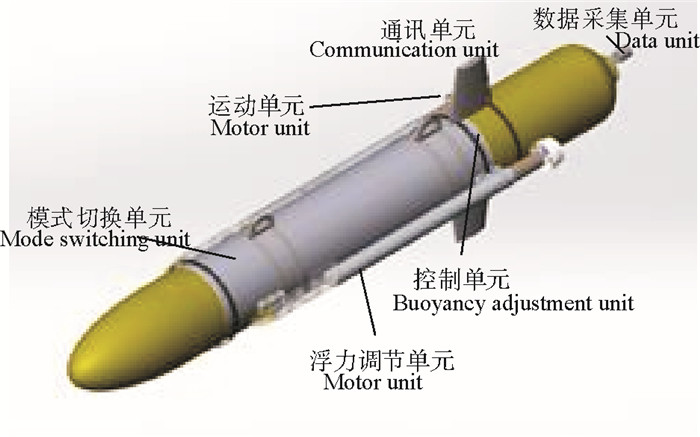
1 亚中尺度观测器的设计 1.1 整体结构设计本文所研究的亚中尺度观测器整体结构如图 1所示,主要包括浮力调节单元、运动单元、模式切换单元、通讯单元、控制单元和数据采集单元。其中对于垂向观测过程起到主要作用的是运动单元、模式切换单元和浮力调节单元。
|
图 1 亚中尺度观测器整体结构 Fig. 1 Overall structure of the sub-mesoscale observer |
当亚中尺度观测器在海面上运行到需要垂向观测的位置后,模式切换单元开始工作,将观测器由水平状态切换至垂直状态,在接到垂向观测任务开启的命令后,浮力调节单元和运动单元开始工作,亚中尺度观测器实现垂向的下潜和上浮,对海洋现象进行观测。
1.2 浮力调节单元和运动控制单元的设计浮力调节单元为左、右各1个推杆,浮力调节范围为-2~2 N,调节时间仅需70 s,具有调节效率高的特点,满足亚中尺度观测下潜的要求。
运动控制单元主要为左、右两个推进器,单个推进器的推力为5 kg,采用了高效能的伺服电机作为动力源,保证了系统的续航能力。水平运动模式下运动控制单元通过控制推进器的螺旋桨进行正、反转,从而实现观测器的前进和后退;在垂向运动模式下,运动控制单元可以辅助浮力调节单元加快运动速度。
运动单元和浮力调节单元采用了一体化设计,减小了迎流面积,从而减小了航行阻力。
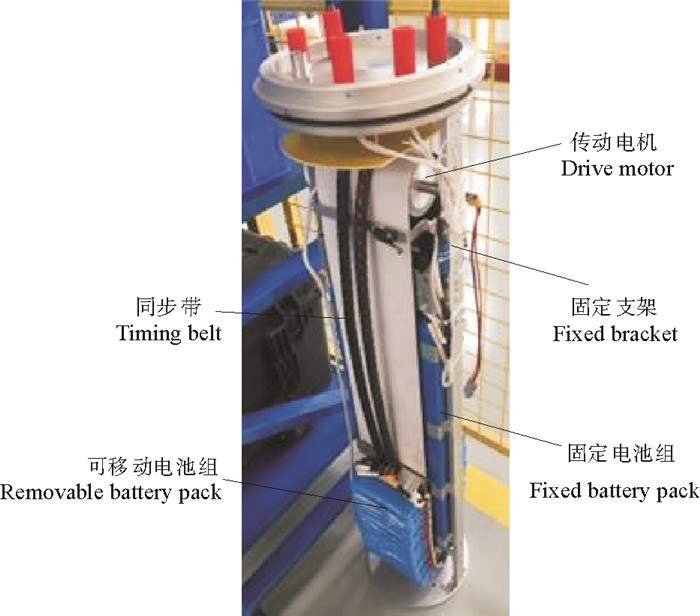
1.3 模式切换单元设计模式切换单元如图 2所示,包括固定电池组、可移动电池组、同步带、固定支架和传动电机。
|
图 2 模式切换单元实物图 Fig. 2 Physical diagram of the mode switching unit |
可移动电池组可以水平移动调节重心的位置,也可以旋转移动对侧,进而大幅度的调节观测器的重心位置,从而实现水平运动模式和垂向运动模式之间的切换。
2 亚中尺度观测器不同流速的建模 2.1 动力学建模本文将自主研制的亚中尺度观测器(见图 3)作为一种刚体进行建模。设该刚体总质量masuv计算式:

|
图 3 亚中尺度观测器实物图 Fig. 3 Physical map of a sub-mesoscale observer |
| $ m_{\text {asuv }}=m_{\mathrm{s}}+m_{\mathrm{m}}+m_{\mathrm{b}} \text { 。} $ | (1) |
式中:ms为固定质量,其包括运动单元、模式切换单元的固定电池包部分、通讯单元、控制单元和数据采集单元;mm为可移动质量部分包括模式切换单元的可移动电池包部分;mb为浮力调节部分,包括重浮力调节单元。
假设亚中尺度观测器整体的位置矢量为rCG,固有:
| $ \boldsymbol{r}_{\mathrm{CG}}=\frac{m_{\mathrm{s}} \boldsymbol{r}_{\mathrm{s}}+m_{\mathrm{m}} \boldsymbol{r}_{\mathrm{m}}+m_{\mathrm{b}} \boldsymbol{r}_{\mathrm{b}}}{m_{\mathrm{s}}+m_{\mathrm{m}}+m_{\mathrm{b}}}\text { 。} $ | (2) |
式中rs、rm和rb分别表示固定质量部分、可移动质量部分和浮力调节部分的位置矢量。
亚中尺度观测器在惯性坐标系下的线动量p和角动量q关系分别为:
| $ \boldsymbol{p}=\boldsymbol{R}_{\mathrm{EB}} \boldsymbol{P}, $ | (3) |
| $ \boldsymbol{q}=\boldsymbol{R}_{\mathrm{EB}} \boldsymbol{Q} \text { 。} $ | (4) |
式中:P和Q分别为亚中尺度观测器在体坐标系下的线动量和角动量;REB表示体坐标系到惯性坐标系的旋转矩阵。
将式(3)和(4)两边同时微分可以得到:
| $ \dot{\boldsymbol{p}}=\boldsymbol{R}_{\mathrm{EB}}(\dot{\boldsymbol{P}}+\Omega P), $ | (5) |
| $ \dot{\boldsymbol{q}}=R_{\mathrm{EB}}(\dot{Q}+\boldsymbol{\Omega} Q)+\boldsymbol{R}_{\mathrm{EB}} \boldsymbol{V} \times \boldsymbol{p}+\boldsymbol{b} \times \dot{\boldsymbol{p}}_{\text {。}} $ | (6) |
式中:V和Ω表示亚中尺度观测器在体坐标系中的线速度和角速度;b表示亚中尺度观测器在惯性坐标系下的位移。
根据平衡方程和动量守恒定理可以得到亚中尺度观测器的动力学模型:
| $ \begin{gathered} \boldsymbol{M} \dot{\boldsymbol{v}}+\dot{\boldsymbol{M}} \boldsymbol{v}=\left[\begin{array}{c} \boldsymbol{P} \times \boldsymbol{\Omega} \\ \boldsymbol{Q} \times \boldsymbol{\Omega}+\boldsymbol{P} \times \boldsymbol{V} \end{array}\right]+ \\ {\left[\begin{array}{l} m_{\mathrm{b}} \boldsymbol{g}\left(\boldsymbol{R}_{\mathrm{EB}}^{\mathrm{T}} \boldsymbol{k}\right) \\ \left(m_{\mathrm{s}} \boldsymbol{r}_{\mathrm{s}}+m_{\mathrm{m}} \boldsymbol{r}_{\mathrm{m}}+m_{\mathrm{b}} \boldsymbol{r}_{\mathrm{b}}\right) \boldsymbol{g} \times \boldsymbol{R}_{\mathrm{EB}} \end{array}\right]+\left[\begin{array}{l} \boldsymbol{F} \\ \boldsymbol{T} \end{array}\right] 。} \end{gathered} $ | (7) |
式中:M表示亚中尺度观测器的惯性矩阵;v为亚中尺度惯性坐标系下的速度; g为重力加速度;k表示重力方向的单位矩阵;F和T分别表示体坐标系下的水动力和水动力矩。
将三维的模型进一步简化得到垂直方向的微分方程如所示:
| $ \left(m_{\text {asuv }}+K_z\right) \dot{\boldsymbol{v}}+K_{\mathrm{q}} \boldsymbol{v}^2=\rho \boldsymbol{g} u_。$ | (8) |
式中:Kz和Kq分别表示亚中尺度航行器惯性和黏性水动力系数;ρ表示海水的密度;u为浮力调节单元的浮力调节量。
当水下机器人受外部水流的阻力干扰时,在进行剖面运动时的平均移动速度往往不超过0.4 m/s[12],在此速度区间内,式中的阻尼二次项如进行线性化处理,误差会同移动速度呈正相关,不会对结果产生较大影响。因此为了使得计算更简单,本文对阻尼二次项进行了线性简化:
| $ \left(m_{\text {asuv }}+K_z\right) \dot{\boldsymbol{v}}+K_q \boldsymbol{v}=\rho \boldsymbol{g} u \text { 。} $ | (9) |
式(9)中v是经式(8)中v线性化处理后的速度。
从而得到线性化状态空间模型的是:
| $ \begin{gathered} \left[\begin{array}{l} \dot{\boldsymbol{X}}_1 \\ \dot{\boldsymbol{X}}_2 \end{array}\right]=\left[\begin{array}{cc} 0 & 1 \\ 0 & -\frac{K_z}{m_{\text {asuv }}+K_q} \end{array}\right]\left[\begin{array}{l} \boldsymbol{X}_1 \\ \boldsymbol{X}_2 \end{array}\right]+ \\ \left[\begin{array}{c} 0 \\ \frac{\rho \boldsymbol{g}}{m_{\text {asur }}+K_q} \end{array}\right] u \text { 。} \end{gathered} $ | (10) |
式中:状态变量X1和X2分别表示亚中尺度航行器在垂向运动的速度和加速度。
2.2 水动力参数求解不同流速下的仿真效果如图 4所示,设定不同仿真流场入口处的水流速度Vinlet和攻角α,通过网格化计算出亚中尺度观测器的沿水流方向所受的阻力D,用最小均差方法求出水动力系数Kz和Kq。

|
图 4 航行器在Vinlet=0.6 m/s下的压强云图 Fig. 4 Pressure nephogram of vehicles at Vinlet=0.6 m/s |
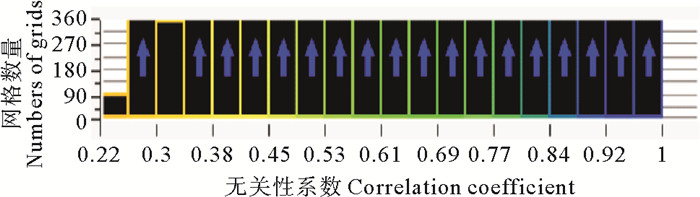
用网格划分软件ICEM的Display Mesh Quality模块显示网格质量,无关性系数越接近1,质量越好,当有无关性系数接近0的网格时,网格不能使用,需重新进行参数设置及其他设置,重新生成网格。本文所划分的网格质量最小值为0.22,如图 5所示,满足后续计算要求。
|
图 5 网格质量图 Fig. 5 Grid quality |
在运动坐标系中,亚中尺度观测器运动方向所受到的阻力D大小为[12]:
| $ \boldsymbol{D}=\left(K_z+K_{\mathrm{q}} \alpha^2\right) \boldsymbol{V}_{\text {inlet }}^2 \text { 。} $ | (11) |
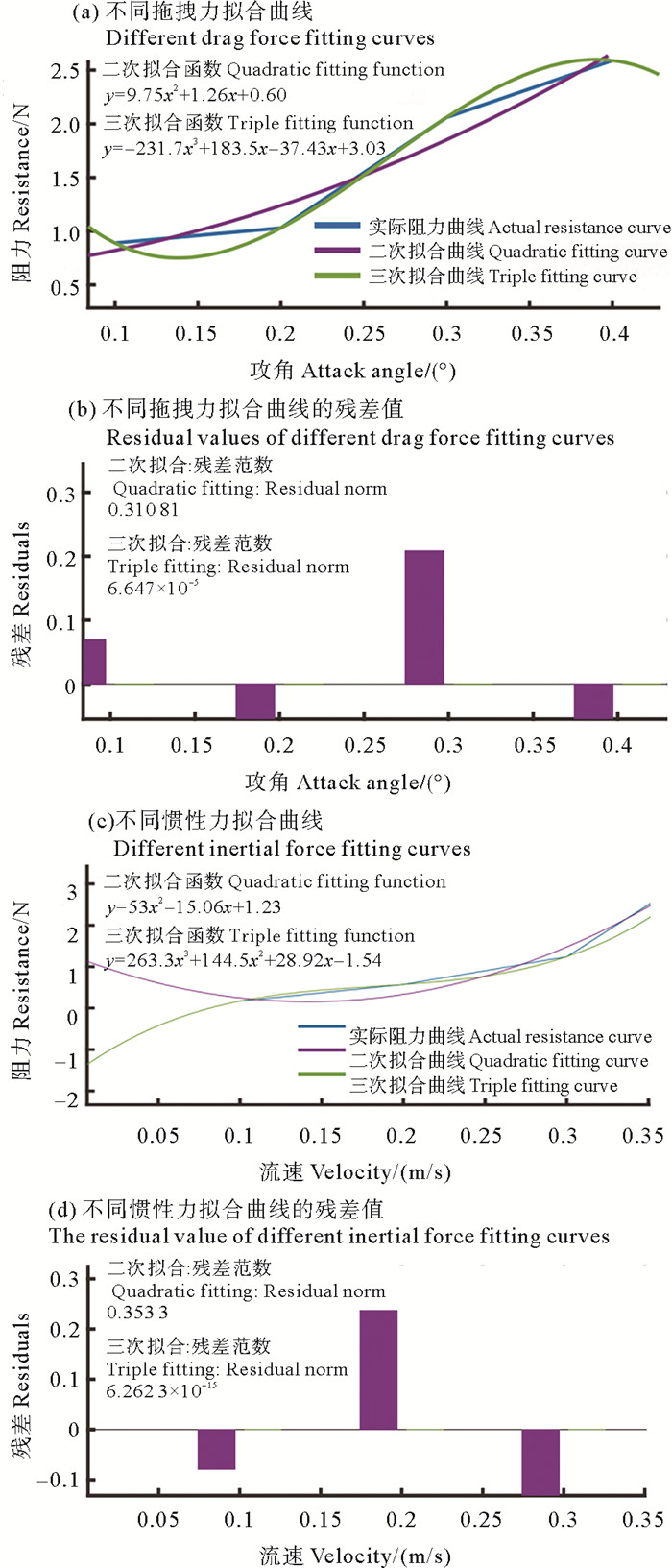
式中:当流场入口处的水流速度保持不变时,阻力D的大小变化只和攻角α有关,因此Kz的求解可以通过使攻角α变化进行拟合,Kq的求解通过控制流速Vinlet的变化进行拟合(见图 6),最终得到不同流速下的水动力系数如表 1所示。
|
图 6 水动力拟合曲线 Fig. 6 Hydrodynamic fitting curve |
|
|
表 1 不同流速下的水动力系数 Table 1 Hydrodynamic parameters at different flow rates |
对于亚中尺度的现场观测,相关的研究较少,因此在流场分层策略上参考研究资料较多的中尺度涡。根据经验,本研究中将亚中尺度观测区域分为表层、中层和深层,同时按照中尺度涡的划分深度[13],将0~50 m定义为表层,50~100 m定义为中层,100~150 m定义为深层。
3.2 无海流下的控制模型预测控制需要对连续时间状态空间模型进行离散化,得到:
| $ x_{\mathrm{m}}(k+1)=\boldsymbol{A}_{\mathrm{m}} x_{\mathrm{m}}(k)+\boldsymbol{B}_{\mathrm{m}} u(k), $ | (12) |
| $ y(k)=\boldsymbol{C}_{\mathrm{m}} x_{\mathrm{m}}(k) \text { 。} $ | (13) |
式中:Am表示状态矩阵,且Am=eAphm, 其中h和m分别表示采样周期和单位矩阵;Bm表示输入矩阵,且Bm=
在模型预测控制(MPC)方法设计中使用了后退地平线控制原理,其中下一阶段的状态矢量是通过未来的预测步长Np采样来进行计算,用于控制控制步长Nc的样本,其中Nc≤Np。对输入量函数Δu的约束和成本J如下:
| $ \Delta u_{\min } \leqslant \Delta u\left(k_{\mathrm{s}}\right) \leqslant \Delta u_{\max }, $ | (14) |
| $ J=\left(R_{\mathrm{s}}-Y\right)^{\mathrm{T}}\left(R_{\mathrm{s}}-Y\right)+\Delta U^{\mathrm{T}} \boldsymbol{R}_{\mathrm{t}} \Delta \boldsymbol{U} $ | (15) |
式中:Δu表示输入量,即可移动电池包的移动距离;ks表示模型离散后算法迭代的步数,模型预测控制算法通过控制第ks步的输入Δu(ks)实现滚动优化;Δumin表示输入量的下限,即可移动电池包到达水平极限位置的移动距离;Δumax表示输入量的上限,即可移动电池包到达竖直极限位置的移动距离;Rt表示转移矩阵;Y表示输出量;ΔU表示输入量的矩阵形式。
3.3 有海流干扰下的控制利用亚中尺度观测器在垂向运动的同时跟随海流做随流运动的特点,根据观测器的出、入水点的位置以及出、入水的时间估算水平流的平均速度。
Argo浮标也是利用这个特点对海流进行估算[13],Park等[14]研究了利用Argo浮标的定位信息估算海洋中层流速。为了获取不同深度段的平均海流速度,本研究对仿真结果的数据进行二次分析,记录当前阶段海流与上层海流的漂流距离差,同时记录周期漂流时间TDE2AE, m,便可以得到平均海流速度Vd_down, m[11]:
| $ \boldsymbol{V}_{\mathrm{d} \_ \text {down }, \mathrm{m}}=\frac{\boldsymbol{P}_{\text {asc_end }, \mathrm{m}}-\boldsymbol{P}_{\text {desc_start }, \mathrm{m}}}{T_{\mathrm{DE} 2 \mathrm{AE}, \mathrm{m}}}-\boldsymbol{E}_{\mathrm{T}, \mathrm{m}} $ | (16) |
式中:Pasc_end, m表示亚中尺度航行器上浮阶段结束后所处的位置;Pdesc_start, m表示其下潜阶段开始前所处的位置;ET, m是由于流速分层时层间流速切变引起的速度误差。相关研究[13]表明,该速度误差项对流速计算的影响较小,因此可以忽略速度切变带来的误差。
针对剖面中存在不同流速的海流干扰的问题,提出了一种基于预测控制理论的分段控制模型。在每个控制阶段,采用分段预测方法求解最优的目标函数。在每段的算法设计过程中,需要找到最优的预测步长Np、控制步长Nc和采样周期T。参数求解的依据是根据垂向模型的控制效果,参考指标主要是稳定时间,因为剖面运动稳定时长决定亚中尺度航行器的水平漂移量,从而决定观测数据是否满足观测的需求。
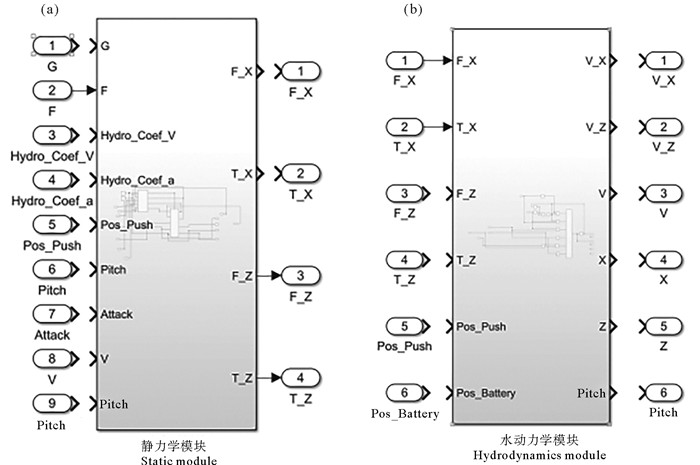
4 亚中尺度观测器垂向运动仿真 4.1 仿真模型的搭建建立一个虚拟的亚中尺度观测器模型,包括推杆、电池包、深度传感器和姿态传感器等,以集成到MATLAB软件的仿真(Simulink)模块中。使用Simulink模块建立亚中尺度航行器在垂直方向上的仿真模型。该仿真模型可以按照平衡关系的类别划分为静力学模块和水动力学模块两个子模块(见图 7)。静力学模块的输出同水动力学模块的输入具有一定的联系,它们共同构建成了水下航行器在垂向上的仿真模型。
|
图 7 亚中尺度航行器仿真模型结构示意图 Fig. 7 Schematic diagram of the structure of the sub-mesoscale vehicle simulation model |
使用Simulink模块和MATLAB软件兼容的脚本编辑器进行控制器的建立。本文的控制目标是使系统的横向漂移量跟踪期望的固定目标值,从而实现对亚中尺度航行器在垂直方向上的有效控制。
4.2 算法最优参数求解本研究中设定的流速剖面的场景:海面海流流速为1 kn海流,深度为0~50、50~100、100~150 m的模拟海流速度分别为35.6、30.8、28.1 cm/s。
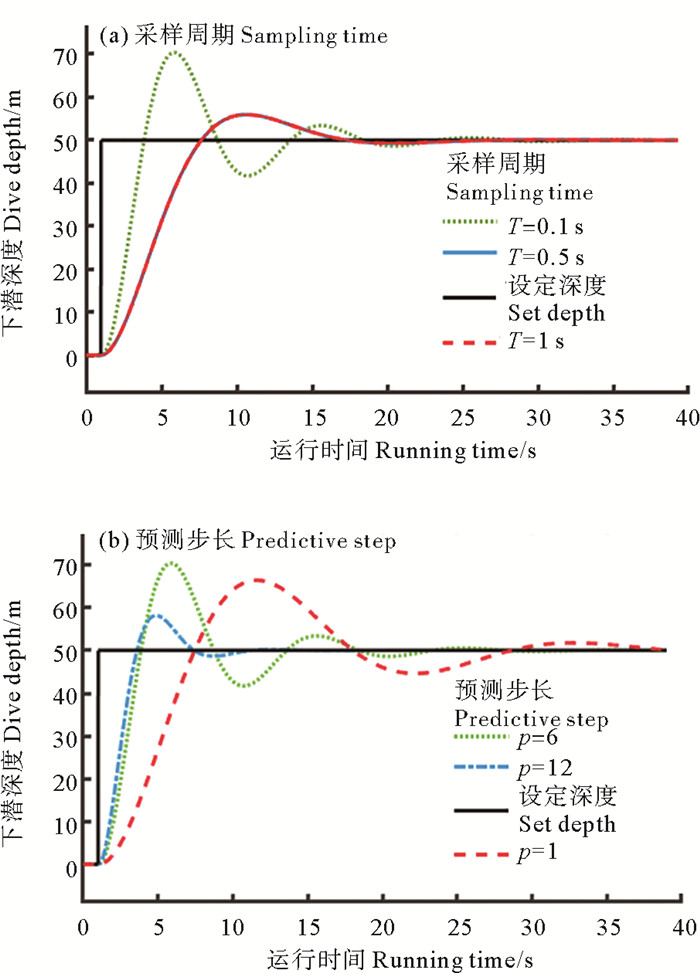
控制稳定性随控制周期减小而增加,符合控制算法规律。对结果进行分析后可以得出,当最优控制周期为0.1 s时,调节时间为30 s左右(见图 8(a))。
|
图 8 模型预测控制参数对控制效果的影响 Fig. 8 The model predicts the impact of control |
在一定范围内,控制稳定性随着预测步长的增加而增加,同时考虑到计算成本问题,最终选择最优的预测步长为6,调节时间为35 s左右(见图 8(b))。
在要求的控制精度中误差为终值的2%且超调量为终值的5%的条件下,调节时间为180 s,最优的模型预测控制参数如表 2所示。
|
|
表 2 不同流速下的模型预测控制最优参数 Table 2 Model prediction control optimal parameters at different flow rates |
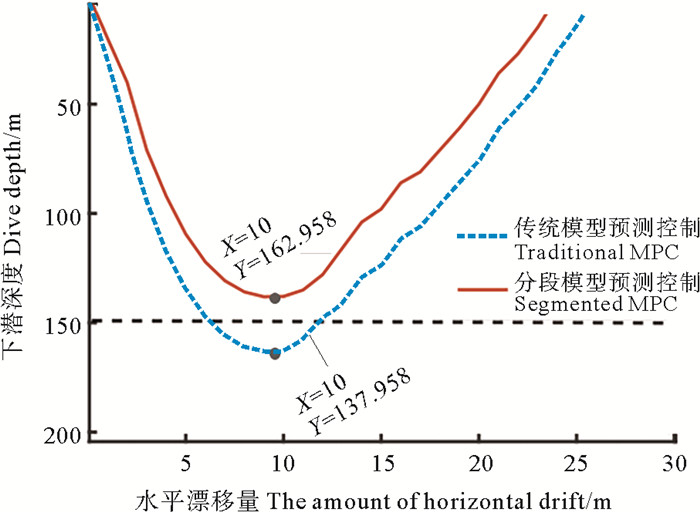
本研究中在垂向运动深度均为150 m的前提下,通过使用优化前、后的MPC控制算法分别对亚中尺度观测器垂向运动过程进行控制,并统计了稳定的时间,最后根据本文4.2节所给出的流速剖面推算出亚中尺度观测器水平漂移量的最优参数(见图 9)。
|
图 9 优化效果对比图 Fig. 9 Optimization performance comparison chart |
通过多次对比分析仿真实验得到的数据,本文所提出的实时分段调整的MPC同具有固定模型和参数的MPC相比,平均水平漂移量从25.45 m减少到23.59 m,减少了1.86 m,优化率约为8%。仿真实验数据表明,对传统MPC的参数进行实时分段调整后,稳定时间可以大幅度减少,进而减少了亚中尺度观测器垂向运动的水平漂移量。
5 仿真有效性分析 5.1 剖面运动实测数据本次试验的目的是对比分析剖面运动的仿真结果和试验数据,从而判断本研究中模型和算法的有效性。为了实现这一目标,本研究中采用了垂直剖面原理测试的方法。在本次试验中,样机需要完成的任务分多个阶段,包括模式初始化阶段、垂向下潜和上浮阶段、姿态调整阶段以及通信传输阶段等。图 10是水下航行器在模式功能验证试验中垂向剖面运动过程的现场记录图。

|
图 10 垂向剖面运动试验过程 Fig. 10 Vertical profile motion test process |
为了探究水下航行器在实际执行任务时的运动状态,本文利用深度传感器和姿态传感器设备采集了航行器进行剖面运动的数据。对实验数据进行可视化处理,以用于仿真数据和实测数据的对比分析。
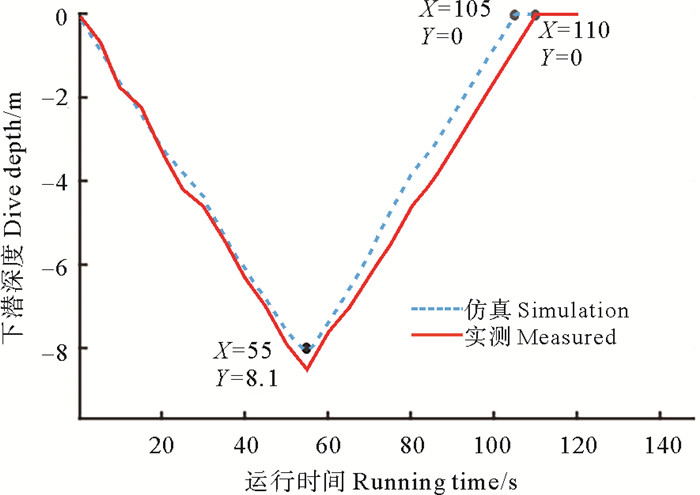
5.2 剖面运动仿真与实测数据对比亚中尺度观测器在垂向上做定深运动的仿真和实测结果如图 11所示。横轴表示运行的时间(单位:s),纵轴表示下潜深度(单位:m)。对比分析后可知:
|
图 11 下潜深度随时间的变化趋势 Fig. 11 Trend of diving depth over time |
(1) 从仿真数据中可以看出,下潜阶段最大深度控制在8.1 m,同实测数据接近且偏小,经分析得知是因为在仿真运行过程中模型预测控制算法的滚动优化过程所用时间没有传感器设备传输数据所用时间长,并且PC端CPU运行速度比树莓派的高。
(2) 整个定深运动仿真和实测的时间差不超过5 s,为整个过程运行时间的4.8%。表明仿真数据与实测数据相似度较高,因此在一定程度上亚中尺度观测器的Simulink仿真模型可以用于代替实物进行任务的分析。
6 总结与展望本文提出了一种分段模型预测控制方法,用于控制亚中尺度观测器的垂直运动,并获取海洋亚中尺度过程的连续时间序列数据。所设计的模型和算法旨在解决洋流引起的不确定性,并通过分段化处理系统模型和控制算法来解决模型变化问题。仿真结果表明,同传统MPC相比,分段MPC具有调整误差小、稳定时间短的优点。
实验结果还表明,本文提出的分段MPC可以显著降低亚尺度观测器剖面周期运动的水平漂移量,并提高垂直运动的稳定性。此外,从Simulink仿真模型中获得的仿真数据同水池试验所测量的数据具有很高的相似性,表明该仿真模型可以用来代替物理对象进行任务分析,为亚中尺度过程数据的获取和认知提供了有效的依据。
未来的工作可以探索将该方法应用于其他航行任务的潜力,例如可以考虑将分段模型预测控制的方法实施到虚拟系泊技术中,从而帮助亚中尺度观测器在执行任务过程中获得可靠的海洋数据。总的来说,本文的研究为海洋学和亚中尺度过程分析领域做出了宝贵的贡献。
| [1] |
Gommenginger C, Chapron B, Hogg A, et al. SEASTAR: A mission to study ocean submesoscale dynamics and small-scale atmosphere-ocean processes in coastal, shelf and polar seas[J]. Frontiers in Marine Science, 2019, 6(12): 457. (  0) 0) |
| [2] |
Siegelman L. Energetic submesoscale dynamics in the ocean interior[J]. Journal of Physical Oceanography, 2020, 50(3): 727-749. DOI:10.1175/JPO-D-19-0253.1 (  0) 0) |
| [3] |
Su Z, Wang J, Klein P, et al. Ocean submesoscales as a key component of the global heat budget[J]. Nature Communications, 2018, 9(1): 775. DOI:10.1038/s41467-018-02983-w (  0) 0) |
| [4] |
Wang Y, Xu Z H, Li Q, et al. Observed internal tides in the deep northwestern Pacific by argo floats[J]. Deep-Sea Research Part Ⅱ, 2023, 5(21): 207. (  0) 0) |
| [5] |
温浩然, 魏纳新, 刘飞. 水下滑翔机的研究现状与面临的挑战[J]. 船舶工程, 2015, 37(1): 1-6. Wen H R, Wei N X, Liu F. Research status and challenges of underwater gliders[J]. Naval Architecture Engineering, 2015, 37(1): 1-6. (  0) 0) |
| [6] |
沈新蕊, 王延辉, 杨绍琼, 等. 水下滑翔机技术发展现状与展望[J]. 水下无人系统学报, 2018, 26(2): 89-106. Shen X R, Wang Y H, Yang S Q, et al. Development status and prospect of underwater glider technology[J]. Journal of Unmanned Systems, 2018, 26(2): 89-106. (  0) 0) |
| [7] |
杨壮滔, 张涛, 段浩, 等. 波浪作用下圆柱型浮标运动仿真方法对比研究[J]. 水下无人系统学报, 2018, 26(4): 291-297. Yang Z T, Zhang T, Duan H, et al. Comparative study on motion simulation methods of cylindrical buoys under wave action[J]. Journal of Unmanned Systems, 2018, 26(4): 291-297. (  0) 0) |
| [8] |
赵洪坛, 朱大奇. UUV水下模型预测滑模跟踪控制算法[J]. 控制工程, 2022, 29(7): 1195-1203. Zhao H T, Zhu D Q. Predictive sliding mode tracking control algorithm for UUV underwater model[J]. Control Engineering, 2022, 29(7): 1195-1203. (  0) 0) |
| [9] |
Shen C, Shi Y, Buckham B. Trajectory tracking control of an autonomous underwater vehicle using Lyapunov-based model predictive control[J]. IEEE Transactions on Industrial Electronics, 2017, 65(7): 5796-5805. (  0) 0) |
| [10] |
蒋亚丽, 邹媛媛, 牛玉刚. 多速率分段线性系统预测控制的显式设计[J]. 自动化学报, 2013, 39(5): 631-636. Jiang Y L, Zou Y Y, Niu Y G. Explicit design of predictive control of multi-rate piecewise linear systems[J]. Journal of Automation, 2013, 39(5): 631-636. (  0) 0) |
| [11] |
冷姚, 赵树恩. 智能车辆横向轨迹跟踪的显式模型预测控制方法[J]. 系统仿真学报, 2021, 33(5): 1177-1187. Leng Y, Zhao S E. Explicit model predictive control method for lateral trajectory tracking of intelligent vehicles[J]. Journal of System Simulation, 2021, 33(5): 1177-1187. (  0) 0) |
| [12] |
Zhang S W, Yu J S, Zhang A C, et al. Spiraling motion of underwater gliders: Modeling, analysis, and experimental results[J]. Ocean Engineering, 2013, 60: 1-13. (  0) 0) |
| [13] |
王晓慧, 张卫民, 王品强, 等. 基于Argo历史观测的南海海盆尺度中层流场研究[J]. 海洋学报, 2018, 40(6): 1-14. Wang X H, Zhang W M, Wang P Q, et al. Study on mesostratic flow field at the basin scale of the South China Sea based on Argo historical observation[J]. Journal of Oceanographica, 2018, 40(6): 1-14. (  0) 0) |
| [14] |
Park J J, Kim K, King B A, et al. An advanced method to estimate deep currents from profiling floats[J]. Journal of Atmospheric and Oceanic Technology, 2005, 22(8): 1294-1304. (  0) 0) |
2. Institute for Advanced Ocean Study, Ocean University of China, Qingdao 266100, China;
3. Faculty of of Information Science and Engineering, Ocean University of China, Qingdao 266100, China;
4. Shandong Guoxing Intelligent Technology Company Limited, Yantai 264001, China
 2023, Vol. 53
2023, Vol. 53

