目前,自动调平系统在我们的生产生活中得到了极其广泛的应用,比如车载式起重机、海洋石油钻井平台、高空作业、消防车、导弹发射平台、雷达平台等[1]。自动调平技术也由以前的依靠人工观察气泡水平仪并手动调整千斤顶和丝杠的方式[2]向数字智能调平方式转变。尤其是随着国内外军事形势和国防技术的发展,特别是激光武器的出现,人们对调平系统的速度和精度提出了更高的要求。
根据自动调平系统的传动机理可以分为液压式和机电式[3]。液压式因其重量轻、体积小的优点得到了大量的应用,但因其自身结构的特点使其调平精度较低;机电式调平系统虽然笨重但其调节精度较高,一般应用在对调平精度要求较高的场合。
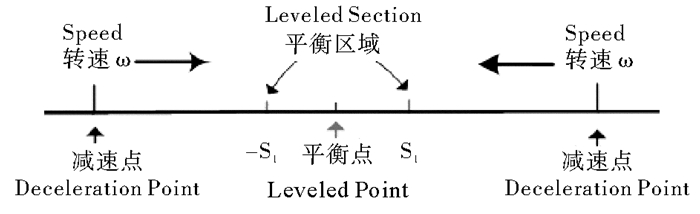
对于一般的调平系统,目前常用的方法就是在平衡区间外频繁正转或反转直至进入平衡区内,系统调平精度由平衡区间约束,精度尚可,调平时间较长(见图 1)。也有一些使用PID控制方法。PID控制算法具有结构简单,控制力强,在对象模型不确知的情况下也可达到有效控制的特点,鉴于在位置控制中所采用的双闭环或三闭环(电流、速度、角度)方式需要整定多个参数,整定难度高、工作量大。
|
图 1 调平系统速度调节示意图 Fig. 1 Diagram of speed regulating on leveling system |
滑模变结构控制算法简单,对系统模型、参数摄动及其外界干扰有很强的鲁棒性,可靠性高[4-5],特别适合电动控制系统。Liu[6]采用滑模变结构控制方法与PID控制方法对含有摩擦的飞行模拟器进行了对比控制研究,得出滑模变结构控制在克服粘性摩擦对系统产生的影响方面明显优于PID控制;Bang-Bang控制作为滑模变结构控制的一种,自诞生起就受到工程界的广泛关注,尤其随着数字控制及大功率开关器件的发展,Bang-Bang控制的应用是越来越广泛。Rubaai A[7]等研究了模糊Bang-Bang控制理论,并将其应用于无刷电动机的角度控制。Nagi F[8]设计了时间次优的模糊Bang-Bang控制器,并将其应用于卫星的姿态控制,实验表明该控制器具有响应迅速和性能稳定的特点。Xu等[9]针对直流电机伺服系统的未建模动态进行了分析和描述,设计了基于插补平滑算法的滑模控制器,实现了非连续切换控制的连续化,有效的消除了未建模动态对直流电动机伺服系统造成的抖振等。
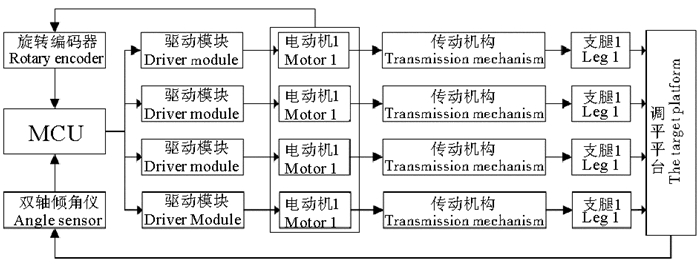
本文所涉及的高精度快速调平系统为某导弹发射车,此系统采用四点式机电调平方式[10],其整体控制结构见图 2。
|
图 2 自动调平系统结构图 Fig. 2 Structure of automatic leveling systems |
本文结合导弹发射车支撑模型、直流电动机模型、Bang-Bang变结构控制及模糊控制理论,提出了变切换线的Bang-Bang变结构高精度快速调平方法。最后通过仿真和现场实验证明该方法是有效的和快速的。相对于在平衡区间来回穿越的方法,该方法使调平速度得到了提升;相对PID控制方法,该方法的参数调整更加简单、快捷。
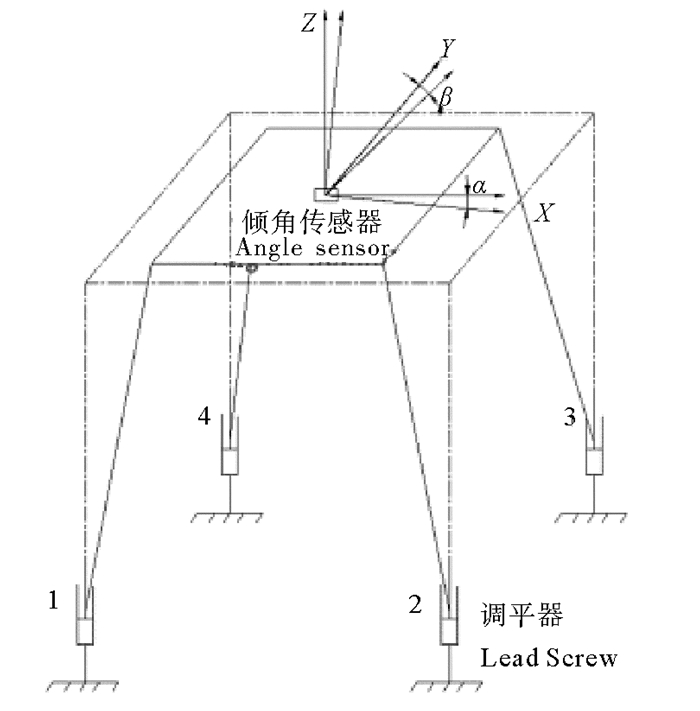
1 调平系统倾角模型本文采用四点式全刚性支撑平衡系统,四点支撑式平衡系统在实际调平过程中存在的静不定及虚腿的问题,可以通过支腿试探举升或设置承重传感器的方法进行解决。实际的四点支撑式调平系统的结构模型[11]见图 3。
|
图 3 四点支撑式平衡系统结构示意图 Fig. 3 Diagram of leveling system with four point supported |
在图 3中以倾角传感器平面建立的坐标系和以水平面建立的水平坐标系的夹角分别为α, β。假令四条支腿的距离分别为L1(腿1与腿2)和L2(腿2与腿3),则当腿1为最高且采用“最高点追逐法”进行调平时,各条支腿需要伸长的长度的数学模型为:
| $ \left[ \begin{array}{l} {d_1}\\ {d_2}\\ {d_3}\\ {d_4} \end{array} \right] = \left[ {\begin{array}{*{20}{c}} 0&0\\ {\tan \alpha }&0\\ {\tan \alpha }&{\tan \beta }\\ 0&{\tan \beta } \end{array}} \right]\left[ \begin{array}{l} {L_1}\\ {L_2} \end{array} \right]。$ | (1) |
在本系统中,各条支腿的长度是通过光电传感器采样电动机光电码盘的脉冲次数来进行测算的,其线数为k1,电动机到支腿的传动减速比为k2, 支腿导程为s,平衡区间边界点为k2; 所以计算出的各条支腿的长度转换为电动机转动的脉冲数为:
| $ {P_i} = \frac{{{k_1}{k_2}}}{s}{d_i},i = 1,2,3,4, $ | (2) |
当Pi∈(-s1, s1), 系统的调平精度为:
| $ \left\{ \begin{array}{l} {\varepsilon _{L1}} = \arctan \left( {\frac{{ \pm {s_1}}}{p}\frac{1}{{{L_1}}}} \right)\\ {\varepsilon _{L2}} = \arctan \left( {\frac{{ \pm {s_1}}}{p}\frac{1}{{{L_2}}}} \right) \end{array} \right., $ | (3) |
其中:s1为平衡区间的端点;p为支腿举升1 mm旋转编码器输出的脉冲数。
2 直流电动机启动、能耗制动模型调平系统传动部分主要有直流电动机、减速器、丝杠丝母及支腿组成。所以调平系统的传动模型就是各个组成构件模型的串联。
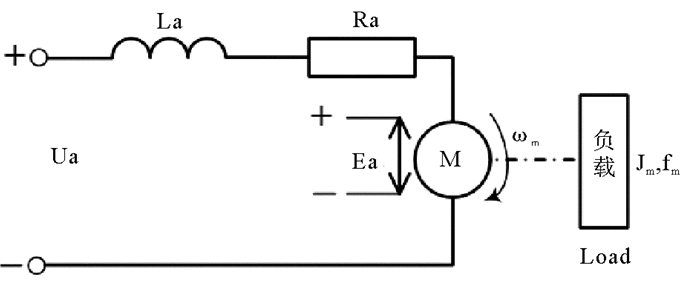
2.1 永磁直流电动机的模型直流电动机具有调速平稳,输出扭矩大和快速启动的特点,特别适合导弹发射车恶劣环境下大负载启动的应用需求。永磁直流电动机的原理图见图 4。
|
图 4 永磁直流电动机原理图 Fig. 4 Diagram of permanent magnetic DC motor |
永磁直流电动机的数学模型为:
| $ \left\{ \begin{array}{l} {U_a} = {L_a}\frac{{d{i_a}}}{{dt}} + {R_a}{i_a} + {E_a},{E_a} = {C_e}\omega \\ {M_m} = {C_m}{i_a}\\ {J_m}\frac{{d\omega }}{{dt}} + {f_m}\omega = {M_m} - {M_c} \end{array} \right., $ | (4) |
其中:La为电动机的电枢电感(mH);Ra为电动机的电枢电阻(Ω);ia为电动机的电枢电流(A);Ea为电动机旋转产生的反电动势(V);Cm为电动机转矩系数(N·m/A);Mm为电枢电流产生的电磁转矩(N·m);Mc折合到电动机上的总的负载扭矩(N·m);Jm为电动机和负载总的转动惯量(Kg·m2);fm为电动机和负载折总的黏性摩擦系数(N·m·s/rad);Ce为反电动势常数(V·s/rad)。
忽略较小参数La、LaJm、Lafm,并令
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {x_2}\\ {{\dot x}_2} = \left( { - \frac{{{f_m}}}{{{J_m}}} - \frac{{{C_m}{C_e}}}{{{R_a}{J_m}}}} \right){x_2} + \frac{{{C_m}}}{{{R_a}{J_m}}}{U_a} - \frac{{{M_c}}}{{{J_m}}} \end{array} \right., $ | (5) |
说明:Ua=0时为短接能耗制动[12]。
2.2 调平系统的传递模型在调平系统中,减速器、丝杆丝母为驱动电机与调平支腿的连接桥梁,其作用为将电动机的转动转换为支腿的伸缩。由于机械结构的长距离传动不可避免的存在着传导的延时。所以系统最终的传递模型可以定义为:
| $ {x_3} = k{x_2}\left( {t - \tau } \right), $ | (6) |
式中:x3为电动机支腿丝母的转速;x2(t)为电动机的转速;τ为传动总延时;k传动变比。
另外,由于机械齿轮之间不可避免的存在间隙,系统的转角传递会产生延时效应,其数学模型如下:
| $ \begin{array}{l} {\theta _3}\left( t \right) = \\ \left\{ \begin{array}{l} {\theta _2}\left( t \right) - \alpha ,{{\dot \theta }_3}\left( t \right) > 0\;且\;{\theta _3}\left( {{t^ - }} \right) = {\theta _2}\left( {{t^ - }} \right) - \alpha \\ {\theta _3}\left( {{t^ - }} \right),其他\\ {\theta _2}\left( t \right) + \alpha ,{{\dot \theta }_3}\left( t \right) < 0\;且\;{\theta _3}\left( {{t^ - }} \right) = {\theta _2}\left( {{t^ - }} \right) + \alpha \end{array} \right., \end{array} $ |
式中t-表示控制过程发生的前一时刻。
在实际应用中由于传递延时及总的间隙很小且对系统几乎无影响,所以在此应用中并未予以考虑。
3 Bang-Bang控制器的设计在调平系统中,令x1=θ, x2=
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {x_2}\\ {{\dot x}_2} = - A{x_2} - C{M_c} + B{U_a} \end{array} \right., $ | (7) |
其中:A>0, B>0, C>0。
令位置参考输入为rin,选取位置误差为e,位置误差变化率
| $ \left\{ \begin{array}{l} e = {r_{in}} - {x_1}\\ \dot e = {{\dot r}_{in}} - {x_2} \end{array} \right.。$ | (8) |
在Bang-Bang变结构控制中为了保证系统的稳定性,如果我们选取切换函数s和控制律Ua为[13-14]:
| $ \left\{ \begin{array}{l} s = ae + \dot e\\ {U_a} = \frac{1}{2}{u_0} \cdot \left[ {\mathit{sgn}\left( s \right) + 1} \right] \end{array} \right., $ | (9) |
其中:u0为系统的供电电压(比如310 V),
| $ {\mathop{\rm sgn}} \left( s \right) = \left\{ \begin{array}{l} 1,s > 0\\ - 1,s < 0 \end{array} \right.。$ | (10) |
定理1 如果切换函数s中参数
证明 选取李雅普诺夫函数
| $ \begin{array}{l} \dot V = s\dot s = \left( {ae + \dot e} \right)\left( {a\dot e + \ddot e} \right) = \\ \left( {a{r_{in}} - a{x_1} - {x_2}} \right)\left( { - a{x_2} - {{\dot x}_2}} \right) = \\ - \left( {a{r_{in}} - a{x_1} - {x_2}} \right)\left( {a{x_2} - A{x_2} + B{U_a} - C{M_c}} \right) = \\ - \left( {a{r_{in}} - a{x_1} - {x_2}} \right)\left( {a{x_2} - A{x_2} + } \right.\\ \left. {\frac{{B{u_0}\left[ {{\mathop{\rm sgn}} \left( s \right) + 1} \right]}}{2} - C{M_c}} \right)。\end{array} $ | (11) |
为保证系统稳定需使
(1) s>0时,根据式(9)可得Ua=u0;令
| $ \dot s = - \left( {a{x_2} - A{x_2} + B{u_0} - C{M_c}} \right) < 0, $ |
可以得到:
| $ a > - \frac{{ - A{x_2} + B{u_0} - C{M_c}}}{{{x_2}}}。$ | (12) |
考虑到注1,式(12)右端为非正数,所以取a>0,满足
(2) s < 0时,根据式(9)可得。令
| $ \dot s = - \left( {a{x_2} - A{x_2} - C{M_c}} \right) > 0, $ |
得
(3) s=0时,在公式(9)中sgn(0)未定义,所以Ua是不确定的。从纯数学意义上讲,对于s=ax+
| $ ax + \dot x = 0, $ |
此方程描述的运动可以解出为:
| $ x = x\left( {{t_1}} \right){{\rm{e}}^{ - a\left( {t - {t_1}} \right)}}, $ | (13) |
其中:x(t1)是x刚进入切换线时的状态;t1为刚进入切换线时的时间。
通过(13)式可以看出,当a>0时,状态x呈指数衰减,最终为0,对于式(9)即误差e趋近于0;该状态为变结构控制中最理想的滑动模态,在实际中是不可能一直保持的。因为由于系统惯性的影响,其任何状态都会逃离出切换线并使s>0或s < 0,即在切换线附近来回穿梭。
综上所述,当a∈(0, CMc/ωn+A)时,系统是渐近稳定的,误差系统(8)会逐渐趋近于原点。
注1 在实际电动机系统式(5)中,一个系统若要能运转,必须保证-Ax2+Bu0-CMc≥0。反之,则该系统是一直在减速的系统,与现实相悖。另外,对于式(9)的控制率,在一次控制中电动机只有正向转动和短接制动两种方式,该过程中转速x2≥0。
性质1 从a∈(0, CMc/ωn+A)可以看出a取值范围由负载的大小决定,负载越重a的取值范围越大,反之亦然。
性质2 系统中的配置参数a越小调节精度越高,调节时间越长;反之亦然。
性质3 相同的系数a,重载时调节的精细度高于轻载时。
所以参数a的选择很关键,选择得当则能够使系统仅需切换一次即可完成控制目的,而且不会造成过大的超调。这也是本系统设计的最终目的。
4 模糊变切换线设计由上面的性质可知:参数a越小,系统的调节精度会越高,耗时越大,系统在切换线附近的抖振越厉害,反之亦然。
所以设计一个模糊控制器来代替Bang-Bang控制中相对稳定的参数a,可以优化系统的性能,降低系统的耗时与抖振[15]。令
| $ a = {K_{fuzz}}\left( {{x_2},{{\dot x}_2}} \right)。$ |
式中
考虑到调平系统传动模型与电动机模型的相似性,本文以一台24 V的永磁直流电动机为例进行仿真实验,电动机参数见表 2。
|
|
表 2 24 V永磁直流电动机参数 Table 2 Parameters of 24 V permanent magnetic DC mmotor |
根据表 1所示的参量及公式(5)建立该电动机满载模型:
|
|
表 1 模糊控制规则表 Table 1 Rule table of fuzzy control |
| $ \left[ \begin{array}{l} {{\dot x}_1}\\ {{\dot x}_2} \end{array} \right] = \left[ {\begin{array}{*{20}{c}} 0&1\\ 0&{ - 272} \end{array}} \right]\left[ \begin{array}{l} {x_1}\\ {x_2} \end{array} \right] = \left[ {\begin{array}{*{20}{c}} 0\\ {5659} \end{array}} \right]{U_a} - \left[ {\begin{array}{*{20}{c}} 0\\ {8412} \end{array}} \right]。$ | (14) |
假设令电动机满载转动15rad,根据公式(8)我们得到
| $ \left\{ \begin{array}{l} e = {r_{in}} - {x_1} = 15 - {x_1}\\ \dot e = {{\dot r}_{in}} - {x_2} = - {x_2} \end{array} \right.。$ | (15) |
当a=350时,选取切换函数s和控制律u为
| $ \left\{ \begin{array}{l} s = 350 \cdot e + \dot e\\ u = \frac{1}{2}{u_0} \cdot \left[ {sign\left( s \right) + 1} \right] = 12 \cdot \left[ {sign\left( s \right) + 1} \right] \end{array} \right.。$ | (16) |
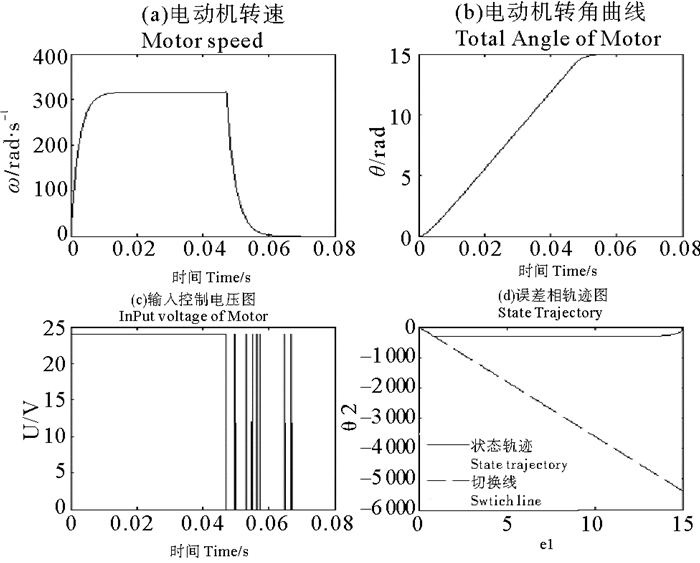
按照式(8)、(9)、(10)所示的误差系统及其控制规律,利用matlab仿真满载运行下的系统状态如图 5所示,图中的e1和e2分别为e和
|
图 5 24V电机满载Bang-Bang控制运行状态图 Fig. 5 The control and running state of DC 24V motor on rated load with Bang-Bang method |
从图 5(c)和(d)中可以看出系统状态从第一次穿越切换线后便一直在切换线附近来回穿越,最终到达原点。与此同时输入电压同样也多次通断,电动机转速也略微波动。电动机的转速的波动导致电动机并非是以一种高效的状态趋近于原点;尤其是重载时, 控制器对电动机的通断控制会更加频繁和密集;所以合理的选择系数a,使系统仅一次切换,便达到控制目标,既能降低了系统切换的频率,也能加快了系统达到原点的速度,图 6所示是选择切换系数a=440后的运行图。
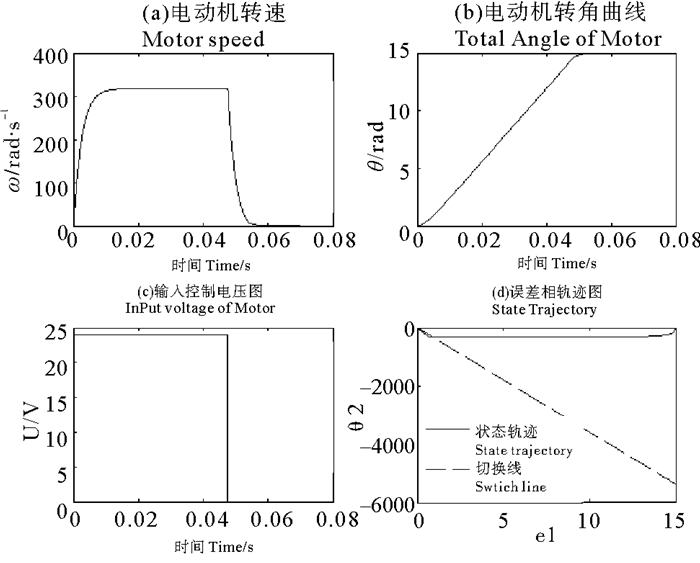
|
图 6 24 V电动机Bang-Bang控制一次切换状态图 Fig. 6 The state of DC 24 V motor of once time controlling with Bang-Bang method |
从图 6中可以看出,通过合理的选择切换系数a使电动机只切换一次便准确的停止在15 rad的位置,系统没有抖振发生,同时加快了系统达到原点的速度。
6 调平试验平台验证在实际应用中调平系统使用的电动机为300 V永磁直流电动机,功率800 W, 额定电流5 A;旋转编码器为1 000线;电源采用车载AC220 V发电机,经全桥整流滤波后直接供电,供电电压约为310 V, 如图 7所示。
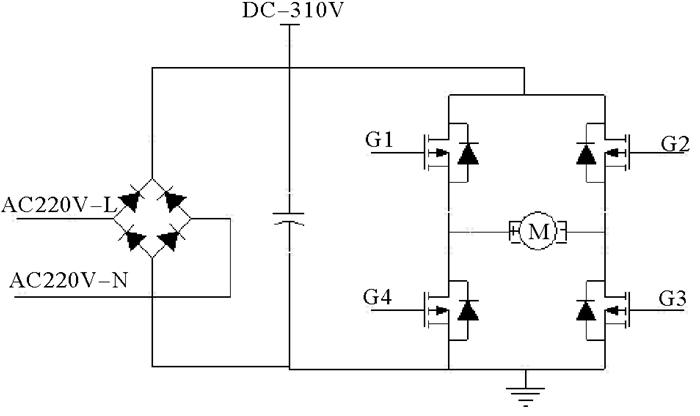
|
图 7 调平系统电气结构示意图 Fig. 7 Diagram of electric structure of leveling systems |
为保证实验验证的方便性,制作了与导弹发射车相似的调平实验平台如图 8所示,本实验过程全部在实验平台上完成。

|
图 8 调平系统实验平台 Fig. 8 Testing platform of leveling system |
控制器采用自主开发的Bang-Bang变结构调平系统控制器, 如图 9所示。该控制器采用stm32F103zet6单片机作为主控芯片,使用uCos操作系统对四条支腿进行实时调度控制。

|
图 9 调平系统控制器 Fig. 9 Controller of leveling system |
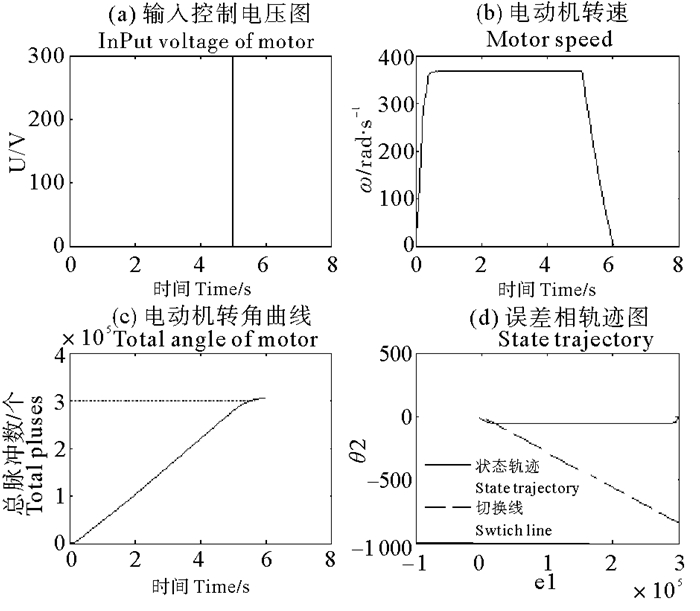
|
图 10 调平系统单条支腿状态图 Fig. 10 Leg state of leveling system |
在实验过程中首先采用Bang-Bang控制方法进行测试,目标脉冲是300 000,分别选取不同大小的a,测得数据如表 3所示。
|
|
表 3 调平系统参数调整性能对比 Table 3 Comparison of different parameters of Bang-Bang method on leveling system |
从表 3中可以看出当参数a较小时系统的调节时间较长,超调脉冲较少,调节精度较高;当参数a在0.02时系统的调节时间和超调脉冲数达到最优,随着参数a的继续增大调节时间和超调脉冲均开始增大,且超调脉冲数增加迅速。所以能够让系统自动选择出合适的参数,是Bang-Bang变结构控制高精度调节的关键。采用如表 1所示的模糊控制规则,并直接将PS、PM、PB解模糊为0.01、0.02和0.04,即对应系统的轻载、满载和重载三个状态,系统运行后的状态图如图 9所示。
在本次调节中系统根据模糊控制规则自动计算a为0.4,从图 9中可以看出在本次调节中系统仅需要一次切换即达到目标转数,系统在切换线附近仅穿插一次,略有超调,调节时间仅为5 s左右,没有抖振产生。
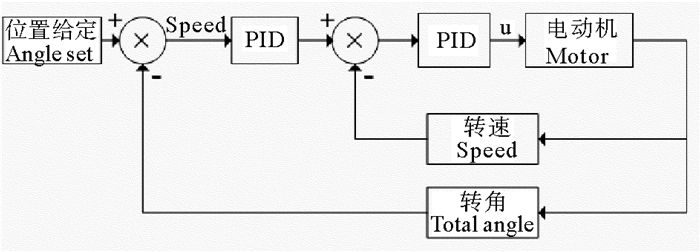
对于采用双闭环PID控制的自动调平系统,其控制结构如图 11所示,当设置外环PID的比例系数Kp=0.6,积分系数和微分系数均为0,内环的比例系数Kp=1.05,积分系数Ki=0.1,微分系数Kd=0时,系统的运行状态如图 12所示。
|
图 11 双闭环PID控制结构图 Fig. 11 Diagram of double closed-loop PID |
|
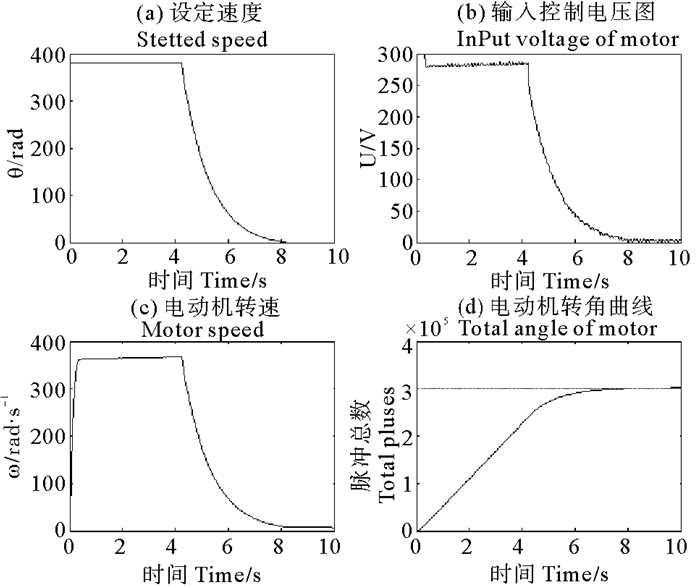
图 12 双闭环PID控制单条支腿运行图 Fig. 12 Leg state of leveling system controlled by double closed-loop PID |
从图 12(a)中可以看出在系统启动瞬间误差值较大时,外环PID给出一个较大的速度设定值让内环PID进行跟踪,内环PID通过对电动机实际转速与外环PID给定的设定值计算出电动机的控制电压,如图 12(b)所示,其对外环所设定速度的跟踪效果如图 12(c)所示;且随着速度误差的不断积分,控制电压在0.5~4.5 s是逐渐上升的。随着总转角误差的逐渐减小,外环的速度给定和内环的电压输出逐渐减小至0。从图 12(b)中可以看出在双闭环PID的控制过程中的电动机转速并不是立即达到最大值而是逐渐趋近于最高转速;而且存在着主动缓慢减速的过程-在电动机总转角逐渐接近目标转角的过程中,控制电压逐渐减小至零,转速是缓慢降低的。而Bang-Bang控制则可以在恰当的位置直接停机,保证了电动机是一直以最高的速度趋近目标位置的。在该双闭环PID控制中整个控制过程耗时约为8 s,比Bang-Bang控制多耗时2 s左右;PID控制需要调节多个参数,Bang-Bang控制仅需调整1个参数,降低了参数整定的难度。
7 结语本文结合电动机启动制动模型从理论上对变切换线Bang-Bang变结构控制应用于调平系统进行理论上的研究,并证明了该控制方法是渐近稳定的,并利用matlab仿真和实际调平系统进行了验证。实验表明该方法简单、可靠,是一种比较简便实用的控制算法,比较适合工程应用。
| [1] |
Ling X, Cao S, Zhu YQ. Fuzzy self-adapting automatically leveling method for four supports hydraulic platform[J]. Machine Tool & Hydraulics, 2007, 35(12): 84-86.
(  0) 0) |
| [2] |
褚新风, 杨曙东. 车载雷达电液自动调平系统[J]. 液压与气动, 2007, 5: 56-58. Chu Xinfeng, Yang Shudong. Electro-hydraulic leveling system for vehicle-borne radars[J]. Chinese Hydraulics & Pneumatics, 2007, 5: 56-58. (  0) 0) |
| [3] |
Feng Y, Chen B J. Control system of automatically leveling of vehicle-borne radars[J]. Huazhong Univ. Of sci. & Tech (Nature Science Edition), 2004, 36(6): 6-71.
(  0) 0) |
| [4] |
王洪斌, 王思文, 王跃灵, 等. 直驱式液压伺服系统建模及变增益滑模控制[J]. 电机与控制学报, 2013, 17(11): 110-116. Wang Hongbin, Wang Siwen, Wang Yueling, et al. Modeling and variable-gain sliding-mode control for adirect drive hydraulic servo system[J]. Electric Machines and Control, 2013, 17(11): 110-116. DOI:10.3969/j.issn.1007-449X.2013.11.017 (  0) 0) |
| [5] |
Lai C K, Shyu K K. A novel motor drive design for incremental motion system via sliding-mode control method[J]. IEEE Transactions on Industrial Electronics, 2005, 52(2): 499-507. DOI:10.1109/TIE.2005.844230
(  0) 0) |
| [6] |
Liu J K, Er L J. Sliding mode controller design for position and speed control of flight simulator servo system with large friction[J]. System Engineering and Electronics, 2003, 14(3): 59-62.
(  0) 0) |
| [7] |
Rubaai A, Jerry J. dSPACE DSP-Based Real-Time Implementation of Fuzzy Switching Bang-Bang Controller for Automation and Appliance Industry[C]. IEEE Industry Applications Society Annual Meeting(IAS), 2010: 1-8.
(  0) 0) |
| [8] |
Nagi F, Zulkarnain A T, Nagi J. Tuning fuzzy Bang-bang relay controller for satellite attitude control system[J]. Aerospace Science and Technology, 2013, 26(1): 76-86. DOI:10.1016/j.ast.2012.02.016
(  0) 0) |
| [9] |
Xu J X, Lee T H, Pan Y J. On the sliding mode control for DC servo mechanisms in the presence of unmodeled dynamics[J]. Mechatronics, 2003, 13(7): 755-770. DOI:10.1016/S0957-4158(02)00062-4
(  0) 0) |
| [10] |
李勇建, 魏贵玲, 邓劲松, 等. 自动调平技术研究[J]. 压电与声光, 2010, 32(6): 949-952. Li Yongjian, Wei Guiling, Deng Jinsong, et al. Study on automatic leveling technology[J]. Piezoelectrics & Acoustooptics, 2010, 32(6): 949-952. (  0) 0) |
| [11] |
房晓明, 姜沛然, 王立权, 等. 波浪影响下导管架调平系统最优控制[J]. 电机与控制学报, 2012, 16(11): 104-108. Fang Xiaoming, Jiang Peiran, Wang Liquan, et al. Optimal control for the jacket leveling system under the influence of wave[J]. Electric Machines and Control, 2012, 16(11): 104-108. DOI:10.3969/j.issn.1007-449X.2012.11.017 (  0) 0) |
| [12] |
张寅孩, 葛金法, 汪松松. 基于Bang-Bang最优理论的感应电机能耗制动相轨迹分析[J]. 电工技术学报, 2011, 26(2): 74-80. Zhang Yinhai, Ge Jinfa, Wang Songsong. Energy-consumed braking phase trajectory of induction motor based on Bang-Bang optimal theory[J]. Transactions of china electrotechnical society, 2011, 26(2): 74-80. (  0) 0) |
| [13] |
李运德, 张淼. 无刷直流电机的指数趋近律滑模变结构控制[J]. 电机与控制应用, 2011, 38(3): 32-35. Li YunDe, Zhang Miao. Sliding mode control of brushless DC motor with exponential reaching law[J]. Electric Machines & Control Application, 2011, 38(3): 32-35. (  0) 0) |
| [14] |
安树, 杨新霞. 无刷直流电动机模糊滑模变结构控制的研究[J]. 计算机仿真, 2010, 27(4): 172-175. An Shu, Yang Xinxia. Research on fuzzy sliding mode changeable structure control of brushless DC motor[J]. Computer Simulation, 2010, 27(4): 172-175. (  0) 0) |
| [15] |
Wai R J, Lin C M, Hsu C F. Adaptive fuzzy sliding mode control for electrical servo drive[J]. Fuzzy Sets and Systems, 2004, 143: 295-310. DOI:10.1016/S0165-0114(03)00199-4
(  0) 0) |
| [16] |
徐逢秋, 许贤泽, 乐意, 等. 基于模糊控制的快速自动安平激光扫平仪[J]. 光学精密工程, 2012, 20(8): 1870-1876. Xu Fengqiu, Xu Xianze, Le Yi, et al. Fast automatic rotating laser construction based on fuzzy control[J]. Optics and Precision Engineering, 2012, 20(8): 1870-1876. (  0) 0) |
 2018, Vol. 48
2018, Vol. 48


