2. 上海交通大学 船舶海洋与建筑工程学院,上海 200240;
3. 中国船舶及海洋工程设计研究院,上海 200011
海底拥有丰富的油气资源,海洋工程中常采用海底管道对开采的油气进行提升运输。其中,钢制悬链线式立管由于形态细长且柔性大,同时受到重力和浮力作用且顶端悬挂,故常在水中呈现悬链线式布置。钢制悬链线式立管可以分为悬垂段、触地段以及拖地段。其中,触地段因为受到海流以及漂浮结构物运动的影响,会同海床发生复杂的管土作用,影响管道结构安全性。为了获取垂向与侧向土体反力变化规律,2H Offshore Engineering公司利用激振器模拟了立管上端慢漂、垂荡、纵荡以及横荡等运动,对触地点管土相互作用问题进行了分析与研究[1]。Aubeny等[2-4]多次进行垂向管土作用实验,将非线性滞后的管土作用过程分为初始嵌入、线性回升、部分管土分离、完全管土分离和重新嵌入。在此基础上发展出了常用的Aubeny-Biscontin(AB)模型。Bruton等[5]进行了管道侧向大位移运动的离心机试验,并收集到了来自联合工业项目(Joint industry project, JIP)实验的数据,总结出管道做侧向大位移运动时的土反力曲线可分为4个阶段。除了实验手段,建立有限元模型也可以探索管土作用的机理与力学规律,Konuk等[6]与Yu等[7]分别建立二维和三维有限元模型,研究了管土相互作用和管道横向屈曲问题,发现三维管道模型计算量大,管道行为极其复杂,而二维模型相对简单,同时可以作为三维研究的基础,有必要先进行二维层面的机理研究。
二维层面上管土作用研究主要专注于垂向与侧向的复杂受力:垂向管土作用中土体对管道的作用力具有滞后效应,存在多种作用模式;侧向管土作用中土体反力具有很强的非线性,且垂向与侧向管土作用之间又存在显著的耦合效应。
有限元分析技术中对物体较为常见的数值描述为拉格朗日(Lagrange)描述与欧拉(Euler)描述。由于管土作用中土体会发生很大的变形,拉格朗日网格易产生畸变导致计算结果不可信,而欧拉描述中,物体可在网格间运动,不会出现网格畸变的问题,但求解难度较大、速度慢,一般用于流体的计算。在研究海底管道管土作用这类有大变形的动力学问题时,目前运用较多的有任意拉格朗日-欧拉(Arbitrary Lagrange-Euler,ALE)法和欧拉-拉格朗日耦合(Coupled Eulerian-Lagrangian,CEL)法。
ALE法基于拉格朗日单元描述,并在特定增量步下重新分布节点位置,使得单元节点独立于材料移动,分析过程中可以保持高质量平滑网格。在Abaqus软件中有3种平滑方法:(1)体积平滑法,通过计算共节点单元中心的体积加权平均值以平滑节点;(2)拉格朗日平滑法,将同目标节点直接相连节点的平均坐标作为目标节点的新坐标;(3)等势平滑法,通过计算临近单元所有节点的高阶加权平均值以平滑节点[8]。蒋建东等[9]利用ALE法计算了土壤受到深耕铲切削时的阻力变化问题。研究管土作用时,程宇骁[10]利用Abaqus软件,基于ALE自适应网格技术和修正硬接触算法模拟悬链线初次贯入、管线回弹与脱离的全过程,重点模拟土体吸力的产生和释放过程,并将数值模拟结果与NGI试验结果进行对比,验证了ALE法分析的可行性。
CEL法则将拉格朗日法与欧拉法相结合,大变形物体采用欧拉法描述,小变形物体或刚体采用拉格朗日法进行描述。在运动过程中,小变形物体用拉格朗日单元描述并占据欧拉网格的空间[11],大变形物体以流体的形式在欧拉网格中运动,并通过接触算法自动计算2种结构间的界面,实现不同类型单元之间的相互作用。Dutta Sujan等[12]采用CEL方法对埋置管道侧向相互作用进行模拟。施若苇[13]利用CEL法建立管土作用模型,发现光滑管道的计算结果与前人研究接近。吴瑞[14]采用CEL法研究了管道在土体中浅贯入时土体材料参数对阻力的影响以及深贯入时的土体破坏机理。
总结来看,CEL法与ALE法均能在一定程度上解决管土作用数值仿真中几何大变形求解困难,但原理不同。目前仍存在以下问题:针对方法层面的论证工作较少,适用性有待模型实验验证;CEL法和ALE法相对较新,有许多技术细节值得深入研究;两种方法之间的对比分析较少,其对网格的要求、计算精度、效率等方面有待研究。此外,海底管道管土作用的相关研究很少考虑到速度效应。本文分别采用拉格朗日法、ALE法以及CEL法对海底管土垂向及侧向作用进行数值仿真,探索不同方法的差异,并进行了管土作用试验,以回答上述仍存在的问题。
1 计算模型 1.1 有限元仿真对象挪威岩土工程研究院(NGI)曾对管土作用做了较为全面的实验研究,实验设备如图 1所示[15]。其中:实验水箱长3.6 m、高1.7 m; 测试管道长1 300 mm; 直径174 mm。土体密度为ρ=2 000 kg/m3,弹性模量为E=1 MPa,泊松比v=0.499,黏聚力c=2 kPa。
本文在Abaqus中按照NGI实验的参数条件进行有限元仿真并取单一横截面做平面应变双精度计算。管道截面视为刚体,土体选用弹塑性模型,用摩尔库伦塑性模型描述土体塑性。限制土体模型左、右两边水平(X方向)运动,底部限制垂向(Y方向)运动,此外模型整体限制在截面法向(Z方向)上的运动以保证是平面应变问题。由于ALE法与CEL法在原理及软件设置上不同,需要各自进行建模:在ALE方法中,采用二维四节点平面应变单元离散土体模型,管土间的接触采用面-面接触;在CEL法中采用三维立体欧拉单元离散土体模型,分析管土间接触采用Abaqus软件中常规接触的自接触(Self contact)。接触过程中,土体法向不能穿透管道,且同时存在一定的黏性,但黏性在管道贯入与侧移过程中影响较小,故忽略黏性影响。法向采用硬接触,当接触面间距大于0时,没有作用力,当接触面间距为0时,正向压力可为无穷大以保证不穿透。接触面切向存在摩擦力,采用罚函数(Penalty)算法描述,摩擦系数f=0.5,最大剪切应力为1 kPa。
1.2 网格无关性验证本文算例中,远离管土作用区域的单元长度取30 mm,为了提升计算精度,需要对管土作用区域的网格进一步细化并验证网格无关性。采用垂向贯入仿真结果进行比较:从管道接触土体开始,保持垂向贯入速度0.5 mm/s,计时100 s,得到不同贯入深度下的单位长度土体反力,并比较网格大小对单位长度土体反力的影响。
针对ALE法,管土作用细化区分别选取超大网格(10 mm)、大网格(4 mm)、中网格(2 mm)以及小网格(1.5 mm)4种情况,得到图 2所示结果。

|
图 2 不同大小网格下ALE法土体反力计算结果 Fig. 2 Calculation results of soil resistance by ALE method under different grids |
由图 2结果可知,单元大小为10 mm时,ALE法计算得到的单位长度反力波动很大,结果不收敛。当网格单元大小为1.5~4 mm时,单位长度反力波动较小且相近,可认为数值计算结果已收敛。在后续的研究中,ALE法将采用2.5 mm的网格进行计算。
针对CEL法,管土作用细化区域分别选取超大网格(20 mm)、大网格(12 mm)、中网格(8 mm)以及小网格(6 mm)4种情况,计算得到的单位长度反力如图 3所示。

|
图 3 不同大小网格下CEL法土体反力计算结果 Fig. 3 Calculation results of soil resistance by CEL method under different grids |
由图 3可知,当网格单元大小为6~20 mm时单位长度反力基本一致,可认为CEL法计算已经收敛。在后续的研究中,CEL法将采用8 mm的网格进行计算。
通过网格无关性验证可知,ALE法计算所需的网格单元尺寸更小,相比而言需要的计算资源更多,且单位长度反力结果波动更大;而CEL法计算时对单元细化的要求更低,结果波动更小。
2 垂向及侧向管土作用分析 2.1 垂向管土作用分析令管体初始位置同土体界面相切,控制与NGI实验同样的垂向贯入速度0.5 mm/s,计算时长为100 s,即最大贯入深度为50 mm,分别采用普通的拉格朗日单元法、ALE法以及CEL法计算垂向贯入时的土体反力。达到最大贯入深度时的土体网格如图 4所示。

|
( (a) 拉格朗日法Lagrange Method;(b) ALE法ALE Method;(c) CEL法CEL Method. ) 图 4 三种方法的网格对比结果 Fig. 4 Grid comparison results of the three methods |
对比发现,在管道垂向贯入时,拉格朗日法的网格将产生极大的变形并扭曲;ALE法所得的网格光滑、过渡自然;CEL法的欧拉网格固定,以流体形式模拟的土体也较为光滑。在土体形态轮廓上,3种方法得到的土体形态相似,隆起光滑,但土堆隆起程度上,CEL法最大,ALE法次之,拉格朗日法最小。利用三种方法计算垂向贯入土体反力结果见图 5。
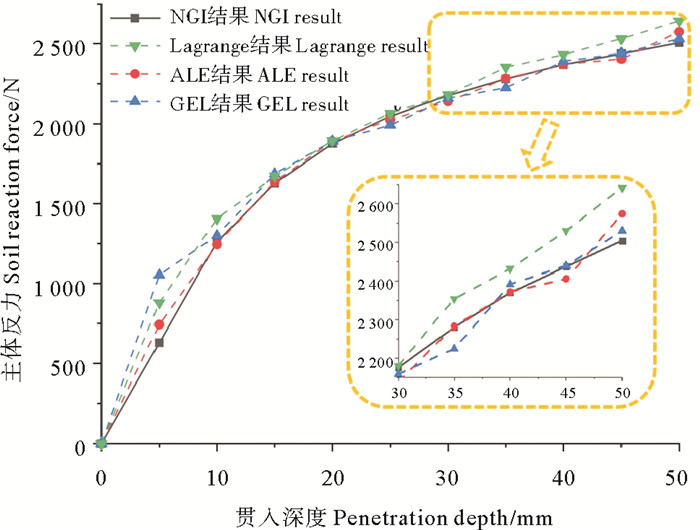
|
图 5 三种方法计算结果与NGI实验结果对比 Fig. 5 Comparison of soil resistance obtained by three methods with NGI experiment |
由图 5可知,在模拟管道垂向贯入中,3种方法计算结果与NGI的结果相近,但初始贯入的土体反力均偏大。方法对比来看,当贯入深度增大时(本模型中为超过10 mm),ALE法与CEL法均能较好反映土体反力变化情况,而拉格朗日法拟合程度稍差。
此外,利用ALE法与CEL法计算得到垂向管土作用的结果与NGI实验结果相近,有理由认为本文的数值建模方法对于垂向管土作用具有一定的可信度。在此基础上,由于缺少NGI的侧向管土试验数据,故仅从有限元计算角度对侧向管土作用进行分析。
2.2 侧向管土作用分析在研究管土侧向作用时,先使管道以0.5 mm/s的速度贯入到深度分别为5、10、20、30、40和50 mm处,接着固定深度,使管道以0.5 mm/s的速度水平运动,水平运动时长为350 s。
ALE法在拉格朗日法基础上发展而来,故先对比拉格朗日单元法和ALE法在侧向管土作用计算中的适用性,后比较ALE与CEL两种适用于大变形问题的网格技术,以得到两种方法各自的优劣。
2.2.1 拉格朗日法与ALE法计算结果对比在垂向贯入深度为50 mm且侧向位移为66 mm时,拉格朗日网格因扭曲而计算终止,如图 6所示。即利用拉格朗日法模拟侧向管土作用时单元会极度扭曲,并且在单元变形超过软件可接受的范围时计算将终止。

|
图 6 拉格朗日网格的扭曲 Fig. 6 Distortion of the Lagrangian grid |
图 7为不同深度下ALE法与拉格朗日法计算土体侧向力的结果对比图。图 7中拉格朗日法曲线不完整的原因是单元过度扭曲计算终止。对比不同深度下拉格朗日法的结果可知,贯入深度越大,侧向位移时引起的土体变形越大,计算更早终止。而ALE法能够得到模拟时间内完整的时历结果。另外,拉格朗日法计算结果较ALE法偏大,仅在侧向位移较小时与ALE法相近。随着侧向位移的进一步增大,两者差距也将进一步增大。

|
图 7 ALE法与拉格朗日法对比图 Fig. 7 Comparison between ALE method and Lagrangian method |
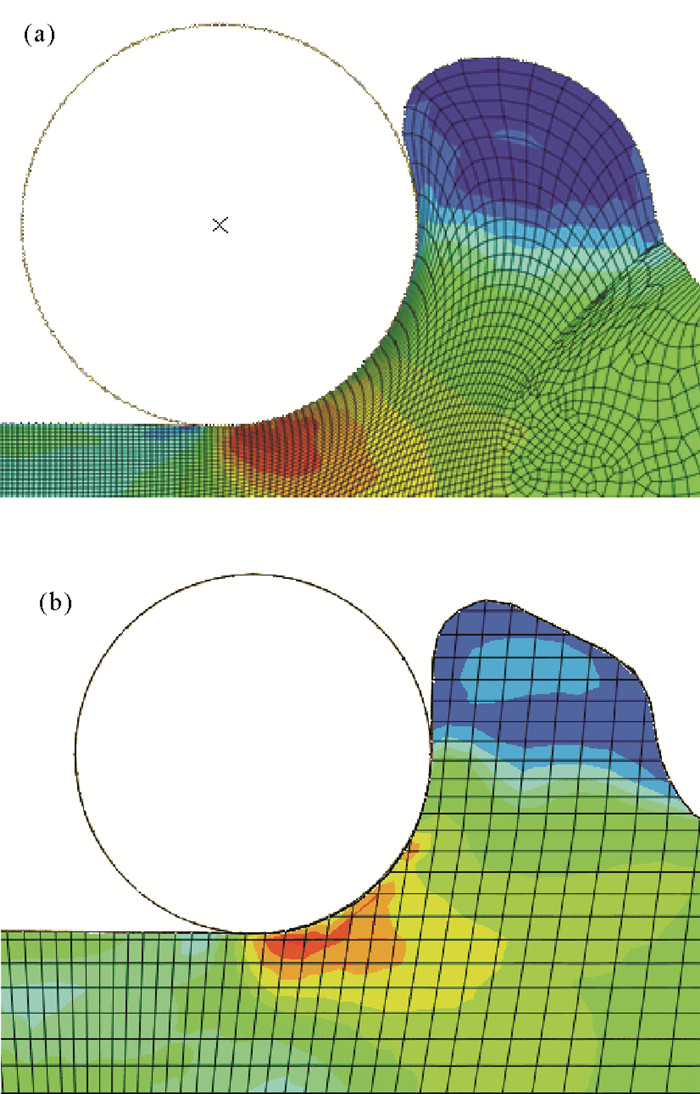
ALE法以及CEL法计算所得的土体变形如图 8所示。
|
( (a) ALE法ALE Method;(b) CEL法CEL Method. ) 图 8 ALE法与CEL法的土体变形对比结果 Fig. 8 Comparison results of soil deformation between ALE method and CEL method |
由图 8可知,得益于计算过程中可以重新划分拉格朗日网格,ALE法在物体产生大变形时能一定程度上保证网格单元光顺并控制长宽比,但受限于上一次网格分布情况,变形的累积依旧可能导致单元产生扭曲与变形。CEL法的网格固定,而土体视为流体,变形光滑,不受变形的大小及复杂程度限制。从单元变形的角度看,CEL法比ALE法更适用于大变形物体的有限元分析研究。此外,2种方法计算得到的土体形态类似,但ALE法得到的土体有回卷的趋势。
ALE法与CEL法的侧向土体反力计算结果见图 9。对比可知,在相同的工况参数下,2种方法计算结果相近,变化趋势相同。但ALE法计算结果相较CEL法计算结果偏小,且波动更大,CEL法计算结果波动更小、更平稳。此外,需要注意的是,ALE法在输出数据中可能出现某点土体反力降低的情况,笔者认为可能的原因是ALE法在重新定位节点位置时会造成“松弛”,使得单元应力降低,可能需要根据相邻数据点取平均值以获得较为平滑的反力变化曲线。
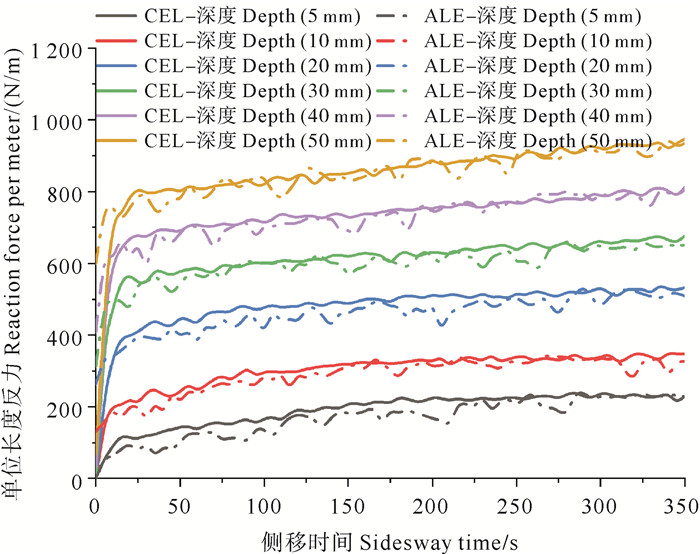
|
图 9 ALE法与CEL法仿真结果对比 Fig. 9 Comparison of simulation results between ALE method and CEL method |
本文对直径50 mm、长度300 mm的管道进行了垂向管土作用试验。管道材料为304不锈钢,壁厚10 mm,两端封闭,表面抛光,可以视为刚体。土样选取中砂。初始位置管道与土体表面相切,贯入深度为直径D,控制垂向贯入速度为1、10、20与50 mm/s,共计4种工况。实验过程中利用六分力仪获取垂向土体反力,同时运动机构记录对应的垂向位移,得到反力随时间变化的曲线。试验设备如图 10和11所示。

|
图 10 实验设备简图 Fig. 10 Schematic diagram of experimental equipment |

|
图 11 试验设备图 Fig. 11 Test equipment |
试验结果表明管土作用中存在一定的速度效应,速度越大土体反力越大,其原因是土体颗粒应变率增大使得土体强度增强,同时变形加速度增大,变形所需的力也更大。用CEL法进行仿真计算,并将计算结果与试验结果进行对比(见图 12)。对比4种速度下的工况,CEL法计算结果与试验结果基本一致,仅在贯入初期有所区别,分析其原因是实验中表层土体较下层土体更为松散,使得土体反力有所减小。试验结果表明,利用CEL法能较好地反映速度对土体反力的放大作用。

|
图 12 CEL法与实验结果对比 Fig. 12 Comparison of CEL method and experimental results |
(1) 在模拟海底管道管土作用问题时,拉格朗日网格单元易畸变甚至结果失真,CEL法与ALE法能较好反映土体反力变化情况。
(2) 在同等条件下,CEL法对网格单元细化要求较低,而ALE法需要更小的网格单元才能保证网格无关性,对计算资源需求更高。
(3) 在侧向管土作用模拟中,ALE法计算结果相较CEL法偏小且波动更大。管土作用这类大变形问题更适合采用CEL法进行仿真分析。
(4) 通过试验比对,CEL法能够较好地反映管土作用土体反力的速度放大效应。
| [1] |
白兴兰, 姚锐, 段梦兰, 等. 深水SCR触地区管-土相互作用试验研究进展[J]. 海洋工程, 2014(5): 107-112. Bai X L, Yao R, Duan M L, et al. Review of experimental research on the interaction of deepwater steel catenary risers with seafloor[J]. The Ocean Engineering, 2014(5): 107-112. (  0) 0) |
| [2] |
Aubeny C P, Biscontin G. Seafloor-riser interaction model[J]. International Journal of Geomechanics, 2009, 9(3): 133-141. (  0) 0) |
| [3] |
Aubeny C P, Biscontin G. Interaction model for steel compliant riser on soft seabed[J]. SPE Projects, Facilities & Construction, 2008, 3(3): 1-6. (  0) 0) |
| [4] |
Aubeny C P, Gaudin C, Randolph M F. Cyclic tests of model pipe in Kaolin[J]. SPE Projects, Facilities & Construction, 2008, 3(4): 1-6. (  0) 0) |
| [5] |
Bruton D, White D, Cheuk C, et al. Pipe/soil interaction behavior during lateral buckling, including large-amplitude cyclic displacement tests by the safebuck JIP[C]// Houston, Texas: Offshore Technology Conference, 2006.
(  0) 0) |
| [6] |
Yu S, Konuk I. Continuum FE modeling of lateral buckling[C]// Houston, Texas: Offshore Technology Conference, 2007.
(  0) 0) |
| [7] |
Konuk I, Yu S. Continuum FE modeling of lateral buckling: Study of soil effects[C]// Proceedings of 26th International Conference on Offshore Mechanics and Arctic Engineering. Mexico: American Society of Mechanical Engineers,, 2007: 347-354.
(  0) 0) |
| [8] |
Dassault Systèmes Simulia Corp. Abaqus/CAE User's Guide[M]. RI: Dassault Systèmes Simulia Corp, 2014.
(  0) 0) |
| [9] |
蒋建东, 高洁, 赵颖娣, 等. 基于ALE有限元仿真的土壤切削振动减阻[J]. 农业工程学报, 2012, 28(S1): 33-38. Jiang J D, Gao J, Zhao Y D, et al. Numerical simulation on resistance reduction of soil vibratory tillage using ALE equation[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(S1): 33-38. (  0) 0) |
| [10] |
程宇骁. 考虑管土接触效应的悬链线立管动力响应特性研究[D]. 上海: 上海交通大学, 2018. Chen Y X. Study on Dynamic Response of Steel Catenary Riser Considering Pipe-Soil Contact Effect[D]. Shanghai: Shanghai Jiaotong University, 2018. (  0) 0) |
| [11] |
胡奇, 王明振, 张家旭, 等. 基于耦合欧拉-拉格朗日方法的浮筒着水数值仿真[J]. 系统仿真技术, 2019, 15(1): 18-22+40. Hu Q, Wang M Z, Zhang J X, et al. Numerical simulation on water impact of float based on coupled Eulerian-Lagrangian method[J]. System Simulation Technology, 2019, 15(1): 18-22+40. (  0) 0) |
| [12] |
Dutta Sujan, Hawlader Bipul, Phillips Ryan. Finite element modeling of partially embedded pipelines in clay seabed using coupled Eulerian-Lagrangian method[J]. Canadian Geotechnical Journal, 2014, 52(1): 58-72. (  0) 0) |
| [13] |
施若苇. 海底管道热屈曲及管土相互作用研究[D]. 杭州: 浙江大学, 2014. Shi R W. Global Buckling of Subsea Pipelines and Pipe-Soil Interaction[D]. Hangzhou: Zhejiang University, 2014. (  0) 0) |
| [14] |
吴瑞. 深水黏土中海底管道与土体相互作用的机理研究[D]. 青岛: 中国石油大学(华东), 2018. Wu R. Study on Mechanism of Pipeline-Soil Interaction in Deep Water Clay[D]. Qingdao: China University of Petroleum (East China), 2018. (  0) 0) |
| [15] |
Langford T E, Aubeny C P. Large scale soil-riser model testing on high plasticity clay[C]//The Proceeding of the Eighteenth International Offshore and Polar Engineering Conference. Vancouver: International Society of Offshore and Polar Engineers, 2008.
(  0) 0) |
2. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240;
3. Marine Design and Research Institute of China, Shanghai 200011
 2023, Vol. 53
2023, Vol. 53



