随着信息时代的到来及信息技术的飞速发展,人们越来越多的接触到高维数据,如航天遥感数据、人的基因分布以及受光照影响的多姿态和表情的人脸图像等。这些数据能够提供更加丰富完整的信息,但同时随着维数的增加会引发维数灾难,给数据分析带来了重大挑战[1]。为了解决维数灾难的问题,人们期望从高维数据中提取有效的、紧致的描述,因此对高维数据进行降维处理是十分有必要的。作为非线性降维的有效算法,近年来,国内外的学者都大力展开了对局部线性嵌入(Locally linear embedding)(LLE)[2]和深度自编码网络[3]的研究。
机器学习中,非线性降维算法包括LLE,Isomap[4],Laplacian Eigenmap[5],Hessian Eigenmap[6],LTSA[7],MVU[8],diffusion maps[9-12],t-SNE[13]和自动编码器等等。LLE是Roweis和Saul于2000年针对高维空间中的非线性流行提出的一种无监督的的降维方法。其核心主要是基于用局部的线性来逼近全局的非线性,将流形上的近邻点映射到低维空间的近邻点,保存原流行中的局部几何特性,以达到高维数据映射到低维全局坐标系中的目的。深度自编码网络是Hinton于2006年提出的一种在无监督数据上建立多层神经网络,学习输入数据隐含特征的有效方法。该方法通过“逐层初始化”解决了含多隐层的传统神经网络在训练上的难度,不仅是神经网络的一种,也为后来深度学习的发展构建框架。LLE和深度自编码网络被广泛应用于数据挖掘、模式识别、故障诊断等多种领域[14-21]。
1 LLE算法的简单描述(1) 根据欧式距离,LLE为高维空间的每个样本点xi(i=1, 2, …, N)寻找离它最近的k(k是定值)个点作为其近邻点。
(2) 对于每个样本点xi(i=1, 2, …, N),LLE从k个近邻点出发,计算出该样本点满足约束条件
| $ {{W}_{i}}=arg\ \text{min}\varepsilon ({{W}_{i}})={{\left| {{x}_{i}}-\sum\limits_{i=1}^{N}{{{w}_{ij}}{{x}_{i}}j} \right|}^{2}}。$ |
(3) 最小化如下损失函数,在满足
| $ \text{min}{\mathit{\Phi}} \left( Y \right)={{\sum\limits_{i=1}^{N}{\left| {{y}_{i}}-\sum\limits_{j=1}^{k}{{{w}_{ij}}{{y}_{ij}}} \right|}}^{2}}。$ |
深度网络可以使用,自动编码器和RBM堆对训练样本进行无监督的预训练。本文选取自动编码器建立深度网络模型。深度自编码网络通过令输出等于输入对网络参数进行无监督的预训练。在训练过程中,深度自编码网络首先通过逐层地编码训练,然后再利用反向传播算法训练模型,在可接受的误差范围内,将模型参数优化到最优值附近。
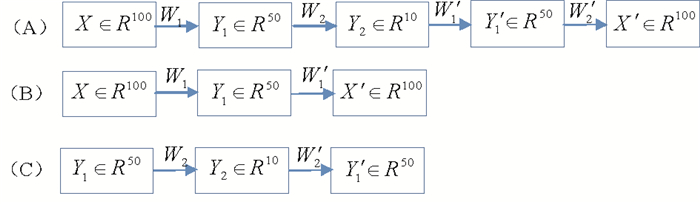
图 1显示了自编码网络无监督学习特征的过程,假设输入样本数据X∈R100,第一层隐含层神经元为50个,第二层隐含层神经元为10个,经过两层编码和两层译码最终使得输入等于输出。输入样本数据X∈R100,经过第一个编码层,输出Y1,然后Y1用于下一层的输入,经过第二个编码层,输出Y2。Y2作为下一层的输入,经过第一个译码层,得到Y′1作为第二个译码层的输入,输出X′。其中W1、W2、W′1、W′2分别对应着自编码网络的编码权值和译码权值。通过使得X′重构X的误差尽可能的小,将模型参数优化到最优值附近。网络的整个过程是无标签的,这就是深度自编码网络对网络参数进行无监督预训练的整个过程。
|
(A)是网络自编码的整体过程,在具体实现的时候,自编码深度网络模型需要拆分成(B)和(C)两个过程。第一个过程(B)训练100-50-100自编码,第一个过程(C)训练50-10-50自编码。 图 1 自编码网络过程得到100-50-10 Fig. 1 Pre-training a deep autoencoder network |
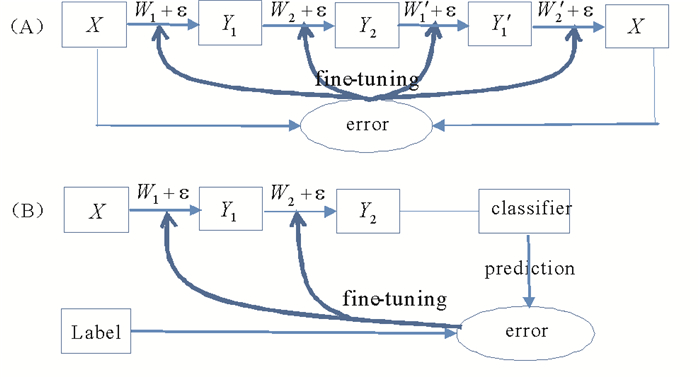
输入训练样本X∈R100通过两层编码生成的数据Y2∈R10,以实现网络降维的目的。通过对以上深度自编码网络的预训练,将模型参数优化到最优值附近。进一步连接X的信息,建立输入和输出之间的联系,有监督地微调网络得到网络模型参数的最优值。微调参数可分为以下两种,如图 2所示。
|
(A)连接X的信息,利用编码和译码过程微调整个网络。(B)连接X的标签信息,建立输入样本和输入标签之间的联系,对网络的编码参数W1和W2进行微调,常用于以分类为目的的微调。 图 2 深度自编码网络模型参数的有监督微调过程 Fig. 2 Fine-tuning deep autoencoder networks |
为了对比研究LLE算法和深度自编码网络的降维效果,选取以下四组数据集,分别从可视化,人脸识别以及文本检索方面出发,结合数值实验结果,对两种降维方法进行详细探讨。
(1) hand手握杯子旋转数据集[22]。该数据集由于其特有的明显的旋转特性,在机器学习领域得到广泛应用,被多次应用于图像降维可视化评价降维算法的性能,共包含481张手握杯子旋转的图像,每张图像的像素为512×480,如图 3所示。

|
图 3 hand手握杯子旋转数据集的手势旋转图像示例 Fig. 3 Motions samples in the hand database |
(2) MNIST手写数字数据集[23]。该数据集有60 000张训练图像和10 000张测试图像,被多次应用于深度学习和图像识别的研究。每张图像的像素为28×28,如图 4所示,由0到9的手写阿拉伯数字构成。
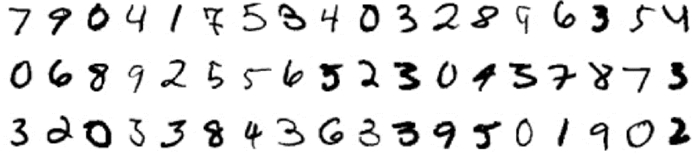
|
图 4 MNIST手写数字数据库的手写数字图像示例 Fig. 4 Handwritten digits samples in the MNIST database |
(3) ORL人脸数据集[24]。该数据集采样于40个不同的人,每个人都呈现出10种多姿势和不同照明方向,共包含400张人脸图像,每张图像的像素为92×112,如图 5所示。ORL人脸数据集是人脸识别领域应用最广泛的人脸数据集之一。

|
图 5 ORL人脸数据集的人脸图像示例 Fig. 5 Facial images samples in the ORL database |
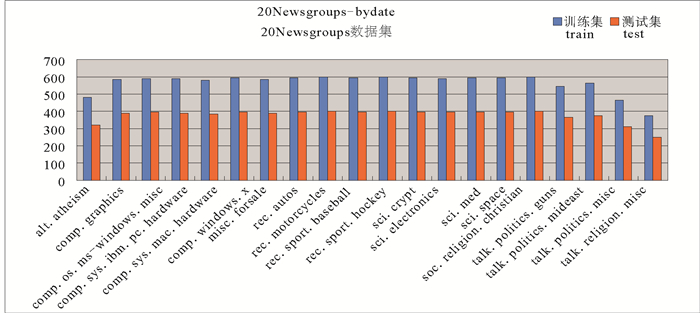
(4) 20Newsgroups数据集[25]。20newsgroups数据集共有18846个文本数据,包含11314个训练文本和7531个测试文本。该语料数据集被划分为20个不同的新闻组,每个新闻组都对应着一个新闻主题,即共有20个新闻主题,如图 6所示。在机器学习领域中,20Newsgroups数据集已成为文本应用实验中(如文本分类和文本聚类)最常用的一个标准数据集之一。
|
图 6 20Newsgroups数据集的训练文本和测试文本数量分布 Fig. 6 Distribution of training and testing in 20 Newsgroups database |
降维可视化旨在尽量保持数据集主要特征的基础上降低维度,进而将高维数据在低维可视空间展开,最终实现图形化分析[26]。降维可视化可以把高维数据投影到低维空间,特别是人眼可观测的二维空间或三维空间,可以实现高维数据的可视化。由于认知能力固有局限性的存在,在面对高维空间结构和数据信息时,人类信息认知活动面临着巨大的挑战,因此无法直观体现数据集中多维对象在各维上的分布情况[27]。降维可视化在图像识别,图像检索,预测膜蛋白类型,地震的预测研究,分辨地表物质和提供商业决策中都得到了广泛的应用[28-30]。
降维是手段,认识数据是目的。因此面对复杂数据表现的大容量、高维度、关系复杂的特点,应用降维可视化有利于我们深入理解和全面掌握高维数据集,再结合人类特有的认知能力,从而对数据进行更深入的观察和分析有着非常重大的现实指导意义[31]。比如,Gordon Berman将降维可视化应用于动物行为的研究[32-33],通过比较图谱,发现了果蝇性别上的行为差异。之后,作者又进一步依据果蝇行为图谱中的层级性,首次给出了关于什么是层级的可靠的定义以及如何理解不同层级之间的关系,对后来研究行为的神经学基础有着深远的意义。
本文选取hand手握杯子旋转数据集和MNIST手写数字数据集,如图 3-4所示,用于LLE算法和深度自编码网络的降维可视化研究。为了减轻计算机的运算负担,我们将手握杯子旋转数图像标准化至10×10,从60 000张MNIST手写数字训练集中随机抽取800幅图像进行实验。采用MATLAB 2015b的实验环境,在CPU为2.3GHz的Intel i3-2350,内存为2GB的计算机上,分别对手握杯子旋转数据集和手写数字数据集进行二维投影,运行实验输出结果。
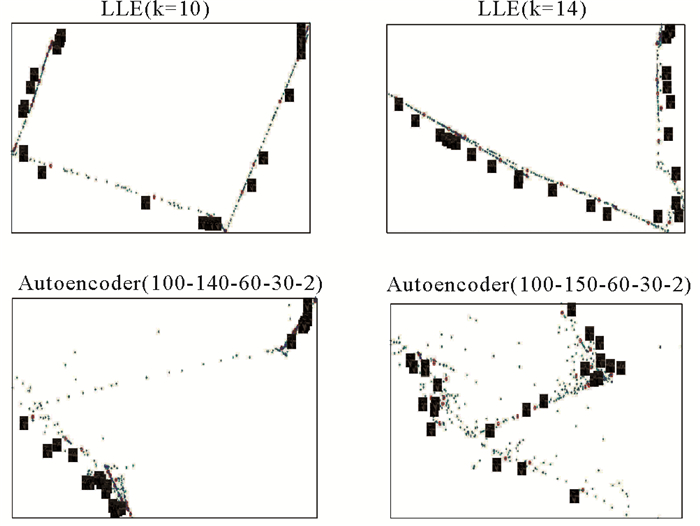
图 7展示了两降维方法在hand手握杯子旋转集上的二维可视化的数值实验结果。实验中,我们依照经验设计LLE算法(k=10和k=14)和深度自编码网络(100-140-60-30-2和100-140-60-30-2)。通过比较,我们发现,虽然两降维方法都能呈现出手握杯子旋转图像的旋转规律,但显然,在本次实验中,无论近邻点k=10或k=14,LLE算法的二维可视化效果都要优于深度自编码网络。
|
图 7 hand手握杯子旋转图像的二维嵌入图 Fig. 7 2-D embedding space of hand rotated cups |
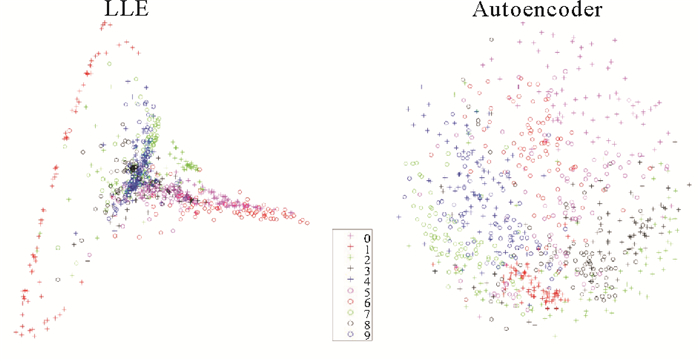
如图 8所示,对随机抽取800幅图像进行降维,将28×28维的数字图像进行二维投影。结果显示,深度自编码网络都能够挖掘出了800幅手写数字图像中存在的重要规律,降至二维后的数据具有良好的区分度,而使用LLE算法降维可视化的结果并不能很好地呈现出数字在各维度上的分布情况。
|
图 8 800幅MNIST手写数字图像的二维嵌入图 Fig. 8 2-D embedding space of real handwritten digits |
人脸识别作为生物特征识别的技术之一,如虹膜识别、指纹识别、掌纹识别等,由于具有成本低、用户易接受、可靠性高等优点,研究人脸识别在理论上和技术上都有重要的意义:一是可以推进对人类视觉系统本身的认识;二是可以满足人工智能应用的需要[34]。采用人脸识别技术,建立自动人脸识别系统,用计算机实现对人脸图像的自动识别,在身份认证、安防监控、人机交互等领域具有广泛的应用前景[35]。
人脸识别过程是由训练和测试两个阶段组成。设在训练阶段X={x1, x2, …, xN}∈RD为训练样本集,其中xi是一幅人脸图像的向量表示形式。通过降维得到训练样本的输出为Y={y1, y2, …, yN}∈Rd(d < D)。在测试阶段,LLE算法和深度自编码网络对于待识别的人脸图像会通过不同的方式寻求低维投影。
由于LLE没有给出重建测试图像的简单方法,采用以下步骤处理测试图像样本集,设为待识别人脸图像集,LLE算法图像识别步骤如下:(1)选取,在训练样本空间中寻找的个近邻点;(2)计算xN+1与其k个近邻点间的局部重建权值WN+1(满足
通过Logistic函数解决深度自编码网络的图像分类问题。该网络将人脸图像的底层视觉特征作为模型的输入,输出图像的高层类别特征,即输出神经元的数目等于图像类别数。即若人脸图像属于第k类,则相应的输出神经元的状态应该是,除去第k个神经元为1外,其余全为0。如前所述,首先预训练深度自编码网络的参数,将模型参数优化到最优值附近。其次,在训练好的网络模型中,连接训练图像的类别信息,建立训练图像和训练类别之间的联系,通过
在ORL人脸数据集运行LLE算法和深度自编码网络进行人脸识别研究。如图 5所示,对于数据集中的每一类,随机抽取50%的人脸作为训练集,剩下的50%作为测试集,为减轻计算机的运行负担,将人脸图像标准化至28×28,采用以上方法,完成实验。
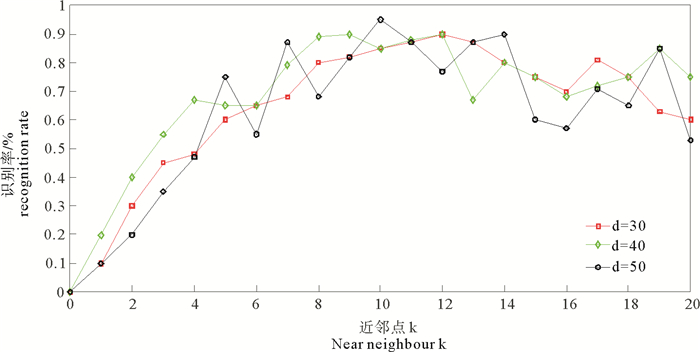
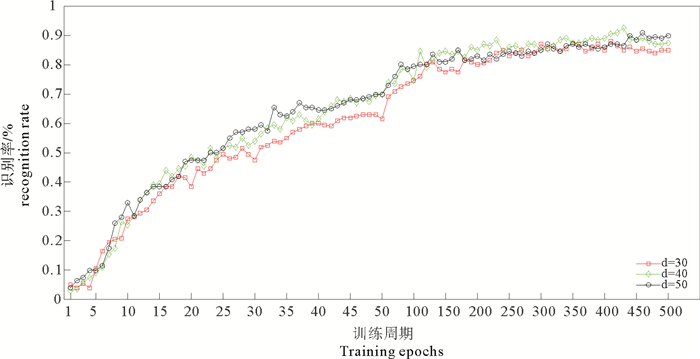
如图 9-10所示,LLE算法和深度自编码网络784-800-d-40在嵌入维数为30, 40, 50时的识别率变化。通过观察,无论高维的人脸图像数据最终降到多少维,当近邻点个数k从1到20变化时,LLE算法总能在某个k处使得识别率达到最大,这一点同样适用于以周期形式训练的深度自编码网络。特别地,LLE算法在降至50维时最高识别率可达91%,与深度自编码网络784-800-d-40相比,网络在d=40的识别率也为91%,但当d=50时,网络测试集上的识别率为92.5%。故从测试样本在ORL数据集上的人脸识别表现来看,两种降维方法不相上下。
|
图 9 LLE算法在嵌入维数为30,40,50时的识别率变化 Fig. 9 The varied recognition rate of LLE |
|
图 10 深度自编码网络在嵌入维数为30,40,50时的识别率变化(dropout=0.5) Fig. 10 The varied recognition rate of deep autoencoder networks |
文本检索的任务主要是指从给定的文本集中找出与用户相关的文本子集,并依据相关度排序把检索结果返回给用户[37]。那么,如何从海量的信息资源中快速并准确地检索出满足用户需求的信息子集,是文本检索的主要问题。本文是基于词频统计的向量空间模型[38]对文本检索展开讨论。首先,我们将文本和检索简化为关键词串及权重集合的向量表示,从而把检索操作变成向量空间上的向量运算。其次,把高维向量表示的文本映射到低维潜在语义空间中, 用向量之间的距离来逼近文本之间的语义相似性,适合于大规模语料库的文本检索。近年来,中英文的文本检索研究受到了国内外许多学者的重视[39-42],在信息检索领域具有非常广泛的发展前景和现实的指导意义。
首先,我们预处理文本数据:(1)去除数字,连字符,标点符号和特殊字符,将所有大写字母都转换为小写,避免某些词会因无法解析导致错误的结果;(2)去除功能词和停用词。将文本中出现频率过高而失去检索意义的单词剔除,如it,the,able,about之类的介词,副词或其他无检索意义的词,从而得到处理过的所有文档中的词,形成单词表;(3)抽取词干,确定基词。这是一种语法层次的处理措施,通过移除前后缀消除词形、时态变化对检索性能的影响并降低索引向量的维度。其次,我们主要选取能表达文本内容的实词作为关键词。通过上述预处理,任何一篇英文文本都可转化为一个由英文26个字母组成的有序字符串,进一步应用切词技术可得到一个一个的词串。通过基于词串在整个文档集中出现的频率,按照由高至低的顺序,我们从中选取一定数量的词串构成关键词[43]。
本节应用20Newsgroups数据集研究文本检索任务,如图 6所示。基于以上原理,我们从文本数据的训练集中选取2 000个高频词作为关键词,从而任一篇文本都可由一个2 000维的向量来表示,其中词串在文本中出现的频率为该向量中各个分量的值。同样的,每一个查询也可表示一个向量,故我们把检索操作变成向量空间上的向量运算。文本检索过程类似于图像识别过程,是由训练和测试两个阶段组成。首先,在训练阶段,由训练样本通过降维得到训练样本的低维输出,力求能够快速并准确地检索出相关文本。其次,在测试阶段,LLE算法和深度自编码网络对于待检索的文本会通过不同的方式寻求低维投影。与图像识别不同的是:(1)我们是用余弦相似度代替LLE算法中的欧氏距离;(2)降维处理后,对于每个待检索的文本,我们利用汉明距离计算低维空间中它与其他所有测试文本的相似性并排序;(3)为了评估两种降维方法在文本检索任务上的性能,规定检索精度为正确检索的文本数(和被检索文本主题一致的文本数)与实际检索返回的总文本数的比值。
选取图 6中的20Newsgroups数据集,根据前人的研究[44],运行LLE算法和深度自编码网络降低文本向量维度,得到数值实验结果,对两种降维方法的文本检索性能进行比较分析。
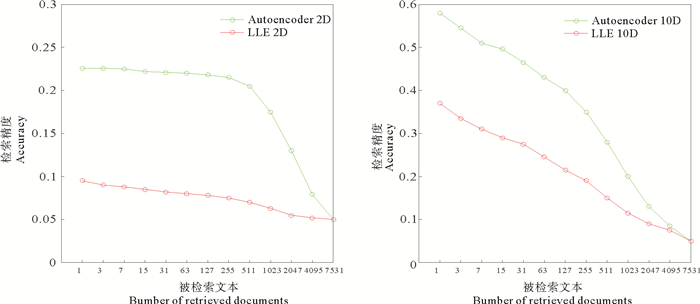
|
图 11 LLE算法和深度自编码网络在不同维度下的文本检索精度 Fig. 11 Accuracy curves of retrieved documents |
从以上的实验结果可以看出,降到2维的时候,深度自编码网络(2000-500-250-125-2)的检索精度要优于LLE算法(k=10)。进一步,保留更高维的特征比较二者的性能,我们发现,当文本向量降到10维的时候,LLE算法(k=25)检索文本的能力仍然不如深度自编码网络(2000-500-250-125-10)精确。
4 结论为了对比研究LLE算法和深度自编码网络的降维性能,本文采用定性与定量相结合的方法,对两种非线性降维方法进行了对比研究。我们看到,两种方法基于各自的降维理论都表现出优异的特征学习能力。在可视化实验中,LLE在手握杯子旋转数据集上的二维可视化效果优于深度自编码网络,而对于随机抽取的800幅手写数字图像,深度自编码网络降至二维后的数据相比于LLE,能更好地呈现出数字在各维度上的分布情况,故两种降维方法在不同数据集上的可视化效果各有千秋。在人脸识别实验中,二者的测试样本在ORL数据集上的识别表现不相上下。在文本检索实验中,我们发现LLE检索文本的能力不如深度自编码网络精确。另外,在识别和检索任务中,LLE没有给出重建测试样本的简单方法,故对于每个待测试的样本,都要在训练样本中寻找其近邻点。而对于深度自编码网络,一旦训练好网络结构,就可以将待测试的样本输入网络,进而完成测试。在参数选取方面,LLE的表现依赖于邻域参数k值的选择。而在深度自编码网络模型的训练过程中,网络层数,学习速率,训练周期以及批次训练的样本数的设置也同样对模型的表现有着非常重要的影响。故在实际的应用中,无论是LLE算法还是深度自编码网络,参数到底取多少合适,这是一个值得考虑的问题。
| [1] |
谭璐.高维数据的降维理论及应用[D].长沙: 国防科学技术大学, 2005. Tan L. Theory and Application of Dimension Reduction for High-Dimensional Data[D]. Changsha: National University of Defense Technology, 2005 (  0) 0) |
| [2] |
Roweis S T, Saul L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290(5500): 2323-2326. DOI:10.1126/science.290.5500.2323
(  0) 0) |
| [3] |
Hinton G E, Salakhutdinov R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504-507. DOI:10.1126/science.1127647
(  0) 0) |
| [4] |
Tenenbaum J B, Silva V D, Langford J C. A global geometric framework for nonlinear dimensionality reduction[J]. Science, 2001, 290(5500): 2319-2323.
(  0) 0) |
| [5] |
Belkin M, Niyogi P. Laplacian Eigenmaps for Dimensionality Reduction and Data Representation[M]. MIT Press, 2003: 1373-1396.
(  0) 0) |
| [6] |
Donoho D L, Grimes C. Hessian eigenmaps: Locally linear embedding techniques for high-dimensional data[J]. Proceedings of the National Academy of Sciences, 2003, 100(100): 5591-5596.
(  0) 0) |
| [7] |
Zhang Z, Zha H. Principal manifolds and nonlinear dimensionality reduction via tangent space alignment[J]. Society for Industrial and Applied Mathematics, 2005, 26(4): 406-424.
(  0) 0) |
| [8] |
Weinberger K Q, Saul L K. Unsupervised learning of image manifolds by semidefinite programming[J]. International Journal of Computer Vision, 2006, 70(1): 77-90. DOI:10.1007/s11263-005-4939-z
(  0) 0) |
| [9] |
Coifman R R, Lafon S. Diffusion maps[J]. Applied & Computational Harmonic Analysis, 2006, 21(1): 5-30.
(  0) 0) |
| [10] |
Nadler B, Lafon S, Coifman R R, et al. Diffusion maps, spectral clustering and reaction coordinates of dynamical systems[J]. Applied & Computational Harmonic Analysis, 2006, 21(1): 113-127.
(  0) 0) |
| [11] |
Lafon S, Lee A B. Diffusion maps and coarse-graining: A unified framework for dimensionality reduction, graph partitioning, and data set parameterization[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2006, 28(9): 1393-1403.
(  0) 0) |
| [12] |
Coifman R R, Kevrekidis I G, Lafon S, et al. Diffusion maps, reduction coordinates, and low dimensional representation of stochastic systems[J]. Siam Journal on Multiscale Modeling & Simulation, 2009, 7(2): 842-864.
(  0) 0) |
| [13] |
Laurens V D M, Hinton G. Visualizing Data using t-SNE[J]. Journal of Machine Learning Research, 2008, 9(2605): 2579-2605.
(  0) 0) |
| [14] |
侯澍旻, 李友荣, 刘光临. 局部线性嵌入算法及其在信号处理中的应用[J]. 仪器仪表学报, 2006, 27(s2): 1337-1339. Hou S M, Li Y R, Liu G L. Locally linear embedding algorithm and its application in signal processing[J]. Chinese Journal of Scientific Instrument, 2006, 27(s2): 1337-1339. (  0) 0) |
| [15] |
尹峻松.流形学习理论与方法研究及在人脸识别中的应用[D].长沙: 国防科学技术大学, 2007. Yin J S. Research on Theory and Method of Manifold Learning and Its Application in Face Recognition[D]. Changsha: National University of Defense Technology, 2007. (  0) 0) |
| [16] |
董安, 潘宏侠, 龚明. 基于局部线性嵌入算法的柴油机故障诊断研究[J]. 计算机工程与应用, 2013, 49(22): 236-240. Dong A, Pan H X, Gong M. Research on fault diagnosis of diesel engine Based on locally linear embedding algorithm[J]. Computer engineering and Application, 2013, 49(22): 236-240. DOI:10.3778/j.issn.1002-8331.1305-0011 (  0) 0) |
| [17] |
胡昭华, 宋耀良. 基于一种连续自编码网络的图像降维和重构[J]. 数据采集与处理, 2010, 25(3): 318-323. Hu S H, Song Y L. Dimensionality reduction and image reconstruction based on continuous autoencoder network[J]. Data Acquisition and Processing, 2010, 25(3): 318-323. DOI:10.3969/j.issn.1004-9037.2010.03.010 (  0) 0) |
| [18] |
石鑫, 朱永利, 宁晓光, 等. 基于深度自编码网络的电力变压器故障诊断[J]. 电力自动化设备, 2016, 36(5): 122-126. Shi X, Zhu Y L, Ning X G, et al. Transformer fault diagnosis based on deep auto-encoder network[J]. Electric Power Automation Equipment, 2016, 36(5): 122-126. (  0) 0) |
| [19] |
Han T, Goodenough D G. Nonlinear feature extraction of hyperspectral data based on locally linear embedding (LLE)[J]. IEEE International Geoscience & Remote Sensing Symposium, 2005, 2: 1237-1240.
(  0) 0) |
| [20] |
Chandar A P S, Lauly S, Larochelle H, et al. An autoencoder approach to learning bilingual word representations[J]. International Conference on Neural Information Processing Systems, 2014, 3: 1853-1861.
(  0) 0) |
| [21] |
Li J, Luong M T, Dan J. A hierarchical neural autoencoder for paragraphs and documents[EB/OL]. Computer Science, https://arxiv.org/abs/1506.01057, 2015.
(  0) 0) |
| [22] |
Liang Zhao, The Robotics Institute, Carnegie Mellon University.GMU Image Data: hand[EB/OL]. http://vasc.ri.cmu.edu/idb/html/motion/hand/index.html.
(  0) 0) |
| [23] |
Yann Le Cun, Corinna Cortes, Christopher J C Burges.THE-MNIST DATABASE of handwritten digits[EB/OL]. http://yann.lecun.com/exdb/mnist/.
(  0) 0) |
| [24] |
Speech Vision, Robotics Group.Cambridge University Engineering Department.The ORL Database of Faces[EB/OL]. http://am.ac.uk/research/dtg/attarchive/facedatabase.html.
(  0) 0) |
| [25] |
Ken Lang, Jason Rennie.The 20 Newsgroups data set[EB/OL]. http://www.qwone.com/~jason/20Newsgroups/.
(  0) 0) |
| [26] |
刘天桢. 高维数据可视化研究[M]. 武汉: 武汉理工大学, 2005.
(  0) 0) |
| [27] |
孙扬, 封孝生, 唐九阳, 肖卫东. 多维可视化技术综述[J]. 计算机科学, 2008, 35(11): 1-7. Yang Y, Feng X S, Tang J Y, Xiao W D. Overview of multidimensional visualization technology[J]. Computer Science, 2008, 35(11): 1-7. DOI:10.3969/j.issn.1002-137X.2008.11.001 (  0) 0) |
| [28] |
余肖生, 周宁. 高维数据降维方法研究[J]. 情报科学, 2007, 25(8): 1248-1251. Yu X S, Zhou N. Research on dimensionality reduction for high-dimensional data[J]. Intelligence Science, 2007, 25(8): 1248-1251. DOI:10.3969/j.issn.1007-7634.2007.08.029 (  0) 0) |
| [29] |
徐志节, 杨杰, 王猛. 利用非线性降维方法预测膜蛋白类型[J]. 上海交通大学学报, 2005, 39(2): 279-283. Xu Z J, Yang J, Wang M. Predict membrane protein types by nonlinear dimensionality reduction[J]. Journal of Shanghai Jiaotong University, 2005, 39(2): 279-283. DOI:10.3321/j.issn:1006-2467.2005.02.026 (  0) 0) |
| [30] |
何怀玉. LLE算法在地震属性参数降维中的应用[M]. 成都: 成都理工大学, 2006. He H Y. The Application of LLE Algorithm in Dimensionality Reduction of Seismic Attribute Parameters[M]. Chengdu: Chengdu University of Technology, 2006. (  0) 0) |
| [31] |
袁晓如, 郭翰琦, 肖何, 等. 高维数据可视化[J]. 中国计算机协会通讯, 2011, 7(4): 13-16. Yuan X R, Guo H Q, Xiao H, et al. The visualization of high-dimensional data[J]. China Computer Association Newsletter, 2011, 7(4): 13-16. (  0) 0) |
| [32] |
Berman G J, Choi D M, Bialek W, et al. Mapping the structure of drosophilid behavior[M]. Biorxiv, 2013. http://arxiv.org/abs.
(  0) 0) |
| [33] |
G Berman, D Choi, W Bialek, J Shaevitz. Discovery of stereotypy through behavioral space embedding[C]. Aps Meeting, 2013.
(  0) 0) |
| [34] |
闫娟, 程武山, 孙鑫. 人脸识别的技术研究与发展概况[J]. 电视技术, 2006(12): 81-84. Yan J, Cheng W S, Sun X. Research and development of face recognition[J]. Television Technology, 2006(12): 81-84. DOI:10.3969/j.issn.1002-8692.2006.12.025 (  0) 0) |
| [35] |
贾川. 浅谈人脸识别技术应用及发展趋势[J]. 中国安防, 2010(3): 83-86. Jia C. Application and development trend of face recognition[J]. China Security, 2010(3): 83-86. DOI:10.3969/j.issn.1673-7873.2010.03.028 (  0) 0) |
| [36] |
Srivastava N, Hinton G, Krizhevsky A, et al. Dropout: A simple way to prevent neural networks from overfitting[J]. Journal of Machine Learning Research, 2014, 15(1): 1929-1958.
(  0) 0) |
| [37] |
袁飞, 王成良, 文俊浩. 一种融合文本重要性的文本检索算法[J]. 计算机工程与应用, 2014, 50(3): 93-96. Yuan F, Wang C L, Wen J H. A text retrieval algorithm integrating text importance[J]. Computer engineering and Application, 2014, 50(3): 93-96. DOI:10.3778/j.issn.1002-8331.1203-0460 (  0) 0) |
| [38] |
Salton G, Wong A, Yang C S. A vector space model for automatic indexing[J]. Communications of the Acm, 1975, 18(11): 613-620. DOI:10.1145/361219.361220
(  0) 0) |
| [39] |
Dumais S T, Furnas G W, Landauer T K, Deerwester S, Harshman R. Using latent semantic analysis to improve access to textual information[J]. Sigchi Conference on Human Factors in Computing Systems, 1988, 281-285.
(  0) 0) |
| [40] |
Cao Y, Xu J, Liu T Y, et al. Adapting Ranking SVM to Document Retrieval[M]. Sigir: International Acm Sigir Conference on Research & Development in Information Retrieval, 2006: 186-193.
(  0) 0) |
| [41] |
李媛媛.基于潜在语义索引的中文文本检索研究[D].成都: 西南交通大学, 2008. Li Y Y. Research on Chinese Text Retrieval Based on Latent Semantic Indexing[D]. Chengdu: Southwest Jiaotong University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10613-2008179161.htm (  0) 0) |
| [42] |
潘炜深. 基于深度学习的手写英文单词检索算法研究及其在历史文本上的应用[M]. 广州: 华南理工大学, 2006. Pan W S. Retrieval Algorithm for Handwritten English Words Based Deep Learning and Its Application in Historical Texts[M]. Guangzhou: South China University of Technology, 2006. (  0) 0) |
| [43] |
高仕龙. 基于奇异值分解的英文文本检索算法[J]. 计算机工程, 2011, 37(1): 78-80. Gao S L. English text retrieval algorithm based on singular value decomposition[J]. Computer Engineering, 2011, 37(1): 78-80. DOI:10.3969/j.issn.1000-3428.2011.01.027 (  0) 0) |
| [44] |
Hinton G E, Salakhutdinov R R. Supporting online material for "reducing the dimensionality of data with neural networks"[J]. Science, 2006, 313(5786): 504-507. DOI:10.1126/science.1127647
(  0) 0) |
 2018, Vol. 48
2018, Vol. 48


