2. 山东省海洋工程重点实验室,山东 青岛 266100;
3. 中国交通建设股份有限公司 交第二航务工程局有限公司,湖北 武汉 430000
起重船是港口装卸的重要设备,在海上安装运维、桥梁建筑、打捞作业、资源探测和深海钻井等海洋工程领域有着重要地位[1-2]。海上作业受风、浪和流等环境载荷作用,船舶产生六自由度运动,吊物会随着吊臂悬吊点运动而发生摆动,进而增加海上作业危险系数,并影响吊装作业效率。在中国交建中马友谊大桥施工期间,当波浪周期在8~12 s,有义波高大于0.8 m时,起重船空钩状态下吊钩的摆动幅度最高可达16 m[3]。因此,分析波浪作用下起重船-吊物系统耦合运动响应并提出吊物减摆方法,对于保障起重船海上吊装作业的安全及效率具有重要意义。
在对船舶-吊物系统进行耦合动力学分析时,通常将船体对吊物的作用简化为吊点对吊物系统的激励,通过船舶六自由度运动方程估算吊点运动,再将其作为激励用于分析吊物的运动。Masoud等[4]建立了刚性无质量吊索与吊物组成的吊装系统模型,并研究了吊臂的回转和变幅运动对吊物摆振影响; Coric等[5]和任会礼等[6]将吊臂升沉作为激励,推导吊物三自由度摆振方程,得到了其运动响应; Lee[7]研究了吊物抬升过程中重心和起重船压载水变化对系统运动响应的影响; 张梁娟等[8]和Idres等[9]建立了八自由度起重船-吊物耦合模型,得到了不同条件下系统的运动响应; 杨晓蓉等[10]和Witz[11]建立了不规则波条件下起重船-吊物耦合运动方程; Cha等[12]建立了六自由度起重船运动方程和五自由度吊物运动方程,分析了不同波浪条件对起重船-吊物系统的影响。
此外,一些学者和科研单位对波浪补偿问题进行了深入研究。孙友刚等[13]提出了一种主动式波浪补偿系统,抑制了波浪对起重船海上作业的动态影响; 孙泳涛[14]提出了补偿技术的工作原理,研制了带有主动波浪补偿功能的30 t起重机。Nam等[15]基于起重船-吊物耦合动力学模型,分析了被动升沉减摇装置对水下作业系统安装作业的影响。文献[16]通过实时测量船舶运动信息以控制六个液压缸的伸缩,实现对船舶浪致运动进行主动补偿,用于解决货物和人员的海上转移问题。荷兰Barge Master公司设计生产了BM-T40三自由度主动式波浪补偿起重机,通过底部的三自由度补偿装置和基座升沉补偿装置可补偿横摇、纵摇和垂荡三自由度运动[17]。Tong等[18]分析了浮式起重机的升沉补偿原理,并将升沉补偿装置与浮式起重机的升降系统集成,为浮式起重机在深海作业提供了一种解决方案。起重船-吊物系统在风、浪和流等环境载荷的影响下会发生摆振,影响作业效率与吊装定位精度,因此研究起重船-吊物在海洋环境载荷作用下的运动响应和吊物减摆方法对于提高海上作业的安全性和效率具有重要意义。
由于“新振浮7”起重船具备起重、运输和打捞等功能,可用于海上电场风机运输和海上升压活模块吊装任务,因此本文以该型号起重船吊装作业为研究背景,建立带有补偿装置的起重船-吊物耦合动力学模型,对机械系统动力学自动分析(Automatic dynamic analysis of mechanical systems, ADAMS)软件进行二次开发,实现海洋载荷仿真,研究波浪环境下起重船-吊物系统耦合运动响应特性,开展有无补偿机构起重船-吊物耦合运动响应分析,研究波浪条件对吊物摆动响应幅值的影响。
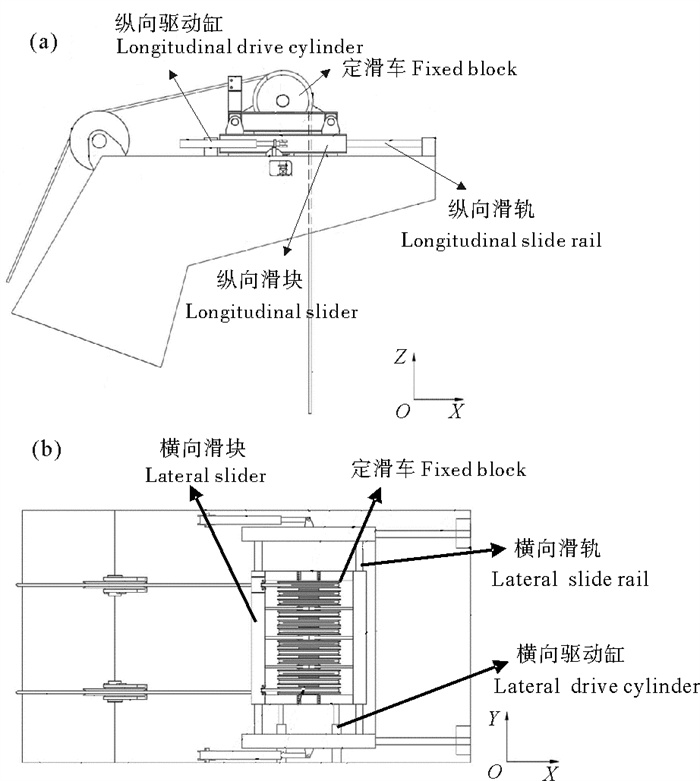
1 起重船吊物系统运动补偿装置图 1所示为起重船吊物系统运动补偿装置简图[19],该装置由横移机构、纵移机构和定滑车组成。其中横移机构由横向滑轨、横向滑块和横向驱动缸组成; 纵移机构由纵向滑轨、纵向滑块和纵向驱动缸组成; 定滑车固定在横向滑块上,其上设置有定滑轮,吊索绕过定滑轮与吊钩连接。横向滑块在横向驱动缸的作用下沿横向导轨移动,纵向滑块在纵向驱动缸的作用下沿纵向导轨移动,从而带动定滑车、定滑轮及吊索横向+纵向移动,通过横移机构和纵移机构可以实时调整定滑车位置,形成横向和纵向双向阻尼调节吊钩摆幅,实现吊装作业过程的抑摆。
|
( ((a)运动补偿装置主视图Front view of motion compensation device; (b)运动补偿装置俯视图Top view of motion compensation device.) ) 图 1 运动补偿装置简图 Fig. 1 Motion compensation device diagram |
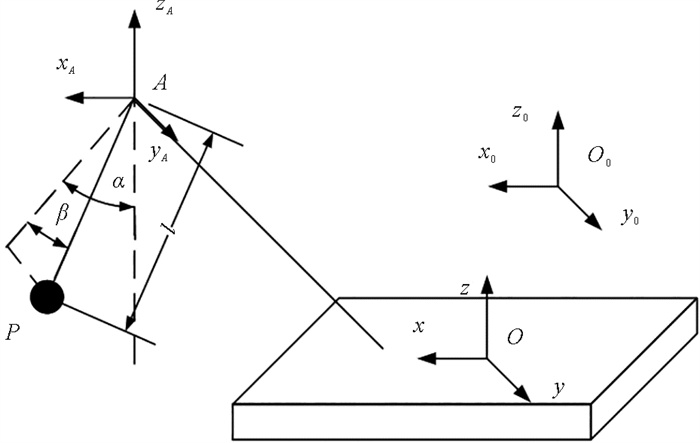
设O为船体中心,A为吊点,P为吊物质心,建立如图 2所示的起重船-吊物系统坐标系。其中O0-x0y0z0为惯性坐标系,用来描述船体在坐标轴方向上的位移,在初始时刻的船体中心,x0轴指向船首,y0轴指向左舷方向,z0轴垂直甲板向上。O-xyz为船体固定坐标系,坐标系方向与惯性系相同,初始时刻惯性与船体坐标系重合,当船体运动时,船体坐标系与船体运动保持一致。A-xAyAzA为吊点坐标系,吊物的摆动可用面内角α和面外角β描述。
|
图 2 起重船-吊物系统坐标系 Fig. 2 Coordinate system of float crane-lifting load system |
在建立船舶运动模型时,将船舶视为单一刚体; 然后根据船体在波浪中的运动响应得到吊点的运动响应,继而将吊点响应作为激励,建立吊物运动方程。设吊索悬垂段长度为l,则吊物在O0-x0y0z0坐标系中的坐标值为:
| $ \left\{\begin{array}{l} x_{P_0}=x_{A_0}+l \cos \alpha \\ y_{P_0}=y_{A_0}+l \sin \alpha \cos \beta \\ z_{P_0}=z_{A_0}-l \sin \alpha \sin \beta \end{array} 。\right. $ | (1) |
进而,可以得到吊物的动力学方程为:
| $ \left\{\begin{array}{l} m_P \ddot{x}_{P_0}=-T \cos \alpha \\ m_P \ddot{y}_{P_0}=-T \sin \alpha \cos \beta \\ m_P \ddot{z}_{P_0}=T \sin \alpha \cos \beta-m_P g \end{array} 。\right. $ | (2) |
式中:xP0、yP0、zP0分别为吊物质心在O坐标系中x、y、z方向的坐标值; xA0、yA0、zA0分别为吊点坐标中x、y、z方向的坐标值; T为吊索张力; mP为吊物质量。
结合式(1)和(2)可以计算吊索的张力,进而可得到张力对船体作用的各个分量。
船舶在海洋环境中所受到的外干扰力和力矩主要是由风、浪和流等组成,根据船舶耐波性模型,吊装作业时起重船-吊物耦合动力学方程可表示为:
| $ \left(\boldsymbol{M}+\boldsymbol{M}_A\right) \ddot{\boldsymbol{\eta}}+(\boldsymbol{C}+\boldsymbol{D}) \dot{\boldsymbol{\eta}}+\boldsymbol{G} \boldsymbol{\eta}=\boldsymbol{\tau}_\eta $ | (3) |
式中:M为起重船-吊物耦合系统质量矩阵; MA为起重船附加质量矩阵; η=x, y, z, φ, θ, ψ, α, β为位移矩阵; C为科氏力矩阵; D为阻尼矩阵; G为刚度矩阵; τη为外力矩阵。
2.2 载荷计算方法在计算船体水动力时,应用切片理论对船体水动力学系数进行估算[20-22],将船体沿艏向分为若干薄型切片,用二维绕流对每一薄片的参数进行计算,最后对船体纵向积分,得到附加质量各分量:
| $ \left\{\begin{array}{l} -X_{\dot{\mathrm{u}}}=\int_{-L / 2}^{L / 2} A_{11}^{(2 D)}(y, z) \mathrm{d} x \approx 0.05 m \\ -Y_{\dot{\mathrm{v}}}=\int_{-L / 2}^{L / 2} A_{22}^{(2 D)}(y, z) \mathrm{d} x= \\ \ \ \ \ \ \ \frac{1}{2} \int_{-L / 2}^{L / 2} \rho \pi D^2(x) \mathrm{d} x=\frac{1}{2} \rho \pi d^2 L \\ -Z_{\dot{\mathrm{w}}}=\int_{-L / 2}^{L / 2} A_{33}^{(2 D)}(y, z) \mathrm{d} x= \\ \ \ \ \ \ \ \int_{-L / 2}^{L / 2} \frac{1}{4} \rho \pi B^2 \mathrm{~d} x=\frac{\pi}{4} \rho B^2 L \\ -K_{\dot{\mathrm{p}}}=\int_{-L / 2}^{L / 2} A_{44}^{(2 D)}(y, z) \mathrm{d} x= \\ \ \ \ \ \ \ \int_{-L / 2}^{L / 2} \frac{1}{8} \rho \pi\left(\frac{1}{4} B^2-\frac{1}{4} H^2\right) \mathrm{d} x= \\ \ \ \ \ \ \ \frac{1}{32} \pi \rho\left(B^2-H^2\right) L \\ -M_{\dot{\mathrm{q}}}=\int_{-L / 2}^{L / 2} A_{55}^{(2 D)}(y, z) \mathrm{d} x= \\ \ \ \ \ \ \ \int_{-L / 2}^{L / 2} x^2 A_{33}^{(2 D)}(y, z) \mathrm{d} x+\int_{-H / 2}^{H / 2} z^2 A_{11}^{(2 D)}(x, y) \mathrm{d} z \approx \\ \ \ \ \ \ \ \frac{1}{48} \rho \pi B^2 L^3+\frac{1}{120} \frac{m L H^3}{B} \\ -N_{\dot{\mathrm{r}}}=\int_{-L / 2}^{L / 2} A_{66}^{(2 D)}(y, z) \mathrm{d} x= \\ \ \ \ \ \ \ \frac{1}{2} \int_{-B / 2}^{B / 2} y^2 \frac{0.1 m}{B} \mathrm{~d} y+\frac{1}{2} \int_{-L / 2}^{L / 2} x^2 \rho \pi d^2(x) \mathrm{d} x= \\ \ \ \ \ \ \ \frac{1}{24}\left(0.1 m B^2+\rho \pi d^2 L^3\right) \end{array}\right. $ | (4) |
式中:
起重船在横荡和艏摇下的二维线性阻尼是无限水深条件下圆柱(起重船近似)半径和波浪圆频率的函数,船舶在横荡和艏摇方向的阻尼Yv和Nr分别为:
| $ \left\{\begin{array}{l} -Y_{\mathrm{v}}=\frac{1}{2} \int_{-L / 2}^{L / 2} B_{22}^{(2 D)}(y, z) \mathrm{d} x=0.4 \sqrt{\frac{g}{R}} \rho A L \\ -N_{\mathrm{r}}=\frac{1}{2} \int_{-L / 2}^{L / 2} x^2 B_{22}^{(2 D)}(y, z) \mathrm{d} x=\frac{L^3}{30} \sqrt{\frac{g}{R}} \rho A \end{array} 。\right. $ | (5) |
式中:Yv为横荡方向的阻尼力; Nr为艏摇方向的阻尼力; B22为二维阻尼系数; g为重力加速度; R为无限水深条件下起重船近似圆柱半径。
除阻尼力以外,起重船还受到由重力和浮力引起的恢复力作用,恢复力主要影响起重船的横摇、纵摇和垂荡,船体关于体坐标系xz平面和yz平面对称[22],具体各项系数计算如下:
| $ \left\{\begin{array}{l} Z_z=-\rho g A_{\omega \mathrm{p}} \\ K_{\varphi}=-\rho g V_{\mathrm{D}}\left(z_B-z_G\right)+\rho g \iint_{A_{\omega \mathrm{p}}} y^2 \mathrm{~d} A \triangleq-\rho g \Delta \overline{G M}_{\mathrm{T}} \\ M_\theta=-\rho g V_{\mathrm{D}}\left(z_B-z_G\right)+\rho g \iint_{A_{\omega \mathrm{p}}} x^2 \mathrm{~d} A \triangleq-\rho g \Delta \overline{G M}_{\mathrm{L}}\ \end{array}。\right. $ | (6) |
式中:Zz为垂荡方向恢复力; Kφ为横摇方向恢复力; Mθ为纵摇方向恢复力; g为重力加速度; Aωp为吃水面面积; VD为排水量; GMT和GML分别为横向和纵向稳心高度。
波浪激励力是导致船体产生受迫运动的重要扰动作用力,其与波浪中的水体运动有关。根据弗劳德-克雷诺夫假设[23]“舰船在受到规则波激励时,船身存在不影响波浪自身的动压力分布”得到波浪激励力各分量如下:
| $ \left\{\begin{array}{l} F_x=2 \rho g a \frac{\sin (k B \cos \varphi / 2)}{k B \sin \varphi / 2} \mathrm{e}^{-k d} B d \sin (k L \sin \varphi / 2) \sin \left(\omega_{\mathrm{e}} \mathrm{t}\right) \\ F_y=-2 \rho g a \frac{\sin (k L \cos \varphi / 2)}{k B \cos \varphi / 2} \mathrm{e}^{-k d} L d \sin (k B \sin \varphi / 2) \sin \left(\omega_{\mathrm{e}} t\right) \\ F_z=\rho g a k \frac{\sin (k B \sin \varphi / 2)}{k B \sin \varphi / 2} \mathrm{e}^{-k d} B d L \frac{\sin (k L \cos \varphi / 2)}{k L \cos \varphi / 2} \cos \left(\omega_{\mathrm{e}} t\right) \\ M_x=\rho g a \frac{\sin (k B \sin \varphi / 2)}{k B \sin \varphi / 2} \mathrm{e}^{-k d} \sin \varphi \cdot \\ \quad \frac{d^2 \sin \varphi \sin (k L \cos \varphi / 2)}{\cos \varphi} \sin \left(\omega_{\mathrm{e}} t\right) \\ M_y=\rho g a \frac{\sin (k B \sin \varphi / 2)}{k B \sin \varphi / 2} \mathrm{e}^{-k d} d \cdot \\ \quad \frac{2 \sin (k L \cos \varphi / 2)-k L \cos \varphi \cos (k L \cos \varphi / 2)}{k^2 \cos ^2 \varphi} \sin \left(\omega_{\mathrm{e}} t\right) \\ M_z=\rho g a \frac{\sin (k B \sin \varphi / 2)}{k B \sin \varphi / 2} \mathrm{e}^{-k d} d \sin \varphi \\ \frac{2 \sin (k L \cos \varphi / 2)-k L \cos ^2 \cos (k L \cos \varphi / 2)}{k^2 \cos ^2 \varphi} \cos \left(\omega_{\mathrm{e}} t\right)。\ \end{array}\right. $ | (7) |
式中:Fx为纵荡方向波浪力; Fy为横荡方向波浪力; Fz为垂荡方向波浪力; Mx为横摇方向波浪力; My为纵摇方向波浪力; Mz为艏摇方向波浪力; a为波幅; k为波数; φ为遭遇浪向角; ωe为遭遇频率。
锚泊系统可以限制起重船的水平运动,能够为起重船横纵荡和艏摇方向提供非线性恢复力和力矩,其非线性恢复力可以通过三次多项式来模拟,考虑到恢复力由系泊缆的弹性变形提供,可得锚泊力[24]Fmoor计算式:
| $ F_{\text {moor }}=\left[\begin{array}{c} -C_1 x-C_2 x^2 \operatorname{sgn}(x)-C_3 x^3 \\ -C_1 y-C_2 y^2 \operatorname{sgn}(y)-C_3 y^3 \\ 0 \\ 0 \\ 0 \\ -C_1 \psi-C_2 \psi^2 \operatorname{sgn}(\psi)-C_3 \psi^3 \end{array}\right] 。$ | (8) |
式中:C1、C2、C3分别为系泊系统的一次、二次和三次恢复力系数; x为起重船纵荡位移; y为起重船横荡位移; ψ为起重船艏摇转角。
船体所受风载荷可以应用模块法进行计算[25],先计算船体分段所受风载荷,通过叠加得到总载荷。当船舶航速为0时,风载荷Fwind通过以下经验公式估算:
| $ F_{\text {wind }}=\frac{1}{2} \rho_{\mathrm{a}} V_{\mathrm{w}}^2\left[\begin{array}{c} C_x\left(\gamma_{\mathrm{w}}\right) A_{\mathrm{Fw}} \\ C_y\left(\gamma_{\mathrm{w}}\right) A_{\mathrm{Lw}} \\ C_{\mathrm{z}}\left(\gamma_{\mathrm{w}}\right) A_{\mathrm{Fw}} \\ C_k\left(\gamma_{\mathrm{w}}\right) A_{\mathrm{Lw}} H_{\mathrm{Lw}} \\ C_m\left(\gamma_{\mathrm{w}}\right) A_{\mathrm{Fw}} H_{\mathrm{Fw}} \\ C_n\left(\gamma_{\mathrm{w}}\right) A_{\mathrm{Lw}} L \end{array}\right] \text { 。} $ | (9) |
式中:ρa为空气密度; Vw为风速; γw为船头与相对风速的角度; AFw和ALw分别为船体水线以上纵向和横向投影面积; HFw为水平方向上形心与重心间距; HLw为水平方向上形心与重心间距; Cx、Cy和Cz分别为纵荡、横荡和垂荡方向上的流体黏性阻尼系数; Ck、Cm、Cn分别为横摇、纵摇和艏摇方向的流体力矩系数。流载荷可以通过与风载荷类似的方法得到。
2.3 补偿装置控制方案通过对方程(3)求解,可得到起重船-吊物系统的动态响应,根据坐标关系,可得到吊点在惯性坐标系下的坐标值为:
| $ \left[\begin{array}{l} x\ _{\mathrm{A} 0} \\ y\ _{\mathrm{A} 0} \\ z\ _{\mathrm{A} 0} \end{array}\right]=\left[\begin{array}{l} x\ _0 \\ y\ _0 \\ z\ _0 \end{array}\right]+\left[\begin{array}{ccc} 1 & -\psi & \theta \\ \psi & 1 & -\varphi \\ -\theta & \varphi & 1 \end{array}\right]\left[\begin{array}{l} x\ _{\mathrm{A}} \\ y\ _{\mathrm{A}} \\ z\ _{\mathrm{A}} \end{array}\right] 。$ | (10) |
将时域计算过程中每个时间步的吊点坐标变化量反馈给控制器,根据吊点位置的变化量控制横移机构和纵移机构双向运动,从而抑制吊物的摆动,主动转轮收放吊索以补偿吊物的垂荡位移。
3 起重船-吊物系统耦合运动响应分析方法 3.1 起重船计算模型本文以“新振浮7”起重船吊装作业为研究对象,基于上述船舶六自由度运动方程,采用ADAMS软件对起重船-吊物的耦合运动响应进行数值模拟。该起重船参数如表 1所示。
|
|
表 1 起重船和吊物参数 Table 1 Parameters of crane ship |
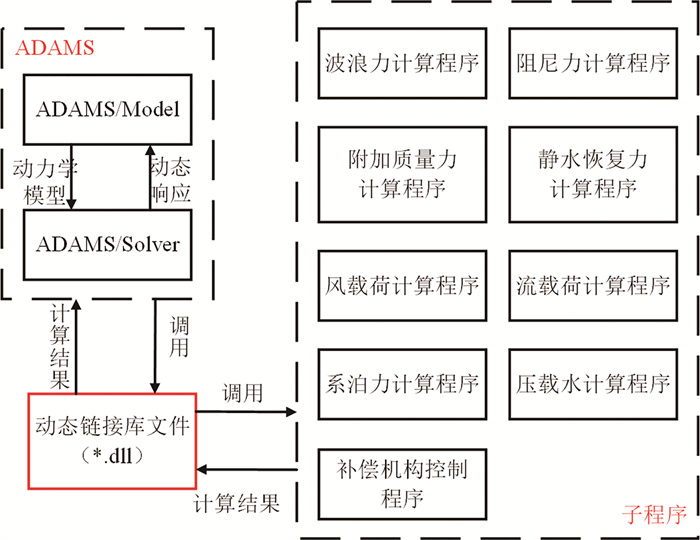
目前AQWA和OrcaFlex等商业软件在建模过程中将浮体视为单体系统,难以实现对带有补偿装置的起重船-吊物多体系统建模仿真。因此,本文为了更准确分析起重船-吊物耦合运动响应,本文考虑吊装过程中船体所受的环境载荷,对ADAMS软件对进行二次开发,基于起重船六自由度运动方程编写ADAMS子程序,再编译为动态链接库文件(DLL)供ADAMS计算调用,实现在ADAMS中计算船舶附加质量力、阻尼力、静水恢复力、波浪力、风载荷和流载荷等功能。采用预估-校正算法进行求解,在仿真的每个时间步,DLL文件将被调用,如图 3所示。
|
图 3 起重船-吊物耦合运动响应计算流程 Fig. 3 Calculation process of coupled motion response of float crane-lifting load system |
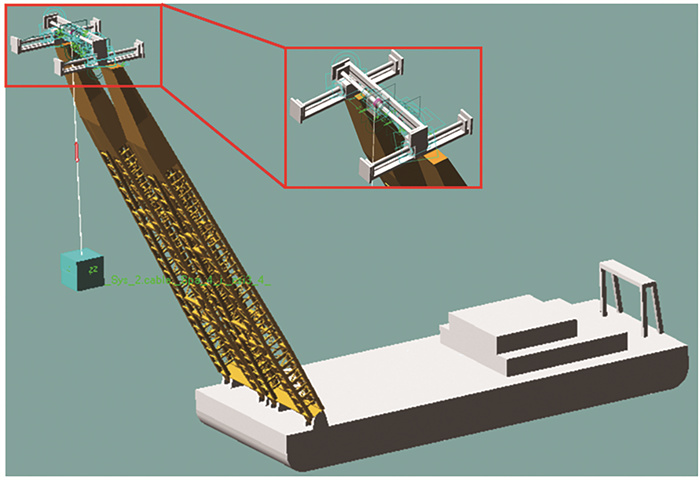
基于上述子程序对带有补偿机构的起重船-吊物耦合系统进行多体动力学分析,通过添加运动约束建立起重船吊装作业动力模型,以真实模拟在海洋环境下起重船与吊物的动态响应,如图 4所示。在建模过程中认为船体与吊臂是一个刚体系统,采用ADAMS的六维力模型(GFORCE)模拟海洋环境载荷。将GFORCE计算模式设置为子程序(Subroutine),在每个时间步内,ADAMS将船体和吊物的位移、速度和加速度等计算结果传递给DLL文件,同时DLL文件将环境载荷计算结果返回给ADAMS,从而实现外部环境载荷计算程序与ADAMS的耦合计算。
|
图 4 具有运动补偿的起重船-吊物动力学模型 Fig. 4 Dynamic model of float crane-lifting load with motion compensation |
运动补偿装置设有纵移机构和横移机构,可以双向驱动定滑车移动,从而改变在滑轮的位置,实现对吊物的运动补偿。为了模拟滑轮组功能,使用Cable模块建立吊索连接吊臂与吊物。使用该模块建立滑轮组时,需先在船体和吊物上分别设置锚点固定吊索,然后将滑轮设置在定滑车上,最后输入吊索弹性模量、直径和阻尼比等参数(见表 2)建立滑轮组模型。由于纵移机构和横移机构运动模式为横向和纵向移动,因此可在定滑车与纵移滑轨之间设置移动副(Translation joint)模拟纵移机构,同样在定滑车与横移滑轨之间设置移动副模拟横移机构。
|
|
表 2 吊索参数 Table 2 Parameters of sling |
采用水动力软件AQWA对不带有运动补偿装置的起重船建立仿真模型,并进行水动力计算, 在建模过程对起重船进行简化,如图 5所示。计算条件:3级海况(波幅1.25 m,波浪周期10 s); 浪向角90°; 仿真步长0.1 s。

|
图 5 起重船计算模型面元网格划分 Fig. 5 Panel mesh generation of crane ship calculation model |
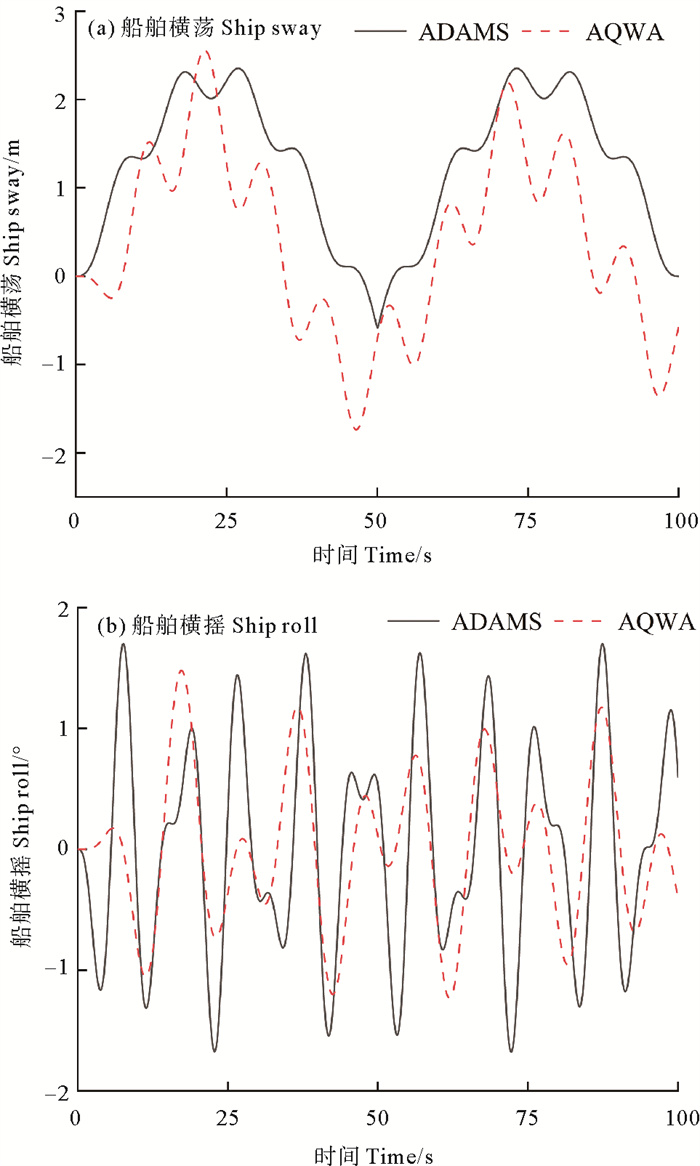
当船舶遭遇浪向角为90°时,波浪前进方向与船舶x轴惯性主轴重合,其主要运动集中在横荡和横摇上,因此将AQWA横荡和横摇计算结果和动力学计算结果对比,如图 6所示,在规则波条件下起重船运动响应计算结果吻合较好,趋势整体一致,说明海洋载荷外部计算程序能够较好的模拟环境载荷对系统响应的影响。
|
图 6 起重船运动响应 Fig. 6 Crane ship motion response |
采用本文“3起重船-吊物系统耦合运动响应分析方法”计算起重船及吊物在规则波下的运动响应,对不同的波浪条件下补偿装置的有效性进行分析。根据Vaughers[26]研究结果,当海浪等级超过3级(根据Pierson-Moskowitz海浪谱的定义,有效波高范围为1.066 8~1.524 m)时,应停止作业。因此,为了确定运动补偿装置对提高作业窗口的有效性,本文对带有补偿机构的起重船-吊物系统进行了4级和5级海况条件下的仿真计算。
4.1 5级海况下起重船-吊物耦合系统动力学仿真在波浪激励作用下,船体运动会引起吊索的受迫运动。计算条件:吊物质量为1 000 t,吊索悬垂段长度为80 m,吊物摆动频率为0.056 Hz; 吊臂倾角为64°; 5级海况对应的波幅、波浪周期和波长分别3 m、9.7 s、147 m; 横浪条件:浪向角为90°; 仿真时间步为0.1 s。
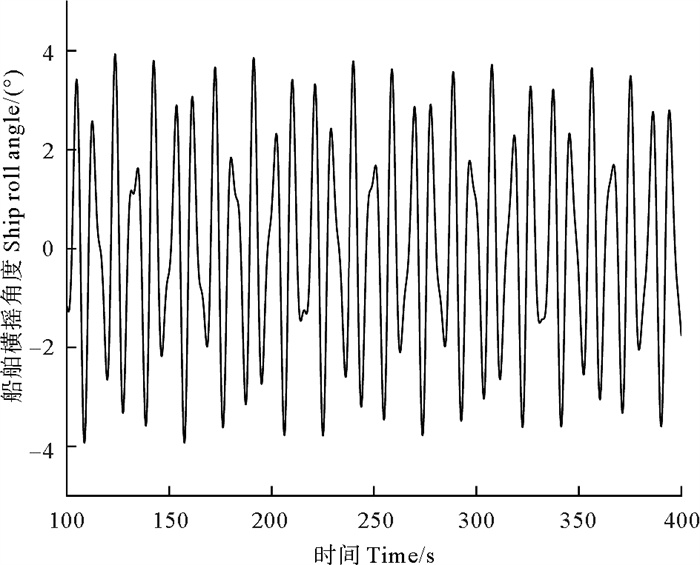
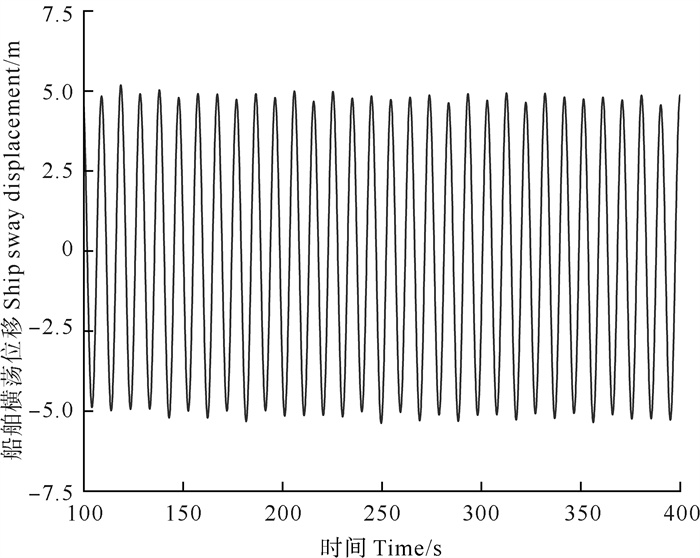
图 7、8分别为5级海况下船体稳定运动的横摇和横荡曲线,仿真起始时起重船运动不稳定,经过一段时间后其运动趋于稳定。5级海况下船体的最大横摇角度为3.93°,最大横荡位移为5.12 m。
|
图 7 5级海况下船舶横摇角度 Fig. 7 Ship roll angle under level 5 sea state |
|
图 8 5级海况下船舶横荡位移 Fig. 8 Ship sway displacement under level 5 sea state |
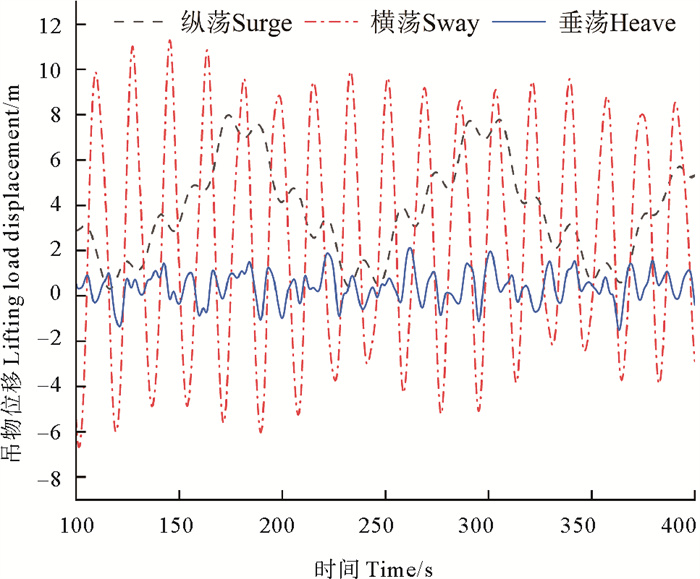
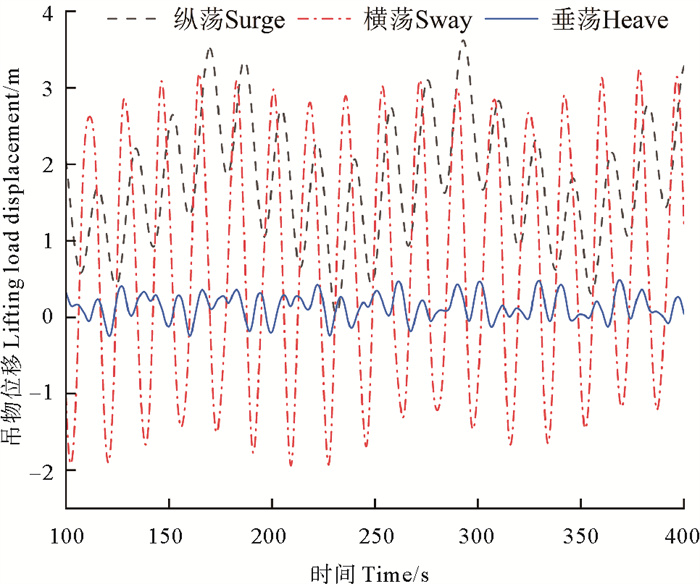
在风、浪和流等环境载荷作用下,起重船-吊物多体系统存在六个自由度运动,即纵荡、横荡、垂荡、纵摇、横摇和艏摇。考虑到吊点仅有纵荡、横荡和垂荡三个方向的位移,且运动补偿装置能够对该三个方向运动进行补偿,因此在5级海况下船舶在遭遇横浪时,分别给出不带有补偿装置和带有补偿装的吊物相对于初始位置的运动响应,如图 9、10所示。从图中可以看出: 在无运动补偿时,吊物最大纵荡位移为8.15 m,最大横荡位移为11.30 m,最大垂荡位移为2.12 m; 在有运动补偿时,吊物最大纵荡位移为3.62 m,最大横荡位移为3.37 m,最大垂荡位移为0.52 m。对比两次计算数据可知,补偿机构的补偿率最少为65%,可以认为补偿装置构起到了较好的补偿作用。
|
图 9 5级海况下无补偿装置的吊物位移 Fig. 9 Lifting load displacement without compensation device under level 5 sea state |
|
图 10 5级海况下有补偿机构的吊物位移 Fig. 10 Lifting load displacement with compensation device under level 5 sea state |
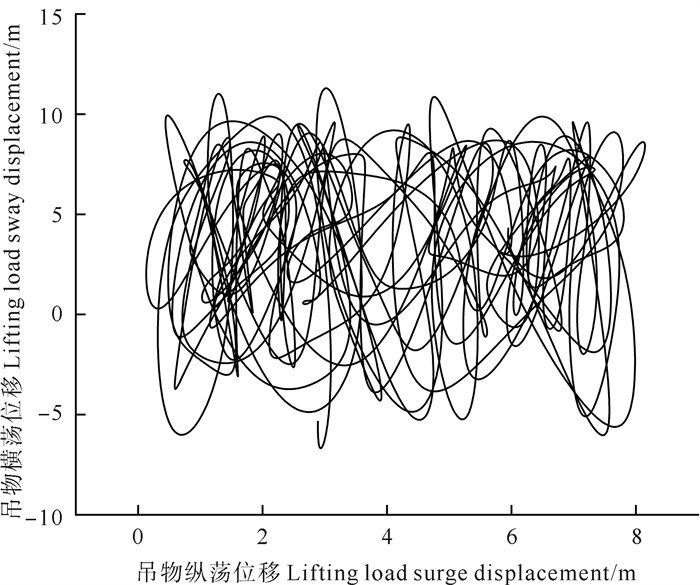
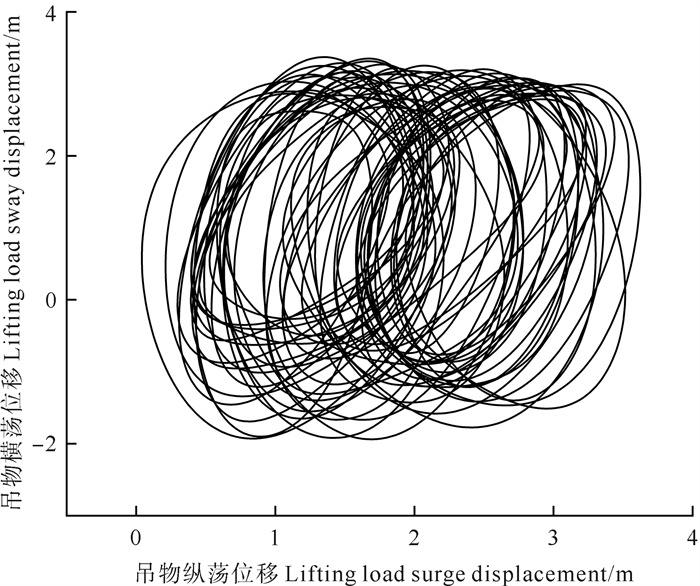
图 11、12分别为5级海况下无、有补偿机构吊物相对于初始位置在水平面上的投影:在无运动补偿时吊物在空间中倾向于无规则运动; 在进行运动补偿时吊物在空间中倾向于规则运动,运动轨迹显示为交替椭圆运动。
|
图 11 5级海况下无补偿机构吊物相对位移 Fig. 11 Lifting load relative displacement without compensation device under level 5 sea state |
|
图 12 5级海况下有补偿机构吊点相对位移 Fig. 12 Lifting load relative displacement with compensation device under level 5 sea state |
从图 7—12可知,由于存在系泊力等非线性载荷,即使在规则波激励下,起重船和吊物运动并非是简谐运动。在吊点设置补偿装置可有效抑制吊物摆振,并保持吊点稳定。
4.2 4级海况下起重船-吊物耦合系统动力学仿真为进一步分析波浪条件对起重船-吊物耦合系统动态响应,采用相同的方法对4级海况(波高2 m,波浪周期8.8 s,波长121 m)下起重船和吊物运动进行动力学仿真。
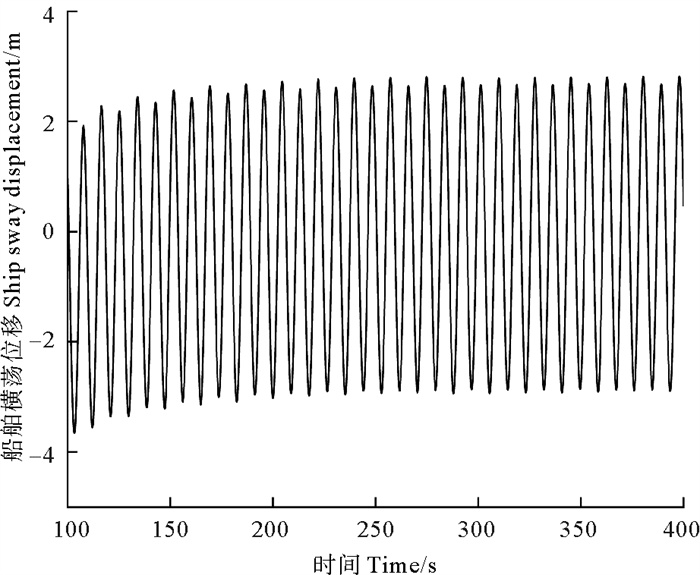
图 13、14分别为4级海况下船体稳定运动的横摇和横荡曲线。4级海况下船体的最大横摇角度为2.02°,最大横荡位移为2.82 m。
|
图 13 4级海况下船舶的横荡位移 Fig. 13 Ship sway displacement under level 4 sea state |

|
图 14 4级海况下船舶的横摇角度 Fig. 14 Ship roll angle under level 4 sea state |
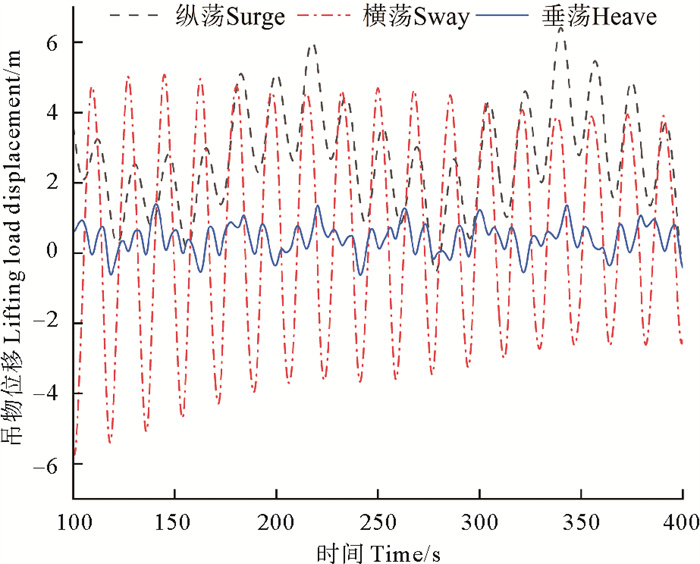
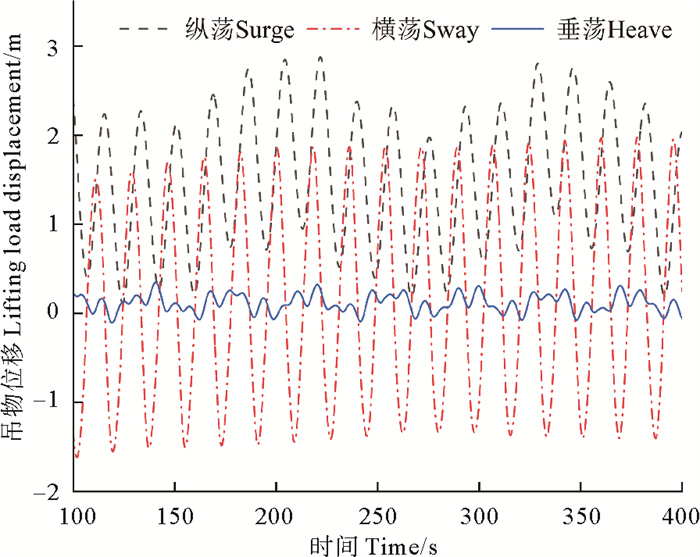
图 15、16分别为4级海况下船舶在遭遇横浪时,不带有补偿装置和带有补偿装置的吊物相对于初始位置的运动响应。可以看出:在无运动补偿时,吊物最大纵荡位移为6.53 m,最大横荡位移为5.08 m,最大垂荡位移为1.39 m; 在有运动补偿时,吊物最大纵荡位移为3.00 m,最大横荡位移为1.98 m,最大垂荡位移为0.35 m。对比两次计算数据可知,补偿机构的补偿率最少为55%。
|
图 15 4级海况下无补偿机构吊物位移 Fig. 15 Lifting load displacement without compensation device under level 4 sea state |
|
图 16 4级海况下有补偿机构吊物位移 Fig. 16 Lifting load displacement with compensation device under level 4 sea state |
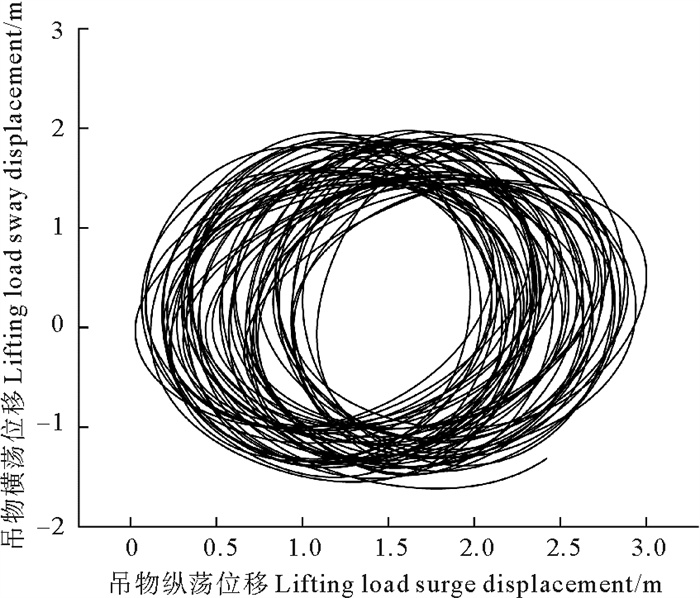
图 17、18分别为4级海况下无、有补偿机构的吊物相对于初始位置在水平面上的投影。可以发现在4级海况下,吊物空间运动轨迹呈现出与5级海况下不同的状态。

|
图 17 4级海况下无补偿机构吊物相对位移 Fig. 17 Lifting load relative displacement without compensation device under level 4 sea state |
|
图 18 4级海况下有补偿机构吊物相对位移 Fig. 18 Lifting load relative displacement with compensation device under level 4 sea state |
从本节仿真计算结果可以看出: 海况条件越差,船舶受波浪作用运动响应越大; 船载起重机随船运动会导致吊物发生一定频率和幅值的摆动,同时吊物摆振还受到风载荷影响。说明吊物的摆振是波浪诱导船体运动响应、船载起重机随船运动和风载荷共同作用下的结果,即使船体在横浪作用下,吊物也存在多种运动轨迹。吊物摆动固有频率同吊索长度相关,当吊物所受激励频率接近其固有频率时,吊物运动幅值增大,本研究中,相对于4级海况计算条件,5级海况下吊物所受激励频率更接近其摆动固有频率,因而具有更大的摆动幅值。
5 结论(1) 通过在吊机悬吊点设置运动补偿机构可以有效抑制吊物的摆动。5级海况下补偿装置可以使吊物运动幅值最少降低65%,4级海况下补偿装置可以使吊物运动幅值最少降低55%,运动补偿装置能够起到较好的补偿效果,且海况等级越高补偿效果越好。
(2) 通过运动补偿的作用可以使悬吊点保证稳定。在波浪作用下,起重船-吊物系统呈现复杂的耦合运动,吊物做空间摆动,无运动补偿时吊物呈现无规则空间轨迹,进行运动补偿时吊物趋向于规则运动。
(3) 波浪条件对吊物运动轨迹影响较大。由于存在系泊力等非线性载荷,规则波下起重船的运动并非是简谐运动,吊物在空间内存在多种运动轨迹。
| [1] |
王文浩, 王跃齐, 贾国强, 等. 大型起重船在规则波中的频域响应分析[J]. 舰船科学技术, 2022, 44(22): 36-42. Wang W H, Wang Y Q, Jia G Q, et al. Frequency domain response analysis of large crane ship in regular waves[J]. Ship Science and Technology, 2022, 44(22): 36-42. (  0) 0) |
| [2] |
王哲骏, 谢金辉, 高剑, 等. 波浪补偿技术现状和发展趋势[J]. 舰船科学技术, 2014, 36(11): 1-7. Wang Z J, Xie J H, Gao J, et al. Current status and development tendency of waves compensation system[J]. Ship Science and Technology, 2014, 36(11): 1-7. (  0) 0) |
| [3] |
陈进, 杨树, 帅立华, 等. 波浪作用下起重船-吊物系统耦合运动响应数值模拟[J]. 船舶工程, 2021, 43(5): 60-65+78. Chen J, Yang S, Shuai L H, et al. Numerical simulation of coupled motion response of a heavy lift vessel in waves[J]. Ship Engineering, 2021, 43(5): 60-65+78. (  0) 0) |
| [4] |
Masoud Z N, Nayfeh A H, Mook D T. Cargo peculation reduction of ship mounted cranes[J]. Nonlinear Dynamics, 2004, 35(3): 299-311. DOI:10.1023/B:NODY.0000027917.37103.bc (  0) 0) |
| [5] |
Coric V, Catipovic I, Shapnicar V. Floating crane response in sea waves[J]. Brodogradnja/Shipbuilding, 2014, 65(2): 111-122. (  0) 0) |
| [6] |
任会礼, 王学林, 胡于进, 等. 起重船吊物系统动力响应仿真分析[J]. 系统仿真学报, 2007, 19(12): 2665-2668. Ren H L, Wang X L, Hu Y J, et al. Dynamic response simulation of lifting load system of ship-mounted cranes[J]. Journal of System Simulation, 2007, 19(12): 2665-2668. (  0) 0) |
| [7] |
Lee J H. Dynamic analysis of topside module in lifting installation phase[J]. Journal of Ocean Engineering and Technology, 2011, 25(4): 7-11. DOI:10.5574/KSOE.2011.25.4.007 (  0) 0) |
| [8] |
张梁娟, 朱昌明, 包继虎. 浮吊物-吊物耦合矢量建模[J]. 中国机械工程, 2011, 22(5): 561-565. Zhang L J, Zhu C M, Bao J H. Coupling vector modeling of floating crane and suspended load[J]. China Mechanical Engineering, 2011, 22(5): 561-565. (  0) 0) |
| [9] |
Idres M, Youssef K, Mook D, et al. A nonlinear 8-dof coupled crane-ship dynamic model[C]//Proceeding of 44th AIAA Structures, Structural Dynamics and Materials Conference. Reston, VA: American Institute of Aeronautics and Astronautics, 2003.
(  0) 0) |
| [10] |
杨晓蓉, 周永波, 王艳红. 不规则波下起重船吊索动张力特性分析[J]. 海军工程大学学报, 2018, 30(4): 87-94. Yang X R, Zhou Y B, Wang Y H. Sling dynamic tension analysis of crane ship under irregular wave[J]. Journal of Naval University of Engineering, 2018, 30(4): 87-94. (  0) 0) |
| [11] |
Witz J A. Parametric excitation of crane loads in moderate sea states[J]. Ocean Engineering, 1995, 22(4): 411-420. (  0) 0) |
| [12] |
Cha J H, Roh M L, Lee K Y. Dynamic response simulation of a heavy cargo suspended by a floating crane based on multibody system dynamics[J]. Ocean Engineering, 2010, 37(14): 1273-1291. (  0) 0) |
| [13] |
孙友刚, 李万莉, 刘祥勇. 海上浮吊平台作业的波浪补偿系统的仿真与研究[J]. 中国工程机械学报, 2016, 14(3): 198-205. Sun Y G, Li W L, Liu X Y. Simulation on heave compensation system for floating cranes during offshore operation[J]. Chinese Journal of Construction Machinery, 2016, 14(3): 198-205. (  0) 0) |
| [14] |
孙泳涛. 基于补偿技术的起重机深水波浪补偿系统研发[J]. 起重运输机械, 2018(3): 124-127. Sun Y T. Research and development of crane deep-water wave compensation system based on compensation technology[J]. Hoisting and Conveying Machinery, 2018(3): 124-127. (  0) 0) |
| [15] |
Nam B W, Kim N W, Hong S Y. Experimental and numerical study on coupled motion responses of a floating crane vessel and a lifted subsea manifold in deep water[J]. International Journal of Naval Architecture and Ocean Engineering, 2017, 9(5): 552-567. (  0) 0) |
| [16] |
Hu B, Yung C. Global Offshore Wind Access Report 2020[R]. Brussels, Belgium: Global Wind Energy Council, 2020.
(  0) 0) |
| [17] |
顾永凤, 邱广庭. 基于ADAMS的船用浮式起重机补偿装置平台运动学分析与研究[J]. 广州航海学院学报, 2018, 26(3): 9-13+23. Gu Y F, Qiu G T. Motion analysis and study of the floating crane's compensation system based on ADAMS[J]. Journal of Guangzhou Maritime University, 2018, 26(3): 9-13+23. (  0) 0) |
| [18] |
Tong M H, Wang Y M, Qiu H Q. Research on dynamic heave compensation on large floating crane in deep sea[C]//2013 Fifth International Conference on Measuring Technology and Mechatronics Automation. Los Alamitos: IEEE Computer Society, 2013: 898-901.
(  0) 0) |
| [19] |
张永涛, 黄灿, 王紫超, 等. 浮吊吊物系统主动抑摆方法及装置: CN202011564258.6[P]. 2021-04-06. Zhang Y T, Huang C, Wang Z C, et al. Active Anti-Swing Device of Floating Crane Lifting System: CN202011564258.6[P]. 2021-04-06. (  0) 0) |
| [20] |
Fossen T I. Handbook of Marine Craft Hydrodynamics and Motion Control[M]. Chichester, United Kingdom: John Wiley & Sons Limited, 2011.
(  0) 0) |
| [21] |
Sen D T, Vinh T C. Determination of added mass and inertia moment of marine ships moving in 6 degrees of freedom[J]. International Journal of Transportation Engineering & Technology, 2016, 2(1): 8-14. (  0) 0) |
| [22] |
Fossen T I. Guidance and Control of Ocean Vehicles[M]. Norway: University of Trondheim Norway, 1994.
(  0) 0) |
| [23] |
张秀凤, 尹勇, 金一丞. 规则波中船舶运动六自由度数学模型[J]. 交通运输工程学报, 2007, 7(3): 40-43. Zhang X F, Yin Y, Jin Y C. Ship motion mathematical model with six degrees of free domin regular wave[J]. Journal of Traffic and Transportation Engineering, 2007, 7(3): 40-43. (  0) 0) |
| [24] |
王学林, 尤心一, 胡于进. 规则波作用下起重船吊重动力学仿真[J]. 中国机械工程, 2010, 21(9): 1077-1082. Wang X L, You X Y, Hu Y J. Cargo pendulation analysis of moored crane ship under regular waves[J]. China Mechanical Engineering, 2010, 21(9): 1077-1082. (  0) 0) |
| [25] |
Veritas D N. Recommended Practice DNV-RP-C205 on Environmental Conditions and Environmental Loads[S]. Det Norske Veritas, 2010.
(  0) 0) |
| [26] |
Vaughters T G. Joint logistics over the shore operations[J]. Naval Engineers Journal, 1994, 106(3): 256-263. (  0) 0) |
2. Key Laboratory of Ocean Engineering of Shandong Province, Qingdao 266100, China;
3. China Communications Construction Company Limited, Second Harbor Engineering Company Limited, Wuhan 430000, China
 2023, Vol. 53
2023, Vol. 53

