空气质量指数(Air Quality Index,简称AQI)[1],是定量研究空气质量状况的无量纲指数,其数值越大,表明空气质量状况越差,对人类健康、生态、环境的消极影响越大。Neha Khanna在2000年提出用空气污染指数(API)体系来评价空气质量[2];刘峰等人在2003年提出了半参数回归模型在空气质量指数分析和预测中的应用[3],模型建立过程中采用了主成分分析法,使得模型结果难以直接与污染因素相对应;郭本初、沈陆明在2016年基于二元回归分析对杭州市的空气质量指数建立回归模型[4],其建立的模型只采用了PM2.5和PM10两项指标作为预测变量对AQI进行回归,具有一定的片面性;滕延芹在2016年基于主成分分析对空气质量指数评价方法进行了优化[5],同样存在建立的模型难于解释而且预测结果误差较大的问题;刘萍在2015年基于主成分分析和多元线性回归模型对空气质量评价方法进行了研究[6],但模型的建立忽视了多元回归对变量的假设。
针对以上问题,本文提出用多元回归分析的方法对空气质量进行分析。本文首先针对AQI原始计算模型进行介绍,根据原始模型的特点提出本文建立AQI计算模型的方法,最后根据青岛地区空气质量数据建立模型验证本文方法的合理性。
1 空气质量指数(AQI)空气质量指数(AQI)是通过监测PM2.5、PM10、二氧化氮、二氧化硫、一氧化碳、臭氧六项指标的浓度计算得出的。随着我国现代化程度的加深,各种能源资源的消耗不断增加,各种污染因素日益增多,给空气质量造成了很大的影响。空气质量指数作为一项评价空气质量的定量指标,在指导积极人类生活、经济社会发展、环境变化等方面有着重大意义。因此,对空气质量指数准确、高效、全面的计算和分析是十分重要的。这也将为我国今后在改善空气质量方面采取更加经济、高效的措施提出建设性的意见和建议。
目前,空气质量指数的计算采取如下步骤:首先,根据公式
| $ IAQ{{I}_{p}}=\frac{IAQ{{I}_{{{H}_{i}}}}-IAQ{{I}_{{{L}_{0}}}}}{B{{P}_{{{H}_{i}}}}-B{{P}_{{{L}_{0}}}}}({{C}_{p}}-B{{P}_{{{L}_{0}}}})+IAQ{{I}_{{{L}_{0}}}}, $ | (1) |
计算出各项监测指标的分指数IAQIp,其中Cp表示监测指标的浓度,BPHi、BPL0分别表示Cp相近的污染物浓度限值的低位值与高位值,这些低位值与高位值均为常数,IAQIHi、IAQIL0分别为BPHi、BPL0对应的空气质量分指数。计算得到各监测指标的分指数后,取
| $ AQI=\underset{p}{\mathop{\text{max}}}\, \{IAQ{{I}_{p}}\}, $ | (2) |
作为最终的空气质量分析结果。
由上述AQI计算模型可以看出,AQI仅仅是取各监测指标的分指数的最大值作为最终结果,也就是AQI的取值,只考虑了监测指标中污染最大的指标作为衡量空气质量的标准。然而实际上,对于空气质量的检测指标,不仅监测指标中污染最大的指标具有重要作用,其他指标以及指标间的相互作用也不可忽视。尤其是在各类污染物的分指数差异较大时,仅利用AQI来评价空气质量是比较片面,并且上述计算模型较为复杂,特别是当引入更多监测指标之后,各监测指标间的存在相互作用的概率更大,其计算结果就容易出现偏差,并且上述计算方法要针对每一个指标计算取最大,其计算量也比较大,这些都不利于对AQI的预测以及空气质量的评价和分析。为了解决上述问题,我们考虑运用多元回归的方法,引入多元回归模型对AQI进行计算,利用多元回归模型对AQI进行计算,可以通过一次回归就分析出影响空气质量的因素,简化模型,提高模型的计算效率,增强模型的可解释性。并且,若引入更多的监测指标,在高维和超高维的情况下,可以利用针对线性模型的相关变量选择的方法,分析得出对于各监测指标对空气质量指数的影响的相关结论。
2 AQI与其他检测指标的多元回归分析多元回归分析[7]是在相关分析的基础上,研究两个或两个以上的自变量与一个因变量之间的数量关系,并用回归模型进行描述与分析。建立多元回归模型需要变量满足各变量服从正态分布以及E(Xi|Xj)≈α0+α1Xj的假设[8]。
因此,在进行回归建模之前应该先对变量进行Box-Cox变换使其服从建立多元回归模型的假设。故我们建立的模型形式如下:
| $ Y=\sum\limits_{i=1}^{6}{{{\beta }_{i}}{{X}_{i}}}, $ | (3) |
其中:Y为AQI经过Box-Cox变换得到的AQI的函数;Xi, i=1, …, 6分别表示PM2.5、PM10、二氧化氮、二氧化硫、一氧化碳、臭氧六项指标的浓度经过Box-Cox变换得到相应的指标浓度的函数,βi, i=1, …, 6为待估参数,ε为误差项。针对模型(3)进行参数估计、模型诊断以及变量选择,从而建立起形式简单、计算效率高、可解释性强、预测准确的模型。
该模型可以根据相关指标对AQI进行预测,模型简单、高效、直观,可以快速分析出变量之间的关系。根据模型中保留的变量、变量的变换形式以及回归系数,还可以判断变量之间的相互关系和影响程度,可以为改善空气质量提出更加有针对性的措施。建立起的回归模型中所保留的协变量以及系数较大的协变量对空气质量的影响程度会相对较大,因此,在提出空气质量改善措施时,可以着重对模型中保留的协变量和系数较大的协变量进行改良。这样也就能提出更加经济高效且有针对性的空气质量改善措施。
3 青岛市空气质量多元回归分析本文通过对青岛市空气质量数据的分析,来展示本方法的应用。本文的数据研究的是2016年1月1日—2017年3月31日青岛每日空气质量数据,数据包括每日空气质量等级、AQI指数、当天AQI排名、以及PM2.5、PM10、二氧化氮、二氧化硫、一氧化碳、臭氧几个指标的浓度。
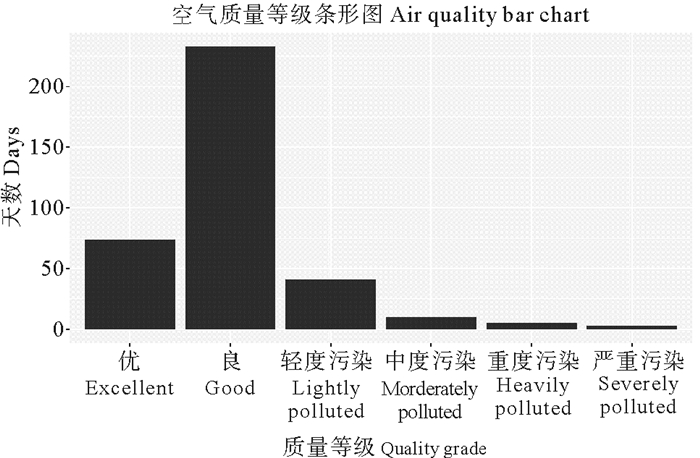
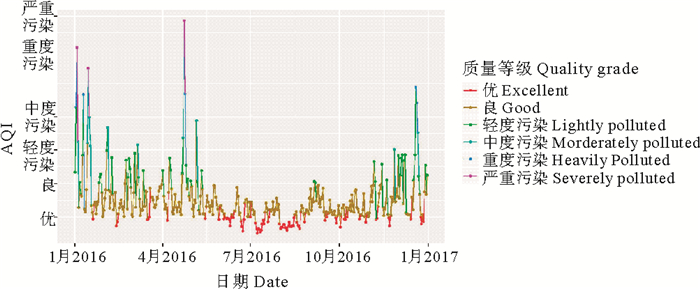
为了研究青岛市空气质量状况,对收集的数据分别绘制了空气质量等级的条形图、AQI分布直方图、AQ变化图。观察前图 1、2可知,青岛的空气质量等级主要集中在“优”、“良”、“轻度污染”这三类当中,且空气质量等级为良的天数明显高于其他几类,说明青岛市的空气质量总体来说是很好的。观察图 3不难看出,6月到11月期间AQI较低,空气质量等级比较高,这几个月正值青岛的夏秋两季,这两个季节属于青岛空气和气候比较舒适的季节;1、2两月以及12月AQI指数较高、空气质量等级较低的天数多,主要考虑到这几个月是青岛的冬季,需要供热取暖,燃煤会对空气质量有较大的影响,所以这几个月青岛的空气质量相对其他几个季节来说最差;3月到5月期间是青岛的春季,属于沙尘暴多发的季节,会对空气质量有较大的影响,所以较夏秋两季来说,春季的空气质量总体上较差,但还是要优于冬季的空气质量的。这就证明,青岛市的空气质量具有明显的季节性。
|
图 1 空气质量条形图 Fig. 1 Air quality bar chart |
|
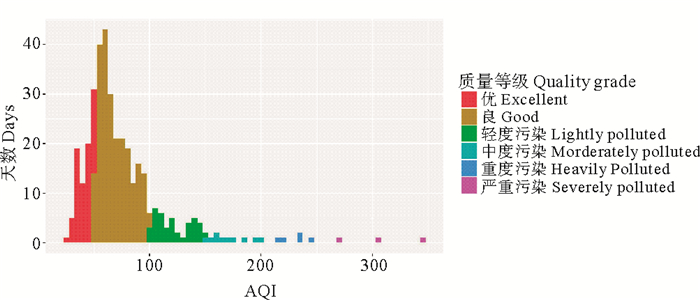
图 2 AQI分布直方图 Fig. 2 Histogram of AQI |
|
图 3 AQI变化图 Fig. 3 Line chart of AQI |
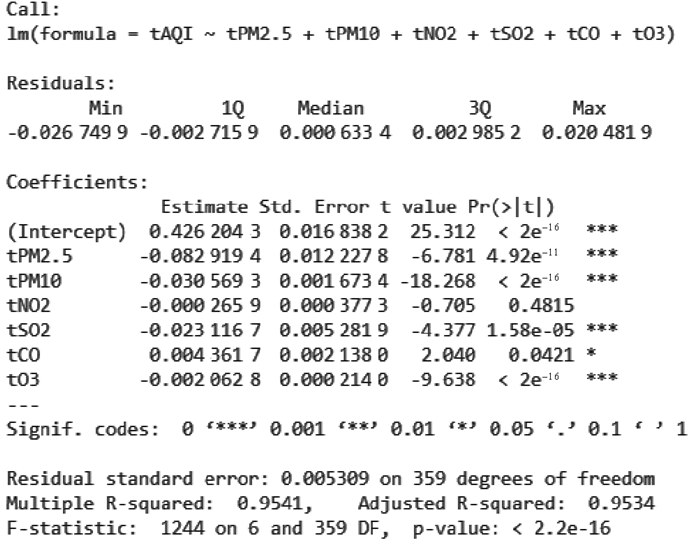
利用2016年全年的数据建立回归模型,用2017年前三个月的数据进行模型的测试。建立多元回归模型需要变量满足各变量服从正态分布的和E(Xi|Xj)≈α0+α1Xj的假设,因此在进行回归建模之前首先利用R语言对各变量进行了如下形式的Box-Cox变换:
|
图 4 变换数据建模结果 Fig. 4 Result of modeling with transformed data |
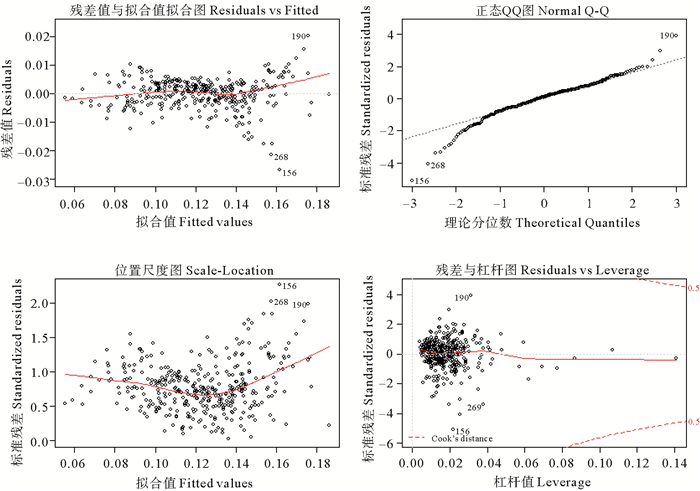
模型的系数均显著,Adjust R-squared=0.953很接近1,F检验的p值,p < 2.2×10-16是一个极小的数,从估计结果上暂且认为模型是合适的,绘制该模型的诊断图如图 5。
|
图 5 模型诊断图 Fig. 5 Diagonal chart of the model |
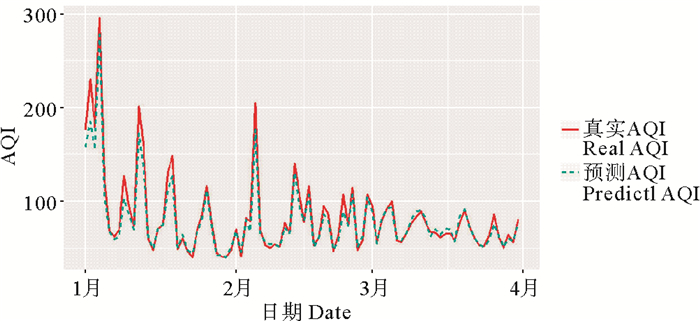
诊断图形显示模型的拟合效果比较好。用2017年前三个月数据对建立的模型进行测试,绘制了AQI真实值、预测值如图 6。
|
图 6 拟合比较图 Fig. 6 Comparison chart of fitness |
同时对测试结果进行汇总,见表 1。结果显示,预测值与真实值能够很好地吻合,真实值均在模型的预测区间内,并且有70%以上的测试数据的真实值与预测值之间的绝对差小于5,这说明建立的模型是准确合理的。
|
|
表 1 测试结果汇总 Table 1 Summary of test results |
最终确定AQI的计算模型:
| $ \begin{align} &\ \ \sqrt{\gamma }=-0.064\ 950\ 2\times {{m}_{1~}}^{0.1}-0.031\ 815\ 1\times \text{log}{{m}_{2~}} \\ &\ \ -0.018\ 811\ 4\times {{g}_{2~}}^{0.12}-0.002\ 067\ 6\sqrt{{{g}_{4~}}}+ \\ &0.396\ 889\ 2 。\\ \end{align} $ | (4) |
其中:γ为AQI;m1为PM2.5浓度;m2为PM10浓度;g2为二氧化硫浓度;g4为臭氧浓度。由模型(4)可以看出,我们建立的模型引入了多个变量对AQI进行计算,这就避免了原始模型中只取分指数最大的一个作为AQI的片面性,同时增强了模型的可解释性。
经过上述空气质量指数回归分析过程建立起回归模型可以直接对空气质量指数进行计算,我们只需要在建立模型时对所有变量进行1次Box-Cox变换,以及1次参数估计和变量选择,一旦建立回归模型AQI的计算则只需要带入变量值进行计算即可。如果运用原始的模型进行计算则每次的计算过程需要进行6次分指数的计算以及多次比较才能的出最终的计算结果,显然本文的方法计算起来更加简便。其次,回归模型经过变量选择后,涉及到的协变量个数少,我们只需要获取保留变量的数据,所以更加经济和高效。
另外,根据建立的模型可以给出更加有针对性且经济的空气质量改善措施。根据模型(4)青岛市在2017年可以出台主要控制PM2.5、PM10、二氧化硫、臭氧四个指标的相关措施。从这几个指标的产生来源来看,主要是汽车尾气和煤炭资源的燃烧,有关部门可以出台相关政策鼓励市民乘坐公共交通工具出行,扩大绿化面积,同时充分利用海洋资源开发新能源来从根本上控制模型中的相关指标的浓度。
4 结论(1) 利用多元回归分析的方法建立起简单、直观、高效的AQI计算模型,引入了多项监测指标对AQI进行计算,增强了AQI的可解释性和准确性,解决了原始模型中只考虑污染程度最大的监测指标作为AQI的评价指标而造成结果具有片面性和误差大的问题,对多元回归全模型进行变量选择后不仅充分考虑了所有污染物对AQI的影响,还大大降低了模型的复杂程度。
(2) 通过观察模型中保留的变量以及变量所对应的系数,可以考虑更加侧重于控制模型中保留的几项监测指标的浓度并根据其系数决定控制力度,从而出台更加经济高效的环保措施来改善空气质量。
| [1] |
中华人民共和国环境保护部. 《环境空气质量指数(AQI)技术规定(试行)》(HJ 633—2012)[S].北京: 中国环境科学出版社, 2012. Ministry of Environmental Protection of the People's Republic of China. AQI Technical Regulations (Tentative) (HJ 633-2012)[S]. Beijing: China Environmental Science Press, 2012. (  0) 0) |
| [2] |
Neha Khanna. Measuring environmental quality: An index of pollution[J]. Ecological Economics, 2000, 35: 191-202. DOI:10.1016/S0921-8009(00)00197-X
(  0) 0) |
| [3] |
刘锋, 银利, 张星. 半参数回归模型在空气质量指数分析和预测中的应用[J]. 数学理论与应用, 2013, 33(4): 94-98. Liu Feng, Yin LI, Zhang Xing. Analysis and prediction of air quality indexes with a semi-parametric regression model[J]. Mathematical Theory and Applications, 2013, 33(4): 94-98. (  0) 0) |
| [4] |
郭本初, 沈陆明. 基于二元线性回归的杭州市空气质量指数研究[J]. 市场周刊(理论研究), 2016, 9: 86-87. Guo Benchu, Shen Luming. Study on Hangzhou AQI based on binary linear regression[J]. Market Weekly, 2016, 9: 86-87. (  0) 0) |
| [5] |
滕延芹. 基于主成分分析的空气质量指数评价方法优化[J]. 内蒙古煤炭经济, 2016, 5: 9-10. Teng Yangqin. Optimization of AQI evaluation method based on principal component analysis[J]. Inner Mongolia Coal Economy, 2016, 5: 9-10. (  0) 0) |
| [6] |
刘萍.基于主成分分析和多元线性回归模型的空气质量评价方法研究[D].云南: 云南大学, 2015. Liu Ping. Based on Principal Conponent Analysis and Multivariate Linear Regression Model of Air Quality Eveluation Method Research[D]. Yunnan: Yunnan University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10673-1016041073.htm (  0) 0) |
| [7] |
何晓群, 刘文卿. 应用回归分析[M]. 北京: 中国人民大学出版, 2015: 57. He Xiaoqun, Liu Wenqing. Applied Regression Analysis[M]. Beijing: China Renmin University Press, 2015: 57. (  0) 0) |
| [8] |
Simon J, Sheather. A Modern Approach to Regression with R[M]. New York: Springer, 2008: 5.
(  0) 0) |
 2018, Vol. 48
2018, Vol. 48

