中国是抗生素生产量和消费量最大的国家之一[1]。进入机体的抗生素绝大部分不能被完全吸收代谢,约有90%会以原形或者中间代谢产物的形式经由患者或畜禽的粪便、尿液进入环境中[2]。然而这些排出机体外的抗生素及其代谢产物仍然具有一定的生物活性且能在水体中持续存在,从而对水环境质量以及人体健康产生威胁[3]。
自1924年青霉素被发现并临床应用以来,人们已经开始研究有关抗生素废水的处理技术,其中主要的方法包括:生物法、物理方法与高级氧化技术等。Turkdogan等[4]研究发现,使用生物法从生态系统中去除抗生素药物的效率非常低。这是因为污水中的抗生素对微生物具有很强的抑制作用。另外,抗生素工业废水大多是高浓度有机废水,传统的生物法难以承受COD≥10 mg/L的废水,这就需要对原水进行大量的稀释使得生物技术处理抗生素废水收到了限制。混凝、吸附等一些物理方法只是将抗生素从液相转移到固相,没有实现真正意义上的去除[5]。电催化氧化法作为化学处理方法的一种,由于具有操作简单、反应速率快和处理效率高等优点,已被成功的应用于降解自然水体和污水中的抗生素[6]。电催化氧化水中抗生素的过程十分复杂,通常认为抗生素分子的降解可能通过以下两种途径进行:一是直接氧化:有机物直接将电子转移到阳极而被氧化;二是间接氧化反应:电解过程中产生具有强氧化性物质(如羟基自由基·OH,活性氯,或硫酸根自由基·SO42-),这些具有强氧化性物质与水体中的有机物发生反应去除目标物质。
随着计算机科技和算法技术的迅速发展,以建立模型的方式进行废水处理研究成为了一个新的热点。目前,废水处理的模型侧重于对动力学模型与理想化模型的研究,而针对物理化学工艺模型的研究比较欠缺。在电催化氧化法过程中,电流密度、溶液的初始pH、电解质浓度和有机物的初始浓度等单因素以及各因素的交互作用对有机物的去除率都有一定影响[7]。另外,电催化氧化技术在处理废水的过程中涉及直接氧化和间接氧化两个复杂的过程,不利于在实际工程中对其进行控制与预测,这也使得研究电催化氧化技术的工艺模型显得尤为重要。目前,对于涉及多个因素的电催化氧化法过程,常用的建模方法有响应面法(RSM)和人工神经网络(ANN)等。RSM是集建模和过程优化于一体的数学统计技术,它不仅能够有效的模拟各因素对响应值的影响,而且还能分析各因素之间的交互作用,确定因素水平的最优域[8]。李虹雨等[9]利用响应曲面拟合自变量和响应值之间的函数关系,COD去除率与预测值的相对偏差仅1.8%。Vahidian等[10]构建人工神经网络模型来模拟电化学处理酸性粽14偶氮染料,以反应时间、初始pH、电流密度、电解质与染料浓度为输入值,电流效率与能耗为输出值,模型拟合的相关系数分别为0.988与0.983。与RSM相比,ANN在数据拟合和预测方面具有更高的准确性[11]。在模型研究的基础之上,对各种水处理工艺的操作条件进行优化逐渐成为一个新的研究方向。遗传算法(GA)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法[12]。将ANN与GA两者结合起来既能得到准确的拟合预测模型,又能起到优化实验条件的效果。为了探究适合于电催化氧化磺胺甲恶唑条件的优化方法,有必要将两种优化模型的方法进行对比,从而达到优化实验条件的目的。
因此,本研究选取具有代表性的抗生素磺胺甲恶唑(SMX)为研究对象,进行了电催化氧化降解实验。从建立准确的优化模型角度出发,通过中心组合设计(CCD)设计实验,建立RSM和ANN两种模型,并评价两种模型的准确性和预测能力。在此基础上分别通过RSM和GA对所得模型进行优化,对比两种优化方式确定最佳电催化氧化SMX的条件。
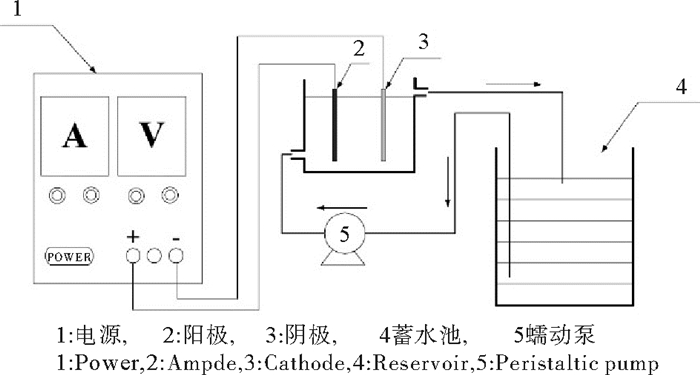
1 材料与方法 1.1 实验装置实验装置由电解槽、蠕动泵、直流电源、蓄水池、磁力搅拌器等组成,装置示意图见图 1。电解槽采用有机玻璃加工制成,长为60 mm,宽为50 mm,高为60 mm,有效容积为180 mL。电解过程中,模拟的SMX废水在蓄水池与电解槽之间循环流动,蓄水池总体积约1 200 mL,废水体积为1 000 mL。为保证整个循环过程中水质均匀,使用磁力搅拌器进行充分搅拌。在电催化氧化实验中,采用不锈钢304作为阴极,钴掺杂的二氧化铅电极作为阳极[13],阳极尺寸为100 mm×80 mm×2 mm,阳极实际的工作尺寸为100 mm×80 mm×2 mm。
|
图 1 实验装置示意图 Fig. 1 Schematic diagram of experimental apparatus |
以SMX为目标污染物配制模拟废水;所有实验均在恒电流状态下进行,保持每次实验时液体流速为0.05 m/s,磁力搅拌器转速均为400 r·min-1,极板间距为1.5 cm;以NaCl作为电解质,使用NaOH与H2SO4溶液调节pH值;电解60 min后取水样进行测试SMX的浓度。SMX浓度采用紫外可见分光光度计进行检测,选用上海仪电分析仪器有限公司生产的L5紫外分光光度计测定SMX的吸收曲线,SMX标准溶液在λ=262 nm处有最大的吸收峰,因此选择λ=262 nm作为SMX的特征吸收波长。配制SMX浓度为0.0,0.5,1.0,2.0,5.0,8.0, 10.0 mg·L-1的标准溶液,在λ=262 nm下,分别测定SMX溶液的吸光度值,绘制SMX标准曲线。
1.3 实验设计采用中心复合设计实验对影响SMX抗生素去除率的电流密度(X1)、溶液的初始pH(X2)、电解质浓度(X3)和SMX的初始浓度(X4)4个因素进行优化。以SMX的去除率(Y)为响应值。单因素实验结果显示:电流密度15 mA/cm2,初始pH=7,NaCl浓度0.3 mol/L,SMX的初始浓度100 mg/L时SMX的去除率最大。因此确定各因素的范围为:电流密度10~20 mA/cm2,初始pH=5~9,NaCl浓度0.2~0.4 mol/L,SMX的初始浓度80~120 mg/L。因素水平编码表如表 1所示。
|
|
表 1 影响因子编码及水平 Table 1 Code and level of independent variables |
响应值与自变量之间的关系采用二阶响应曲面方程进行拟合:
| $ Y = {\beta _0} + \sum\limits_{i = 1}^k {{\beta _i}} {X_i} + \sum\limits_{i = 1}^k {{\beta _{ii}}} X_i^2 + \sum\limits_{i = 1}^{k - 1} {\sum\limits_{j = 2}^k {{\beta _{ij}}} } {X_i}{X_j} + \varepsilon 。$ | (1) |
其中i≠j。
式中: β0为常数项; Xi和Xj为自变量; βi、βii、βij分别表示交互作用项的回归系数; k为影响因素的数量; ε为误差[14]。
1.5 人工神经网络模型本研究采用三层的BP人工神经网络(输入层、隐含层、输出层)创建优化模型。实验设计选取电流密度、溶液的初始pH、电解质浓度和SMX的初始浓度四个变量的实验数据作为网络模型的输入参数。为了统一输入量的数量级,运用公式(2)将数据样本归一化处理在0.1~0.9之间。
| $ {x_i} = \frac{{0.8\left( {{X_i} - {X_{\min }}} \right)}}{{{X_{\max }} - {X_{\min }}}} + 0.1。$ | (2) |
其中:Xi、xi分别为实验数据归一化前、后的值;Xmax、Xmin分别为数据中的最大值和最小值。
通过比较在不同神经元数训练的均方误差(MSE)来确定隐含层神经元的个数。之后对经过CCD设计得到的30组实验数据进行人工神经网络训练。以均方误差(MSE)、平均绝对误差(MAE)和决定系数(R2)大小作为评价模型的指标[15]。MSE、MAE和R2如公式(3)、(4)和(5)所示:
| $ MSE = \frac{1}{n}{\left( {\sum\limits_{i = 1}^n {\left( {{Y_{{\rm{pre}}}} - {Y_{{\rm{exp}}}}} \right)} } \right)^2}。$ | (3) |
| $ MAE = \frac{1}{n}\sum\limits_{i = 1}^n {\left( {\left| {{Y_{{\rm{pre}}}} - {Y_{{\rm{exp}}}}} \right|} \right)} 。$ | (4) |
| $ {R^2} = \frac{{{{\left( {\sum\limits_{i = 1}^n {\left( {{Y_{{\rm{exp}}}} - \overline {{Y_{{\rm{exp}}}}} } \right)} \left( {{Y_{{\rm{pre}}}} - \overline {{Y_{{\rm{pre}}}}} } \right)} \right)}^2}}}{{\sum\limits_{i = 1}^n {{{\left( {\left( {{Y_{{\rm{exp}}}} - \overline {{Y_{{\rm{exp}}}}} } \right)\left( {{Y_{{\rm{pre}}}} - \overline {{Y_{{\rm{pre}}}}} } \right)} \right)}^2}} }}。$ | (5) |
式中:Ypre为SMX去除率的实验值;Yexp为SMX去除率的计算值;n为试验次数(30)。
2 结果与讨论 2.1 响应曲面法实验结果 2.1.1 模型建立与显著性检验根据CCD设计进行实验,所得的实验方案和结果见表 2。其中实验序号由软件Design-Expert 8.0.6 Trial自动产生。运用SPSS对实验数据进行回归、显著性和方差分析。表 3所示为中心复合设计条件下,预测SMX去除率的回归方程系数和各因素项的显著性检验,从而得出电流密度,pH,电解质浓度和SMX的初始浓度与SMX去除率之间的回归方程(6)。
| $ \begin{array}{l} \begin{array}{*{20}{l}} {Y = 56.3768 + 0.8596{X_1} + 2.6103{X_2} + }\\ {89.0917{X_3} - 0.3542{X_4} + 0.0376{X_1}{X_2} - } \end{array}\\ \begin{array}{*{20}{c}} {2.9425{X_1}{X_3} + 0.0233{X_1}{X_4} - 2.5875{X_2}{X_3} - }\\ {0.0110{X_2}{X_4} + 0.3081{X_3}{X_4} - 0.0488X_1^2 - } \end{array}\\ 0.1234X_2^2 - 25.9792X_3^2 - 0.0008X_4^2。\end{array} $ | (6) |
|
|
表 2 基于中心组合实验设计方案与结果 Table 2 Design and results based on CCD methodology |
|
|
表 3 回归方程方差分析 Table 3 ANOVA and regression analyses |
表 3可以看出:该模型的F值为43.54,P < 0.000 1,说明该回归方程是极显著的,即该模型在整个的回归区域内的拟合很好;模型的多元相关系数R2 = 0.976,说明模型的相关性较好,预测模型拟合程度高,能很好地预测实际的处理效果;模型校正决定系数RAdj2=0.954,说明该模型可以解释95.4%的响应值变化,实验误差小,数据合理;失拟项P=0.323 8>0.05,失拟不显著,说明方程拟合充分,回归方程高度显著,可以较好地描述各因素与响应值之间的真实关系[16-17]。
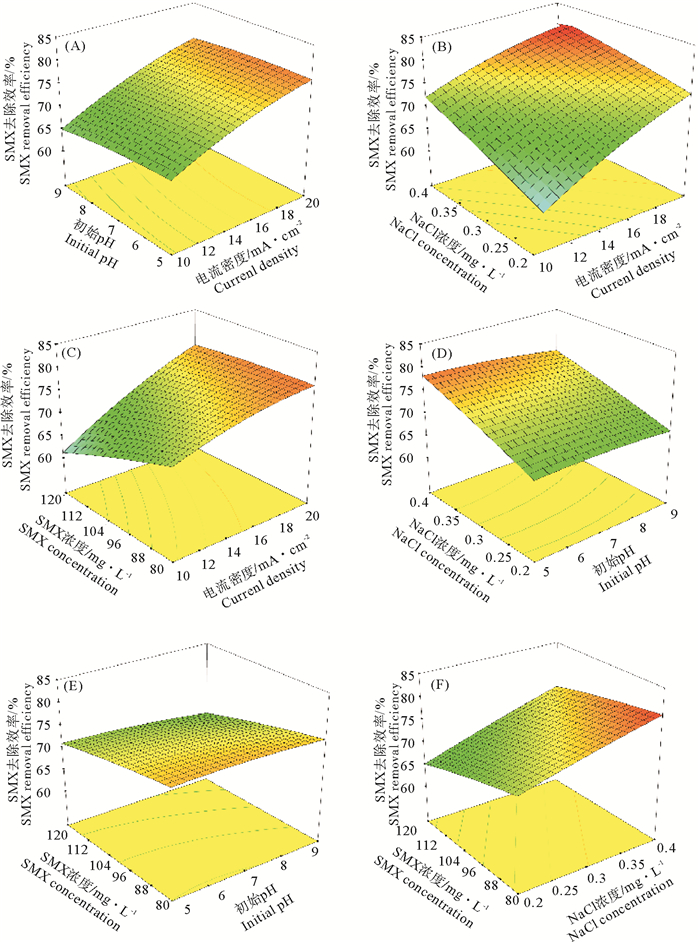
2.1.2 SMX去除率的响应面分析采用响应曲面法分析交互作用对SMX去除率的影响程度,借助三维曲面图形进行判断。如图 2所示,各图表示电流密度、初始pH、NaCl浓度和SMX浓度任意两个变量取中间水平时,其余两个变量对SMX去除率的影响。这些图可以直观发映出各因素对SMX去除率的影响,确定最佳去除SMX参数范围区间以及各参数之间的相互作用。从理论上而言,如果曲面的坡度较大说明影响因素之间的交互作用对响应值的影响较为显著。
|
图 2 各试验因素对SMX去除率的交互影响 Fig. 2 Interactive effects of the experimental factors on the removal efficiency of SMX |
从图 2(A)可知,在小的电流密度下,pH值的变化对SMX去除率的影响较为显著,当电流密度高于15 mA/cm2时,SMX去除效率随pH值的增加持续降低,造成这一现象的主要原因是碱性环境不利于废水中具有强氧化性的活性基团(如·OH)的存在,且其数量和存在形式既受到pH值控制也受到电流密度的影响。从图 2(B)可以看出,三维曲面图形的坡度较大且等高线分布较为密集,说明电流密度和NaCl浓度之间的交互作用对SMX去除效果有显著的影响。在NaCl浓度固定时,电流密度的提高可以显著加强电化学氧化降解SMX的能力,与低电流密度区域比较,在高电流密度条件下,NaCl浓度的增加在一定范围内可以显著提高SMX的去除效果。此外,当电流密度一定时,SMX去除率会随着NaCl浓度的提高有较小范围的先增加后减小的趋势,这可能是因为当NaCl浓度过量时部分盐的析出在电极表面形成一层盐膜,阻碍电化学氧化的进行。从图 2(D)可以判断出pH值与NaCl浓度之间的交互作用对SMX去除率也有较为显著的影响。当反应体系中NaCl浓度一定时,pH的增加会使SMX去除率呈现先增加后减小的趋势。当体系为碱性时,SMX去除率会随NaCl浓度的增加而增加,但酸性环境下比碱性环境提升的幅度更大。
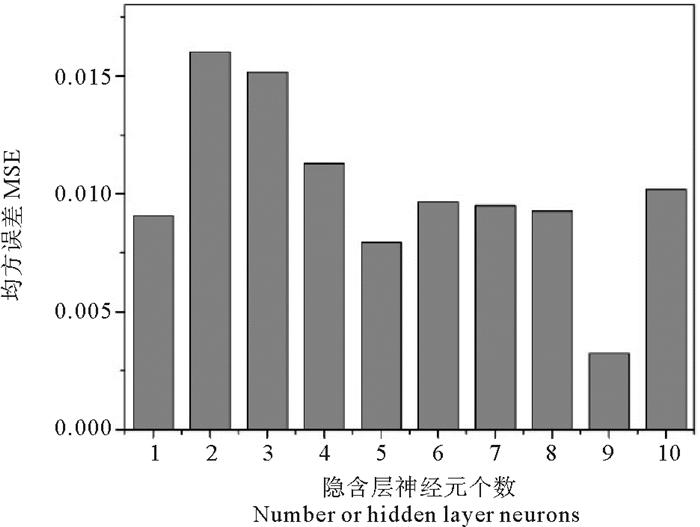
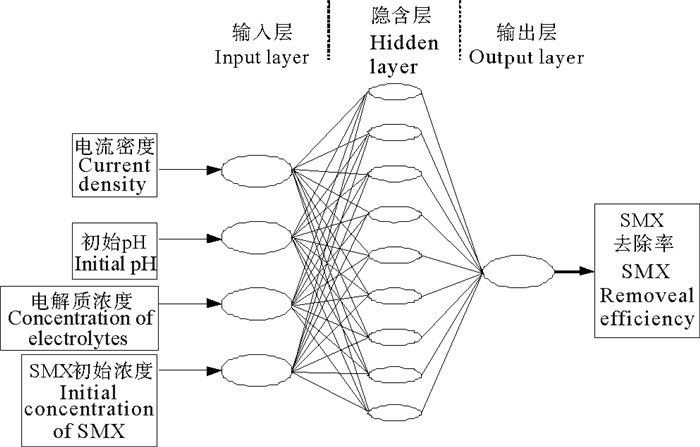
2.2 神经网络模型 2.2.1 神经网络结构神经网络的拓扑结构和参数主要包括:输入/输出层,网络层数,隐含层的神经元个数,训练函数和传递函数等。在本研究中隐含层的传递函数采用对数S型函数,输出层的传递函数为线性函数,隐含层的层数为一层。通过改变隐含层神经元的个数来提高模型的精度。图 3为隐含层神经元个数对网络性能的影响,由图 3可以看出当神经元个数为9时,MSE最下。经过多次实验迭代,最终确定隐含层神经元个数为9。训练函数采用L-M法的trainlm函数来克服标准BP神经网络收敛速度慢的缺陷。训练步数为1 000,学习率0.5。当实验值与预测值误差达到10-2时停止训练。从而得出神经网络的拓扑结构如图 4。
|
图 3 隐含层节点数对网络性能的影响 Fig. 3 Influence of hidden nodes on the network performance |
|
图 4 BP神经网络结构 Fig. 4 BP neural network architecture |
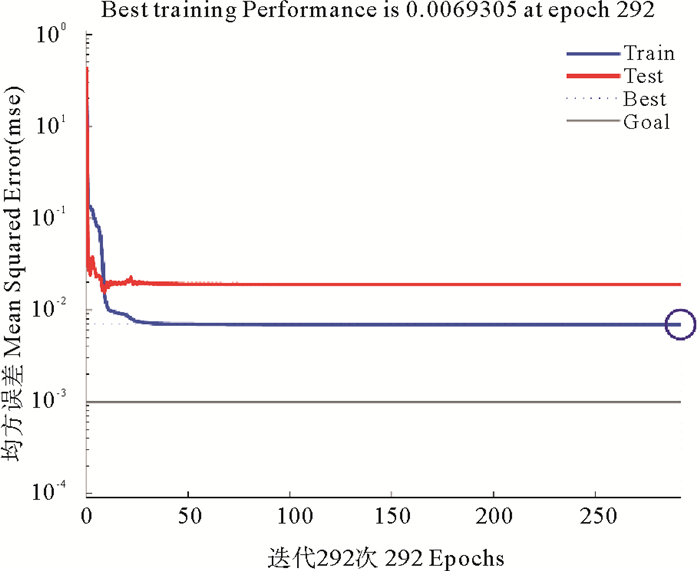
建立神经网络需要训练数据和测试数据,因此本研究随机选取CCD设计中的25组数据对网络进行训练,剩余5组数据用于测试网络。所有神经网络的仿真都是在Matlab R 2012a上进行。训练步数为1 000,学习率0.5,训练步长为10、动量因子为0.1,直到目标误差达到为10-2或训练到1 000步时训练结束。图 5给出了该神经网络训练过程中误差的变化曲线,从图中可以看出该神经网络模型在第292次迭代时达到设定的目标精度。神经网络预测结果如表 2,可以看出实验值与其对应预测值的吻合度较好,二者的相对误差均小于1%。
|
图 5 神经网络模型的训练误差曲线 Fig. 5 Curve of training error of network model |
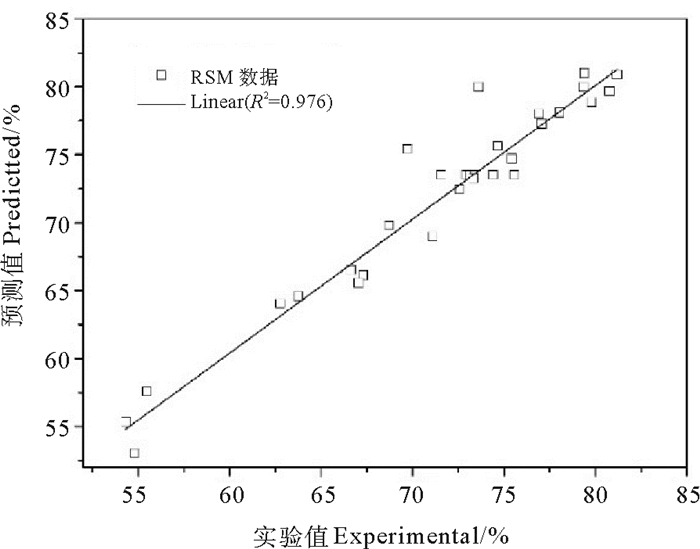
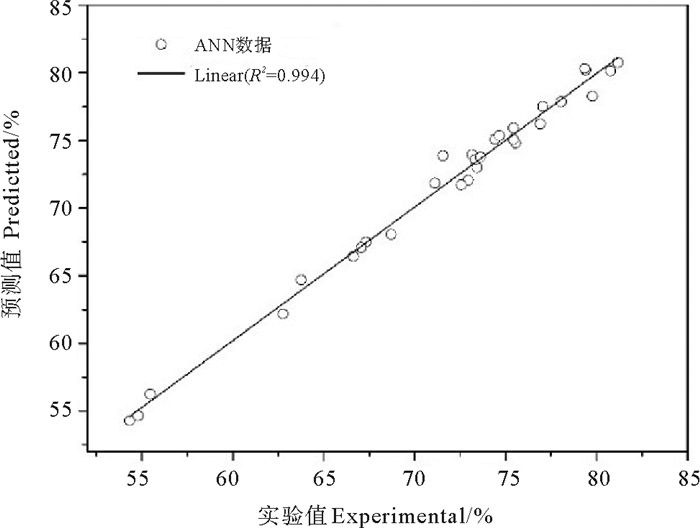
响应曲面模型能够利用二次回归模型的系数来反映各个因素对响应值影响的程度。使用RSM可以分辨哪些是主要因素,以及各因素之间是否有交互作用,从而可以降低问题的复杂程度。但是在这种方法中所有因素的范围必须提前确定,如果因素范围的选择不当则得不到理想的优化结果[18]。本节比较了电催化氧化磺胺甲恶唑的响应曲面模型和人工神经网络模型。基于均方误差(MSE)、平均绝对误差(MAE)决定系数(R2)进行比较。在表 2中,列出了RSM和ANN模型的预测值。对实验设计的RSM和ANN模型对电催化氧化磺胺甲恶唑进行回归分析,结果如图 6和图 7所示。根据方程(3)、(4)和(5)计算得出RSM和ANN的MSE、MAE、R2的值分别为2.62、1.13、0.976和0.59、0.62、0.994。表 4列出了相对应的MSE,MAE和R2。结果表明,ANN模型比RSM模型具有更高拟合度、精度和预测能力。
|
图 6 响应曲面模型预测值与实验值的相关性 Fig. 6 Correlativity of Predicted and Experimental Values of RSM |
|
图 7 人工神经网络模型预测值与实验值的相关性 Fig. 7 Correlativity of Predicted and Experimental Values of ANN |
|
|
表 4 RSM和ANN模型预测能力的比较 Table 4 Comparison of the predictive capacity of RSM and ANN |
通过对RSM模型进行典型性分析,得到最佳实验条件:电流密度20 mA/cm2、初始pH=5、电解质浓度0.4 mol/L、SMX初始浓度116.54 mg/L,SMX的理论去除率为81.01%。为验证该优化方法的可靠性,在此条件下,实验重复3次,SMX去除率的平均值为87.84%,预测值与实验值的相对误差为4.83%。说明了响应曲面模型优化电催化氧化SMX的可行性。
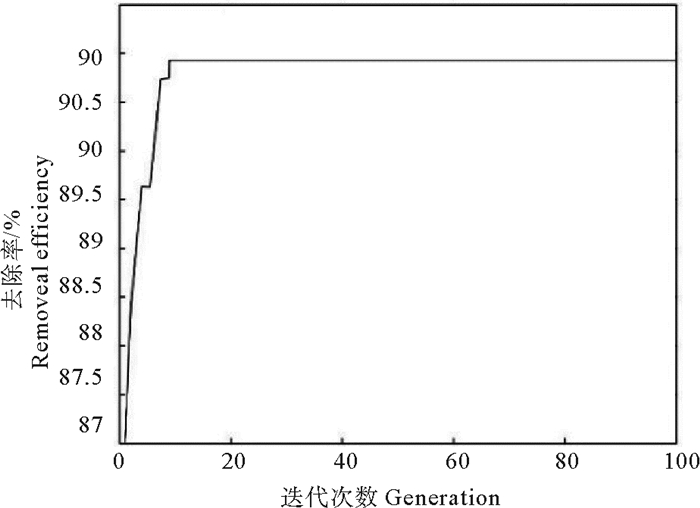
鉴于建立的ANN模型比RSM模型具有更高拟合度、精度和预测能力等特点[19],利用基因算法对建立的ANN模型的输出值进行寻优,最终确定了最佳的电催化氧化磺胺甲恶唑工艺条件。将表 2中心组合设计的实验结果作为初始群体,通过人工神经网络模型来调试函数的适应度,以SMX的去除率作为其函数的输出值,将神经网络建模和遗传优化算法结合对电催化过程进行全局寻优,获得最佳的实验条件。在优化计算过程中,设定最大进化代数为100,种群大小为5,交叉概率为0.6,变异概率为0.05[20],得到每代种群最优适应度和平均适应度及其变化结果如图 8。由图可知,经过13代的迭代适应度达到最大即SMX的去除率已达到最大值,随后基本保持不变,经遗传算法对电催化氧化条件进行全局寻优,获得的SMX去除率的最大值为90.62%,其工艺参数为:电流密度10.73、初始pH=5.6、电解质浓度0.32、SMX初始浓度99.26。在此条件下,实验重复3次,SMX去除率的平均值为88.47%,预测值与实验值相差1.52%。
|
图 8 神经网络模型的训练误差曲线 Fig. 8 Curve of training error of network model |
将响应曲面优化、遗传算法优化结果进行比较,其结果如表 5所示。由表 5可以看出,遗传算法优化结果的相对误差明显低于响应曲面的优化结果。这表明遗传算法优化结果可信度更高,用该方法进行优化电催化氧化磺胺甲恶唑条件是可行的。
|
|
表 5 优化结果比较 Table 5 Comparison of optimization results |
采用中心组合设计原理设计组合实验。基于实验数据建立了响应曲面模型和BP人工神经网络模型。并对模型进行了验证和对比;随后对所得回归方程进行分析,采用遗传算法对所得BP人工神经网络进行优化并对比两种优化模型的结果,得出以下结论:
(1)响应曲面模型的MSE,MAE明显高于BP人工神经网络模型,R2低于BP人工神经网络模型,表明BP人工神经网络模型的预测和拟合能力高于响应曲面模型。
(2)遗传算法的优化结果与实验所得结果的相对误差仅为0.74%,明显低于响应面的优化结果,遗传算法法人优化结果可信度更高,证明用遗传算法进行优化电催化氧化磺胺甲恶唑条件是可行的。
| [1] |
Richardson B J, Lam P K S, Martin M. Emerging chemicals of concern: Pharmaceuticals and personal care products (PPCPs) in Asia, with particular reference to Southern China[J]. Marine Pollution Bulletin, 2005, 50(9): 913-920. DOI:10.1016/j.marpolbul.2005.06.034
(  0) 0) |
| [2] |
Ching-Hua Huang, Renew J E, Smeby K L, et al. Assessment of potential antibiotic contaminants in water and preliminary occurrence analysis[J]. Journal of Contemporary Water Research & Education, 2001, 120(1): 30-40.
(  0) 0) |
| [3] |
Bu Q, Wang B, Huang J, et al. Estimating the use of antibiotics for humans across China[J]. Chemosphere, 2016, 144: 1384. DOI:10.1016/j.chemosphere.2015.10.010
(  0) 0) |
| [4] |
Jiang M X, Wang L H, Rong J. Biotic and abiotic degradation of four cephalosporin antibiotics in a lake surface water and sediment[J]. Chemosphere, 2010, 80(11): 1399-1405. DOI:10.1016/j.chemosphere.2010.05.048
(  0) 0) |
| [5] |
张昱, 唐妹, 田哲, 等. 制药废水中抗生素的去除技术研究进展[J]. 环境工程学报, 2018, 12(1): 1-14. Zhang Y, Tang M, Tian Z, et al. Research progress of removal technology of antibiotics from antibiotic production wastewater[J]. Chinese Journal of Environmental Engineering, 2018, 12(1): 1-14. (  0) 0) |
| [6] |
孙子为, 归谈纯, 高乃云, 等. 高级氧化技术降解水体中抗生素的研究进展[J]. 四川环境, 2014, 33(5): 146-153. Sun Z W, Gui T C, Gao N Y, et al. Research progress on degradation of antibiotics Via advanced oxidation processes[J]. Sichuan Environment, 2014, 33(5): 146-153. DOI:10.3969/j.issn.1001-3644.2014.05.028 (  0) 0) |
| [7] |
Wang Y, Shen C, Zhang M, et al. The electrochemical degradation of ciprofloxacin using a SnO2 -Sb/Ti anode: Influencing factors, reaction pathways and energy demand[J]. Chemical Engineering Journal, 2016, 296: 79-89. DOI:10.1016/j.cej.2016.03.093
(  0) 0) |
| [8] |
Wu J, Zhang H, Oturan N, et al. Application of response surface methodology to the removal of the antibiotic tetracycline by electrochemical process using carbon-felt cathode and DSA (Ti/RuO2-IrO2) anode[J]. Chemosphere, 2012, 87(6): 614-620. DOI:10.1016/j.chemosphere.2012.01.036
(  0) 0) |
| [9] |
李虹雨, 王可, 邢璇, 等. 响应曲面法优化新型电化学系统深度处理垃圾渗滤液生化出水[J]. 环境化学, 2018, 37(4): 713-719. Li H Y, Wang K, Xing X, et al. Landfill leachate treatment by novel electrochemical system: Optimization of experimental conditions by Response Surface Methodology[J]. Environmental Chemistry, 2018, 37(4): 713-719. (  0) 0) |
| [10] |
Vahidian H R, Ali Reza Soleymani, Parsa J B. Development of a four-layered ANN for simulation of an electrochemical water treatment process[J]. Desalination & Water Treatment, 2015, 56(2): 388-398.
(  0) 0) |
| [11] |
Fan M, Hu J, Cao R, et al. Modeling and prediction of copper removal from aqueous solutions by nZVI/rGO magnetic nanocomposites using ANN-GA and ANN-PSO[J]. Sci Rep, 2017, 7(1): 18040. DOI:10.1038/s41598-017-18223-y
(  0) 0) |
| [12] |
Jiang B, Zhang F, Sun Y, et al. Modeling and optimization for curing of polymer flooding using an artificial neural network and a genetic algorithm[J]. Journal of the Taiwan Institute of Chemical Engineers, 2014, 45(5): 2217-2224. DOI:10.1016/j.jtice.2014.03.020
(  0) 0) |
| [13] |
Dai Q, Zhou J, Weng M, et al. Electrochemical oxidation metronidazole with Co modified PbO2, electrode: Degradation and mechanism[J]. Separation & Purification Technology, 2016, 166: 109-116.
(  0) 0) |
| [14] |
Aghaeinejad-Meybodi A, Ebadi A, Shafiei S, et al. Modeling and optimization of antidepressant drug Fluoxetine removal in aqueous media by ozone/H2O2, process: Comparison of central composite design and artificial neural network approaches[J]. Journal of the Taiwan Institute of Chemical Engineers, 2015, 48: 40-48. DOI:10.1016/j.jtice.2014.10.022
(  0) 0) |
| [15] |
Estahbanati M R K, Feilizadeh M, Iliuta M C. Photocatalytic valorization of glycerol to hydrogen: Optimization of operating parameters by artificial neural network[J]. Applied Catalysis B Environmental, 2017, 209: 483-492. DOI:10.1016/j.apcatb.2017.03.016
(  0) 0) |
| [16] |
高爱舫, 李爱国, 张莹, 等. 基于响应曲面法的US/UV/Fenton联合处理抗生素制药废水优化[J]. 安全与环境学报, 2014, 14(3): 180-183. Gao A F, Li A G, Zhang Y, et al. Application of response surface methodology for optimization of US/UV/Fenton combination process for antibiotic pharmaceutical wastewater[J]. Journal of Safety and Environment, 2014, 14(3): 180-183. (  0) 0) |
| [17] |
Li J, Liu Q, Ji Q Q, et al. Degradation of p-nitrophenol (PNP) in aqueous solution by Fe 0-PM-PS system through response surface methodology (RSM)[J]. Applied Catalysis B Environmental, 2017, 200: 633-646. DOI:10.1016/j.apcatb.2016.07.026
(  0) 0) |
| [18] |
王栗, 岳琳, 王开红, 等. 响应曲面法优化电化学氧化技术处理染料废水[J]. 环境工程学报, 2014, 8(3): 990-996. Wang L, Yue L, Wang K H, et al. Optimization of electrochemical oxidation of dye wastewater using response surface methodology[J]. Chinese Journal of Environmental Engineering, 2014, 8(3): 990-996. (  0) 0) |
| [19] |
Zhang Y, Pan B. Modeling batch and column phosphate removal by hydrated ferric oxide-based nanocomposite using response surface methodology and artificial neural network[J]. Chemical Engineering Journal, 2014, 249: 111-120. DOI:10.1016/j.cej.2014.03.073
(  0) 0) |
| [20] |
Liu B, Jin C, Wan J, et al. Modeling and optimizing an electrochemical oxidation process using artificial neural network, genetic algorithm, and particle swarm optimization[J]. Journal of the Serbian Chemical Society, 2018, 83(3): 379-390. DOI:10.2298/JSC170721101L
(  0) 0) |
 2019, Vol. 49
2019, Vol. 49


