2. 中国海洋大学海洋与大气学院,山东 青岛 266100;
3. 挪威科技大学海洋技术系,挪威 特隆赫姆 7491
振荡流中的静止圆柱以及静止流中的振荡圆柱在海洋工程和水动力学领域有着极大研究价值。该物理模型适用于很多海洋工程设施,如研究液化天然气运输船在受到波浪力摆动时,液舱中泵塔的受力;由多个圆柱组成的波能吸收器在波浪中的振动;水下防喷器受到扰动在流速较小的海水中的振荡[1]等。对于上述工程应用,涡激振动产生的力学问题会对建筑设施产生极大的影响,忽视这种影响可能酿成灾害性后果,因此研究圆柱体在振荡过程中的受力载荷至关重要。实际工程中,圆柱的数量和摆放方式各异,而并列排布的双圆柱系统是其中较为典型的一种。对双圆柱体在振荡过程中的受力载荷研究对于大量的实际工程应用问题具有突出的指导意义。
该问题的流体动力学模型可以简化为振荡流体中的结构物相互作用。该结构上沿振动方向的力可以由莫里森方程表示:
| $ F = \frac{1}{2}\rho D{C_{\rm{d}}}\left| U \right|U + \frac{1}{4}{\rm{ \mathsf{ π} }}\rho {D^2}{C_{\rm{m}}}\frac{{{\rm{d}}u}}{{{\rm{d}}t}}。$ |
而垂直于振动方向的力可以表示为:
| $ F = \frac{1}{2}\rho {U^2}D{C_{\rm{l}}}。$ |
其中:Cd为阻力系数;Cm为附加质量系数;Cl为升力系数。Keulegan[11]指出,这三个关键的水动力学系数依赖于无量纲数KC。KC数被定义为KC=UmT/D,Um为圆柱最大的振荡速度,T是圆柱的振荡周期,D为圆柱直径。在简单正弦振动中,KC数可以简化为2πA/D, A为圆柱振荡的振幅。Sarpkaya[12]指出,这三个水动力学系数不仅依赖于KC数,也同时依赖于另一个无量纲数β,β被定义为β=D2/Tν,ν为流体的运动学粘度系数。因为雷诺数Re定义为Re=UmD/v因此雷诺数Re也可表示为Re=β×KC。
单个圆柱在均匀流中的水动力特性已经得到了广泛的研究。Bearman等[3]实验测量了KC数范围为4~55和β范围为100~166时的圆柱体上的流体力合力,小KC数范围内,阻力系数Cd与理论结果吻合较好。Sarpkaya[4]实验在稳定流场所对应的KC数范围下,合理的预测阻力系数和附加质量系数随着KC数上升的变化趋势。Tatsuno和Bearman[5]在不同的KC数值下进行了实验,并确定了8种不同的流动状态。
与单个圆柱相比,多体圆柱在静止流场中振荡的水动力特性会复杂很多。这是圆柱的尾流之间的相互作用所导致的。对于串联圆柱系统,下游圆柱受到上游圆柱尾流作用,在间隙比较小时会产生驰振现象(Wake-induced galloping)[6]。Chen等[7]对雷诺数为100,间隙比为2.0~5.0的双圆柱系统进行了数值模拟,并分析了不对称振动的现象。为了进一步研究双圆柱系统水动力特征和其受力载荷,本文首先进行了了静水中振荡的并列双圆柱动力特性的模型实验。此外,为了更好的理解双圆柱的流场特征及其机理,本文同时对并列双圆柱系统在静止流场中的运动进行了数值模拟,从能量的角度对阻力系数增大进行了机理分析。
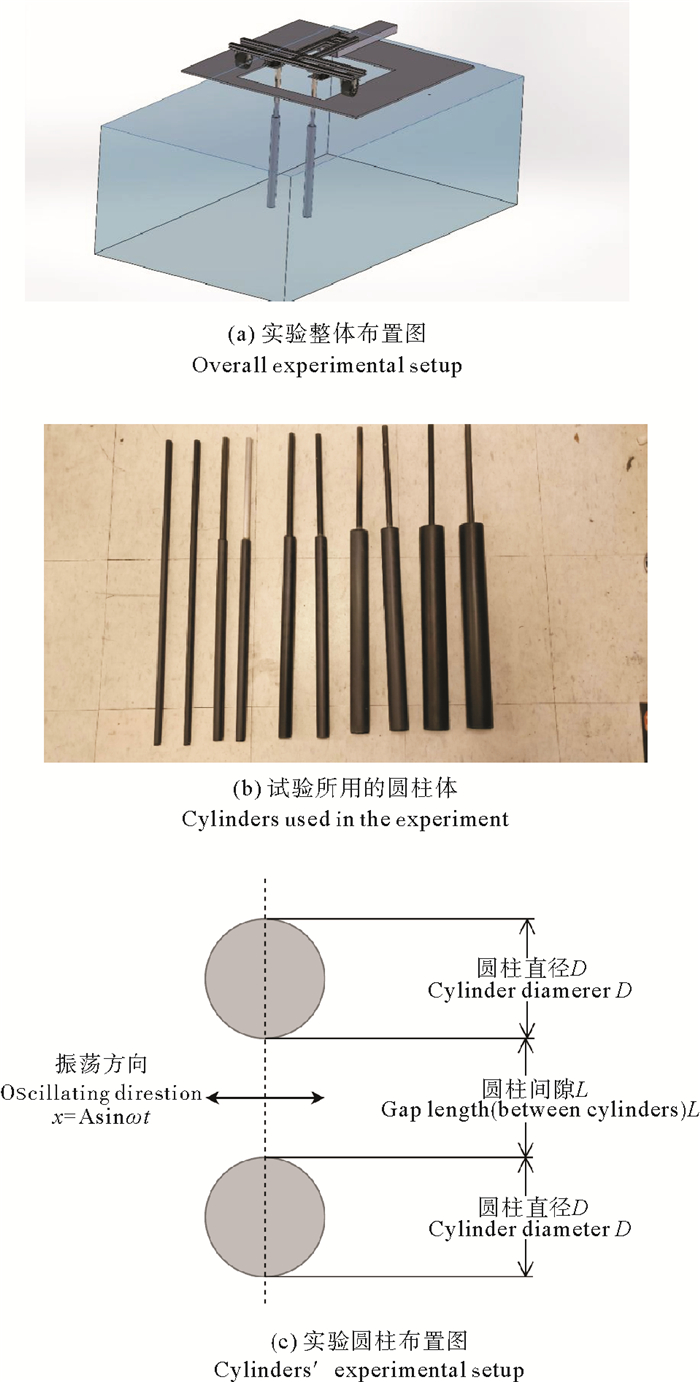
1 实验设置 1.1 实验装置与器材本研究实验在麻省理工学院拖曳水池实验室的拖曳水池中进行,研究静水中振荡圆柱的水动力特性,实验整体布置如图 1(a)所示, 水池长1.5 m,宽和高均为1 m。实验所使用圆柱的表面经过电镀,以保持其表面光滑,从而减小因表面粗糙引起的误差,圆柱直径包括2.54、3.81、5.08与6.35 cm。圆柱被固定在拖曳平台上,拖曳平台与力传感器相连;拖曳平台下方有2个滑轮,实验时,由电脑控制的拖曳平台在搭建在水池上方的平板上做正弦式往复运动。只有圆柱浸入水中,其他的装置均不会对圆柱的水动力学结果产生影响。实验使用ATI Gamma六分力传感器对力进行实时记录。本次实验采用直径为3.81 cm的圆柱,与该尺寸的圆柱相比,实验水池范围(1.5 m×1 m×1 m)足够大,当圆柱在水池中心位置处振荡时,产生的涡街和尾流无法传播到水池边界处,因而可忽略边界效应,将该振荡视为圆柱在无限大的水域中进行的振荡。并列圆柱的布置如图 1(c)所示,L为两圆柱之间的间隙,D为圆柱直径,为了便于说明,实验引入间隙比(gap ratio=L/D)的概念,即两圆柱间距与圆柱直径的比值。振动位移随时间的变化可表示为x=Asinωt, 其中,A是振幅,ω是振动的角速度。
|
图 1 实验布置和模型 Fig. 1 Experiment setup and models |
振荡圆柱体在静止流体中所受的力可以被分解为2个部分,第一部分为沿振动方向的力,可以用莫里森方程表示:
| $ {F_{\rm{d}}} = \frac{1}{2}\rho D{C_{\rm{d}}}\left| U \right|U + \frac{1}{4}{\rm{ \mathsf{ π} }}\rho {D^2}{C_{\rm{m}}}V。$ |
第二部分为垂直于振动方向的力(称为升力),可以表示为:
| $ {F_1} = \frac{1}{2}\rho {U_2}D{C_1}。$ |
其中Cd、Cm和Cl分别是阻力系数,附加质量系数和升力系数。三者主要由KC数(2πA/D)、β数(D2/Tυ)和间隙比(L/D)三个无量纲数决定,其中,T是振动周期,υ是流体的运动学粘度系数。实验中,KC数从1~20变化,β数的选取范围是350~2 810。双圆柱的间隙比设定为0.5、1.0、2.0和3.0。每个实验工况重复3次,以保证实验结果的可靠性。
2 实验结果与分析 2.1 实验验证并列排列,KC =12.1,β=550,L/D=0.5。
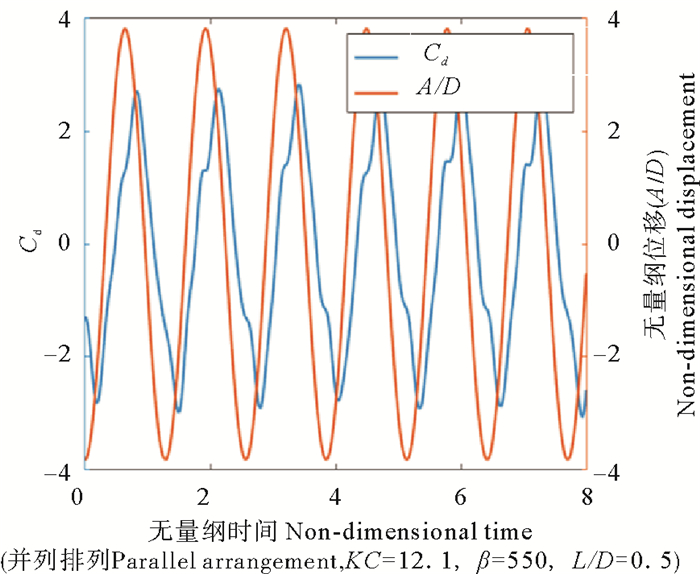
图 2给出了在静水中,并列双圆柱(直径5.08 cm,间隙比0.5,KC数12.1,β数550)的位移和阻力系数Cd随时间的变化图中,圆柱的位移随时间正弦变化,阻力呈现多频变化,且相位落后于位移。
|
图 2 无量纲位移和振动方向的阻力系数随着时间的关系 Fig. 2 non-dimensional motion and drag force vs non-dimensional time |
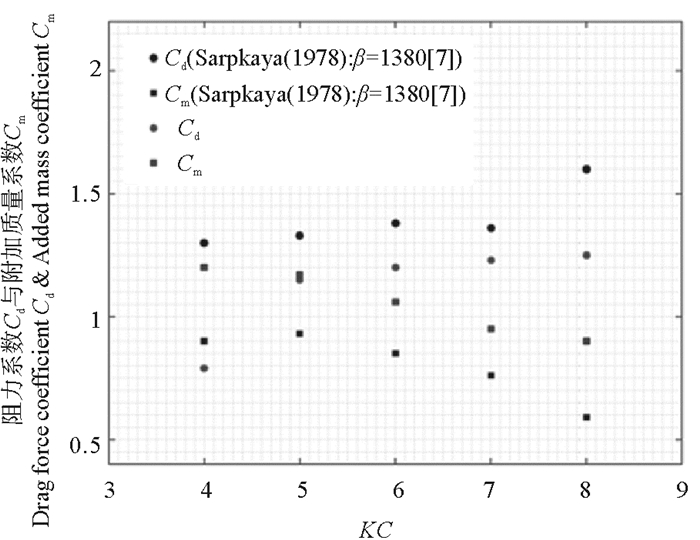
Bearman和Sarpkaya分别对振荡流体中的静止圆柱进行了类似实验,图 3比较了本文结果与Sarpkaya[7]的结果,可以发现两组实验的趋势相同,但数值上一定差异。两组实验的区别在于,在Sarpkaya[7]的实验中,静止圆柱被置于振荡流场中,而本次实验是将做标准正弦振荡的圆柱置于静止流场。此外,两组实验选取的β数略有差异(本文实验β数为1 400,Sarpkaya[7]中β数为1 380)。然而两种实验方法的结果都表明,随着KC数的增加,附加质量系数Cm有所下降,而阻力系数Cd基本呈上升趋势。
|
( 本次研究 β=1 400;Sarpkaya: β=1 380[7] ) 图 3 Cd和Cm随着KC数的变化以及本次实验和Sarpkaya实验结果对比 Fig. 3 Comparison of Cd and Cm vs KC number between our experiment β=1 400 and Sarpkaya's experiment β=1 380 |
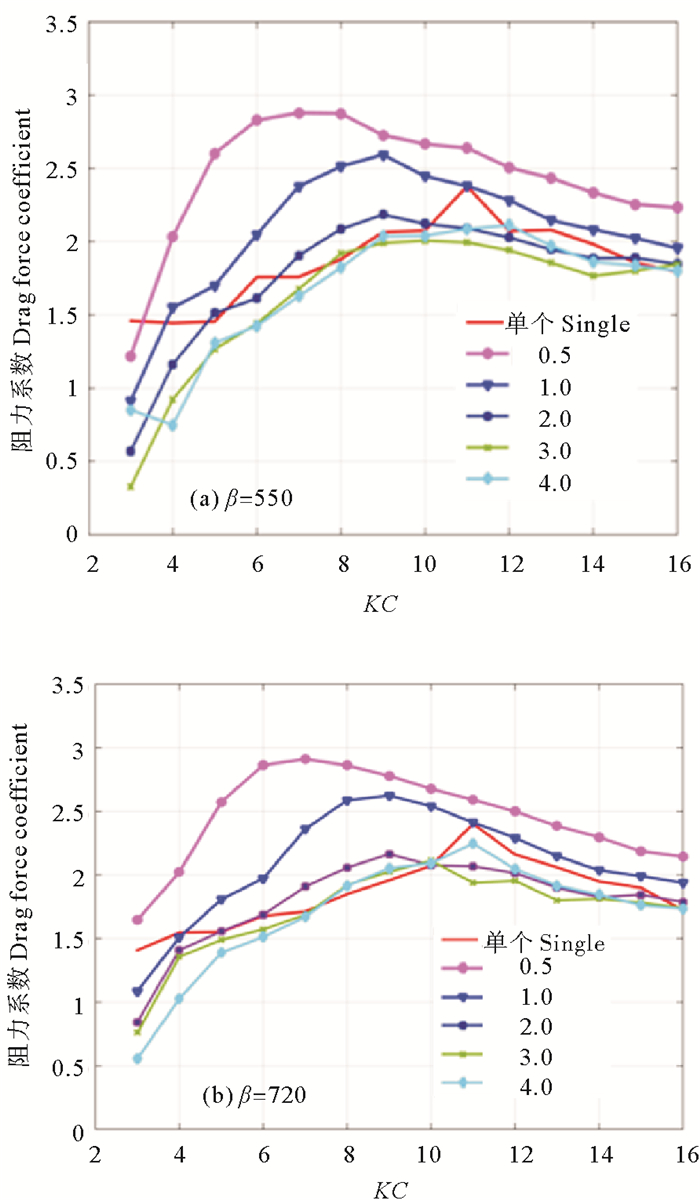
阻力系数Cd是莫里森公式中的一个关键系数。与单圆柱相比,双圆柱系统在流场中振荡时,两圆柱之间会产生相互作用,因而会使得并列双圆柱的流场比单圆柱的复杂。图 4(a)和(b)分别给出了β数为550和720工况,不同间隙比情况下的平均阻力系数Cd随着KC数的变化。随着间隙比减小,双圆柱平均阻力系数Cd有增大趋势,在间隙比为0.5(试验中所采用的最小的间隙比),KC数大于5时,阻力系数Cd明显大于单圆柱振荡时的阻力系数Cd。而在KC数较小(3, 4)时,二者差异不大。这是由于正弦振荡中的圆柱,KC数可以表示为KC=2πA/D,A是圆柱振荡的振幅,D是圆柱的直径,小KC数对应的圆柱振幅较小,激发的尾流较弱,双圆柱之间的相互作用因而也相对较弱,很难观察到阻力系数Cd的增强现象。当间隙比较大(3.0)时,两者数值相近。这是由于当两个圆柱距离较远时,两圆柱之间的水动力相互作用很弱,故呈现出与单圆柱相一致的水动力特性。
|
图 4 不同间隙比下的并列双圆柱平均阻力系数Cd随KC数的变化 Fig. 4 Drag coefficient vs KC number under different gap ratio |
附加质量系数Cm是莫里森公式中的另一个关键系数。由于双圆柱振荡引起的流场与单个圆柱的流场不一致,流体质点的运动情况发生了明显变化,从而导致附加质量系数Cm不同。
图 5(a)和(b)分别给出了β数等于550和720时,附加质量系数Cm随KC数的变化。由图可见,Cm随着KC数的增大而基本呈减小趋势;且圆柱之间的距离越近,附加质量系数Cm越大。与阻力系数Cd类似,当间隙比较大(3.0)时,由于两个圆柱相互作用弱,因此附加质量系数Cm也与单个圆柱的情况相类似。但是在间隙比为0.5时,尽管在小KC数下两者数值相近,但是当KC数大于6时,0.5间隙比下双圆柱的附加质量系数明显大于单圆柱的附加质量系数,而且前者很快趋于平稳。

|
图 5 不同间隙比下的并列双圆柱平均附加质量系数随KC数的变化 Fig. 5 Added mass coefficient vs KC number under different gap ratio |
同时,图 5(a)和(b)显示,同样的β数下,当间隙比为1.0时,Cm约在KC数等于6时开始趋于稳定。当间隙比为2.0时,Cm约在KC数等于8时趋于稳定。当间隙比为3.0时,Cm约在KC数等于11时趋于稳定。单圆柱的情况下(也可以理解为间隙比为∞),β=550时,Cm在实验的KC数范围内未出现稳定,β=720时,Cm在KC数等于13时趋于稳定。很明显,随着间隙比的增大,Cm在更大的KC数达到稳定。在到达稳定之前,Cm随着KC的增加而减小。
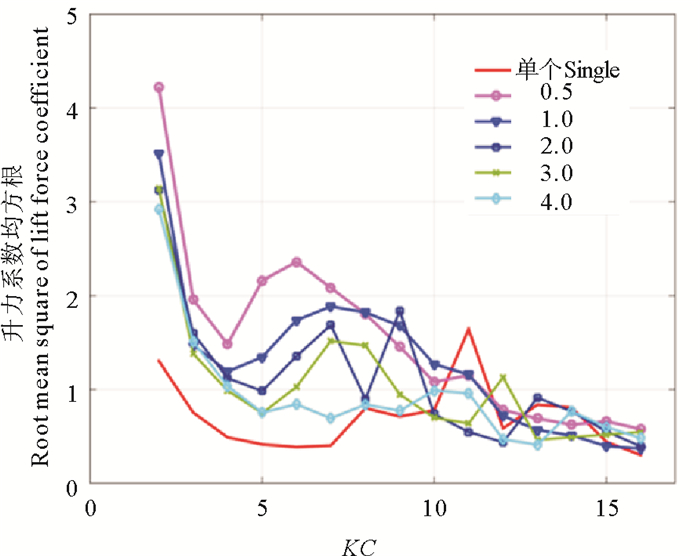
2.4 升力系数图 6为β数为550时,不同间隙比下的升力系数的均方根Cl, rms随KC数变化的情况。
|
图 6 β=550时,间隙比为0.5~4.0下升力系数均方根随KC数的变化 Fig. 6 Root mean square of lift force coefficient vs KC number (β=550, gap ratio=0.5~4.0) |
由图可知,在KC数等于5~10的范围内,并列圆柱的升力系数均方根值要大于单圆柱的。同时,随着KC数的增大,升力系数均方根值逐渐降低,但存在波动,而且间隙比越小, 该波动对应的KC数也越小。比如单个圆柱的波动出现在KC数等于11的位置,间隙比为1.0的情况中,波动出现在KC数等于7的位置,而间隙比为0.5的情况中,波动出现在KC数等于6的位置。
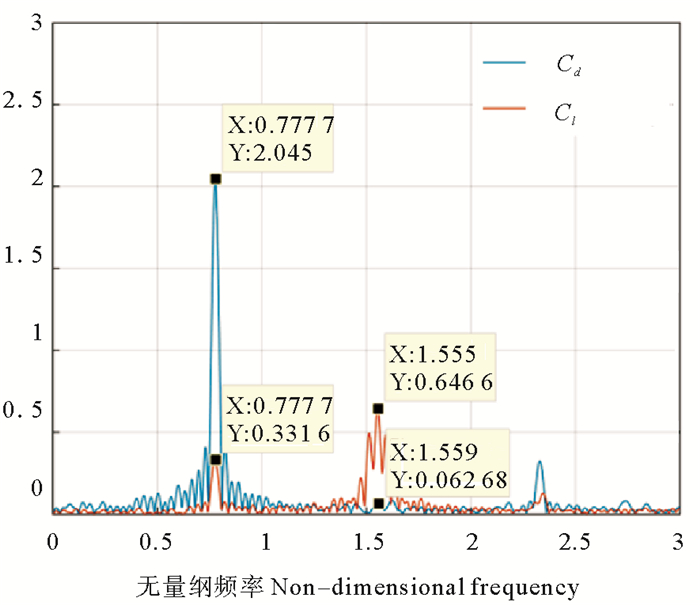
为进一步对比并列圆柱和单圆柱阻力系数Cd和升力系数Cl的不同,实验选取单圆柱(KC=9,β=550),将所测升力系数Cl和阻力系数Cd的时域数据经过傅立叶变换,得到Cl和Cd的频谱(见图 7)。可以看到,两个系数的一阶频均在0.77处,同时升力系数Cl在1.55(约二倍频率处)处出现了明显的二阶分量,且二阶分量占优。阻力系数Cd在2.33处出现较明显的二阶分量(约三倍频率处),但一阶分量占优。
|
图 7 单圆柱(KC=9, β=550)情况下Cl和Cd的傅里叶频谱 Fig. 7 Fourier spectrum for single cylinder (KC=9, β=550) |
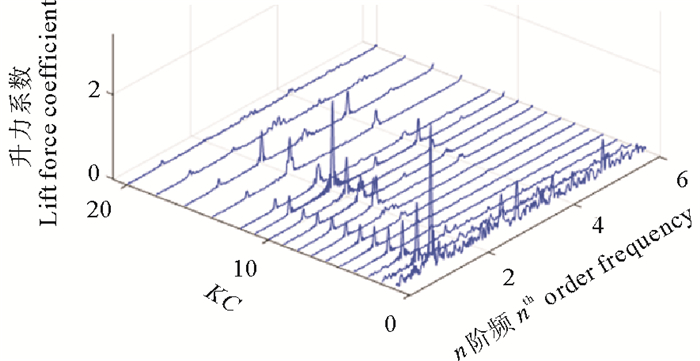
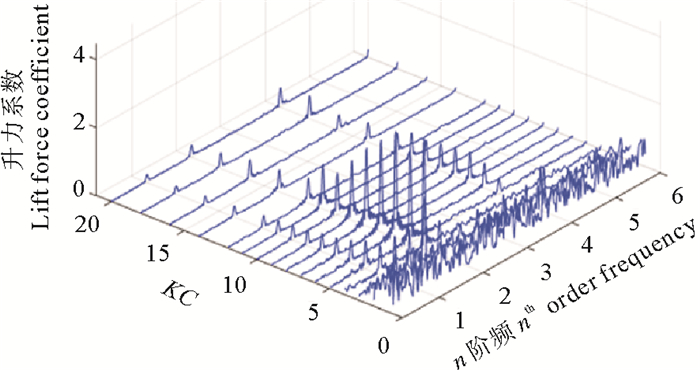
此外,对β=550条件下,不同KC数(1~20)的单圆柱和双圆柱(L/D=0.5)的实验数据进行傅立叶变换,得到x坐标为阶频数,y坐标为KC数,z坐标为谱密度的3D频谱图(见图 8、9)。
|
图 8 单个圆柱情况下傅里叶变化得到的Cl频谱图 Fig. 8 Fourier spectrum for single cylinder's lift coefficient |
|
图 9 双圆柱并列振荡情况下(间隙比0.5)傅里叶变化得到的Cl频谱图 Fig. 9 Fourier spectrum for dual cylinders' lift coefficient (gap ratio=0.5) |
对比图 8、9,可以看到单圆柱情况下,随着KC数的增大,圆柱的升力系数频率先是一阶占优,而后逐渐过渡到二阶占优(KC=11)。并列圆柱情况下,升力系数主要表现为二阶频率占优,并且存在较为明显的四阶频率分量。
3 数值模拟结果与分析由于在水槽中进行的实验很难将流场清晰地展现出来,因此,为了进一步分析双圆柱并列振荡和单圆柱振荡的流场特征,本次研究开展了基于BDIM(Boundary Data Immersion Method)的数值模拟,得到不同振荡形式下的流场实时数据和流场的涡量云图。研究将通过数值模拟实时数据计算升力系数、阻力系数和附加质量系数,并设置控制体,从能量的角度解释水槽实验中阻力系数增大的现象。Zhao[10]的研究证明,与三维模型相比,二维数值模型也能够清晰的描绘出流场特征并准确的计算圆柱的水动力学载荷,因此,本次研究使用二维模型进行模拟。
数值模拟的计算中将所有物理量都无量纲化:(x, y)=(x’, y’)/D、(u, v)=(u’, v’)/Um、p=p’/ρUm、t=Umt’/D。(x, y)是网格上的坐标。(u, v)是x、y方向上的速度分量t、p、ρ和Um分别是时间,压强,流体密度和圆柱的最大振荡速度,则无量纲化的控制方程化为:
| $ \begin{array}{l} \frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} + \frac{{\partial p}}{{\partial x}} - \frac{1}{{{\mathop{\rm Re}\nolimits} }}{\nabla ^2}u = 0。\\ \frac{{\partial u}}{{\partial t}} + u\frac{{\partial v}}{{\partial x}} + v\frac{{\partial v}}{{\partial y}} + \frac{{\partial p}}{{\partial y}} - \frac{1}{{{\mathop{\rm Re}\nolimits} }}{\nabla ^2}v = 0。\\ \;\;\;\;\;\;\;\;\;\;\;\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} = 0。\end{array} $ |
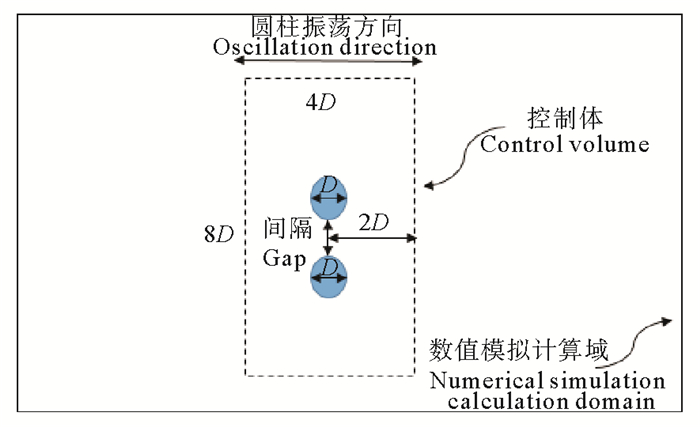
数值模拟布置如图 10所示,虚线表示控制体的边界。控制体长度为8D,宽度为4D,以满足大运动幅度的要求。因为数值模拟的边界是不可穿透的,因此将计算域的大小设置为40D×20D,以达到消除边界效应和阻挡效应。Lily-Pad的求解器不需要我们建立网格,屏幕的像素将直接成为网格的节点并建立非结构化网格。然而,求解器要求必须以像素为单位定义柱面和计算域的大小,因此在计算中,为了平衡计算效率和精度,每个圆柱体的直径D被设置为50个像素。
|
图 10 数值模拟布置图 Fig. 10 Numerical simulation setup |
首先采用三种不同全局精度的网格(delta/D=0.025、0.02和0.016)对振荡单圆柱绕流进行数值模拟,以检验网格的收敛性。收敛性验证中,KC数目设置为6,雷诺数Re设置为120。计算所得的附加质量系数和阻力系数见表 1。以delta/D=0.016所得到的Cm值(1.975)和Cd值(1.979)为参考,计算不同网格精度条件下,附加质量系数Cm和阻力系数Cd的相对误差和。
|
|
表 1 网格收敛性验证 Table 1 Grid convergence verification |
由表 1可知,与delta/D=0.016的工况相比,delta/D=0.02工况的附加质量系数的相对误差为0.2%,阻力系数的相对误差为0.56%。相比之下,delta/D=0.025工况的附加质量系数的相对误差为6.26%,阻力系数的相对误差为8.38%,远大于delta/D=0.02工况的相对误差,证实了delta/D=0.02的网格满足收敛性要求。图 11(b)和(c)进一步给出了delta/D为0.02和0.016时,圆柱向右以最大速度通过平衡位置的的涡量云图(其相位定义为π/2),可以看到两者几乎相同。然而,图 11(a)中delta/D为0.025的结果明显不同,流线对称,未观察到圆柱两侧交替泄涡现象。

|
图 11 在KC=6时间为65时,不同网格的涡旋场的比较 Fig. 11 Comparison of vortices in different grids when KC=6, non-dimensional time=65 |
为了证明数值模拟算法的正确性,在进行数值模拟研究前,研究首先使用前人在精度更高的网格上计算得到的结果进行比对:另取与Tong[9]相同的工况参数设置,即KC数为5、雷诺数Re为100,并将该工况下使用三种精度更高的网格计算得到的Cm和Cd的结果和Tong[9]进行对比,见表 2。
|
|
表 2 Tong(2015)[9]数值模拟参数和本次数模拟参数的对比 Table 2 Comparison between Tong (2015)[9] numerical simulation parameters and current simulation parameters |
Tong[9]设置的三种网格delta/D分别为0.003, 0.001, 0.000 75,其精度较本次研究使用的网格更高,其计算得到的(Cd,Cm)分别为(2.11,2.43)、(2.11,2.43)、(2.11,2.42)、最终Tong[9]选取了网格2即delta/D为0.001的网格进行数值模拟。与网格2相比对,本次研究中网格4计算的结果(2.29,2.23)与之差距较大,网格5得到的Cd和Cm略小于网格2计算的结果,网格6计算的Cd小于网格2计算的Cd,而Cm略大于网格2。同时,与网格6相比,网格5计算的Cd更接近于Tong[9]使用的精度更高的网格2的Cd值。因此网格5和网格6满足收敛性验证,且其计算结果与前人在精度更高的网格上的计算结果更为接近,满足正确性验证。同时,从网格5和网格6中都可以观察到交替泄涡的现象。为了提高运算效率,研究采取网格5(delta/D=0.02)进行数值模拟计算。
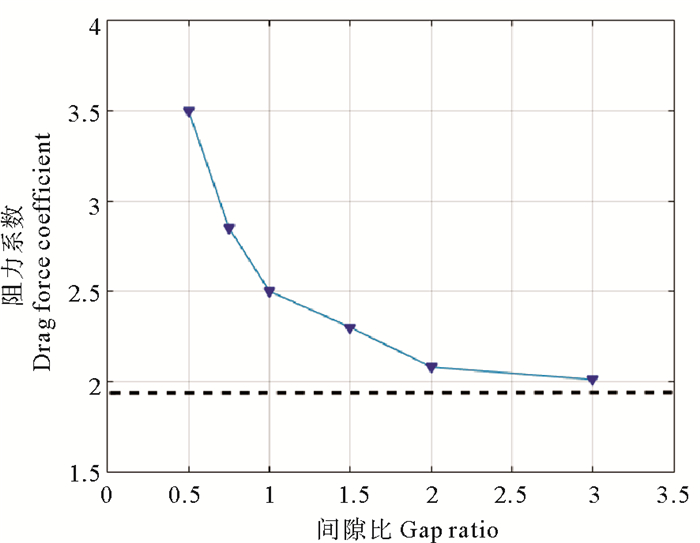
3.2 阻力系数Cd分析在并列双圆柱的数值模拟中,雷诺数Re选定为120,KC数为6,β数(Re/KC)为20,间隙比选定为0.50、0.75、1.00、1.25、1.50、2.00和3.00,同时选取单个圆柱振荡进行对比(见图 12),图中的虚线所对应的纵坐标值代表同一KC数和β数下的单个圆柱阻力系数Cd的值。
|
图 12 KC=6时的阻力系数Cd Fig. 12 Drag Coefficient (KC=6) |
可见,振荡并列圆柱的阻力系数Cd比单圆柱的较大,随着间隙比的增大,阻力系数Cd单调减小,并趋近于单圆柱的阻力系数。这与实验结果的趋势一致。
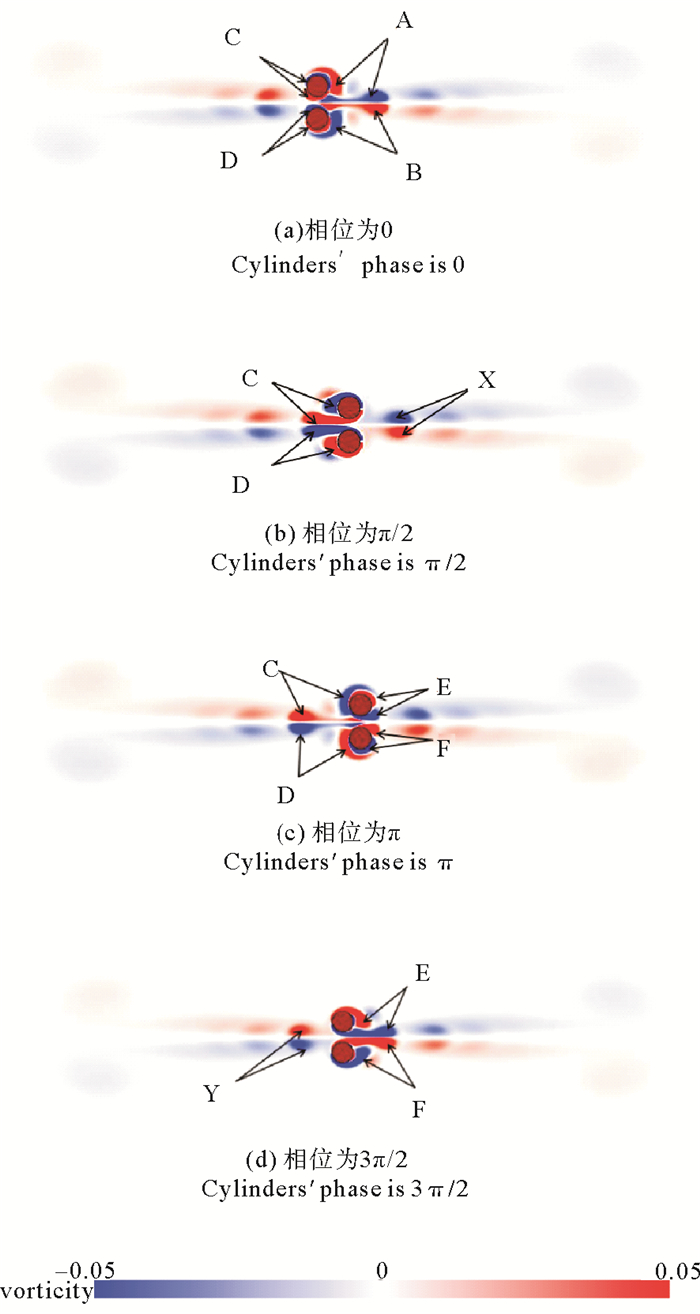
4 数值模拟的流场分析 4.1 振荡双圆柱流场图 13给出了间隙比为0.5振荡双圆柱绕流在一个周期内的4个特征时刻的流场,在这4个时刻圆柱的运动状态分别表示左侧最大位移处(定义相位为0),向右通过平衡位置处(定义相位为π/2),右侧最大位移处(定义相位为π),向右通过平衡位置处(定义相位为3π/2),以此描述一个运动周期内的流场变化。图 13(a)是圆柱运动到最左侧位置(相位为0)时的流场,此时圆柱泄出涡对A和B,A的下部涡流(蓝色的逆时针漩涡)和B的上部涡流(红色的顺时针漩涡)携带了大量能量。并在间隙中产生强相互作用,形成强喷射流X,快速远离圆柱,其速度超过了圆柱的振荡速度。当圆柱移动到右侧最大位移时,如图 13(c)所示,涡对C和D泄出,与A和B类似,C的下部涡流和D的上部涡流在间隙中形成了新的涡流对Y。与X类似,Y携带了大量能量并快速远离圆柱。同时圆柱激发了新的涡流对E与F。随后,如图 13(d)所示,此后圆柱将运动到左侧最大位移处,间隙中产生新的射流涡对。这些携带能量且具有较快速度的涡对,是双圆柱系统阻力系数增大的原因。
|
图 13 双圆柱的流场发展(KC数为6, 间隙比为0.5) Fig. 13 Flow field development of double cylinders (KC=6, gap ratio=0.5) |
为了从能量角度定量的解释双圆柱系统阻力系数增大的现象,本文引入平均能量流出率(Mean Energy Outflow Rate,简称),其定义式为:
| $ \overline {EOR} = \frac{1}{T}\int\limits_0^T {\oint {\frac{1}{2}} } \left| \mathit{\boldsymbol{u}} \right|\mathit{\boldsymbol{u}} \cdot \mathit{\boldsymbol{n}}{\rm{d}}s{\rm{d}}t。$ |
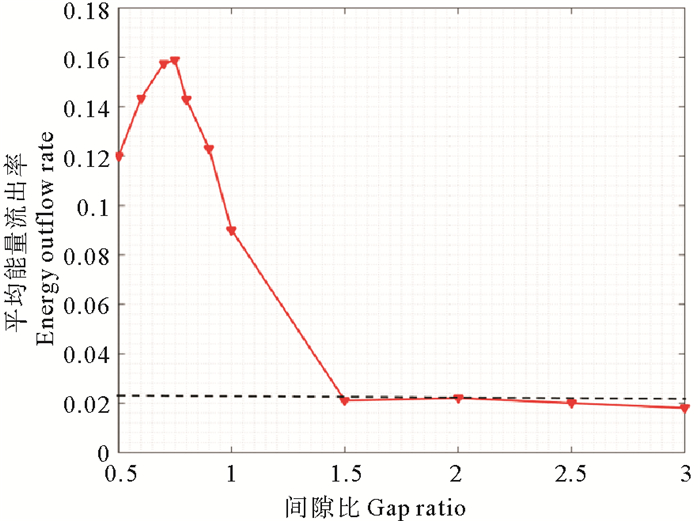
其中:u为无量纲流体速度,其方向是控制体的外法线方向;ds是控制体的无量纲的单位边长,控制体设置示意图见图 10。平均能量流出率的物理含义是指:一个完整的振荡周期中,选定控制体在单位时间内能量的流出,其大小体现了该情况下由于圆柱振荡而流出的能量多少。选取KC数等于6的情况,对不同间隙比下的双圆柱系统求得平均能量流出率(控制体内包含圆柱体),如图 14所示,其中水平虚线表示振荡单圆柱工况的平均能量流出率。
|
图 14 KC数等于6时不同间隙比下圆柱求得平均能量流出率 Fig. 14 Energy outflow rate of cylinder withdifferent gap ratio(KC=6) |
可以看出,间隙比较小时,$\overline {{\rm{EOR}}} $远大于单个圆柱的情况。随着间隙比的增大,$\overline {{\rm{EOR}}} $先增大,当间隙比达到0.75时$\overline {{\rm{EOR}}} $达到顶峰,随后随着间隙比的增大而减小;当间隙比增大到1.5左右的时候,双圆柱系统的$\overline {{\rm{EOR}}} $已经与单圆柱的接近,随后随着间隙比的增大,双圆柱系统的$\overline {{\rm{EOR}}} $保持稳定。双圆柱系统的$\overline {{\rm{EOR}}} $在间隙比为0.75时而非0.5时达到最大,这是由于0.5的间隙比下,尽管圆柱之间的相互作用最强,但是由于距离较近,无法排出体积较大的涡,因而无法携带很大的能量;而0.75的间隙比下,圆柱之间仍然有较强的相互作用,同时该间隙比可以使涡充分的成长,进而携带较多的能量。随着间隙比的进一步增大,圆柱之间的相互作用减弱,当间隙比达到1.5时,由于两个圆柱间距较远,泄出的涡之间的距离也较大,几乎无法产生相互作用,故此时的平均能量流出率也非常接近单圆柱的。此后进一步增加间隙比,由于双圆柱之间流场的相互作用几乎不存在,因此更大的间隙比对能量流出的影响不大,平均能量流出率的大小也与单圆柱的类似。
因为平均能量流出率是对圆柱相对于水的相对速度进行边界积分,而相对速度的大小影响了莫里森公式中的阻力,系数Cd,因此平均能量流出率随间隙比的变化从能量的角度解释了小间隙比条件下阻力系数Cd增大的机制。
5 结语本文对做正弦式往复振荡的并列双圆柱系统在静止流场里的水动力性能进行了实验和数值模拟。实验发现,小间隙比并列振荡的情况与单个圆柱相比,阻力系数Cd在KC数>5时出现明显的增大现象,附加质量系数Cm在小KC数下提前趋于稳定,升力系数Cl的方均根增大,而且Cl在小KC数下提前出现二阶频率分量。随后,使用基于BDIM的数值模拟,针对KC数为6,β数为20(Re=120)的情况进行水动力学载荷计算和流场分析。数值模拟通过使用delta/D=50的网格,发现双圆柱系统在小间隙比下并列振荡时,由于两圆柱流场之间的相互作用,在间隙中会产生间隙流和携带能量的涡流。通过计算各系统中流出的能量,研究发现小间隙比下双圆柱系统产生的涡流携带的能量高于单圆柱系统,这一携带更多能量的涡流导致了小间隙比下双圆柱系统阻力系数Cd的增大,而较大间隙比下双圆柱之间的作用比较微弱,流出的能量也接近与单圆柱振荡流出的能量。
| [1] |
Chen Y, Fu S, Xu Y, et al. High order force components of a near-wall circular cylinder oscillating in transverse direction in a steady current[J]. Ocean Eng, 2013, 74(7): 37-47.
(  0) 0) |
| [2] |
Xu Y, Fu S, Chen Y, et al. Experimental investigation on vortex induced forces of oscillating cylinder at high Reynolds number[J]. Ocean Syst Engi, 2013, 3: 167-180. DOI:10.12989/ose.2013.3.3.167
(  0) 0) |
| [3] |
Bearman P W, Graham J M R, Downie M J, et al. Forces on cylinders in viscous oscillatory flow at low Keulegan-Carpenter numbers[J]. J Fluid Mech, 1985, 154: 337-356. DOI:10.1017/S0022112085001562
(  0) 0) |
| [4] |
Sarpkaya T. Force on a circular cylinder in viscous oscillatory flow at low Keulegan-Carpenter numbers[J]. J Fluid Mech, 1986, 165: 61-71. DOI:10.1017/S0022112086002999
(  0) 0) |
| [5] |
Tatsuno M, Bearman P W. A visual study of the flow around an oscillating circular cylinder at low Keulegan-Carpenter numbers and low Stokes numbers[J]. J Fluid Mech, 1990, 211: 157-182. DOI:10.1017/S0022112090001537
(  0) 0) |
| [6] |
Chen W, Ji C, Williams J, et al. Vortex-induced vibrations of three tandem cylinders in laminar cross-flow: Vibration response and galloping mechanism[J]. J Fluids and Struc, 2018, 78: 215-238. DOI:10.1016/j.jfluidstructs.2017.12.017
(  0) 0) |
| [7] |
Chen W, Ji C, Xu W, et al. Response and wake patterns of two side-by-side elastically supported circular cylinders in uniform laminar cross-flow[J]. J Fluids and Struc, 2015, 55: 218-236. DOI:10.1016/j.jfluidstructs.2015.03.002
(  0) 0) |
| [8] |
Weymouth GD, Yue D K. Boundary data immersion method for Cartesian-grid simulations of fluid-body interaction problems[J]. J Comput Phys, 2011, 230(16): 6233-6247. DOI:10.1016/j.jcp.2011.04.022
(  0) 0) |
| [9] |
Feifei Tong, Liang Cheng, Ming Zhao, et al. Oscillatory flow regimes around four cylinders in a square arrange-ment under small KC and Re conditions[J]. J Fluid Mech, 2015, 769: 298-336. DOI:10.1017/jfm.2015.107
(  0) 0) |
| [10] |
An H, Cheng L, Zhao M. Two-dimensional and three-dimensional simulations of oscillatory flow around a circular cylinder[J]. Ocean Eng, 2015, 109: 270-286. DOI:10.1016/j.oceaneng.2015.09.013
(  0) 0) |
| [11] |
Keulegan G H. Forces on cylinders and plates in an oscillating fluid[J]. J Res National Standards, 1956, 60(5): 423-440.
(  0) 0) |
| [12] |
Sarpkaya T. In-Line and Transverse Forces on Smooth and Sand-Roughened Cylinders in Oscillatory Flow at High Reynolds Numbers[D]. Monteray, California: Naval Postgraduate School, 1976.
(  0) 0) |
2. College of Oceanic and Atmospheric Sciences, Ocean University of China, Qingdao 266100, China;
3. Department of Marine Technology, Norwegian University of Science and Technology, Trondheim 7491, Norway
 2019, Vol. 49
2019, Vol. 49

