2. 中国海洋大学数学科学学院,山东 青岛 266100
随着计算机技术的发展,偏微分方程在物理学、气象学、天文学、海洋、航空与航天等学科和工程技术科学中发挥着越来越重要的作用,利用其可以刻画物理科学中的基本规律,如纳维-斯托克斯方程反映了粘性流体流动的基本力学规律。然而在复杂的场景下,偏微分方程的精确解析解很难求解出来。此时可以利用传统数值求解方法对其进行近似求解。常用的数值求解方法包括有限差分法、有限体积法、有限元法等。这些数值方法将偏微分方程的求解区域离散成若干网格点,之后在离散的网格点上提供解值,从而得到方程的近似解。王敞亮[1]分析讨论了计算机流体力学中控制方程有限差分法数值求解,具体从有限差分法的概念及基本思路进行了分析。廖敦明等[2]利用有限差分法对铸件凝固过程热应力场进行了数值求解及模拟,并且开发了基于有限差分法应力场模拟系统。文中阐述可将铸件成形过程划分成许多的小变形增量步,并且利用基于小变形热弹塑性理论来对每个小变形增量步进行求解。刘铁锤等[3]总结了国内外基于有限体积法对溃坝水流模拟的研究进展,其中介绍了应用于有限体积法的非结构网格、有限体积法中方程离散的步骤以及法向数值通量计算等。成思源[4]详细阐述和讨论了有限元法的原理及产生方法论。
虽然这些传统数值求解方法能够对于一些难以求出解析解的复杂的偏微分方程进行求解,但是当需要求解精度越高时,计算速度会非常缓慢,并且耗费的内存及磁盘空间等计算资源都非常惊人,差商所依赖的网格节点也会越多,此时会使得边界条件也不好处理。
最近几年,随着卷积神经网络(CNNs)的迅速发展,其在加速偏微分方程数值求解方面取得了重大突破。例如Bar-Sinai Y等[5-6]将CNN嵌入传统数值求解过程中,用它代替有限差分系数的计算,而其余的步骤仍使用传统方法,如计算通量、做时间步进。机器学习组件与传统数值求解方案紧密集成,并通过端到端可微编程框架进行训练。Kochkov D等[7]提出了一种新型的数值求解器,它不平均未解析的自由度,而是使用离散方程,在未解析网格上给出逐点精确解。Sirignano等[8]提出了一个深度学习偏微分方程模型(DPM),它是一种基于深度学习的偏微分方程增强方法,该方法优化了偏微分方程的函数形式。Um K等[9]针对偏微分方程离散化过程中出现的数值误差,离散化误差可以通过神经网络进行学习,训练好的网络可以在本地进行评估,从而可以减少数值误差,改进偏微分方程求解器的解。Pathak J等[10]引入了一种新的ML-PDE混合体系结构,该技术可以修正高雷诺数下湍流的粗网格模拟引起的数值误差,同时恢复高分辨率场的估计,并且能在以低分辨率求解系统PDE的同时获得高分辨率解轨迹。Tompson J等[11]提出了一种数据驱动方法,即利用深度学习的近似能力和标准求解器的精度来获得快速和高度真实的模拟。Obiols-Sales O等[12]提出了一个深度学习和物理模拟耦合的框架(CFDNet),实验结果表明使用CFDNet显著加快了数值求解的速度。
虽然这些方法在偏微分方程数值求解加速领域都取得了重大的突破,但是这些方法这些方法仍存在两个关键的缺点:缺乏物理先验知识的指导。多数方法建模时由于没有考虑物理先验知识的指导,在预测方程解的过程中忽略了部分物理信息,从而导致求解精度下降。忽略了多层级空间联结关系和全局信息。多数方法利用神经网络进行数值求解加速时,建模过程中采用扁平化建模,没有进行结构化的建模,因此并没有将多层级复杂空间联结关系考虑在内。除了目标节点周围节点会对该点产生影响,其他节点也会影响到目标节点,而多数方法仅仅考虑了目标节点周围的节点,忽略了全局空间的影响,从而引起全局信息缺失。
针对以上问题,本文利用经典图模型构建空间图结构,所有空间网格点作为图结点,并基于物理先验知识确定图结点间关系,构造融合全局信息的图邻接矩阵。因此,本文提出了基于图卷积的空间离散化数值求解加速方法,并利用该方法来加速求解一维平流方程。
1 方法 1.1 一维平流方程平流方程指的是任意变量水平输送导致该变量的局地变化的微分方程,它是大气运动中重要过程之一,因此,对平流方程的研究对大气运动的研究具有非常重要的意义。平流方程最简单的形式是一维平流方程,它被写成:
| $ \frac{\partial C}{\partial t}+\vec{v} \frac{\partial C}{\partial x}=0 。$ | (1) |
式中:C为标量浓度场C(x, t);
利用用欧拉格式对空间导数
| $ \left.\frac{\partial C}{\partial x}\right|_{x_i}=\sum\limits_{j=-k}^k \alpha_j C_{i+j} \text { 。} $ | (2) |
式中:{x1,…,xN}为空间网格点;Ci+j为点xi+j处的浓度;{α-k,…,αk}为预定义的有限差分系数。
利用欧拉格式进行数值求解可以在高阶情况下得到高精度的解,但是其计算速度极其缓慢,并且在复杂速度场下,如湍流速度场下,还会引起极大的数值扩散。
1.2 物理先验知识在进行一维平流方程空间离散化数值求解时,将方程的连续的定解区域进行离散,由于本文采用6点有限差分模板,因此之后将当前时刻每个点处的空间导数由预测得到空间离散化有限差分系数与上一时刻的该点处的浓度值及该点周围的6个点处的浓度值相结合来表示,由此可得到当前时刻每个点处的浓度值。6点有限差分模板是借鉴的传统数值求解方法,之后本文在此基础上进一步根据物理场的性质定义并设计了物理先验知识,从而对初始系数进行了设定。因此本文的物理先验知识分为两种:①对于每个节点周围的6个点,离目标节点越近的点对其影响越大;②除了这6个点以外,其他节点也会对目标节点产生影响。在通过图模型对一维平流方程空间离散化结构建模时,基于这两个物理先验知识确定图结点间关系,从而构造融合全局信息的图邻接矩阵。基于这两个物理先验知识,通过图模型构建空间结构邻接矩阵,根据先验知识①,对于每个节点周围的6个点,在邻接矩阵上将离目标节点更近的点的值设置的更大;根据先验知识②,由于除了每个点周围的6个点外的其他点也会对目标节点产生影响,因此不应将其他节点一概设置为0,将它们设置为与0接近的值。例如下面的矩阵。

|
(3) |
本文利用图卷积预测出有限差分系数,即系数
|
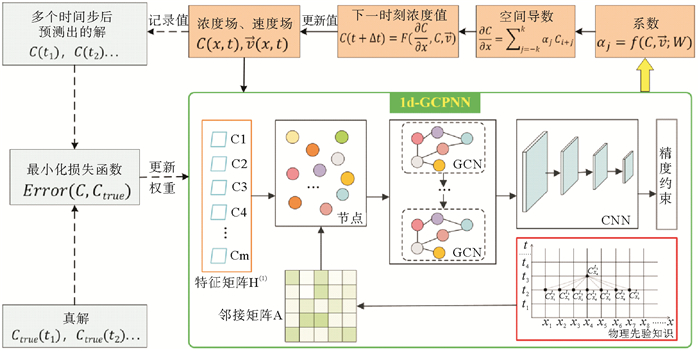
( 前向求解过程中,使用图卷积物理神经网络(红色框部分)预测出每一层的有限差分系数,之后去计算空间差分、时间步进,从而得到每一层的浓度值。在训练时,使用由基线求解器求解得到的高分辨率解下采样后的低分辨率数据集对模型进行优化。In the forward solution process, the physical neural network of graph convolution (red box part) is used to predict the finite difference coefficient of each layer, and then the spatial difference and time step are calculated to obtain the concentration value of each layer. During training, the low resolution data set sampled from the high resolution solution obtained by the baseline solver is used to optimize the model. ) 图 1 基于图卷积的一维平流方程空间离散化数值求解器整体框架 Fig. 1 Overall framework of spatial discretization numerical solver for one-dimensional advection equation based on graph convolution |
本文利用GCPNN(图 1红色框部分)来预测出有限差分系数,在该部分使用由第一层浓度值得到的输入特征矩阵(Feature matrix) H(1)和由网格节点间的空间结构关系得到的邻接矩阵(Adjacency matrix)A相乘,之后将得到的结果经过全连接层,从而得到第二层的特征,接着再将该层的特征与邻接矩阵相乘后经过全连接层,得到第三层的特征,重复上述操作,直到得到第n层的特征,之后再经过CNN卷积操作。
在最后加入了多项式精度约束(Polynomial constraint),它可以强制机器学习预测系数满足n阶多项式约束,从而使近似误差衰减为O(Δxn),如果学习的离散化适合于网格尺度上平滑的解,多项式精度约束将确保可以恢复经典的有限差分方法。
1.3.3 构建图结构及邻接矩阵基于图模型的一维平流方程空间离散化结构建模需要构建网格节点间的图结构关系,首先确定图结构的结点和边。
结点:将空间离散化后的高分辨率网格点下采样后得到的低分辨率点作为图结构的结点。
边:基于物理先验知识通过距离远近空间多层级化来设计图结构的边的权重。
之后建立所有网格点的空间结构关系;具体如下:假设空间离散化后共有m个网格点,每个网格点都有浓度值,每个网格点的浓度值由上一层该点处的值和该点周围2k个网格点的值来表示(即该点左边和右边各k个点。这里k是经实验得到的最优周围点数量,即通过k个周围点预测得到的中心点浓度值与真解间误差最小,在本文中取k为3,即6点有限差分模板。)。根据每个网格点的浓度值得到输入特征矩阵H(1),H(1)形状为(m,1),如下为特征矩阵H(1),其中C1,…,Cm分别为m个网格点上的浓度值。
| $ \boldsymbol{H}^{(1)}=\left[\begin{array}{c} C_1 \\ C_2 \\ C_3 \\ \cdots \\ C_{m-1} \\ C_m \end{array}\right] \text { 。} $ | (4) |
由空间结构关系可得到邻接矩阵A(m×m)为:

|
(5) |
通过邻接矩阵A可计算得到
| $ \boldsymbol{H}^{(l+1)}=\sigma\left(\check{\boldsymbol{D}}^{-\frac{1}{2}} \check{\boldsymbol{A}} \check{\boldsymbol{D}}^{-\frac{1}{2}} \boldsymbol{H}^{(l)} \boldsymbol{W}^{(l)}\right)。$ | (6) |
其中,H为预测出的每一时间层的特征矩阵,输入层为H(1);σ是非线性激活函数。
1.3.4 多步损失函数在训练过程中,本文使用多步损失函数,相对于单个时间步,多步损失函数可以稳定前向积分。多步损失函数即累积预测10个时间步的前向求解器预测结果,然后在整个空间域上与该时间段内的真解计算平均绝对误差(MAE)来做为损失函数:
| $ { loss }=\frac{1}{N \cdot M} \sum\limits_{i=1}^N \sum\limits_{j=1}^M\left|\boldsymbol{C}_j^{\text {predict }}\left(t_i\right)-\boldsymbol{C}_j^{\text {true }}\left(t_i\right)\right| 。$ | (7) |
其中:N表示10个时间步;M表示每个时间步上的网格节点个数。
2 实验过程及实验结果 2.1 数据集本文使用带有单调通量限制器的二阶VanLeer平流方案来作为基线求解器,之后以64×64的分辨率来运行基线求解器来获得参考真解(ground truth)。之后对获得的较高分辨率结果进行下采样得到32×32低分辨率的结果,即可为以粗糙网格训练的机器学习模型生成训练和测试数据集。
2.2 训练优化方法本文使用Tensorflow框架实现模型的构建,并采用8 000个解作为训练样本,2 000个解作为测试样本。在训练时,迭代次数(epoch)设置为300,批量大小(batch size)设置为128。
本文将基于图卷积的数据驱动离散化应用于一维平流,对于每个实验,本文都使用了6点有限差分模板,即公式(2)中的k为3,每个网格点处的浓度值由该点周围6个点的值来表示。本文应用含32个网格点的一维周期网格。本文分别设置Δt=0.5,Δx=1,u=1,然后计算
对于训练过程,采用1.3.4小节中的多步损失函数
| $ M A E=\frac{1}{N} \sum\limits_{i=1}^N\left|\boldsymbol{C}_i^{\text {predict }}-\boldsymbol{C}_i^{\text {true }}\right|。$ | (8) |
其中N表示网格节点的个数。
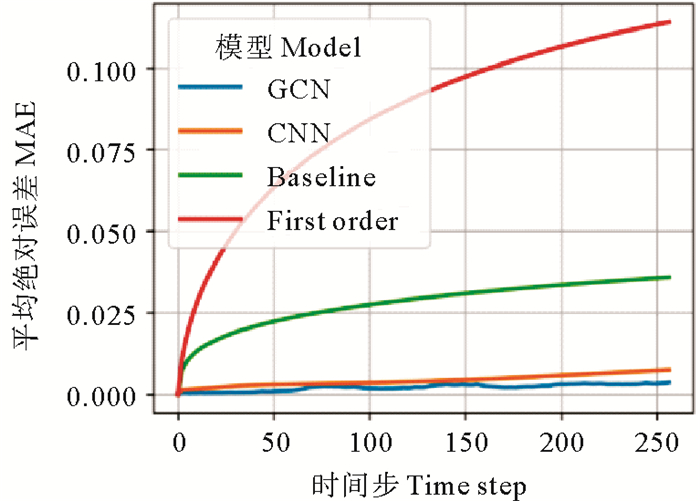
2.4 实验设计 2.4.1 对比实验本文将基于图卷积模型的求解器与基线求解器、一阶Vanleer平流格式求解器、基于cnn模型的求解器进行对比,将预测出的解与真解(Ground truth)之间的平均绝对误差(MAE)作为对比指标,图 2展示了在这些求解器上所有测试样本的平均绝对误差(MAE)随时间的变化,图卷积模型的误差最小且比基线二阶VanLeer格式求解器小8倍,并且图卷积模型比cnn模型的误差小。
|
图 2 在测试样本上得到的误差 Fig. 2 Error obtained on the test sample |
在测试样本上图卷积模型单步预测时间为0.35 s,cnn模型单步预测时间为0.29 s。在经过了250个时间步后,使用CNN模型的平均绝对误差的值约为0.007,使用图卷积模型的平均绝对误差的值约为0.002。因此虽然图卷积单步预测时间与cnn模型相比多消耗了20%,但精度却比CNN模型提高了71%。
2.4.2 消融实验(1) 基于物理先验知识①的邻接矩阵值更换
为了验证离某个网格节点越近的点对其影响越大的假设成立,本文在之前的邻接矩阵基础上进行了改动,且设计出了三种邻接矩阵,即将矩阵中的6个1替换为另外6个接近于1的数,且越靠近该节点的点处的值越大,三种模板设计分别为[0.97,0.98,0.99,0.99,0.98,0.97]、[0.75,0.85,0.95,0.95,0.85,0.75]、[0.7,0.8,0.9,0.9,0.8,0.7],并用这三种模板得到的邻接矩阵去进行训练,训练得到的test loss如表 1所示。从表中可以看出使用这三种邻接矩阵训练得到的test loss与使用原邻接矩阵训练得到的test loss相差无几,且使用[0.75,0.85,0.95,0.95,0.85,0.75]这种模板得到的test loss最低,由此可以得出离某个网格节点越近的点对其产生的影响越大,且邻接矩阵使用[0.75,0.85,0.95,0.95,0.85,0.75]这种模板来进行设计所得结果会更好。
|
|
表 1 不同邻接矩阵模板训练结果对比 Table 1 Comparison of training results of different adjacency matrix templates |
(2) 基于物理先验知识②的邻接矩阵值更换
为了验证对于某个网格节点,不仅该点周围的6个点对其有影响,其他点也会对该点产生影响,本文又设计了四种邻接矩阵,这次替换原邻接矩阵中的0,分别为①将所有0替换为0.1;②将所有0替换为0.2;③将所有0替换为0.001;④将所有0替换为0.003。并使用这四种邻接矩阵去进行训练,训练得到的test loss如表 2所示。从表中可以看出使用将所有0替换为0.001得到的test loss最低,由此可以看出除了某个点周围的6个点对该点有影响,其他点也对该点会产生影响,且邻接矩阵使用将所有0替换为0.001来进行设计所得结果会更好。
|
|
表 2 不同邻接矩阵模板训练结果对比 Table 2 Comparison of training results of different adjacency matrix templates |
(3) 有限差分模板更改实验
为了得到更好的有限差分模板,本文又设计了三种邻接矩阵,这次改变原邻接矩阵中每行1的个数(原邻接矩阵中为6),分别将其改为5、7、8个,使用这些邻接矩阵训练得到的test loss如表 3所示,从表中可以看出原邻接矩阵比其他三种矩阵训练得到的test loss都低,由此可以看出,6点有限差分模板是更好的。
|
|
表 3 不同邻接矩阵模板训练结果对比 Table 3 Comparison of training results of different adjacency matrix templates |
本文针对一维平流方程,在目前现有数据驱动离散化方法的基础上创新性的提出了基于图卷积的一维平流方程空间离散化数值求解加速方法,该方法在物理先验指导下基于图模型对一维平流方程空间离散化进行结构建模,并利用图卷积算法构建出预测模型,利用该模型学习最优的有限差分系数,实现加速数值求解。之后并进行了实验分析,包括对比实验和消融实验,主要结论如下:
(1) 本文提出的基于图卷积的一维平流方程空间离散化数值求解加速方法不仅可以在低分辨率下得到高精度的解,并且能加速求解,同时该方法的预测结果显著优于基线求解器和CNN模型求解器。
(2) 根据物理先验知识①进行邻接矩阵值更换,可得出结论即离某个网格节点越近的点对其产生的影响越大,且邻接矩阵使用[0.75,0.85,0.95,0.95,0.85,0.75]这种模板来进行设计所得结果会更好。
(3) 根据物理先验知识②进行邻接矩阵值更换,可得出结论即除了某个点周围的6个点对该点有影响,其他点也对该点会产生影响,且邻接矩阵使用将所有0替换为0.001来进行设计所得结果会更好。
(4) 通过更改有限差分模板中1的个数来进行实验可得出结论即使用6点有限差分模板达到的效果最好。
后续工作将考虑将本文方法应用到其他数值离散方案上,如有限体积法、有限元法、伪谱方法等。另外,在后续工作中还将考虑将本文方法推广到高维平流方程数值求解问题。
| [1] |
王敞亮. CFD控制方程中有限差分法的分析[J]. 中国新通信, 2019, 21(9): 149-150. Wang Changliang. Analysis of finite difference method in CFD control equations[J]. China New Telecommunications, 2019, 21(9): 149-150. (  0) 0) |
| [2] |
廖敦明, 刘瑞祥, 陈立亮, 等. 基于有限差分法的铸件凝固过程热应力场数值模拟的研究[J]. 铸造, 2003, 52(6): 420-425. Liao Dunming, Liu Ruixiang, Chen Liliang, et al. Research on numerical simulation of thermal stress field in casting solidification process based on finite difference method[J]. China Foundry, 2003, 52(6): 420-425. (  0) 0) |
| [3] |
刘铁锤, 李光炽, 蔡华钦. 基于有限体积法的二维溃坝水流模拟研究进展[J]. 水电能源科学, 2011, 29(8): 50-54. Liu Tiechui, Li Guangchi, Cai Huaqin. Research progress on two-dimensional dam break flow simulation based on finite volume method[J]. Water Resources and Power, 2011, 29(8): 50-54. (  0) 0) |
| [4] |
成思源. 有限元法的方法论[J]. 重庆大学学报(社会科学版), 2001(4): 61-63. Cheng Siyuan. Methodology of finite element method[J]. Journal of Chongqing University (Social Science Edition), 2001(4): 61-63. (  0) 0) |
| [5] |
Bar-Sinai Y, Hoyer S, Hickey J, et al. Learning data-driven discretizations for partial differential equations[J]. Proceedings of the National Academy of Sciences of the United States of America, 2019, 116(31): 15344-15349. (  0) 0) |
| [6] |
Zhuang J, Kochkov D, Bar-Sinai Y, et al. Learned discretizations for passive scalar advection in a two-dimensional turbulent flow[J]. Physical Review Fluids, 2021, 6(6): 064605. DOI:10.1103/PhysRevFluids.6.064605 (  0) 0) |
| [7] |
Kochkov D, Smith J A, Alieva A, et al. Machine learning accelerated computational fluid dynamics[J]. Proceedings of the National Academy of Sciences of the United States of America, 2021, 118(21): e2101784118. (  0) 0) |
| [8] |
Sirignano J, MacArt J F, Freund J B, et al. DPM: A deep learning PDE augmentation method with application to large-eddy simulation[J]. Journal of Computational Physics, 2020, 423(1): 109811. (  0) 0) |
| [9] |
Um K, Brand R, Fei Y, et al. Solver-in-the-Loop: Learning from differentiable physics to interact with iterative PDE-Solvers[C]//Neural Information Processing System. Advances in Neural Information Processing Systems. San Diego, CA: Neural Information Processing Systems Foundation Incoporated company, doi: 10.48550/arXiv.2007.0001633.
(  0) 0) |
| [10] |
Pathak J, Mustafa M, Kashinath K, et al. Using machine learning to augment coarse-grid computational fluid dynamics simulations[J]. Computer Physics. DOI:10.48550/arXiv.2010.00072 (  0) 0) |
| [11] |
Tompson J, Schlachter K, Sprechmann P, et al. Accelerating Eulerian Fluid Simulation with Convolutional Networks[C]. [s. l.]: 34th International Conference on Machine Learning, 2017.
(  0) 0) |
| [12] |
Obiols-Sales O, Vishnu A, Malaya N, et al. CFDNet: A deep learning-based accelerator for fluid simulations[C]//Universitat Politechica de Catalunya, Barcelona Supercomputing Center. Proceedings of the International Conference on Supercomputing. New York: Association for Computing Machinery, doi: 10.1145/3392717.3392772.
(  0) 0) |
2. School of Mathematical Sciences, Ocean University of China, Qingdao 266100, China
 2024, Vol. 54
2024, Vol. 54


