2. 青岛海洋科学与技术试点国家实验室 海洋矿产资源评价与探测技术功能实验室, 山东 青岛 266237;
3. 南方科技大学 地球与空间科学学院, 广东 深圳 518000
地震全波形反演是利用非线性最优化方法反演地震波形记录,获取地下弹性参数分布的一种方法,它具有揭示复杂地质背景下构造细节和岩性的潜力[1]。因此,若全波形反演技术在实际生产中能得到成功应用,必然能为波动方程偏移等处理环节提供更为准确的弹性参数模型,提高地震数据的成像精度,其还可为后续的层位划分、储层预测、井位标定等工作提供依据,降低勘探风险。
地震全波反演的研究最早起源于Tarantola等[2]提出的基于最小二乘理论的二维声波方程时间域全波形反演方法,之后学术界对这种方法进行了补充与完善,先后研究了声波方程的时间域多尺度反演策略[3],基于相位编码技术的时间域多炮同时反演方法[4],全波形反演的边界存储问题[5]及并行加速策略[6-9]等,这些成果丰富了时间域全波形反演的理论体系,推动了该技术的实用化进程。但时间域多尺度反演存在巨大的计算量问题,且当时很难为波场延拓提供一个满意的单频波场。为解决上述问题,Pratt等[10]将全波形反演理论拓展到频率域,他应用LU分解算法求解阻抗矩阵,提高了多炮反演的计算效率,且由于在频率域更易于实现从低频到高频的多尺度反演,因此频率域全波形反演得到了广泛关注,相关理论与算法不断完善[11-14],并在二维反射纵波数据的全波形反演中取得了应用。但时间域反演和频率域反演都存在严重的低频依赖问题,当野外记录中缺少有效的低频信息时,多尺度反演往往会失效,同时,三维情况下频率域全波形反演还存在存储消耗大和矩阵迭代计算效率低等缺陷。为解决此问题,Shin等[15-16]又基于拉普拉斯域对频率不敏感的特性发展了拉普拉斯域全波形反演方法,降低了全波形反演对于低频数据的依赖程度,但这种方法仍存在计算效率过低的问题,不利于工业应用。由此,学术界又提出了基于时间域正演和拉普拉斯域反演的混合域反演算法[17-19],这种算法将波场模拟放在时间域进行,避开了波阻抗矩阵的求逆运算,再将模拟结果变换到拉普拉斯域进行梯度寻优计算。混合域反演算法联合了拉普拉斯域反演和时间域正演的优点,在波场模拟过程中利用傅里叶变换直接求解频率域的解,不增加额外的计算量,可同时获得多个频率的波场信息,不需要超大内存空间,方便实现多尺度算法且便于并行处理。
弹性波全波形反演技术的实现思路与声波全波形反演类似,其发展历程也与声波全波反演技术相似。Tarantola[20]和Mora[21]首先将二维时间域全波形反演从声波扩展到弹性波领域,实现了基于多分量数据的纵、横波速度和密度反演。Pratt[22]将频率域声波波形反演理论推广到了弹性波反演领域,Pyun等[23]发展了Laplace域的全波反演技术,Jun H等[24]研究了弹性波方程混合域全波反演方法。由于弹性波全波形反演和声波全波形反演具有相似的实现思路与方程,因此声波反演中的大部分技术(如多尺度算法、相位编码技术、边界存储技术和并行加速技术等)都能扩展到弹性波形反演中,在实现过程中只需要将弹性波方程与对应技术结合即可。同时,时间域、频率域、拉普拉斯域以及混合域的弹性波全波反演技术的优缺点与相同条件下的声波全波形反演类似。
弹性波全波形反演的特殊性主要表现在两方面:(1)多参数反演。弹性波全波形反演需要同时反演纵波速度和横波速度,多种参数的耦合效应增加了反演难度,其不适定性和计算量过大的问题也比声波全波形反演更严重,同时,横波速度的反演需要输入数据中包含更丰富的低频信息;(2)反演隐含了输入的多分量地震记录具有相同频谱的假设,由于波场模拟时是纵波源激发,波在模型空间中以弹性波的形式传播,此时炮点波场中各分量在时间域必然具有相同的频谱,这就要求实际接收到的三分量地震记录也必须具有相同的频谱。但实际上,由于地层对纵、横波的吸收机理不同,横波高频成分的衰减远较纵波严重,导致纵横波的频谱出现明显差异,这对弹性波全波形反演中的震源设置问题造成了困扰,且目前没有合适的解决方案。
本文主要研究弹性波全波形反演的低频依赖问题,利用Laplace-Fourier域反演与时间域反演相结合的方法,降低低频能量缺失对弹性波全波形反演的影响。具体步骤为:首先通过Laplace-Fourier域反演对低频缺失的地震数据指数衰减获得低频分量,由此重建纵、横波速度的中、长波长分量模型;然后将Laplace-Fourier域的反演结果作为混合域反演[24]的初始模型采用多尺度反演策略逐步恢复出纵、横波速度模型的短波长分量,实现了低频缺失时的弹性波全波形反演。
1 Laplace域波场的获取及其特征分析 1.1 指数衰减对时间域数据低频成分的恢复作用现有一信号d(t),对其施加一个随时间的指数衰减项,得到一个衰减后的信号:
| $ \hat d\left( t \right) = d\left( t \right)\exp \left( { - \alpha t} \right)。$ | (1) |
式中:t为时间;α为衰减因子;
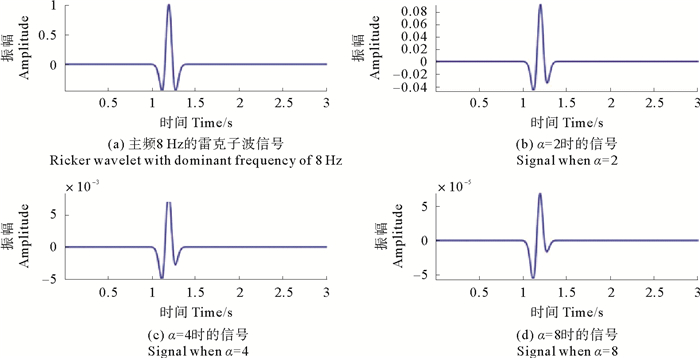
现假设d(t)为一雷克子波信号,中心频率为5 Hz。利用衰减因子α=2,4,8对此信号进行衰减,图 1显示了衰减前和衰减后的信号。图中可以看出,衰减因子的作用不仅改变了信号的振幅,也改变了信号的波形。随着衰减因子的增大,信号的第二个波谷逐渐消失。
|
图 1 原信号及衰减信号 Fig. 1 Original signal and attenuated signal |
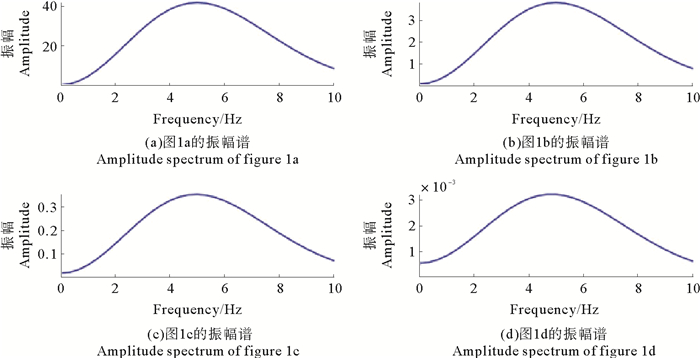
对图 1中的4个信号进行傅里叶变换得到其振幅谱(见图 2),图中可以看出,随着衰减因子的增大,信号低频成分产生了明显的变化,并且衰减因子越大,低频率成分的相对振幅越强。同时,当衰减因子α较大时,从衰减后波场的振幅谱中能够明显看到零频率处有值,而原信号的零频率振幅几乎为零。由此可见,时间域指数衰减使得原信号中产生了原信号不存在的零频率成分和低频成分,Ha和Shin的研究也证明了这一点[25]。Shin等[25]的研究表明:这些由于对地震波场指数衰减而新产生的低频成分对于地震波全波反演来说是有效并且可用的。因此,在对缺失低频的地震数据进行全波反演时,如果在反演前对地震数据进行指数衰减使其产生新的低频成分,就可以依靠这些低频信息反演出弹性参数的中、长波长成分,并由此建立一个比较可靠的全波反演初始模型。
1.2 Laplace域波场的获取| $ P\left( s \right) = \int_0^\infty {p\left( t \right){e^{ - st}}} {\rm{d}}t = \int_0^\infty {p\left( t \right){e^{ - \sigma t}}} {e^{ - {\rm{i}}\omega t}}{\rm{d}}t。$ | (2) |
式中:t为时间;ω为角频率,
由式(2)可知,Laplace变换的本质是对指数衰减后的信号进行傅里叶变换,它是一种线性变换,可直接作用于波动方程。因此,对时间域的二阶弹性波动方程[16]沿时间维度作Laplace变换可得Laplace域波动方程:
| $ \left\{ {\begin{array}{*{20}{l}} {{s^2}\rho U = \frac{\partial }{{\partial x}}\left[ {\lambda \left( {\frac{{\partial U}}{{\partial x}} + \frac{{\partial W}}{{\partial z}}} \right) + 2\mu \frac{{\partial U}}{{\partial x}}} \right] + \frac{\partial }{{\partial z}}\left[ {\mu \left( {\frac{{\partial U}}{{\partial z}} + \frac{{\partial W}}{{\partial x}}} \right)} \right] + Fx}\\ {{s^2}\rho W = \frac{\partial }{{\partial z}}\left[ {\lambda \left( {\frac{{\partial U}}{{\partial x}} + \frac{{\partial W}}{{\partial z}}} \right) + 2\mu \frac{{\partial W}}{{\partial z}}} \right] + \frac{\partial }{{\partial x}}\left[ {\mu \left( {\frac{{\partial U}}{{\partial z}} + \frac{{\partial W}}{{\partial x}}} \right)} \right] + Fz} \end{array}} \right.。$ | (3) |
式中:x、z分别为直角坐标系的两个方向;U和W为Laplace域弹性波场的x分量和z分量;ρ为密度;λ和μ为拉梅常数;Fx和Fz为Laplace域震源项。
本文求解式(3)的方法如下:首先采用有限差分技术在时间域直接求解时间域弹性波方程,在求解的时间循环中加入离散Laplace变换, 以最小成本提取任意频率的Laplace域波场。根据式(2),离散Laplace变换及其反变换表示为[26]:
| $ \left\{ {\begin{array}{*{20}{l}} {P\left( {{s_n}} \right) = \sum\limits_{k = 0}^{nt} {{e^{ - snk\Delta t}}} p(k\Delta t)}\\ {p(k\Delta t) = \sum\limits_{\omega = 0}^{{n_\omega }} {{e^{{s_n}k\Delta }}} P\left( {{s_n}} \right)} \end{array}} \right.。$ | (4) |
式中:Δt为采样间隔;nt为时间序列的长度;nω为频率序列的长度;Sn=σn+iωn。
式(4)和离散傅里叶变换的区别仅在于一个时间衰减因子,时间域波动方程正演过程中在每一个时间步均利用(4)式进行变换即可得到Laplace域的波场值。Shin等[15-16]的研究表明,对于声波方程,利用Laplace域的零频率波场进行反演能够获得模型的长波长分量,同时使用零频和低频分量进行反演能够获得模型的长、中波长分量。Shin等[15-16]将这种方法称为Laplace-Fourier域反演。由于声波和弹性波全波形反演具有相同的数学基础,这种方法很容易推广到弹性波全波反演领域。
1.3 Laplace域波场特征分析Laplace域波场的形态较常规频率域波场抽象,本文以一个简单模型为例来说明Laplace域波场特征。模型网格规模为150×200,网格大小10 m×10 m。炮点位于模型表面的中间位置,采用主频8 Hz的Ricker子波,衰减常数为2。
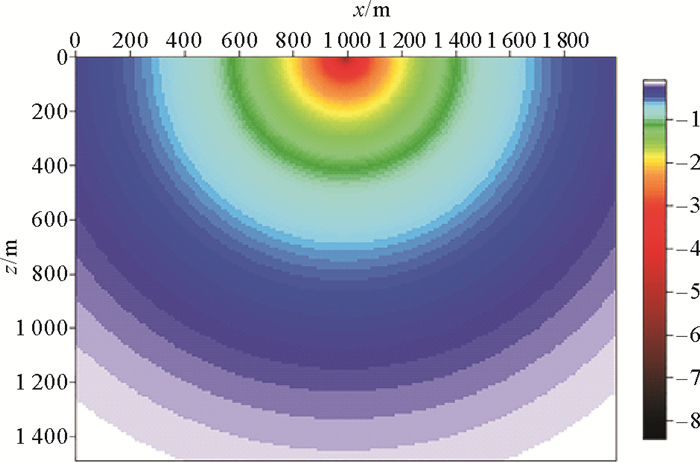
图 3为衰减常数2对应的零频率Laplace域波场,可以看出,零频率Laplace域波场的主要特征为:波场峰值位于炮点处,随着与炮点间距也来越远,波场振幅逐步降低,呈指数规律衰减。
|
图 3 零频率的Laplace域波场形态 Fig. 3 Wave field pattern in laplacedomain with zero frequency |
接下来讨论Laplace域波场与介质速度的关系,用一个两层速度模型来计算Laplace域波场,上层速度为1 500 m/s,下层速度分别为1 600和2 500 m/s, 界面深度为100 m, 纵横波速度比为1.73。接收点位于模型表面,计算得到零频率Laplace域地震记录见图 4。图中不同下层速度对应的Laplace域零频率波场振幅不一致,说明衰减波场的零频率分量对速度值高低是有响应的,它包含了介质速度信息。

|
图 4 零频率的Laplace域地震记录(水平分量) Fig. 4 Seismic records in laplacedomain with zero frequency(horizontal component) |
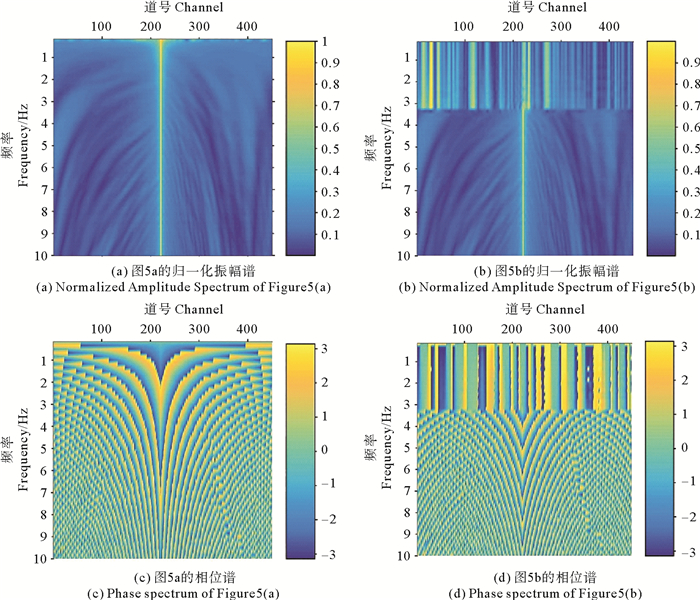
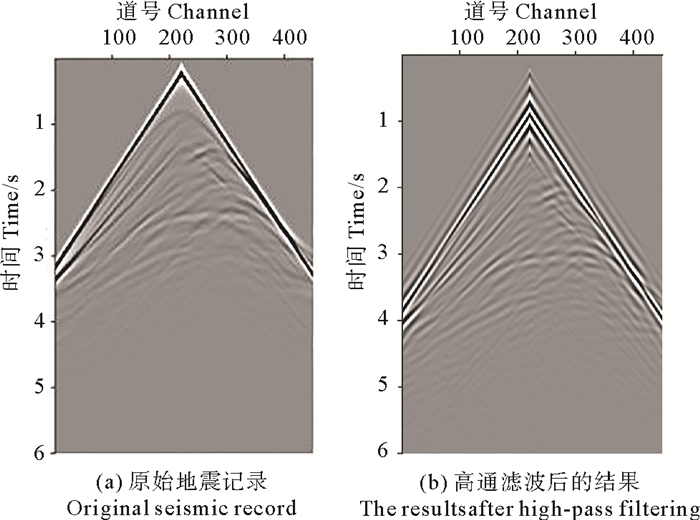
Shin等[15-16]的研究结果表明对信号进行指数衰减会增加原本不存在的低频成分,下面通过一个地震记录实例来分析这些低频成分的有效性。图 5(a)为某一单炮记录,图 5(b)是图 5(a)高通滤波(截断频率3 Hz)后的结果。图 6为图 5的归一化振幅谱和相位谱,其中归一化振幅谱是对傅里叶变换计算出的振幅谱的每一个频率对应的多道振幅值作归一化得到,由图 6可见,对于3 Hz以上的频率段,滤波后的地震记录保持了原地震记录的频谱特征,但3 Hz以下的频谱产生了很大变化,此频率段并不是原信号的有效成分,对反演不可用。
|
图 5 某一单炮地震记录以及高通滤波后的结果 Fig. 5 A single shot seismic record andits results after high pass filtering |
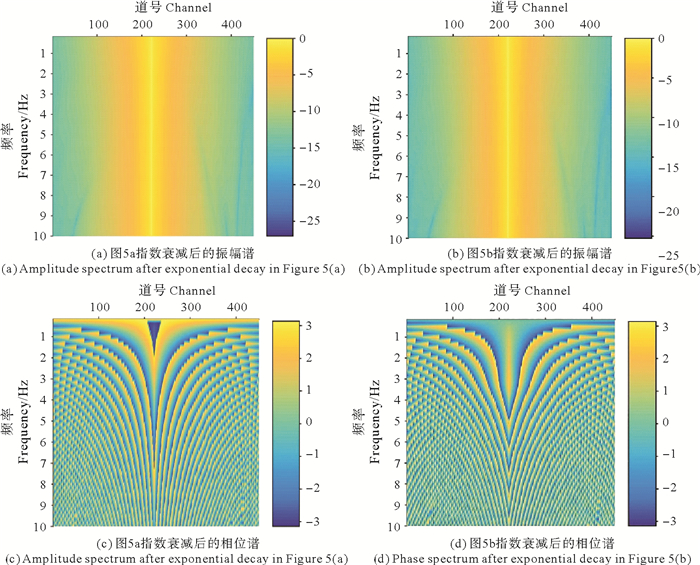
利用衰减常数2对缺失了3 Hz以下信号的炮记录(见图 5(b))进行衰减并求取振幅谱和相位谱(见图 7),图 7中振幅谱是通过对图 6中归一化振幅谱取对数得到,由图 7可知,对于滤波后的地震记录,其衰减后的频谱与原始记录存在明显的相似性,因此可以认为衰减后波场包含了有效的低频成分,合理利用这些人工操作产生的低频成分则能够恢复模型的大尺度信息。
|
图 7 对图 5进行指数衰减后的振幅谱和相位谱 Fig. 7 Amplitude spectrum and phase spectrum after exponential attenuation of Fig. 5 |
在Laplace-Fourier域反演过程中会出现远道信息缺失、探测深度变浅的问题。这一现象的产生原因是远道初至时间大,致使Laplace域能量衰减剧烈,波场振幅变弱。此时如果采用L2范数作为目标函数进行反演会失去大部分远道信息,使探测深度变浅。本文中采用L1范数作为Laplace-Fourier域的反演目标函数。
基于L1范数的目标函数为:
| $ E = \sum\limits_{i = 1}^{Ns} {\left| {{U_i} - {D_i}} \right|} 。$ | (5) |
式中:E为目标函数; U、D分别为正演模拟记录和观测记录的Laplace变换; Ns为炮数。
此目标函数对应的伴随震源表示为:
| $ r_i^ * = \frac{{\Delta d_i^ * }}{{\left| {\Delta {d_i}} \right|}}。$ | (6) |
上式中Δdi为第i炮的波场残差,ri可视为归一化后的残差波场。为避免因Δdi数值过小而产生发散,通常利用一个较小的实数对ri作如下处理:
| $ r_i^ * = \left\{ {\begin{array}{*{20}{c}} {\frac{{\Delta d_i^ * }}{{\left| {\Delta {d_i}} \right|}}, \left| {\Delta {d_i}} \right| \ge \varepsilon }\\ {0, \left| {\Delta {d_i}} \right| < \varepsilon } \end{array}} \right.。$ | (7) |
由式(7)可知,由于归一化处理消除了残差波场的振幅差异,因此它不会对伴随震源的振幅产生影响,这实际上起到了增强Laplace域远道波场振幅的作用,增大了反演深度。
解决了上述理论问题后,采用如下步骤实现弹性波的Laplace-Fourier域全波形反演,获取纵、横波的长波长模型:①读入初始模型,地震记录,子波等;②进行多炮的时间域正演,过程中插入Laplace变换以获得Laplace域波场;③对观测地震记录进行Laplace变换,计算Laplace域的残差波场和伴随震源;④将伴随震源从Laplace域反变换到时间域;⑤将伴随震源在时间域进行反传,过程中插入Laplace变换以获得Laplace域的反传波场;⑥计算梯度;⑦计算步长,并完成模型更新;⑧检验是否达到迭代终止条件,若没有则返回步骤②。
3 弹性波混合域全波形反演Laplace-Fourier域反演通过对低频缺失的地震数据指数衰减获得了地震记录的低频分量,并可由此反演出模型的中、长波长成分。以Laplace-Fourier域反演的反演结果作为初始模型即可进行弹性波混合域全波形反演。
混合域反演的特征是在时间域进行正演和反传,在频率域进行梯度的计算和处理。其中炮点波场的正向延拓和残差波场的反传采用高阶有限差分法实现,时间域正演中的炮点波场重构采用有效边界存储策略实现[5]。频率域的梯度计算需要频率域波场,因此混合域反演实现的关键在于如何在时间域正演中获得频率域的波场。本文在正演的时间循环中用离散傅里叶变换来提取所需的频率域波场:
| $ \hat P\left( \omega \right){\rm{ = }}\sum\limits_{t = 0}^{{T_{\max }}} {\exp \left( { - i\omega t} \right)} P\left( t \right)。$ | (8) |
式中:P(ω)和
炮点波场和残差波场的时间域延拓过程中,应用(8)式进行变换即可获得梯度计算所需的频率域波场。
在混合域中,当使用几个频率同步反演时,傅里叶变换可以用很小的运算代价在一次时间域正演中得到多个频率的波场,不需要像频率域正演那样单独计算每一个频率波场。
获得频率域波场后,即可采用史才旺[27]的方法进行梯度的计算与模型的更新,直至得到最终反演结果。
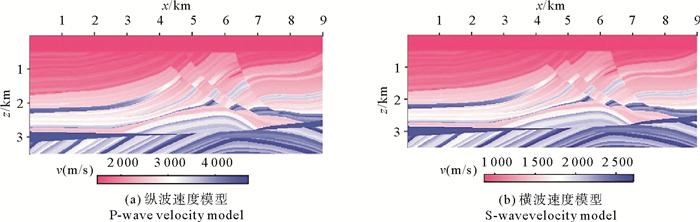
4 数值算例用图 8所示模型的正演记录验证本文算法的有效性,该模型中纵波速度模型是休斯顿大学应用地球物理实验室的Marmousi2模型的一部分,横波速度模型是将纵波速度除以1.73得到的。该模型大小为8 980 m×3 480 m,网格大小20 m×20 m。正演所用的观测系统如下:地表纵波源激发,震源为主频5 Hz的Ricker子波,中间放炮,炮点均匀分布于地表,第一炮位于0 m处,炮间距100 m,每炮450道接收,道间距20 m,在模型两边排列固定不动,炮点滚动,共得到90炮两分量记录,各炮记录长度均为8 s,采样间隔2 ms。
|
图 8 纵横波速度模型 Fig. 8 P-and S-wave velocity model |
首先对两分量正演记录进行高通滤波,滤除3 Hz以下的频率,利用滤波后的记录进行常规频率域多尺度反演。反演所用初始模型中纵、横波速度均在深度方向上线性变换,在水平方向上无变化(见图 9)。

|
图 9 反演初始纵、横波速度模型 Fig. 9 Inversion of initial P-wave and S-wave velocity models |
由于输入数据的频带限制,反演过程中所采用的频率组信息见表 1。
|
|
表 1 用于反演的频率组信息 Table 1 frequency group information for inversion |
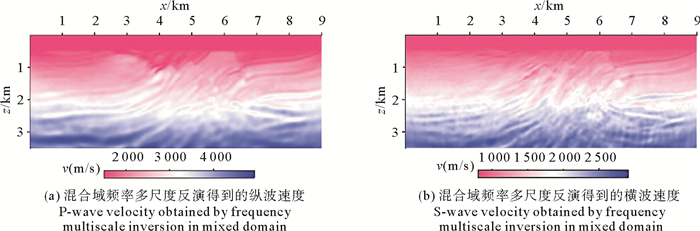
每个频带的迭代次数设为20次,最终得到常规混合域多尺度反演结果见图 10。可以看到,反演结果与真实模型在形态上偏差较大,这说明对于缺乏低频成分的多分量数据,常规混合域多尺度反演方法是失败的。
|
图 10 混合域频率多尺度反演结果 Fig. 10 Multiscale frequency inversion in mixed domain |
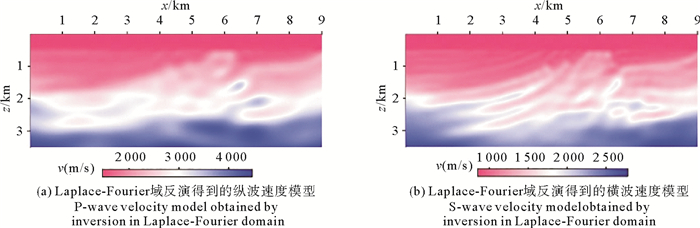
同样以图 9作为初始模型,利用本文给出的Laplace-Fourier域反演算法来对滤除了低频成分的多分量数据进行反演。Laplace-Fourier域反演需要事先确定使用的频率和衰减常数,本文使用的频率为0、0.5、0.8、1.4、2 Hz,衰减常数为2。图 11显示了Laplace-Fourier域的反演结果。容易看出,Laplace-Fourier域反演结果正确反映了原模型的大尺度信息。
|
图 11 Laplace-Fourier域反演结果 Fig. 11 Laplace-fourier domain inversion results |
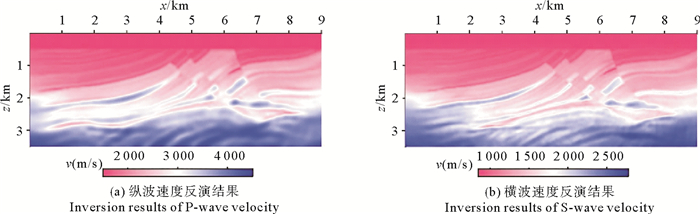
把图 11所示的Laplace-Fourier域反演结果作为初始模型,利用混合域多尺度反演方法得到的最终反演结果见图 12。Laplace-Fourier域反演和混合域多尺度联合反演的最终结果明显优于单纯的混合域多尺度反演方法(见图 10),证实了本文的反演方法针对低频缺失数据的有效性。
|
图 12 以图 11作为初始模型的混合域频率多尺度反演结果 Fig. 12 Multiscale frequency inversion in mixed domain using Figure 11 as the initial model |
(1) 弹性波全波形反演中,当地震数据缺失低频成分时,低精度的初始模型极易使反演陷入局部极值,得到错误的反演结果。对时间域波场施加指数衰减项能够产生人工的低频成分,基于此的Laplace-Fourier域反演能够在地震数据缺失低频信息时恢复模型的中、长波长分量。
(2) 当多分量数据缺失低频信息时,可以通过Laplace-Fourier域反演获得一个相对可靠的初始模型,在此基础上使用混合域频率多尺度反演能够更好地重建地下介质的弹性参数,得到更为准确的纵、横波速度模型。
| [1] |
杨勤勇, 胡光辉, 王立歆. 全波形反演研究现状及发展趋势[J]. 石油物探, 2014, 53(1): 77-83. Yang QinYong, Hu Guanghui, Wang Lixin. Current situation and development trend of full waveform inversion[J]. Petroleum Geophysical Exploration, 2014, 53(1): 77-83. DOI:10.3969/j.issn.1000-1441.2014.01.011 (  0) 0) |
| [2] |
Tarantola, Albert. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754
(  0) 0) |
| [3] |
Bunks Cetal. Multiscale seismic waveform inversion[J]. Geophysics, 1995, 60(5): 1457-1473. DOI:10.1190/1.1443880
(  0) 0) |
| [4] |
Krebs J R, Anderson J E, David H, et al. Fast full-wavefield seismic inversion using encoded sources[J]. Geophysics, 2009, 74(6): 177-188. DOI:10.1190/1.3230502
(  0) 0) |
| [5] |
Zhang Qingchen, Zhou Hui, Wang Jie. Efficient Boundary Storage for Three-Dimensional Elastic Full-Waveform Inversion in Time Domain. 84th Annual International Meeting[C]. SEG: Expanded Abstracts, 2014: 1142-1146.
(  0) 0) |
| [6] |
Mao Jian, Wu Rushan, Wang Baoli. Multiscale Full Waveform Inversion Using GPU, 82nd Annual International Meeting[C]. SEG: Expanded Abstracts, 2012: 1-7.
(  0) 0) |
| [7] |
Wang Baoli, Jinghuai Gao. CUDA-base Acceleration of Full Waveform Inversion on GPU. 81st Annual International Meeting[C]. SEG: Expanded Abstracts, 2011: 2528-2533.
(  0) 0) |
| [8] |
Song Peng, Tan Jun, Li Jinshan, et al. CUDA-based Acceleration of Full Waveform Inversion with Phase Encoding on GPU[C].[s.l.]: International Conference on Computer Science and Technology, 2014: 135-143.
(  0) 0) |
| [9] |
张猛, 王华忠, 任浩然, 等. 基于CPU/GPU异构平台的全波形反演及其实用化分析[J]. 石油物探, 2014, 53(4): 461-467. Zhang Meng, Wang Huazhong, Ren Haoran, et al. Full waveform inversion and its practical analysis based on CPU / GPU heterogeneous platform[J]. Petroleum Geophysical Exploration, 2014, 53(4): 461-467. DOI:10.3969/j.issn.1000-1441.2014.04.012 (  0) 0) |
| [10] |
Pratt G, Shin C. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion[J]. Geophysical Journal International, 1998, 133(2): 341-362. DOI:10.1046/j.1365-246X.1998.00498.x
(  0) 0) |
| [11] |
刘璐, 刘洪, 张衡, 等. 基于修正拟牛顿公式的全波形反演[J]. 地球物理学报, 2013, 56(7): 2447-2451. Liu Lu, Liu Hong, Zhang Heng, et al. Full waveform inversion based on modified quasi Newton formula[J]. Journal of Geophysics, 2013, 56(7): 2447-2451. (  0) 0) |
| [12] |
Choi Y, Min D J, Shin C. Frequency-domain elastic full waveform inversion using the new pseudo-Hessian matrix: Experience of elastic Marmousi-2 synthetic data[J]. Bulletin of the Seismological Society of America, 2008, 98(5): 2402-2415. DOI:10.1785/0120070179
(  0) 0) |
| [13] |
Han Miao, Han Liguo, Liu Chuncheng, et al. Auto-adapting full waveform inversion with blended source and frequency-group encoding[J]. Applied Geophysics, 2013, 10(1): 41-52. DOI:10.1007/s11770-013-0367-3
(  0) 0) |
| [14] |
Sirgue L, Pratt R G. Efficient waveform inversion and imaging: A strategy for selecting temporal frequencies[J]. Geophysics, 2004, 69(1): 231-248.
(  0) 0) |
| [15] |
Shin C, Ho Cha Y. Waveform inversion in the Laplace domain[J]. Geophysics Journal International, 2008, 173(3): 922-931. DOI:10.1111/j.1365-246X.2008.03768.x
(  0) 0) |
| [16] |
Shin C, Ho Cha Y. Waveform inversion in the Laplace-Fourier domain[J]. Geophysics Journal International, 2009, 177(3): 1067-1079. DOI:10.1111/j.1365-246X.2009.04102.x
(  0) 0) |
| [17] |
Kim Y, Shin C, Calandra H, et al. An algorithm for 3D acoustic time-Laplace-Fourier-domain hybrid full-waveform inversion[J]. Geophysics, 2013, 78(4): 151-166. DOI:10.1190/geo2012-0155.1
(  0) 0) |
| [18] |
Xu Kun, McMechan G A. 2D frequency-domain elastic full-waveform inversion using time-domain modeling and a multistep-length gradient approach[J]. Geophysics, 2014, 79(2): 41-53.
(  0) 0) |
| [19] |
Jun H, Kim Y, et al. Laplace-Fourier-domain elastic full-waveform inversion using time-domain modeling[J]. Geophysics, 2014, 79(5): 195-208.
(  0) 0) |
| [20] |
Tarantola A. A strategy for nonlinear elastic inversion of seismic reflection data[J]. Geophysics, 1986, 51: 1893-1903. DOI:10.1190/1.1442046
(  0) 0) |
| [21] |
Mora P. Nonlinear two-dimensional elastic inversion of multioffset seismic data[J]. Geophysics, 1987, 52: 1211-1228. DOI:10.1190/1.1442384
(  0) 0) |
| [22] |
Pratt R G. Inverse theory applied to multi-source cross-hole tomography. Part 2: Elastic wave-equation method[J]. Geophysical Prospecting, 1990, 38(3): 311-329. DOI:10.1111/j.1365-2478.1990.tb01847.x
(  0) 0) |
| [23] |
Pyun S, Shin C, Lee H. 3D Elastic Full Waveform Inversion in the Laplace Domain[C]. 78th Annual International Meeting. SEG: Expanded Abstracts, 2008: 1976-1980.
(  0) 0) |
| [24] |
Jun H, Kim Y. Laplace-Fourier-domain elastic full-waveform inversion using time-domain modeling[J]. Geophysics, 2014, 79(5): 195-208.
(  0) 0) |
| [25] |
Ha W, Shin C. Proof of the existence of both zero-and low-frequency information in a damped wavefield[J]. Journal of Applied Geophysics, 2012, 83(4): 96-99.
(  0) 0) |
| [26] |
Jun H, Kim Y, Shin J, et al. Laplace-Fourier-domain elastic full-waveform inversion using time-domain modeling[J]. Geophysics, 2014, 79(5): 195-208.
(  0) 0) |
| [27] |
史才旺, 何兵寿. 基于主成分分析和梯度重构的全波形反演[J]. 石油地球物理勘探, 2018, 53(1): 95-104+7. Shi CaiWang, He BingShou. Full waveform inversion based on principal component analysis and gradient reconstruction[J]. Petroleum Geophysical Exploration, 2018, 53(1): 95-104+7. (  0) 0) |
2. Functional Laboratory of Marine Mineral Resources Evaluation and Exploration Technology, Pilot National Laboratory of Marine Science and Technology (Qingdao), Qingdao 266237, China;
3. College of Earth and Space Sciences, Southern University of Science and Technology, Shenzhen 518000, China
 2020, Vol. 50
2020, Vol. 50