水声数据采集对海洋通信、导航定位、目标识别等研究领域具有重要意义[1],但是海洋环境噪声以及其他干扰声源的复杂多变使得目标信号的检测和提取变得异常困难。因此进行水声去噪处理,提高信号质量非常重要。
水声信号具有典型的非平稳性,相比于传统的傅里叶分析,小波变换具有多分辨率特性,能够对信号进行多尺度的细化处理[2]。由于鱼群、风浪和船舶等影响,水声信号频率成分复杂,利用变分模态分解(Variational mode decomposition,VMD)可以实现复杂信号在频域的有效分离[3]。相比于传统的经验模态分解(EMD)及其改进的算法[4],VMD具有分解速度快、精度高等优点,在信号处理方面得到了广泛应用。例如,朵慕社等[5]利用VMD和卷积神经网络来诊断轴承故障,李宏等[6]将VMD应用于语音信号的去噪,杨洁等[7]提出一种基于VMD和熵特征的雷达辐射源分类方法。
VMD算法进行信号分解时需要确定分解模态数和惩罚因子。许多文献中仅凭经验或者不能综合考虑二者的相关性以及不同输入信号的特点来选取参数,都会导致信号分解效果变差。
在小波分析方面,小波阈值(WT)去噪算法由于原理简单,易于实现的特点,成为信号去噪领域的重要方法。但是传统的软、硬阈值函数具有不连续和存在固定阈值偏差的缺陷,容易导致重构信号出现伪吉布斯现象以及边缘模糊等失真问题。此外,在传统的阈值选取方式下,不同小波分解层数对应的阈值固定不变,并没有考虑到噪声小波系数随着分解尺度增加而表现出的衰减特性。文献[8]提出一种改进的小波阈值函数,并且结合中值滤波改善了去噪效果;文献[9]提出利用VMD和小波阈值去噪的联合算法(VMD-WT),进一步提升了去噪性能,但是没有考虑到信号VMD分解的参数设置问题,仅凭经验选取参数模型,存在很大的偶然性与误差问题,并没有对阈值区间的小波系数进行处理,容易丢失信号的细节信息;文献[10]对小波阈值函数与阈值选取方式都进行了改进,但是调节参数过多,去噪效率还有待提高。根据上述算法的优缺点,本文提出一种优化VMD和改进小波阈值处理相结合的去噪方法。通过改进的鲸鱼优化算法自适应地选取VMD的最佳参数组合,将水声信号分解成多个相对平稳且具有不同特性的模态分量。通过计算各模态分量的中心频率以及与原始信号的互相关系数,确定有效信号分量,最后使用改进的可调阈值函数和分层阈值对有效分量进行小波去噪处理。实验结果表明,本文算法与传统FIR、IIR滤波方法、EMD-WT(经验模态分解-小波阈值去噪)、EEMD-WT(集合经验模态分解-小波阈值去噪)、文献[8]所提的小波阈值与中值滤波结合的算法、文献[9]提出的VMD-WT方法、文献[10]中的改进小波阈值去噪算法相比,去噪效果更好且能够有效地提升水声信号的信噪比。
1 VMD算法利用VMD将输入信号f(t)分解成K个具有不同频率和带宽的模态分量[11],实现信号在频域内的有效分离。其对应的带宽约束变分问题为:
| $ \min _{\{\mu k\}, \{\omega k\}}\left\{\begin{array}{l} \sum\limits_k\left\|\partial_t\left[\left(\delta(t)+\frac{j}{\pi t}\right) * \mu_k(t)\right] e^{-j \omega t}\right\|_2^2 \\ s . t . \sum\limits_k \mu_k=f(t) \end{array}\right\}。$ | (1) |
式中:{μk}={μ1, …, μK}和{ωk}={ω1, …, ωK}分别表示各IMF分量及其对应的中心频率;*表示卷积,∂t为梯度运算。
求解式(1)时,引入Lagrange乘子λ和惩罚因子α,得到非约束的Lagrange表达式:
| $ \begin{gathered} L\left(\left\{\mu_k\right\}, \left\{\omega_k\right\}, \lambda\right)= \\ \alpha \sum\limits_k\left\|\partial_t\left[\left(\delta(t)+\frac{j}{\pi t}\right) * \mu_k(t)\right] e^{-j \omega t}\right\|_2^2+ \\ \left\|f(t)-\sum\limits_k \mu_k(t)\right\|_2^2+\left[\lambda(t), f(t)-\sum\limits_k \mu_k(t)\right] \end{gathered}。$ | (2) |
最后迭代求出上述模型的最优解,具体步骤为:
(a) 初始化
(b) 对μk、ωk和λ进行更新,公式分别为:
| $ \begin{gathered} \hat{\mu}_k^{n+1}(\omega)= \\ \frac{\hat{f}(\omega)-\sum _{i<k} \hat{\mu}_i^{n+1}(\omega)-\sum _{i>k} \hat{\mu}_i^n(\omega)+\frac{\hat{\lambda}^n(\omega)}{2}}{1+2 \alpha\left(\omega-\omega_k^n\right)^2}。\end{gathered} $ | (3) |
| $ \omega_k^{n+1}=\frac{\int_0^{\infty} \omega\left|\hat{\mu}_k^{n+1}(\omega)\right|^2 \mathrm{~d} \omega}{\int_0^{\infty}\left|\hat{\mu}_k^{n+1}(\omega)\right|^2 \mathrm{~d} \omega}。$ | (4) |
| $ \hat{\lambda}^{n+1}(\omega)=\hat{\lambda}^n(\omega)+\tau\left(\hat{f}(\omega)-\sum\limits_k \hat{\mu}_k^{n+1}(\omega)\right) 。$ | (5) |
(c) 判断是否满足终止条件:
| $ \frac{\sum _k\left\|\hat{\mu}_k^{n+1}-\hat{\mu}_k^n\right\|_2^2}{\left\|\hat{\mu}_k^n\right\|_2^2}<\varepsilon。$ | (6) |
式中ε表示精度。满足则停止迭代,否则回到步骤(b)。
2 鲸鱼优化算法WOA是一种新提出的群智能优化算法,模拟座头鲸的狩猎行为并建立数学模型[12]。座头鲸在捕食时主要包含以下三种机制:
(1) 缩小包围机制
鲸群发现猎物后会不断收缩包围圈,并根据当前种群最优个体更新位置,对应公式为:
| $ \boldsymbol{D}=C \cdot \boldsymbol{X}^*(t)-\boldsymbol{X}(t)。$ | (7) |
| $ \boldsymbol{X}(t+1)=\boldsymbol{X}^*(t)-A \cdot \boldsymbol{D}。$ | (8) |
其中:t是当前迭代次数;X(t)代表鲸鱼个体的位置矢量;X*(t)代表当前最优个体的位置矢量;系数A和C定义为:
| $ A=2 m r-m。$ | (9) |
| $ C=2 r。$ | (10) |
| $ m=2-\frac{2 t}{T_{\max }}。$ | (11) |
式中:r为[0, 1]的随机值;Tmax表示最大迭代次数。
(2) 螺旋气泡攻击
座头鲸在围困猎物的同时,还会有50%的概率制造出螺线形气泡网实施攻击,数学模型对应为:
| $ \boldsymbol{D}^{\prime}=\boldsymbol{X}^*(t)-\boldsymbol{X}(t)。$ | (12) |
| $ \boldsymbol{X}(t+1)=\boldsymbol{D}^{\prime} \cdot e^{b l} \cdot \cos (2 \pi l)+\boldsymbol{X}^*(t)。$ | (13) |
式中:D′表示鲸鱼个体到当前最佳解的距离矢量;l是[-1, 1]区间的任意值;b是常数,本文取值为1。
(3) 随机搜索机制
在搜索猎物阶段,当系数|A|≥1时,鲸群将通过随机搜索在全局范围内寻找优质猎物(候选解),其位置更新表达式为:
| $ \boldsymbol{D}=C \cdot \boldsymbol{X}_{\text {rand }}(t)-\boldsymbol{X}(t)。$ | (14) |
| $ \boldsymbol{X}(t+1)=\boldsymbol{X}_{\text {rand }}(t)-A \cdot \boldsymbol{D}。$ | (15) |
上式中,Xrand(t)是选的随机个体的位置矢量。当|A| < 1时,鲸群会选择在局部范围内进行更加精细的搜索,同时根据式(8)更新个体位置。
2.1 WOA的改进策略传统的WOA通过系数A来调节全局和局部搜索,A的值主要与m有关,然而线性变化的收敛因子m并不利于算法的非线性寻优过程。对此,本文提出一种余弦收敛因子,公式如下:
| $ m=1+\cos \left(\frac{\pi t}{T_{\max }}\right)^{1.3}。$ | (16) |
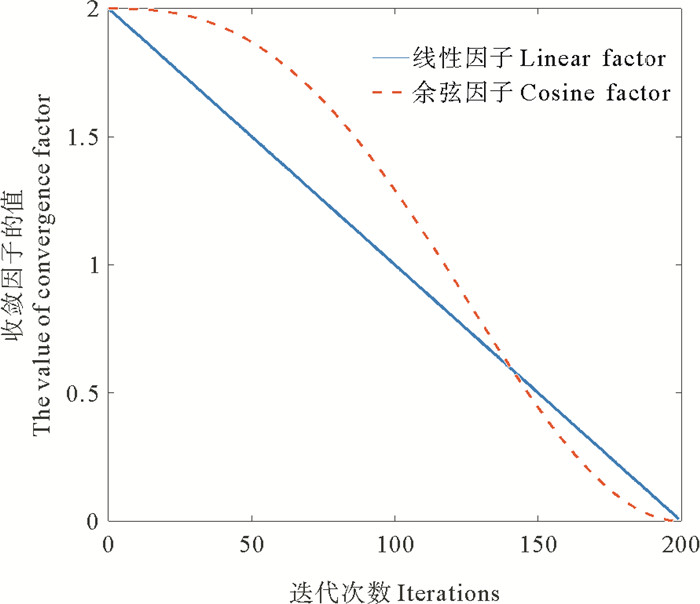
m的变化情况如图 1所示。在整个迭代过程中,收敛因子非线性递减。前期和中期阶段,m的值较大且变化较快,可以扩大|A|≥1的比例且能够尽快地在全局范围内确定优质解,增强算法的全局寻优性能,同时较大步长更有利于摆脱局部最优极值[13]。算法后期,m以较小步长进行局部的细致搜索,可以提高算法收敛精度。
|
图 1 余弦收敛因子曲线图 Fig. 1 Cosine convergence factor curve |
此外,引入自适应权重β控制当前最优个体对鲸群位置更新的影响。前期较大的权值可以防止陷入局部最优,后期较小的权值更利于鲸群对猎物的精确定位,改进WOA的局部搜索能力。β定义为:
| $ \beta=0.4+0.6 e^{\frac{-5 t}{T_{\max }}}。$ | (17) |
同时,式(8)、(13)将更新为:
| $ \boldsymbol{X}(t+1)=\beta \cdot \boldsymbol{X}^*(t)-A \cdot \boldsymbol{D}。$ | (18) |
| $ \boldsymbol{X}(t+1)=\boldsymbol{D}^{\prime} \cdot e^{b l} \cdot \cos (2 \pi l)+\beta \cdot \boldsymbol{X}^*(t)。$ | (19) |
小波阈值去噪[14]的主要步骤为:
(1) 确定小波基函数和分解层数,对含噪信号进行小波变换,得到各尺度下的小波系数。
(2) 设置每层的阈值,利用阈值函数对原始小波系数ωj, k进行量化处理,得到小波估计系数
(3) 对
上述过程中,阈值、阈值函数的选取对最终去噪效果具有重要影响。本文在传统算法的基础上,引入一种新的阈值函数和分层确定阈值的方法。
3.1 改进的小波阈值函数针对传统的硬、软阈值函数存在的不连续和恒定差值问题,本文提出一种可调阈值函数,表达式为:
| $ \begin{aligned} & \hat{\omega}_{j, k}= \\ & \left\{\begin{array}{l} \operatorname{sign}\left(\omega_{j, k}\right) \cdot \sqrt{\left|\omega_{j, k}\right|^2-\frac{a \lambda^2}{e^{\frac{\left|\omega_{j, k}\right|-\lambda}{N}}}, \left|\omega_{j, k}\right| \geqslant \lambda} \\ \operatorname{sign}\left(\omega_{j, k}\right) \cdot \sqrt{1-a} \cdot\left|\omega_{j, k}\right| \cdot e^{10 *\left(\left|\omega_{j, k}\right|-\lambda\right)}, \left|\omega_{j, k}\right|<\lambda \end{array}\right.。\\ & \end{aligned} $ | (20) |
式中:j表示分解尺度;λ表示阈值;k为系数标号;a是可调参数且0≤a≤1。
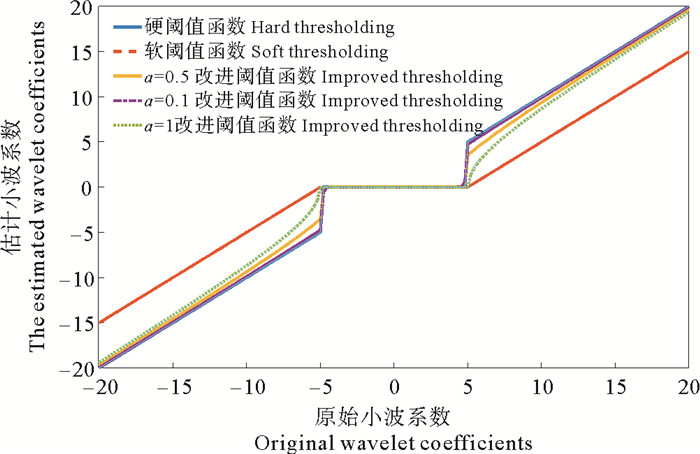
新阈值函数连续,当|ωj, k| < λ时,利用指数函数的逼近性使得阈值处理更加平滑,有利于保留信号的细节信息。同时,引入参数a实现阈值函数的动态调整,改善了软阈值函数中
|
图 2 基于参数调整的阈值函数曲线图 Fig. 2 Curve of threshold function based on parameter |
传统的阈值固定不变,考虑到噪声系数会随着分解尺度的增加而逐渐衰减,阈值也应该逐层降低。文献[10]指出第j层噪声小波系数大约是第j+1层的
| $ \left\{\begin{array}{l} \lambda_1=\sigma \sqrt{2 \lg N} \\ \lambda_j=\frac{\sqrt{2}}{2} \lambda_{j-1}, j=2, 3, \cdots, L \end{array}\right.。$ | (21) |
式中:σ表示噪声标准差;N表示序列长度;L表示小波分解尺度。
4 基于改进WOA-VMD的小波阈值去噪使用VMD分解信号时需要预先设定参数:分解模态个数K和惩罚因子α。本文利用鲸鱼优化算法选取最佳[K, α]参数组合,选取功率谱熵作为WOA的适应度函数,假设在第t次迭代过程中,输入信号f(t)被分解出K个模态分量,则功率谱熵的计算公式如下:
| $ \left\{\begin{array}{l} p_k=\frac{|X(k)|^2}{\sum _{k=0}^{N-1}|X(k)|^2}, (k=0, 1, 2, \cdots, N-1) \\ H=-\sum _{k=1}^N p_k \log p_k \end{array}\right. $ | (22) |
式中:N为信号序列的长度;k为标号;X(k)是第k个模态分量x(k)对应的离散傅里叶变换;pk表示第k个功率谱值占总功率谱的比重;H表示对应的功率谱熵。
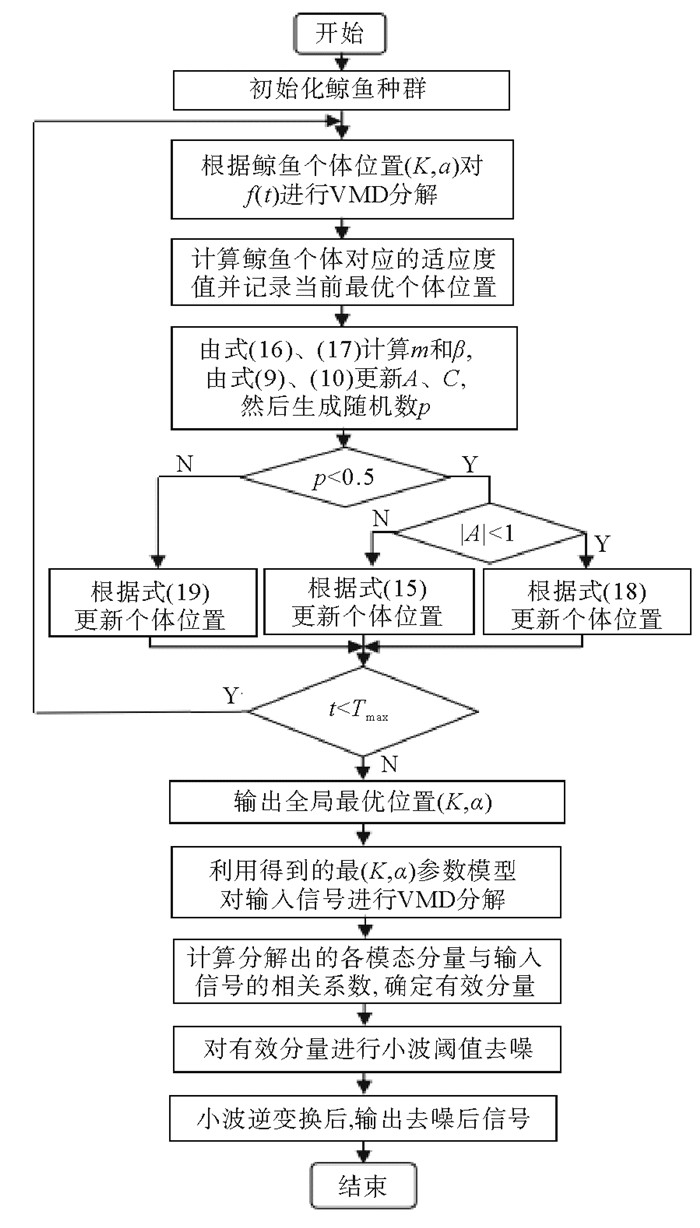
如图 3所示,本文算法的实现步骤如下:
|
图 3 算法流程图 Fig. 3 Algorithm flowchart |
(1) WOA优化VMD参数。将需要寻优的参数组合(K, α)作为鲸鱼个体的位置,根据每个鲸鱼的位置对输入信号f(t)进行VMD分解,计算对应的功率谱熵值并记录当前功率谱熵值最小时对应的个体位置(K, α)。随着迭代次数的增加,适应度值的变化将逐渐趋于平稳,最后在满足终止条件后输出最优位置(K, α),作为输入信号f(t)进行VMD分解的最佳参数组合。
(2) 使用上述得到的最佳参数模型对输入信号f(t)进行VMD分解,得到对应的K个模态分量IMFs。
(3) 计算各IMF对应的中心频率以及与输入信号f(t)的相关系数,根据设定的相关系数阈值,最终确定有效分量和噪声分量。
(4) 舍弃噪声分量,使用本文改进的小波阈值算法对有效分量进行去噪处理。
(5) 最后重构有效模态分量得到去噪后信号。
5 实验验证 5.1 算法仿真实验在MATLAB软件平台下进行仿真实验分析。本文采用的仿真信号如下:
| $ \left\{\begin{array}{l} x_0(t)=\sin (2 \pi 200 t) \\ x_1(t)=0.4 \sin (2 \pi 50 t) \\ x_2(t)=0.6 \sin (2 \pi 100 t) \\ x_3(t)=0.5 \sin (2 \pi 250 t) \\ x_4(t)=0.5 \sin (2 \pi 500 t) \\ f(t)=x_0(t)+x_1(t)+x_2(t)+ \\ \\ \quad x_3(t)+x_4(t)+n(t) \end{array}\right.。$ | (23) |
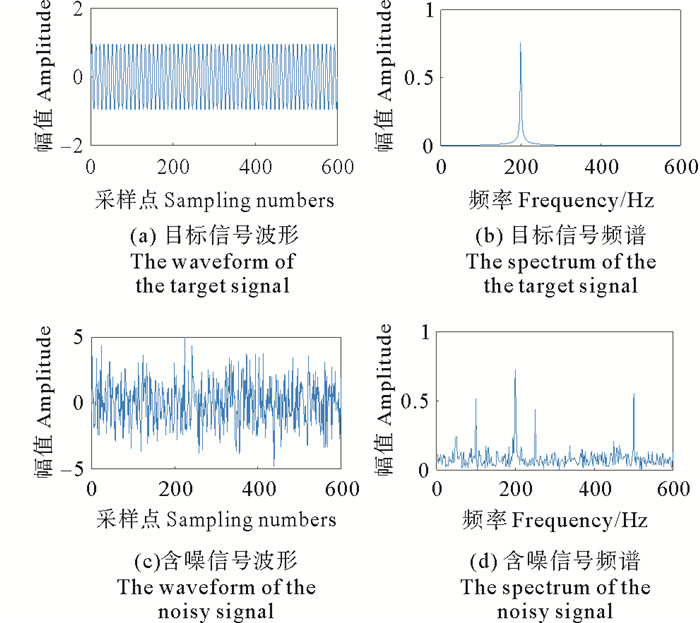
式中:仿真信号f(t)代表含噪输入信号;由各谐波分量与高斯白噪声组成;x0(t)代表目标信号,主频为200 Hz;x1(t)、x2(t)、x3(t)和x4(t)分别表示频率为50、100、250和500 Hz的干扰信号;n(t)代表高斯白噪声。设置采样频率为2 000 Hz,采样点数为1 024,当含噪信号的信噪比为-2.975 0 dB时,仿真信号及其对应的频谱如图 4所示,原始信号包含明显的频率干扰和噪声。
|
图 4 目标信号、含噪信号时频图 Fig. 4 Time frequency diagram of target signal and noisy signal |
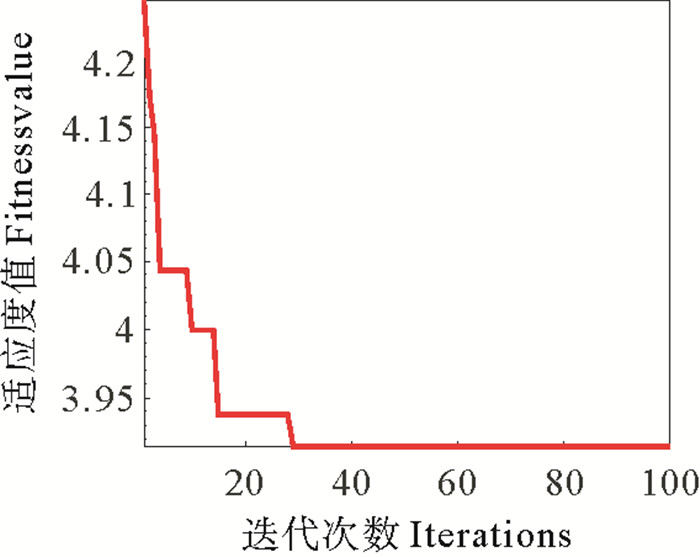
利用本文算法进行去噪处理。首先,通过WOA获得含噪信号VMD分解的最优参数模型。设置种群数为50,最大迭代次数为100,k∈[2, 9],α∈[1 000, 9 000]。仿真信号的VMD参数寻优过程如图 5所示,最终获得的最佳参数组合是K=8,α=7 230。
|
图 5 WOA优化VMD参数迭代曲线 Fig. 5 Iterative curve of WOA optimized VMD parameters |
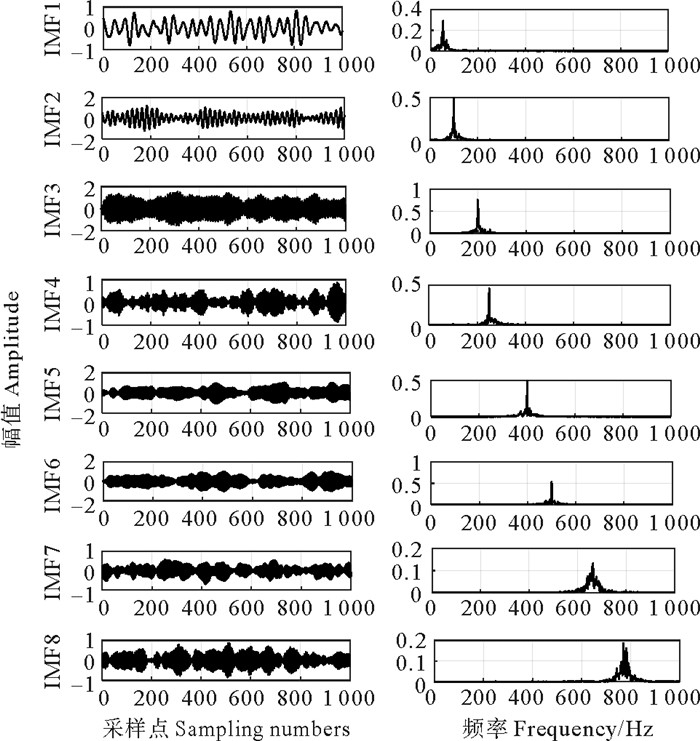
然后,利用该参数模型对含噪信号f(t)进行VMD分解,最终得到的8个模态分量对应的时频波形如图 6所示。观察分解结果可以发现,经本文WOA-VMD算法选取的最佳参数模型能够实现复杂信号的有效分离,仿真信号中的多个频率相近的分量都被很好地分解到不同的频段,每一个模态分量谱中的频率都是单一的,没有出现频谱混叠问题。计算各IMF分量与输入信号f(t)的相关系数,结果分别为0.287 5、0.390 5、0.599 4、0.349 5、0.348 7、0.182 6、0.169 4、0.190 9,其中IMF3分量对应的相关系数最高且中心频率在200 Hz左右,最接近目标信号,因此选定IMF3为有效分量并进行小波阈值去噪。
|
图 6 IMF分量及其对应频谱 Fig. 6 IMF component and its corresponding spectrum |
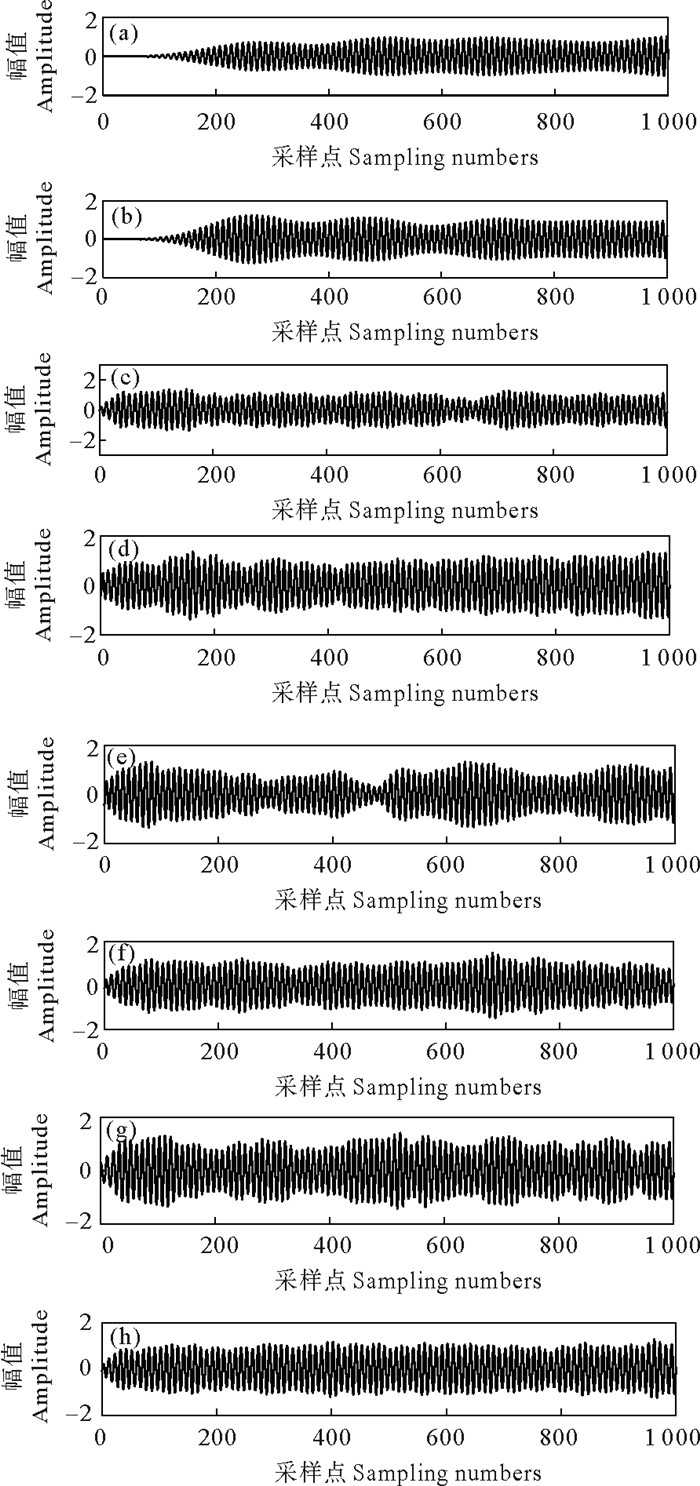
选择db4小波基,采用本文方法与传统FIR、IIR滤波方法、EMD-WT、EEMD-WT、文献[8]所提的小波阈值与中值滤波结合的算法、文献[9]提出的VMD-WT方法、文献[10]中的改进小波阈值去噪算法进行去噪对比实验,去噪后信号如图 7所示。
|
(((a)FIR滤波Finite Impulse Response filter;(b)IIR滤波Infinite Impulse Response filter;(c)EMD-WT;(d)EEMD-WT;(e)文献[8]算法The algorithm in literature[8];(f)文献[9]算法The algorithm in literature[9];(g)文献[10]算法The algorithm in literature[10];(h)本文算法The algorithm proposed in this paper.)) 图 7 不同算法去噪效果 Fig. 7 Denoising effects of different algorithms |
采用信噪比和均方根误差对最终去噪效果进行衡量,结果如表 1所示。
|
|
表 1 不同算法的去噪性能指标 Table 1 Denoising performance indexes of different algorithms |
观察表 1与图 7可以发现,与其他算法相比,本文算法的去噪效果最好,去噪后信号的信噪比最大,均方误差最小,本文算法重构后的波形光滑,没有出现明显的毛刺,与目标信号的波动偏差也是最小的,说明本文算法去噪的信号能够更好地拟合目标信号,在去噪方面更具优势。
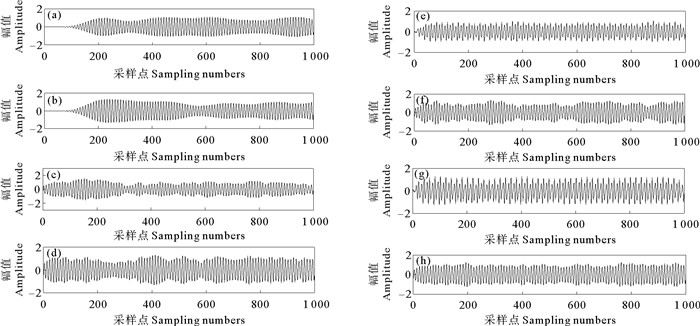
为进一步验证本文算法的效果,分别加入不同强度的噪声并进行去噪对比实验,记录对应算法的SNR和RMSE,结果如表 2所示。从表 2可以看出,在不同的噪声强度下,本文算法的去噪性能指标均优于其他五种算法,能够有效提升目标信号的信噪比。图 8记录了SNR=-4.514 1时的不同算法的去噪效果。
|
|
表 2 八种算法在不同信噪比条件下的去噪性能指标 Table 2 Denoising performance indexes of eight algorithms under different signal-to-noise ratios |
|
(((a)FIR滤波Finite Impulse Response filter;(b)IIR滤波Infinite Impulse Response filter;(c)EMD-WT;(d)EEMD-WT;(e)文献[8]算法The algorithm in literature[8];(f)文献[9]算法The algorithm in literature[9];(g)文献[10]算法The algorithm in literature[10];(h)本文算法The algorithm proposed in this paper.)) 图 8 八种不同算法去噪效果 Fig. 8 Denoising effects of eight different algorithms |
将水声信号采集板集成到海洋牧场环境监测系统中,然后投放到莱州湾附近的海域,整个系统采用原位坐底的布放方式,距离岸线约26 km,水深约10 m。
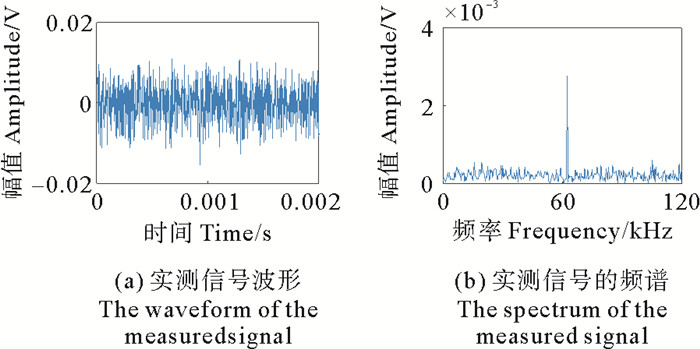
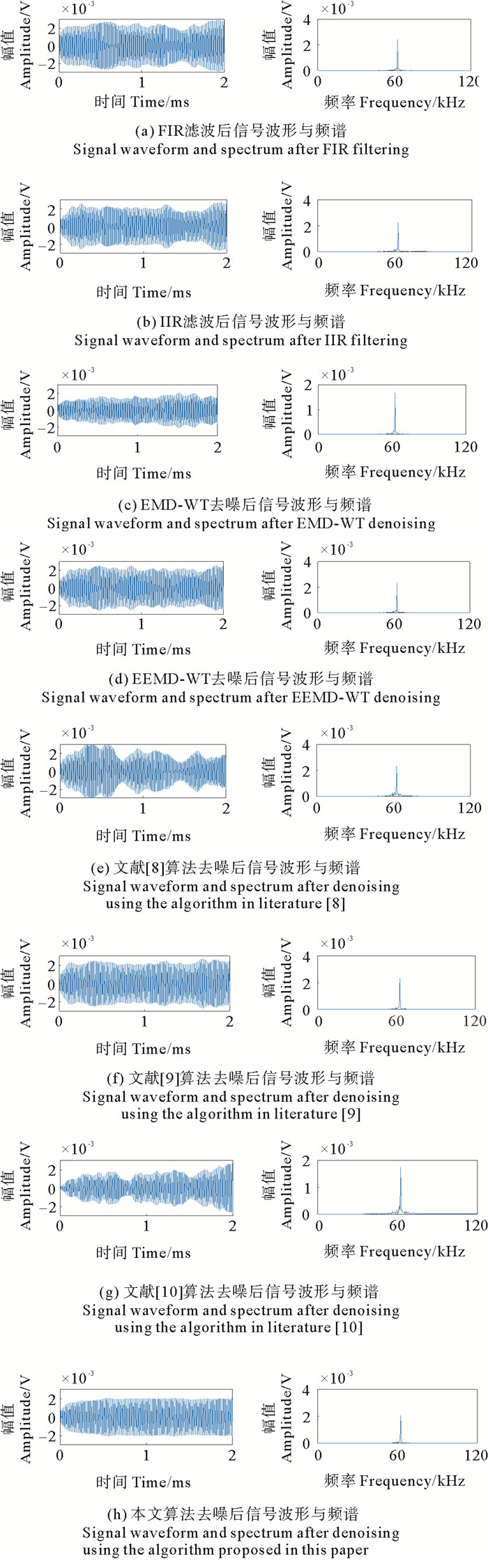
水下控制系统通过光电复合缆和接驳盒与岸基监测平台进行数据传输,通过岸基监测站发送配置命令并控制数据采集,采样频率为250 kHz,采样精度为16bit,数据实时上传到岸基服务器。选择10月24日保存的一段数据进行去噪实验,实测数据如图 9所示。对比本文算法与其他不同算法的去噪效果,结果如图 10所示。其中目标信号的频率是62 kHz,对比几种算法去噪后的波形与频谱,可以看出:VMD-WT算法优于EMD-WT、EEMD-WT,说明了VMD方法在复杂信号分解方面更具优势。FIR与IIR滤波的效果比较接近,去噪效果仍低于本文优化的WOA-VMD-WT方法。利用本文算法可以更好地去除信号中的次要频率干扰,去噪后的信号波形更加平稳,波动偏差更小,进一步证明了该算法的有效性与实用价值。
|
图 9 实测信号波形与频谱 Fig. 9 The measured signal and corresponding spectrum |
|
图 10 不同算法的实测信号去噪效果图 Fig. 10 Measured signal denoising effects of different algorithms |
本文根据水声信号的特点,提出一种基于改进WOA-VMD和小波阈值处理结合的去噪方法。在进行小波阈值处理之前,引入VMD算法对含噪信号进行分解,将复杂的信号划分到不同的频段进行分析,并根据各模态分量的中心频率以及与含噪信号的互相关系数,最终确定有效分量。从而有利于根据应用场景和目标信号的特点来进一步提取有用信息,提高目标信号的信噪比。
此外,针对信号VMD处理过程中参数选择的关键影响,将需要选择的参数组合(K, α)作为种群寻优的位置,选取功率谱熵作为适应度函数,然后利用WOA算法获得含噪信号VMD分解的最佳参数模型。为了提高模型的精度,引入余弦收敛因子和指数权重,改进传统WOA的寻优能力和收敛速度。实验证明,采用本文改进的WOA-VMD方法可以实现复杂信号在频域的有效分离,不会出现频谱混叠的现象。
在对有效分量进行小波阈值处理时,考虑到噪声小波系数随着分解尺度的不断增加而呈现出的衰减特性,本文提出改进的可调阈值函数和分层自适应阈值,改善了传统阈值量化过程中存在的固定偏差问题,可以根据含噪信号的特点,灵活调整阈值函数的形状以及设置合适的阈值。在不同噪声强度下进行仿真实验,结果表明了本文算法的去噪性能指标均优于其他七种算法,去噪的同时能够保留更多的细节信息。实测信号的去噪对比分析,也进一步验证本文算法可以有效去除水声信号中的次要频率干扰,去噪后的波形比较光滑,更加接近目标信号,说明该算法在信号去噪方面具有一定的实用性与优越性。
| [1] |
Li Y, Wang S, Jin C, et al. A survey of underwater magnetic induction communications: Fundmental issues, recent advances, and challenges[J]. IEEE Communications Surveys & Tutorials, 2019, 21(3): 2466-2487. (  0) 0) |
| [2] |
晏建洋, 吴建星. 基于小波变换的微震信号去噪研究[J]. 科技通报, 2016, 32(3): 185-188. Yan J Y, Wu J X. Reserach on microseismic signal denoising based on wavelet transform[J]. Bulletin of Science and Technology, 2016, 32(3): 185-188. DOI:10.3969/j.issn.1001-7119.2016.03.042 (  0) 0) |
| [3] |
陈鹏, 赵小强. 基于优化VMD与改进阈值降噪的滚动轴承早期故障特征提取[J]. 振动与冲击, 2021, 40(13): 146-153. Chen P, Zhao X Q. Early fault extraction of rolling bearing based on optimized VMD and improved threshold denoising[J]. Journal of Vibration and Shock, 2021, 40(13): 146-153. (  0) 0) |
| [4] |
丁明宽, 石志勇, 韩兰懿, 等. 基于优化VMD-小波阈值的MEMS陀螺信号降噪[J]. 兵器装备工程学报, 2021, 42(8): 191-197. Ding M K, Shi Z Y, Han L Y, et al. MEMS gyro signal noise reduction based on optimized VMD-Wavelet threshold[J]. Journal of Ordnance Equipment Engineering, 2021, 42(8): 191-197. DOI:10.11809/bqzbgcxb2021.08.031 (  0) 0) |
| [5] |
朵慕社, 纪国宜, 朱海龙, 等. 基于VMD降噪和CNN的轴承故障诊断[J]. 噪声与振动控制, 2021, 41(5): 155-160. Duo M S, Ji G Y, Zhu H L, et al. Bearing fault didgnosis based on VMD noise reduction and CNN[J]. Noise and Vibration Control, 2021, 41(5): 155-160. DOI:10.3969/j.issn.1006-1355.2021.05.025 (  0) 0) |
| [6] |
李宏, 李定文, 朱海琦, 等. 一种优化的VMD算法及其在语音信号去噪中的应用[J]. 吉林大学学报(理学版), 2021, 59(5): 1219-1227. Li H, Li D W, Zhu H Q, et al. An optimized VMD algorithm and its application in speech signal denoising[J]. Journal of Jilin University(Science Edition), 2021, 59(5): 1219-1227. (  0) 0) |
| [7] |
杨洁, 岳美君, 曾耀平. 基于VMD和熵特征的雷达辐射源信号识别[J]. 计算机技术与发展, 2021, 31(10): 13-17. Yang J, Yue M J, Zeng Y P. Radar emitter signal recognition based on VMD and entropy features[J]. Computer Technology and Development, 2021, 31(10): 13-17. DOI:10.3969/j.issn.1673-629X.2021.10.003 (  0) 0) |
| [8] |
傅琪, 闫坤, 甘海铭, 等. 小波阈值函数优化算法在金属零件上的应用[J]. 微电子学与计算机, 2022(2): 92-100. Fu Q, Yan K, Gan H M, et al. Application of wavelet threshold function optimized algorithm in metal pars[J]. Microelectronics & Computer, 2022(2): 92-100. (  0) 0) |
| [9] |
施晶, 朱明, 沈华, 等. 基于VMD和小波阈值的水听器信号去噪方法[J]. 传感技术学报, 2020, 33(7): 1003-1012. Shi J, Zhu M, Shen H, et al. Denoising method of hydrophone signal based on VMD and wavelet threshold[J]. Chinese Journal of Sensors and Actuators, 2020, 33(7): 1003-1012. DOI:10.3969/j.issn.1004-1699.2020.07.013 (  0) 0) |
| [10] |
杜诗强, 宋宇鲲, 张玄, 等. 一种改进的小波阈值去噪算法[J]. 微电子学与计算机, 2021, 38(2): 40-46. Du S Q, Song Y K, Zhang X, et al. Improved wavelet threshold denoising algorithm[J]. Microelectronics & Computer, 2021, 38(2): 40-46. (  0) 0) |
| [11] |
Dragomiretskiy K, Zosso D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544. (  0) 0) |
| [12] |
Mirjalili S, Lewis A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67. (  0) 0) |
| [13] |
郭冬宝. 改进萤火虫算法及其在约束优化中的应用[D]. 广州: 暨南大学, 2018. Guo D B. Research on Firefly Algorithm and Its Application In Constrained Optimization[D]. Guangzhou: Jinan University, 2018. (  0) 0) |
| [14] |
宋洁, 石明全, 张霞. 小波阈值去噪在动态扭矩检测中的应用[C]. 济南: 017中国自动化大会(CAC2017)暨国际智能制造创新大会(CIMIC2017)论文集, 2017: 794-798. Song J, Shi M Q, Zhang X. Application of wavelet threshold denoising in dynamic torque detection[C]. Jinan: Proceedings of 2017 Chinese Automation Congress(CAC2017)& Intelligent Manufacturing International Conference(CIMIC2017), 2017: 794-798. (  0) 0) |
 2023, Vol. 53
2023, Vol. 53


