2. 青岛市保密技术服务中心,山东 青岛 266000;
3. 青岛市保密科技测评中心,山东 青岛 266000
信息系统安全可能受到外部攻击破坏、内部威胁以及系统本身所产生的意外事故,这些问题都可能导致数据泄露和更严重的后果,包括服务的被迫中断、敏感信息的泄露甚至威胁到国家安全[1]。要确保信息系统安全,需要依据风险管理的核心理论[2],对内外部威胁与资源进行解析,降低安全风险发生概率,任何可能引发风险发生的环节都要妥善处理。因此,对信息系统进行持续性的安全风险评估是十分必要的。
基于概率推理的贝叶斯网络(Bayesian network,BN)具有强大的推理能力,能够处理不确定和不完整性问题,特别是对于安全风险分析领域具有较好的适用性,常用于解决复杂系统不确定性和关联性故障诊断、风险预测、关键风险因素识别等问题。
本文通过探索信息系统在不同威胁风险因素影响下可能导致的不同状态,构建多态事件树,演化贝叶斯网络以实现对系统的风险评估,在此基础上提供对网络安全威胁进行深入分析的定量依据,有助于形成有效处理机制,最终达到识别威胁、区分风险优先级的目的。
1 贝叶斯网络 1.1 概念贝叶斯网络,又称信念网络(Belief network),是一种概率图形模型,它使用贝叶斯推理进行概率计算。贝叶斯网络的目标是通过在有向图中用边表示条件依赖来模拟条件依赖,从而模拟因果关系。贝叶斯网络广泛用于概率推理,具有非常广泛的适用性,能够实现从大量样本数据中进行机器学习、诊断推理和因果推理。
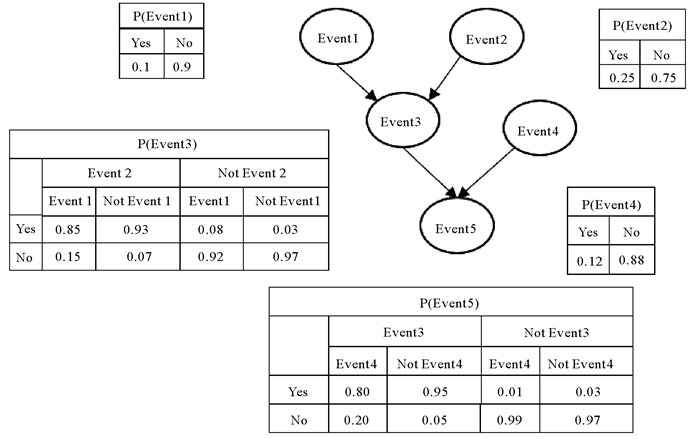
贝叶斯网络是一个有向无圈图,其中节点代表随机变量,节点间的边代表变量之间的直接依赖关系。每个节点都附有一个概率分布,根节点X附带的是它的边缘分布,而非根节点X附带的是条件概率分布。图 1是一个典型的贝叶斯网络示意图,其中每个节点都是一个变量,可以处于有限数量的状态之一,节点之间的链接或箭头表示这些节点之间的因果关系。图 1中的所有变量都是布尔变量,但是变量可以拥有的状态数没有限制,如果两个节点之间没有边则意味着条件独立性,此时节点的概率分布可以通过考虑其父节点的分布来确定。以此类推,可以指定整个网络的联合概率分布,这种关系可以用微积分中的链式法则从数学上捕捉。
|
图 1 典型贝叶斯网络示意图 Fig. 1 The schematic diagram of typical Bayesian network |
贝叶斯网络中,在对特定一组证据变量进行赋值后,可以推断目标变量的精确概率分布(边际分布和条件分布),但在大规模连通网络中,随着极大团规模增大,计算复杂度呈指数增长,无法完全实施精确推理,此时会采用近似推理算法,能够以较低的复杂度和较高的计算效率获得近似解。近似推理算法主要有基于搜索的方法和蒙特卡洛算法。常见的精确推理算法包括:
(1) 树传播推理算法(Polytree propagation)
该算法仅适用于具有多变结构的网络,也称为单连通网络,这一算法是贝叶斯网络中最早的推理算法之一,由于算法可以给执行的每个子计算赋予特定的概率意义,因此从计算意义上赋予了不同的认知维度,这一算法是循环信念传播算法这种近似推理算法的基础。
(2) 连接树推理算法(Junction tree propagation)
连接树算法的思想是一种将联合概率的全局计算分解成局部计算链接集的方法,这种算法明确了图论局部性和有效概率推理之间的重要关系。
(3) 符号推理(Symbolic probabilistic inference,SPI[3])
SPI算法是目标导向的,只执行那些响应查询所需的计算,多适用于具有离散值变量的贝叶斯网络。
为提高运算速度,开发出很多贝叶斯网络工具,这些工具提供不同的推理算法,有些工具还配有引擎机制,配合这些算法可以完成模型应用,常见推理引擎有联合树推理引擎、全局联合树推理引擎、信念传播推理引擎以及消除推理引擎等。
2 贝叶斯网络在信息系统风险评估过程的应用 2.1 方法的适用性概率安全评估是以定量评估为主,定性与定量结合的一种评估工作,可以分为两大类:静态方法和动态方法。静态方法以事件树/故障树、二元决策图等方法为代表;动态方法主要包括Petri网、Markov状态转移矩阵、动态逻辑分析法、连续事件树和时间序列图等方法。近年来快速发展的贝叶斯网络技术可以根据需要构建静态评估和动态评估模型,具有很多优点,非常适用于信息系统安全风险评估:
(1) 贝叶斯网络类似神经元网络,具有可靠地数据理论基础,可以很好的描述非单调性、关联性以及非确定性逻辑关系等能力,能够充分描述人的推理过程。
(2) 贝叶斯网络可以定量化描述评估过程,其中的因果关系易于理解,可通过专家经验获取先验知识。
(3) 贝叶斯概率所具有的连续性和积累性非常符合安全评估场景需要,评估不仅体现了现有状态,还是历史和先验信息的反应。
(4) 目前存在很多成熟的推理算法和软件工具。
2.2 国内外研究现状鉴于贝叶斯网络模型对于当今复杂多样的信息系统建模非常有用,有很多研究提出了信息安全风险评估的贝叶斯网络模型。Frigault等[3-4]将相关安全风险因素,如漏洞代码或补丁的可用性结合到基于攻击图的安全度量中,形成动态贝叶斯网络的模型来测量网络安全性。Wang等[5]创建了基于风险评估过程的动态贝叶斯网络模型,通过对信息系统进行分析计算风险的概率,同时进行了动态贝叶斯网络模型与静态贝叶斯网络模型的分析和比较实验。Sevilay等[6]提出了一种基于贝叶斯网络和模糊推理系统的信息安全风险评估方法,相关模型被开发用于分析软件服务公司的测试过程,以便评估信息安全风险,其利用威胁、漏洞、风险以及它们之间的关系实现贝叶斯网络建模,并为每个风险因素计算边际概率。
我国很多高等院校和科研机构在数据挖掘、医疗诊断、辅助智能决策等方面对贝叶斯网络进行了大量研究[7-10],取得了部分成果。有一些研究团队将贝叶斯网络用于信息系统风险评估过程:李欢等[11]利用贝叶斯网络攻击图来判断网络中可能存在的攻击路径,实现了攻击者为达到攻击目标而采取的所有可能攻击方法的可视化,便于发现网络中存在的所有可能发生的潜在攻击过程;王文思等[12]将并行随机森林方法与贝叶斯网络相结合,建立了网络安全态势评估模型,通过计算当前网络在某些条件下发生危险的概率,来判断网络是否处于安全状态,并及时发现导致网络不安全的最大潜在因素。
总体来讲,国内在这一领域的整体研究还处于起步阶段,应用也比国外少得多,特别是对复杂状态下的信息系统安全风险评估还缺乏相关研究。
3 基于贝叶斯网络的信息系统多态概率安全风险评估方法 3.1 多态系统事件树工业领域对故障的判断最初只有两种状态:正常和故障。传统的故障树方法对事件也只有二态性的假设,即发生和不发生,分别用1和0表示[13]。网络系统安全评估不同于对故障的判断,它的状态更为复杂,会存在多态形式,比如定义某种安全威胁的严重等级为:低风险(Low)、一般风险(General)、高风险(High)和严重风险(Severe)。
贝叶斯网络可以描述出事件的多态性,通过贝叶斯网络构建多态系统安全评估模型,可以计算出评估结果发生的概率、重要度,同时可以进行预测或诊断,帮助评估者获取更多辅助决策信息。
进行网络安全评估过程之前,应提前收集很多辅助信息,特别是有一些安全日志可以为构建网络安全的多态事件树[14]提供依据,而多态事件树通过相关算法可直接转化为贝叶斯网络模型。多态事件树是在A.Papazoglou的事件树[15]基础上定义的,其中树的节点由对系统的状态有影响的各种因素或者事件构成,叶子节点表示基本事件,可以用E1,E2,……来表示,基本事件Ei的所有状态构成了Ei的状态空间,具有j种状态的事件Ei可以表示为
例如,EAEB两事件各自有a和b种状态,则两事件的联合状态空间可以表示为笛卡尔积的形式,设其状态空间分别为
| $ \boldsymbol{S}_{\mathrm{E}_{1} \mathrm{E}_{2} \cdots \cdots \mathrm{E}_{n}}=\boldsymbol{S}_{\mathrm{E}_{1}} \otimes \boldsymbol{S}_{\mathrm{E}_{2}} \otimes \cdots \otimes \boldsymbol{S}_{\mathrm{E}_{n} 。} $ |
用发生事件的状态空间笛卡尔积表示的多态事件树,其组成事件的所有状态都是由同一事件节点发出的,用图形表示为一个节点对应多个分支状态,分支的尾部与后续事件的起始节点相连,并不断持续形成其他事件分支。从形式上看,多态事件树并没有多复杂,但计算过程中会出现状态爆炸的情况,特别是不同事件存在相互依赖关系时,目前还没有适合的算法。本文提出在使用贝叶斯网络进行多态风险事件树的求解,能够利用建模工具部分缓解状态爆炸影响,可用于识别信息系统的有限威胁状态并进行风险评估。
具有3个事件E1、E2和E3的任何事件树可以由贝叶斯网络表示,其中有两种类型的边组成了网络:
结果关系边(贝叶斯网络中一般由实线所示)将每个事件节点连接到结果节点。这种关系是确定性的,可基于结果节点的概率表对事件和结果之间的逻辑关系进行编码。
因果关系边(贝叶斯网络中一般由虚线表示)将每个事件节点连接到稍后的所有事件,例如事件E1指向E2的虚线边即E1影响E2的概率(或者E1是事件E2的因果因素)。这种表示方法具有通用性,因为节点和边只取决于事件的数量。然而,在贝叶斯网络仅用于确定后果概率时,因果关系边是不必要的,需对贝叶斯网络进行简化,本文中不考虑因果关系边。
3.2.2 算法多态事件树转化为贝叶斯网络的过程如下:
设初始事件E0有三种状态,分别是:L、M和H,第一个事件E1有两种状态,分别是:Y和N,第二个事件E2有两种状态F和S,则最后结果节点O的条件概率分布如下:
| $ \begin{gathered} P\left(O=O_{1} \mid E_{0}=L, E_{1}=Y, E_{2}=F\right)=p_{1}, \\ P\left(O=O_{2} \mid E_{0}=L, E_{1}=Y, E_{2}=S\right)=p_{2}, \\ \cdots \cdots\\ P\left(O=O_{11} \mid E_{0}=H, E_{1}=N, E_{2}=F\right)=p_{11}, \\ P\left(O=O_{12} \mid E_{0}=H, E_{1}=N, E_{2}=S\right)=p_{12} 。\end{gathered} $ |
由此可见,多态事件树中的任一事件序列,表示的是该事件序列中的各环节状态转换顺序,在此基础上可得多态事件树(Polymorphic event tree,PET)转换为贝叶斯网络的基本算法:
Step1:进入PET,将Initial Event作为BN初始二态节点(Initial node,IN);
Step2:根据事件树顺序遍历PET,将其他事件对应在在中建立相应节点,建立PET与BN状态空间映射关系;
Step3:建立多态输出结果向量O,其输出状态为{Oi},O的每个状态对应事件树的一个结果,BN中的每个NEi与Oi节点相连接;
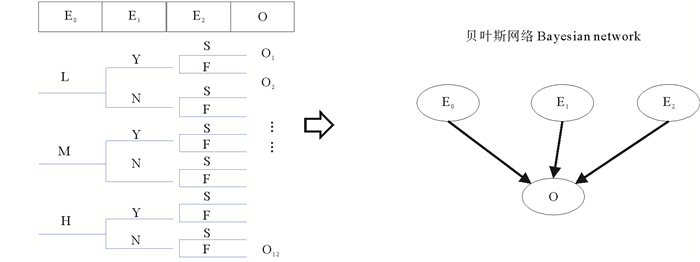
Step4:根据多态事件树的逻辑分支建立输出结果向量O的条件概率分布(见图 2)。
|
图 2 多态事件树向贝叶斯网络的转化过程示意图 Fig. 2 The schematic diagram of transformation process from an polymorphic event tree to the Bayesian network |
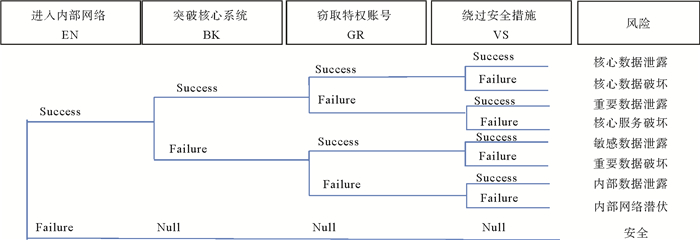
以外部攻击导致信息系统安全事件为例,首先攻击者要先进入系统内部网络(假设可能通过web漏洞攻击或者水坑攻击进入内网),进入内部网络后假设需要寻找应用系统漏洞来突破核心系统,在此基础上通过弱口令、暴力破解等方法获取特权账号,然后通过绕过存储介质管控或打印刻录管控等内网安全措施的方式完成数据窃取,可以得到面对特定外部攻击的信息系统安全事件树(见图 3)。
|
图 3 面对特定外部攻击的信息系统安全事件树 Fig. 3 The information system security event tree facing external attacks |
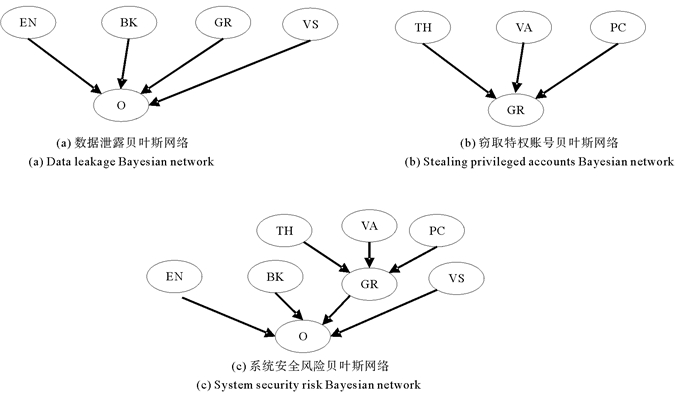
4个根节点——进入内部网络(EN)、突破核心系统(BK)、窃取特权账号(GR)和绕过安全措施(VS)概率分布暂不赋值,对应数据泄露贝叶斯网络(见图 4(a)),整个网络中各环节可以进一步分解其对应事件树。以窃取特权账号(GR)事件为例,可能通过木马植入(TH)、漏洞攻击(VA)和密码破解(PC)等事件实现,对应的事件图不再分析,可以得到窃取特权账号对应的贝叶斯网络(见图 4(b))。
|
图 4 系统安全风险贝叶斯网络 Fig. 4 The Bayesian network of system security risk |
从图 3可以看出,共有9种类型结果,分别是内部及敏感数据泄露、重要数据泄露、核心数据泄露、核心服务无法运行、核心数据和重要数据被破坏、内网潜伏和处于安全状态,对上述9种状态进行归并,最终得到4种状态,分别是数据泄露(DR)、系统被破坏(SD)、内网潜伏(IL)和安全(SE),作为系统安全风险评估的4种结果。将细化后的窃取特权账号根节点整合入原有贝叶斯网络,得到整合后的数据泄露贝叶斯网络(见图 4(c))。
已确定贝叶斯网络的情况下,需要根据已知证据节点变量的概率分布,利用条件概率的计算方法,计算出所关注节点变量发生的概率。在本示例中,利用已知贝叶斯网络图 4(c),根据木马植入、漏洞攻击和密码破解等节点事件发生概率,可推理系统安全风险发生的概率。
整个推理过程需要借助贝叶斯网络推理工具来实现。目前有很多贝叶斯网络构建工具,例如Hugin Expert、BayesBuider、BN Toolkit、JavaBayes、Netica等。其中Netica是基于Java开发的使用较广泛的贝叶斯网络开发软件[16],其设计目的是简单可靠和高性能。贝叶斯网络中的未知变量可以通过多种形式来表示其适当的值或概率,包括条形图和仪表盘,设计好的案例可以方便地保存到文件中,在任何变量或参数发生变化时,可以再代入网络以进行进一步推理分析。
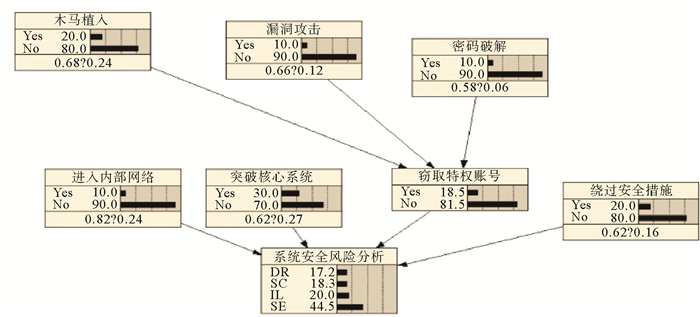
利用Netica软件构建贝叶斯网络时,初始的信度栅均为50(50%),在本例中即木马植入、漏洞攻击和密码破解等节点事件的发生风险的可能性为50%。通过学习大量上述风险事件统计数据(Netica调用样本数据集后执行参数学习功能),最终获得基于实际样本数据集的推理网络。如图 5所示,经过某特定信息系统风险事件统计样本学习后,木马植入事件的发生概率为20%,漏洞攻击事件发生概率为10%,密码破解事件发生概率为10%,此时窃取到特权账号的可能性可以推理出来为18.5%;根据样本数据学习到攻击者进入内部网络事件发生概率为10%,突破核心系统的可能概率为30%,绕过安全措施的可能概率为20%,最后可以获得系统安全风险评估分析结果,其中数据泄露(DR)概率为17.2%、系统被破坏(SD)的概率为18.3%、内网潜伏(IL)的概率为20%,系统处于安全状态(SE)的概率为44.5%。
|
图 5 系统安全风险分析贝叶斯网络模型(Netica v5.18) Fig. 5 The Bayesian network model for system security risk analysis (Netica v5.18) |
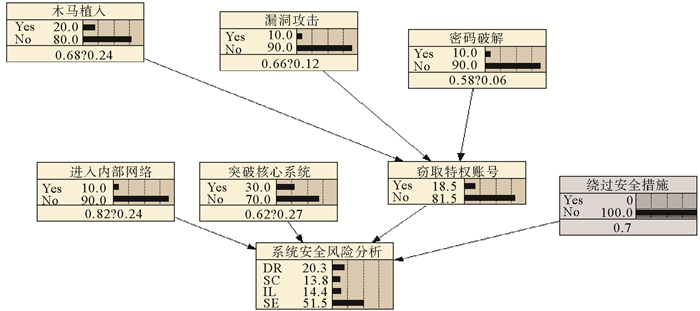
根据调整某些特定事件的发生概率,可以获得状态更新后的推理网络(见图 6),在其他安全事件发生概率不变,绕过安全措施的风险事件不可能发生的情况下,系统安全风险评估分析结果有所变化,其中安全状态(SE)的概率提升为51.5%,内部潜伏的可能性降低为14.4%。
|
图 6 调整后的系统安全风险分析贝叶斯网络模型(Netica v5.18) Fig. 6 The adjusted Bayesian network model for system security risk analysis (Netica v5.18) |
香农的信息论中,互信息(Mutual information,MI)是衡量父节点对子节点重要度的指数[17]。在信息系统风险分析过程中,特定事件所导致的风险传类似信息流通,Netica将MI作为衡量敏感性分析的重要指标。除此以外还有熵减百分比(Percent)和方差(Variance)[18]。根据图 6所示的贝叶斯网络,以“系统安全风险分析”为查询节点的敏感性分析如表 1所示。
|
|
表 1 以“系统安全风险分析”为查询节点的事件敏感性分析 Table 1 Event sensitivity analysis with "system safety analysis" as query node |
基于特定攻击事件发生的先验概率贝叶斯网络,当给定各个风险事件发生概率,同时结合各自的联合概率,即可计算出特定事件概率与导致数据泄露风险的MI值,据此评估出攻击事件的重要度。由表 1可知,对“数据泄露”最有影响力的节点是“突破核心系统”,同时其熵减百分比和方差也最大,说明“数据泄露”概率对“突破核心系统”节点概率变化的敏感程度最大。
4 结论贝叶斯网络应用于信息系统风险评估时,可通过严格的数学方式来模型化信息系统风险分析过程,具有很高的计算效率和很强的适应性,但其仍具有局限性:
(1) 系统在实际使用中会有意想不到的风险事件发生,从而造成系统用户对各类系统风险估计不足。系统通常会遇到以下异常或意外情况,如:外部非法入侵、内部窃密、恶意软件攻击、物理损害(包括:自然灾害、环境破坏等)、无作为或操作失误、安全管理不到位、越权或滥用、信息篡改等[19-20],但仍有一些风险事件无法预知,即便这些风险属于小概率事件,也容易造成整个系统的风险被低估。所以必须考虑系统因无法预测而遭遇其他风险。
(2) 注意在贝叶斯推理处理中使用先验知识的质量和程度。贝叶斯网络仅在先验知识可靠时才有用,对这些先验知识的质量过于乐观或悲观会扭曲整个网络并使结果无效,特别是对数据建模时所依赖的统计分布选择。选择合适的分布模型来描述某类风险的发生概率,对网络评估结果的质量有着显著影响。
因此,对信息系统进行风险评估时,应充分分析相似系统曾经发生的风险事件,并统计其发生的可能性,分析和统计工作的充分性将能够提高贝叶斯网络风险评估的可靠性。
| [1] |
张焕国. 网络空间安全综述[J]. 中国科学(信息科学), 2016, 46(2): 125-164. Zhang Huan-Guo. Overview of cyberspace security[J]. Science China Information Sciences, 2016, 46(2): 125-164. (  0) 0) |
| [2] |
郭新. 信息安全风险评估手册[M]. 北京: 机械工业出版社, 2017: 23-34. Guo Xin. Information Security Risk Assessment Manual[M]. Beijing: China Machine Press, 2017: 23-34. (  0) 0) |
| [3] |
Zagorecki A, Druzdzel M J. Knowledge engineering for Bayesian Networks: How common are Noisy-MAX distributions in practice[J]. IEEE Trans on Systems Man and Cybernetics: Systems, 2013, 43(1): 186-195. DOI:10.1109/TSMCA.2012.2189880 (  0) 0) |
| [4] |
Frigault M, WANG L, Singhal A, et al. Measuring Network Security using Dynamic Bayesian Network[C]. Alexandnia VA, USA: Proceedings of the 4th ACM Workshop on Quality of Protection, 2008: 23-30.
(  0) 0) |
| [5] |
WANG J, FAN K, MO W, et al. A Method For Information Security Risk Assessment Based on The Dynamic Bayesian Network[C]. Hakodate: IEEE International Conference on Networking and Network Applications, 2016: 279-283.
(  0) 0) |
| [6] |
Sevilay BEKENi, Mete EMINAAOLUii. An Information security risk assessment model based on bayesian Network and fuzzy inference system[J]. Journal of Strategic Research, 2019, 10(1): 13-33. (  0) 0) |
| [7] |
吕海敏. 城市地铁系统沉涝灾害风险评估方法与防灾对策[D]. 上海: 上海交通大学, 2019. LYU Hai-Min. Risk Assessment Method and Disaster Prevention Counter Measures of Urban Subway System[D]. Shanghai: Shanghai Jiao Tong University, 2019. (  0) 0) |
| [8] |
刘瑞. 基于贝叶斯网络的洪水灾害风险评估与建模研究[D]. 上海: 华东师范大学, 2016. LIU Rui. Research on Flood Disaster Risk Assessment and Modeling Based on Bayesian Network[D]. Shanghai: East China Normal University, 2016. (  0) 0) |
| [9] |
徐磊. 基于贝叶斯网络的突发事件应急决策信息分析方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2013. XU Lei. Research on Analysis Method of Emergency Decision Information Based on Bayesian Network[D]. Harbin: Harbin Institute of Technology, 2013. (  0) 0) |
| [10] |
那孜古丽. 斯拉木. 面向非常规突发时间应急管理的临机决策计算模型研究[D]. 天津: 天津大学, 2016. Naziguli Slamu. Research on the Calculation Model of Temporary Decision-making for Unconventional Emergency Management[D]. Tianjin: Tianjin University, 2016. (  0) 0) |
| [11] |
李欢. 基于贝叶斯网络攻击图的动态风险评估方法研究[D]. 秦皇岛: 燕山大学, 2019. Li Huan. Research on Dynamic Risk Assessment Method Based on Bayesian Network Attack Graph[D]. Qinhuangdao: Yanshan University, 2019. (  0) 0) |
| [12] |
王文思. 基于贝叶斯网络和支持向量机的网络安全态势评估和预测方法研究[D]. 南京: 南京邮电大学, 2020. Wang Wen-Si. Research on Network Security Situation Assessment and Prediction Method Based on Bayesian Network and Support Vector Machine[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2020. (  0) 0) |
| [13] |
Boudali Hichem, Dugan Joanne B. A New Bayesian Network Approach To Solve Dynamic Fault Trees[C]. Proceedings of the Annual Reliability and Maintainability Symposium on Product Quality and Integrity. Alexandria: IEEE, 2005.
(  0) 0) |
| [14] |
田宏, 陈宝智, 吴穹, 等. 广义多态事件树模型[J]. 中国安全科学学报, 2000, 10(6): 35-39. Tian Hong, Chen Bao-Zhi, Wu Qiong, et al. Generalized polymorphic event tree model[J]. China Safety Science Journal, 2000, 10(6): 35-39. DOI:10.3969/j.issn.1003-3033.2000.06.008 (  0) 0) |
| [15] |
Papazoglou I A. Mathematical foundations of event trees[J]. Reliability Engineering and System Safety, 1998, 61(3): 169-183. DOI:10.1016/S0951-8320(98)00010-6 (  0) 0) |
| [16] |
陈静, 蒋正凯, 付敬奇. 基于Netica的自学习贝叶斯网络的构建[J]. 电子测量与仪器学报, 2016, 30(11): 1687-1693. Chen Jing, Jiang Zheng-Kai, Fu Jing-Qi. Construction of self-learning Bayesian Network based on Netica[J]. Journal of Electronic Measurement and Instrument, 2016, 30(11): 1687-1693. (  0) 0) |
| [17] |
Liam Paninski. Estimation of entropy and mutual information[J]. Neural Computation 15, Massachusetts Institute of Technology, 2003, 15(6): 1191-1253. (  0) 0) |
| [18] |
Peng H, Long F, Ding C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(8): 1226-1238. DOI:10.1109/TPAMI.2005.159 (  0) 0) |
| [19] |
Ammann P, Wijesekera D, Kaushik S. Scalable Graph-based Network Vulnerability Analysis[C]. Acm Conference on Computer & Communications Security. Washington: IEEE Press, 2002: 217-224.
(  0) 0) |
| [20] |
Kerem Kaynar, Fikret Sivrikaya. Distributed attack graph generation[J]. IEEE Transactions on Dependable and Secure Computing, 2016, 13(5): 519-532. DOI:10.1109/TDSC.2015.2423682 (  0) 0) |
2. Qingdao Security Technology Service Center, Qingdao 266000, China;
3. Qingdao Security Technology Evaluation Center, Qingdao 266000, China
 2022, Vol. 52
2022, Vol. 52

