1960年, 卡尔曼提出了基于贝叶斯估计的递推滤波方法—卡尔曼滤波[1], 用以处理线性系统的状态估计。面对非线性问题, 有学者提出基于线性化的扩展卡尔曼滤波EKF(Extended Kalman filter), 这是一种用欧拉折线近似替代非线性方程的方法, 只能应用于线性化误差比较小的系统方程。后来又产生了用特征点近似状态的概率密度函数的方法——Sigma点滤波:基于无迹变换的无迹卡尔曼滤波UKF(Uncented Kalman Filter)[2]、基于插值法的高斯滤波器[3]和基于重要性采样的粒子滤波PF(Particle Filter)[4]。它们或数学基础不严密, 或计算量会随着系统维度的增加而急剧增大。学者Arasaratnam提出了基于容积计算的容积卡尔曼滤波器CKF(Cubature Kalman Filter)[5], 此后又研究了连续系统的容积卡尔曼滤波算法[6], 但并未给出带约束系统的容积卡尔曼滤波算法。对于约束问题, Simon在其专著[7]中给出了4种方法:降维、完美观测、约束优化、概率重写, Rawlings将预测控制中的滚动优化方法[8]引入状态估计领域并于推导出递推滚动最优估计算法MHE(Moving Horizion Estimation)[9], 通过解带约束的最优化方程的方法同步解决约束和估计问题。同时发展的还有其近亲算法——非线性动态数据均衡RNDDR(Recursive Nonlinear Dynamic Data Reconciliation)[10], 这种方法与N=1的MHE算法很像, 这两种方法有能够处理多种约束条件的优点, 但最优化计算会产生很大的运算量, 同时RNDDR在递推过程中需要用到黎卡提方程, 对于非线性系统则需借助线性化的手段来实现[10], 或借用Sigma点滤波来实现黎卡提方程的参数更新功能[11], 本文将CKF算法和带约束的非线性动态数据均衡算法NDDR(Nonlinear Dynamic Data Reconciliation)相结合, 弥补计算精度低或UKF数学基础不严密的缺点。完全讨论所有的约束会使问题过于复杂, 本文只讨论边界约束。对于文献[12]中所使用的约束方法, 其仿真效果在很多情况下并不理想, 所以本文在此基础上改进, 将容积点完全约束在边界之内, 重新计算对应的权重, 同时与数据均衡算法结合, 使CKF算法更适用于边界约束的非线性系统, 推导出约束容积卡尔曼滤波Constrainted Cubature Kalman filter(CCKF)。
1 容积卡尔曼滤波对于非线性系统模型
| $ {\mathit{\boldsymbol{x}}_k} = f\left( {{\mathit{\boldsymbol{x}}_{k - 1}}} \right) + {\mathit{\boldsymbol{w}}_{k - 1}}, $ | (1) |
| $ {\mathit{\boldsymbol{z}}_k} = g\left( {{\mathit{\boldsymbol{x}}_k}} \right) + {\mathit{\boldsymbol{v}}_k}, $ | (2) |
其中:xk∈Rn、zk∈Rm分别表示k时刻系统状态和系统输出;wk∈Rn、vk∈Rm分别为k时刻系统噪声和输出噪声;f:Rn→Rn, g:Rn→Rm为非线性函数。
| $ E{\mathit{\boldsymbol{w}}_i} = 0,E{\mathit{\boldsymbol{w}}_i}\mathit{\boldsymbol{w}}_j^{\rm{T}} = \mathit{\boldsymbol{Q}} \cdot {\delta _{ij}}, $ |
| $ E{\mathit{\boldsymbol{v}}_i} = 0,E{\mathit{\boldsymbol{v}}_i}\mathit{\boldsymbol{v}}_j^{\rm{T}} = \mathit{\boldsymbol{R}} \cdot {\delta _{ij}}, $ |
| $ E{\mathit{\boldsymbol{w}}_i}\mathit{\boldsymbol{v}}_j^{\rm{T}} = 0, $ |
其中:Q、R分别为正定对称矩阵;δij为Kronecker函数。
Bayes估计求出状态的概率分布之后, 通过求期望来获得状态估计的滤波方差, CKF的本质是将积分求期望的问题用积分插值方法解决, 即
对任意函数f(x), 其容积积分为
| $ \begin{array}{l} {I_N}\left( f \right) = \int_{{R^n}} {f \cdot N\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}},\mathit{\boldsymbol{P}}} \right){\rm{d}}x} \approx \\ \frac{1}{{2n}}\sum\limits_{i = 1}^{2n} {f\left( {\mathit{\boldsymbol{u}} + \sqrt {\mathit{\boldsymbol{P}}} \cdot {\xi _i}} \right)} , \end{array} $ | (3) |
其中点集{ξi}为标准容积点:
| $ \sqrt {\mathit{\boldsymbol{n}}} \left\{ {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} 1\\ 0\\ \vdots \\ 0 \end{array}} \right]}& \cdots &{\left[ {\begin{array}{*{20}{c}} 1\\ 0\\ \vdots \\ 0 \end{array}} \right]}&{\left[ {\begin{array}{*{20}{c}} 1\\ 0\\ \vdots \\ 0 \end{array}} \right]}& \cdots &{\left[ {\begin{array}{*{20}{c}} 1\\ 0\\ \vdots \\ 0 \end{array}} \right]} \end{array}} \right\}。$ |
在Bayes估计的框架下, k时刻的后验概率估计为
CKF的滤波步骤如下:
(1) 预测更新。计算方差平方根和容积点
| $ {\mathit{\boldsymbol{S}}_{k - 1/k - 1}} = {\rm{chol}}\left( {{\mathit{\boldsymbol{P}}_{k - 1/k - 1}}} \right), $ | (4) |
| $ {\mathit{\boldsymbol{x}}_{k - 1/k - 1,i}} = {\mathit{\boldsymbol{S}}_{k - 1/k - 1}} \cdot {\xi _i} + {{\mathit{\boldsymbol{\hat x}}}_{k - 1/k - 1}}, $ | (5) |
其中:chol(·)表示cholesky分解;Sk-1/k-1为Pk-1/k-1的矩阵平方根;ξi是上文中的标准容积;xk-1/k-1, i为实际计算需要的容积点。容积点对应的预估点为
| $ {\mathit{\boldsymbol{x}}_{k/k - 1,i}} = f\left( {{\mathit{\boldsymbol{x}}_{k - 1/k - 1,i}}} \right), $ | (6) |
预估状态和预估方差
| $ {{\mathit{\boldsymbol{\hat x}}}_{k/k - 1}} = \sum\limits_{i = 1}^{2n} {{\omega _i}{\mathit{\boldsymbol{x}}_{k/k - 1,i}}} , $ | (7) |
| $ {\mathit{\boldsymbol{P}}_{k/k - 1}} = \sum\limits_{i = 1}^{2n} {{\omega _i}\left( {{\mathit{\boldsymbol{x}}_{k/k - 1,i}} - {{\mathit{\boldsymbol{\hat x}}}_{k/k - 1}}} \right){{\left( {{\mathit{\boldsymbol{x}}_{k/k - 1,i}} - {{\mathit{\boldsymbol{\hat x}}}_{k/k - 1}}} \right)}^{\rm{T}}}} , $ | (8) |
其中:ωi为表示权重,且ωi=1/2n。
(2) 状态更新。计算此时的容积点
| $ {\mathit{\boldsymbol{S}}_{k /k - 1}} = {\rm{chol}}\left( {{\mathit{\boldsymbol{P}}_{k /k - 1}}} \right), $ | (9) |
| $ {\mathit{\boldsymbol{x}}_{k /k - 1,i}} = {\mathit{\boldsymbol{S}}_{k /k - 1}} \cdot {\xi _i} + {{\mathit{\boldsymbol{\hat x}}}_{k /k - 1}}, $ | (10) |
容积点对应的输出
| $ {\mathit{\boldsymbol{z}}_{k/k - 1,i}} = h\left( {{\mathit{\boldsymbol{x}}_{k /k - 1,i}}} \right), $ | (11) |
系统输出的预估
| $ {{\mathit{\boldsymbol{\hat z}}}_{k/k - 1}} = \sum\limits_{i = 1}^{2n} {{\omega _i}{\mathit{\boldsymbol{z}}_{k/k - 1,i}}} , $ | (12) |
相关协方差
| $ {\mathit{\boldsymbol{P}}_{xz,k}} = \sum\limits_{i = 1}^{2n} {{\omega _i}\left( {{\mathit{\boldsymbol{x}}_{k/k - 1,i}} - {{\mathit{\boldsymbol{\hat x}}}_{k/k - 1}}} \right){{\left( {{\mathit{\boldsymbol{z}}_{k/k - 1,i}} - {{\mathit{\boldsymbol{\hat z}}}_{k/k - 1}}} \right)}^{\rm{T}}}} , $ | (13) |
| $ {\mathit{\boldsymbol{P}}_{xx,k}} = \sum\limits_{i = 1}^{2n} {{\omega _i}\left( {{\mathit{\boldsymbol{x}}_{k/k - 1,i}} - {{\mathit{\boldsymbol{\hat x}}}_{k/k - 1}}} \right){{\left( {{\mathit{\boldsymbol{x}}_{k/k - 1,i}} - {{\mathit{\boldsymbol{\hat x}}}_{k/k - 1}}} \right)}^{\rm{T}}}} , $ | (14) |
状态增益为
| $ {\mathit{\boldsymbol{K}}_k} = {\mathit{\boldsymbol{P}}_{xz,k}}\mathit{\boldsymbol{P}}_{zz,k}^{ - 1}, $ | (15) |
| $ {{\mathit{\boldsymbol{\hat x}}}_{k/k}} = {{\mathit{\boldsymbol{\hat x}}}_{k/k - 1}} + {\mathit{\boldsymbol{K}}_k}\left( \hat{{\mathit{\boldsymbol{z}}_k} - {\mathit{\boldsymbol{z}}_{k/k - 1}}} \right), $ | (16) |
滤波方差
| $ {\mathit{\boldsymbol{P}}_{k/k}} = {\mathit{\boldsymbol{P}}_{k/k - 1}} - {\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{P}}_{zz,k}}K_k^{\rm{T}}。$ | (17) |
在噪声为高斯噪声的假设下,Bayes估计退化为Kalman滤波, 因此即使是非线性系统的状态滤波也具有了线性Kalman滤波的一般形式, 但二者绝不是简单类比, 而是同源于Bayes估计。CKF用容积求积规则逼近求系统状态期望的步骤, 因而不是最优估计。在滤波算法中引入非线性动态数据均衡方法可以一定程度地提高算法精度,这一方法很好地处理了滤波过程中约束条件的影响。
2 非线性动态数据均衡算法非线性动态数据均衡算法是一种尽可能充分利用已知信息进行状态估测的方法, 其主要思想是对已知的信息利用惩罚因子的方法予以平衡, 获取可信度相对高的状态估计,这是一种广泛应用于非线性的化工生产之中的算法[10], 同时可以处理广泛的非线性约束问题, 相对于MHE算法, 这是一种很好的平衡算法运算量和运算精度的方法。
即计算:
| $ \begin{array}{l} {{\mathit{\boldsymbol{\hat x}}}_{k/k}} = \arg \mathop {\min }\limits_{{\mathit{\boldsymbol{x}}_k}} \left\{ {{{\left( {{\mathit{\boldsymbol{x}}_k} - {{\mathit{\boldsymbol{\hat x}}}_{k/k - 1}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{P}}_{k/k - 1}^{ - 1}\left( {{\mathit{\boldsymbol{x}}_k} - {{\mathit{\boldsymbol{\hat x}}}_{k/k - 1}}} \right) + } \right.\\ \left. {{{\left( {{\mathit{\boldsymbol{z}}_k} - g\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right)}^{\rm{T}}}\mathit{\boldsymbol{R}}_k^{ - 1}\left( {{\mathit{\boldsymbol{z}}_k} - g\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right)} \right\}, \end{array} $ | (18) |
上式的约束条件为
| $ {\mathit{\boldsymbol{x}}_L} \le {\mathit{\boldsymbol{x}}_k} \le {\mathit{\boldsymbol{x}}_H}, $ |
| $ h\left( {{\mathit{\boldsymbol{x}}_k}} \right) \le 0, $ |
| $ e\left( {{\mathit{\boldsymbol{x}}_k}} \right) = 0。$ |
当约束条件去除, 系统为线性化系统时, 以上方法退化为Kalman滤波。
3 约束容积卡尔曼滤波本文只讨论具有边界约束的状态滤波, 边界约束定义如下:xL≤xk≤xU, 此时整个空间的概率函数将形成截断函数, 理想假设中的高斯分布变成了截断高斯分布。此外对于连续不等式fi(x)≤0, 会形成空间{ x|fi(x)≤0}:将不等式约束化为特殊的边界约束。容积卡尔曼滤波(CKF)是用容积点近似模拟整个空间的概率分布。假如约束空间为凸空间, 容积点还可以一定程度近似截断高斯分布。只是其容积点和权重的取法需要改进。
当容积点位于边界点之外时, 将容积点强制约束至边界。即:对于容积点,
同时对于滤波结果的求取, 使用更精确和对约束处理更直接的非线性动态数据均衡算法。
综合以上假设和推理, 得到
(1) 预估阶段。
| $ {S_{k - 1/k - 1}} = {\rm{chol}}\left( {{P_{k - 1/k - 1}}} \right), $ | (19) |
求出每个Δxi方向边界与容积点的相对关系
| $ {\theta _i} = \min \left\{ {\left( {{b_j} - {{\hat x}_j}} \right)/\Delta {x_{i,j}}} \right\}, $ | (20) |
其中
Δxi=[Sk-1/k-1 -Sk-1/k-1]的第i个纵量, 令λi=min{1, θ},
则容积点为
| $ {{\mathit{\boldsymbol{\hat x}}}_{k - 1/k - 1,i}} = {\lambda _i}{\mathit{\boldsymbol{S}}_{k - 1/k - 1}}{\xi _i} + {{\mathit{\boldsymbol{\hat x}}}_{k - 1/k - 1}}, $ | (21) |
其对应的权重为
| $ {\mathit{\boldsymbol{x}}_{k/k - 1,i}} = f\left( {{{\mathit{\boldsymbol{\hat x}}}_{k - 1/k - 1,i}}} \right), $ | (22) |
| $ {{\mathit{\boldsymbol{\hat x}}}_{k/k - 1}} = \sum\limits_{i = 1}^{2n} {{\omega _{k/k - 1,i}}{\mathit{\boldsymbol{x}}_{k/k - 1,i}}} , $ | (23) |
预估方差
| $ {\mathit{\boldsymbol{P}}_{k/k - 1}} = \sum\limits_{i = 1}^{2n} {{\omega _i}\left( {{\mathit{\boldsymbol{x}}_{k/k - 1,i}} - {{\mathit{\boldsymbol{\hat x}}}_{k/k - 1}}} \right){{\left( {{\mathit{\boldsymbol{x}}_{k/k - 1,i}} - {{\mathit{\boldsymbol{\hat x}}}_{k/k - 1}}} \right)}^{\rm{T}}}} 。$ | (24) |
(2) 状态更新。重复以上求容积点的规则得到相应的容积点
| $ \begin{array}{l} {\mathit{\boldsymbol{x}}_{k/k,i}} = \arg \mathop {\min }\limits_{{x_k}} \left\{ {{{\left( {{\mathit{\boldsymbol{x}}_{k,i}} - {{\mathit{\boldsymbol{\hat x}}}_{k/k - 1,i}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{P}}_{k/k - 1}^{ - 1}\left( {{\mathit{\boldsymbol{x}}_{k,i}} - } \right.} \right.\\ \left. {\left. {{{\mathit{\boldsymbol{\hat x}}}_{k/k - 1,i}}} \right) + {{\left( {{\mathit{\boldsymbol{z}}_k} - g\left( {{\mathit{\boldsymbol{x}}_{k,i}}} \right)} \right)}^{\rm{T}}}\mathit{\boldsymbol{R}}_k^{ - 1}\left( {{\mathit{\boldsymbol{z}}_k} - g\left( {{\mathit{\boldsymbol{x}}_{k,i}}} \right)} \right.} \right\}。\end{array} $ | (25) |
优化约束条件为
| $ {\mathit{\boldsymbol{x}}_L} \le {\mathit{\boldsymbol{x}}_k} \le {\mathit{\boldsymbol{x}}_H}, $ |
滤波值为
| $ \begin{array}{l} {{\mathit{\boldsymbol{\hat x}}}_{k/k}} = \sum\limits_{i = 1}^{2n} {{\omega _{k/k,i}}{\mathit{\boldsymbol{x}}_{k/k,i}}} , \end{array} $ | (26) |
滤波方差为
| $ {\mathit{\boldsymbol{P}}_{k/k}} = \sum\limits_{i = 1}^{2n} {{\omega _{k/k,i}}\left( {{\mathit{\boldsymbol{x}}_{k/k,i}} - {{\mathit{\boldsymbol{\hat x}}}_{k/k}}} \right){{\left( {{\mathit{\boldsymbol{x}}_{k/k,i}} - {{\mathit{\boldsymbol{\hat x}}}_{k/k}}} \right)}^{\rm{T}}}} 。$ | (27) |
对于边界约束的容积滤波算法, 最精确的方式是利用文献[7]中的方法对截断空间的期望x和方差P进行重新计算, 这样容积点就会全部落入约束区域, 但这种方法处理过于复杂, 因此本文基于相似的理念给出了一种替代方法。在本方法中, 预估阶段的期望、方差和状态更新阶段的期望、方差, 均考虑了约束条件。
4 仿真算例本文讨论的算例来自化工气体化合过程[13]的改写,其化学反应为:2A → B
| $ \frac{{{\rm{d}}{P_A}}}{{{\rm{d}}t}} = - 2{k_1}P_A^2, $ | (28) |
| $ \frac{{{\rm{d}}{P_B}}}{{{\rm{d}}t}} = {k_1}P_A^2, $ | (29) |
| $ \begin{array}{l} {k_1} = 0.16,\\ P = {P_A} + {P_B}。\end{array} $ | (30) |
其对应的离散化模型为
| $ {\mathit{\boldsymbol{x}}_k} = \left[ {\begin{array}{*{20}{c}} {{x_k}\left( 1 \right)}\\ {{x_k}\left( 2 \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{P_A}\left( k \right)}\\ {{P_B}\left( k \right)} \end{array}} \right], $ |
式中:PA、PB分别为A和B的分压;P为总压强, 采样速率为ΔT=0.1s。
| $ \left[ {\begin{array}{*{20}{c}} {{x_k}\left( 1 \right)}\\ {{x_k}\left( 2 \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{x_{k - 1}}\left( 1 \right) - 2{k_1}x_{k - 1}^2\left( 1 \right)\Delta T}\\ {{x_{k - 1}}\left( 2 \right) - 2{k_1}x_{k - 1}^2\left( 1 \right)\Delta T} \end{array}} \right] + {\mathit{\boldsymbol{w}}_k}, $ | (31) |
输出方程为
| $ {\mathit{\boldsymbol{z}}_k} = \left[ {\begin{array}{*{20}{c}} 1&1 \end{array}} \right]{\mathit{\boldsymbol{x}}_k} + {\mathit{\boldsymbol{v}}_k}, $ | (32) |
各参数设置如下:
wk的方差为
| $ {\mathit{\boldsymbol{x}}_L} \le \mathit{\boldsymbol{x}} \le {\mathit{\boldsymbol{x}}_H}, $ |
| $ {\mathit{\boldsymbol{x}}_L} = {\left[ {\begin{array}{*{20}{c}} 0&0 \end{array}} \right]^{\rm{T}}}, $ |
| $ {\mathit{\boldsymbol{x}}_H} = {\left[ {\begin{array}{*{20}{c}} {100}&{100} \end{array}} \right]^{\rm{T}}}。$ |
|
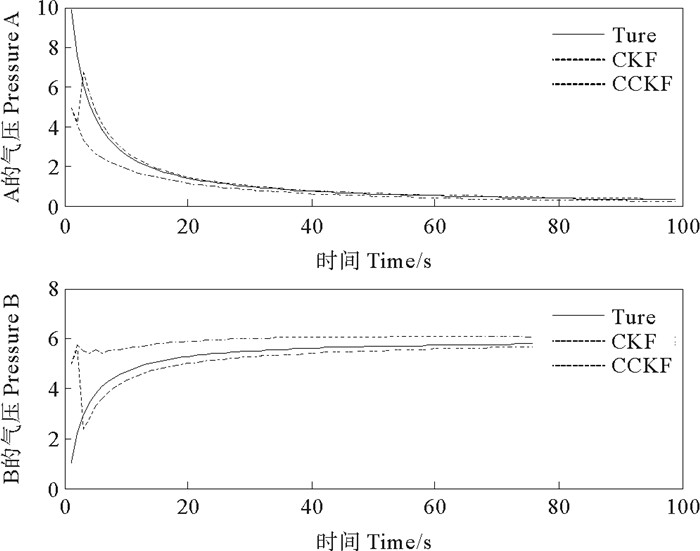
(“——”表示真值; “----”表示CKF的滤波结果; “……”表示CCKF的滤波结果。"——"denotes the ture state; "----"denotes the state estimated by CKF; "……"denote the state estimated by CCKF) 图 1 CKF和CCKF的滤波效果对比 Fig. 1 The comparation of the estimated states by CKF and by CCKF |
|
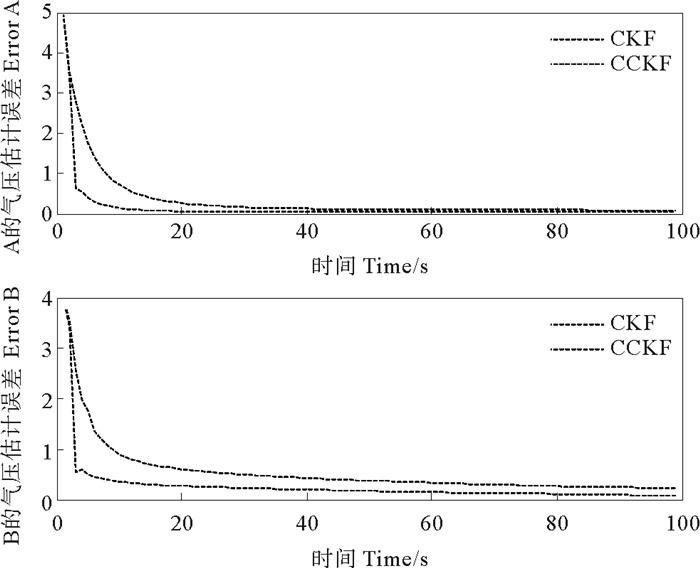
(“----”表示CKF的绝度滤波误差; “……”表示CCKF的绝度滤波误差。"----"denotes the absolute errors using CKF; "……"denote the absolute errors using CCKF.) 图 2 两种算法的绝对误差比较 Fig. 2 The comparation of the absoluote errors between the double algorithms |
图 1为A和B分压的真实状态及两种滤波算法的滤波结果对比,图 2为两种滤波算法的绝对误差对比。
从图 1和2中可以看出CCKF的收敛速度和收敛精度均高于CKF, 说明约束算法有效。
在仿真算例中发现一类使大多数算法失效的情况。即当非线性系统的系统方程的一阶项系数—梯度矩阵接近单位阵时, 由于计算的舍入误差, EKF及其衍生算法随机稳定, 即有时可以跟踪真值, 有时不能跟踪真值, 对于UKF、CKF及其衍生算法中未结合非线性动态数据均衡算法的, 跟踪效果也不稳定,本文算法表现稳定。
5 结语本文在容积卡尔曼滤波(CKF)和非线性动态数据均衡算法(NDDR)的基础上提出了处理一类边界约束的容积卡尔曼滤波, 将CKF的容积点约束在求积空间中, 提出相应的求权重的方法, 同时将非线性动态数据均衡的方法融入到状态估计过程中, 提高滤波精度, 并使滤波的每个过程都在约束之内。仿真表明, 本文算法在滤波收敛速度、滤波精度和鲁棒性等方面均优于原有的容积卡尔曼滤波。
本文提出的算法并非最优估计算法。一个高斯分布的概率密度函数在通过非线性系统之后, 其概率密度会产生畸变, 新的概率密度将不再是高斯函数, 甚至完全变形。而目前大部分非线性滤波仍假设是高斯分布, 因此本文算法是次优的,但大量仿真表明本算法的有效性。
| [1] |
Kalman R E. A new approach to linear filtering and prediction problems[J]. Journal of Basic Engineering, 1960, 82(1): 35. DOI:10.1115/1.3662552
(  0) 0) |
| [2] |
Julier S J, Uhlmann J K. Unscented filtering and nonlinear estimation[J]. Proceedings of the IEEE, 2004, 92(3): 401-422. DOI:10.1109/JPROC.2003.823141
(  0) 0) |
| [3] |
Alspach D L, Sorenson H W. Nonlinear bayesian estimation using Gaussian sum approximations[J]. Automatic Control, IEEE Transactions on, 1972, 17(4): 439-448. DOI:10.1109/TAC.1972.1100034
(  0) 0) |
| [4] |
Arulampalam M S, Maskell S, Gordon N, et al. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J]. IEEE Transactions on Signal Processing, 2002, 50(2): 174-188. DOI:10.1109/78.978374
(  0) 0) |
| [5] |
Arasaratnam I, Haykin S. Cubature Kalman Filters[J]. Automatic Control, IEEE Transactions on, 2009, 54(6): 1254-1269. DOI:10.1109/TAC.2009.2019800
(  0) 0) |
| [6] |
Arasaratnam I, Haykin S, Hurd T R. Cubature Kalman Filtering for Continuous-Discrete Systems: Theory and Simulations[J]. IEEE Transactions on Signal Processing, 2010, 58(10): 4977-4993. DOI:10.1109/TSP.2010.2056923
(  0) 0) |
| [7] |
Simon D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches[M]. New York: Wiley-Interscience, 2006.
(  0) 0) |
| [8] |
Frank P M, Wer F A, Badgwell T A, et al. Nonlinear Predictive Control and Moving Horizon Estimation - An Introductory Overview[M]. London: Springer London, 1999, 391-449.
(  0) 0) |
| [9] |
Robertson D G, Lee J H, Rawlings J B. A moving horizon-based approach for least-squares estimation[J]. AIChE Journal, 1996, 42(8): 2209-2224. DOI:10.1002/(ISSN)1547-5905
(  0) 0) |
| [10] |
Vachhani P, Narasimhan S, Rengaswamy R. Recursive state estimation in Nonlinear processes[C]. Proceedings of the American Control Conference. New York: IEEE, 2004: 200-204.
(  0) 0) |
| [11] |
Vachhani P, Narasimhan S, Rengaswamy R. Robust and reliable estimation via Unscented Recursive Nonlinear Dynamic Data Reconciliation[J]. Journal of Process Control, 2006, 16(10): 1075-1086. DOI:10.1016/j.jprocont.2006.07.002
(  0) 0) |
| [12] |
Zarei J, Shokri E. Nonlinear and Constrained State Estimation Based on the Cubature Kalman Filter[J]. Industrial & Engineering Chemistry Research, 2014, 53(10): 3938-3949.
(  0) 0) |
| [13] |
Haseltine E L, Rawlings J B. Critical evaluation of extended Kalman filtering and moving-horizon estimation[J]. Industrial & Engineering Chemistry Research, 2005, 44(8): 2451-2460.
(  0) 0) |
 2018, Vol. 48
2018, Vol. 48


