涡旋是自然界中一种普遍存在的流动现象,大到行星尺度的极地涡旋,小到大气与海洋中的湍流现象,对涡旋运动的研究对地球物理学、环境科学、工程以及军事都具有重要意义。室内实验室实验在涡研究方面有着无与伦比的优势:一方面可以通过控制实验室参数,模拟不同维度不同层结下的背景场,消除涡旋个体差异对理论总结的影响;另一方面,实验室实验可以完整地获取涡旋水平以及垂向结构场,并且可以模拟其随时间演化的全过程;同时实验室实验还有获取数据成本低等优势。
前人针对涡旋展开了多种形式的实验室实验,采用了多种造涡方法,并总结出了一定的规律。Bush J.W.M等[1]分析了旋转层结流体中浮力线型羽流产生连续涡旋结构的过程,通过在水槽底部布设一均匀开孔的注水管,在旋转层结流体中生成了高度可控的地转涡旋,并总结出了用于预测涡旋结构和规模的简易模式。Kloosterziel等[2]通过二维数值模拟和实验室实验模拟了小型气旋型旋涡与地形的相互作用。通过向旋转平台的水槽内注入垂向速度均一的水平急流,发现在较宽的山谷地形下,急流产生的涡旋会以围绕中心的气旋式螺旋爬升出山谷地形;而在宽山脊地形的情况下,涡旋趋向于以反气旋绕山峰爬升,其运动机制与β平面上气旋的西北向传播相同。Paul Billant等[3]通过双瓣装置生成垂向结构一致的涡旋,在层结流体中研究了一种新的涡旋不稳定机制,其涡旋流场与lamb-chaplygin涡的理论解有很好的拟合性。Andersen等[4]通过实验生成了所谓“bathtub vortex”,并给出了理论解,这种涡旋通过将流体从旋转的圆柱容器底部小孔中排出产生,发现通过这种方法生成的涡旋有明显的内外两层结构,内层为快速向下流动的流体,来源于自由表面,外层为Ekman上升流,两层流体涡度方向相反,并且流出容器的流体绝大部分来源于容器底部的Ekman层。Heijst等[5]总结了实验室生成正压涡旋的一般方法,发现涡旋结构可以归结为两类,给出了各自的拟合公式,并着重讨论了底地形对涡旋演化的作用。
海洋中的涡旋运动会受到地转效应的影响,同时由于海洋本身是一个层结流体,这都使得海洋中的涡旋运动进入到了地球流体力学的研究领域,同时也使得海洋涡旋具有与一般涡旋运动不同的影响因素及独特性质[6]。
通常针对涡旋的实验大多专注于涡旋的不稳定性研究[7-9],以及涡旋与地形的相互作用[10-15],所以在造涡方法方面,多采取“扰动”式造涡方法,涡旋结构不能长时间保持。而且使用上述方法造涡不可避免的会造成层结的变化甚至破坏,影响数据的完整性以及实验结果的准确性。本文作者提出了一种实验室造涡方法,通过强迫表层流场的方法输入涡度,可以在实验室中生成一个定常涡旋。相比于过去的研究,本实验不仅没有破坏线性层结,而且在持续涡度输入的情况下,涡旋可以保持稳定,更符合海洋中涡旋的存在特征。最后,通过测量水平速度分布,研究涡旋的三维结构,并总结不同物理量沿径向和垂向的分布规律。
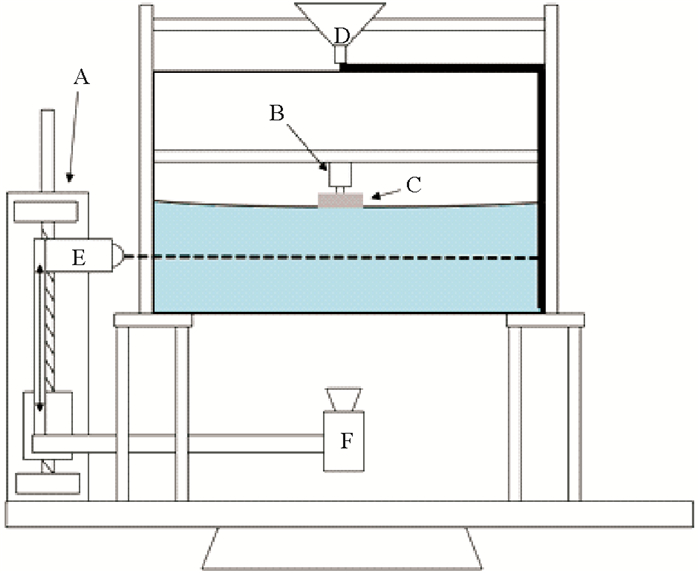
1 实验装置与测量方法实验依托中国海洋大学物理海洋实验室地转平台进行,本实验装置主要由转平台,试验水槽和强迫装置三部分组成(见图 1)。
|
(A为电动平移台,B为马达,C为强迫圆盘,D为漏斗,E为激光器,F为CCD。图中淡蓝色部分为实验水体,其右上部加粗折线为排水管道。与C接触的曲面表示水面。A: The electric displacement platform, B: The motor, C: The coercing disk, D: The Funnel, E: The Laser, F: CCD.The light blue area represents the experimental water, and the thick solid line is the water pipelines.Surface in contact C is water level.) 图 1 实验装置设置 Fig. 1 Experiment set-up |
地转平台为直径为1 m的圆形转台,用水平仪器调整到水平,旋转平稳。加载实验仪器后工作稳定。转台上架设一金属框架,抬高水槽,便于从底部采集图像[16]。本文的实验中,设置转台转速Ω=0.25 rad/s,逆时针旋转,对应北半球科氏参量f=0.5 rad/s。
矩形实验水槽为有机玻璃材质,为50.0 cm×50.0 cm×40.0 cm (长×宽×高),水槽壁厚为0.5 cm。在水槽中放置一环形透明有机玻璃圆环,下方开有多处豁口便于放置分层水,目的是消除方形水槽角落生湍的影响,强迫装置为在距离水槽底部21 cm处放置的一直径为4 cm的实心圆盘,在马达的带动下匀速旋转,马达转速可调。考虑到使涡旋结构清晰、便于数据提取,本实验中强迫圆盘选取转速ω=4.19 rad/s。圆盘入水深度1~2 mm,转台与圆盘的旋转方向相同,均为逆时针旋转,模拟北半球气旋式涡旋。实验过程中保持圆盘匀速旋转,待实验完成后停止转动。
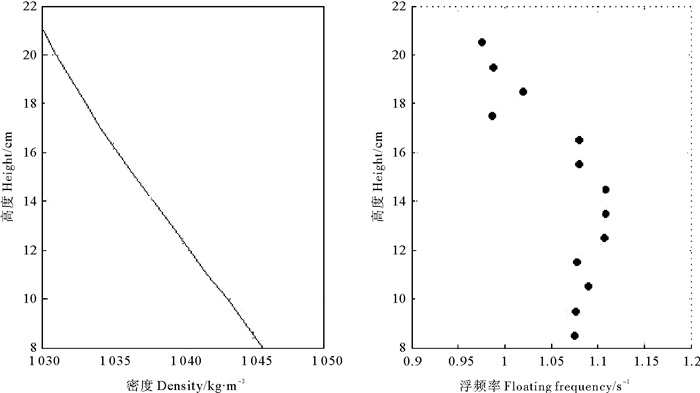
使用前人[18]研究所用的“双缸法”布设线性分层水,双缸内溶液保持相同的初始高度。本实验中设置为13 cm,但是最终只在试验水槽中布设20 cm高的线性分层水。开始测量前,使用电导率仪测量实验水体电导率,并反演出实验水体密度垂向分布。根据双缸法理论,N≈1.1s-1,与使用电导率仪测得的浮频率分布结果(见图 2)基本吻合。
|
图 2 放制线性分层水密度与浮频率分布 Fig. 2 The linear stratified water density and the floating frequency distribution |
本实验采取Particle Image Velocimetry[19](以下简称PIV)方法采集流场速度。本次实验装置布置了两套PIV系统,分别采集水平断面和垂直断面的流速信息。同组的激光器和CCD固定在同一个电动平移台上,可以同步升降,实现了一次实验中对多个水平断面信息的采集。实验中使用的CCD分辨率为1 920×1 080,激光器功率为3 W,激光波长为450 nm,采用聚苯乙烯为示踪粒子,其密度为1 040 kg/m3,粒径为20 μm。CCD拍摄帧率为10 fps。
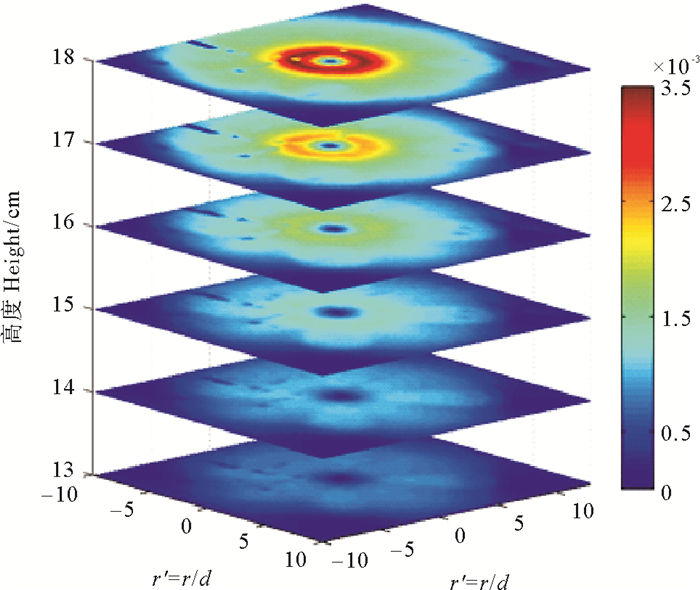
2 涡旋的三维结构 2.1 涡旋的水平结构本实验中共拍摄18~11 cm共8个间隔1 cm的水平断面,图为各水平断面速度大小的空间分布,13 cm层以深断面速度量级很小,故只展示了上6个断面。图 3中,x、y轴代表水槽的长、宽,具体数值已经使用强迫圆盘半径d进行了归一化处理,z轴为距离水槽底部的高度,单位均为cm,颜色表示流速的大小,单位为m/s。图像左上角的长条状低值区为实验仪器遮挡所致。
|
图 3 各层速度大小水平分布 Fig. 3 Horizontal distribution of velocity in each layer |
首先可以看到在涡旋结构的中央存在一个速度低值区,此区域对应着强迫圆盘直接作用的区域;在这一区域外速度大小迅速增加至最大值,在近表层18 cm处速度最大可达3.5 mm/s;后速度沿径向缓慢衰减。强迫圆盘边际处线速度约为8 cm/s,数值上比近表层最大速度大一个量级。垂向上看,不同深度断面的速度水平分布有着基本相同的分布特征,但是速度的量级随深度增加明显衰减。
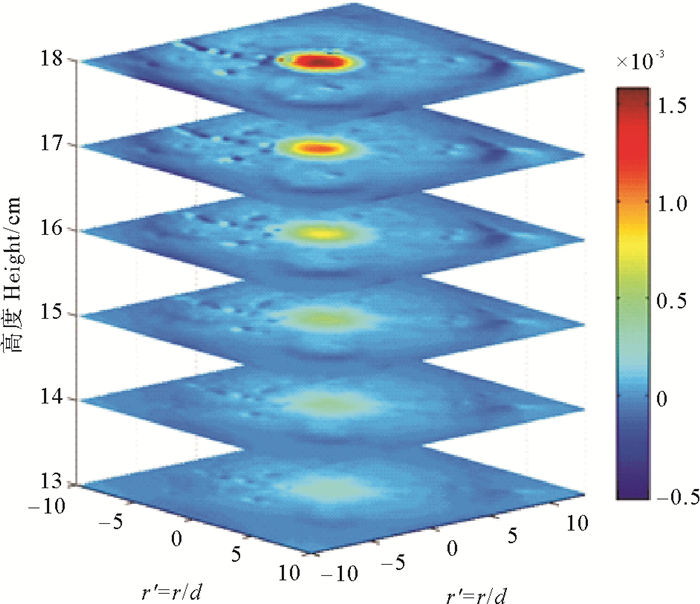
涡度与速度的水平分布在形态上有较大差异。图 4为涡旋各深度层涡度水平分布图,速度的低值区对应着涡度的高值区,涡度在涡旋涡心高度集中,但是涡度在水平方向上衰减较速度更为迅速。与速度分布规律相同的是,垂向上不同深度层的涡度水平分布也具有相同的特征,随着深度的增加涡度逐渐衰减。
|
图 4 各层涡度大小水平分布 Fig. 4 Horizontal distribution ofvorticity in each layer |
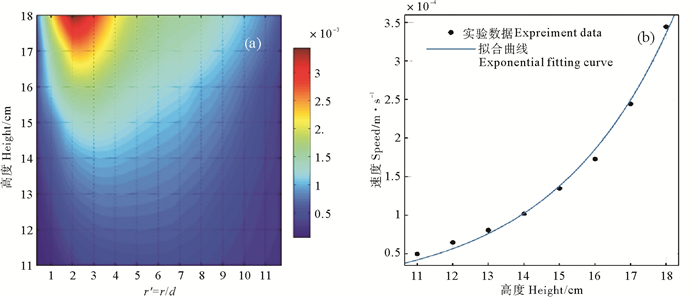
在实验中作者发现,涡旋的速度分布和涡度分布都有以涡心为中心各向同性的特征,本文利用这一现象,取过涡心一条半径上两个物理量的分布来代表整体分布,做出不同深度速度和涡度的径向衰减曲线(见图 5、6),定量的描述速度在垂向上的衰减过程。图 5为各深度水平断面速度大小的径向分布,横坐标为归一化的距心距离,单位为cm;纵坐标距底面深度,颜色表示速度大小,单位为m/s。通过这张图可以更清楚的看到速度由中心低值沿径向增长到高值后缓慢衰减的过程。
|
图 5 速度大小垂向分布(a)和各层速度最大值垂向衰减趋势(b) Fig. 5 Vertical distribution of velocity (a)and fading tendency trend of maximum velocity of each layer (b) |
|
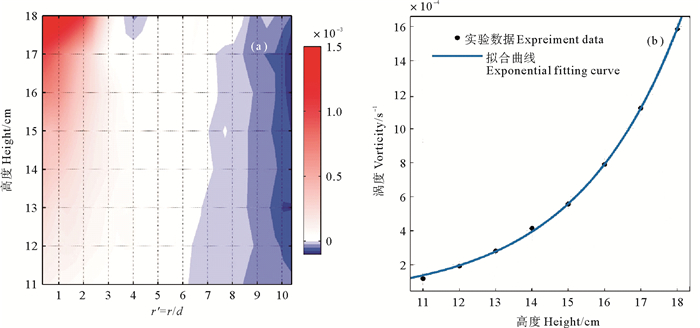
图 6 涡度大小垂向分布(a)和各层涡度最大值垂向衰减趋势(b) Fig. 6 Vertical distribution of vorticity (a) and fading tendency trend of maximum vorticity of each layer (b) |
由于存在着垂向密度层结,速度在层与层之间的传递存在着能量衰减,且各深度层的速度最大值衰减规律可以用一简单的指数函数拟合(见图 5(b))。另一个明显的现象是,随着深度加深,各层速度最大值点逐渐远离涡心。在近表层18 cm处最大速度涡心距为5 cm,大概位于2倍圆盘半径处,在11~12 cm处已几乎难以用肉眼确认速度极大值位置。这体现了随着深度的增加,能量从集中于涡心附近,到渐渐“摊平”在整个平面上。
与速度分布规律相反,各深度水平断面上的涡度最大值位于涡心处(见图 6(a)),后沿径向迅速减小,在距涡心8 cm处涡度达到最低值,此时的涡度小于零,随后涡度开始向正值移动,靠近边界处的涡度值再次下降,但是并不是每一深度的涡度径向分布都可以用这一规律描述。从图中可以看到,12 cm层以深涡度径向衰减接近线性,而在中层深度,涡度分布也与表层有较大偏差。同速度最大值的垂向衰减情况相同,各深度层涡度最大值的垂向衰减也符合指数规律(见图 6(b))。
2.3 涡旋结构的统一性Trieling和van Heijst[20]曾在实验室中用一简单的解析函数描述实验室中涡旋的径向分布:
| $ w\left( r \right) = \left( {1 - \frac{{\alpha {r^\alpha }}}{2}} \right) \times \exp \left( { - {r^\alpha }} \right)。$ |
其中α为一常数。Trieling在其实验中中取2,取得了很好的拟合结果。
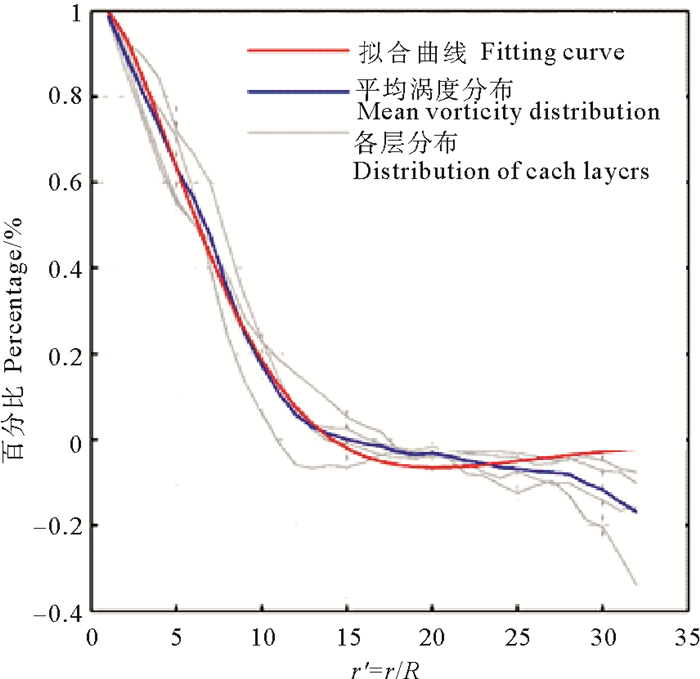
本实验使用了相同的函数对涡旋的涡度径向分布进行了拟合(见图 7),图中纵轴为测点涡度值与本层最大涡度的比值,横轴为使用速度最大值距涡心距离进行归一化后的相对涡心距,灰色曲线为各深度层涡度实际分布,蓝线为涡度平均分布,红线为解析函数,本实验中参数α取1.43,可以看到这一解析函数可以基本代表涡度的径向分布规律,二者在边界处存在的趋势差异,我们认为是边界效应导致。
|
图 7 不同深度层归一化涡度径向分布与拟合函数对比 Fig. 7 Comparison of radial distribution and fitting function of normalized vorticity in different depth layers |
在本实验中,完成了旋转的情况下,层结流体中定常涡旋生成、维持、测量的全过程,解决了旋转情况下创造线性分层环境的问题,避免了传统造涡方法对层结的破坏;涡旋可以长时间维持,为涡旋三维结构场的精细测量创造了条件。本实验对涡旋三维结构进行了分析,得到了以下结论:
(1) 发现在强迫圆盘直接作用区域存在速度低值区,速度最大值位于二倍圆盘半径处,达到最值后速度沿径向缓慢衰减。
(2) 涡度在强迫直接作用区为高值,离开此区域后涡度迅速衰减并反号,后沿径向缓慢恢复至零涡度。
(3) 涡旋结构随着深度的加深变得不明显,相邻深度层与层之间的涡度与速度衰减符合统一的指数型规律。
(4) 涡度的径向分布可以用一简单的解析函数拟合,但这一拟合的准确性随着深度的下降渐渐降低。
| [1] |
Bush J W M, Woods A W. Vortex generation by line plumes in a rotating stratified fluid[J]. Journal of Fluid Mechanics, 1999, 388(388): 289-313.
(  0) 0) |
| [2] |
Kloosterziel R C, Carnevale G F, Phillippe D. Propagation of barotropic dipoles over topography in a rotating tank[J]. Dynamics of Atmospheres & Oceans, 1993, 19(233): 65-100.
(  0) 0) |
| [3] |
Billant P, Chomaz J M. Experimental evidence for a new instability of a vertical columnar vortex pair in a strongly stratified fluid[J]. Journal of Fluid Mechanics, 2000(418): 167-188.
(  0) 0) |
| [4] |
Andersen A, Bohr T, Stenum B, et al. Anatomy of a bathtub vortex[J]. Physical Review Letters, 2003, 91(10): 104502. DOI:10.1103/PhysRevLett.91.104502
(  0) 0) |
| [5] |
Heijst G J F V, Clercx H J H. Laboratory modeling of geophysical Vortices[J]. Annual Review of Fluid Mechanics, 2009, 41(1): 143-164. DOI:10.1146/annurev.fluid.010908.165207
(  0) 0) |
| [6] |
张正光.中尺度涡[D].青岛: 中国海洋大学, 2014. Zhang Z. Mesoscale Eddy[D]. Qingdao: Ocean University of China, 2014. (  0) 0) |
| [7] |
张晓爽, 吕红民. 利用旋转平台模拟Rossby波现象的实验研究[J]. 中国海洋大学学报(自然科学版), 2010, 40(S1): 9-15. Zhang X, Lyu H. The experimental study of simulation of rossby wave by using rotating platform[J]. Periodical of Ocean University of China, 2010, 40(S1): 9-15. (  0) 0) |
| [8] |
Kloosterziel, Carnevale, Orlandi. Inertial instability in rotating and stratified fluids: barotropic vortices[J]. Journal of Fluid Mechanics, 2007, 583(583): 379-412.
(  0) 0) |
| [9] |
Stegner A, Zeitlin V. From quasi-geostrophic to strongly nonlinear monopolar vortices in a paraboloidal shallow-water-layer experiment[J]. Journal of Fluid Mechanics, 2000, 356(356): 1-24.
(  0) 0) |
| [10] |
Mittal S, Raghuvanshi A. Control of vortex shedding behind circular cylinder for flows at low Reynolds numbers[J]. International Journal for Numerical Methods in Fluids, 2015, 35(4): 421-447.
(  0) 0) |
| [11] |
Scolan H, Su S, Wright S, et al. Numerical and experimental study of flows in a rotating annulus with local convective forcing[C]. // EGU General Assembly Conference.[s.1.]: EGU General Assembly Conference Abstracts, 2016. http://adsabs.harvard.edu/abs/2016EGUGA..1816194S
(  0) 0) |
| [12] |
Scolan H, Read P L. A rotating annulus driven by localized convective forcing: a new atmosphere-like experiment[J]. Experiments in Fluids, 2017, 58(6): 75-81. DOI:10.1007/s00348-017-2347-5
(  0) 0) |
| [13] |
Terhaar S, Reichel T G, Schrödinger C, et al. Vortex breakdown types and global modes in swirling combustor flows with axial injection[J]. Journal of Propulsion & Power, 2015, 31(1): 219-229.
(  0) 0) |
| [14] |
Vega L. The dynamics of vortex filaments with corners[J]. Communications on Pure & Applied Analysis, 2017, 14(4): 1581-1601.
(  0) 0) |
| [15] |
Karch A, Tong D. Particle-vortex duality from 3d bosonization[J]. Physical Review X, 2016, 6.
(  0) 0) |
| [16] |
陈琛.水平温差驱动环流的机制探讨及实验研究[D].青岛: 中国海洋大学, 2009. Chen C. Lab Experiment and Theoretical Model for Horizontal Convection[M]. Qingdao: Ocean University of China. 2009. http://cdmd.cnki.com.cn/Article/CDMD-10423-2009172305.htm (  0) 0) |
| [17] |
Wain D. Laboratory Experiments on the Effect of Baroclinic Eddies on a Dense Plume in a Rotating Stratified Fluid[R].[s.l.]: Woods Hole Oceanog. Inst Tech Rept, WHOI-2005-08: 239-259.
(  0) 0) |
| [18] |
Economidou M, Hunt G R. Density stratified environments: the double-tank method[J]. Experiments in Fluids, 2009, 46(3): 453-466. DOI:10.1007/s00348-008-0571-8
(  0) 0) |
| [19] |
Fincham A, Delerce G. Advanced optimization of correlation imaging velocimetry algorithms[J]. Exp Fluids, 200, 29(1): 13-22.
(  0) 0) |
| [20] |
Trieling R R, Heijst G J F V. Decay of monopolar vortices in a stratified fluid[J]. Fluid Dynamics Research, 1998, 23(1): 27-43. DOI:10.1016/S0169-5983(97)00046-4
(  0) 0) |
| [21] |
万伟, 屈玲, 周生启. 双扩散对流中台阶结构的实验研究[J]. 力学学报, 2014, 46(2): 217-223. Wan W, Qu L, Zhou S. Laboratory studies on the staircase structure of double-diffusive convection[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(2): 217-223. (  0) 0) |
| [22] |
Illingworth S J. Model-based control of vortex shedding at low Reynolds numbers[J]. Theoretical & Computational Fluid Dynamics, 2016, 30(5): 1-20.
(  0) 0) |
 2019, Vol. 49
2019, Vol. 49


