2. 青岛市海洋可再生能源重点实验室,山东 青岛 266100
潮流能是海洋可再生能源的一个重要门类,开发潮流能对于缓解中国的能源短缺和环境污染问题具有重要意义[1]。水平轴水轮机是目前应用最为广泛的一种潮流能捕获装置,其叶片直接承受水动力并将其转化为转子的机械能,叶片的性能与各剖面的翼型密切相关[2]。
国内外研究机构对风力机叶片翼型进行了相关研究。荷兰Delft大学设计出DU风力机翼型系列[3];丹麦RISØ国家实验室研发出适用于风力机的专用翼型,命名为RISØ翼型系列[4];美国可再生能源实验室(NREL)相继开发出9个不同的NREL-S翼型系列[5];瑞典航空研究院对翼型的研究也进行多年,研究开发出FFA-W1-XXX、FFA-W2-XXX和FFA-W3-XXX三个翼型族系列[6]。国内也相继开始对翼型进行了研究,西北工业大学开发出NPU-WA风力机翼型族系列[7];中国科学院工程热物理研究开发出CAS-W1-XXX风力机翼型族系列[8-9]。另外,重庆大学、北京航空航天大学等高校也在风力机翼型研究方面取得一定的成果[10]。
在水平轴潮流能叶片设计方面,目前普遍采用的多是航空翼型或风力机专用翼型[2]。为提高潮流能水轮机工作性能,开发适合潮流能水轮机工作环境的专用翼型是很有必要的。为提高潮流能水轮机的设计效率,中国海洋大学的王树杰等[11]利用Visual C++开发了水平轴潮流能水轮机设计软件(HAT design)。本文采用多目标优化遗传算法对潮流能叶片进行优化设计,将优化后的专用翼型数据应用到水平轴潮流能水轮机设计软件(HAT design)中,实现对专用翼型数据的调用,提高潮流能水轮机专用叶片的设计效率。
1 多目标遗传算法遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法[12]。多目标问题的基本思想就是求解在满足所有约束条件和各个目标函数的条件下的一组最优解集[13]。其通用的数学表达式为:
| $ \begin{array}{*{20}{l}} {{\rm{min}}F(x) = [{f_1}(x),{f_2}(x),L,{f_m}(x)]}\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}\left\{ {\begin{array}{*{20}{l}} {{g_i}(x) \le 0,i = 1,2,L,k}\\ {{h_1}(x) = 0,i = 1,2,L,p}\\ {{a_i} \le {x_i} \le {b_i},i = 1,2,L,n}\ \ \ \ \ \ \ \ 。\end{array}} \right.} \end{array} $ | (1) |
式中:m, n-目标函数,设计变量个数;k, p-不等式约束,等式约束个数;ai、bi第i个设计变量的上限值和下限值[14]。遗传算法步骤如下:
(1) 初始种群选取。本文初始翼型的翼型坐标为初始化种群。设种群的大小为N,每一个个体按r+1递增。选用三阶B样条曲线,因此控制点个数至少为4个,本文选取控制点个数为13个。
| $ \begin{array}{*{20}{c}} {u = (1:n - k) = sort (G(1:n - k))}。\\ {n = length{\rm{ }}(G) - length{\rm{ }}(Q)}。\end{array} $ |
其中:Q-初始数据序列;k-B样条次数;length(G)-计算序列G中元素个数;sort(G)-对序列G排序;X(n:m)-序列X中第n个到第m个组成的序列[15]。
(2) 适应度函数。因翼型曲线上的控制点是随着不同的参数选择而变化的。拟合的翼型曲线不一定为最优结果,所以需要另加约束,采用近弧长约束[15],B(t)的弧长为:
| $ s = uk + 1\int\limits_{uk + 1}^{un + 1} {\left| {{B^\prime }(t)} \right|{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{d}}t} = \int\limits_{uk + 1}^{un + 1} {\sqrt {{{({x^\prime }(t))}^2} + {{({y^\prime }(t))}^2}{\rm{d}}t} } 。$ | (2) |
化简计算得:
| $ S \le len = \sqrt {\int\limits_{uk + 1}^{un + 1} {({{({x^\prime }(t))}^2} + {{({y^\prime }(t))}^2}){\rm{d}}t} } 。$ | (3) |
该约束使所得到的拟合曲线为最优拟合曲线。
(3) 选择算子。若个体Gi(i=1, 2, …, NIND)适应值为Di(i=1, 2, …, NIND),则Gi被选中的概率为
(4) 剪切和拼接算子。种群中的染色体可以随着剪切拼接操作而变化,并产生新染色体,染色体也是可以变化的,这样在拟合过程中产生更多的控制点,可以使样条曲线拟合曲线匹配到更多的合适点。过程为:首先要选择一个剪切点r1=Rand(1, L1); r2=Rand(1, L2),其中Rand(n, m)表示随机产生的[n, m]中的随机的一个数,并且此数为整数[15]。在拼接和剪切过程中,容易产生非法染色体,为了避免此问题,需要对剪切点位置进行限制,因此需编写程序实现限制,具体程序如下:
L1=Length(G1); L2=Length(G2);
r1=Rand(1, L1); r2=Rand(1, L2);
while(
(r1+L2-r2) < k+1+m或(r2+L1-r1) < k+1+m
r1=Rand(1, L1);
r2=Rand(1, L2);
)end
从而实现对翼型曲线弧长进行约束,使翼型曲线更加光顺,避免拟合曲线拟合过程中出现剧烈震荡。(5)变异。通过改变每个个体的一些基因来恢复种群群体的多样性,使搜索达到整个空间,这就是变异算子的操作[15]。
算法流程:
步骤1 输入B样条曲线次数K、平面有序坐标点{Pj(xj, yj), j=1, 2, …, r},种群大小为N,选择概率p0,最大迭代次数tmax,初始种群迭代次数记为t=1[12]。取控制点个数为13,种群大小N=40,tmax=300。
步骤2 选择最优结果保存方法,将种群中适应度较大的个体记为最优个体,适应度函数为
步骤3 按照适应度函数大则被选择机率大的原则,对当代种群进行随机抽样,得到N个新选择的个体,计算每个个体的适应度值,种群的平均适应度值和最大、最小适应度值[12]。
步骤4 将种群中个体随机配对,计算交叉概率,运用线性交叉,得到新个体[12],既为得到新的翼型坐标点,交叉概率取0.8。
步骤5 对交叉后的种群,先计算种群中每个个体的适应度,种群的平均和最大适应度值,从而计算出每个个体的变异概率pm,再对每个个体的每个基因执行单点变异操作,变异概率取0.05。
步骤6 对变异后的种群,采用最差去除策略,将当代种群中适应度较小的个体去除,并把先前的最优个体集添加到当代种群中,这样可保证算法最终收敛于全局最优[12]。
步骤7 令t = t+1,重复步骤,直到满足条件为止。可用t大于最大进化代数tmax或者误差平方和SSE小于给定误差作为迭代的终止条件,数据点误差平方和为0.002。
2 翼型参数化建模 2.1 B样条曲线拟合翼型曲线翼型的曲线形状为前圆后尖、表面光滑的流线图形,要对翼型的曲线进行优化,就要先了解分析翼型的几何特性。采用B样条曲线对翼型曲线进行拟合,首先要确定翼型曲线上的控制点,则此处设翼型上的坐标控制点为P={pj(xj, yj), j=1, K, r},其次选择参数向量,此处的参数向量为T={tj, j=1, K, r},在非递减节点向量上,定义一条k次B样条曲线可表示为[16]:
| $ \mathit{\boldsymbol{U}} = \{ {u_1} = {u_2} = \cdots \le {u_{k + 1}} \le \cdots \cdots \le {u_{n + k + 1}}\} 。$ | (4) |
节点向量定义为:
| $ B(t) = \sum\limits_{i = 1}^n {{d_j}} {N_{j,k}}。$ | (5) |
其中:D={di, i=1, K, n}表示控制点,Ni, k(t)为基函数,定义为:
| $ \left\{ {\begin{array}{*{20}{l}} {{N_{i,0}}(t) = \left\{ {\begin{array}{*{20}{l}} {1,\quad {u_i} \le t < {u_{i + 1}}}\\ {0,\quad {\rm{ 其他 }}} \end{array}} \right.}\\ {{N_{j,k}}(t) = \frac{{t - {u_i}}}{{{u_{i + k}} - {u_i}}}{N_{i,k - 1}}(t) + \frac{{{u_{i + k + 1}} - t}}{{{u_{i + k + 1}} - {u_{i + 1}}}}{N_{i + 1,k - 1}}(t)}。\end{array}} \right. $ | (6) |
选用三次B样条曲线对翼型进行参数化表达,通过选择翼型上的控制点就可以控制翼型曲线,用B样条曲线拟合翼型曲线得到点能使得最小二乘拟合误差平方和达到最小。则满足条件的B样条曲线写成矩阵形式为[16]:
| $ \mathit{\boldsymbol{Q}} = \mathit{\boldsymbol{ND}}。$ | (7) |
其中:N为B样条基函数阵,D为有序数据点阵。若事先确定参数向量T和节点向量U,可求得控制顶点阵D的近似解[12]:
| $ \mathit{\boldsymbol{D}} = {({N^T}N)^{ - 1}}{N^T}P。$ | (8) |
则得到翼型拟合曲线:
| $ {P^C} = N{({N^T}N)^{ - 1}}{N^T}P。$ | (9) |
记pjc为翼型拟合曲线上对应参数tj的点,则误差平方和(Sum of Square Error, SSE)为:
| $ SE = \sum\limits_{j = 1}^r | {p_j} - p_j^c{|^2}。$ | (10) |
如果求出控制顶点集D,使得:
| $ \begin{array}{*{20}{c}} {{p_1} = B({t_1}) = {D_1};}\\ {{p_r} = B({t_r}) = {D_n};}\\ {{P^c} = {\rm{min}}SSE}。\end{array} $ | (11) |
则称该翼型拟合曲线Pc为插值于端点的最小二乘拟合曲线,此次选取13个控制点来进行翼型曲线的拟合[17]。
2.2 翼型曲线优化模型翼型设计与多个学科领域相关,比如可靠性设计、结构设计、流体力学等。在设计过程中也会遇到翼型的结构需求与水动力性能相矛盾的情况。例如:追求高的升力系数会得到更加敏感的前缘,翼型的升阻比会受到翼型相对厚度增加的限制[8]。多目标优化问题的计算过程中,各子目标之间是相互竞争的,对翼型的水动力性能进行优化设计必须考虑到将会出现的矛盾冲突,协调好将会出现的冲突和矛盾,从而得到最优解[14]。
(1) 设计变量:用B样条曲线进行参数化建模,以翼型拟合曲线上的控制点为设计变量,设计变量为13个控制点,将设计变量表达为:
| $ \begin{array}{*{20}{c}} {P = ({P_1},{P_2},{P_3},{P_4},{P_5},{P_6},{P_7},}\\ {{P_8},{P_9},{P_{10}},{P_{11}},{P_{12}},{P_{13}})}。\end{array} $ |
(2) 目标函数:设计目标主要是初始翼型取得最大升阻比和最大升力系数的攻角处,取得最优解。翼型在设计攻角处的升阻比最大作为目标函数之一:
| $ {f_1}(X) = {\rm{max}}({C_L}/{C_D})。$ |
式中:CL-翼型升力系数;CD -翼型阻力系数。
翼型在设计攻角处的升力系数最大也作为目标函数:
| $ {f_1}(X) = {\rm{max}}({C_L})。$ |
(3) 约束条件:多目标优化时,目标之间有时会相互冲突,因此,在满足优化目标的同时还需约束其他因素。在设计攻角处,升阻比寻得最优解时,升力系数也必须加以限制,不得小于初始翼型的升力系数,即CL≥X0;同理,当设计攻角处升力系数最大时,升阻比不得小于初始翼型的升阻比值,即CL/CD≥Y0。
最大相对厚度为x,为了保证优化后的翼型的相对厚度仍是x,施加约束:
| $ t/c = x。$ | (12) |
式中:t—翼型的最大厚度;c—翼型弦长。
初始翼型的最大厚度所在位置是距前缘35%~50%弦长位置处,因此施加约束[10]:
| $ 35\% \le {x_t}/c \le 50\% 。$ | (13) |
式中,xt—最大厚度所在位置距前缘的距离。
翼型的弯度与翼型的升阻比与强度有关,弯度增大可增大翼型升阻比,但又要对弯度进行限制[10],因为弯度过大又影响翼型的强度,综合以上因素施加约束[9]:
| $ 3\% \le f/c \le 5\% 。$ | (14) |
式中,f为翼型弯度。
弯度位置适当向后缘移动,有利于提高潮流能水轮机翼型的最大升阻比,施加约束[10]:
| $ 50\% \le {x_j}/c \le 55\% 。$ | (15) |
式中,xf为弯度位置距翼型前缘的距离。
考虑到翼型的强度要求,需要对它的截面积进行约束:
| $ \frac{{|S - {S_0}|}}{{{S_0}}} \le 3\% 。$ | (16) |
式中:S-优化后翼型的截面积;S0 -优化前翼型的截面积。
翼型的尾缘是噪声的主要来源,其尾缘噪声随着尾缘厚度的增加而增大,因此,需要对尾缘进行约束[18]:
| $ {y_{u,0.99}} - {y_{1,0.99}} \le 0.01。$ | (17) |
式中yu, 0.99、y1, 0.99为默认弦长为1时,弦长位置处上翼面及下翼面的y坐标值[18]。
3 翼型设计结果分别以FX60-126、NACA65019、NACA63-215、EPPLER 862 STRUT和EPPLER 864 STRUT为初始翼型,用B样条曲线参数化建模,通过多目标遗传算法求的五种新翼型,最大相对厚度分别为12.6%、19%、21.5%、32.4%和38.8%,分别命名为OUC-TT-1260、OUC-TT-1900、OUC-TT-2150、OUC-TT-3240和OUC-TT-3880。五种新翼型的几何形状如图 1所示。
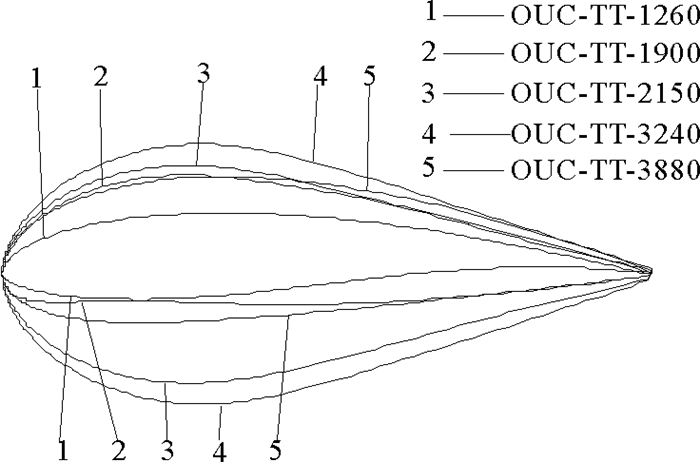
|
图 1 OUC-TT-XXX0翼型族几何形状图 Fig. 1 Geometrical shape of OUC-TT-XXX0 hydrofoil family |
(1) OUC-TT-1260翼型优化结果
在来流速度V=1.5 m/s工作环境下,因FX60-126翼型在α=15°时的升力系数最大,在α=2°时升阻比最大,因此选择α=15°时的升力系数和α=2°时的最大升阻比作为优化目标。以FX60-126翼型为初始翼型,通过用遗传算法进行编程求解得到新的潮流能水轮机专用翼型OUC-TT-1260曲线坐标。通过对FX60-126翼型和翼型OUC-TT-1260进行网格划分和CFD分析得到如图 2、3所示的仿真分析结果,水动力特性参数对比如图 4所示。
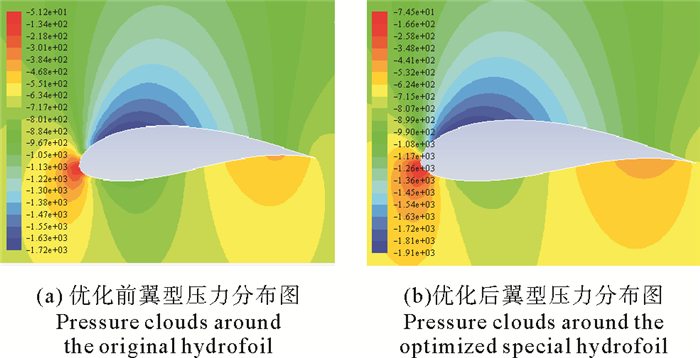
|
图 2 专用翼型多目标优化前后翼型附近压力云图(V=1.5 m/s,α=2°) Fig. 2 Pressure clouds around the original hydrofoil and optimized special hydrofoil(V=1.5 m/s, α=2°) |
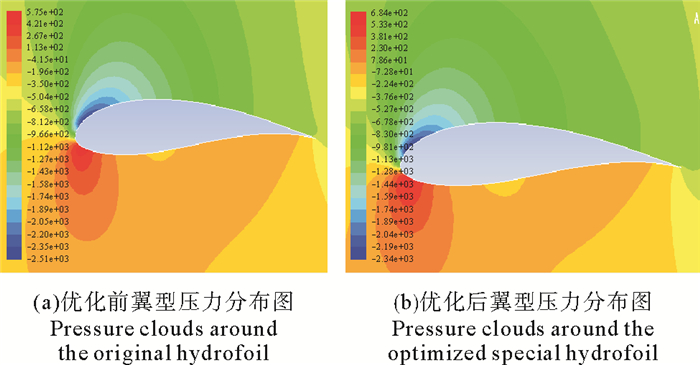
|
图 3 专用翼型多目标优化前后翼型附近压力云图(V=1.5 m/s,α=15°) Fig. 3 Pressure clouds around the original hydrofoil and optimized special hydrofoil(V=1.5 m/s, α=15°) |
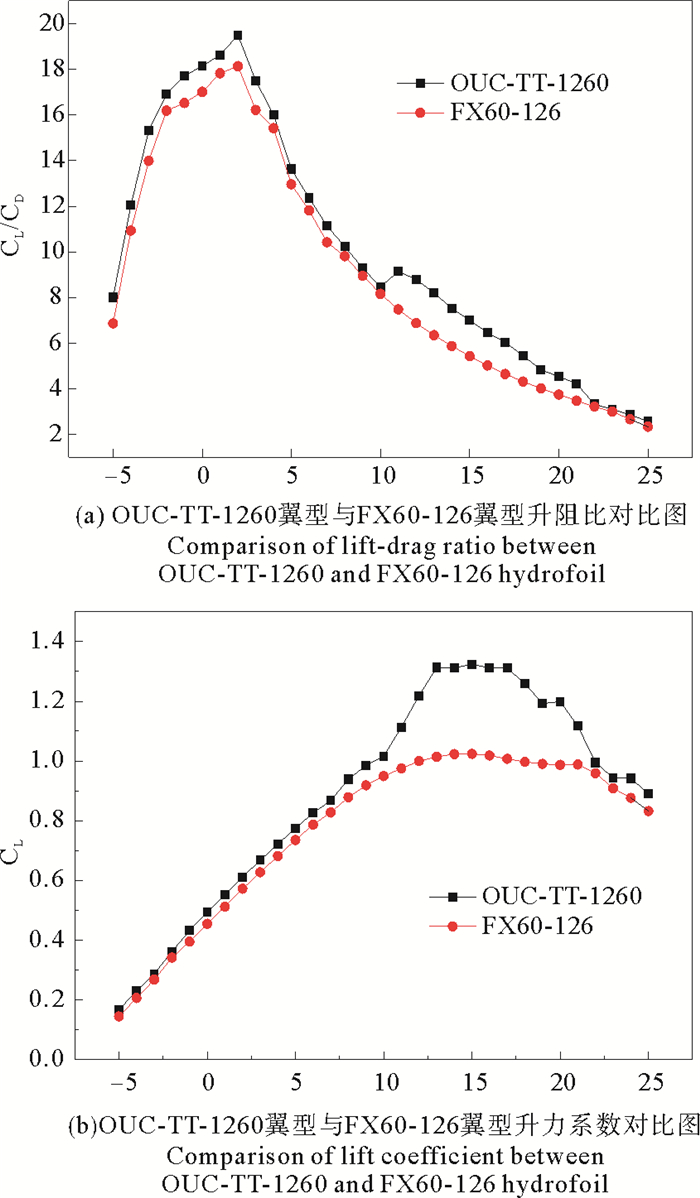
|
图 4 OUC-TT-1260翼型与FX60-126翼型水动力参数对比 Fig. 4 Comparison of hydrodynamic parameters between OUC-TT-1260 and FX60-126 hydrofoil |
如图 4所示为OUC-TT-1260翼型与FX60-126翼型的水动力参数对比,如图 2、3所示为CFD仿真分析结果,由CFD仿真分析结果和水动力参数结果对比可知,OUC-TT-1260翼型的升阻比和最大升力系数比FX60-126翼型整体较高,攻角范围在10°~20°时,OUC-TT-1260翼型的升力系数和升阻比明显高于FX60-126翼型,则优化结果符合要求。
(2) OUC-TT-1900翼型优化结果
以NACA65019翼型为初始翼型,因对NACA65019翼型进行分析得到的水动力性能参数,升力系数在α=20°时取得最大值,在α=10°时,升阻比取得最大值,因此选择这两种攻角环境下翼型的水动力学性能为优化目标。
通过用遗传算法进行编程求解得到新的潮流能水轮机专用翼型OUC-TT-1900曲线坐标,得到潮流能水轮机专用翼型OUC-TT-1900后进行网格划分和CFD分析得到如图 5、图 6所示的仿真分析结果,水动力特性参数对比如图 7所示。
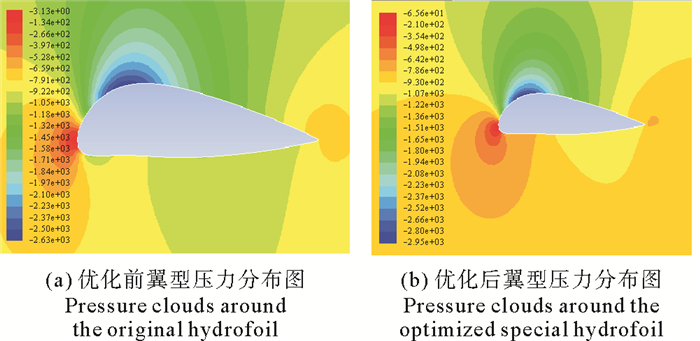
|
图 5 专用翼型多目标优化前后翼型附近压力云图(V=1.5 m/s,α=10°) Fig. 5 Pressure clouds around the original hydrofoil and optimized special hydrofoil (V=1.5 m/s, α=10°) |
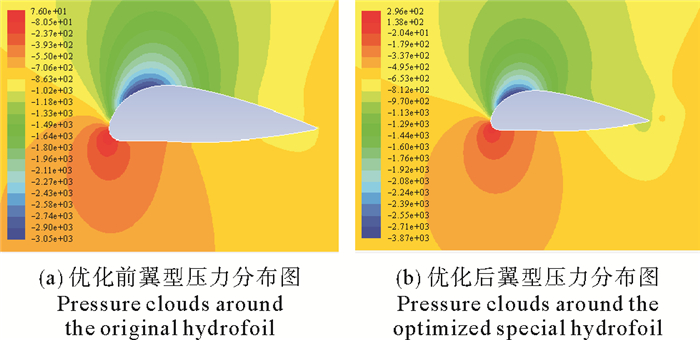
|
图 6 专用翼型多目标优化前后翼型附近压力云图(V=1.5 m/s,α=20°) Fig. 6 Pressure clouds around the original hydrofoil and optimized special hydrofoil (V=1.5 m/s, α=20°) |
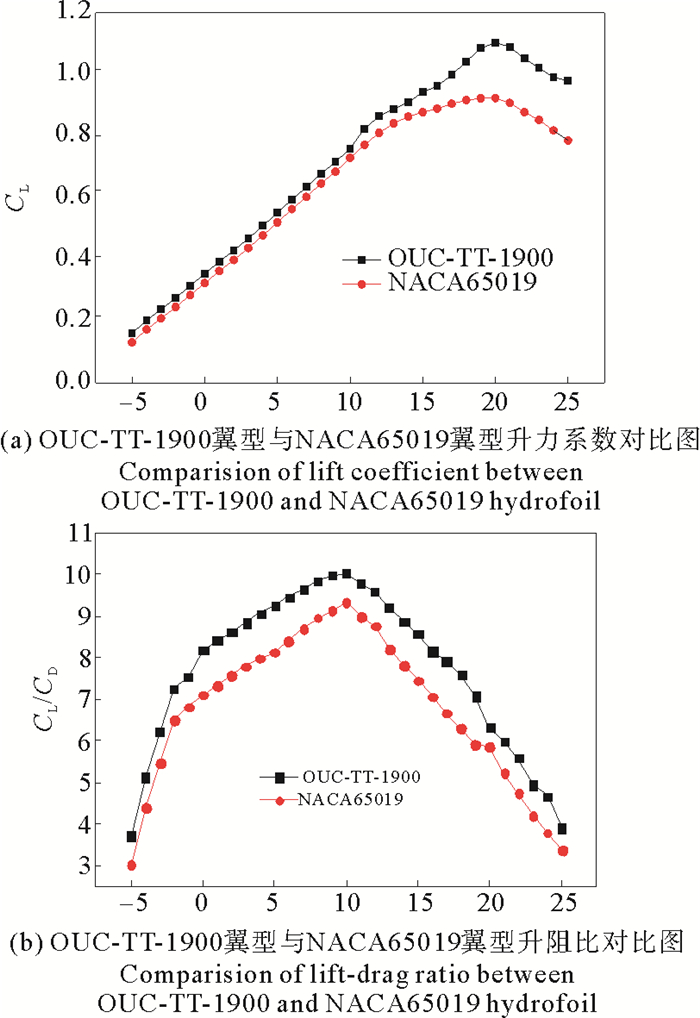
|
图 7 OUC-TT-1900翼型与NACA65019翼型水动力参数对比 Fig. 7 Comparison of hydrodynamic parameters between OUC-TT-1900 and NACA65019 hydrofoil |
通过对如图 5、图 6所示的CFD仿真分析结果进行分析,对如图 7所示为OUC-TT-1900翼型与NACA65019翼型的水动力参数进行对比可知,OUC-TT-1900翼型的升阻比和最大升力系数比NACA 65019翼型整体较高,攻角范围在15°~25°时,OUC-TT-1900翼型升力系数明显高于NACA 65019翼型,优化结果符合要求。
(3) OUC-TT-XXX0翼型族主要水动力参数结果
五种翼型的升力系数和升阻比都有相应的提高,其中OUC-TT-1260翼型的升力系数提高最多,OUC-TT-1260翼型的升阻比提高最多。
由表 1可知,优化后的OUC-TT-XXX0翼型族具有较好的水动力特性。
|
|
表 1 OUC-TT-XXX0翼型族主要水动力特性参数 Table 1 Major parameters of hydrodynamic performance of OUC-TT-XXX0 hydrofoil family |
专用翼型族是针对潮流能水轮机工作环境而获得的翼型系列。由以上研究可知,专用翼型族具有较好的水动力性能。水轮机的整体性能取决于翼型的水动力性能参数,翼型的水动力性能参数复杂繁多,搭建数据库进行翼型数据管理,可以更加高效地获取翼型的性能参数,从而快速地设计水轮机叶片[11]。
4.1 数据库设计方案为了实现在水平轴潮流能水轮机设计软件中调用专用翼型族数据,将优化后的潮流能水轮机专用翼型族数据进行整理,导入到SQL Server中,搭建专用翼型族数据库。在水平轴潮流能水轮机设计软件中对数据库中的专用翼型族数据进行调用,完成后续的专用潮流能水轮机叶片的设计。水平轴潮流能水轮机设计软件及其专用叶片翼型数据库的整体设计方案如图 8所示。
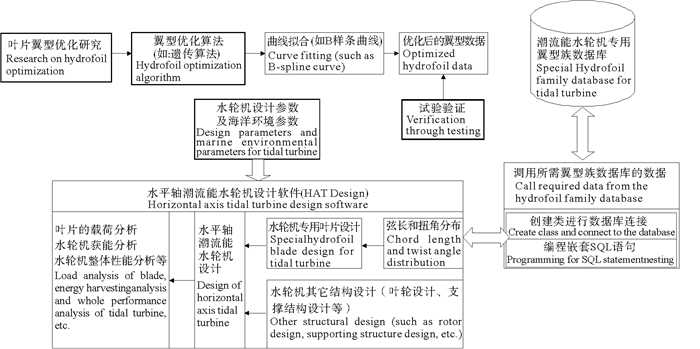
|
图 8 专用翼型族数据库设计方案 Fig. 8 Design scheme of special hydrofoil Database |
通过编程完成了水平轴潮流能水轮机设计软件与专用翼型族数据库之间的连接和数据调用。在水平轴潮流能水轮机设计软件的翼型数据界面中,通过下拉框选择专用翼型族数据库中已有的翼型,从数据库中调用专用翼型的几何数据和水动力学参数等信息,通过二维图形显示翼型的外形,并显示翼型的水动力特性曲线。潮流能水轮机设计软件翼型数据界面如图 9所示。水平轴潮流能水轮机设计软件也实现了叶片设计、叶片载荷分析、水轮机获能分析等功能。叶片的载荷分析如图 10所示。水轮机叶片载荷主要是流体动力作用在水轮机叶片上的载荷,包括叶片受到的弯矩、扭矩及其它作用于叶片上的载荷。
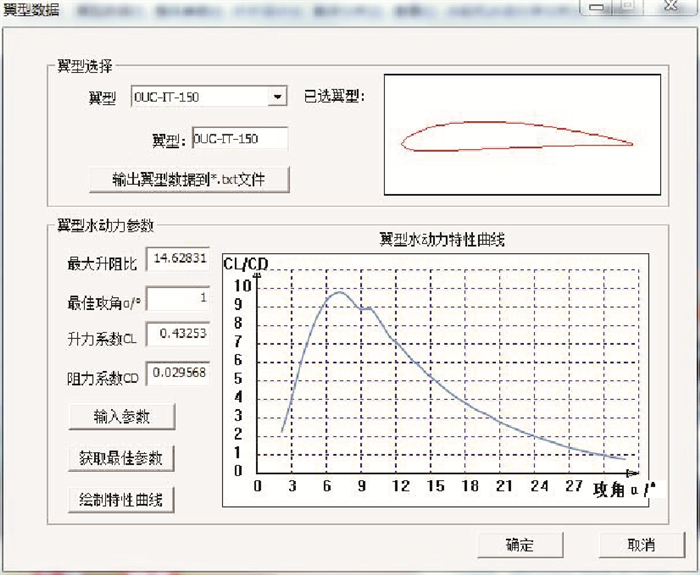
|
图 9 专用翼型数据选择与数据显示界面 Fig. 9 Implementation interface of hydrofoil data selection from Database |

|
图 10 载荷分析界面 Fig. 10 Load analysis interface |
本文介绍了潮流能水轮机专用翼型族设计采用的多目标遗传算法思路、翼型的参数化建模方法及翼型的设计实例。得到五种潮流能水轮机专用叶片翼型,最大相对厚度范围为12.6%~38.8%,分别命名为OUC-TT-1260、OUC-TT-1900、OUC-TT-2150、OUC-TT-3240和OUC-TT-3880。优化后的潮流能叶片翼型族具有较好的水动力特性。整理优化后的潮流能水轮机专用翼型族数据,搭建了潮流能水轮机专用翼型族数据库,实现了潮流能水轮机设计软件与专用翼型族数据库的连接及翼型数据选取功能,提高了水轮机叶片的设计效率。
| [1] |
张理, 李志川. 潮流能开发现状、发展趋势及面临的力学问题[J]. 力学学报, 2016, 48(5): 1019-1032. Zhang Li, Li Zhichuan. Development status, trend and the problems of mechanics of tidal current energy[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(5): 1019-1032. (  0) 0) |
| [2] |
刘雪峰.潮流能水轮机叶片设计及其性能研究[D].舟山: 浙江海洋学院, 2014. Liu Xuefeng. Blade Design and Performance Analysis of Tidal Current Energy Turbine[D]. Zhoushan: Zhejiang Ocean University, 2014. (  0) 0) |
| [3] |
Timmer W A, Van R A. Summary of delft university wind turbine dedicated airfoils[J]. ASME, 2003, 125: 488-496.
(  0) 0) |
| [4] |
Fuglsang P, Bak C. Development of risø wind turbine airfoils[J]. Wind Energy, 2004, 7(2): 145-162. DOI:10.1002/we.117
(  0) 0) |
| [5] |
Tangler J L, Somers D M. NREL Airfoil Families for HAWTs[M]. Colorado: National Renewable Energy Laboratory, 1995.
(  0) 0) |
| [6] |
Bjork A. Coordinates and Calculations for the FFA-W1-xxx, FFA-W2-xxx, FFA-W3-xxx Series of Airfoils for HAWTS[R]. Sweden: FFA, 1990.
(  0) 0) |
| [7] |
乔志德, 宋文萍, 高永卫. NPU-WA系列风力机翼型设计与风洞实验[J]. 空气动力学学报, 2012, 30(2): 260-265. Qiao Zhide, Song Wenping, Gao Yongwei. Design and experiment of the NPU-WA airfoil family for wind turbines[J]. Journal of Aerodynamics, 2012, 30(2): 260-265. DOI:10.3969/j.issn.0258-1825.2012.02.023 (  0) 0) |
| [8] |
白井艳, 杨科, 李宏利, 等. 水平轴风力机专用翼型族设计[J]. 工程热物理学报, 2010, 31(4): 589-592. Bai Jingyan, Yang Ke, Li Hongli, et al. Design of the horizontal axis wind turbine airfoil family[J]. Journal of Engineering Thermophysics, 2010, 31(4): 589-592. (  0) 0) |
| [9] |
白井艳.水平轴风力机专用翼型族试验分析及优化设计[D].北京: 中国科学院工程热物理研究, 2010. Bai Jingyan. The Experimental Analysis, and Optimal Design of Dedicated Airfoil Family for Horizontal-Axis Wind Turbines[D]. Beijing: Institute of Engineering, Thermophysics, Chinese Academy of Sciences, 2010. (  0) 0) |
| [10] |
王旭超.潮流能水平轴水轮机翼型族设计理论与方法研究[D].青岛: 中国海洋大学, 2017. Wang Xuchao. Study on the Design Theory and Method of the Horizontal Axis Tidal Turbine Hydrofoil Family[D]. Qingdao: Ocean University of China, 2017. (  0) 0) |
| [11] |
王树杰, 王宽宽, 袁鹏, 等. 潮流能水平轴水轮机设计软件框架设计与应用[J]. 太阳能学报, 2017, 38(11): 186-187. Wang Shujie, Wang Kuankuan, Yuan Peng, et al. Framework design of horizontal axis tidal current turbine design software and application[J]. Acta Energiea Solaris Sinica, 2017, 38(11): 186-187. (  0) 0) |
| [12] |
孙越泓, 魏建香, 夏德深. 基于自适应遗传算法的B样条曲线拟合的参数优化[J]. 计算机应用, 2010, 30(7): 1879-1880. Sun Hongyue, Wei Jianxiang, Xia Deshen. Parameter optimization for b-spline curve fitting based on adaptive genetic algorithm[J]. Journal of Computer Applications, 2010, 30(7): 1879-1880. (  0) 0) |
| [13] |
张荣聪.风力机专用翼型的优化设计及气动性能数值分析[D].大连: 大连交通大学, 2014. Zhang Rongcong. Optimization Design and Numerical Analysis of Aerodynamic Performance on Wind Turbine Airfoil[D]. Dalian: Dalian Jiaotong University, 2014. (  0) 0) |
| [14] |
杨硕.风力发电机翼型多目标优化设计方法研究[D].太原: 太原理工大学, 2012. Yang Shuo. Study on Multi-objective Optimization Design Method of Wind Turbine Airfoil[D]. Taiyuan: Taiyuan University of Technology, 2012. (  0) 0) |
| [15] |
张石强, 陈进, PeterEeeen, 等. 基于多目标遗传算法的风力机翼型形状优化[J]. 太阳能学报, 2011, 32(8): 1269-1272. Zhang Shiqiang, Chen Jin, PeterEeeen, et al. Multi-objective optimization of wind turbine airfoil profile based on genetic algorithm[J]. Acta Energiea Solaris Sinica, 2011, 32(8): 1269-1272. (  0) 0) |
| [16] |
周文明, 秦明, 代海涛, 等.风力机翼型自由Bezier造型方法及优化[C].北京: 中国科学技术协会年会, 2010. Zhou Wenming, Qin Ming, Dai Hai, et al. Wind Turbine Blade Design and Optimization Based on Free Modeling with Bezier Curve[C]. Beijing: China Science and Technology Association Annual Conference, 2010. (  0) 0) |
| [17] |
周明华, 汪国昭. 基于遗传算法的B样条曲线和Bézier曲线的最小二乘拟合[J]. 计算机研究与发展, 2005, 42(1): 134-143. Zhou Minghua, Wang Guozhao. Genetic algorithm based least square fitting of b-spline and bezier curves[J]. Journal of Computer Research and Development, 2005, 42(1): 134-143. (  0) 0) |
| [18] |
任毅如, 张田田, 曾令斌. 基于遗传算法的潮流能水轮机翼型优化设计[J]. 湖南大学学报(自然科学版), 2015, 42(10): 59-64. Ren Yiru, Zhang Tiantian, Zeng Lingbin. Tidal turbine hydrofoil design method based on genetic algorithm[J]. Journal of Hunan University (Natural Sciences), 2015, 42(10): 59-64. DOI:10.3969/j.issn.1674-2974.2015.10.010 (  0) 0) |
2. Ocean Engineering Key Lab of Shandong Province, Qingdao 266100, China
 2020, Vol. 50
2020, Vol. 50

