2. 上海大学,上海 200444
风暴潮是指由于气压骤变和强风等剧烈的大气扰动所导致的潮位异常升降现象,是最严重的自然灾害之一,自上世纪50年代以来一直是本领域重要的研究课题[1]。而在全球变暖趋势和沿海人口增长的影响下,预计未来风暴潮会带来更大风险[2-3]。厦门岛位于福建省东南沿海,濒临台湾海峡,是强台风的频发地区。由厦门站1959—2012年风暴潮资料统计分析得出,厦门沿海因为台风影响引起增水超过50 cm的风暴潮有145次,约每年出现2.7次[4]。风暴潮引起的极端水位给厦门地区造成非常严重的影响,因此,准确预测风暴潮就显得尤其重要。台风引起的风暴潮的主要因素包括强风和低气压。强风引起水体堆积,气压降低引起海面上升。除了大气强迫外,海洋物理过程(例如与波浪的相互作用)和浅水区的地形也会进一步影响风暴潮的规模[5]。
风暴潮的预报类型分为三种:第一种类型为经验公式法[6]。该种方法根据对观测数据统计分析,利用经验将不同的预测效果量化成一个或多个参数。这种方法可以将最大风暴潮水位和台风特征例如气压和风速通过经验公式的方式结合起来。通常这种简单的关系能够解释风暴潮60%的变化[5]。第二种类型为流体动力学模型法。利用流体动力学和大气驱动建立直接的或者耦合的数值模式来预测风暴潮[7]。一般采用Boussineq近似的非线性浅水方程结合深度积分的二维正交网格来模拟风暴潮[8],驱动场可采用参数化的台风模型[9-10]。此外,流体动力学模型方法是当前最通用的方法,在过去数十年间研究人员花费了大量精力用于数值模型的发展和改进[17-19]。该方法的缺点是需要精确而详细的流体动力学方程、地形数据、台风模型、边界条件以及很大的运算量,而在实际运行中,我们通常没有准确而详细的地形数据、台风模型和边界条件[5]。最后一种方法为人工神经网络,它模仿人脑从数据中有效学习有关自然现象的复杂规则[20],在气象、水文、水资源和海岸工程多个领域都有应用[21-25]。人工神经网络方法不需要建立复杂数据模型,只需要输入数据调节网络内部连接,依靠其强大的自学习、自组织和自适应性,能够通过对系统输入输出样本对的学习,自动提取组合其中的映射规则,自动调整网络结构参数以适应环境变化,具有强大的逼近能力和拟合能力[26]。基于此,人工神经网络能够有效模拟风暴潮和气象条件之间的非线性关系并得到广泛应用。常用的模型包括SVR、RBF和BP神经网络等。其中,应用最广泛的为BP神经网络。BP神经网络是一种常见的基于误差反向传播算法的多层前馈型网络,包括输入层、隐藏层和输出层。BP神经网络将输出层误差反方向通过隐藏层传导至输入层来调整权值,网络的学习训练过程就是权值不断调整的过程。进行风暴潮模拟时,通过输入台风因子和当地气候因子来得到风暴潮增水值[27]。然而,BP神经网络的算法较为低效并且容易陷入梯度消失的陷阱,在实际预测中可能会造成训练失败或者误差无法降低的情景。基于此,本文采用LSTM模型来模拟风暴潮。LSTM是循环神经网络(RNN)的变体模型,它弥补了RNN的梯度消失和梯度爆炸、长期记忆能力不足等问题,使得循环神经网络能够真正有效地利用长距离的时序信息,LSTM网络被证明比传统的RNN更加有效[28]。目前LSTM得到了广泛应用,并在数据预测领域中有着优异的表现[29-32]。
1 数据来源台风数据来源于中国天气台风网(http://typhoon.weather.com.cn/index.shtml),要素包括台风实时路径、最大风速、中心气压、七级风圈半径等,时间间隔1 h,选取了2005—2019年期间影响厦门市的台风数据,共包括61个台风过程。其中,2005—2015年共46个台风过程用于训练,剩下15个台风过程用于测试验证。
厦门潮位数据来源于国家海洋信息中心,数据时间为2005—2019年,时间间隔1 h,数据都经过质量控制,质量良好。厦门海洋站位置见图 1。

|
图 1 厦门测站位置及代表性台风路径 Fig. 1 Location of Xiamen station and typical typhoon track |
本文利用LSTM模型强大的长短期记忆能力预测厦门市台风期间的风暴潮增水,合理选择影响风暴潮增水的因子,预测增水的变化趋势,为厦门沿海防灾减灾提供支持和参考。
2.1 LSTM模型LSTM结构包含输入门、输出门、遗忘门和记忆单元,输入门、输出门。遗忘门都是逻辑单元,它们不会将自己的输出发送给其他神经元,而是负责在神经网络的其他部分与记忆单元连接的边缘处设定权值,用来选择性记忆反馈的误差函数随梯度下降的修正参数,其具体结构如图 2。

|
图 2 LSTM模型结构 Fig. 2 LSTM model structure |
输入门、输出门用来接收以及输出参数和修正参数,分别记为i,o。遗忘门表示是否保留当前隐藏层节点存储的历史信息,记为f。记忆单元(Cell)表示神经元状态的记忆,记为c。3个门以及独立的Cell单元的设计,使得LSTM单元有保存、读取、重置和更新长距离历史信息的能力。它们的计算过程如下式:
| $\left\{\begin{array}{l}i_t=\sigma\left(W_i \cdot\left[h_{t-1}, x_t\right]+b_i\right) \\ f_t=\sigma\left(W_f \cdot\left[h_{t-1}, x_t\right]+b_f\right) \\ o_t=\sigma\left(W_o \cdot\left[h_{t-1}, x_t\right]+b_o\right) \\ g=\tanh \left(W_g \cdot\left[h_{t-1}, x_t\right]+b_g\right)^{\circ} \\ C_t=f_t \otimes C_{t-1}+i_t \otimes g_t \\ h_t=o_t \otimes \tanh \left(C_t\right)\end{array}\right.$ | (1) |
其中:h表示隐藏状态;W和b分别为对应的权重系数矩阵和偏置项;σ和tanh分别为sigmoid函数和双曲正切激活函数。
2.2 数据归一化不同数据由于单位和量级的差别会对模型训练产生不利影响,为消除这种影响,需将数据进行去量纲化处理。同时本LSTM模型中采用的sigmoid函数作为激活函数,该函数对于较大的输入数据变化不敏感,所以为解决数据之间的可比性,方便模型训练,本模型训练中将数据进行归一化处理,将数据映射到[-1, 1]之间。公式如下:
| $x^*=\frac{2 x-x_{\max }-x_{\min }}{x_{\max }-x_{\min }}$ | (2) |
其中:x*为归一化后的数值;x为原始样本数据;xmax和xmin分别为原始样本数据的最大和最小值。
2.3 模型评估指标为了评估模型训练和预测结果,根据风暴潮增水特性,采用平均绝对误差、相关系数和有效系数来对模型效果进行评估。
(1) 平均绝对误差MAE。平均绝对误差代表预测值和实际值的误差程度,相对于常用的均方根误差评价指标,平均绝对误差能更好地反映预测值误差的实际情况。
| $M A E=\frac{1}{n} \sum\limits_{i=1}^n\left|y_i-x_i\right|$ | (3) |
(2) 相关系数CC。用以评估预测值和实际值之间的相关程度,数值越接近1,说明相关程度越大。
| $C C=\frac{\sum\limits_{i=1}^n\left(y_i-\bar{y}\right)\left(x_i-\bar{x}\right)}{\sqrt{\sum\limits_{i=1}^n\left(y_i-\bar{y}\right)^2 \sum\limits_{i=1}^n\left(x_i-\bar{x}\right)^2}} 。$ | (4) |
(3) 有效系数CE。评判预测模型相对于基准模型的好坏程度。所谓基准模型是指用样本均值代表预测值,代表预测的基本标准。如果模型结果=1,说明预测和实际完全吻合。如果等于0,说明预测模型和基准模型效果相当。如果小于0,说明预测模型还不如基准模型。
| $C E=1-\frac{\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(y_i-x_i\right)^2}}{\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(y_i-\overline{y_i}\right)^2}} 。$ | (5) |
(4) 极值偏差ΔH。一个台风过程期间的实际最大增水和预测最大增水之间的偏差值。增水极值和灾害等级密切相关,对增水极值的准确预测对准确评估灾害风险有重要作用。
| $\Delta H=\left|y_{\max }-x_{\max }\right| 。$ | (6) |
台风期间观测的潮位数据包括天文潮和台风引起的风暴增水。在分析风暴潮时,应先从实际潮位中去除天文潮部分。将天文潮分离出来的方法包括kalman滤波[33-34]和最小二乘法等[35-36],本文使用了基于最小二乘法开发的t_tide程序包用于天文潮的计算[37]。
3 影响因子影响风暴潮增水的因素众多,总体分为三类。一类是台风相关因子,包括台风中心位置、台风中心风速、中心最低气压、中心最大风速、七级风半径(边缘距测站的距离)、台风中心距测站的距离、台风移动方向、台风相对于测站的方位和中心气压等;一类是测站气象因子,例如测站气压、测站风速风向、测站天文潮位;还有一类是测站当地的固定影响因子,例如测站周边水深、地形地貌和底摩擦系数等,这一类因子不在模型的考虑范围内,因为训练数据本身已经包含了此类影响,而这些难以量化的具体参数也是数值模式方法难以确定的,这也一定程度上体现了神经网络的优势。上述因子中,有些因子如风和气压,会通过大气扰动直接影响风暴潮增水,有些参数如七级风半径、台风方位和移动路径也会对台风产生影响[26, 38],天文潮位也会因为和风暴潮的非线性相互作用而对风暴潮产生影响[39]。除此之外,考虑风暴潮增水本身趋势的影响,将增水值也作为输入加入到预报模型中。另外,有些因子对增水的影响有重复性,例如台风位置和台风距测站的距离和角度,为了排除这种干扰,本模型仅采用距离和角度作为台风位置的输入参数。综上,模型共考虑中心气压(Pc)、最大风速(Uc)、台风中心和测站的距离(L)、七级风圈和测站的距离(R,当测站位于七级风圈内此值为负)、台风入侵角度(θc,台风中心和测站之间相对于正北方向的夹角,取值-180~180)、台风移动角度(θm,台风移动方向相对于正北方向的夹角,取值-180~180)、测站气压(Pt)、测站风速(Ut)、天文潮位(A)和增水值H共10个因子。
确定风暴增水影响因子一般采用相关性分析结合超前滞后相位分析来确定,但是此种方法有一定局限性,因为相关性并不能说明存在因果关系,并且对于两个时间序列,相关分析是双向的,无法准确判定在一个周期变化中,相位差是由滞后还是超前引起的。因此,依靠滞后相关分析无法准确表征因果关系。为了能够表征两个时间序列的因果关系,基于如果序列X1的发展演变独立于序列X2,那么X2到X1的信息流为0这一信息流与因果律定理,Liang利用Liang-Kleeman信息流理论[40-41],构建因果关系表征系数,刻画两个序列间的因果关系。
对于两个时间序列X1,X2,序列X2到序列X1的信息流率的最大似然估计为:
| $T_{2 \rightarrow 1}=\frac{C_{11} C_{12} C_{2, d 1}-C_{12}^2 C_{1, d 1}}{C_{11}^2 C_{22}-C_{11} C_{12}^2}$ | (7) |
其中:Cij为样本协方差;Ci, dj是xi和由xj导出的级数之间的样本协方差,当T2→1≠0,表示X2是X1变化的因。在推断因果关系时,我们只需关注信息流传递速率的大小的绝对值。
分别使用除了增水自身以外的9个因子和增水进行因果分析,结果见图 3。信息流速率会随着序列长短而产生不同,但当序列足够长时,将会趋于一个稳定值。图 3(c)中,T1→2和T2→1都不等于0,说明天文潮和增水呈现互为因果的关系,除了图 3(i),其它均为T1→2大于0,T2→1基本等于0,说明此8个因子均是增水的因,均能对增水产生影响,反之不成立。

|
(其中T1→2表示其他因子到风暴潮增水的信息流,T2→1则相反。这些因子分别为:(a)台风中心气压,(b)台风最大风速,(c)测站气压,(d)测站风速,(e)台风中心与测站距离,(f)台风七级风圈距离,(g)台风入侵角度,(h)台风移动角度,(i)天文潮位。T1→2 represents the information flow from other factors to the storm surge, and T2→1 is the opposite. These factors are: (a) typhoon center pressure; (b) typhoon maximum wind speed; (c) local pressure; (d) local wind speed; (e) distance between typhoon center and Xiamen station; (f) Distance between Xiamen station and force 7 wind circle; (g) typhoon intrusion angle; (h) typhoon moving angle; (i) astronomical tide level.) 图 3 信息流速率随时间的变化 Fig. 3 Information flow rate changes with time |
为了验证各台风影响因子对风暴潮增水的具体影响,设计了如下4个模型进行分析。
模型A:仅用t时刻的增水值H(t)来预测t+1时刻的增水值H(t+1), 模型表示如下:
| $H(t+1)=f(H(t))$ | (8) |
模型B:仅利用t时刻台风因子来预测t+1时刻的增水值H(t+1), 模型表示如下:
| $H(t+1)=f(P \mathrm{c}(t), U \mathrm{c}(t), L(t), \\R(t), \theta \mathrm{c}(t), \theta \mathrm{m}(t)) 。$ | (9) |
模型C:利用t时刻台风因子和增水值来预测t+1时刻的增水值H(t+1), 模型表示如下:
| $H(t+1)=f(\operatorname{Pc}(t), U \mathrm{c}(t), L(t), \\ R(t), \theta \mathrm{c}(t), \theta \mathrm{m}(t), H(t)) 。$ | (10) |
模型D:利用t时刻的所有因子,包括台风因子和测站气象因子、天文潮和增水值来预测t+1时刻的增水值H(t+1), 模型表示如下:
| $H(t+1)=f(\operatorname{Pc}(t), U \mathrm{c}(t), L(t), R(t)$ $\theta \mathrm{c}(t), \theta \mathrm{m}(t), P \mathrm{t}(t), U \mathrm{t}(t), A(t), H(t))$ | (11) |
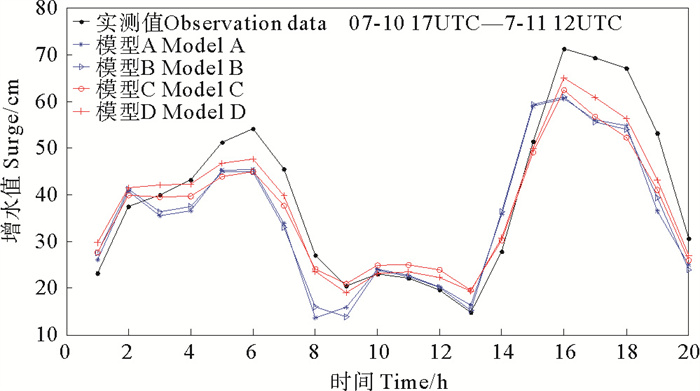
利用LSTM模型对模型A~D进行风暴潮增水模拟,其中80%的样本用于训练,20%的样本用于测试验证。为了分析不同台风路径引起的增水的模拟效果,选取了3个台风期间的增水作为验证,分别为2018年8号台风“玛莉亚”,2015年21号台风“杜鹃”和2016年14号台风“莫兰蒂”。此三台风分别从台湾海峡以北、台湾海峡中部和台湾海峡以南经过,并对厦门市造成了巨大影响,台风“杜鹃”甚至造成了厦门历史上第二高潮位。这也分别代表了三种不同的影响厦门的台风路径,即北部、中部和南部路径。为了表述方便,下文分别以台风N,M和S代表台风“玛利亚”、“杜鹃”和“莫兰蒂”。三种台风路径引起的风暴潮增水的变化各不相同,总体来说,北部路径虽距离厦门较远,但是由于台湾海峡引起的狭管效应会导致海水不断堆积引起海峡内高水位,海峡西岸会在台风登陆前较长时间内产生持续较强和波动较大的风暴潮增水;中部路径往往会引起厦门沿海的风暴潮增水产生较规律的双增水峰或多增水峰的现象;南部路径的台风在行进过程中,厦门沿海都处于其右半旋向岸大风区内,增水增长较为迅速,并在登陆前几个小时达到极值。台风登陆后厦门沿海处于左半旋离岸风区内,增水迅速减小[42]。模型A~D表现见图 4~6及表 1。
|
图 4 台风N期间不同影响因子模拟风暴潮增水与实测对比 Fig. 4 Comparison of simulated and measured storm surge water increase with different influencing factors during typhoon N |
|
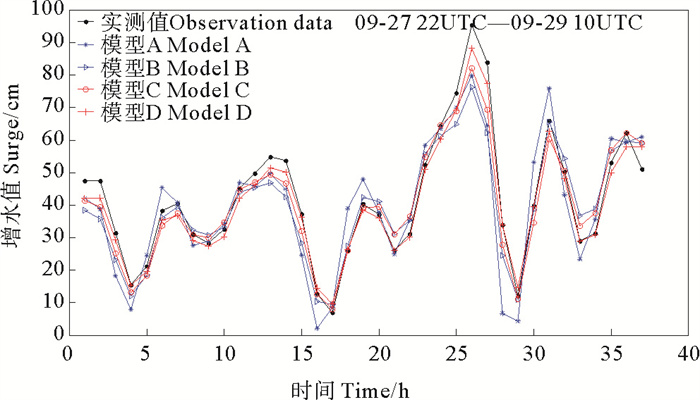
图 5 台风M期间不同影响因子模拟风暴潮增水与实测对比 Fig. 5 Comparison of simulated and measured storm surge water increase with different influencing factors during typhoon M |
|
图 6 台风S期间不同影响因子模拟风暴潮增水与实测对比 Fig. 6 Comparison of simulated and measured storm surge water increase with different influencing factors during typhoon S |
|
|
表 1 不同影响因子下平均绝对误差、相关系数、有效系数和极值误差分析表 Table 1 Mean average absolute error, correlation coefficient, effective coefficient and extreme deviation of different impact factors |
由图 4~6可知,LSTM的四种模型均能较好模拟出风暴潮增水的变化曲线。对三种路径台风的增水曲线均贴合较好,能预测出增水的不同阶段和极值发生时间。对于台风M,增水变化最为复杂,期间高低极值交叉反复出现,最大值出现在第25小时;对于台风S,增水值呈现逐渐变大的趋势,并且在登陆前达到极值;台风N期间的增水分成两个阶段,增水极值分别出现在前期和后期,LSTM模型能较好预测出这种趋势。
由表 1可知,模型A和B的平均绝对误差在7 cm左右,模型D最小,为4.35 cm;模型A和B的相关系数和有效系数大体一致,均小于模型C和D;模型D的极值偏差最小。模型A仅考虑增水值,模型B仅考虑台风因素,模型C考虑了台风和增水,说明台风和增水均能对预测精度产生影响,综合考虑二者能提高预测精度,模型D在模型C的基础上考虑了当地气象因子,精度比模型C更高,说明台风因子、当地气象因子以及潮位本身都能对增水产生影响,将这些因子纳入模型可以增加预测精度和准确率。
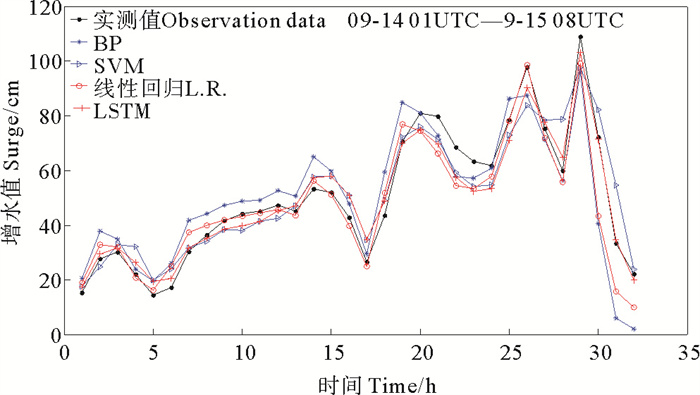
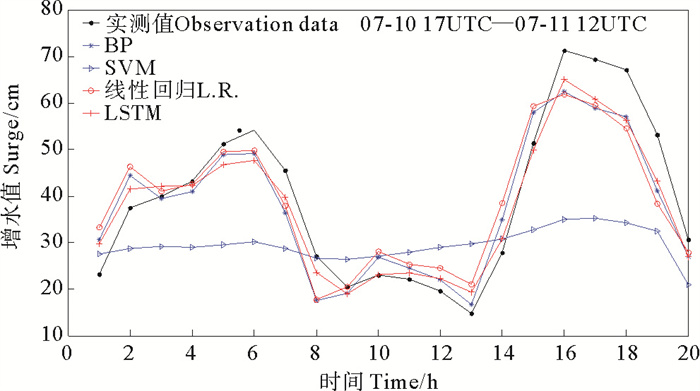
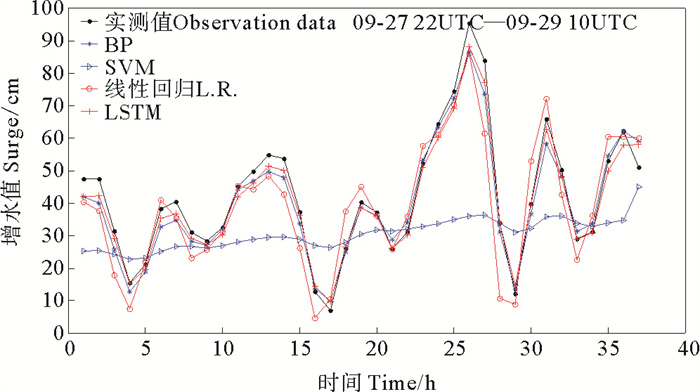
4.2 不同模型对比为了进一步说明LSTM模型在风暴潮模拟上的表现,我们将LSTM和常用的BP神经网络模型、SVM模型和线性回归模型做同步对比,方案同模型D,即利用t时刻10种输入要素模拟t+1时刻增水值,其中SVM模型为支持向量机模型,线性回归模型是利用回归方法来确定两种或两种以上变量间相互依赖关系。模型对比结果见图 7~9及表 2。
|
图 7 台风N期间不同模型模拟风暴潮增水与实测对比 Fig. 7 Comparison of simulated and measured storm surge water increase with different model during typhoon N |
|
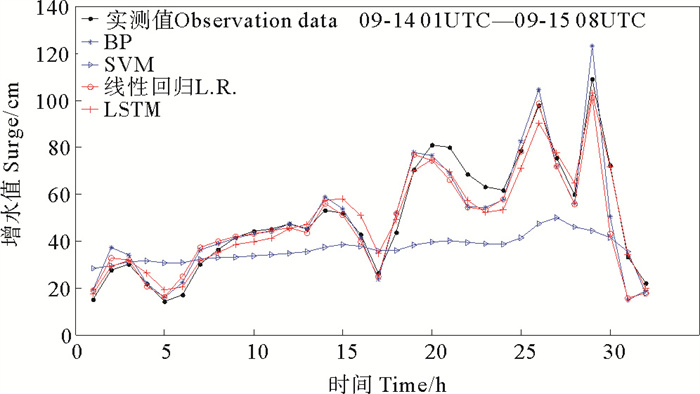
图 8 台风M期间不同模型模拟风暴潮增水与实测对比 Fig. 8 Comparison of simulated and measured storm surge water increase with different model during typhoon M |
|
图 9 台风S期间不同模型模拟风暴潮增水与实测对比 Fig. 9 Comparison of simulated and measured storm surge water increase with different model during typhoon S |
|
|
表 2 不同模型平均绝对误差、相关系数、有效系数和极值误差分析表 Table 2 Average absolute error, correlation coefficient, effective coefficient and extreme deviation of different model |
由图 7~9可以看出,SVM模型表现很差,基本无法模拟出增水趋势,BP神经网络、线性回归模型均能模拟出增水曲线的变化。由表 2可知,BP神经网络模型和线性回归模型表现大体一致,这两个模型的平均MAE值在6 cm左右。相关系数CC值在0.9左右,有效系数CE在0.6左右,ΔH在9 cm左右。这两个模型指标均低于LSTM模型。说明LSTM模型在风暴潮增水预测精度和准确性上要优于一般常用的机器学习模型。
另外,张莉等[43]利用耦合数值模型对福建沿岸风暴潮进行后报模拟,5个站位平均绝对误差在20 cm以上,平均最大极值误差为20 cm,LSTM模型在这两个指标上的表现均优于传统数值模型。
4.3 多时刻输入比较以上试验仅使用一个时刻要素值预测后一个时刻,为了验证前一个时刻的要素值是否对模型有影响,设计如下模型E:
| $H(t+1)=f(P \mathrm{c}(t-1), U \mathrm{c}(t-1), L(t-1,\\R(t-1), \theta \mathrm{c}(t-1), \theta \mathrm{m}(t-1), P \mathrm{t}(t-1), U \mathrm{t}(t-1)\\A(t-1), H(t-1), P \mathrm{c}(t), U \mathrm{c}(t), L(t), R(t), \theta \mathrm{c}(t)\\\theta \mathrm{m}(t), P \mathrm{t}(t), U \mathrm{t}(t), A(t), H(t)) 。$ | (12) |
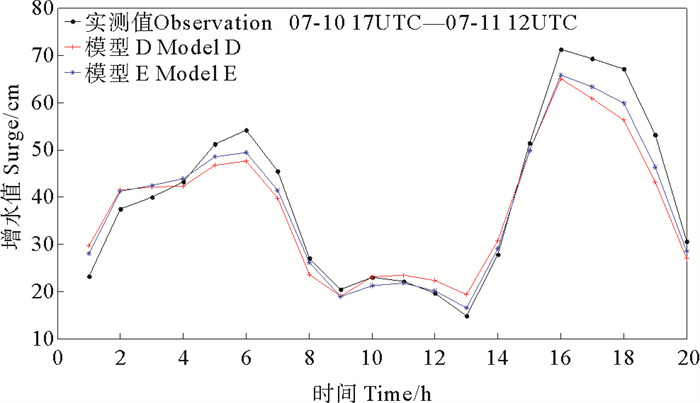
即利用t-1时刻和t时刻要素值来预测t+1时刻增水值,结果见图 10~12和表 3。
|
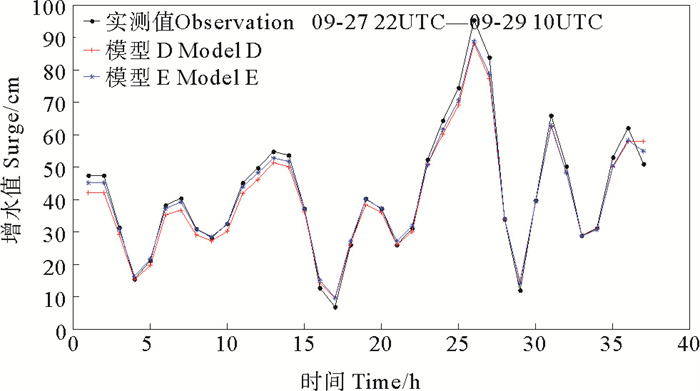
图 10 台风N期间模型D和E模拟风暴潮增水与实测对比 Fig. 10 Comparison of simulated and measured storm surge water increase between model D and E during typhoon N |
|
图 11 台风M期间模型D和E模拟风暴潮增水与实测对比 Fig. 11 Comparison of simulated and measured storm surge water increase between model D and E during typhoon M |
|
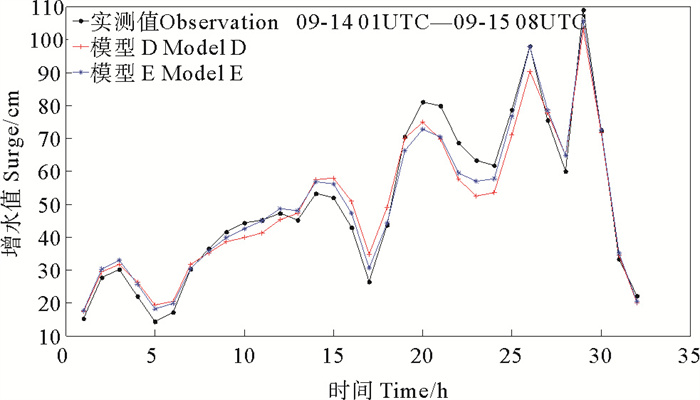
图 12 台风S期间模型D和E模拟风暴潮增水与实测对比 Fig. 12 Comparison of simulated and measured storm surge water increase between model D and E during typhoon S |
|
|
表 3 模型E平均绝对误差、相关系数、有效系数和极值误差分析表 Table 3 Average absolute error, correlation coefficient, effective coefficient and extreme deviation of model E |
由图 10~12和表 3可以看出,模型E同样能较好模拟风暴潮增水曲线变化,并且相对于模型D,模型E能更贴近实测曲线。各项指标也比模型D更优,平均绝对误差MAE的平均值仅有3 cm,极值偏差为5.4 cm,相关系数和有效系数也优于模型D。
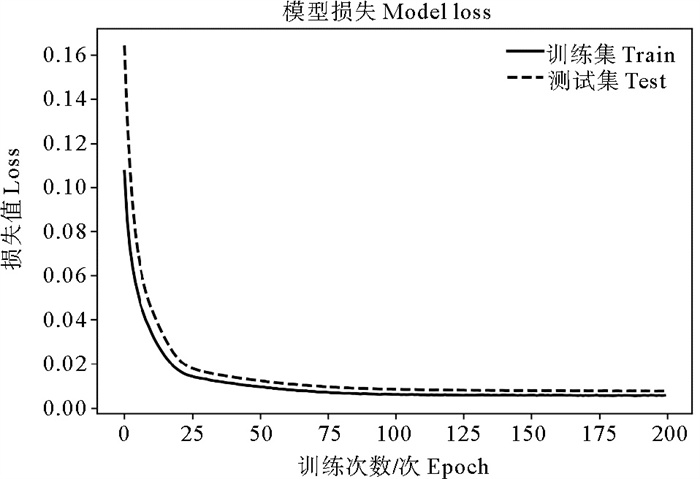
为了进一步说明模型训练情况,图 13给出了模型E的训练过程中的模型损失情况。由图可知,训练集和测试集的损失值随训练次数迅速收敛并趋于稳定,说明模型学习情况良好,模型适应性强,未出现过拟合等问题。具体而言,损失值训练次数在25次以内迅速下降,25~100次趋于平缓下降,100次以上基本稳定,损失值不再变化。表 4给出了三个台风平均MAE随训练次数变化情况。由表 4可知,模型误差和模型损失曲线表现一致,在训练次数100次左右误差基本稳定。
|
图 13 模型训练损失变化 Fig. 13 Model loss of train and test dataset |
|
|
表 4 模型E的平均绝对误差随训练次数变化 Table 4 MAE variations with the number of training of model E |
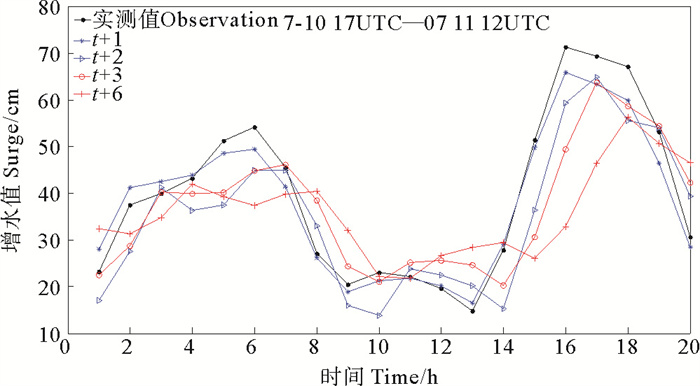
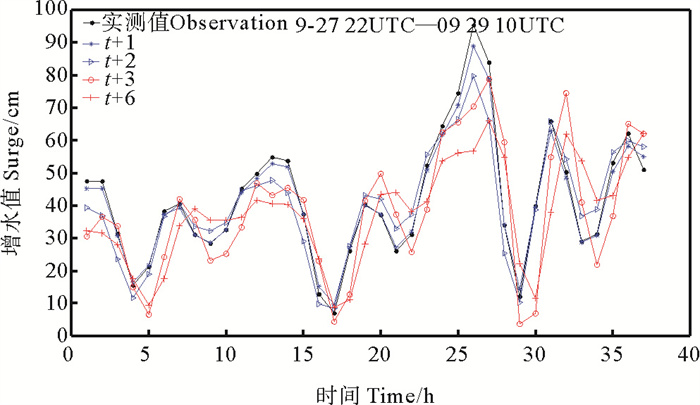
为展示LSTM在模拟较长时刻的风暴潮增水效果,分别预测t+1,t+2,t+3和t+6时刻的增水值,模型使用模型E。t+2时刻增水值的预测方式是先预测出t+1时刻增水值,利用此增水值作为输入预测t+2时刻增水值,依次类推得到t+3和t+6时刻增水值。模拟结果见图 14~16及表 5。
|
图 14 台风N期间不同时长模拟风暴潮增水与实测对比 Fig. 14 Comparison of simulated and measured storm surge water increase of different forecast duration during typhoon N |
|
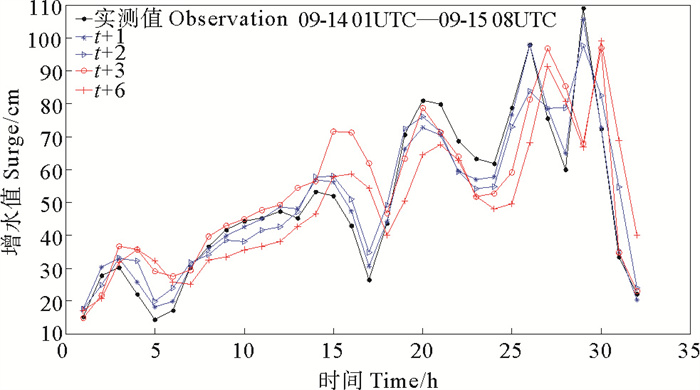
图 15 台风M期间不同时长模拟风暴潮增水与实测对比 Fig. 15 Comparison of simulated and measured storm surge water increase of different forecast duration during typhoon M |
|
图 16 台风S期间不同时长模拟风暴潮增水与实测对比 Fig. 16 Comparison of simulated and measured storm surge water increase of different forecast duration during typhoon S |
|
|
表 5 不同预报时长平均绝对误差、相关系数、有效系数和极值误差分析表 Table 5 Average absolute error, correlation coefficient, effective coefficient and extreme deviation of different forecast duration |
由图 14~16可以看出,随着预测时长的增加,预测精度开始下降,t+3和t+6时刻出现了滞后现象,并且增水值也出现了较大偏差。由表 5可知,平均绝对误差由t+1时刻的3 cm增加到t+6时刻的11 cm,极值偏差由5 cm增加至15 cm,相关系数和有效系数也随之下降。总体而言,t+1和t+2时刻的预报结果表现出较高的准确率和相关度,t+3和t+6时刻的预报结果精度虽然有所下降,但是仍有较高精度,最低的台风N的相关系数也有0.6左右,具有较强的相关性,可描述出风暴潮增水的变化趋势。就三种台风路径而言,t+1和t+2时刻的台风M期间平均绝对误差最小,预测精度最高,t+3和t+6时刻的台风N期间的平均误差最小。
5 结论风暴潮是一种由台风引起的海水水位变化,它受台风、当地气象条件和海岸地形的影响。本文根据信息流理论,选取影响风暴潮增水的10个因子并分析了与增水的因果关系,基于分析结果,利用长短期记忆神经网络建立厦门沿海风暴潮增水预报模型,探讨了在3种不同路径下的各模型表现好坏,并和其它常用机器学习模型进行对比,结论如下。
(1) 根据不同影响因子组合建立了预报模型,发现台风因子、当地气象因子和风暴潮增水都能对增水产生影响,将所有10个因子纳入模型可以增加预测精度和准确率。
(2) 将LSTM模型和常用的BP神经网络模型、SVM模型和线性回归模型做同步对比,预报因子选用10个因子,发现SVM模型表现最差,BP神经网络模型和线性回归模型基本一致,LSTM模型表现最优。
(3) 同时使用t-1和t时刻影响因子来预报t+1时刻增水值的表现优于仅使用t时刻因子进行预报。利用t-1和t时刻影响因子继续预报了t+2、t+3和t+6时刻的增水值,发现随着预测时长的增加,预测精度开始下降。t+1和t+2时刻的预报结果表现出较高的准确率和相关度,t+3和t+6时刻的预报结果精度虽然有所下降,但是仍有较高精度。
(4) 预报精度和台风路径类型有关,t+1和t+2时刻的台风M期间预报值平均绝对误差最小,预测精度最高,t+3和t+6时刻的台风N期间预报值平均误差最小。
综上所述,本模型相对于一般机器学习预报模型能更好地预报台风引起的风暴潮增水变化,不论增水值还是增水时间都具有较高精度,并且本模型训练简单,收敛速度快,具有较高的可行性,可为风暴潮业务化预报提供辅助和参考。
| [1] |
Doodson A T. Tides and storm surges in a long uniform gulf[J]. Proc Math Phys Eng Sci, 1956, 237: 325-343. (  0) 0) |
| [2] |
Webster P J, Holland G J, Curry J A, et al. Changes in tropical cyclone number, duration, and intensity in a warming environment[J]. Science, 2005, 309: 1844-1846. DOI:10.1126/science.1116448 (  0) 0) |
| [3] |
Emanuel K A. Increasing destructiveness of tropical cyclones over the past 30 years[J]. Nature, 2005, 436: 686-688. DOI:10.1038/nature03906 (  0) 0) |
| [4] |
朱星桦. 基于改进联合概率模型的厦门岛极端水位预测研究[D]. 南京: 东南大学, 2018. Zhu Xinghua. Estimating Extreme Water Levels with Joint Probability Optimal Sampling Method in Xiamen Island[D]. Nanjing: Southeast University, 2018. (  0) 0) |
| [5] |
Chao W T, Young C C, Hsu T W, et al. Long-lead-time prediction of storm surge using artificial neural networks and effective typhoon parameters: Revisit and deeper insight[J]. Water, 2020, 12(9): 1-24. (  0) 0) |
| [6] |
Conner W C, Kraft K H, Harris D L. Empirical methods for forecasting the maximum storm tide due to hurricanes and other tropical storms[J]. Monthly Weather Review, 1957, 85: 113-116. DOI:10.1175/1520-0493(1957)085<0113:EMFFTM>2.0.CO;2 (  0) 0) |
| [7] |
Welander P. Numerical predictions of storm surges[J]. Advances in Geophysics, 1961, 8: 315-379. (  0) 0) |
| [8] |
Platzman G W. The dynamical prediction of wind tides on Lake Erie[J]. Meteorol Monogr, 1963, 4: 1-44. (  0) 0) |
| [9] |
Jelesnianski C P. A numerical calculation of storm tides induced by a tropical storm impinging on a continental shelf[J]. Monthly Weather Review, 1965, 93: 343-358. DOI:10.1175/1520-0493(1993)093<0343:ANCOS>2.3.CO;2 (  0) 0) |
| [10] |
Holland G J. An analytic model of the wind and pressure profiles in hurricanes[J]. Monthly Weather Review, 1980, 108: 1212-1218. DOI:10.1175/1520-0493(1980)108<1212:AAMOTW>2.0.CO;2 (  0) 0) |
| [11] |
Weserink J J, Luettich R A, Baptista A M, et al. Tide and storm surge predictions using a finite element model[J]. Journal of Hydraulic Engineering, 1992, 118: 1373-1390. DOI:10.1061/(ASCE)0733-9429(1992)118:10(1373) (  0) 0) |
| [12] |
Shen J, Zhang K, Xiao C, et al. Improved prediction of storm surge inundation with a high-resolution unstructured grid model[J]. Journal of Coastal Research, 2006, 22: 1309-1319. (  0) 0) |
| [13] |
Kim S Y, Yasuda T, Mase H. Numerical analysis of effects of tidal variations on storm surges and waves[J]. Applied Ocean Research, 2008, 30: 311-322. DOI:10.1016/j.apor.2009.02.003 (  0) 0) |
| [14] |
Chen W B, Liu W C, Hsu M H. Computational investigation of typhoon-induced storm surges along the coast of Taiwan[J]. Natural Hazards, 2012, 64: 1161-1185. DOI:10.1007/s11069-012-0287-1 (  0) 0) |
| [15] |
Wu G, Shi F, Kirby J T, et al. Modeling wave effects on storm surge and coastal inundation[J]. Coastal Engineering, 2018, 140: 371-382. DOI:10.1016/j.coastaleng.2018.08.011 (  0) 0) |
| [16] |
Dietrich J C, Zijlema M, Westerink J., et al. Modeling hurricane waves and storm surge using integrally coupled scalable computations[J]. Coastal Engineering, 2011, 58: 45-65. DOI:10.1016/j.coastaleng.2010.08.001 (  0) 0) |
| [17] |
Torres M J, Hashemi M R, Hayward S, et al. Role of hurricane wind models in accurate simulation of storm surge and waves[J]. Journal of Waterway Port Coastal and Ocean Engineering, 2019, 145(1): 04018039. DOI:10.1061/(ASCE)WW.1943-5460.0000496 (  0) 0) |
| [18] |
Dietrich J C, Zijlema M, Westerink J, et al. Modeling hurricane waves and storm surge using integrally coupled scalable computations[J]. Coastal Engineering, 2011, 58: 45-65. DOI:10.1016/j.coastaleng.2010.08.001 (  0) 0) |
| [19] |
Kohno N, Dube S K, Entel M, et al. Recent progress in storm surge forecasting[J]. Tropical Cyclone Research and Review, 2018, 7: 128-139. (  0) 0) |
| [20] |
Rumelhart D E, Hinton G E, Williams R J. Learning representations by back-propagating errors[J]. Nature, 1986, 323: 533-536. DOI:10.1038/323533a0 (  0) 0) |
| [21] |
Bajo M, Umgiesser G. Storm surge forecast through a combination of dynamic and neural network models[J]. Ocean Model, 2010, 33: 1-9. DOI:10.1016/j.ocemod.2009.12.007 (  0) 0) |
| [22] |
Erdil A, Arcaklioglu E. The prediction of meteorological variables using artificial neural network[J]. Neural Computing & Applications, 2013, 22: 1677-1683. (  0) 0) |
| [23] |
Young C C, Liu W C. Prediction and modelling of rainfall-runoff during typhoon events using a physically-based and artificial neural network hybrid model[J]. Hydrologccal Sciences Journal, 2015, 60: 2102-2116. DOI:10.1080/02626667.2014.959446 (  0) 0) |
| [24] |
Young C C, Liu W C, Chang C E. Genetic algorithm and fuzzy neural networks combined with the hydrologic modeling system for forecasting watershed runoff discharge[J]. Neural Computing & Applications, 2015, 26: 1631-1643. (  0) 0) |
| [25] |
SK A, SP B, HM C. Artificial neural network-based storm surge forecast model: Practical application to Sakai Minato, Japan[J]. Applied Ocean Research, 2019, 91: 101871. DOI:10.1016/j.apor.2019.101871 (  0) 0) |
| [26] |
卢君峰, 李少伟, 袁方超. 基于BP神经网络的厦门沿海风暴潮预报应用[J]. 海洋预报, 2016, 33(4): 9-16. Lu J F, Li S W, Yuan F C. Application of storm surge forecasting by BP artificial neural network off coast of Xiamen[J]. Marine Forecasts, 2016, 33(4): 9-16. (  0) 0) |
| [27] |
李未, 王如云, 卢长娜, 等. 神经网络在珠江口风暴潮预报中的应用[J]. 热带海洋学报, 2006(3): 10-13. Li W, Wang R Y, Lu C N, et al. Forecast of storm surge in Zhujiang River estuary by means of artificial neural network[J]. Journal of Tropical Oceanography, 2006(3): 10-13. DOI:10.3969/j.issn.1009-5470.2006.03.002 (  0) 0) |
| [28] |
Deng L, Yu D. Deep learning: Methods and applications[J]. Foundations and Trends in Signal Processing, 2014, 7(3/4): 197-387. (  0) 0) |
| [29] |
Yang Y, Dong J, Sun X, et al. A CFCC-LSTM Model for sea surface temperature prediction[J]. IEEE Geoence & Remote Sensing Letters, 2017(2): 1-5. (  0) 0) |
| [30] |
Zhang Q, Wang H, Dong J, et al. Prediction of sea surface temperature using long short-term memory[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(10): 1745-1749. DOI:10.1109/LGRS.2017.2733548 (  0) 0) |
| [31] |
石绥祥, 王蕾, 余璇. 长短期记忆神经网络在叶绿素a浓度预测中的应用[J]. 海洋学报, 2020, 42(2): 134-142. Shi Suixiang, Wang lei, Yu Xuan, et al. Application of long term and short term memory neural network in prediction of chlorophyll a concentration[J]. Haiyang Xuebao, 2020, 42(2): 134-142. DOI:10.3969/j.issn.0253-4193.2020.02.014 (  0) 0) |
| [32] |
Yang C H, Wu C H, Hsieh C M. Long short-term memory recurrent neural network for tidal level forecasting[J]. IEEE Access, 2020(99): 1-13. (  0) 0) |
| [33] |
Jan C D, Tseng C M, Wang J S, et al. Empirical relation between the typhoon surge deviation and the corresponding typhoon characteristics: A case study in Taiwan[J]. Journal of Marine Science & Technology, 2006, 11(3): 193-200. (  0) 0) |
| [34] |
Yen P H, Jan C D, Lee Y P, et al. Application of Kalman filter to short-term tide level prediction[J]. Journal of Waterway Port Coastal & Ocean Engineering, 1998, 122(5): 226-231. (  0) 0) |
| [35] |
Doodson A T. Oceanic Tides. Advances in Geophysics[M]. New York: Academic Press, 1958: 117-152.
(  0) 0) |
| [36] |
Pan H, Lv X, Wang Y, et al. Exploration of tidal-fluvial interaction in the Columbia River Estuary using S_TIDE[J]. Journal of Geophysical Research: Oceans, 2018, 123: 6598-6619. DOI:10.1029/2018JC014146 (  0) 0) |
| [37] |
Pawlowicz R, Beardsley B, Lentz S. Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE[J]. Computers & Geosciences, 2002, 28(8): 929-937. (  0) 0) |
| [38] |
许金电, 郭小钢, 黄奖. 2006年夏季福建近海台风风暴潮特征分析[J]. 台湾海峡, 2011, 30(4): 473-482. Xu J D, Guo X G, Huang J. Analysis of the characteristics of typhoon storm surges in Fujian offshore area during 2006 summer[J]. Journal of Oceanography in Taiwan Strait, 2011, 30(4): 473-482. DOI:10.3969/J.ISSN.1000-8160.2011.04.004 (  0) 0) |
| [39] |
黄森军. 浙江近海台风暴潮及冲淤研究[D]. 杭州: 浙江大学, 2017. Huang Senjun. Research on Storm Surge and Erosion and Deposition of Typhoon Offshore in Zhejiang[D]. Hangzhou: Zhejiang University, 2017. (  0) 0) |
| [40] |
Liang X S. Information flow and causality as rigorous notions abinitio[J]. Physical Review E, 2015, 94(5): 1-49. (  0) 0) |
| [41] |
Liang X San. Entropy evolution and uncertainty estimation with dynamical systems[J]. Entropy, 2014, 16: 3605-3634. DOI:10.3390/e16073605 (  0) 0) |
| [42] |
张文舟, 胡建宇, 商少平, 等. 福建沿海风暴潮特征的分析[J]. 海洋通报, 2004, 23(3): 12-19. Zhang W Z, Hu J Y, Shang S P, et al. On the characteristics of storm surges along Fujian Coast[J]. Marine Science Bulletin, 2004, 23(3): 12-19. DOI:10.3969/j.issn.1001-6392.2004.03.002 (  0) 0) |
| [43] |
张莉, 商少平, 谢燕双, 等. 基于有限元法的福建沿岸天文潮-风暴潮耦合预报模式研究[J]. 应用海洋学报, 2016, 35(2): 256-265. Zhang L, Shang S P, Xie Y S, et al. A tide-storm surge coupled model based on finite element method for Fujian coast[J]. Journal of Applied Oceanography, 2016, 35(2): 256-265. (  0) 0) |
2. Shanghai University, Shanghai 200444, China
 2022, Vol. 52
2022, Vol. 52


