鹰爪虾(Trachysalambria curvirostris)广泛分布于印度洋-西太平洋区,是海洋捕捞中的重要虾类之一[1],在中国虾类年捕捞量中占比约为20%[2],同时还是韩国张网和拖网渔业的目标种,占韩国虾类渔获总量的50%以上[3],也是东北亚近海的重要商业捕捞种之一[4]。海州湾拥有丰富的渔业资源,但随着开发程度的日益提高,资源衰退严重[5]。鹰爪虾作为海州湾海域的主要经济渔获物之一[6],国内对其生物学参数以及开发状况的研究较少,致使鹰爪虾资源的管理和利用缺乏理论支撑。为此,本研究依据海上调查的实际数据,对鹰爪虾的单位补充量产量进行计算,为该海域鹰爪虾资源管理策略的科学制定提供理论依据。
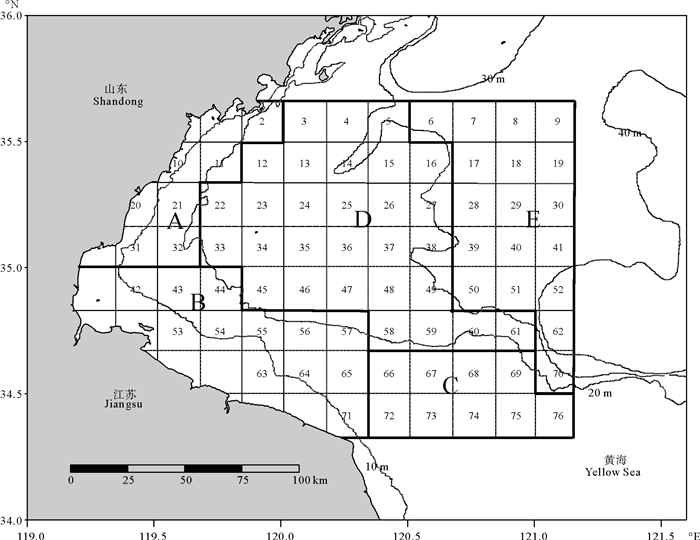
1 材料与方法 1.1 数据来源本研究的鹰爪虾取样自2011年在海州湾及邻近海域进行的渔业资源底拖网调查,调查范围为119°20′E~121°10′E、34°20′N~35°40′N(见图 1),每10′×10′的方格内设一个站位,共76个站位,从中随机选取了24个调查站位。调查船采用功率为220 kW的单拖渔船,拖速为2~3 kn,在每个调查站位的拖网时间约60 min。调查网具网口宽约25 m,囊网网目为17 mm。在5、7、9和12月分别捕获鹰爪虾106、171、261和379尾,共917尾,其中雌性637尾,体长范围为3.8~11.9 cm;雄性280尾,体长范围为3.7~8.9 cm。
|
图 1 海州湾及邻近海域渔业资源调查区域图 Fig. 1 Map of bottom trawl survey area in the Haizhou Bay and adjacent waters |
已有研究[7-8]发现鹰爪虾雌性个体的体型一般大于雄性,因此本研究利用R中TropFishR[9]包对雌、雄性鹰爪虾生长参数、死亡系数及单位补充量产量分别进行分析。
1.2.1 体长-体重关系应用于拟合体长与体重数据的关系式为:
| $ W = a{L^b}。$ |
式中:W为体重(g);L为体长(cm);a为生长条件因子;b为异速生长因子,b=3时表示等速生长,b≠3时表示异速生长[10]。
1.2.2 生长参数使用von Bertalanffy生长方程描述鹰爪虾的生长[10]:
| $ {L_t} = {L_\infty }\left( {1 - {{\rm{e}}^{ - K\left( {t - {t_0}} \right)}}} \right)。$ |
式中:Lt表示在年龄为t龄时的体长;L∞表示渐近体长;t0为理论上体长为零时的年龄,通常为负数;K为生长曲线趋近渐近值的相对速率。生长参数L∞和K的估算使用ELEFAN(Electronic LEngth Frequency ANalysis)方法[11],这一方法常用于年龄鉴定困难的渔业资源种类中,近年来在R语言中得到实现[12],其中TropFishR包对获取生长方程参数的拟合算法进行了扩展[13]。本研究选用响应面分析(Response surface analysis, RSA)、模拟退火(Simulated annealing, SA)与遗传算法(Genetic algorithm, GA)三种算法获得鹰爪虾生长方程的最优拟合。体长组划分参考之前研究[14]的建议,在本研究中采用0.6和0.4 cm分别作为雌、雄鹰爪虾体长分组的组距。三种算法所得结果的优化程度以Rn[15]区分:
| $ {R_n} = \frac{{{{10}^{{\rm{ESP}}/{\rm{ASP}}}}}}{{10}}。$ |
式中:ASP(Available sum of peaks)与ESP(Explained sum of peaks)分别代表可用波峰的最大得分之和与已用波峰的得分之和[16]。此外,TropFishR中引入tanchor以确定生长曲线的起始点,其取值在0~1之间,对应于产卵高峰期出现的月份,有研究[17]指出鹰爪虾的产卵期为7月初至9月初,产卵盛期为7月中旬至8月上旬,Rn相同的情况下,以tanchor与产卵盛期的接近程度作为优化效果的判断标准。t0的估算使用Pauly经验公式[18]:
| $ \lg \left( { - {t_0}} \right) = - 0.3922 - 0.2752 \times \lg {L_\infty } - 1.038 \times \lg K。$ |
总死亡系数Z使用变换体长渔获曲线法(Length-Converted Catch Curves, LCCC)估算:
| $ \ln (C/{\rm{d}}t) = a + b{t^\prime }。$ |
式中:C为给定体长组的样本数量;dt为生长过程中体长从该体长组下限增长至上限所需时间;t′为所属该体长组样品的相对年龄;-b即为总死亡系数。所选数据点应符合“未达补充年龄和接近渐近体长的数据点不能使用”原则[10]。自然死亡系数M的计算使用Pauly经验公式[19]:
| $ \begin{array}{l} \;\;\;\lg M = - 0.0066 - 0.279 \times \lg {L_\infty } + 0.6543 \times \lg K + \\ 0.4634 \times \lg T。\end{array} $ |
式中:渐近体长L∞的单位为cm;T为年平均水温的摄氏度数。调查区域2011年的年平均表层水温利用来自美国国家海洋和大气管理局(NOAA) CoastWatch网站(https://coastwatch.pfeg.noaa.gov/) (Accessed on 8 September 2019)的卫星遥感海洋表面温度(SST)数据计算,计算结果为14.79 ℃。捕捞死亡系数F可根据F=Z-M得出,开发率E由E=F/Z求得。
1.2.4 渔具选择性及开捕体长利用变换体长渔获曲线拟合的方程,向后推算未被选用的各点对应的预期值,计算观测值(Numbers caught)与预期值(Numbers expected)之比,得出的比率即为各体长组对应的选择性,渔具选择性(PL)和体长(L)的关系可以表示为Logistic曲线[20]:
| $ {P_L} = \frac{1}{{1 + {{\rm{e}}^{{S_1} - {S_2}L}}}}。$ |
式中:S1和S2为常数;L和PL即体长组的组中值及其对应的选择率。选择率为50%时所对应的体长L50即为开捕体长(Lc)。
1.2.5 单位补充量产量Beverton-Holt模型[21]是常用的单位补充量产量求算方法,后经Pauly和Soriano结合渔具选择性进行了改进[22],在本研究中使用刀刃式选择假设模型和结合渔具选择性改进的Beverton-Holt模型两种方法计算鹰爪虾的单位补充量产量。
使用刀刃式选择假设模型计算相对单位补充量产量(Y′/R)的方法为[23]:
| $ Y^{\prime} / R=E \cdot U^{M / K}\left\{1-\frac{3 U}{(1+m)}+\frac{3 U^{2}}{(1+2 m)}-\frac{U^{3}}{(1+3 m)}\right\}。$ |
其中,
| $ \begin{array}{*{20}{c}} {U = 1 - \left( {{L_c}/{L_\infty }} \right);}\\ {m = (1 - E)/(M/K) = (K/Z)。} \end{array} $ |
使用结合渔具选择性改进的Beverton-Holt模型计算Y′/R的方法为[23]:
| $ {Y^\prime }/R = \sum {{P_i}} \left( {\left( {{{\left( {{Y^\prime }/R} \right)}_i} \cdot {G_{i - 1}}} \right) - \left( {{{\left( {{Y^\prime }/R} \right)}_{i + 1}} \cdot {G_i}} \right)} \right)。$ |
式中:(Y′/R)i即根据第i个体长组下限计算的相对单位补充量产量;Pi为第i个体长组的拖网渔具选择性;Gi由下式定义:
| $ {G_i} = \Pi {r_j}。$ |
其中,
| $ \begin{array}{*{20}{c}} {{r_j} = {{\left( {1 - {c_i}} \right)}^{{S_i}}}/{{\left( {1 - {c_{i - 1}}} \right)}^{{S_i}}};}\\ {{S_i} = (M/K)(E/(1 - E)){P_i};}\\ {{c_i} = {L_i}/{L_\infty }。} \end{array} $ |
式中:Li为第i个体长组的上限。单位补充量产量(Y/R)与相对单位补充量产量(Y′/R)之间的关系为[20]:
| $ (Y/R) = \left( {{Y^\prime }/R} \right) \cdot {W_\infty } \cdot {{\rm{e}}^{M\left( {{T_r} - {t_0}} \right)}}。$ |
式中:雌性鹰爪虾和雄性鹰爪虾的补充年龄Tr分别使用雌虾的最小产卵体长和最小交尾体长[24]根据生长方程计算获得;W∞为渐近体重,由W∞=a(L∞)b求得。
此外,本研究计算了保持当前开捕体长不变的情况下单位补充量产量达到最大值时的捕捞死亡系数(Fmax)和开发率(Emax),以及单位补充量边际产量相当于未开发状态的10%时的捕捞死亡系数(F0.1)[25]和开发率(E0.1)。
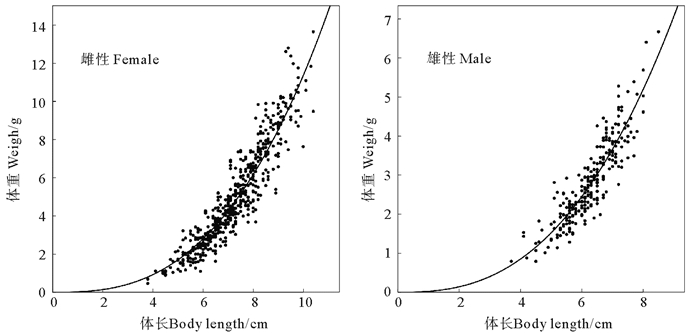
2 结果 2.1 体长-体重关系对雌、雄性鹰爪虾体长与体重数据进行拟合(见图 2),得出的体长与体重关系分别为:
| $ \begin{array}{l} W_{F}=0.0206 \times\left(L_{F}\right)^{2.74}, R^{2}=0.865; \\ W_{M}=0.0227 \times\left(L_{M}\right)^{2.61}, R^{2}=0.807。\end{array} $ |
|
图 2 海州湾及邻近海域鹰爪虾的体长-体重关系拟合曲线 Fig. 2 Length-weight relationships of Trachysalambria curvirostris in the Haizhou Bay and adjacent waters |
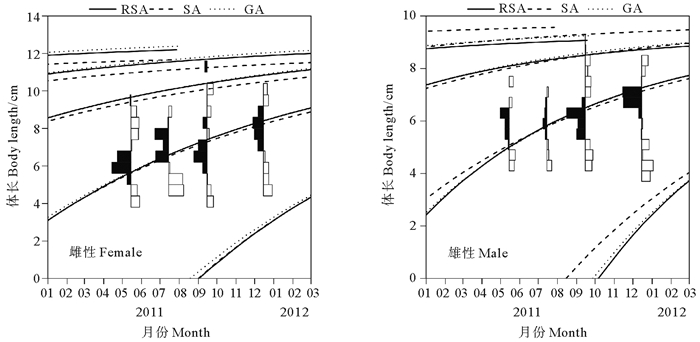
根据鹰爪虾的体长频率数据,应用三种拟合算法获得了ELEFAN方法的不同结果(见图 3)。
|
(RSA为响应面分析,SA为模拟退火,GA为遗传算法。RSA means response surface analysis, SA means simulated annealing, GA means genetic algorithm.) 图 3 使用ELEFAN方法的不同拟合算法得出的海州湾及邻近海域鹰爪虾的生长曲线 Fig. 3 Growth curves of T. curvirostris in the Haizhou Bay and adjacent waters estimated by ELEFAN method using different algorithms |
将Rn相同时得到的tanchor与产卵盛期的接近程度进行比较(见表 1),选择三种算法结果中的较优值。
|
|
表 1 比较通过TropFishR的三种算法获得的von Bertalanffy生长参数 Table 1 Comparison of growth parameters by three fit algorithms in TropFishR |
雌、雄性鹰爪虾的生长参数最终分别选用遗传算法和模拟退火拟合算法的结果,并用Pauly经验公式得出t0值,获得雌性鹰爪虾的体长生长方程为:
| $ {L_t} = 12.97 \times \left( {1 - {{\rm{e}}^{ - 0.79(t + 0.26)}}} \right)。$ |
雄性鹰爪虾的体长生长方程为:
| $ {L_t} = 9.77 \times \left( {1 - {{\rm{e}}^{ - 0.98(t + 0.22)}}} \right)。$ |
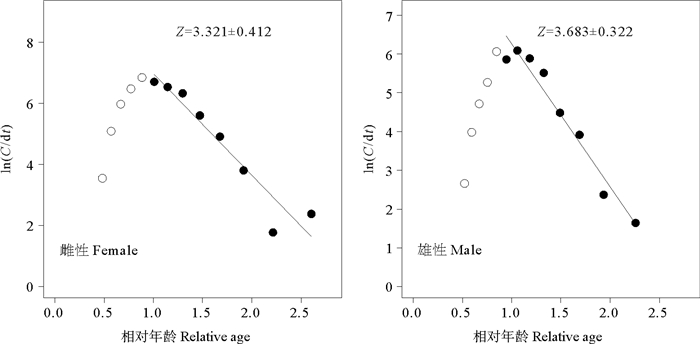
雌、雄鹰爪虾的总死亡系数(见图 4)分别为3.321和3.683 a-1,自然死亡系数分别为1.435和1.791 a-1,捕捞死亡系数分别为1.886和1.892 a-1,开发率分别为0.568和0.514。
|
图 4 海州湾及邻近海域鹰爪虾的变换体长渔获曲线分析 Fig. 4 Analysis of length-converted catch curves of T. curvirostris in the Haizhiou Bay and adjacent waters |
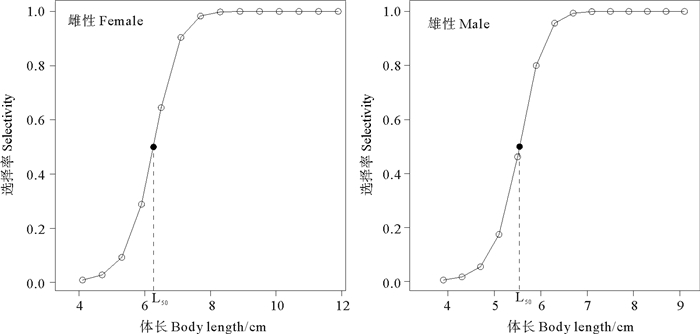
对图 4中的点计算观测值和预期值之比(见图 5),得出雌、雄性鹰爪虾的开捕体长分别为6.27和5.54 cm。
|
(L50为开捕体长。L50 is length at first capture.) 图 5 海州湾及邻近海域鹰爪虾的捕捞选择性曲线 Fig. 5 Selectivity curves of T. curvirostris in the Haizhou Bay and adjacent waters |
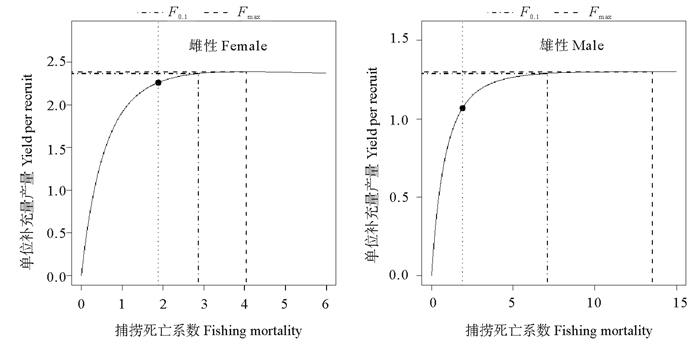
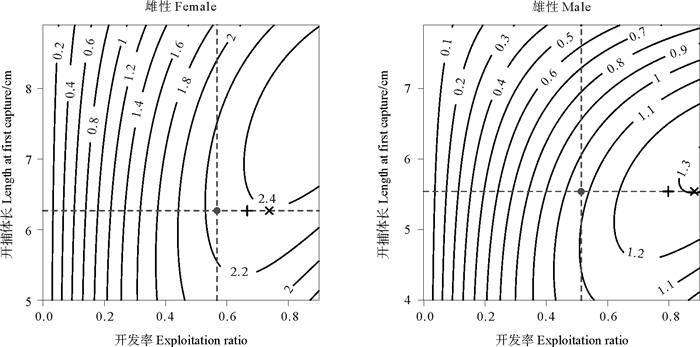
应用两种方法计算单位补充量产量并通过Y/R随捕捞死亡系数F的变化图和单位补充量产量等值线图表示海州湾鹰爪虾的资源开发程度。使用刀刃式选择假设模型时,雌、雄性鹰爪虾的单位补充量产量分别为2.264和1.068 g,F0.1分别是2.866和7.078 a-1,Fmax分别为4.050和13.527 a-1(见图 6),E0.1分别为0.666和0.798,Emax分别为0.738和0.883(见图 7)。
|
(图中圆点表示实际捕捞死亡系数,F0.1为单位补充量边际产量相当于未开发状态的10%时的捕捞死亡系数,Fmax为单位补充量产量最大时的捕捞死亡系数。The black dots represent current fishing mortality, F0.1 means the fishing mortality at which marginal increase in yield per recruit (YPR) is 10% of that at F of 0, Fmax means the fishing mortality which maximum YPR value is attained.) 图 6 使用刀刃式选择假设模型时海州湾及邻近海域鹰爪虾的单位补充量产量曲线 Fig. 6 Yield per recruit curves of T. curvirostris in the Haizhou Bay and adjacent waters using knife-edge selection option |
|
(图中圆点表示实际捕捞压力,加号表示单位补充量边际产量相当于未开发状态10%时的开发率(E0.1),叉号表示单位补充量产量最大时的开发率(Emax)。The grey dots represent current fishing pressure, plus symbols indicate the exploitation rate (E0.1) at which marginal increase in yield per recruit (YPR) is 10% of that at E of 0, cross symbols indicate the exploitation rate (Emax) which maximum YPR value is attained.) 图 7 使用刀刃式选择假设模型时海州湾及邻近海域鹰爪虾的单位补充量产量等值线图 Fig. 7 Yield per recruit isopleth diagrams of T. curvirostris in the Haizhou Bay and adjacent waters using knife-edge selection option |
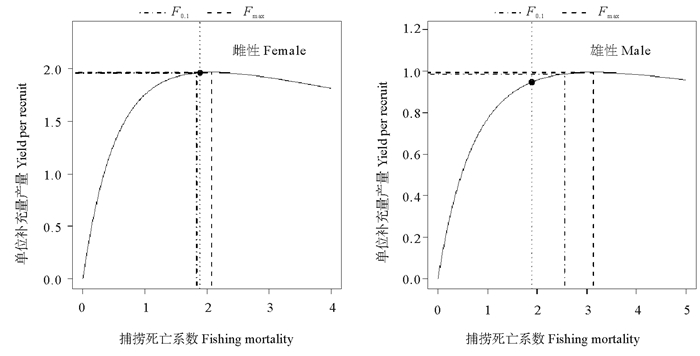
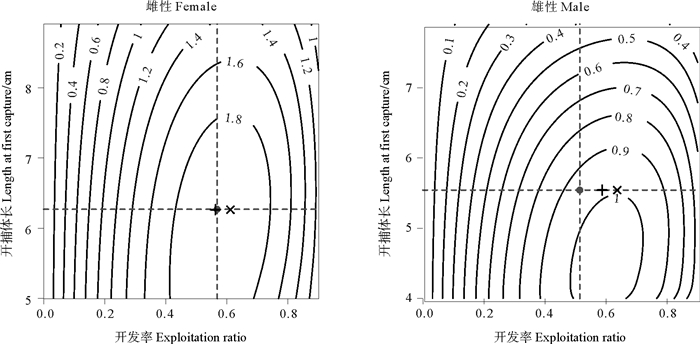
使用结合渔具选择性改进的Beverton-Holt模型时,雌、雄性鹰爪虾的单位补充量产量分别为1.963和0.946 g,F0.1分别为1.833和2.548 a-1,Fmax分别为2.077和3.135 a-1(见图 8),E0.1分别为0.561和0.587,Emax分别为0.591和0.636(见图 9)。
|
(图中圆点表示实际捕捞死亡系数,F0.1为单位补充量边际产量相当于未开发状态的10%时的捕捞死亡系数,Fmax为单位补充量产量最大时的捕捞死亡系数。The black dots represent current fishing mortality, F0.1 means the fishing mortality at which marginal increase in yield per recruit (YPR) is 10% of that at F of 0, Fmax means the fishing mortality which maximum YPR value is attained.) 图 8 使用结合渔具选择性改进的Beverton-Holt模型时海州湾及邻近海域鹰爪虾的单位补充量产量曲线 Fig. 8 Yield per recruit curves of T. curvirostris in the Haizhou Bay and adjacent waters using selection ogive option |
|
(图中圆点表示实际捕捞压力,加号表示单位补充量边际产量相当于未开发状态10%时的开发率(E0.1),叉号表示单位补充量产量最大时的开发率(Emax)。The grey dots represent current fishing pressure, plus symbols indicate the exploitation rate (E0.1) at which marginal increase in yield per recruit (YPR) is 10% of that at E of 0, cross symbols indicate the exploitation rate (Emax) which maximum YPR value is attained.) 图 9 使用结合渔具选择性改进的Beve-rton Holt模型时海州湾及邻近海域鹰爪虾的单位补充量产量等值线图 Fig. 9 Yield per recruit isopleth diagrams of T. curvirostris in the Haizhou Bay and adjacent waters using selection ogive option |
使用本研究得出的雌性鹰爪虾生长方程结合鹰爪虾的最小产卵体长[24]求算初次产卵年龄,认为该海域鹰爪虾孵化后到次年繁殖季节进行产卵,与纪伊水道西部海域鹰爪虾的初次产卵年龄[26]相似,且使用该生长方程对鹰爪虾生长进行的拟合与在人工养殖实验[27]中观测到的结果相近,因此认为本研究得出的生长方程可以近似描述该海域鹰爪虾体长和年龄的关系。
3.2 单位补充量产量的计算方法本研究使用了两种方法对单位补充量产量进行计算,并参考Gulland提出的生物学参考点[28]对得出的E0.1进行比较以评价两种方法在鹰爪虾资源群体中的适用性程度。Gulland认为最适捕捞死亡系数与自然死亡系数相等,即Eopt=0.5。根据计算结果可以看出,相比刀刃式选择假设模型得出的雌、雄性鹰爪虾的E0.1(0.666,0.798),使用结合渔具选择性改进的Beve-rton-Holt模型得出的E0.1(0.561,0.587)与Gulland提出的最适开发率更为接近,因此本研究认为结合渔具选择性改进的Beverton-Holt模型更适用于鹰爪虾的种群评估中。
有研究认为在使用刀刃式选择假设模型评估小型鱼和虾类的种群资源时会导致单位补充量产量被高估[29],并且即使以F0.1作为生物学参考点仍然会对资源开发程度做出过于乐观的评价[30],本研究对鹰爪虾种群资源的评估结果同样反映了使用刀刃式选择假设模型得出的单位补充量产量和F0.1偏高的问题。在维持当前开捕体长不变时,雄性鹰爪虾的F0.1高达7.078 a-1,推测这一结果的得出不仅与使用刀刃式选择假设模型有关,还与雄性鹰爪虾的样本量偏少有关,综合考虑计算方法和样本量对评估结果的影响,本研究选择使用结合渔具选择性改进的Beverton-Holt模型对雌性鹰爪虾单位补充量产量的计算结果评估该海域鹰爪虾的资源开发状况。
3.3 鹰爪虾的资源利用状况在保持当前开捕体长不变的情况下应用结合渔具选择性改进的Beverton-Holt模型估算雌性鹰爪虾的F0.1,F0.1作为比较保守的参考点,在渔业管理中被认为比Fmax更具参考价值[31-33]。结果显示,当前的捕捞死亡系数FF(1.886 a-1)大于F0.1(1.833 a-1),当雌性鹰爪虾捕捞死亡系数减小至F0.1时,Y/R从1.963 g降低至1.960 g,仅减少了0.003 g(< 1%),即降低捕捞强度至生物学参考点F0.1时对单位补充量产量造成的损失较小。因此认为应适当降低开发程度,这与之前对东海鹰爪虾资源变动状况的研究[34]结论一致。从单位补充量产量等值线图(见图 9)中可以看出,雌性鹰爪虾当前的开捕体长已接近获得最大单位补充量产量时的开捕体长,所以认为可保持当前开捕体长不变,但考虑到逃逸存活率的问题,为减小拖网捕捞对初孵幼体的影响,在鹰爪虾孵化初期(秋季)捕捞作业时最小网目尺寸的制定需在今后做套网试验进一步研究。
综上,本研究认为海州湾及邻近海域鹰爪虾面临的捕捞压力略大,为保护该海域的鹰爪虾资源,应降低捕捞强度。根据渔业统计年鉴中的数据,鹰爪虾的海洋捕捞产量从2015[35]到2018年[2]逐年下降,2018年的产量相较于2015年下降了超过12万t,减少幅度约为33.07%,反映出我国鹰爪虾资源正日渐衰退。凡守军等[27]曾进行过鹰爪虾的人工繁殖实验,证实了鹰爪虾人工养殖的可行性,但国内目前尚未实现鹰爪虾的产业化人工养殖。为确保鹰爪虾资源的可持续利用,建议在减小捕捞压力的同时发展鹰爪虾的人工养殖产业。
4 结语本研究表明,通过ELEFAN方法得出的鹰爪虾生长方程能够近似描述其体长与年龄的关系,对鹰爪虾开发状况的评估结果显示,当前开发率高于Gulland提出的最适开发率,在对鹰爪虾的单位补充量产量进行估算时,建议使用结合渔具选择性改进的Beverton-Holt模型,分析结果同样表明当前对鹰爪虾的捕捞强度过大,因此建议减小对该海域鹰爪虾的捕捞压力以促进渔业生产的可持续发展。
| [1] |
吴长功, 周令华, 相建海, 等. 鹰爪虾与中国对虾雌虾纳精囊的形态结构[J]. 水产学报, 1999, 23(3): 223-228. Wu C G, Zhou L H, Xiang J H, et al. Morphology and structure of thelycum in Trachypenaeus curvirostris and Penaeus chinensis[J]. Journal of Fisheries of China, 1999, 23(3): 223-228. (  0) 0) |
| [2] |
农业农村部渔业渔政管理局. 2019中国渔业统计年鉴[Z].北京: 中国农业出版社, 2019. Bureau of Fisheries of the Ministry of Agriculture and Rural Affairs of the People's Republic of China. 2019 China Fishery Statistical Yearbook[Z]. Beijing: China Agriculture Press, 2019. (  0) 0) |
| [3] |
Cha H K, Oh C W, Choi J H. Biology of the cocktail shrimp, Trachysalambria curvirostris (Decapoda: Penaeidae) in the Yellow Sea of Korea[J]. Journal of the Marine Biological Association of the United Kingdom, 2004, 84(2): 351-357. DOI:10.1017/S0025315404009270h
(  0) 0) |
| [4] |
Sakaji H, Hayashi K I. A review of the Trachysalambria curvirostris species group (Crustacea: Decapoda: Penaeidae) with description of a new species[J]. Species Diversity, 2003, 8(2): 141-174. DOI:10.12782/specdiv.8.141
(  0) 0) |
| [5] |
章守宇, 张焕君, 焦俊鹏, 等. 海州湾人工鱼礁海域生态环境的变化[J]. 水产学报, 2006, 30(4): 475-480. Zhang S Y, Zhang H J, Jiao J P, et al. Change of ecological environment of artificial reef waters in Haizhou Bay[J]. Journal of Fisheries of China, 2006, 30(4): 475-480. (  0) 0) |
| [6] |
黄六一, 陈燕, 高慧良, 等. 坛子网方形网目逃逸窗选择性研究[J]. 中国海洋大学学报(自然科学版), 2018, 48(9): 15-23. Huang L Y, Chen Y, Gao H L, et al. Study on selectivity of square mesh escape window of Tanzi net[J]. Periodical of Ocean University of China, 2018, 48(9): 15-23. (  0) 0) |
| [7] |
Oh T Y, Choi J H, Cha H K, et al. Maturation and growth of Trachysalambria curvirostris in the coastal water of Geomundo, Korea[J]. Bulletin of the Korean Society of Fisheries Technology, 2003, 39(2): 120-127. DOI:10.3796/KSFT.2003.39.2.120
(  0) 0) |
| [8] |
叶孙忠, 张壮丽, 叶泉土, 等. 闽东北外海鹰爪虾数量的时空分布及其生物学特性[J]. 福建水产, 2012, 34(2): 141-146. Ye S Z, Zhang Z L, Ye Q T, et al. The quantitative distribution and biological characteristics of Trachypenaeus curvirostris in northeast Fujian outer-sea[J]. Journal of Fujian Fisheries, 2012, 34(2): 141-146. (  0) 0) |
| [9] |
Mildenberger T K, Taylor M H, Wolff M. TropFishR: An R package for fisheries analysis with length-frequency data[J]. Methods in Ecology and Evolution, 2017, 8(11): 1520-1527. DOI:10.1111/2041-210X.12791
(  0) 0) |
| [10] |
詹秉义. 渔业资源评估[M]. 北京: 中国农业出版社, 1995. Zhan B Y. Fishery Stock Assessment[M]. Beijing: China Agricultural Press, 1995. (  0) 0) |
| [11] |
Pauly D, David N. ELEFAN I, a BASIC program for the objective extraction of growth parameters from length-frequency data[J]. Berichte der Deutschen Wissenschaftlichen Kommission für Meeresforschung, 1981, 28(4): 205-211.
(  0) 0) |
| [12] |
Schwamborn R, Mildenberger T K, Taylor M H. Assessing sources of uncertainty in length-based estimates of body growth in populations of fishes and macroinvertebrates with bootstrapped ELEFAN[J]. Ecological Modelling, 2019, 393: 37-51. DOI:10.1016/j.ecolmodel.2018.12.001
(  0) 0) |
| [13] |
Taylor M H, Mildenberger T K. Extending electronic length frequency analysis in R[J]. Fisheries Management and Ecology, 2017, 24(4): 330-338. DOI:10.1111/fme.12232
(  0) 0) |
| [14] |
陈国宝, 李永振, 陈丕茂, 等. 鱼类最佳体长频率分析组距研究[J]. 中国水产科学, 2008, 15(4): 659-666. Chen G B, Li Y Z, Chen P M, et al. Optimum interval class size of length-frequency analysis of fish[J]. Journal of Fishery Sciences of China, 2008, 15(4): 659-666. (  0) 0) |
| [15] |
Kleiber P, Pauly D. Graphical representations of ELEFAN I response surfaces[J]. Fishbyte, 1991, 9(2): 45-49.
(  0) 0) |
| [16] |
Pauly D. A review of the ELEFAN system for analysis of length-frequency data in fish and aquatic invertebrates[C].// Pauly D, Morgan G R. Length-Based Methods in Fisheries Research. Manila: ICLARM Conference Proceedings, 1987, 13: 7-34.
(  0) 0) |
| [17] |
张树德, 宋爱勤. 鹰爪虾及其渔业[J]. 生物学通报, 1992(11): 12-14. Zhang S D, Song A Q. Trachypenaeus curvirostris (Stimpson) and its fishery[J]. Bulletin of Biology, 1992(11): 12-14. (  0) 0) |
| [18] |
Pauly D. Some simple methods for the assessment of tropical fish stocks[J]. FAO Fisheries Technical Paper, 1983(234): 1-52.
(  0) 0) |
| [19] |
Pauly D. On the interrelationships between natural mortality, growth parameters, and mean environmental temperature in 175 fish stocks[J]. ICES Journal of Marine Science, 1980, 39(2): 175-192.
(  0) 0) |
| [20] |
Sparre P, Venema S C. Introduction to tropical fish stock assessment. Part 1. Manual[J]. FAO Fisheries Technical Paper, 1998, 306(1): 1-407.
(  0) 0) |
| [21] |
Beverton R J H, Holt S J. Manual of methods for fish stock assessment. Part 2. Tables of yield functions[J]. FAO Fisheries Technical Paper, 1996(38): 1-67.
(  0) 0) |
| [22] |
Pauly D, Soriano M L. Some practical extensions to Beverton and Holt's relative yield-per-recruit model[C].// Maclean J L, Dizon L B, Hosillo L V. The First Asian Fisheries Forum. Manila: Asian Fisheries Society, 1986: 491-496.
(  0) 0) |
| [23] |
Gayanilo Jr F C, Sparre P, Pauly D. FAO-ICLARM Stock Assessment Tools Ⅱ (FiSAT Ⅱ). User's guide[J]. FAO Computerized Information Series (Fisheries), 2005(8): 1-168.
(  0) 0) |
| [24] |
张树德. 黄渤海鹰爪虾Trochypenaeus curvirostris (Stimpson)种群结构特征的初步研究[J]. 生态学报, 1990, 10(2): 145-149. Zhang S D. Preliminary study on population structure of Trachypenaeus curvirostris (Stimpson) in Huanghai and Bohai Seas[J]. Acta Ecologica Sinica, 1990, 10(2): 145-149. (  0) 0) |
| [25] |
Deriso R B. Optimal F0.1 criteria and their relationship to maximum sustainable yield[J]. Canadian Journal of Fisheries and Aquatic Sciences, 1987, 44: 339-348. DOI:10.1139/f87-335
(  0) 0) |
| [26] |
Ueta Y. Reproduction and growth of Trachypenaeus curvirostris (Penaeidae, Decapoda, Crustacea) in Kii Channel[J]. Aquaculture Science, 1987, 35(3): 161-169.
(  0) 0) |
| [27] |
凡守军, 周令华, 于奎杰, 等. 鹰爪虾人工繁殖技术研究[J]. 海洋科学, 1999, 23(3): 1-3. Fan S J, Zhou L H, Yu K J, et al. Studies on breeding and propagation techiniques for Trachypenaeus curvirostris[J]. Marine Sciences, 1999, 23(3): 1-3. (  0) 0) |
| [28] |
Gulland J A. The Fish Resources of the Ocean[M]. Surrey: Fishing News Books, 1971.
(  0) 0) |
| [29] |
Silvestre G T, Soriano M, Pauly D. Sigmoid selection and the Beverton and Holt yield equation[J]. Asian Fisheries Science, 1991, 4(1): 85-98.
(  0) 0) |
| [30] |
Pauly D. Beyond our original horizons: The tropicalization of Beverton and Holt[J]. Reviews in Fish Biology and Fisheries, 1998, 8(3): 307-334. DOI:10.1023/A:1008863215253
(  0) 0) |
| [31] |
Hilborn R, Walters C J. Quantitative Fisheries Stock Assessment: Choice, Dynamics and Uncertainty[M]. London: Chapman and Hall, 1992.
(  0) 0) |
| [32] |
曹少鹏, 刘群. 把不确定性引入生物学参考点F0.1和Fmax的估计以评估东海带鱼渔业资源[J]. 南方水产, 2007, 3(2): 42-48. Cao S P, Liu Q. Stock assessment of the hairtail (Trichiurus haumela) fishery in the East China Sea by incorporating uncertainty into the estimation of the biological reference points F0.1 and Fmax[J]. South China Fisheries Science, 2007, 3(2): 42-48. (  0) 0) |
| [33] |
童玉和, 陈新军, 田思泉, 等. 渔业管理中生物学参考点的理论及其应用[J]. 水产学报, 2010, 34(7): 1040-1050. Tong Y H, Chen X J, Tian S Q, et al. Theory and application of biological reference points in fisheries management[J]. Journal of Fisheries of China, 2010, 34(7): 1040-1050. (  0) 0) |
| [34] |
宋海棠, 俞存根, 姚光展. 东海鹰爪虾的数量分布和变动[J]. 海洋渔业, 2004, 26(3): 184-188. Song H T, Yu C G, Yao G Z. Study on biomass distribution and variation of Trachypenaeus curvirostris in East China Sea[J]. Marine Fisheries, 2004, 26(3): 184-188. (  0) 0) |
| [35] |
农业部渔业渔政管理局. 2017中国渔业统计年鉴[Z].北京: 中国农业出版社, 2017. Bureau of Fisheries of the Ministry of Agriculture of the People's Republic of China. 2017 China Fishery Statistical Yearbook[Z]. Beijing: China Agriculture Press, 2017. (  0) 0) |
 2020, Vol. 50
2020, Vol. 50


