2. 四川大学水力学与山区河流开发保护国家重点实验室, 四川 成都 610065
开孔沉箱能够有效降低结构的反射系数和波浪力,并降低工程造价,因此在港口工程中经常被用于修建防波堤和码头。开孔沉箱防波堤最早由Jarlan[1]在1960年代提出,基本结构型式是在实体直立墙前放置一道开孔墙,在开孔墙和实体墙之间形成消浪室。在实际应用中,为了提高防波堤的消浪效果,经常采用多消浪室开孔沉箱结构。
许多学者研究了波浪作用下开孔沉箱的反射特性。Tanimoto等[2]早期通过物理模型试验研究了不规则波作用下开孔沉箱结构的反射系数。Suh等[3]将理论分析和物理模型试验相结合,研究了不规则波作用下开孔沉箱防波堤的反射系数,发现:当消浪室宽度与消浪室内有效波长之比约为0.2时,防波堤具有最优消浪效果。Takahashi等[4]利用流体体积函数(VOF)法数值分析了开孔沉箱防波堤的反射特性。Kondo[5]发展了一种解析模型,可以计算单消浪室和双消浪室开孔沉箱的反射系数。Li等[6-7]利用匹配特征函数法,建立了斜向波对单消浪室和双消浪室开孔沉箱防波堤作用的解析解。Bergmann[8]利用大尺度物理模型试验,研究了单消浪室和多消浪室开孔沉箱的反射特性。Twu和Lin[9]对实验水槽中多消浪室开孔消浪装置的反射系数进行了理论分析,发现:开孔板数量、开孔板间距以及开孔率是影响结构反射系数的主要因素。赵洋等[10]基于线性势流理论,建立了波浪与多消浪室局部开孔沉箱防波堤相互作用的理论模型,分析了不同影响因素对结构反射特性的影响规律。Neelamani等[11]通过物理模型试验,研究了不规则波作用下多消浪室开孔沉箱结构的反射特性。以上研究工作主要集中在理论分析与物理模型试验方面,主要研究开孔沉箱结构的反射系数,关于开孔沉箱周围流场特性和消浪机理的数值分析不足。特别是,针对波浪与多消浪室开孔沉箱相互作用的数值研究成果报道较少,有必要开展进一步的数值分析工作,深入理解多消浪室开孔沉箱的消浪特性。
本文通过建立二维波浪数值水槽,对多消浪室开孔沉箱的消浪特性进行数值分析。首先将开孔沉箱前波面和反射系数的数值分析结果与物理模型试验结果进行对比分析,验证数值水槽的合理性。之后,基于数值分析结果,研究开孔沉箱的反射特性,分析单消浪室和多消浪室开孔结构附近的速度矢量和湍流强度分布。研究结果对深入理解开孔沉箱的消浪机理具有借鉴意义,可为开孔沉箱的工程设计提供参考依据。
1 数学模型采用不可压缩粘性流体的Navier-Stokes(N-S)方程作为控制方程,同时考虑湍流运动,引入时均化概念,得到基于雷诺平均的N-S方程:
| $ \frac{\partial \bar{u}_{i}}{\partial x_{i}}=0, $ | (1) |
| $ \begin{array}{c} \frac{\partial \bar{u}_{i}}{\partial t}+\bar{u}_{j} \frac{\partial \bar{u}_{i}}{\partial x_{j}}= \\ -\frac{1}{\rho} \frac{\partial \bar{p}}{\partial x_{i}}+g_{i}+\frac{1}{\rho} \frac{\partial}{\partial x_{j}}\left(\mu\left(\frac{\partial \bar{u}_{i}}{\partial x_{j}}+\frac{\partial \bar{u}_{j}}{\partial x_{i}}\right)-\rho \overline{u_{i}^{\prime} u_{j}^{\prime}}\right) \end{array} $ | (2) |
式中:对于二维流体运动,
为了封闭上述方程,引入k-ε湍流模型[12],湍动能k和湍动能耗散率ε的方程为如下形式:
| $ \begin{array}{c} \frac{\partial k}{\partial t}+\bar{u}_{j} \frac{\partial k}{\partial x_{j}}=\frac{\partial}{\partial x_{j}}\left[\left(\frac{\nu_{t}}{\sigma_{k}}+\nu\right) \frac{\partial k}{\partial x_{j}}\right]+ \\ \nu_{t}\left(\frac{\partial \bar{u}_{i}}{\partial x_{j}}+\frac{\partial \bar{u}_{j}}{\partial x_{i}}\right) \frac{\partial \bar{u}_{i}}{\partial x_{j}}-\varepsilon ,\end{array} $ | (3) |
| $ \begin{array}{l} \frac{\partial \varepsilon}{\partial t}+\bar{u}_{j} \frac{\partial \varepsilon}{\partial x_{j}}=\frac{\partial}{\partial x_{j}}\left[\left(\frac{\nu_{t}}{\sigma_{\varepsilon}}+\nu\right) \frac{\partial \varepsilon}{\partial x_{j}}\right]+ \\ C_{1 \varepsilon} \frac{\varepsilon}{k} \nu_{t}\left(\frac{\partial \bar{u}_{i}}{\partial x_{j}}+\frac{\partial \bar{u}_{j}}{\partial x_{i}}\right) \frac{\partial \bar{u}_{i}}{\partial x_{j}}-C_{2 \varepsilon} \frac{\varepsilon^{2}}{k} 。\end{array} $ | (4) |
式中:
对于自由表面运动,采用流体体积法(Volume of Fluid,VOF)进行追踪,流体体积函数F的基本方程为:
| $ \frac{\partial F}{\partial t}+\bar{u}_{i} \frac{\partial F}{\partial x}=0 。$ | (5) |
式中,F函数定义为网格内流体体积与网格总体积之比。F = 1,为流体单元;F = 0,为空单元;0 < F < 1,为混合单元,即确定自由表面单元。
本文数值模型采用交错网格法和有限差分法对计算区域进行离散,并用两步映射法求解雷诺平均N-S方程,具体离散格式及求解技术可见Lin[13]。
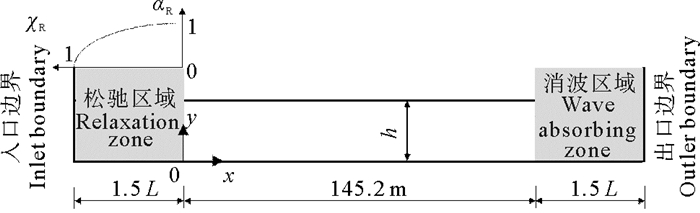
2 数值波浪水槽设置 2.1 边界条件和初始条件参照Bergmann[8]的大水槽物理模型试验,建立如图 1所示的二维波浪数值水槽。坐标原点O取在松弛区域右端和水槽底部的交界面处。水槽底部满足无滑移边界条件。在自由表面处,忽略空气和法向应力的影响,采用简化的边界条件:
| $ \frac{\partial \bar{u}_{\tau}}{\partial x_{n}}=0, \bar{p}=0 。$ | (6) |
|
图 1 数值波浪水槽示意图 Fig. 1 Sketch of numerical wave flume |
式中,下标n和τ为自由表面的外法线方向和切向方向。水槽计算域总长度为3.0 L + 145.2 m(L为波长),高度为7.0 m。左侧为造波区域,采用边界造波方法,在左侧入口边界处输入随时间变化的波面和速度条件。采用二阶斯托克斯造波理论,入口边界处波面η和速度uit为:
| $\eta=A \cos \sigma t+\frac{A^{2} k}{4} \frac{\cosh k h(2+\cosh 2 k h)}{\sinh ^{3} k h} \cos 2 \sigma t ,$ | (7) |
| $ \left\{\begin{array}{l} u_{1 t}=A \sigma\left[\frac{\cosh k(y+h)}{\sinh k h} \cos \sigma t+\frac{3 A k}{4} \frac{\cosh 2 k(y+h)}{\sinh ^{4} k h} \cos 2 \sigma t\right] \\ u_{2 t}=A \sigma\left[\frac{\sinh k(y+h)}{\sinh k h} \sin \sigma t+\frac{3 A k}{4} \frac{\sinh 2 k(y+h)}{\sinh ^{4} k h} \sin 2 \sigma t\right] \end{array}\right.。$ | (8) |
式中:A为振幅;k为波数;σ为圆频率。为消除造波边界处的二次反射,在造波边界前方设置长度为1.5 L的松弛区域[14]。通过调整松弛区域内的速度值,实现入口边界处的无反射造波。松弛区域内的速度满足:
| $ \bar{u}_{i}=\left(1-\alpha_{R}\right) u_{i t}+\alpha_{R} \bar{u}_{i c}, i=1,2 。$ | (9) |
式中:
| $ \alpha_{R}=1-\frac{\exp \left(\chi_{R}^{3.5}\right)-1}{\exp (1)-1}, 0 \leqslant \chi_{R} \leqslant 1。$ | (10) |
水槽右侧为开放边界,并在前侧设置1.5 L消波区域,用来消除出口处的波浪反射。
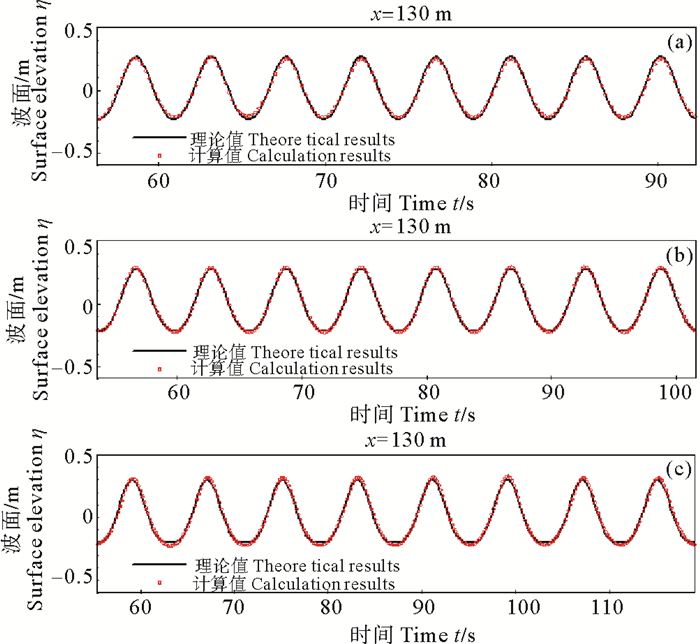
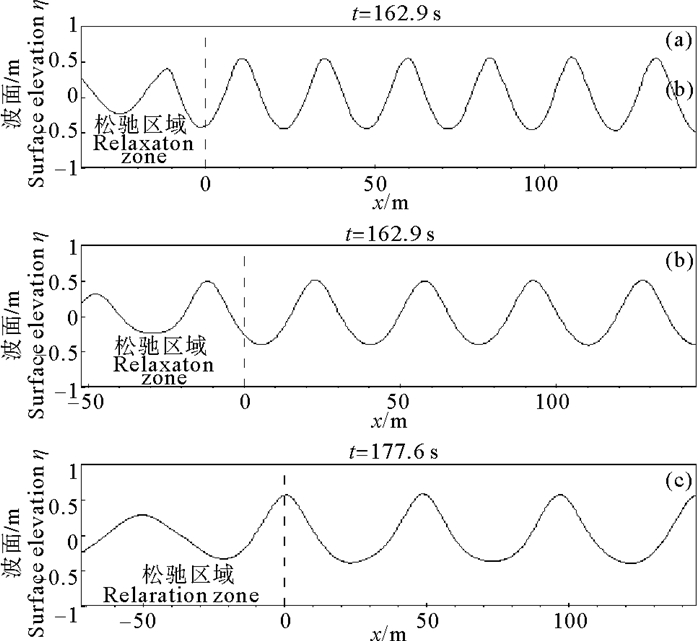
2.2 数值造波经网格收敛性验证,在整个计算区域内划分横向网格尺度为Δ x = 0.3 m,纵向网格尺度为Δ y = 0.02 m。图 2给出数值水槽计算域内x = 130 m位置处,不同波要素条件下,波面历时曲线的计算值与理论值对比。图中实线表示理论值,空心圆点表示本文计算值。由图 2可以看出,计算值与理论值符合良好,数值水槽内能够形成稳定的规则波。将数值水槽中右侧消波区域去掉,出口边界设置为固壁边界(无滑移边界条件),再次进行造波。经过一段长时间模拟后,计算域中沿程波面计算结果如图 3所示。从图 3可以看出,波浪传播到固壁边界产生反射后,在松弛区域前的计算域内形成了稳定的波形图,且叠加后的波高接近于2倍入射波高。说明加入松弛区域后能够有效消除造波边界处的二次反射。
|
( (a)H=0.5 m、T=4.5 s;(b)H=0.5 m、T=6.0 s;(c)H=0.5 m、T=8.0 s。) 图 2 波面历时曲线的计算值与理论值对比 Fig. 2 Comparison of time series between calculation and theoretical results |
|
( (a)H=0.5 m、T=4.5 s;(b)H=0.5 m、T=6.0 s;(c)H=0.5 m、T=8.0 s ) 图 3 末端全反射数值水槽中的计算波形图 Fig. 3 Wave elevation of standing wave in numerical wave flume |
本节将开孔沉箱前波面和反射系数的数值计算结果与Bergmann[8]的大水槽物理模型试验结果进行对比,验证数值模型的合理性,并基于数值模拟结果分析开孔沉箱的消浪特性。
3.1 计算参数设置Bergmann[8]试验中,开孔沉箱后实墙高度为6.0 m,宽度为0.18 m,无越浪现象发生。考虑4种不同的单消浪室开孔沉箱(结构1和2)和多消浪室开孔沉箱(结构3和4)。开孔沉箱开孔形状为矩形横条开孔,单消浪室开孔沉箱的前墙开孔率为e = 20%,消浪室宽度(开孔前墙到后实墙之间的距离)分别为B = 4.8和7.8 m。多消浪室开孔沉箱包括3个消浪室(3排开孔墙):沿入射波的传播方向,3排开孔墙的开孔率依次为e1 = 26.5%、e2 = 20%和e3 = 11%;3个消浪室的宽度依次为B1 = 2.8 m、B2 = 4.4 m、B3 = 7.8 m和B1 = 7.3 m、B2 = 4.3 m、B3 = 3.4 m;消浪室的总宽度为B = 15 m。设置水深为h = 4.0 m,波高为H = 0.5 m,周期为T = 4.5 s、6.0 s、8.0 s和12.0 s。数值试验参数与物理模型试验参数一致,列于表 1。
|
|
表 1 开孔沉箱试验参数 Table 1 Test parameters of perforated caisson |
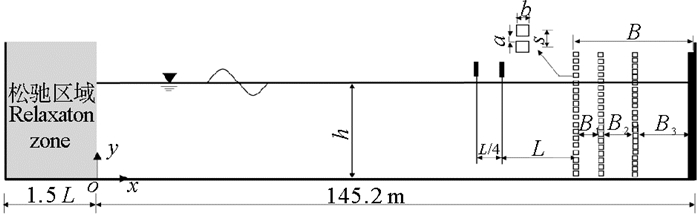
数值模拟过程中,波浪与开孔沉箱相互作用,不发生越浪,为节约计算时间,去掉消波区域,将开孔沉箱放置在水槽右端,并在开孔沉箱部分进行横向网格加密,最小横向网格尺度为Δ x = 0.18 m,纵向网格尺度为Δ y = 0.02 m。在水槽中,距离开孔沉箱第一排开孔墙1.0 L和1.25 L处设置2支数值波高仪记录波面时间历程线,并采用Goda和Suzuki[15]方法分析反射系数。图 4为数值波浪水槽中多消浪室开孔沉箱和波高仪布置图。
|
图 4 数值波浪水槽中多消浪室开孔沉箱和波高仪布置图 Fig. 4 Sketch of multi-chamber perforated caisson and wave gauge in numerical flume |
本小节对波面的数值模拟结果进行分析,将开孔沉箱内外波面最值(最大值和最小值)的计算结果与Bergmann[8]的模型试验结果进行对比验证。
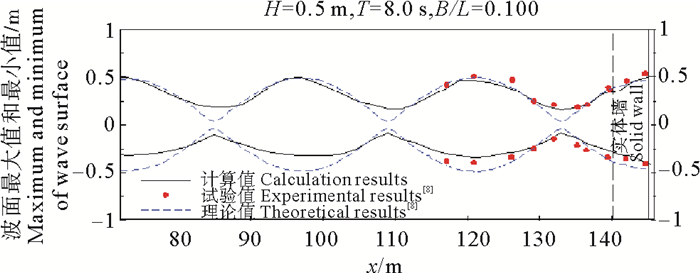
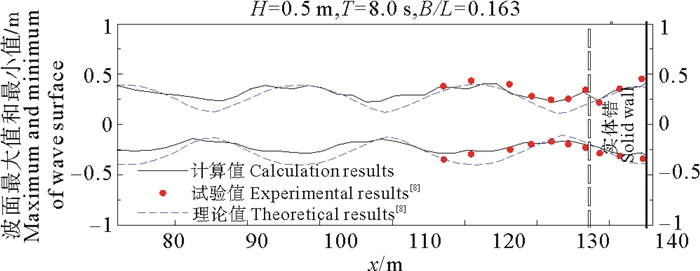
图 5、6分别给出H = 0.5 m、T = 8.0 s时,单消浪室开孔沉箱(结构1和结构2)内外波面最值分布的数值计算结果与Bergmann[8]试验结果对比。
|
图 5 开孔沉箱内外波面最大值和最小值分布(结构1,B = 4.8 m) Fig. 5 Maximum and minimum of wave surface elevation inside and outside perforated caisson (Structure 1, B = 4.8 m) |
|
图 6 开孔沉箱内外波面最大值和最小值分布(结构2,B = 7.8 m) Fig. 6 Maximum and minimum of wave surface elevation inside and outside perforated caisson (Structure 2, B = 7.8 m) |
图中,实线表示本文数值计算结果,圆点表示Bergmann[8]试验结果。为便于对比分析,将Bergmann[8]给出的波面最值分布理论值(基于线性理论叠加)也绘于图 5、6(虚线)。从图中可以看出:波腹与波节点位置的数值模拟结果与Bergmann[8]试验结果和理论结果基本一致。但是,由于波浪的非线性作用,波面最值在波节处的数值计算结果与Bergmann[8]理论值存在一定偏差,但与Bergmann[8]试验结果符合较好。进一步对比图 5、6可以发现:结构2(见图 6)消浪室内外波面最值的变化幅值小于结构1(见图 5)的变化值,说明在此波浪条件下,结构2(相对消浪室宽度为0.163)的消浪效果优于结构1(相对消浪室宽度为0.1)。
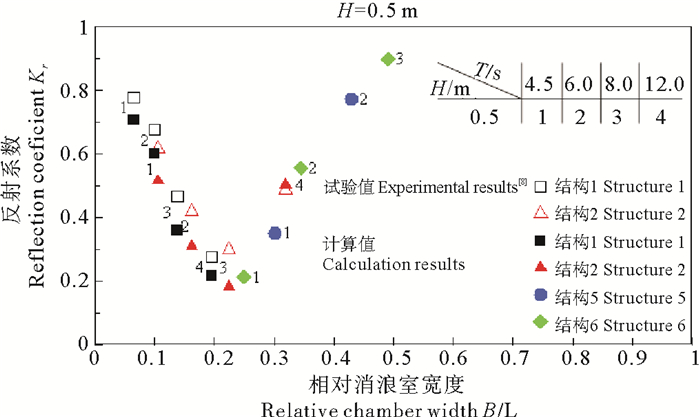
3.2.2 反射系数图 7给出单消浪室开孔沉箱反射系数计算结果与Bergmann[8]试验结果的对比,图中纵坐标为反射系数Kr,横坐标为相对消浪室宽度B/L。从图 7可以看出:反射系数的数值计算结果略小于试验结果,但两者总体符合较好。除了数值和试验结果的对比算例外,进一步数值分析了消浪室宽度B1 = 10.5 m(结构5)和B1 = 12.0 m(结构6)两种算例,并将数值计算结果也绘于图 7。由图 7中可知:对于单消浪室开孔沉箱而言,随着相对消浪室宽度的增大,反射系数先减小后增大,且在B/L ≈ 0.2时,反射系数达到最小值。
|
图 7 单消浪室开孔沉箱反射系数的计算值与试验值对比 Fig. 7 Comparsion of reflection coefficient by single-chamber perforated caisson between calculation and experimental results |
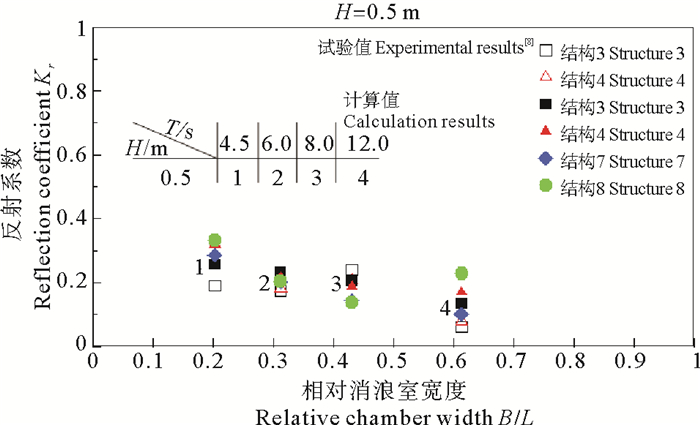
图 8给出多消浪室开孔沉箱反射系数计算结果与试验结果的对比,可以看出两者符合较好,且同一波要素条件下,结构1和结构2反射系数结果相近。对比图 7、8发现:与单消浪室开孔沉箱不同,当相对消浪室宽度从0.2开始增加时,多消浪室开孔沉箱的反射系数呈减小趋势;同一波浪条件下,多消浪室开孔沉箱的反射系数低于单消浪室开孔沉箱的反射系数。为了明确开孔沉箱消浪室内部开孔板间距变化对消浪效果的影响,保持消浪室总宽度和各开孔板开孔率不变,进一步考虑消浪室宽度B1 = 5.0 m、B2 = 5.0 m(结构7)和B1 = 9.4 m、B2 = 4.4 m (结构8)两种算例,并将其反射系数的数值计算结果绘于图 8。从图 8中可以看出:同一波要素下,结构3(B1 = 2.8 m)、结构4(B1 = 7.3 m)、结构7(B1 = 5.0 m)和结构8(B1 = 9.4 m)的反射系数相差不明显。这说明当多消浪室开孔沉箱的开孔率和消浪室总宽度确定后,单纯改变各消浪室宽度,对结构消浪效果的影响不明显。
|
图 8 多消浪室开孔沉箱反射系数的计算值与试验值对比 Fig. 8 Comparsion of reflection coefficient by multi-chamber perforated caisson between calculation and experimental results |
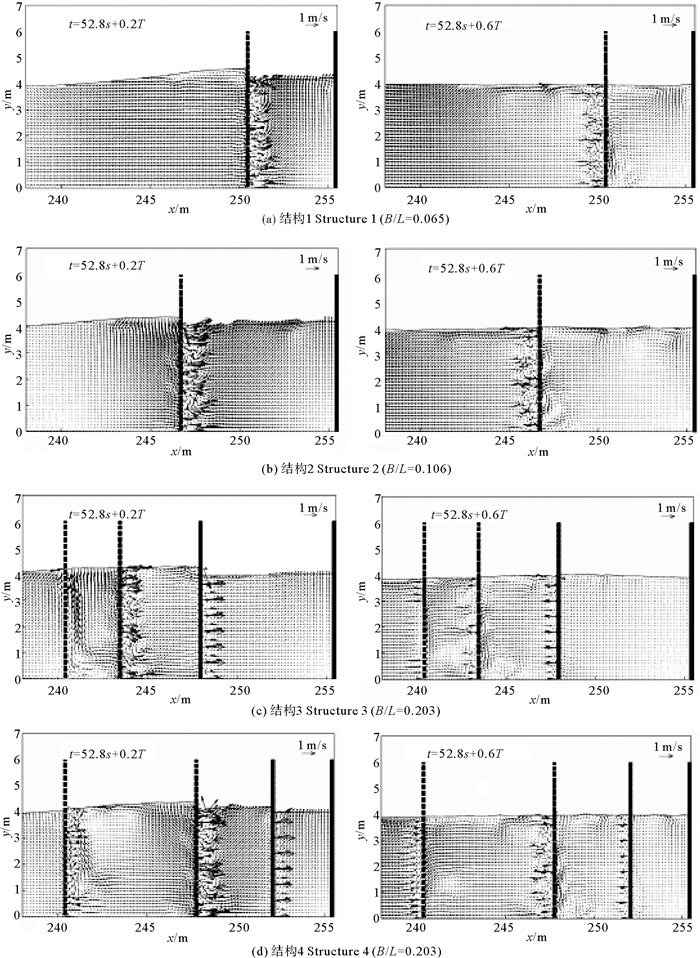
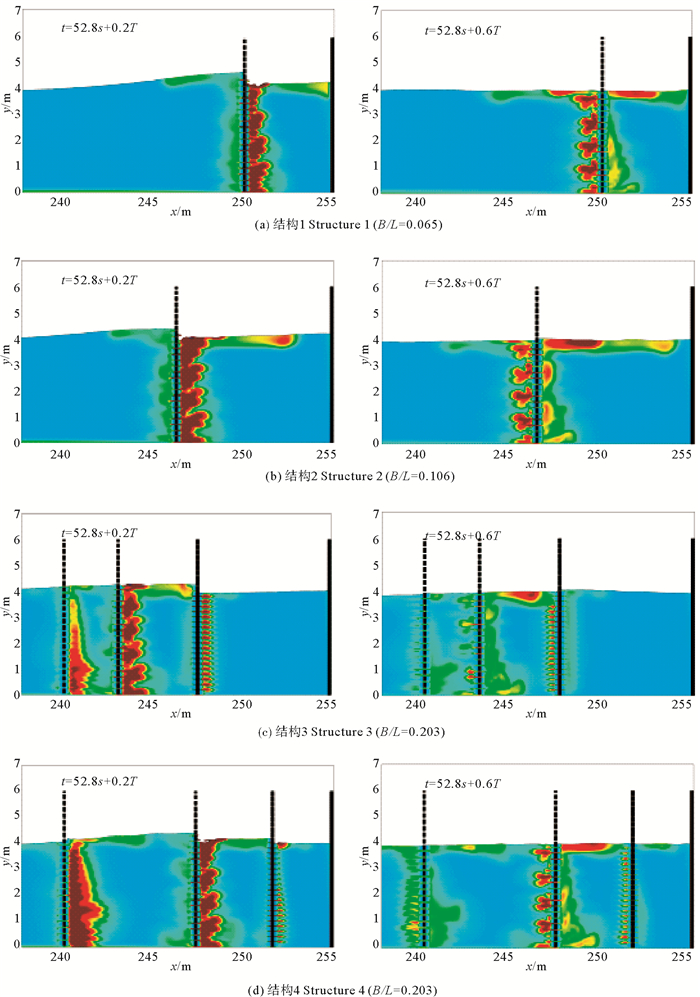
本节以波高H = 0.5 m、周期T = 12.0 s的入射波条件为例,分析开孔沉箱附近的速度矢量和湍流强度分布。
图 9给出4种不同开孔沉箱结构附近的速度矢量分布,可以看出:波浪与单消浪室开孔沉箱相互作用时(结构1和结构2),由于开孔墙的存在,波浪以射流形式进出消浪室,并在开孔墙内外两侧形成涡旋;此外,在消浪室内部靠近自由表面附近也存在较大涡旋。波浪与多消浪室开孔沉箱相互作用时(结构3和结构4),涡旋主要集中在各开孔墙以及第2个消浪室内部自由表面附近。
|
图 9 开孔沉箱附近速度矢量分布(H=0.5 m,T=12.0 s) Fig. 9 Distribution of velocity vector around the perforated caisson (H=0.5 m, T=12.0 s) |
图 10给出4种不同开孔沉箱结构附近的湍流强度分布,湍流强度用I=(2k)1/2表示。从图 10可以看出:波浪与单消浪室开孔沉箱(结构1和结构2)相互作用时,湍动主要分布在开孔墙和消浪室内部自由表面附近;与单消浪室开孔沉箱相比,多消浪室沉箱在各开孔墙周围都存在较大的湍流强度,从而有效耗散波浪能量,进一步降低结构的反射系数。对比图 10(c)和10(d),可以看出:由于开孔沉箱内部开孔墙的位置发生变化,湍流强度大小与分布也随之发生改变,不过湍动仍主要集中在开孔墙和消浪室内部自由表面附近;此外,结合图 8的分析结果可知,尽管这两种结构的湍流强度分布不同,但是结构的反射系数(总的波能耗散)接近。
|
图 10 开孔沉箱附近湍流强度分布(H=0.5 m,T=12.0 s) Fig. 10 Distribution of turbulence intensity around the perforated caisson (H=0.5 m, T=12.0 s) |
本文通过求解雷诺平均Navier-Stokes方程和湍流模型k-ε方程,并引入松弛区域,建立了无反射数值波浪水槽,模拟了波浪与多消浪室开孔沉箱的相互作用,分析了开孔沉箱结构的消浪特性。将开孔沉箱前波面变化和反射系数的数值计算结果与试验结果进行了对比,符合良好。研究结果表明:
(1) 波浪与开孔沉箱相互作用时,涡旋和湍动主要集中在开孔墙和消浪室内部自由表面附近;
(2) 对于单消浪室开孔沉箱,当相对消浪室宽度B/L≈0.2时,反射系数达到最小值;
(3) 对于多消浪室开孔沉箱,当B/L > 0.2时,反射系数随着相对消浪室宽度的增加进一步减小;
(4) 与单消浪室开孔沉箱相比,多消浪室开孔沉箱通过增加消浪室总宽度和开孔墙的数量,进一步耗散波浪能量,降低结构的反射系数。
| [1] |
Jarlan G E. A perforated vertical wall breakwater[J]. Dock Harbour Auth, 1961, 41: 394-398.
(  0) 0) |
| [2] |
Tanimoto K, Haranaka S, Takahashi S, et al. An experimental investigation of wave reflection, overtopping and wave forces for several types of breakwaters and sea walls[C]. // Ministry of Transport. Tokyo: Tech Note of Port and Harbour Res Inst, 1976.
(  0) 0) |
| [3] |
Suh K D, Park J K, Park W S. Wave reflection from partially perforated-wall caisson breakwater[J]. Ocean Engineering, 2006, 33(2): 264-280. DOI:10.1016/j.oceaneng.2004.11.015
(  0) 0) |
| [4] |
Takahashi S, Kotake Y, Fujiwara R, et al. Coastal Engineering 2002—Performance evaluation of perforated-wall caissons by VOF numerical simulations[C]. // World Scientific Publishing Company. Cardiff, Wales: World Scientific Publishing Company Proceedings of the 28th, 2003: 1364-1376.
(  0) 0) |
| [5] |
Kondo H. Analysis of breakwaters having two porous walls[C]. // American Society of Civil Engineers. Virgiain: Proc Coastal Structures' 79, 1979: 962-977.
(  0) 0) |
| [6] |
Li Y C, Liu H J, Teng B, et al. Reflection of oblique incident waves by breakwaters with partially-perforated wall[J]. China Ocean Engineering, 2002, 16(3): 329-342.
(  0) 0) |
| [7] |
Li Y, Dong G, Liu H, et al. The reflection of oblique incident waves by breakwaters with double-layered perforated wall[J]. Coastal Engineering, 2003, 50(1-2): 47-60. DOI:10.1016/j.coastaleng.2003.08.001
(  0) 0) |
| [8] |
Bergmann H. Hydraulische Wirksamkeit und Seegangsbelastung Senkrechter Wellenschutzbauwerke mit Durchlässiger Front[D]. German, Braunschweig: Mitteilungen aus dem Leichtweiss-Institut, 2000.
(  0) 0) |
| [9] |
Twu S W, Lin D T. Wave reflection by a number of thin porous plates fixed in a semi-infinitely long flume[C]. // American Society of Civil Engineers. Delft, Netherlands: 22nd International Conference on Coastal Engineering, 1990.
(  0) 0) |
| [10] |
赵洋, 刘勇, 李华军. 多消浪室局部开孔沉箱防波堤反射特性的理论研究[C]. 舟山: 第十八届中国海洋(岸) 工程学术讨论会论文集(下), 2017: 1044-1048. Zhao Y, Liu Y, Li H J. A Theoretical Study of Wave Reflection with Multi-Chamber Partially-Perforated Caisson Breakwaters[C]. Zhoushan: Proceedings of the 18th China Ocean (Ashore) Engineering Symposium (Part Ⅱ), 2017: 1044-1048. (  0) 0) |
| [11] |
Neelamani S, Al-Salem K, Taqi A. Experimental investigation on wave reflection characteristics of slotted vertical barriers with an impermeable back wall in random wave fields[J]. Journal of Waterway, Port, Coastal and Ocean Engineering, 2017, 143(4): 06017002. DOI:10.1061/(ASCE)WW.1943-5460.0000395
(  0) 0) |
| [12] |
Lin P, Liu P L F. A numerical study of breaking waves in the surf zone[J]. Journal of Fluid Mechanics, 1998, 359: 239-264. DOI:10.1017/S002211209700846X
(  0) 0) |
| [13] |
Lin P. Numerical Modeling of Breaking Waves[D]. Ithaca, NY: Cornell University, 1998.
(  0) 0) |
| [14] |
Jacobsen N G, Fuhrman D R, Fredsøe J. A wave generation toolbox for the open-source CFD library: OpenFoam[J]. International Journal for Numerical Methods in Fluids, 2012, 70(9): 1073-1088. DOI:10.1002/fld.2726
(  0) 0) |
| [15] |
Goda Y, Suzuki Y. Estimation of incident and reflected waves in random wave experiments[C]. // American Society of Civil Engineers. Honolulu, Hawaii: 15th International Conference on Coastal Engineering, 1977: 828-845.
(  0) 0) |
2. State Key Laboratory of Hydraulics and Mountain River Engineering, Sichuan University, Chengdu 610065, China
 2021, Vol. 56
2021, Vol. 56


