2. 浙江大学海洋学院,浙江 舟山 316021;
3. 宁波大学海运学院,浙江 宁波 315211
溃坝,即坝体溃决,是水利工程中一种典型的灾害性水流现象。当坝体由于某种原因发生溃决时,大量水体瞬间失控释放并急剧下泄,形成以涌波形式向下游急速传播的洪水,对下游地区生命、财产造成灾难性损害[1]。近几十年来,全球发生了多起重大溃坝事故,造成了极为严重的人员伤亡和财产损失[2]。预测溃坝自由液面、水深和波浪的演变对减少生命损失和洪水损害具有重要意义。
早期关于溃坝问题的研究主要以理论和物理模型试验为主,随着计算机和数值方法的发展,数值模拟已被证明是一种研究溃坝水流演进的有效手段并被广泛运用[3]。溃坝问题是具有代表性的自由液面大变形流动问题,准确捕捉溃坝过程中的自由液面是模拟该问题的关键,国内外很多研究者对此进行了研究。Kocaman等[4-8]针对溃坝后的复杂水流行为进行了一系列模型试验和数值模拟,为后续研究者提供了较多基准模型。Issakhov等[9]采用VOF法结合离散相模型和宏观颗粒模型对溃坝水流中宏观颗粒在水面的运动进行了数值模拟。Soleimani等[10]采用δ-SPH方法模拟了不同障碍物下双液体溃坝的诱导混合过程。文献[11]中提到,Sheu采用Level-Set法模拟了三维溃坝的流动过程。张永祥等[12]建立了基于CE/SE格式的溃坝洪水波计算模型。缪吉伦等[13]采用SPH法模拟了立面二维溃坝的流动问题,并对下游不同障碍物挑流和消能进行了初步分析。廖斌等[14]采用NASA-VOF法对溃坝水流冲击丁坝的流场进行了数值模拟。郑仙佩等[15]采用SWE-SPH法对下游为湿河床的溃坝水流进行了数值模拟。通过调研可知,目前在溃坝自由液面的数值模拟中,基于欧拉法的VOF模型和基于拉格朗日法的SPH模型是应用最为广泛的两种模型。
作为一种不稳定、快速变化的复杂流动,溃坝除了导致大量人员伤亡和破坏之外,还会产生强烈的洪水波,引起泥沙输送,导致地貌侵蚀和快速变化[16]。溃坝波的传播过程中,水流的形态、最大深度以及波传播速度将很大程度上取决于下游通道的不规则外貌。当河道中存在码头、桥墩等建筑物时,溃坝水流的前进同样会受到阻碍,并在建筑物附近形成绕射和反射流场,严重影响洪水的下泄;另外,建筑物本身也会受到溃坝水流的强烈冲击,建筑物的强度和稳定性将受到严峻的考验[17]。目前已有不少针对不同障碍物下溃坝流动的研究,但对于水流和障碍物的相互作用机理以及障碍物对溃坝波影响的分析仍不够透彻。基于此,本文考虑单一液体的溃坝问题,针对坝体下游具有不同外形障碍物的情况,采用VOF法构建相应的二维简化数值模型,研究不同外形障碍物与溃坝水流之间的相互作用和影响,并分析溃坝中自由液面大变形复杂流动问题的作用机理。本文还给出了闸门抽出与下游带有湿床两种情况的溃坝仿真结果,以期得到一些有价值的结论。
1 数学模型的建立 1.1 控制方程对于二维溃坝水流模拟,其控制方程可以由不可压缩流体的N-S方程组建立。
对于连续性方程:
| $ \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0 \text { 。} $ | (1) |
对于动量方程:
| $ \left\{\begin{array}{l} \frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}+v \frac{\partial u}{\partial y}=f_x+\mu\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}\right)-\frac{1}{\rho} \frac{\partial p}{\partial x} \\ \frac{\partial v}{\partial t}+u \frac{\partial v}{\partial x}+v \frac{\partial v}{\partial y}=f_y+\mu\left(\frac{\partial^2 v}{\partial x^2}+\frac{\partial^2 v}{\partial y^2}\right)-\frac{1}{\rho} \frac{\partial p}{\partial y} \end{array}\right. \text { 。} $ | (2) |
式中:u、v为流体的速度分量;t为时间;fx、fy为体积加速度分量;μ为流体运动黏滞系数;ρ为流体密度;p为流体压强。
1.2 VOF法VOF(Volume of fluid)方法是建立在欧拉网格下的界面追踪方法,根据各个时刻流体在单元网格内所占的体积百分比函数F来追踪构造自由液面。在某一时刻,当F=1时,表示该网格单元内充满指定流体。当F=0时,说明该网格单元内充满另一种流体(本文中为空气)。相比于F=1时的单网格元,该网格单元也被称为空单元。当0 < F < 1时,在该网格单元上存在气液交界面。VOF方法的数学原理为:
定义函数f(x, y, t)为:
| $ f(x, y, t)= \begin{cases}1 & (\text { 在 }(x, y) \text { 处有指定流体质点 }) \\ 0 & (\text { 在 }(x, y) \text { 处无指定流体质点 })^{\circ}\end{cases} $ | (3) |
式中:函数f是随流场变化运动的,F是f在计算单元中的平均值,即:
| $ {F_{i, j}} = \frac{1}{{\Delta {S_{i, j}}}}\iint\limits_{\Delta {S_{i, j}}} {(x, y, t){\rm{d}}x{\rm{d}}y} 。$ | (4) |
守恒形式的传输方程为:
| $ \frac{\partial f}{\partial t}+\frac{\partial(u f)}{\partial x}+\frac{\partial(v f)}{\partial y}=0 \text { 。} $ | (5) |
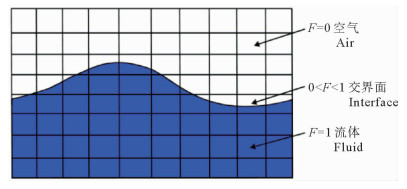
由于体积百分比函数F在交界面的法向上变化最快,因此在确定交界面法向和体积百分比函数F的值后,单元中就可以确定一条用来近似表达两种流体交界面的分割线(见图 1)。
|
图 1 VOF模型 Fig. 1 VOF model |
为了提高自由界面的计算精度,可以对自由界进行重构。VOF法凭借存储量小、计算简单、追踪界面精细等优点,深受广大CFD工作者的喜爱,在众多界面追踪技术中越来越占据主流地位。
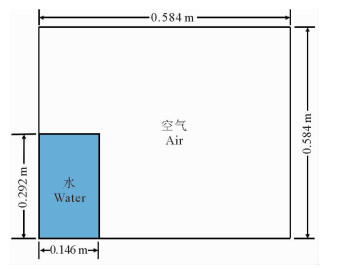
2 下游有不同形状障碍物的单一液体溃坝模拟 2.1 基础计算模型参数为了与模型试验形成充分对比并验证可靠性,数值模拟的计算模型尺寸通常与模型试验的尺寸保持一致[18]。图 2是下游不带有任何障碍物的溃坝基础计算模型,后续不同形状障碍物的模型计算均基于此模型。
|
图 2 溃坝基础计算模型 Fig. 2 Dam-break foundation calculation model |
整个计算域为0.584 m×0.584 m的方形容器,给定溃坝水柱长0.146 m,静水深0.292 m,初始状态放置在容器的左下角,计算开始后水柱将在重力的作用下向下游流动。
2.2 基础溃坝计算模型的网格划分与边界条件根据几何模型进行网格划分。二维网格的类型有四边形、三角形和多边形等,其中四边形网格节点分布规则,奇异点个数少,布局合理,且网格边能够自然的与矩形计算域的特征边对齐,因此在本文采用四边形网格。网格边的尺寸为1.25 mm,矩形边上的网格层数约470层,二维网格的总数量约22万,如图 3所示,矩形计算域的左侧、右侧和底部的边界条件给定无滑移的壁面,顶部给定压力出口。由于正方形计算域顶部连通大气,因此计算域的初始压力与大气压相等。

|
图 3 二维网格 Fig. 3 Two-dimensional grid |
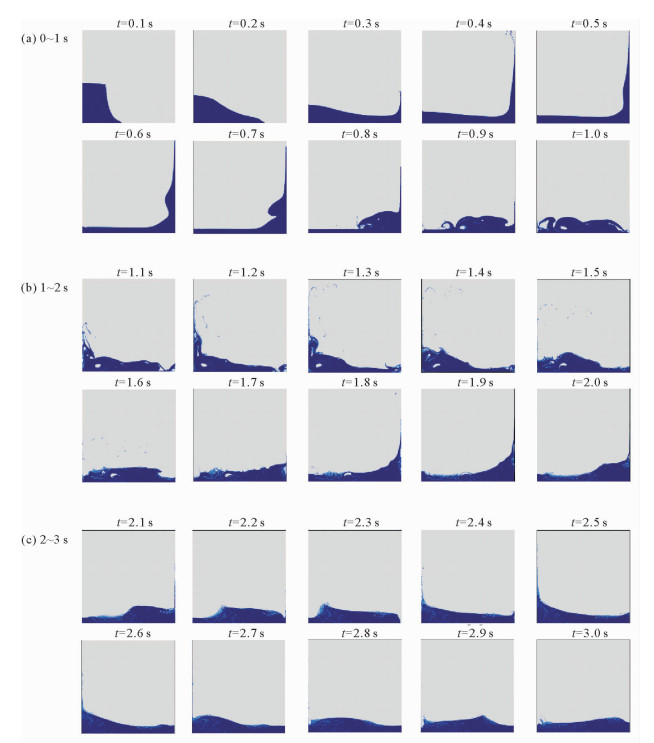
截取0~3 s内典型时刻的自由液面进行分析。由图 4可以看出,下游不带有任何障碍物的溃坝流程可以大致分为四个阶段:第一阶段是从水柱开始下落直至前流到达容器右壁;第二阶段考虑水流与容器右壁的相互作用,包括由重力作用造成的回流和惯性作用导致的流体沿壁向上和向下的运动;第三阶段,从回流第一次弹射回左侧墙面到第二次触碰容器右壁;第四阶段,水流在重力和能量损耗的双重作用下逐渐平稳。
|
图 4 0~3 s内典型时刻的自由液面 Fig. 4 Free surface at typical time in 0~3 s |
第一阶段是整个溃坝的最开始阶段,水流在重力的作用下开始下坠,水体在高速向右运动的同时水位迅即下降。由于与空气接触的最右侧水流的下坠速度远大于贴近墙壁一侧的水流速度,因此水体上端的自由液面从最开始的直线形状变成微微向上拱起的弧形。上游水体在重力的作用下向下游水体挤压,从而在水柱的最右端形成一段较长的向下弯曲的弧形自由液面,该弧形自由液面会在水体下坠的过程中逐渐展平。t=0.25 s时,高速运动的水流前端到达矩形容器的右壁后猛烈撞击壁面并向上爬升,同时整个溃坝过程也进入第二阶段。
溃坝第二阶段,水流沿壁面向上爬升的过程中,不断有水珠从最前端水流脱落出来。t=0.5 s时,水流沿壁面爬升的速度逐渐降低为零,此后在重力的作用下快速跌落翻卷。下落水体撞击到底部向右运动的水面上产生多个大小和形状不一的气泡,同时撞击作用使底部水面和坠落水体的接触部分弹射出一股向左运动的水流,这是底部水面的第一次水跃现象。受到下跌水体的阻碍作用,容器底部向右运动的水体粒子未抵达壁面就产生了第二次水跃,高度较之前大大减小。水流形成的过程中,不断有水珠从中分离又坠回到水流中。水流一边翻卷一边向左做加速运动,当t=1 s时,撞击到容器左壁,这是水体第一次返回到左侧墙壁。
溃坝第三阶段,在重力和动能损耗的双重作用下,水体第一次返回并撞击到容器左壁后向上爬升的高度较上一阶段撞击右壁时的高度大大降低,而在爬升的水流中脱落的水滴则越来越多。在撞击右壁的短暂过程中,靠近左侧墙壁的下游水体产生了一个回旋,这种回旋会增大水流的动能损耗,从而使水流的速度大大降低。值得注意的是,在溃坝第二阶段的槽底发生第一次水跃后,水体中产生了一个较大的气泡,该气泡受到周围流动水体的挤压而变形,并跟随水流一起向左运动,直到水流返回容器右壁的过程中该气泡才会逐渐破灭。爬升的水流在坠回的瞬间空气来不及扩散,与下方水体融合并产生多个大小不一的气泡,坠回后水流推动着下游水质点向容器右壁运动,t=1.7 s时,水流抵达至右壁。这就是溃坝过程的第三阶段。
溃坝第四阶段,水体第二次撞击容器右壁时能量越来越低,重力的作用越来越明显。虽然水体仍会在壁面上爬升并产生回流,但无论是跃升的高度还是回流的流量较前两个阶段均大大降低。当1.7 s < t < 3 s时,水流仍会在惯性作用下左右晃动,但最终会因壁面反复撞击导致能量消耗而趋于平稳。
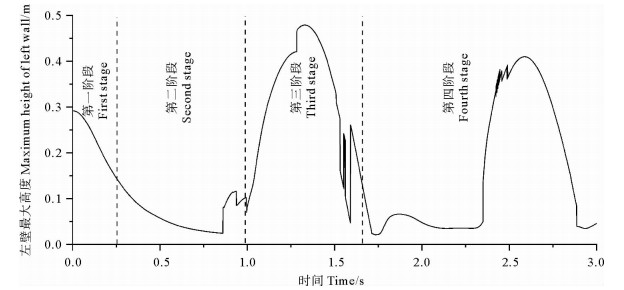
2.3.2 容器左壁的最大高度图 5是容器左壁水柱高度随时间变化的曲线。由图 5可以看出,在溃坝的第一阶段,容器左壁的水柱高度迅速降低,下降水柱的加速度不断增大,在第一阶段结束之前达到最大值。结合图 4可知,t=0.25 s时,水流前段已爬升到容器右壁,此时水柱高度的下落速度明显减缓。t=0.85 s时,容器左壁的水柱高度会有一个小幅度激增,这是水体回流过程中前段产生的分离液珠拍打到左侧壁所造成的结果。t=1 s时,回流的水体已经触碰到容器左壁。当1 s < t < 1.5 s时,左壁上的自由液面高度经历了急速攀升又快速下落的过程。在溃坝过程第三阶段的末期,左壁自由液面的高度有一个反复跳跃的现象,这是由爬升水流前段脱落的水珠又重新吸附到左壁上所形成的。第一次返回容器左壁的水体离开之后,左壁自由液面的高度在很长一段时间内变化微小,直至水体在晃动的过程中又一次返回容器左壁。受到重力和能量损耗的影响,此时自由液面的最大高度较第一次返回时已经有所降低。可以预见,随着时间的推移,左壁自由液面的最大高度会不停降低直到维持在某一固定高度上。
|
图 5 容器左壁的水柱高度变化 Fig. 5 Changes in the height of the water column on the left wall of the container |
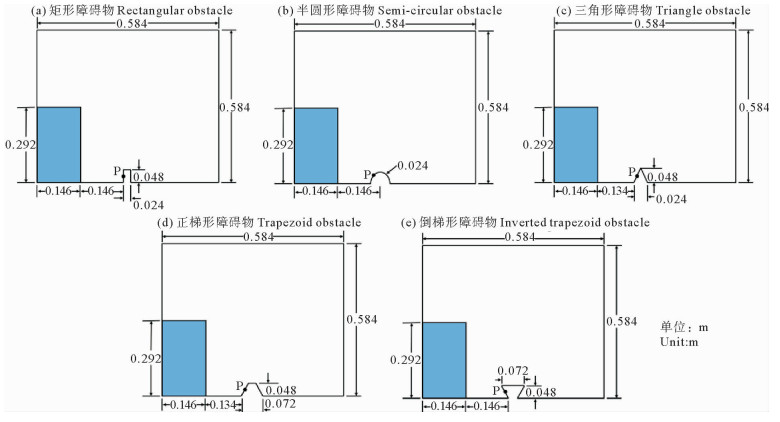
本节选用主视图为矩形、半圆形、三角形、梯形和倒梯形共5种障碍物截面进行计算(下文简称矩形、半圆形、三角形、梯形和倒梯形障碍物),且这几种堤坝都位于下游。为了充分比较不同形状障碍物外形对溃坝水流的影响,在建模过程中最大程度上保证各个障碍物的几何模型的缩尺比保持一致。同时在靠近水流的侧边的一半取一测试点P,用于监测该点随时间的压力变化,反映障碍物的受压情况。图 6是5种障碍物的溃坝计算模型。
|
图 6 不同障碍物计算模型 Fig. 6 Calculation models of different obstacles |
由图 7可以看出,除了下游带有半圆形障碍物的溃坝,其余4种障碍物在0.1~0.5 s的水流演变具有高度的相似性。当t < 0.2 s时,溃坝水流的前沿会抵达障碍物;当t=0.2 s时,水流前沿已经撞击到障碍物。除半圆形障碍物之外,其余4种模型的溃坝水流前端撞击到障碍物后在其右上角转弯,形成一个向右上方行进的水舌。水舌的形状大小以及与水平面形成的夹角取决于障碍物侧壁的高度和坡度。三角形障碍物和正梯形障碍物的侧壁均与水平面有一个坡度,该坡度会降低水流对障碍物的冲击作用,因此三角形障碍物和正梯形障碍物产生的水舌高度和大小均不如矩形障碍物。而倒梯形障碍物的侧壁方向与三角形和正梯形的侧壁方向相反,侧壁对前进的水流有挤压作用,导致前流的部分水体向后运动并和后部水体相互融合。对于圆形障碍物,水流前端并不会像前4种障碍物那样形成水舌,而是在平缓地越过障碍物后,因流动分离在圆形障碍物右半区的底部形成一个封闭的空气区,该区域一直存在到前流爬升左壁的过程,直至前流下坠时才会消失。结合5种障碍物的外形可以看出,形成水舌的4种障碍物前沿均有一个带凸点或尖点的角形区域,水流遭遇到该角形区域会在此处发生剧烈的流动分离,而半圆形障碍物的弧状外形没有突兀的尖点,水体会顺利的从外形上方流通到下游。

|
((从上到下依次为矩形、半圆形、三角形、正梯形和倒梯形。) (From top to bottom, it is rectangular, semi-circular, triangular, regular trapezoid and inverted trapezoid.) ) 图 7 0.1~0.5 s内不同形状障碍物的自由液面流场 Fig. 7 The free surface flow field of obstacles of different shapes in 0.1~0.5 s |
当t=0.3 s时,4种障碍物的水舌继续向右上方延伸,形成鞭状水体,同时不断有水珠从水流前段脱离出来。t=0.4 s时,鞭状水体已撞上容器右壁,在撞击的瞬间空气来不及全部扩散,在水体内形成大小不一的气泡,在重力的作用下水体有沿容器右壁下滑的趋势,而气泡将随水体下滑而扩散出来;与此同时,一些散落的水滴从鞭状水体的下方脱离出来,而在水鞭甩向容器右壁的一瞬间,一条带状水体从障碍物上方的鞭状水体中脱离出来。t=0.5 s时,水体已从容器右壁跌落至容器底部,并与容器底部发生撞击,产生了水珠飞溅的现象。鞭状水体上的大部分水体被后部水体挤压到容器右壁上,同时后部水体持续撞击容器右壁,使水体中的气泡有所增加。与容器右壁撞击的水体一部分沿右壁向下流动,一部分向障碍物流动。半圆形障碍物的水体在0.1 s < t < 0.5 s时,流动状况与图 4中的流动状况比较类似,即水体前段绕过半圆形障碍物后沿容器右壁向上爬升(见图 7)。
当0.6 s < t < 1.0 s时,不同形状障碍物的溃坝水流在容器右侧的区域内的流动变得混乱且无序。后部水体持续不断地越过障碍物,与撞击在容器右壁上的水体相互碰撞,期间有大量水珠从中飞溅出来。从容器右壁下坠并流向障碍物的水体在拍打到障碍物顶部时,受到顶部给水体的作用力后又将翻卷着流回容器左壁。三角形障碍物的受力前端是一个尖点,理论上其与水流之间的相互作用力最小;矩形和梯形的顶部面积相同,因此两者在此刻的自由液面流动变化也大致相当;倒梯形拥有面积最大的受力端,水体在该处的上升幅度最小。对于半圆形障碍物,弧状外形使得水体流经此处时不会像流经前几种障碍物那样发生剧烈的流动而分离,大部分水体只会因障碍物的阻碍作用产生小幅度翻卷(见图 8)。

|
图 8 0.6~1.0 s内不同形状障碍物的自由液面流场 Fig. 8 The free surface flow field of obstacles of different shapes in 0.6~1.0 s |
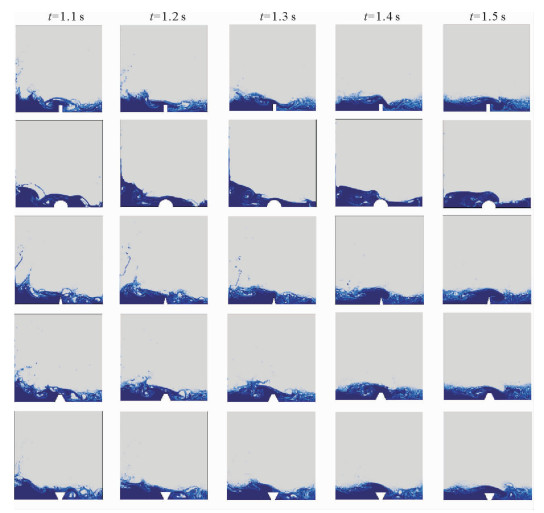
由图 9、10可以看出,由于下游存在障碍物,溃坝水流无论是从第一次返回容器左壁到第二次抵达右壁的时间,还是液体在容器内往返晃动的频率都比不带有障碍物的情况小很多。虽然在水流第一次接触障碍物的前1 s内,自由液面在容器右侧区域变形十分剧烈,但在此后的时间里水体在受到障碍物的阻碍作用后流动逐渐平缓,水流与障碍物撞击的过程中能量被不断耗散。当t>2 s时,5种障碍物溃坝水流的自由液面已经基本趋于平稳。
|
图 9 1.1~1.5 s内不同形状障碍物的自由液面流场 Fig. 9 The free surface flow field of obstacles of different shapes in 1.1~1.5 s |

|
图 10 1.6~2.0 s内不同形状障碍物的自由液面流场 Fig. 10 The free surface flow field of obstacles of different shapes in 1.6~2.0 s |
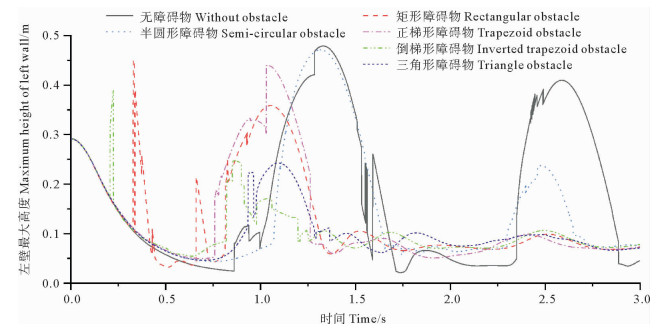
图 11是不同形状障碍物的容器左壁处水柱高度随时间的变化曲线。当t=0.5 s时,各个障碍物的水柱高度变化规律基本相同,此时溃坝水流均处在匀加速下坠过程中。倒梯形和矩形障碍物在t=0.5 s之前的某一时刻出现高度峰值,这是由于水舌在行进过程中,从最前端的水流脱离出的水滴拍打到容器左壁上所导致的。同矩形障碍物比,倒梯形障碍物的水舌形成时间更早、水舌高度更低,因此,倒梯形障碍物的水柱高度峰值出现时间比矩形更早,峰值比矩形更低。
|
图 11 不同形状障碍物容器左壁的水柱最大高度 Fig. 11 The maximum height of the water column on the left wall of the obstruction container of different shapes |
当0.5 s < t < 1.25 s时,不同形状障碍物水柱高度随时间的变化呈现较大的差异。该阶段是溃坝水流第一次返回容器左壁的过程。对于矩形障碍物,水流在返回左壁的过程中,由水流撞击障碍物产生的小部分水体率先流向容器左壁,造成容器左壁水柱的最大高度在短时间内小幅度升高,随后大量水流抵达容器左壁并沿墙壁上爬,造成水柱最大高度的值瞬间增大。受到矩形障碍物的阻碍作用,水流爬升的最大高度比为无障碍物时的高度降低了1/4。三角形障碍物的水柱高度同其他几种类型的障碍物相比,幅值最低。水流前端的水珠爬升速度大于整个水流,且水滴会在墙壁上附着一小段时间,因此反映到图 11中表现为一小段平直的线。梯形障碍物的水流运动到容器左壁上时有一个二次爬升的过程:前进的水流在爬升过程中受到后部分水体挤压,水柱的高度会瞬间增大到最大值。倒梯形障碍物在0.5 s < t < 1.25 s时,水流体左壁最大高度随时间的变化并不像其他4种障碍物的水流一样呈现抛物线状,而是阶梯状,这说明该过程溃坝回流没有直接爬升到容器左壁上,溃坝水流分离的水珠将反复拍打到墙壁上并附着一小段时间,从而形成阶梯状的高度曲线。对于半圆形障碍物在0.5 s < t < 1.25 s时的高度曲线,无论是外形还是幅值,除了在最高点处没有发生跃增现象外,其余状态与无障碍物时的曲线高度相似。当t=2.3 s时,半圆形障碍物的溃坝水流运动像无障碍物时一样,在容器左壁上小幅度爬升,但幅值是无障碍物的1/2,这说明虽然在溃坝水流运动的前半段,半圆形障碍物对水流的阻碍作用十分微弱,但在水流在第一次抵达容器右壁并返回到容器左壁的过程中其仍能一定程度上降低溃坝水流的流速。其他4种障碍物的水流在后半段均趋于平稳,反映到图 11中表现为容器左壁的最大高度在0.1 m以下小幅度波动。
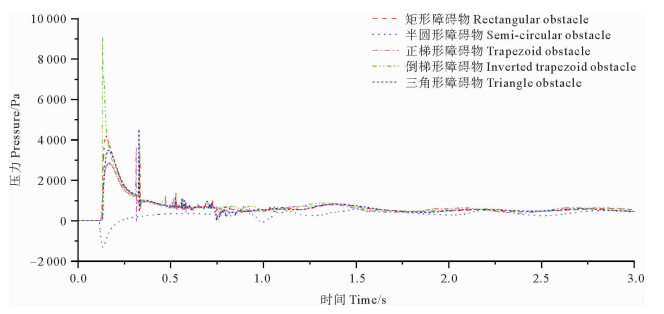
2.4.4 测试点压力图 12是不同形状障碍物测试点P处的压力对比图。由图 12可以看出,测试点P点处的压力值在流动的前1 s内变化最为剧烈。水流在第一次抵达障碍物后,除半圆形外,其余4种障碍物在P处的压力均会瞬间升高。其中,倒梯形障碍物压力升高的幅值远大于矩形、三角形和梯形。这里由于倒梯形坡度的影响,水流对该障碍物的冲击力远大于其他3种。对于半圆形障碍物,水体流经P点后压力反而会降低。水体流过P处后,速度逐渐恢复至正常流速,同时压力也恢复到正常水压值。结合图 7可知当t=0.3 s时,由水流前端形成的水舌撞击到容器右壁上,这一瞬间P点处的流速有一停滞,从而造成了压力值在此刻激增。当0.5 s < t < 1.0 s时,P点处压力值在水流的不规则晃动下不断振动。当t>1.0 s时,水流不断平稳,压力值在波动中逐渐趋于平稳。
|
图 12 不同形状障碍物测试点的压力 Fig. 12 Pressure at test points of obstacles of different shapes |
上文涉及到的溃坝水流问题,初始状态下游均不带有水流(即下游为干床),而对于初始下游湿床情况的溃坝问题也是现在研究的热点之一[15]。本节以Kocaman和Ozmen-Cagatay[7]在2015年进行的下游有湿床的溃坝实验为计算模型来分析下游水流对溃坝自由液面的影响。
2.5.1 有湿床的计算模型下游带有湿床的水槽模型如图 13所示。
|
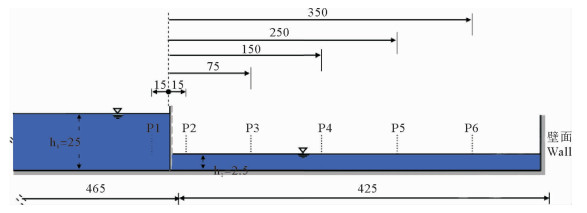
图 13 有湿床计算模型(单位:m) Fig. 13 Calculation model with wet bed(Unit: m) |
溃坝水柱的长4.65 m,高0.25 m,下游水体的长4.25 m,高0.025 m。整个计算域长8.9 m,高0.5 m。Kocaman的模型试验中设置了6个探针,测定6个断面的自由液面高度随时间的变化曲线,本算例依照Kocaman的模型试验在相同的位置设置探针,用来测量自由液面高度随时间变化的情况。
2.5.2 有湿床的计算模型的网格划分下游带湿床计算域的二维网格数量约10万(见图 14)。初始状态下上游水柱和下游湿床的分布如图 15所示。由于水槽计算域顶部连通大气,因此计算域的初始压力也不应该为零,而应与大气压相等。

|
图 14 下游带湿床计算域的二维网格 Fig. 14 Two-dimensional grid with wet bed |

|
图 15 初始状态下上游水柱和下游湿床的分布 Fig. 15 Distribution of upstream water column and downstream wet bed in initial state |
定义无量纲时间:T=t(g/h0)0.5。式中g为重力加速度,取9.81 m/s2。当2.5 < T < 80(间隔2.5)时,自由液面流场分布和演变如图 16~17所示。

|
图 16 2.5 < T < 20的自由液面 Fig. 16 Free surface at 2.5 < T < 20 |

|
图 17 22.5 < T < 40的自由液面 Fig. 17 Free surface at 22.5 < T < 40 |
由图 16可知,溃坝水流在重力的作用下开始运动时,上游水的势能转化为动能向下游流动。当水槽下游有2.5 cm厚的静水时,下游水将阻碍上游水的运动,迫使上游水流以一种类似于卷破波的形式向上运动,在溃坝水流的前端发生明显的卷跃现象,波浪前缘被破坏并在下游形成射流。当T < 5.0(对应物理时间0.79 s)时,在溃坝的初始阶段由下游湿床上的波浪破碎产生的湍流效应导致波前的自由液面上产生了大量的泡沫,水流中掺杂了大量的空气,T>5.0时,空气在随水流运动的过程中逐渐扩散到水槽中。7.5 < T < 15.0时,溃坝波在卷破后,以一种类似于涌浪的波形向前移动,随时间的推移水槽内上下游水位差逐渐降低,导致水流前进速度明显减弱。T=17.5时,(对应物理时间2.79 s)溃坝波抵达水槽右壁,受到壁面的反射后向水槽左壁运动。
当T>22.5时,水面受到右壁面的反射作用形成负波向左运动,此时上下游水位仍存在一个微小的势差迫使上游水体流向右壁。受到墙壁反射的负波和正波相互作用使整个波面的速度下降,同时早期溃坝波的破碎引起的湍流效应在反射波的自由液面上占主导地位,导致反射波前端的波峰将锐化,直至T=35(对应物理时间5.5 s)时出现破波。T>37.5时,上下游的水位差逐渐变为零,反射波在惯性的作用下平缓地向水槽左侧移动(见图 17)。

|
图 18 42.5 < T < 60的自由液面 Fig. 18 Free surface at 42.5 < T < 60 |

|
图 19 62.5 < T < 80的自由液面 Fig. 19 Free surface at 62.5 < T < 80 |
当42.5 < T < 80.0时,水波以一种恒定不变的波形平缓地从水槽的右侧流向左侧。受到上游水体和下游水体的相互挤压,溃坝波回流的过程中在水体前端产生了一个微小的水流凸起,该凸起一直持续到回流撞击到水槽左侧的墙壁。回流抵达左侧壁上动能远小于第一次抵达右壁,因此水流的翻卷程度也大大降低。
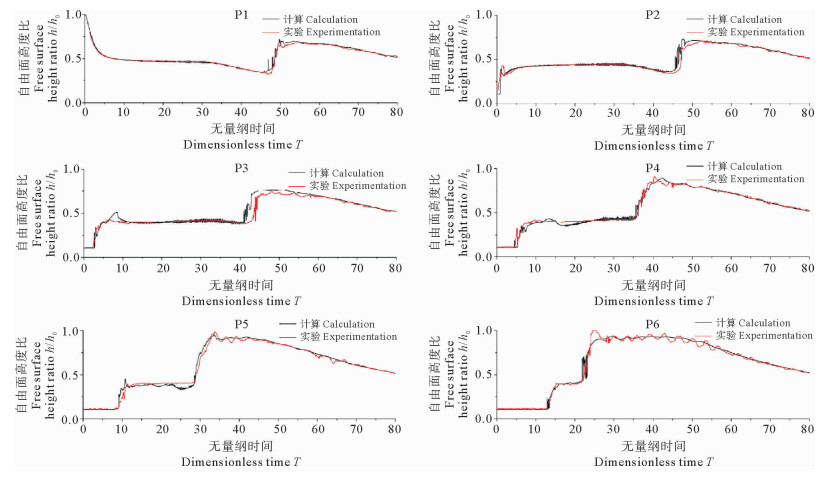
2.5.4 不同位置的自由液面高度变化图 20是6个位置处水位高度随时间的变化曲线,横坐标为无量纲的时间T,纵坐标为瞬时高度h与最大高度h0的比值,红色线代表试验值,黑色线代表计算值。总的来看,6个位置处水位高度的计算值与试验值吻合较好。溃坝开始后,除了P1断面处的自由液面高度会迅速下降之外,其余位置的水位高度均会在溃坝波到达断面后迅速上升,此后在较长的一段时间内水位基本保持不变。P2位置距离上游水柱最近,因此该处的自由液面高度会在溃坝开始后迅速上升,此后在T < 33时,水位高度保持恒定并维持在h/h0=0.43左右。32 < T < 48和33 < T < 46时,P1和P2的水位逐渐下降,然后迅速上升至峰值。各位置处自由液面水位的第二次快速上升是由溃坝波对下游右侧墙壁的反射所产生的反射波引起的。当运动的溃坝波撞击到水槽右侧墙壁后,波在壁面上反射,产生一个深度最大的反射波。反射波在向水槽左壁回流的过程中,到达6个断面后会引起该位置水位的第二次跃升。由溃坝波引起的第一次水位快速上升和由反射波引起的第二次水位快速上升之间的滞后时间向下游(P2~P6)减少,P6处最短。反射波到达上游端后,水位迅速下降。对于P3~P6,水位在第一次快速上升后高度。在保持恒定并维持在h/h0=0.40处,这表明反射波上游的自由表面轮廓是水平的。
|
图 20 6个位置处的高度变化 Fig. 20 Altitude change at 6 positions |
一旦溃坝波冲击到水槽右壁,它就会反射到墙上并到达测量断面,因此,所有测量断面上都会出现波列。波列的振幅随着时间的推移而减小。反射波高度比h/h0在P5和P6处超过1,这可以由向上游方向移动的反射波与向下游方向移动的溃坝波的碰撞以及两者的相互叠加来解释。因此,反射波向上游移动时也会变陡。
靠近下游端壁附近的水面波长小、振幅小,因此出现不明显的波动。在靠近下游水槽右侧墙壁的断面上(P5和P6位置),观测到反射波的时间要比其他断面上的时间早。溃坝波从P2位置运动到P5位置所需的无量纲时间(T)约为9.5,而反射波从P5位置回流到P2位置花费的无量纲时间(T)约为19,因此可以推断出,由于溃坝波抵达水槽右壁后与右壁发生的相互作用导致了波的部分能量损失,使水流的速度降低了约50%。
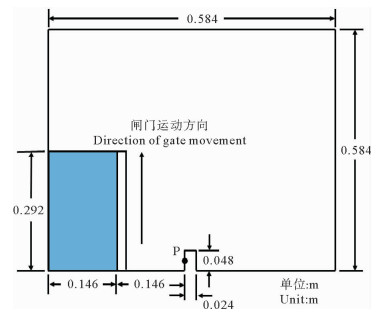
2.6 闸门抽动时的单一液体溃坝模拟与分析 2.6.1 闸门抽动时的溃坝模型本节以前文中下游有矩形障碍物的溃坝模型为例,给出闸门抽动时的溃坝模拟计算流程,同时简单对比闸门抽动对溃坝自由液面流场的影响。带闸门的溃坝计算模型如图 21所示,闸门的运动速度为0.14 m/s,通过重叠网格的平移来实现。重叠域网格数量为3 450,背景域网格数量约8.5万(见图 22)。
|
图 21 带闸门计算模型 Fig. 21 Calculation model with gate |

|
图 22 带闸门的二维网格 Fig. 22 Two-dimensional grid with gate |
闸门对溃坝水流的影响主要集中在闸门抽取的过程中,当闸门脱离水流后悬浮在容器的左上方,此时闸门与水流几乎不发生相互作用。当计算时间大于0.14 s时,闸门平移速度为0,因此本节选取0.15 s之前的溃坝自由液面作为分析对象。
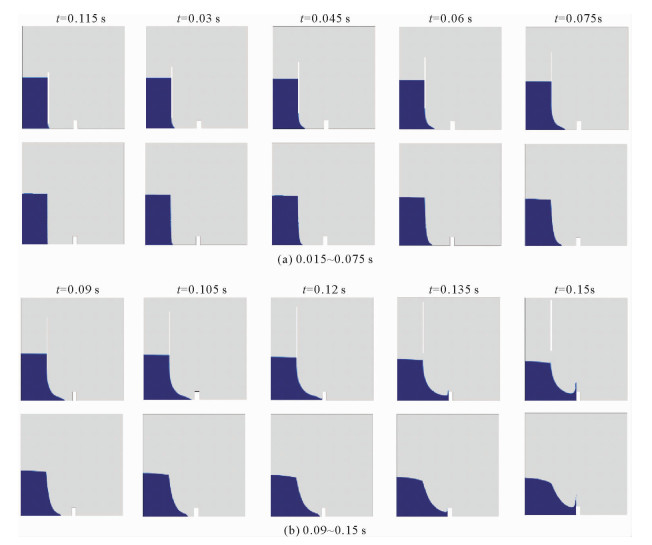
由图 23可以看出,由于受到闸门的挤压约束,在溃坝开始阶段,水柱上游与闸门接触的水体自由液面外形比较固定,在水柱塌陷的过程中自由液面的形状几乎不发生改变。闸门在离开水体之前水体上端的自由液面始终保持直线形状,不会形成拱起的弧形。当闸门离开水体之后,水体不受任何约束的与外界空气接触,在水柱最右端的自由液面受到突然增大的静压力影响而形成一个弯曲程度更大的弧形。
|
图 23 带闸门与不带闸门的自由液面对比 Fig. 23 Free face comparison with and without gate |
闸门平移过程中,水体与闸门之间发生相对滑移作用。从力学的角度上讲,闸门对于水流的作用是向上的,与闸门接触的水体下滑速度有所降低。而闸门平移时水体下部分被瞬间释放,反而会使溃坝水流的最前端更早地抵达矩形障碍物。闸门停止平移后,溃坝过程中飞溅的水珠偶尔会拍打到闸门上(见图 24)但总体上,悬浮的闸门不会对溃坝的后续阶段产生较大的影响。

|
图 24 带闸门溃坝在某一时刻的自由液面 Fig. 24 Free face with gate at certain moment |
下游带有不同形状障碍物的单一液体溃坝仿真结果显示:不同形状障碍物均能对溃坝水流起到一定的阻碍作用,水体在障碍物的角隅处发生的流动分离现象与该处的坡度密切相关;从受压程度上讲,倒梯形障碍物在瞬时状态下受压程度最大,结构强度应是建造该外形障碍物时的首要考虑因素。虽然三角形和梯形障碍物的整体受压程度较其他几种障碍物的整体受压程度低,但其较复杂的外形会给建造的过程带来不便。半圆形障碍物压力变化幅度最小,但该类型的障碍物溃坝水流的阻碍作用甚微。综合来看,矩形障碍物仍是目前用于阻碍溃坝水流的首选之一。
下游有湿床的单一液体溃坝仿真结果显示:下游水将阻碍上游水的运动,迫使上游水流以一种类似于卷破波的形式向上运动,在溃坝水流的前端发生明显的卷跃现象,波浪前缘被破坏并在下游形成射流。
闸门抽动时的单一液体溃坝仿真结果显示:当闸门离开水体之后,水体不受任何约束的与外界空气接触,在水柱最右端的自由液面受到突然增大的静压力影响而形成了弯曲程度更大的弧形;闸门平移过程中,水体与闸门之间发生相对滑移作用。闸门停止运动后,溃坝过程中飞溅的水珠偶尔会拍打到闸门上,但总体上,悬浮的闸门不会对溃坝的后续阶段产生较大的影响。
| [1] |
吴双. 2010年以来美国溃坝统计与分析[J]. 大坝与安全, 2020(5): 61-65. Wu S. Statistics and analysis of dam failures in United States since 2010[J]. Dam and Safety, 2020(5): 61-65. DOI:10.3969/j.issn.1671-1092.2020.05.017 (  0) 0) |
| [2] |
李宏恩, 盛金保, 何勇军. 近期国际溃坝事件对我国大坝安全管理的警示[J]. 中国水利, 2020(16): 19-22, 30. Li H E, Sheng J B, He Y J. Global dam break events raise an alert about dam safety management[J]. China Water Resources, 2020(16): 19-22, 30. (  0) 0) |
| [3] |
黄彬彬, 葛立明, 徐娴, 王悦. HEC-RAS在二维溃坝模拟中的应用——以红旗水库为例[J]. 人民珠江, 2021, 42(5): 73-79. Huang B B, Ge L M, Xu X, Wang Y. Application of HEC-RAS in 2D dam break simulation—A case study of Hongqi Reservoir[J]. Pearl River, 2021, 42(5): 73-79. DOI:10.3969/j.issn.1001-9235.2021.05.010 (  0) 0) |
| [4] |
Yilmaz A, Kocaman S, Demirci M. Numerical modeling of the dam-break wave impact on elastic sluice gate: A new benchmark case for hydroelasticity problems[J]. Ocean Engineering, 2021, 231: 108870. DOI:10.1016/j.oceaneng.2021.108870 (  0) 0) |
| [5] |
Kocaman S, Evangelista S, Guzel H, et al. Experimental and numerical investigation of 3D dam-break wave propagation in an enclosed domain with dry and wet bottom[J]. Applied Sciences, 2021, 11(12): 5638. DOI:10.3390/app11125638 (  0) 0) |
| [6] |
Kocaman S, Dal K. A New Experimental Study and SPH comparison for the sequential dam-break problem[J]. Journal of Marine Science and Engineering, 2020, 8(11): 905. DOI:10.3390/jmse8110905 (  0) 0) |
| [7] |
Kocaman S, Ozmen-Cagatay H. Investigation of dam-break induced shock waves impact on a vertical wall[J]. Journal of Hydrology, 2015, 525: 1-12. DOI:10.1016/j.jhydrol.2015.03.040 (  0) 0) |
| [8] |
Kocaman S, Ozmen-Cagatay H. The effect of lateral channel contraction on dam break flows: Laboratory experiment[J]. Journal of Hydrology, 2012, 432: 145-153. (  0) 0) |
| [9] |
Issakhov A, Imanberdiyeva M. Numerical modelling of the water surface movement with macroscopic particles of dam break flow for various obstacles[J]. Journal of Hydraulic Research, 2020, 59(10): 1-22. (  0) 0) |
| [10] |
Soleimani K, Ketabdari M J. Meshfree modeling of near field two-liquid mixing process in the presence of different obstacles[J]. Ocean Engineering, 2020, 213: 107625. DOI:10.1016/j.oceaneng.2020.107625 (  0) 0) |
| [11] |
Gu Z H, Wen H L, Yu C H, et al. Interface-preserving level set method for simulating dam-break flows[J]. Journal of Computational Physics, 2018, 374: 249-280. DOI:10.1016/j.jcp.2018.07.057 (  0) 0) |
| [12] |
张永祥, 陈景秋. 用守恒元和解元法数值模拟二维溃坝洪水波[J]. 水利学报, 2005(10): 1224-1229. Zhang Y X, Chen J Q. Numerical simulation of 2-D dam-break wave by using conservation element and solution element method[J]. Journal of Hydraulic Engineering, 2005(10): 1224-1229. DOI:10.3321/j.issn:0559-9350.2005.10.015 (  0) 0) |
| [13] |
缪吉伦, 黄成林, 张晓明. 溃坝流动无网格SPH法模拟研究[J]. 中国农村水利水电, 2012(1): 134-136, 140. Miao J L, Huang C L, Zhang Xiaoming. Research on dambreak flow simulation by meshfree SPH method[J]. China Rural Water and Hydropower, 2012(1): 134-136, 140. (  0) 0) |
| [14] |
廖斌, 陈善群. 基于NASA-VOF模型的二维溃坝水流冲击丁坝流场模拟[J]. 安徽工程大学学报, 2012, 27(4): 65-69. Liao B, Chen S Q. Numerical simulation of the collapse of two-dimensional dam-break flow with a dike based on NASA-VOF model[J]. Journal of Anhui Polytechnic University, 2012, 27(4): 65-69. (  0) 0) |
| [15] |
郑仙佩, 顾声龙, 任立群. 基于SWE-SPH的下游为湿河床的溃坝水流模拟[J]. 青海大学学报, 2016, 34(5): 40-44. Zheng X P, Gu S L, Ren L Q. Simulation of dam-break flow with wet bed at downstream based on SWE-SPH[J]. Journal of Qinghai University, 2016, 34(0): 40-44. (  0) 0) |
| [16] |
牟迪, 陈丽芬, 宁德志. 溃坝及其对结构物作用的三维数值模拟研究[J]. 中国造船, 2020, 61(S2): 231-239. Mu D, Chen L F, Ning D Z. Three-D numerical study of interaction between dam-break wave and circular cylinder[J]. Shinbuilding of China, 2020, 61(S2): 231-239. (  0) 0) |
| [17] |
葛立明. 红旗水库溃坝模拟与风险分析[D]. 南昌: 南昌工程学院, 2020. Ge L M. Dam Break Simulation and Risk Analysis of Hongqi Reservoir[D]. Nanchang: Nanchang Institute of Technology, 2020. (  0) 0) |
| [18] |
姚志坚, 彭瑜. 溃坝洪水数值模拟及其应用[M]. 北京: 中国水利水电出版社, 2013. Yao Z J, Peng Y. Numerical Simulation of Dam Break Flood and Its Application[M]. Beijing: China Water & Power Press, 2013. (  0) 0) |
2. Ocean College, Zhejiang University, Hangzhou 316021, China;
3. Faculty of Maritime and Transportation, Ningbo University, Ningbo 315211, China
 2022, Vol. 52
2022, Vol. 52

