收稿日期:2021-04-10;修订日期:2021-05-10
基金项目:山东省重大科技创新工程项目(2019JZZY010301)资助
超大型浮式结构研究对海洋利用和开发具有重要意义[1]。由于此类浮体水平尺寸通常远大于厚度,研究中多将其简化为均质弹性薄板(欧拉板)。Fox和Squire[2]基于线性势流理论发展了波浪作用下半无限浮冰的水弹性响应解析模型。Meylan和Squire[3]采用边界元方法建立了波浪与有限长浮冰相互作用的数值解。对于超大型海洋浮式结构物,通常需要在其端部施加合适的约束,除了自由状态之外的其他端部条件也需要考虑。Sahoo等[4]建立了波浪与半无限漂浮弹性薄板相互作用的解析模型,分别考虑了弹性板的端部自由、简支和固支3种情况。在他们的求解过程中,提出了薄板覆盖水域下的特征函数正交关系,提高了计算结果的精度。Teng等[5]改进了Sahoo等[4]提出的方法,简化了计算步骤,并提高了计算效率。Teng等[6]进一步考虑弹性薄板吃水深度对结构水弹性响应的影响,研究结果表明:在低频入射波情况下,可以忽略吃水深度;但是在高频入射波情况下,吃水深度对水弹性响应的影响较为明显。Guo等[7]基于势流理论研究了不同地形下的斜向波浪与半无限漂浮弹性薄板的相互作用,阐明了波浪发生全反射时的临界入射角度,探讨了地形高度、薄板吃水深度等对弹性板挠度、剪力、弯矩等水动力参数的影响规律。Mohapatra等[8]基于势流理论和薄板理论,建立了波浪与漂浮柔性板或水下柔性板相互作用的一般三维数学模型。
本文研究波浪作用下层合型浮体的水弹性响应,该浮体由上下面板和中间芯材构成。高刚度面板弯曲变形,低刚度芯材剪切变形,芯材密度远小于面板,能够有效减轻浮体整体质量且保持较高的整体刚度。本文结合势流理论与夹芯梁振动理论,采用匹配特征函数展开法建立波浪作用下层合型浮体的水弹性响应分析模型,探讨各层厚度比例、端部约束等对夹芯板水动力参数的影响规律,为海上超大型浮体的实际设计应用提供科学依据。
1 解析模型
1.1 夹芯梁运动理论
考虑由上、下面板和中间芯材构成的夹芯梁,图 1给出单位宽度的夹芯梁截面受力情况。在外荷载作用下,夹芯梁的运动偏微分方程[9]为:
|
$\begin{array}{l}
\;\;\;\;\;\;\;\;\frac{{{\partial ^6}w}}{{\partial {x^6}}} - {G_{\rm{t}}}(1 + Y)\frac{{{\partial ^4}w}}{{\partial {x^4}}} = \\
\frac{1}{{{D_{\rm{t}}}}}\left( {\frac{{{\partial ^2}p}}{{\partial {x^2}}} - {G_{\rm{t}}}\left( { - {m_{\rm{s}}}\frac{{{\partial ^2}w}}{{\partial {t^2}}} + q(x, t)} \right)} \right), \\
{G_{\rm{t}}} = \frac{G}{{{h_2}}}\left( {\frac{1}{{{E_1}{h_1}}} + \frac{1}{{{E_3}{h_3}}}} \right), {D_{\rm{t}}} = {D_1} + {D_3} = \frac{{{E_1}h_1^3}}{{12}} + \frac{{{E_3}h_3^3}}{{12}}, \\
Y = \frac{{{d^2}}}{{{D_{\rm{t}}}}}\left( {\frac{{{E_1}{h_1}{E_3}{h_3}}}{{{E_1}{h_1} + {E_3}{h_3}}}} \right), d = {h_2} + \left( {{h_1} + {h_3}} \right)/2{\rm{。}}
\end{array}$
|
(1) |
式中:ms是夹芯梁的单位面积质量;q为外荷载;h1和h3分别为上面板和下面板厚度;h2为芯材厚度;E1和E3分别为上面板和下面板的弹性模量;G为芯材剪切模量。
关于夹芯梁挠度、弯矩和剪力的计算公式可参阅文献[9]。当夹芯梁做小振幅简谐运动时,分离出时间因子,则有
|
$q(x, t) = Re \left[ {Q(x){{\rm{e}}^{ - i\omega t}}} \right], $
|
(2) |
|
$w(x, t) = Re \left[ {W(x){{\rm{e}}^{ - i\omega t}}} \right], $
|
(3) |
|
$S(x, t) = Re \left[ {\bar S(x){{\rm{e}}^{ - i\omega t}}} \right], $
|
(4) |
|
${M_j}(x, t) = Re \left[ { {{\overline{M}_j}} (x){{\rm{e}}^{ - i\omega t}}} \right]{\rm{。}}$
|
(5) |
式中:Re表示取变量实部;Q(x)表示空间外部荷载;W(x)、S(x)和Mj(x)分别表示空间挠度、剪力和弯矩,均为复数形式;下标j表示夹芯梁的第j层。
将式(2~5)代入式(1),并消去时间因子,可以得到:
|
$\frac{{{\partial ^6}W}}{{\partial {x^6}}} - {G_{\rm{t}}}(1 + Y)\frac{{{\partial ^4}W}}{{\partial {x^4}}} = \frac{1}{{{D_{\rm{t}}}}}\left( {\frac{{{\partial ^2}Q}}{{\partial {x^2}}} - {G_{\rm{t}}}{m_{\rm{s}}}{\omega ^2}W - {G_{\rm{t}}}Q} \right){\rm{。}}$
|
(6) |
|
$\begin{array}{c}
M = {M_1} + {{\bar M}_2} + {M_3} = \\
\frac{{{D_{\rm{t}}}}}{{{G_{\rm{t}}}}}\left[ { - \frac{{{\partial ^4}W}}{{\partial {x^4}}} + {G_{\rm{t}}}(1 + Y)\frac{{{\partial ^2}W}}{{\partial {x^2}}} + \frac{{{m_{\rm{s}}}{\omega ^2}}}{{{D_{\rm{t}}}}}W + \frac{Q}{{{D_{\rm{t}}}}}} \right]{\rm{。}}
\end{array}$
|
(7) |
式中: M1=D1(∂2W/∂x2); M3=D3(∂2W/∂x2)。夹芯梁的剪力为:
|
$\bar S = \frac{{{D_{\rm{t}}}}}{{{G_{\rm{t}}}}}\left[ { - \frac{{{\partial ^5}W}}{{\partial {x^5}}} + {G_{\rm{t}}}(1 + Y)\frac{{{\partial ^3}W}}{{\partial {x^3}}} + \frac{{{m_{\rm{s}}}{\omega ^2}}}{{{D_{\rm{t}}}}}\frac{{\partial W}}{{\partial x}} + \frac{1}{{{D_{\rm{t}}}}}\frac{{\partial Q}}{{\partial x}}} \right]{\rm{。}}$
|
(8) |
上面板的纵向力P1和下面板的纵向力P3为:
|
${P_1} = - {P_3} = \frac{{{D_{\rm{t}}}}}{{{G_{\rm{t}}}d}}\left[ {\frac{{{\partial ^4}W}}{{\partial {x^4}}} - {G_{\rm{t}}}Y\frac{{{\partial ^2}W}}{{\partial {x^2}}} + \frac{{{m_{\rm{s}}}{\omega ^2}}}{{{D_{\rm{t}}}}}W - \frac{1}{{{D_{\rm{t}}}}}Q} \right]{\rm{。}}$
|
(9) |
1.2 边值问题
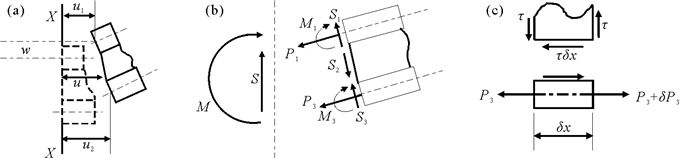
图 2为波浪作用于半无限长夹芯板示意图,忽略夹芯板的吃水。假设流体无黏性、不可压缩,且流体运动无旋,则可以用速度势描述整个流体的运动[10]。考虑圆频率为ω的小振幅正弦波,分离出时间因子,则速度势可以表示为:
|
${\mathit{\Phi}} (x, z, t) = Re \left[ {\varphi (x, z){{\rm{e}}^{ - i\omega t}}} \right]{\rm{。}}$
|
(10) |
式中φ(x, z)表示空间速度势,为复数形式。
整个流体区域划分成2个子区域:左侧的开放水体区域Ω1(x≤0,-h≤z≤0)和夹芯板覆盖的水体区域Ω2(0≤x,-h≤z≤0)。流体的速度势满足拉普拉斯方程和以下边界条件:
|
$\frac{{{\partial ^2}{\varphi _j}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{\varphi _j}}}{{\partial {z^2}}} = 0, (j = 1, 2), $
|
(11) |
|
$\frac{{\partial {\varphi _1}}}{{\partial z}} = \frac{{{\omega ^2}}}{g}{\varphi _1}, z = 0, $
|
(12) |
|
$\frac{{\partial {\varphi _j}}}{{\partial z}} = 0, z = - h, (j = 1, 2), $
|
(13) |
|
$\mathop {\lim }\limits_{x \to - \infty } \left( {\frac{\partial }{{\partial x}} + i{k_0}} \right)\left( {{\varphi _1} - {\varphi _{\rm{I}}}} \right) = 0{\rm{。}}$
|
(14) |
式中:下标j表示流体区域编号;g表示重力加速度;k0表示波数;φI表示入射波的速度势。假设流体与夹芯板之间不存在间隙,则运动学边界条件和动力学边界条件分别为
|
$\frac{{\partial {\varphi _2}}}{{\partial z}} = - i\omega W, z = 0, $
|
(15) |
|
$Q = i\omega \rho {\varphi _2} - \rho gW, z = 0{\rm{。}}$
|
(16) |
式中ρ是流体的密度。将式(15)和式(16)代入式(6),可以得到仅与速度势有关的弹性边界条件:
|
$\begin{array}{c}
\left[ {\frac{{{\partial ^6}}}{{\partial {x^6}}} - {G_{\rm{t}}}(1 + Y)\frac{{{\partial ^4}}}{{\partial {x^4}}} + \frac{{\rho g - {m_{\rm{s}}}{\omega ^2}}}{{{D_{\rm{t}}}}}\left( {\frac{{{\partial ^2}}}{{\partial {x^2}}} - {G_{\rm{t}}}} \right)} \right]\frac{{\partial {\varphi _2}}}{{\partial z}} - \\
\frac{{\rho {\omega ^2}}}{{{D_{\rm{t}}}}}\left( {\frac{{{\partial ^2}}}{{\partial {x^2}}} - {G_{\rm{t}}}} \right){\varphi _2} = 0{\rm{。}}
\end{array}$
|
(17) |
为了求解夹芯板的运动响应,需要在夹芯板端部施加合适的约束,因此本文作者考虑到2种不同约束条件:端部自由和端部简支,数学表达式为
(a) 自由状态:面板的纵向受力为0,即
|
$\left[ {\frac{{{\partial ^4}}}{{\partial {x^4}}} - {G_{\rm{t}}}Y\frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{\rho g - {m_{\rm{s}}}{\omega ^2}}}{{{D_{\rm{t}}}}}} \right]\frac{{\partial {\varphi _2}}}{{\partial z}} - \frac{{\rho {\omega ^2}}}{{{D_{\rm{t}}}}}{\varphi _2} = 0, x = 0{\rm{。}}$
|
(18) |
芯材弯矩为0,即
|
$\begin{array}{c}
\left[ {\frac{{{\partial ^4}}}{{\partial {x^4}}} - {G_{\rm{t}}}(1 + Y)\frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{\rho g - {m_{\rm{s}}}{\omega ^2}}}{{{D_{\rm{t}}}}}} \right]\frac{{\partial {\varphi _2}}}{{\partial z}} - \\
\frac{{\rho {\omega ^2}}}{{{D_{\rm{t}}}}}{\varphi _2} = 0, x = 0{\rm{。}}
\end{array}$
|
(19) |
剪力为0,即
|
$\begin{array}{c}
\left[ { - \frac{{{\partial ^5}}}{{\partial {x^5}}} + {G_t}(1 + Y)\frac{{{\partial ^3}}}{{\partial {x^3}}} - \frac{{\rho g - {m_{\rm{s}}}{\omega ^2}}}{{{D_{\rm{t}}}}}\frac{\partial }{{\partial x}}} \right]\frac{{\partial {\varphi _2}}}{{\partial z}} + \\
\frac{{\rho {\omega ^2}}}{{{D_{\rm{t}}}}}\frac{{\partial {\varphi _2}}}{{\partial x}} = 0, x = 0{\rm{。}}
\end{array}$
|
(20) |
(b) 简支状态:挠度为0,即
|
$\frac{{\partial {\varphi _2}}}{{\partial z}} = 0, x = 0{\rm{。}}$
|
(21) |
面板弯矩为0,即
|
$\frac{{{\partial ^2}\frac{{\partial {\varphi _2}}}{{\partial z}}}}{{\partial {x^2}}} = 0, x = 0{\rm{。}}$
|
(22) |
芯材弯矩为0,即
|
$\left[ {\frac{{{\partial ^4}}}{{\partial {x^4}}} - {G_{\rm{t}}}Y\frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{\rho g - {m_{\rm{s}}}{\omega ^2}}}{{{D_{\rm{t}}}}}} \right]\frac{{\partial {\varphi _2}}}{{\partial z}} - \frac{{\rho {\omega ^2}}}{{{D_{\rm{t}}}}}{\varphi _2} = 0, x = 0{\rm{。}}$
|
(23) |
1.3 速度势求解
满足控制方程(11)和边界条件(12)、(13)和(14)的速度势级数表达式为:
|
$\begin{array}{l}
{\varphi _1} = - \frac{{igH}}{{2\omega }}\left[ {\left( {{{\rm{e}}^{i{k_0}x}} + {R_0}{{\rm{e}}^{ - i{k_0}x}}} \right){Z_0}(z) + } \right.\\
\left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{n = 1}^\infty {{R_n}} {{\rm{e}}^{{k_n}x}}{Z_n}(z)} \right]{\rm{。}}
\end{array}$
|
(24) |
式中:H是入射波的波高;Rn(n≥0)是待定的复展开系数;波数kn满足色散方程:
|
${\omega ^2} = g{k_0}\tanh {k_0}h = - g{k_n}\tan {k_n}h(n \geqslant 1){\rm{。}}$
|
(25) |
Zn(z)是垂向特征函数:
|
$\begin{array}{c}
{Z_0}(z) = \frac{{\cosh {k_0}(z + h)}}{{\cosh {k_0}h}}, \\
{Z_n}(z) = \frac{{\cos {k_n}(z + h)}}{{\cos {k_n}h}}, n \geqslant 1{\rm{。}}
\end{array}$
|
(26) |
满足控制方程(11)、边界条件(13)以及远场辐射边界条件的速度势级数表达式为:
|
${\varphi _2} = - \frac{{igH}}{{2\omega }}\sum\limits_{n = - 2}^\infty {{T_n}} {{\rm{e}}^{ - {\lambda _n}x}}{Y_n}(z){\rm{。}}$
|
(27) |
式中:Tn(n≥-2)是待定的复展开系数;波数λn满足色散方程:
|
$\begin{array}{c}
\left[ {\lambda _n^6 - {G_{\rm{t}}}(1 + Y)\lambda _n^4 + \frac{{\rho g - {m_s}{\omega ^2}}}{{{D_{\rm{t}}}}}\left( {\lambda _n^2 - {G_{\rm{t}}}} \right)} \right]{\lambda _n}\tan {\lambda _n}h = \\
\frac{{\rho {\omega ^2}}}{{{D_{\rm{t}}}}}\left( {\lambda _n^2 - {G_{\rm{t}}}} \right){\rm{。}}
\end{array}$
|
(28) |
Yn(z)是垂向特征函数:
|
${Y_n}(z) = \frac{{\cos {\lambda _n}(z + h)}}{{\cos {\lambda _n}h}}(n \geqslant - 2){\rm{。}}$
|
(29) |
值得注意的是,λ0是式(28)的负纯虚根,对应向右传播的波浪传播模态;λ-2(=α+iβ)和λ-1(=α-iβ)(α>0,β>0)是式(28)的共轭复数根,对应向右传播但幅值不断衰减的传播模态;λn(n≥1)是式(28)的正实根,对应波浪的非传播模态。
在区域交界处(x=0),速度势满足压强连续条件和水平速度连续条件:
|
${\varphi _1} = {\varphi _2}, x = 0, - h \leqslant z \leqslant 0, $
|
(30) |
|
$\frac{{\partial {\varphi _1}}}{{\partial x}} = \frac{{\partial {\varphi _2}}}{{\partial x}}, x = 0, - h \leqslant z \leqslant 0{\rm{。}}$
|
(31) |
将Ω1区域和Ω2区域的速度势表达式代入匹配边界条件(30)和(31),并在式子两边同时乘以特征函数Zm(z),然后对z沿水深积分,可以得到
|
${I_m}{R_m} - \sum\limits_{n = - 2}^\infty {{\Lambda _{nm}}} {T_n} = - {\delta _{m0}}, (m = 0, 1, 2, \cdots ), $
|
(32) |
|
${\tilde k_m}{I_m}{R_m} + \sum\limits_{n = - 2}^\infty {{\lambda _n}} {\Lambda _{nm}}{T_n} = {\tilde k_0}{\delta _{m0}}, (m = 0, 1, 2, \cdots ), $
|
(33) |
|
$
{\Lambda _{nm}} = \int\limits_{ - h}^0 {{Y_n}} (z){Z_m}(z){\rm{d}}z, {I_m} = \int\limits_{ - h}^0 {Z_m^2} (z){\rm{d}}z{\rm{。}}
$
|
式中:δ00=1;δm0=0(m≠0);$ {\tilde k_0}$=-ik0;$ {\tilde k_m}$=km(m≠0)速度势表达式(27)代入端点自由条件(18)~(20)和端点简支条件(21)~(22),得到自由状态:
|
$\begin{array}{l}
\sum\limits_{n = - 2}^\infty {{T_n}} \left[ {{\lambda _n} t a n {\lambda _n}h\left( {\lambda _n^4 - {G_{\rm{t}}}(1 + Y)\lambda _n^2 + } \right.} \right.\\
\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {\frac{{\rho g - m{\omega ^2}}}{{{D_{\rm{t}}}}}} \right) + \frac{{\rho {\omega ^2}}}{{{D_{\rm{t}}}}}} \right] = 0,
\end{array}$
|
(34) |
|
$\begin{array}{l}
\sum\limits_{n = - 2}^\infty {{T_n}} \left[ {{\lambda _n} t a n {\lambda _n}h\left( { - \lambda _n^4 + {G_{\rm{t}}}Y\lambda _n^2 - } \right.} \right.\\
\;\;\;\;\;\;\left. {\left. {\frac{{\rho g - m{\omega ^2}}}{{{D_{\rm{t}}}}}} \right) - \frac{{\rho {\omega ^2}}}{{{D_{\rm{t}}}}}} \right] = 0,
\end{array}$
|
(35) |
|
$\begin{array}{l}
\sum\limits_{n = - 2}^\infty {{T_n}} \left[ {{\lambda _n} t a n {\lambda _n}h\left( {\lambda _n^5 - {G_{\rm{t}}}(1 + Y)\lambda _n^3 + } \right.} \right.\\
\;\;\;\;\;\left. {\left. {\frac{{\rho g - m{\omega ^2}}}{{{D_{\rm{t}}}}}{\lambda _n}} \right) + \frac{{\rho {\omega ^2}}}{{{D_{\rm{t}}}}}{\lambda _n}} \right] = 0{\rm{。}}
\end{array}$
|
(36) |
|
$\sum\limits_{n = - 2}^\infty {{T_n}} {\lambda _n}\tan {\lambda _n}h = 0, $
|
(37) |
|
$\sum\limits_{n = - 2}^\infty {{T_n}} \lambda _n^3\tan {\lambda _n}h = 0, $
|
(38) |
|
$\begin{array}{l}
\sum\limits_{n = - 2}^\infty {{T_n}} \left[ {{\lambda _n} t a n {\lambda _n}h\left( {\lambda _n^4 - {G_{\rm{t}}}Y\lambda _n^2 + } \right.} \right.\\
\;\;\;\;\;\;\;\;\;\left. {\left. {\frac{{\rho g - m{\omega ^2}}}{{{D_{\rm{t}}}}}} \right) + \frac{{\rho {\omega ^2}}}{{{D_{\rm{t}}}}}} \right] = 0
\end{array}$
|
(39) |
将式(32)中的m和n截断到N项,式(33)中的m和n分别截断为N-1项和N项,式(34)~(39)中的n截断到N项,然后联立式(32)和式(33)以及任意端部条件,可以得到含2N+4个未知数的线性方程组,求解方程组便可确定速度势的展开系数Rn和Tn。
1.4 水动力参数
当波浪遇到漂浮夹芯板产生反射和透射,反射系数Kr和透射系数Kt为:
|
${K_{\rm{r}}} = \left| {{R_0}} \right|, $
|
(40) |
|
${K_{\rm{t}}} = \left| {{T_0}\frac{{{\lambda _0}\tanh {\lambda _0}h}}{{{k_0}\tanh {k_0}h}}} \right|{\rm{。}}$
|
(41) |
利用速度势可以计算夹芯板的挠度W(x)、弯矩(x)和剪力(x),具体表达式为:
|
$W(x) = - \frac{{gH}}{{2{\omega ^2}}}\sum\limits_{n = - 2}^\infty {{T_n}} {\lambda _n}\tan {\lambda _n}h, $
|
(42) |
|
$\begin{array}{l}
\bar M(x) = \frac{{{D_{\rm{t}}}}}{{{G_{\rm{t}}}}}\frac{{gH}}{{2\omega ^2}}\sum\limits_{n= - 2}^\infty {{T_n}} \left[ {{\lambda _n} t a n {\lambda _n}h\left( {\lambda _n^4 - } \right.} \right.\\
\left. {\left. {{G_t}(1 + Y)\lambda _n^2 - \frac{{\rho g - {m_{\rm{s}}}{\omega ^2}}}{{{D_{\rm{t}}}}}} \right) + \frac{{\rho {\omega ^2}}}{{{D_{\rm{t}}}}}} \right],
\end{array}$
|
(43) |
|
$\begin{array}{l}
\bar S(x) = \frac{{{D_{\rm{t}}}}}{{{G_{\rm{t}}}}}\frac{{gH}}{{2{\omega ^2}}}\sum\limits_{n = - 2}^\infty {{T_n}} \left[ {{\lambda _n} t a n {\lambda _n}h\left( {\lambda _n^5 - } \right.} \right.\\
\left. {\left. {{G_{\rm{t}}}(1 + Y)\lambda _n^3 - \frac{{\rho g - {m_{\rm{s}}}{\omega ^2}}}{{{D_{\rm{t}}}}}{\lambda _n}} \right) + \frac{{\rho {\omega ^2}}}{{{D_{\rm{t}}}}}} \right]{\rm{。}}
\end{array}$
|
(44) |
无因次挠度、弯矩和剪力定义为
|
${C_{\rm{W}}} = \left| {\frac{{2W}}{H}} \right|, C_{\rm{M}}^ - = \left| {\frac{{2\bar M}}{{\rho gH{h^2}}}} \right|, C_{\rm{S}}^{\overline {\rm{S}} } = \left| {\frac{{2\overline {\rm{S}} }}{{\rho gHh}}} \right|{\rm{。}}$
|
(45) |
2 结果分析与讨论
2.1 收敛性检验
端部自由时,重力加速度为g=9.8 m/s2,流体的密度为1 025 kg/m3,水深为100 m,夹芯板参数为:总厚度1 m,上下面板厚度为0.04 m,弹性模量E1和E3均为192 GPa,芯材厚度为0.92 m,剪切模量G为1.06 GPa。表 1给出不同截断数时夹芯板的反射系数和透射系数,系数随着截断数的增加而逐渐收敛,截断数N=50的计算结果达到4位有效数字精度,因此,在下文计算中截断数均取N=50。
表 1
Table 1
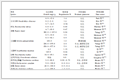
表 1 端部自由状态下夹芯板的反射系数和透射系数随截断数的变化
Table 1 Reflection and transmission coefficient of the structure with free end
截断数N
Truncated number N |
k0h=1 |
|
k0h=4 |
|
k0h=7 |
|
k0h=10 |
| Kr |
Kt |
|
Kr |
Kt |
|
Kr |
Kt |
|
Kr |
Kt |
| 30 |
0.002 8 |
0.993 1 |
|
0.162 1 |
0.539 8 |
|
0.329 2 |
0.314 6 |
|
0.434 6 |
0.219 2 |
| 40 |
0.002 8 |
0.993 1 |
|
0.161 8 |
0.539 9 |
|
0.329 1 |
0.314 6 |
|
0.434 9 |
0.219 1 |
| 50 |
0.002 8 |
0.993 1 |
|
0.161 6 |
0.539 9 |
|
0.329 0 |
0.314 6 |
|
0.435 1 |
0.219 0 |
| 60 |
0.002 8 |
0.993 1 |
|
0.161 6 |
0.539 9 |
|
0.329 0 |
0.314 6 |
|
0.435 1 |
0.219 0 |
| 注:k0h: 无量纲波数。Dimensionless wavenumber. |
|
表 1 端部自由状态下夹芯板的反射系数和透射系数随截断数的变化
Table 1 Reflection and transmission coefficient of the structure with free end |
2.2 极限情况验证
夹芯板上面板和中间芯材的厚度均为零时,浮体退化成单层均质薄板。Teng等[6]基于势流理论研究波浪作用下半无限薄板水弹性响应,采用欧拉梁模型为水面条件。图 3给出退化之后的计算结果与Teng等[6]计算结果的对比,计算中抗弯刚度满足EI/(ρgh4)=0.005,薄板单位面积质量满足ms/(ρh)=0.01,端部自由,2种方法的计算结果符合良好。
2.3 算例分析与讨论
本文作者采用3.1节材料参数,夹芯板总厚度不变,考虑3种不同的芯材厚度:h2=0.92 m、h2=0.96 m和h2=0.98 m。图 4(a)给出3种不同夹芯板端部自由状态下的反射和透射系数随无因次波数k0h的变化:随着波数k0h的增大,反射系数逐渐增大、透射系数逐渐减小,即高频波浪(短波)易被夹芯板所反射,低频波浪(长波)则不容易被反射,而且,芯材厚度增大,透射系数增大,反射系数减小,即芯材厚度的增加导致被反射的波浪能量减少,透射到夹芯板下方水域的波浪能量增加,主要是因为芯材厚度增加使得夹芯板整体等效刚度减小。图 4(b)为夹芯板端部简支状态下的反射系数Kr和透射系数Kt随无因次波数k0h的变化,当无因次波数k0h增大时,反射系数和透射系数的变化趋势与图 4(a)一致;但是,对比同一波数k0h,端部简支夹芯板的反射系数相对端部自由的显著增大,透射系数减小。
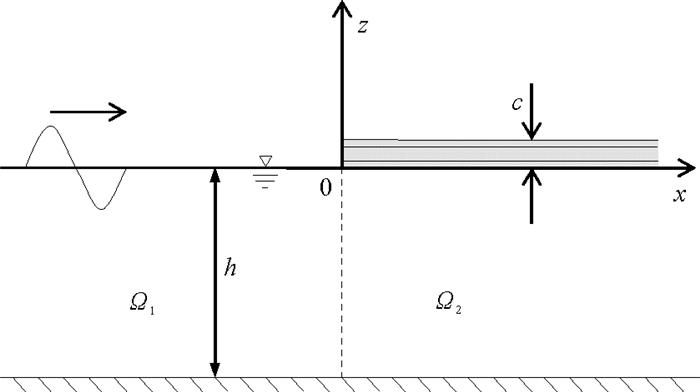
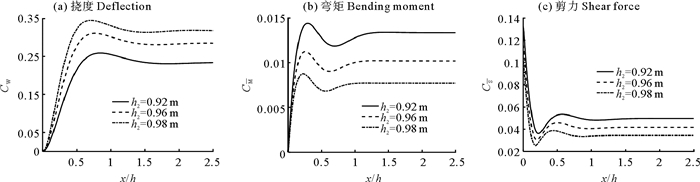
图 5给出端部自由状态下3种不同夹芯板的无因次挠度、弯矩和剪力,无因次波数k0h=6。夹芯板挠度随着芯材厚度的增大逐渐减小,这主要是因为夹芯板的整体刚度增大;面板厚度的变化不影响挠度最大值所对应的位置,3种不同夹芯板的挠度均在端点处达到最大值;随着离端点距离的增加,夹芯板的挠度先减小,然后趋于稳定,这是因为此时流体区域仅存在向右传播的传播波;随着芯材厚度的增加,夹芯梁的弯矩和剪力均逐渐增大。图 6给出端部简支状态下三种不同夹芯板的无因次挠度、弯矩和剪力,计算条件与图 5中的参数一致。芯材厚度影响与端部自由状态时相同,不过,端部简支约束使挠度最大值不再出现在夹芯板左端(此处挠度和弯矩均为0),而且挠度响应最大值明显减小。
3 结语
本文基于夹芯板理论和势流理论,采用匹配特征函数展开法,建立了波浪作用下超大型层合浮体水弹性响应分析的解析模型,不同端部约束都具有很好的收敛性。对波浪反射系数、透射系数以及夹芯板挠度、剪力和弯矩进行分析:相对自由夹芯板,简支板的挠度幅值更大;芯材厚度减小增大板整体刚度,有效降低挠度响应幅值。本文解析模型可为复杂的数值模拟或物理模型试验研究提供理论指导,为超大型层合浮体设计提供快速分析方法和参考依据。
Hydro-Elastic Responses of Very Large Floating Sandwich Structures Under Wave Action
College of Engineering, Ocean University of China, Qingdao 266100, China
Supported by the Key Engineering Innovation Project of Shandong Province(2019JZZY010301)


 0)
0) 0)
0) 0)
0) 0)
0) 0)
0) 0)
0) 0)
0) 0)
0) 0)
0) 0)
0) 2022, Vol. 52
2022, Vol. 52


