2. 山东科技大学信息工程系,山东 泰安 271021;
3. 泰山医学院外国语学院,山东 泰安 271000
变压器是电力网络运行过程中最重要的设备之一,变压器如果产生故障,会给电力网络带来巨大的经济损失。变压器的定期维修和故障及时发现具有重要的意义。目前用于检测变压器是否正常运行的方法很多,其中应用最为广泛的是油中溶解气体分析法(Dissolved Gas Analysis, DGA)。该方法是利用对变压器绝缘油中的五种溶解气体(H2、CH4、C2H6、C2H4和C2H2)浓度进行分析,从而确定变压器的故障类型[1]。
近些年研究者提出了基于机器学习变压器故障诊断方法,主要有基于模糊集理论[2],基于支持向量机[3],基于聚类分析法[4],基于神经网络法[5-7]等。还有研究者提出基于进化理论的变压器故障诊断方法,主要有基于遗传方法[8],基于粒子群方法[9]和基于免疫方法[10]等。这些算法在故障诊断中均取得较好的效果。
2006年由Hinton等人[11],在Science杂志上提出深度信念网络(Deep Belief Network, DBN)模型,被称为神经网络的新生[12]。深度信念网络从结构上来说是由多个受限玻尔兹曼机(Restricted Boltzmann Machine, RBM)组成。Roux和Bengio[13]从理论上证明了,如果隐层的单元数量足够大,RBM能够拟合任意类型的离散分布。近些年基于RBM的深度算法在图像识别[14],语音识别[15],文本识别[16]等领域均取得了成功。然而应用RBM算法在变压器故障诊断领域的研究较为少见。本文基于深度结构的RBM算法与变压器油中DGA技术相结合进行变压器故障诊断。构造由两层RBM和一层BP所组成的深度信念网络DBN。利用RBM进行预训练并提取特征信息,利用BP计算误差并重构DBN。仿真结果表明该方法对变压器故障分类有较高的准确性。
1 变压器故障分类电力变压器大多数都是用绝缘油实现绝缘和散热功能。电力变压器虽然经过密封和干燥处理,但是在运行过程中难免会混入少量空气。这些空气在热力和电力的作用下与绝缘油发生化学反应,产生少量CO、CO2以及一些低分子烃类。
变压器在正常运行的情况下,绝缘油内部的分子结构比较稳定,不会出现化学键的断裂从而产生烃类气体。如果内部发生故障,那么故障点会释放出大量的热量。这些热量就会迫使故障点周围的绝缘油裂变,从而产生CH4(甲烷)、C2H6(乙烷)、C2H4(乙烯)、C2H2(乙炔)、H2(氢气),以及CO(一氧化碳)、CO2(二氧化碳)。某些情况下CO和CO2并不是由设备故障造成的。因此CH4、C2H6、C2H4、C2H2、H2这五种气体就成为检测变压器故障的特征气体[17]。绝缘油的烃分子在300~400 ℃的时候开始发生裂变反应。随着温度的不断增加,H2和烃类气体的含量也会增加,裂变气体的热解顺序为:烷烃-烯炔-炔烃。变压器内部故障主要有机械、热、电三种模式。典型的变压器故障可以概括为局部放电、低能放电、高能放电、低温过热、高温过热这五类。当产生故障时,五种特征气体的含量呈现一些规律性,比如当局部放电时,如果放电密度较低时总烃类含量比较低,H2含量通常会占到总量的90%以上。
当溶解气体超过正常值范围时候,可用表 1判断故障性质。在故障诊断的时候,特征气体的含量与故障类型有着十分密切的联系。因此用特征气体含量来判断变压器故障性质比较方便直观。
|
|
表 1 判断故障性质方法 Table 1 Method of diagnose fault characteristic |
由于不同的故障所含有的特征气体的含量差别较大,一般来说通过对气体的相对含量的统计更加准确,更容易诊断故障类型。因此三比值法,即W(CH4)/W(H2)、W(C2H2)/W(C2H4)、W(C2H4)/W(C2H6)数据往往被用来进行故障分析。
2 模型设计根据DBN的设计原理,网络结构设计采用两层RBM和一层BP的模式。可见层包含3个单元,用来存放输入的变压器故障三比值的数据。输出层T包含5个单元,用来存放三比值数据对应的变压器故障类型。在维数较低的情况下,神经网络每层的单元格数k可以利用kolmogorov定理计算
| $ k = \left[{\sqrt {n + m} } \right] + a, $ | (1) |
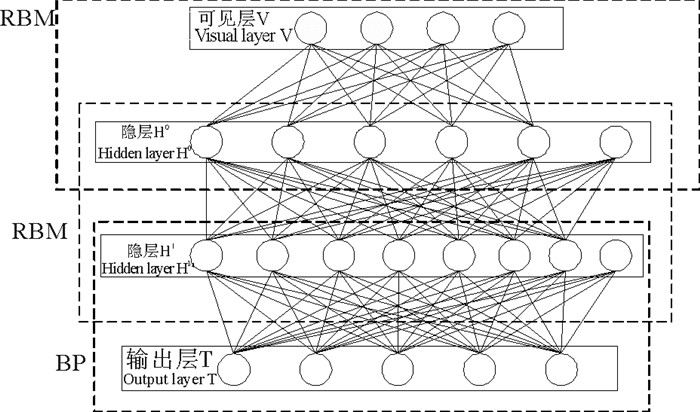
其中:n是可视层单元个数;m为输出层单元个数;a为1~10的随机整数;[·]表示取整。利用式(1)和实际仿真确定第一个隐层H0含有5个单元,第二个隐层H1含有7个单元。另外每层增加一个偏置项,用来存放阈值。可见层V和隐层H0从逻辑结构上组成第一层RBM,隐层H0和隐层H1共同组成第二层的RBM,隐层H0看做是第二层RBM的输入。隐层H1和输出层T在逻辑上组成第三层BP,隐层H1看做是第三层BP的输入。网络结构图如图 2所示。
|
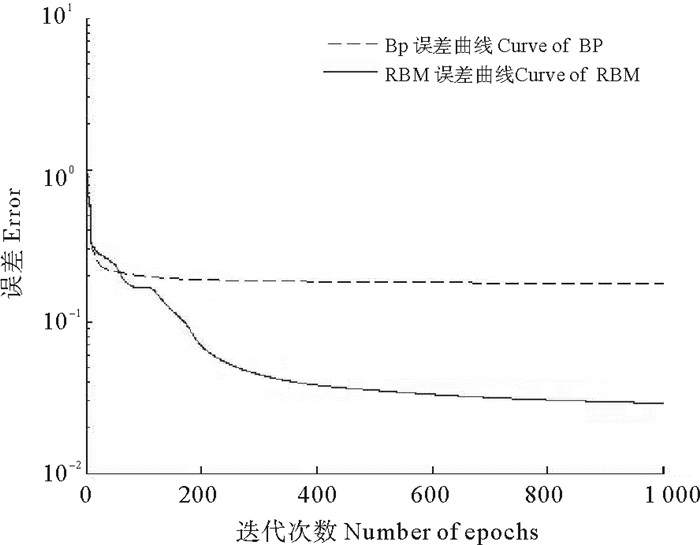
图 2 BP与RBM误差曲线图 Fig. 2 The error curve of BP and RBM |
两层RBM网络状态{v, h0, h1}的能量模型可以定义为
| $ \begin{array}{l} E(v, {h^0}, {h^1}|\theta ) =-\sum\limits_{i = 1}^n {{a_i}{v_i}}-\sum\limits_{j = 1}^m {{b_j}} h_{_j}^{^0}-\sum\limits_{k = 1}^l {{c_k}} h_{_k}^{^1} - \\ \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {{v_i}} } {W_{ij}}h_{_j}^{^0} - \sum\limits_{j = 1}^m {\sum\limits_{k = 1}^l {h_{_j}^{^0}} } {W_{jk}}h_{_k}^{^1}, \end{array} $ | (2) |
其中:vi表示可见层第i个节点的值;hj0表示第一个隐层第j个节点的值;hk1表示第二个隐层第k个节点的值。vi, hj0, hk1的状态取值{0, 1};Wij表示从vi节点到hj0的权重值;Wjk表示hj0到hk1的权重值;ai表示可见层的偏置;bj表示第一个隐层的偏置;ck表示第二个隐层的偏置。根据热力学相关原理,求得联合概率分布为
| $ P\left( {v, {h^0}, {h^1}} \right) = \frac{{{\rm{exp}}\left( {-E\left( {v, {h^0}, {h^1}} \right)} \right)}}{{{\sum _{v, {h^0}, {h^1}}}{\rm{exp}}\left( {-E\left( {v, {h^0}, {h^1}} \right)} \right)}}。$ | (3) |
根据联合概率分布,计算求得条件概率分布为
| $ P\left( {h_{_j}^{^0} = 1|v, {h^1}} \right) = \sigma \left( {{b_j} + \sum\limits_i {{v_i}} {W_{ij}} + \sum\limits_k {h_{_k}^{^1}} {W_{jk}}} \right), $ | (4) |
其中:
由于在可见层单元之间没有直接的链接,并且只与隐层h0关联。因此可见单元之间符合独立条件分布,且条件项为h0。条件概率分布为
| $ P\left( {{v_i} = 1|{h^0}} \right) = \sigma \left( {{a_i} + \sum\limits_j {{W_{ji}}} h_{_j}^{^0}} \right)。$ | (5) |
同理隐层h1的条件概率分布为
| $ P\left( {h_{_k}^{^1} = 1|{h^0}} \right) = \sigma \left( {{c_k} + \sum\limits_j {{W_{jk}}} h_{_j}^{^0}} \right)。$ | (6) |
通过最大化训练样本的极大似然对数函数来求解θ
| $ {\theta ^*} = {\rm{arg}}\mathop {{\rm{max}}}\limits_\theta \left( \theta \right) = \arg \mathop {\max }\limits_\theta \sum\limits_{t = 1}^T {{\rm{ln}}} P\left( {{v^{\left( t \right)}}|\theta } \right)。$ | (7) |
对(θ)求偏导得到
| $ \begin{array}{l} \frac{\partial }{{\partial \theta }} = \sum\limits_{{h^0}, {h^1}} {P\left( {{h^0}, {h^1}|v} \right)} \frac{{\partial \left( {-E\left( {v, {h^0}, {h^1}} \right)} \right)}}{{\partial \theta }} + \\ \sum\limits_{v, {h^0}, {h^1}} {P\left( {{h^0}, {h^1}, v} \right)} \frac{{\partial \left( {-E\left( {v, {h^0}, {h^1}} \right)} \right)}}{{\partial \theta }}。\end{array} $ | (8) |
由于进一步求导时P(h0, h1, v|θ)分布难以获得,所以通过CD算法近似计算其分布。
|
图 1 网络结构图 Fig. 1 The structure of neuro network |
CD算法就是利用Kullback-Leibler距离来计算概率分布的区别性。
| $ KL\left( {q||p} \right) = \sum\limits_{x \in \mathit{\Omega }}^{} q \left( x \right){\rm{ln}}q\left( x \right)-\sum\limits_{x \in \mathit{\Omega }} {q\left( x \right)} {\rm{ln}}p\left( x \right)。$ | (9) |
利用式(9)计算采样概率分布的区别性
| $ KL{\rm{ }}({p_0}||{p_\infty })-KL{\rm{ }}({p_n}||{p_\infty }), $ | (10) |
其中:p0是初始状态的联合概率分布;pn是经过n步MCMC采样以后的联合概率分布;p∞是马氏链最末端的联合概率分布。CD算法就是不断的将pn赋值给p0,通过对参数的修正,让KL距离趋近与0。CD算法的精准度近似于MCMC方法[18],更新参数由下式计算
| $ \begin{array}{l} \Delta {W_{ij}} = \varepsilon \left( {{{\left[{{v_i}h_{_j}^{^0}} \right]}_{data}} - {{\left[{{v_i}h_{_j}^{^0}} \right]}_{recon}}} \right), \\ \Delta {W_{jk}} = \varepsilon \left( {{{\left[{h_{_j}^{^0}h_{_k}^{^1}} \right]}_{data}} - {{\left[{h_{_j}^{^0}h_{_k}^{^1}} \right]}_{recon}}} \right), \\ \Delta {a_i} = \varepsilon \left( {{{\left[{{v_i}} \right]}_{data}} - {{\left[{{v_i}} \right]}_{recon}}} \right), \\ \Delta {b_j} = \varepsilon \left( {{{\left[{h_{_j}^{^0}} \right]}_{data}} - {{\left[{h_{_j}^{^0}} \right]}_{recon}}} \right), \\ \Delta {c_k} = \varepsilon \left( {{{\left[{h_{_k}^{^1}} \right]}_{data}} - {{\left[{h_{_k}^{^1}} \right]}_{recon}}} \right)。\end{array} $ | (11) |
其中:ε表示网络学习率;[·]recon表示重构以后的概率分布。基于CD算法的RBM训练的主要步骤如下:
Step 1 初始化令ΔWij、ΔWjk、Δai 、Δbj、Δck的值为0,Wij、Wjk、ai、bj和ck随机较小的数。然后设置迭代次数E。
Step 2 将训练样本v赋值给的v0利用式(5)、式(6)计算h0、v1、h1。
Step 3 利用式(11),计算ΔWij、ΔWjk、Δai、Δbj、Δck的值,并更新参数θ←θ+Δθ。
Step 4 如果迭代次数小于E,则重复Step 2, 否则结束。
3 训练与仿真变压器油中特征气体的浓度数据,对分析变压器故障有着直接的指导意义。根据收集到的数据进行整理,训练数据分为两个部分,一部分为输入数据,即五种特征气体H2、CH4、C2H2、C2H6、C2H4的样本数据,利用三比值法[19]计算出三个比值的数据,作为测试样本的输入数据。也就是说训练输入样本为三维矩阵。为了减小数据的奇异性,提高训练速。使用数据归一化公式,把训练输入样本的数据归一到[-1, 1]之间。
| $ y = \frac{{({y_{{\rm{max}}}}-{y_{{\rm{min}}}})\left( {x-{x_{{\rm{min}}}}} \right)}}{{({x_{{\rm{max}}}}-{x_{{\rm{min}}}})}} + {y_{{\rm{min}}}}。$ | (12) |
其中:y表示归一化处理后的样本数据,令ymax=1,ymin=-1;xmax为样本中最大值,xmin为样本中的最小值。
训练数据的另外一部分为输出数据,即特征气体的样本数据对应的故障情况,将变压器的故障分为5类,低温过热(00001)、高温过热(00010)、局部放电(00100)、低能放电(01000)和高能放电(10000)。
在实际的训练过程中,除了对初始数据进行归一化外,额外添加部分高斯噪音(Gaussian Noise, GN)。即数据ξ~N(μ, σ2),其中σ2表示随机变量的方差,μ表示随机变量的平均期望。本文中将高斯噪声添加到可视层中。从流形学习的角度分析,高维样本数据通常散布在低维流形上或者附近。流形学习尝试发现嵌入在高维数据空间中的低维流形结构。假设随机算子
训练网络的过程中,一些参数的设置是十分重要的。近来的一些研究表明[20],如果参数设置不当,会影响最终的实验结果。根据经验和在仿真过程中的一些调试,笔者对一些重要的参数做了如下设置。
学习率设置:学习速率的选取很重要,过大会导致系统不稳定,过小会导致训练周期过长、收敛慢,达不到要求的误差。一般倾向于选取较小的学习速率以保持系统稳定,通过观察误差下降曲线来判断。下降较快说明学习率比较合适,若有较大振荡则说明学习率偏大。由于网络规模大小的不同,学习率选择应当针对其进行调整。在本实验中,设置网络的学习率为0.05,此设置收敛速度快,误差曲线波动小。
动量项设置:为了避免受学习率设置影响,在参数更新的时候,增加动量项的设置,使得参数的变化并不完全由似然函数的梯度方向决定。避免了出现过度拟合的问题。在本试验中设置动量项为0.9。
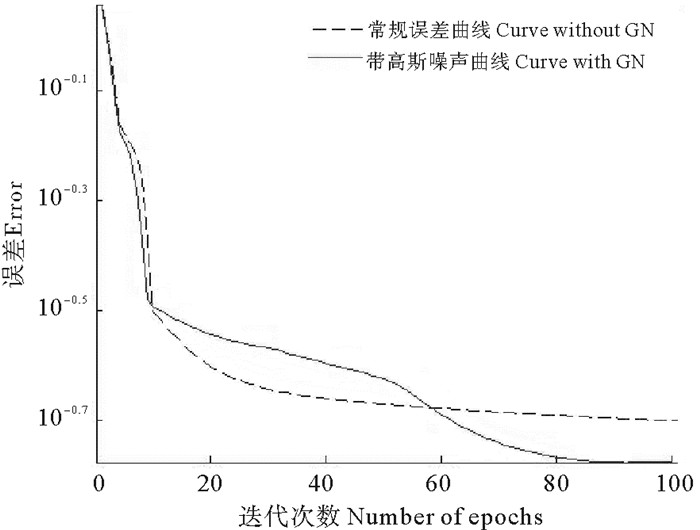
本文以IEC TC 10 Database[21]所提供的134组历史故障案例样本资料作为变压器故障的输入样本。使用K层交叉验证(K-fold)的方式对实验数据进行分类。实验数据分为K组,交叉验证过程重复K次,每次选取其中一个不同的部分作为测试数据,其余K-1组作为训练数据。实验设置K=9,即将数据分为9组。每次选取其中一组作为测试数据,其余8组作为训练数据,重复9次,确保每组数据都被当做测试数据。最终把测试结果取平均值即可得到整体正确率。图 3为经过BP训练的误差曲线图与经过RBM训练的误差曲线图,图中可以发现RBM的误差明显小于BP训练的误差,并且收敛速度更快。经过1 000轮回的训练后,误差能够达到10-2左右。图4为带高斯噪声和不带高斯噪声的RBM的误差曲线图。如图可以看出,增加部分高斯噪声以后,曲线的收敛速度更快。在同样学习率的情况下,训练效果更优。
|
图 3 带高斯噪声与不带高斯噪声误差曲线图 Fig. 3 The error curve of with Gaussian Noise and without Gaussian Noise |
为了验证算法有效性,本文设计BP、K邻近(K-NearestNeighbor, K-NN)、支持向量机(Support Value Machine, SVM)和RBM几种算法的对比试验。表 2所示为K-NN算法的识别率,K=15时,正确率最高为90%。表 3所示为SVM在选择不同核函数(Kernel Function, KF)的情况下的正确率,当选择径向基函数(Radial Basis Function, RBF)作为核函数时,正确率最高为79.9%。
|
|
表 2 K-NN分类正确率 Table 2 Classification accuracy of K-NN |
|
|
表 3 SVM分类正确率 Table 3 Classification accuracy of SVM |
通过对134组训练数据进行了1 000轮回的训练后,表 4列举了BP和RBM的明细正确率。BP算法平均正确率为84.1%。RBM算法在低温过热分类中获得100%的正确率,在局部放电分类中获得最低83.3%的正确率,平均正确率为93.6%。
|
|
表 4 BP和RBM算法结果比较 Table 4 Classification accuracy of BP and RBM |
在已经训练好的网络基础上,本文对10组测试样本进行了检验。使用RBM网络训练结果与实际的故障结果进行比较如表 5所示。可以看出,使用RBM网络诊断的结果与变压器的实际故障具有较高的吻合度。
|
|
表 5 训练结果 Table 5 The training results |
本文研究了一种基于受限玻尔兹曼机模型的变压器故障诊断方法。方法首先根据变压器绝缘油中五种特征气体含量计算三比值数据。然后构造一个由两层RBM和一层BP所组成的DBN网络。利用RBM预训练样本数据,利用BP进行误差计算并判断故障类型。仿真结果验证该方法的有效性。
| [1] |
刘勇辉. 基于DGA的变压器故障诊断[J]. 高电压技术, 2005, 31(6): 87-88. Liu Yonghui. Power Transformer fault diagnosis based-on dissolved gas analysis[J]. High Voltage Engineering, 2005, 31(6): 87-88. (  0) 0) |
| [2] |
杜文霞, 句希源, 吕锋. 基于模糊聚类算法的变压器故障诊断研究[J]. 变压器, 2009, 46(8): 65-69. Du Wenxia, Ju Xiyuan, Lu Feng. Research on transformer fault diagnosis based on fuzzy clustering algorithm[J]. Transformer, 2009, 46(8): 65-69. (  0) 0) |
| [3] |
郭创新, 朱承治, 张琳, 等. 应用多分类多核学习支持向量机的变压器故障诊断方法[J]. 中国电机工程学报, 2010, 30(13): 130-136. Guo Chuangxin, Zhu Chengzhi, Zhang Lin, et al. A fault diagnosis method for power transformer based on multiclass multiple-kernel learning support vector machine[J]. Proceedings of the CSEE, 2010, 30(13): 130-136. (  0) 0) |
| [4] |
符杨, 田振宁, 江玉蓉, 等. 加权模糊核聚类法在电力变压器故障诊断中的应用[J]. 高电压技术, 2010, 36(2): 371-374. Fu Yang, Tian Zhenning, Jiang Yurong, et al. Power transformer fault diagnosis using weighted Fuzzy kernel clustering[J]. High Voltage Engineering, 2010, 36(2): 371-374. (  0) 0) |
| [5] |
付强, 陈特放, 朱佼佼. 采用自组织RBF网络算法的变压器故障诊断[J]. 高电压技术, 2012, 38(6): 1368-1375. Fu Qiang, Chen Tefang, Zhu Jiaojiao. Transformer fault diagnosis using self-adaptive RBF neural network algorithm[J]. High Voltage Engineering, 2012, 38(6): 1368-1375. (  0) 0) |
| [6] |
李霜, 王朗珠, 张为, 等. 基于DGA的改进BP神经网络的变压器故障诊断方法[J]. 变压器, 2010, 47(12): 61-65. Li Shuang, Wang Langzhu, Zhang Wei, et al. Fault diagnosis method of transformer based on improved BP neural network of DGA[J]. Transformer, 2010, 47(12): 61-65. (  0) 0) |
| [7] |
王晓霞, 王涛. 基于BP神经网络的变压器故障诊断[J]. 华东电力, 2008, 36(2): 112-116. Wang Xiaoxia, Wang Tao. Transformer fault diagnosis based on BP networks[J]. East China Electric Power, 2008, 36(2): 112-116. (  0) 0) |
| [8] |
潘翀, 陈伟根, 云玉新, 等. 基于遗传算法进化小波神经网络的电力变压器故障诊断[J]. 电力系统自动化, 2007, 31(13): 88-92. Pan Zhong, Chen Weigen, Yun yuxin, et al. Fault diagnosis of power transformers based on genetic algorithm evolving wavelet neural network[J]. Automation of Electric Power Systems, 2007, 31(13): 88-92. DOI:10.3321/j.issn:1000-1026.2007.13.017 (  0) 0) |
| [9] |
Tang W H, Goulermas J Y, Wu Q H. A probabilistic classifier for tr-ansformer dissolved gas analysis with a particle swarm optimizer[J]. IEEE Transactions on Power Delivery, 2008, 23(2): 751-759. DOI:10.1109/TPWRD.2008.915812
(  0) 0) |
| [10] |
宋绍民, 王耀南, 孙炜, 等. 基于免疫聚类算法的变压器DGA数据故障诊断方法[J]. 变压器, 2008, 45(8): 70-72. Song Shaomin, Wang Yaonan, Sun Wei, et al. Fault diagnosis method with transformer DGA data based on immune recognition algorithm[J]. Transformer, 2008, 45(8): 70-72. (  0) 0) |
| [11] |
Hinton G E, Salakhutdinov R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504-507. DOI:10.1126/science.1127647
(  0) 0) |
| [12] |
Garrison W. Cottrell. New life for neural networks[J]. Science, 2006, 313: 454-455. DOI:10.1126/science.1129813
(  0) 0) |
| [13] |
Roux N L, Bengio Y. Representational power of restricted boltzmann machines and deep belief networks[J]. Neural Computation, 2008, 20(6): 1631-1649. DOI:10.1162/neco.2008.04-07-510
(  0) 0) |
| [14] |
Salakhutdinov R, Larochelle H. Efficient learning of deep Boltzmann machines[J]. Journal of Machine Learning Research: Proceedings Track, 2010, 9(1): 693-700.
(  0) 0) |
| [15] |
Jaitly N, Hinton G E. Learning a better representation of speech sound waves using restricted Boltzmann machines[C]. Proc of the 2011 IEEE Int Conf on Acoustics. Speech and Signal Processing, 2011: 5884-5887. http://ieeexplore.ieee.org/document/5947700/
(  0) 0) |
| [16] |
Dahl G, Yu Dong, Deng Li, et al. Context-dependent pretrained deep neural networks for large vocabulary speech recongnition[J]. IEEE Trans on Audio, Speech and Language Processing, 2012, 20(1): 30-42. DOI:10.1109/TASL.2011.2134090
(  0) 0) |
| [17] |
耿基明, 郭晓峰. 应用变压器油色谱分析判断变压器故障[J]. 变压器, 2006, 43(11): 44-47. Geng Jiming, Guo Xiaofeng. Diagnosis of Transformer Faults by Chromatogr aphic Analysis of Transformer oil[J]. Transformer, 2006, 43(11): 44-47. DOI:10.3969/j.issn.1001-8425.2006.11.011 (  0) 0) |
| [18] |
Hinton G E. Training products of experts by minimizing contrastive divergence[J]. Neural Computation, 2002, 14(8): 1771-1800. DOI:10.1162/089976602760128018
(  0) 0) |
| [19] |
尚勇, 闫春江, 严璋. 基于信息融合的大型油浸电力变压器故障诊断[J]. 中国电机工程学报, 2002, 22(7): 50-55. Shang Yong, Yan Chunjiang, Yan Zhang. Synthetic Insulation Fault Diagnostic Model of Oil-immersed Power Transformers Utilizing Information Fusion[J]. Proceedings of the CSEE, 2002, 22(7): 50-55. (  0) 0) |
| [20] |
Schulz H, Müller A, Behnke S. Investigating Convergence of Restricted Boltzmann Machine Learning[C]. //NIPS 2010 Workshop on Deep Learning and Unsupervised Feature Learning, 2010: 1-9.
(  0) 0) |
| [21] |
Duval M, dePabla A. Interpretation of gas-in-oil analysis using new IEC publication 60599 and IEC TC 10 databases[J]. IEEE on Electrical Insulation Magazine, 2001, 17: 31-41.
(  0) 0) |
2. Department of Information Engineering, Shandong University of Science and Technology, Taian 271021, China;
3. College of Foreign Languages, Taishan Medical University, Taian 271000, China
 2018, Vol. 48
2018, Vol. 48


