2. 国家海洋环境监测中心,辽宁 大连 116023;
3. 海军工程设计研究院工程综合试验研究中心, 山东 青岛 266100
波浪是海洋动力环境中重要的组成部分,是影响港工结构物安全和港内船舶泊稳的主要因素。波浪从外海传播至在近岸的过程中,特别是传至掩护水域附近时,受岛屿、建筑物及地形变化等的影响,会发生折射、绕射、反射及破碎等一系列变形,使得波浪能量重新分布,形成新的波浪场,从而进一步对港区泊稳和港工建筑物的安全产生影响。港口工程中,通常建造防波堤来掩护港池内部不受波浪的直接作用,并开挖港池和航道以满足船舶的通行和使用要求,波浪要素直接影响着近岸建筑物的设计和规模及港内泊稳条件等。因此,在工程施工之前,准确预测掩护水域在完工后的波浪分布和泊稳状况,对设计方案的优化和实施是非常重要的。
随着数值计算方法的快速发展,涌现了许多波浪数值计算模型,其中应用较广泛的主要有波能平衡方程模型、缓坡方程模型和Boussinesq方程模型等。其中Boussinesq方程可以用于模拟波浪的非线性运动和由于水深变化而引起的波群演化等,Madsen[1-2]、Nowgu[3]、Gobbi[4]和邹志利[5]等对经典的Boussinesq方程进行了改进,使之可以适用于较深处的波浪。基于改进的Boussinesq方程开发而成的MIKE21 BW模型,可用于模拟任意地形或平面布置条件下的波浪运动过程,包括波浪的绕射、折射、反射、浅水变形及它们之间的相互作用等,能够精确模拟小范围内的波浪传播情况,现已被广泛应用于海洋、近海工程的水动力数值模拟[6]。
董胜[7]基于考虑绕射作用的能量平衡方程,建立了浅水波浪传播变形的改进数值模型,并对日照帆船港港域波浪场进行数值模拟,计算值与物理模型试验观测值吻合良好。张娜[8]和王中起[9]分别针对某特定工程的总平面布置设计方案,利用MIKE21 BW模型,对工程建成前后的波浪场进行模拟,为方案比选和工程设计提供了科学依据。徐俊峰[10]通过建立MIKE21 BW波浪模型,系统地分析了不同航道条件对港内波浪传播与变形的影响规律。林法玲[11]利用MIKE21 BW模型计算了霞关一级渔港的港内波况,统计确定了渔港的有效避风面积和避风区域,为渔船的安全避风提供了技术支撑。贾晓[12]利用MIKE21 BW模型,通过设定透射系数,准确模拟了透浪建筑物掩护水域的波浪条件,与试验结果吻合良好。吴亚楠[13]采用MIKE21 BW模型对威海船厂港域的泊稳状况进行了数值模拟,与物理模型试验结果吻合良好。冯卫兵[14]采用MIKE21 BW模型分别对平底地形下单突堤的波浪绕射及实际地形下某港港内波浪场进行模拟及验证,探讨了地形旋转处理及谱峰因子γ对港内波浪场模拟结果的影响。
本文对青岛万达游艇码头项目进行港域的波浪物理模型试验研究,并应用MIKE21 BW模型,考虑波浪的折射、绕射、反射及破碎等一系列物理过程,对波浪在港池附近海域的传播变形及港内的泊稳状况进行了数值研究,并与物理模型试验值[15]进行比较,对该项目的设计提供了合理的改进建议。
1 BW模型介绍 1.1 基本方程BW模型控制方程采用改进后的Boussinesq方程:
| $ n\frac{{\partial \xi }}{{\partial t}} + \frac{{\partial P}}{{\partial x}} + \frac{{\partial Q}}{{\partial y}} = 0, $ | (1) |
| $ \begin{array}{l} n\frac{{\partial P}}{{\partial t}} + \frac{\partial }{{\partial x}}(\frac{{{P^2}}}{h}) + \frac{\partial }{{\partial y}}\left( {\frac{{PQ}}{h}} \right) + \frac{{\partial {R_{xx}}}}{{\partial x}} + \frac{{\partial {R_{xy}}}}{{\partial x}} + \\ {F_x} + {n^2}gh\frac{{\partial \xi }}{{\partial x}} + {n^2}P[\alpha + \beta \sqrt {\frac{{{P^2} + {Q^2}}}{{{h^2}}}}] + \\ \frac{{gP\sqrt {{P^2} + {Q^2}} }}{{{h^2}{C^2}}} + n{\psi _1} = 0, \end{array} $ | (2) |
| $ \begin{array}{l} n\frac{{\partial Q}}{{\partial t}} + \frac{\partial }{{\partial y}}(\frac{{{Q^2}}}{h}) + \frac{\partial }{{\partial x}}\left( {\frac{{PQ}}{h}} \right) + \frac{{\partial {R_{xx}}}}{{\partial x}} + \frac{{\partial {R_{xy}}}}{{\partial x}} + \\ {F_y} + {n^2}gh\frac{{\partial \xi }}{{\partial y}} + {n^2}Q[\alpha + \beta \frac{{\sqrt {{P^2} + {Q^2}} }}{{{h^2}}}] + \\ \frac{{gQ\sqrt {{P^2} + {Q^2}} }}{{{h^2}{C^2}}} + n{\psi _2} = 0, \end{array} $ | (3) |
| $ \begin{array}{l} 式中:{\psi _1} = \left( {- B + \frac{1}{3}} \right){\rm{ }}{d^2}({P_{xxt}} + {Q_{xyt}})- \\ nBg{d^3}({\xi _{xxx}} + {\xi _{xyy}})- d{d_x}[\frac{1}{3}{P_{xt}} + \frac{1}{6}{Q_{yt}} + nBgd{\rm{ }}(2{\xi _{xx}} + \\ {\xi _{yy}})] -d{d_y}(\frac{1}{6}{Q_{xt}} + nBgd{\xi _{xy}}); \end{array} $ | (4) |
| $ \begin{array}{l} {\psi _2} = \left( {- B + \frac{1}{3}} \right){d^2}({Q_{yyt}} + {P_{xyt}})- nBg{d^3}({\xi _{yyy}} + \\ {\xi _{xxy}})- d{d_y}[\frac{1}{3}{Q_{yt}} + \frac{1}{6}{P_{xt}} + nBgd{\rm{ }}(2{\xi _{yy}} + {\xi _{xx}})] -\\ d{d_x}(\frac{1}{6}{P_{yt}} + nBgd{\xi _{xy}})。\end{array} $ | (5) |
式中:ξ为波面高度(m);P、Q为x、y方向流速水深积分;B为深水修正系数,取1/15;Fx、Fy为x、y方向水平应力;h为总水深,h=ξ+d;n为孔隙率;C为谢才系数;α、β为多孔介质中的层、湍流阻力系数;Rxx、Rxy为水滚引起的非均匀流动所产生的附加质量。
1.2 消波边界利用BW模型进行波浪的数值计算时,需在模型中无建筑物的边界处进行消波处理。它具有在指定区域吸收多余波能量的功能,既能避免边界产生的多次反射影响计算精度,又能防止计算的溢出。在该模型中,通过设置消波层厚度和消波系数的大小来控制消波效果,消波层的厚度一般设置为波长的1~2倍,以保证消波完全。
1.3 波浪边界在造波边界处,波浪的能量通过水面高程随时间的变化过程或者与边界垂直的流量密度附加给波浪场。波浪的生成是通过内部生波实现,主要通过在入射波浪场中沿着指定的生长线添加流量,可以指定一条生波线,也可以指定两条生成具有角度的波浪。内部生波的优点之一便是可以在波浪生长线后设置消波层,这样超出模型区域的波浪就可以被吸收掉,它与消波层之间是独立的。
数值模型入射波浪采用与物理试验相同的单向不规则波,其波谱采用由英、美、荷、德等国联合进行的“联合北海波浪计划”获得的JONSWAP谱[16]。该谱包括了深、浅水各不同成长阶段的风浪,得到了广泛应用,其表达式为
| $ S\left( \omega \right) = \frac{{0.78}}{{{\omega ^5}}}{\rm{exp}}(- \frac{{3.11}}{{H_{_s}^{^2}{\omega ^4}}}){\gamma _p}{\rm{exp}}[-\frac{{{{(\omega-{\omega _{{\rm{max}}}})}^2}}}{{2{\sigma ^2}\omega _{_{{\rm{max}}}}^{^2}}}]。$ | (6) |
式中:γp称为谱峰因子,γp =1.5~6,一般取平均值γp=3.3;ωmax为谱峰频率;Hs为有效波高H1/3;σ为峰形系数,取为
波浪与建筑物相互作用时,不同型式的建筑物对波浪的反射率各不相同,如直立式无孔建筑物对波浪的反射率接近100%,而斜坡堤等多孔建筑物的反射率约为20%~50%。MIKE21 BW模型通过设置不同的孔隙层层数和孔隙率大小来模拟岸线反射及具有不同反射率的建筑物,同时可以避免计算溢出。
2 物理模型试验为了使青岛万达游艇码头建设具有可靠的科学依据,确保工程建设更加经济合理、安全可靠,进行了本次整体物理模型试验。通过物理模型试验,测定拟建码头附近水域的波浪状况和泊稳条件,测量港内有关建筑物前的波浪要素,并对口门处护岸分别采用直立式和斜坡式的两种不同方案进行比选优化,提出合理的改进措施,为工程建设提供依据。
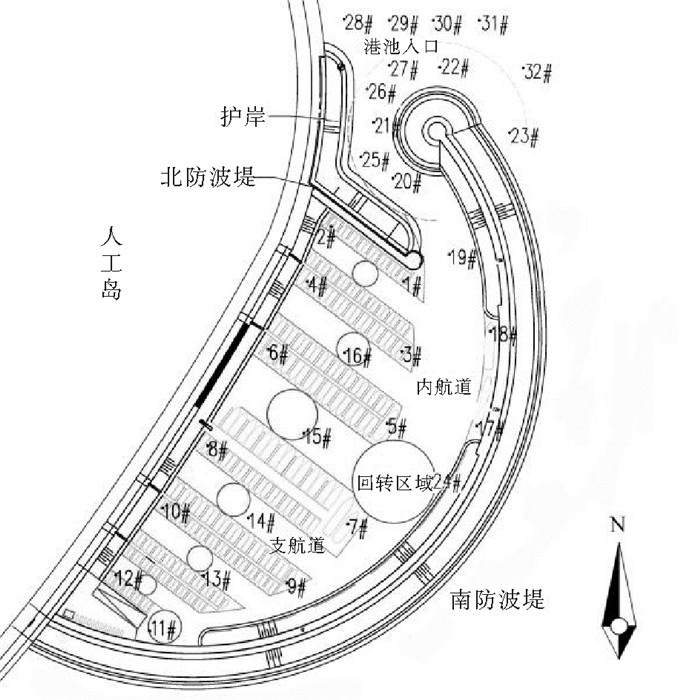
物理模型试验在长60、宽40、深1.2 m的室内水池中进行,水池两侧配备有L型造波系统,模型比尺λ为34,模型布置如图 1。造波机推板单宽均为0.5 m,铰型连接,可以产生多向不规则波,造波总宽度分别为26.0和30.0 m。波高测量采用DS-30系统,共布置波浪测点32个,其中包括港池内22个(1#~20#、24#、25#)、港池外10个(21#~23#、26#~32#),1#~16#测点代表游艇泊位,17#~19#测点代表工作船泊位,测点位置如图 2。

|
图 1 物理模型试验布置图 Fig. 1 Layout of the physical experiment |
|
图 2 试验测点布置图 Fig. 2 Layout of the measurement points |
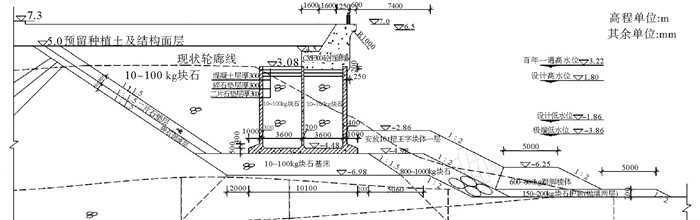
为分析口门处人工岛护岸采用直立结构和斜坡结构对港池平稳度的影响,试验采用NNE、NE、ENE三种方向波浪进行,波浪重现期为2和50 a,设计水位为设计高水位(1.80 m)和设计低水位(-1.86 m),采用单向不规则波浪进行试验。其中人工岛护岸的结构断面及其与特征水位的关系见图 3。
|
图 3 人工岛护岸横断面与特征水位关系图 Fig. 3 The relation graph between the characteristic water level and the cross section of the revetment |
试验结果表明,三个方向的波浪到达南防波堤堤头时均会产生明显的绕射,其中NNE向经绕射进入口门的波浪最多,ENE向最少;NNE向波浪传播至口门处时,波峰线基本与人工岛护岸轴线垂直,护岸对其基本无反射作用,当NE向和ENE向波浪作用时,护岸对波浪反射严重,入射波与反射波相互叠加,致使波况恶化;NNE向和NE向波浪入射到北防波堤处有明显反射和一定的波能集中现象,产生的波高较大。由于南、北防波堤与人工岛护岸在口门处形成了狭小水域,且港池口门正对护岸,致使波浪传播到该区域时受到的障碍较多,各建筑物对入射波的不同作用导致该处波浪状态较为复杂。
试验采用设计高水位下的波浪验证了港内泊稳情况。当护岸采用直立结构时,港池内游艇码头泊位和工作船泊位处波高均超出了系泊允许波高,且不满足游艇上下岸的作业标准;当采用斜坡式结构时,港池内游艇码头泊位满足系泊要求及游艇上下岸作业标准,工作船泊位满足系泊要求,但波高较上下岸标准略大。当护岸形式由直立结构改为斜坡结构后,港池内波高均显著减小,平稳度明显改善,因此建议采用斜坡式护岸,并适当延长现有方案中斜坡式护岸的长度,使港内的泊稳状况得到改善。
3 数值计算 3.1 模型设置对青岛万达游艇码头物理试验过程应用MIKE21 BW模块进行数值计算,水位为设计高水位(1.80 m),重现期为2 a一遇,口门处护岸结构形式为直立和斜坡式两种,共包括3种波况如表 1。
|
|
表 1 BW模型计算工况表 Table 1 Calculated wave cases in BW model |
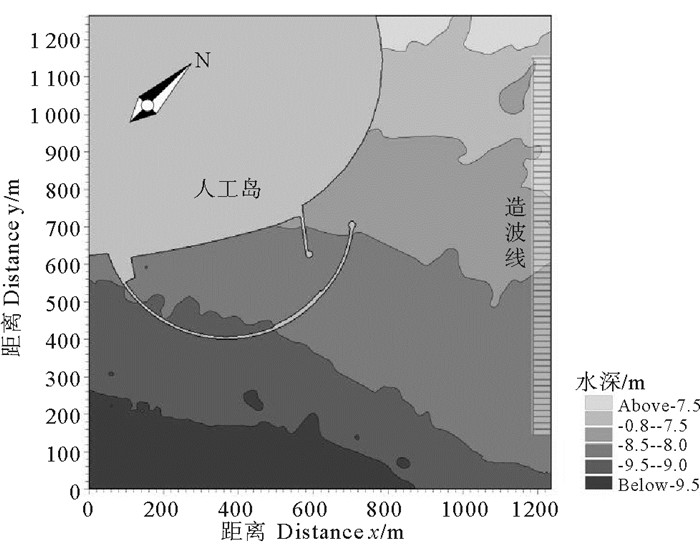
计算区域网格x和y向空间步长均为2 m,计算时间30 min,以保证波浪传播稳定,计算区域水深地形图如图 4。南防波堤中部、北防波堤内侧及港池内护岸为直立式结构,按完全反射处理;南防波堤其余部分及北防波堤外侧为斜坡式结构,按部分反射处理;口门处护岸的两种不同结构形式则分别按完全反射和部分反射处理。其中,部分反射边界的反射率通过设置不同的孔隙层层数和孔隙率大小确定。对孔隙层参数进行不断的调试和优化,使模拟结果与试验结果拟合良好,最终确定其反射率大小。
|
图 4 MIKE21计算区域水深地形图 Fig. 4 Water depth of the computed area in MIKE21 |
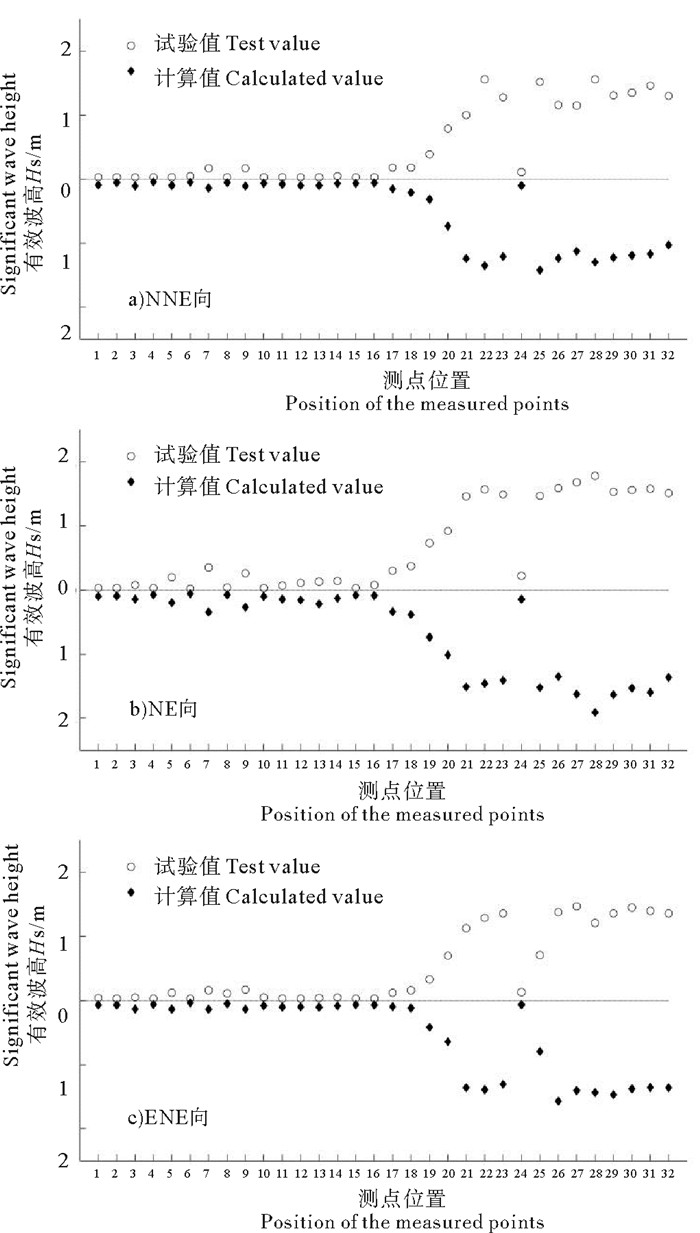
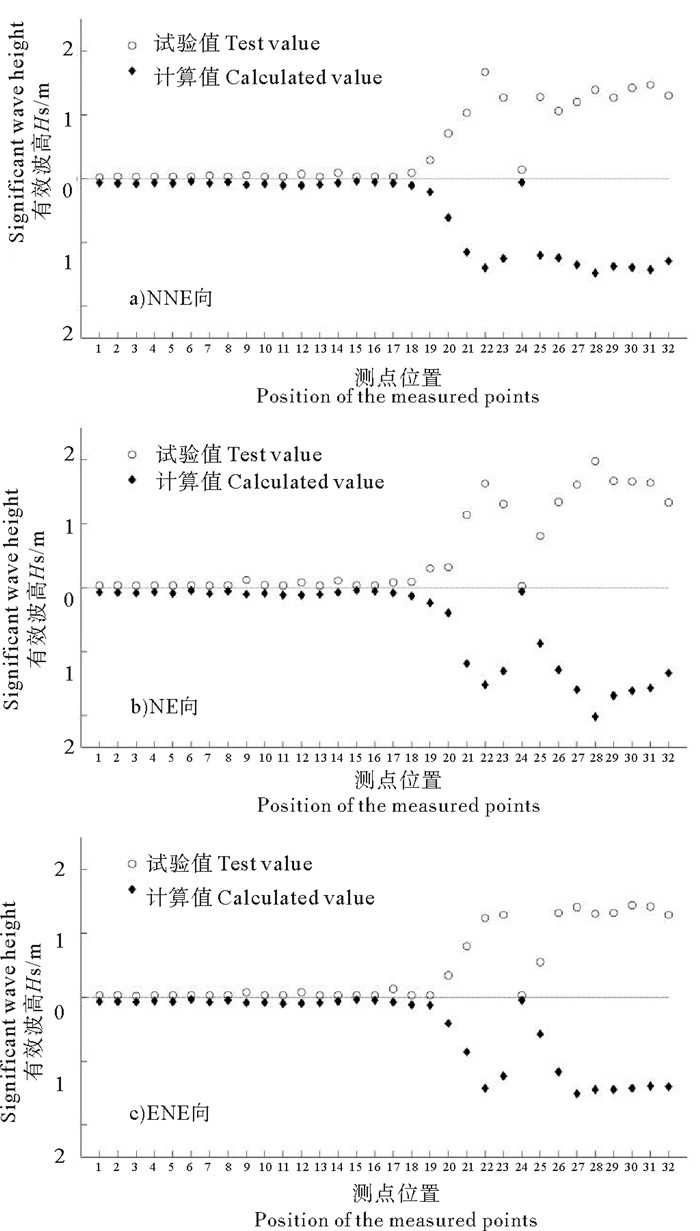
将BW模型计算结果与试验结果进行比较,图 5和6分别为护岸结构为直立式和斜坡式时的各测点在不同方向波浪作用下的波高对比图。从图 5~6中可以看出,各波向作用时计算值与试验值吻合较好,港池内各测点波高最大差值不超过0.1 m,港池外各测点最大差值不超过0.27 m。产生差异的原因是港池内外均有部分测点位于波浪强反射区,即使是两个波高仪之间位置的微小区别都会对模拟结果产生影响。此外,越浪现象的发生也会对试验结果有部分影响,而BW模型没有发生越浪现象。总体来说,数值计算结果是相当理想的,也表明了BW模型在计算近岸波浪传播过程中的可靠性。
|
图 5 口门处人工岛护岸为直立结构时各测点不同方向波高数值计算值与模拟值对比 Fig. 5 Comparison of calculated values and experimental values at the measurement points with a vertical revetment |
|
图 6 口门处人工岛护岸为斜坡结构时各测点不同方向波高数值计算值与模拟值对比 Fig. 6 Comparison of calculated values and experimental values at the measurement points with a sloping revetment |
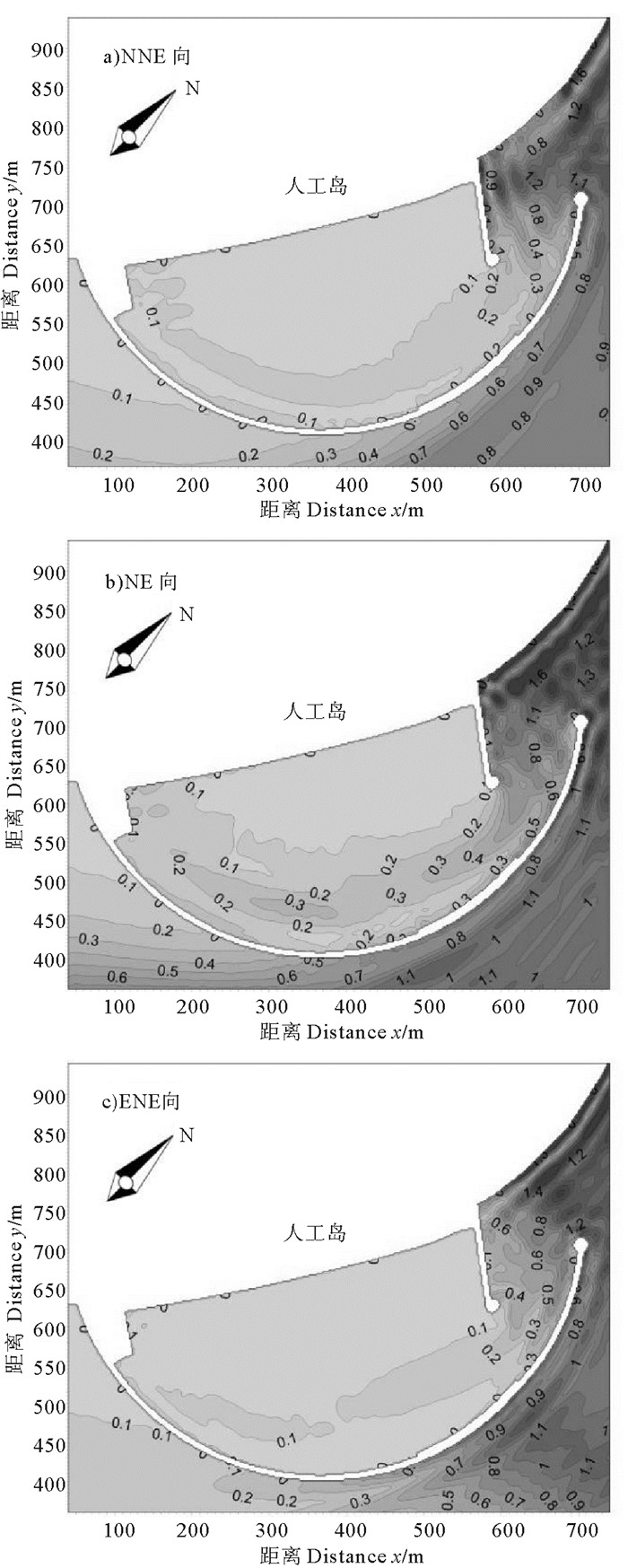
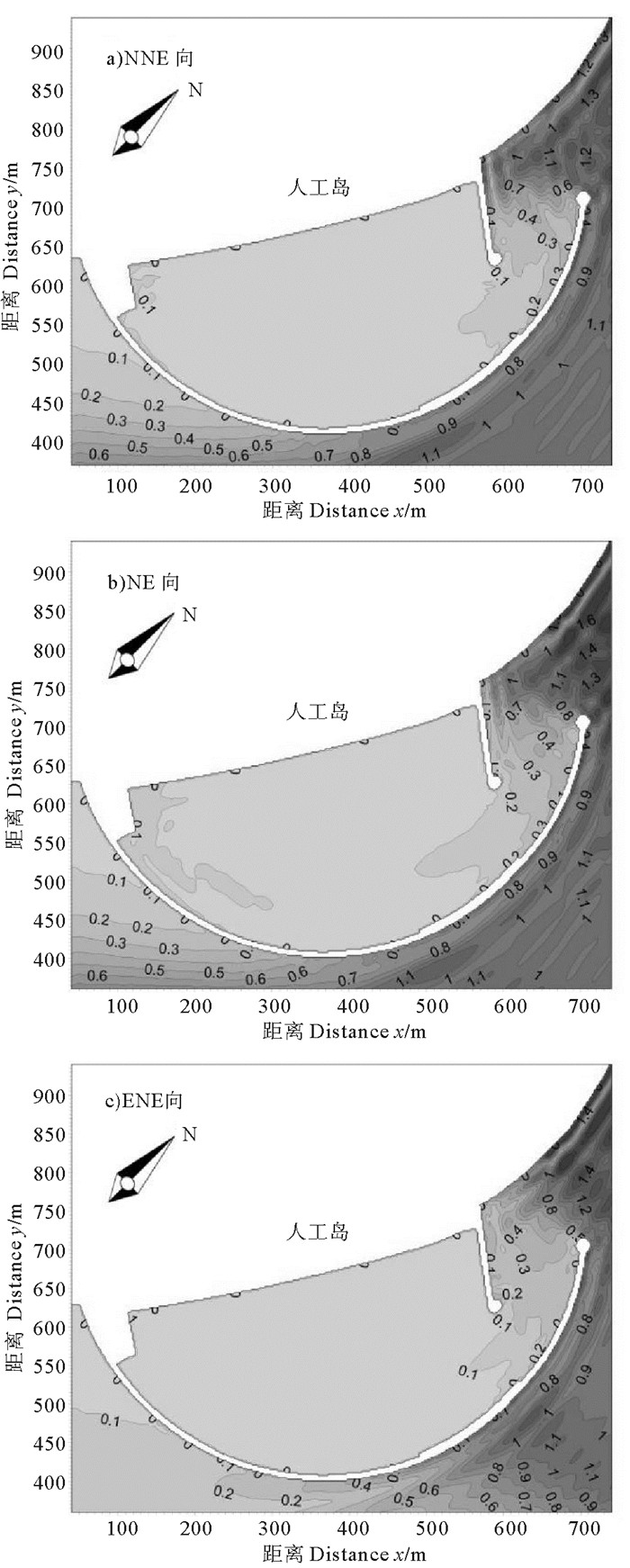
图 7~8给出了在三种不同方向波浪作用下,港池附近海域波浪的比波高的等值分布情况,即等比波高分布图。其中,比波高定义为计算得到的港池内各点实际波高与造波线边界处的入射波高之比。从图中可以看出三个方向的波浪到达南防波堤堤头时均会产生明显的绕射;NNE向波浪传播至口门处时,护岸对其基本无反射作用,当NE向和ENE向波浪作用时,护岸反射严重,此时入射波与反射波相互叠加,使波况较为复杂;NNE、NE向波浪入射到北防波堤处有明显的反射和波能集中,产生较大波高。模拟得到的波高分布情况与物理模型试验结果是一致的,表明可利用BW模型计算港池的波浪分布状况,为相关建筑物的设计和施工提供科学参考。
|
图 7 口门处人工岛护岸为直立结构时港域等比波高分布图 Fig. 7 Distribution of Hm0/Hm0_coming in the harbor basin with a vertical revetment |
|
图 8 口门处人工岛护岸为斜坡结构时港域等比波高分布图 Fig. 8 Distribution of Hm0/Hm0_coming in the harbor basin with a sloping revetment |
本文采用MIKE21 BW模块建立了近岸波浪数学模型,在考虑与物理模型试验相同因素的基础上,对青岛万达游艇码头港域的波浪传播变形进行数值模拟,得到了与试验值相当吻合的结果,表明BW模型在计算近岸波浪传播过程中的可靠性。得到如下结论:
(1) 试验证实,护岸结构采用直立式时,游艇泊位仅在NNE向和ENE向波浪作用下满足泊稳要求,工作船泊位在各方向波浪作用下均不满足泊稳要求;护岸结构为斜坡式时,游艇泊位和工作船泊位在各方向波浪作用下均满足泊稳要求。
(2) 经验证,数值计算的港池泊稳情况与试验情况一致,各验证点对比结果较好。
(3) 试验和数值计算都证实,口门处人工岛护岸采用斜坡式结构时,港内泊稳情况优于直立式结构,港池内波高较后者均有明显减小。因此建议采用斜坡式护岸,并适当延长现有方案中斜坡式护岸的长度,可大大改善港内的泊稳状况。
| [1] |
Madsen P A, Murray R, Sorensen O R. A new form of the Boussinesq equations with improved linear dispersion characteristics[J]. Coastal Engineering, 1991, 15(4): 371-388. DOI:10.1016/0378-3839(91)90017-B
(  0) 0) |
| [2] |
Madsen P A, Sorensen O R. A new form of the Boussinesq equations with improved linear dispersion characteristics:Part 2.A slowly-varying bathymetry[J]. Coastal Engineering, 1992, 18(3-4): 183-204. DOI:10.1016/0378-3839(92)90019-Q
(  0) 0) |
| [3] |
Nwogu O. A alternative form of Boussinesq equations for nearshore wave propagation[J]. Journal of Waterways, Port, Coastal and Ocean Engineering, 1993, 119(6): 618-638. DOI:10.1061/(ASCE)0733-950X(1993)119:6(618)
(  0) 0) |
| [4] |
Gobbi M F, Kirby J T. Wave evolution over submerged sills:tests of a high-order Boussinesq model[J]. Coastal Engineering, 1999, 37(1): 57-96. DOI:10.1016/S0378-3839(99)00015-0
(  0) 0) |
| [5] |
邹志利. 高阶Boussinesq水波方程的改进[J]. 中国科学:E辑, 1999, 29(1): 87-96. Zou Z L. The improvement of higher-order Boussinesq equations[J]. Science in China(Series E), 1999, 29(1): 87-96. (  0) 0) |
| [6] |
DHI group. MIKE21 Boussinesq Wave Module Scientific Documentation[S]. New York: DHI, 2009.
(  0) 0) |
| [7] |
董胜, 冯春明, 张华昌. 日照帆船港港域波高的数值计算[J]. 中国海洋大学学报, 2006, 36(6): 995-998. Dong S, Feng C M, Zhang H C. Numerical calculation of wave height in the basin of Rizhao sailing boat harbor[J]. Periodical of Ocean University of China, 2006, 36(6): 995-998. (  0) 0) |
| [8] |
张娜, 郭科, 王旭辉. MIKE21-BW模型在日照港总平面设计方案可行性研究中的应用[J]. 中国港湾建设, 2007(1): 32-34. Zhang N, Guo K, Wang X H. Application of MIKE21-BW model to feasibility study of general plan layout of Rizhao port[J]. China Harbour Engineering, 2007(1): 32-34. (  0) 0) |
| [9] |
王中起. 某拟建修造船厂工程波浪分析[J]. 水运工程, 2011(5): 45-49. Wang Z Q. Wave deformation near a dockyard[J]. Port & Waterway Engineering, 2011(5): 45-49. (  0) 0) |
| [10] |
徐俊锋, 方春明, 黄烈敏, 等. 应用MIKE21 BW模型分析航道对波浪传播的影响[J]. 中国水利水电科学研究院学报, 2011, 9(4): 292-297. Xu J F, Fang C M, Huang L M, et al. Analysis of the impact of navigation upon wave propagation by using MIKE21 BW module[J]. Journal of China Institute of Water Resources and Hydropower Research, 2011, 9(4): 292-297. (  0) 0) |
| [11] |
林法玲. 渔港有效避风面积计算探讨--以霞关渔港为例[J]. 海洋预报, 2012, 29(6): 92-97. Lin F L. Discussion of effectively sheltered area for fishery port-An example of Xiaguan fishery port[J]. Marine Forecasts, 2012, 29(6): 92-97. DOI:10.11737/j.issn.1003-0239.2012.06.012 (  0) 0) |
| [12] |
贾晓, 张峰, 邵燕华. 透浪建筑物掩护水域波浪数值模拟研究[J]. 水运工程, 2013(11): 153-158. Jia X, Zhang F, Shao Y H. Wave numerical simulation about waters sheltered by permeable hydraulic structures[J]. Port & Waterway Engineering, 2013(11): 153-158. DOI:10.3969/j.issn.1002-4972.2013.11.033 (  0) 0) |
| [13] |
吴亚楠, 董胜, 张华昌. 威海船厂港域泊稳试验研究与数值模拟[J]. 水运工程, 2015(1): 13-18. Wu Y N, Dong S, Zhang H C. Experimental test and numerical simulation of berthing in harbor basin of Weihai shipyard[J]. Port & Waterway Engineering, 2015(1): 13-18. (  0) 0) |
| [14] |
冯卫兵, 黄颖娜, 厉佳卉. BW模型在掩护水域内波浪计算中的应用[J]. 水运工程, 2015(11): 8-13. Feng W B, Huang Y N, Li J H. Application of wave field simulation in sheltered waters based on BW model[J]. Port & Waterway Engineering, 2015(11): 8-13. DOI:10.3969/j.issn.1002-4972.2015.11.002 (  0) 0) |
| [15] |
张华昌, 柳玉良. 青岛万达东方影都人工岛、游艇码头项目游艇码头港池泊稳物理模型试验报告[R]. 青岛: 海军工程设计研究院工程综合试验研究中心, 2014. Zhang H C, Liu Y L. The report of the physical modeling experiment of berthing in Qingdao Wanda marina[R]. Qingdao: Experiment Research Center, Navy Engineering Design and Research Institute, 2014. (  0) 0) |
| [16] |
Hasselmann K, Barnett T P, Bouws E, et al. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP)[J]. Dtsch Hydrogr Z, 1973, 8(12): 1-95.
(  0) 0) |
2. National Marine Environmental Monitoring Center, Dalian 116023, China;
3. Experiment Research Center, Navy Engineering Design and Research Institute, Qingdao 266100, China
 2018, Vol. 48
2018, Vol. 48

