反应器网络综合是化工过程综合的重要组成部分，对化工过程开发和反应器工艺的优化设计等具有重要意义。依据动力学特征，Chitra等^[1-2]、赵文^[3]以及本文作者^[4]都将反应体系分为三类。虽然分类方法不同，但对第三类反应体系的描述都是相同的，即允许反应物到目的产物的过程中含多个中间产品的反应体系。针对第一二类简单反应体系已发展了多种综合方法，如依据反应过程化工知识和经验进行反应器网络综合的直接推断法^[5-7]；可得区法由Horn^[8]最先提出，Hildebrandt等^[9-10]采用几何法更清楚的阐述了可得区的基本思想，赵文等^{[3, 11]}将可得区法用于求解反应器网络废料最少的问题，Glasser等^[12-13]在可得区内引入温度变量，深入研究了可逆放热反应在不同换热操作下的综合问题，但对复杂反应体系可得区法的应用受维数限制。Kokossis等^[14-15]提出了针对等温和非等温问题的超结构优化法，Marquardt等^[16]提出流程和分散控制系统同时优化的超结构法，及耿宁^[17]提出基于功能性催化剂排列的反应路径和反应器网络同步优化的超结构法，超结构法虽不受维数限制，但开发合适的数学算法困难。胡仰栋等^[18-19]针对简单反应体系提出了用目标函数瞬时值的导数与反应器选型之间的关系进行反应器网络综合的导数分析法，并应用于几个实例证明了导数分析法的有效性和简捷性。

本文发展了适用于复杂反应体系反应器网络综合的导数分析法，提出以反应步数为依据的新分段策略，对分段副产物瞬时选择性进行导数分析选择各阶段合适的反应器，以目的产物总选择性为目标函数优化反应器网络。

1 导数分析法

导数分析法是用目标函数瞬时值的导数与反应器选型之间的关系进行反应器网络综合的方法^[18]。

本文将目标函数瞬时值与反应器类型选择之间的关系简要概括为在最优反应器网络中采用CSTR型反应器的必要条件是：目标函数瞬时值对关键反应物浓度或转化率的全导数：$\frac{{{\rm d}B}}{{{\rm d}{C_A}}} \le 0 $或$ \frac{{{\rm d}B}}{{{\rm d}{X_A}}} \ge 0$；采用PFR型反应器的必要条件是：目标函数瞬时值对关键反应物浓度或转化率的全导数：$\frac{{{\rm d}B}}{{{\rm d}{C_A}}} \ge 0 $或$ \frac{{{\rm d}B}}{{{\rm d}{X_A}}} \le 0$。

2 第三类反应体系的反应器网络综合 2.1 反应分段策略

本文作者曾提出复杂反应的分段策略^[20]，该策略将反应过程中$ \frac{{{\rm d}{C_i}\left( \tau \right)}}{{{\rm{{\rm d}}}t}} < 0$的组分i称为瞬时反应物，$ \frac{{{\rm d}{C_j}\left( \tau \right)}}{{{\rm{d}}t}} > 0$的组分j为瞬时产物，依据瞬时反应物和瞬时产物组成不同将反应分段。该策略将分段过程复杂化，故本文结合实际工业中反应器设计的分段方法提出将串联反应以反应物到目的产物的反应步数为依据进行分段，简化分段过程。以Denbigh反应为例介绍分段策略。

Denbigh反应式：

$ \begin{align} & A\xrightarrow{{{r}_{1}}}B\xrightarrow{{{r}_{3}}}D, \\ & A\xrightarrow{{{r}_{2}}}C, \\ & B\xrightarrow{{{r}_{_{4}}}}E \\ \end{align} $

串联反应过程为A→B→D，A为关键反应物，D为最终的目的产物。从反应物A到目的产物D的反应步数为两步，故将Denbigh反应分为A→B和B→D两个阶段。将反应物相同的副反应归为同一阶段，则最终第一阶段为A→B和A→C，第二阶段为B→D和B→E。

当反应的中间产品增多，如A→B→C→D→E的串联反应，其中A为反应物，E为目的产物。从反应物到目的产物的反应步数为四步，则将反应分为A→B，B→C，C→D和D→E四个阶段。

2.2 过程参数分析与反应器网络综合

由于复杂反应的中间产品和副产物种类繁多，原简单反应体系速率瞬时值或目的产物瞬时选择性不再适用，须寻找新目标函数瞬时值描述复杂反应的过程特性。本文所研究的反应均为恒温、恒容过程。

通过Denbigh反应为例介绍本文设计的四种目标函数瞬时值S，分别是反应在不分段时目的产物对关键反应物的瞬时选择性S₁，中间产品和目的产物共同组成目的产物对关键反应物的瞬时选择性S₂，以及反应分段时两个阶段目的产物瞬时选择性S₃₁和S₃₂，两个阶段副产物瞬时选择性S₄₁和S₄₂。对这四种目标函数瞬时值导数分析后选择的反应器进行比较，选择最合适的参数进行反应器网络综合。四种不同瞬时选择性S及S~X_A曲线如下所示：

$ {S_1} = \frac{{{\rm{d}}{C_D}}}{{{\rm{ - d}}{C_A}}} = \frac{{{r_3}}}{{{r_1} + {r_2}}}。$

(1)

$ {S_2} = \frac{{{\rm{d}}{C_B} + {\rm{d}}{C_D}}}{{{\rm{ - d}}{C_A}}} = \frac{{{r_1} - {r_3} - {r_4} + {r_3}}}{{{r_1} + {r_2}}} = \frac{{{r_1} - {r_4}}}{{{r_1} + {r_2}}}。$

(2)

$ \begin{array}{l} {S_{31}} = \frac{{{\rm{d}}{C_B}}}{{ - {\rm{d}}{C_A}}} = \frac{{{r_1} - {r_3} - {r_4}}}{{{r_1} + {r_2}}},\\ {\rm{ }}{S_{32}} = \frac{{{\rm{d}}{C_D}}}{{ - {\rm{d}}{C_B}}} = \frac{{{r_3}}}{{{r_3} + {r_4} - {r_1}}}。\end{array} $

(3)

$ {S_{41}} = \frac{{{\rm{d}}{C_C}}}{{ - {\rm{d}}{C_A}}} = \frac{{{r_2}}}{{{r_1} + {r_2}}},{S_{42}} = \frac{{{\rm{d}}{C_E}}}{{ - {\rm{d}}{C_B}}} = \frac{{{r_4}}}{{{r_3} + {r_4} - {r_1}}}。$

(4)

由图 1可知不分段时，S₁对X_A的导数结果为$ \frac{{{\rm d}{S_1}}}{{{\rm d}{X_A}}} < 0$，依据反应器选择的必要条件选择CSTR。S₂对X_A的导数结果先负后正，则反应器网络为PFR+CSTR。

由图 2可知反应分段时，分段目的产物瞬时选择性S₃₁对X_A的导数结果为$\frac{{{\rm d}{S_{31}}}}{{{\rm d}{X_A}}} < 0 $，依据必要条件第一阶段选择PFR。S₃₂对X_A的导数结果先负后正，第二阶段选择PFR+CSTR。分段副产物瞬时选择性S₄₁对X_A的导数结果为$ \frac{{{\rm d}{S_{41}}}}{{{\rm d}{X_A}}} > 0$，得到适合副产物生成的反应器为返混较大的CSTR，但反应目标是减少副产物的生成，故选返混较小的PFR。同理因$\frac{{{\rm d}{S_{42}}}}{{{\rm d}{X_A}}} < 0 $，则第二阶段选择CSTR减少副产物生成。

由S₄₁和S₃₁均选择PF可知S₁选择单个CSTR反应器不是最优的，优化结果也证明了该点，S₂存在负值，故不分段时的S₁和S₂均无法准确描述反应过程。S₄₁和S₄₂选择了各阶段合适的反应器，但S31存在负值且S₃₂在一阶段内确定了两个反应器，故分段副产物瞬时选择性优于分段目的产物瞬时选择性。

分析分段目的产物瞬时选择性不如分段副产物瞬时选择性准确的原因，是中间产品参与两个阶段的反应，将其作为某一阶段的过程参数是不准确的。如S₃₁中dC_B的变化与A的反应速率r₁和D、E的生成速率r₃、r₄有关，仅将其作为第一阶段参数会出现负值则无法准确描述第一阶段的反应过程。而分段副产物瞬时选择性无此类问题，因为副产物仅由各阶段的反应物生成，分段副产物瞬时选择性仅与该阶段反应物有关。如第一阶段副产物C仅由A反应生成，S₄₁仅与C_A有关，其导数分析选择的是该阶段最优的反应器。故本文以分段副产物瞬时选择性作为参数，对其采用导数分析进行反应器网络综合。

采用分段副产物瞬时选择性导数分析法得到Denbigh反应的最优反应器网络为PFR+CSTR。当反应更复杂时，本方法能确保各阶段为最优的反应器，串联得到最优反应器网络。故本方法得到的最优反应器网络是CSTR和PFR组成的串联结构，最优反应器网络和工艺参数由这些串联结构依据不同目标优化得到。

2.3 工艺参数优化

由分段副产物瞬时选择性的导数分析得出反应器网络结构后，需要依据不同的工业目标优化工艺参数。如本文优化模型的目标函数为最终目的产物对关键反应物的总选择性S_t最大，决策变量为各反应器出口处关键反应物的转化率X_An。

目标函数：

$ {\rm{max}}{S_t} = \frac{{\Delta {C_D}}}{{\Delta {C_A}}}\varphi = \frac{{{C_{Dexit}} - {C_{D0}}}}{{{C_{A0}} - {C_{Aexit}}}}\varphi 。$

(5)

式中：C_A表示关键反应物A的浓度，C_D表示目的产物D的浓度；C_A0和C_D0表示进料时A和D的浓度；C_Aexit和C_Dexit表示反应器网络出口处A和D的浓度；φ与计量系数有关，本文取为1。

约束条件：

$ \left\{ \begin{array}{l} 0 \le {X_{A1}} < 1\\ {X_{A1}}A2 < 1\\ \ldots \\ {X_{An}}An + 1 < 1\\ n = 1,2,...N - 1 \end{array} \right.。$

(6)

PFR:

$ \frac{{{\rm{d}}C_m^p}}{{{\rm{d}}\tau }} = r\left( {C_m^p} \right). $

(7)

CSTR:

$ C_{exit,m}^C - C_{i,m}^C = \tau \cdot r\left( {C_m^C} \right)。$

(8)

式(6)中X_An为第n个反应器出口处A的总转化率，N为反应器个数。式(8)中C_{i, m}^C和C_{exit, m}^C表示组分m在CSTR进口和出口处浓度，同理C_{i, m}^p和C_{exit, m}^p分别表示组分m在PFR进口和出口处浓度。则在CSTR+PFR结构中存在关系式C_{exit, m}^C=C_{i, m}^p，在PFR+CSTR的结构中存在关系式C_{exit, m}^p=C_{i, m}^C，且C_{exit, m}^C与C_{exit, m}^p由反应器出口处X_A决定。

本文采用遗传算法优化反应器网络^[21]。优化时种群数为50，交叉和变异概率分别为0.8和0.01，采用轮盘赌选择父辈并进行交叉和变异操作，产生的子代个体不断重复以上操作直至S_t最优。其中第一个转化率的边界为[0, 1)，第二个转化率的边界条件为(X_A1, 1)。

3 算例研究 3.1 Denbigh反应

其反应动力学参数如下：

r₁ = k₁ C_A², r₂ = k₂ C_A, r₃ = k₃ C_B, r₄ = k₄ C_B² k₁ = 1l/(mol·s), k₂ = 0.6 s^-1, k₃ = 0.6 s^-1, k₄ = 0.1l/(mol·s)

采用遗传算法对不同反应器网络进行优化，并对结果进行比较。优化结果列于表 1，其中X_A1和X_A2为各反应器出口处A的总转化率。图 3、4分别为PFR+DSR和循环PFR+CSTR结构图。

从表 1可知，PFR+CSTR结构的总选择性大于其他结构，故PFR+CSTR为Denbigh反应的最优反应器网络，且本文的总选择性比文献值更高。

3.2 九组分反应

九组分反应式和动力学参数如下：

$ \begin{align} A\xrightarrow{{{r}_{1}}}B\xrightarrow{{{r}_{3}}}C\xrightarrow{{{r}_{3}}}D\xrightarrow{{{r}_{7}}}E, \\ A\xrightarrow{{{r}_{2}}}F\xrightarrow{{{r}_{4}}}G\text{ }C\xrightarrow{{{r}_{6}}}H\text{ }D\xrightarrow{{{r}_{s}}}I, \\ {r_1} = {k_1}C_A^2,{r_2} = {k_2}{C_A},{r_3} = {k_3}{C_B},{r_4} = {k_4}C_B^2,{\rm{ }}\\ {r_5} = {k_5}C_C^2,{r_6} = {k_6}{C_C},{r_7} = {k_7}{C_D},{r_8} = {k_8}C_D^2,{\rm{ }}\\ {k_1} = 5{\rm{ }}l/({\rm{mol}}\cdot{\rm{s}}),{k_2} = 0.5{{\rm{s}}^{ - 1}},\\ {k_3} = 5{{\rm{s}}^{ - 1}},{k_4} = 0.5l/({\rm{mol}}\cdot{\rm{s}}),\\ {k_5} = 5{\rm{ }}l/({\rm{mol}}\cdot{\rm{s}}),{k_2} = 0.5{{\rm{s}}^{ - 1}},\\ {k_3} = 5{{\rm{s}}^{ - 1}},{k_4} = 0.5l/({\rm{mol}}\cdot{\rm{s}}). \end{align} $

其中：A为关键反应物；E为最终目的产物；B、C、D为中间产品；F、G、H、I为副产物。反应进料为纯A，C_A0=10 mol/L。

先将反应按新分段策略分为四个阶段，第一阶段为A→B和A→F，第二阶段为B→C和B→G，第三阶段为C→D和C→H，第四阶段为D→E和D→I。

计算各阶段的副产物瞬时选择性，依据导数分析确定最终的反应器网络结构为：PFR+CSTR+PFR+CSTR。各阶段瞬时选择性结果如图 5所示：

用遗传算法求解不同反应器网络进行求解，并对结果进行比较，不同结构的最优结果列于表 2，其中X_A1, X_A2, X_A3, X_A4, X_A5为对应各反应器出口处A的总转化率。

从表 2可知，PFR+CSTR+PFR+CSTR结构的总选择性优于其他结构，且比文献结果更优，说明本方法得到的PFR+CSTR+PFR+CSTR结构是最优反应器网络。第四阶段的反应器内A变化很小，舍去CSTR后的PFR+CSTR+PFR结构也能获得较高的总选择性。

3.3 Van de Vusse反应

Van de Vusse反应式是第二类反应体系中的典型反应，其反应式如下：

$ \begin{align} & A\xrightarrow{{{r}_{1}}}B\xrightarrow{{{r}_{2}}}C,2A\xrightarrow{{{r}_{3}}}D\text{ } \\ & {{r}_{1}}={{k}_{1}}{{C}_{A}},{{r}_{2}}={{k}_{2}}{{C}_{B}},{{r}_{3}}={{k}_{3}}C_{A}^{2} \\ & ~{{k}_{1}}=10~{{\text{s}}^{-1}},{{k}_{2}}=1~{{\text{s}}^{-1}},{{k}_{3}}=1\prime l/(\text{mol}\cdot \text{s})。\\ \end{align} $

目的产物为B，反应进料为纯A，C_A=5.8mol/L。由于反应的中间产品B即为反应的目的产物，故本例将反应分为一个阶段，即A→B和2A→D。其副产物瞬时选择性的导数如式(9)所示：

$ \frac{{{\rm{d}}S}}{{{\rm{d}}{C_A}}} = \frac{{10}}{{{{\left( {10 + {C_A}} \right)}^2}}} > 0。$

(9)

由导数分析结果可知van de Vusse反应的最优反应器网络为单个CSTR，对其总选择性进行优化并与PFR和CSTR+PFR结构的结果比较。各结构的优化结果列于表 3，其中X_A1和X_A2为各反应器出口处A的总转化率。

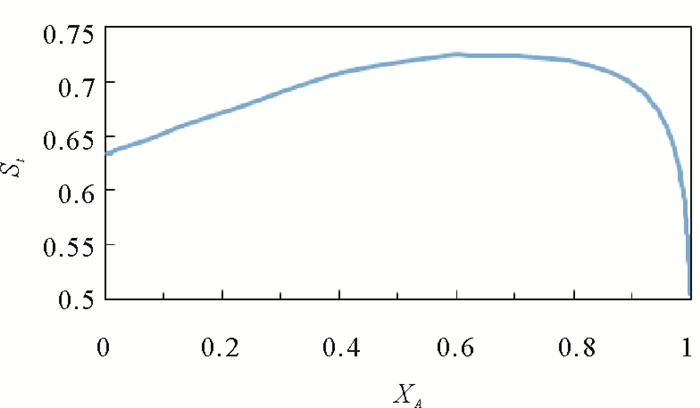
从表 3可知CSTR和CSTR+PFR结构的选择性均优于单个PFR，且前两者选择性基本相等，即仅CSTR就可使总选择性最大；图 6是传统以C_B最大为目标得到的CSTR+PFR结构在最优反应器网络中目的产物总选择性与转化率X_A的关系图，可知总选择性在PFR中呈下降趋势，表明CSTR+PFR结构中的PFR对提高总选择性不利，故最优反应器网络为CSTR。

Van de Vusse反应是第二类反应体系中的典型反应，其结果证实本方法选择的过程参数和目标函数是准确的，且本方法同样适用于第二类反应体系。

4 结论

针对复杂反应体系中间产品较多的特点，发展了适用于复杂反应体系反应器网络综合的导数分析法。

(1) 本文提出将串联反应以反应物到目的产物的反应步数为依据的分段策略，通过对分段副产物瞬时选择性进行导数分析确定反应器类型，运用遗传算法进行求解确定最优的反应器网络。

(2) 采用三个算例验证了以分段副产物瞬时选择性的导数分析进行反应器网络综合的有效性和简捷性，且得到的最优反应器网络是由CSTR和PFR的串联而成。其中，van de Vusse反应的综合结果说明本方法同样适用于第二类反应体系。

符号说明：