基因重组是生物进化中的一个重要过程,它能够产生基因组序列的多样性[1]。目前研究表明,不同物种之间或同一物种的不同染色体(甚至是同一染色体的不同区域)之间,重组率都是不同的[2]。重组频率高的区域称为重组热点,重组频率低的区域称为重组冷点[3]。
正确识别重组热点和重组冷点对理解重组机制和生物进化过程十分重要。常规的生化实验和基因比较方法可以识别重组位点[2, 4-5],但随着生物信息学的发展,所研究的基因数量呈爆炸式增长,常规的生化实验显得既费时又费力,所以急需开发快速且有效识别重组位点的方法。目前,已经提出了一些基于DNA序列内容信息识别重组位点的计算方法。首先,Jiang等提出了间隙二核苷酸的随机森林分类模型,得到82.05%的准确率[6]。Zhou等提出了基于密码子组合的支持向量机分类模型[7];Liu等建立了基于序列k-mer频率的二次判别分析模型[8]。但这些方法都忽略了DNA序列的一些顺序信息,而这些信息在文献[9]中被证明是重要的。因此,一些研究者提出了基于DNA序列顺序信息的计算方法。Chen等基于伪氨基酸(PseAAC)[9]并结合DNA的6个特性,提出iRSpot-PseDNC模型[10]识别重组位点;Qiu等将3-gram组成与伪氨基酸组成相结合识别重组位点,建立了iRSpot-TNCPseACC分类模型[11];之后,Liu等利用加权特征识别重组位点[12];Long等建立了集成分类器模型识别重组位点,该模型称为iRSpot-EL[13];近年来,Zhang等通过将相关二核苷酸产物模型整合到Chou的伪成分中,提出了iRSpot-ADPM模型识别重组位点[14];Yang等将六聚体整合到一般的K元伪成分中识别重组位点,提出了iRSpot-Pse6NC模型[15];Al Maruf等通过融合不同的特征识别重组位点,提出了iRSpot-SF模型[16];Khan等将深度神经网络用在二级序列信息和理化衍生特征上识别重组位点,提出了iRSpot-SPI模型[17]。过去,Asgari和Mofrad成功地将自然语言处理技术应用到生物学中[18]。受到上述启发,Do等利用自然语言处理中的FastText模型处理DNA序列实现了重组位点的识别,且得到了92.6%的准确率[19]。
本文基于DNA序列提出了一个新的特征提取方法。首先,通过自然语言处理中的Word2Vec模型编码3-gram向量来表示DNA序列,获得一组新特征。然后,基于DNA特性设计一个新的计算公式,且沿着DNA序列量化不同位置二核苷酸对的关系求得另一组新特征。最后,将这两组新特征与文献[19]的特征进行组合,将组合特征输入支持向量机(Support vector machine, SVM)算法中构建一个分类器模型。在基准数据集上采用5倍交叉验证评估该模型的识别效果,结果优于现有的其他方法,证明了本文提出的方法在重组位点识别方面的有效性。
1 材料和方法 1.1 数据集本文使用的数据集来自http://lin-group.cn/server/iRSpot-Pse6NC/网站。Liu等人通过实验数据计算出重组位点率构建了该数据集,他们在Gerton等人和Jiang等人研究的基础上确定了“热”和“冷”的开放阅读框,使用UCSC基因浏览器检索上游和下游序列。因此,本文使用的基准数据集在预测重组位点方面十分有效可靠,且多次用于重组位点分类研究[10-17, 19]。该基准数据集包含490个DNA热点样本和591个冷点样本。方便起见,将基准数据集记为S,表示如下:
| $ S=S^{+} \cup S^{-}, $ | (1) |
式中:S+为重组热点集合;S-为重组冷点集合。
1.2 特征提取方法数据集S中的每一个DNA样本表示如下:
| $ D=R_1 R_2 \cdots R_i \cdots R_{L }。$ | (2) |
式中:Ri表示DNA序列第i个位置上的核苷酸,Ri={A1T1C1G}; L是DNA序列长度。
文献[19]利用FastText模型(包括子词信息)对DNA序列进行处理,获得一部分特征, 维数为100,表示如下:
| $ F_f=\left(a_1, a_2, \cdots, a_{100}\right)^{\mathrm{T}} \text { 。} $ | (3) |
式中T为转置符号。下面章节将详细介绍新特征的提取方法。
1.2.1 基于DNA特性表示DNA序列DNA特性包含二核苷酸的灵活性值、结构和热力学参数(见表 1)。首先,利用公式(4)对表 1中的参数进行标准化:
| $ \frac{P-P_{\min }}{P_{\max }-P_{\min }} 。$ | (4) |
|
|
表 1 DNA原始特性(二核苷酸属性) Table 1 Original property of DNA(the dinucleotide property) |
式中:P为原始属性值;Pmin为最小属性值;Pmax为最大属性值。
将表征DNA序列的特征向量[20]表示如下:
| $ F_P=\left(f_{1, 1, 1}, f_{1, 1, 2}, \cdots, f_{s, t, g}\right)^{\mathrm{T}} \text { 。} $ | (5) |
式中:s=1, 2, ⋯, 15;t=s, s+1, ⋯,15;g=1, 2, ⋯, G。s, t是表 1中二核苷酸特性对应的索引,g是一个间隙因子,它决定了沿着序列的二核苷酸的分隔程度(见图 1),G是g的最大值。l是DNA序列长度,Θi, g, s, t称为差积因子,如(6)式所定义:
| $ \varTheta_{i, g, s, t}=\left(P_{i, s}-P_{i+g, s}\right) \times\left(P_{i, t}-P_{i+g, t}\right) \text { 。} $ | (6) |
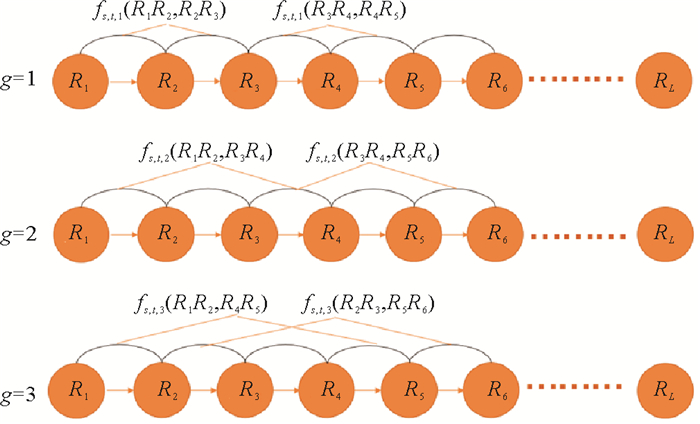
|
图 1 g的分隔程度和特征FP产生过程 Fig. 1 Separation degree of g and the generation process of feature FP |
式中:Pi, s表示第i个位置上的二核苷酸(RiRi+1)的第s个属性;Θi, g, s, t反映了不同位置二核苷酸之间的联系。利用(5)式可以把每一个DNA序列转化为维数是120×G的特征向量Fp。
特征向量Fp的维数随着G的变化而变化,当G=1时,Fp的维数是120,而当G=13时,维数增加到了1 560维,虽然维数增加,但结果并没有改善。本文基于基准数据集分别计算了G=1, 2, ⋯⋯, 13对应的特征向量,将特征向量Ff和不同G值对应的新特征向量组合进行训练,如图 2所示,当G=4时准确率达到最大值。因此,选取间隙因子G=4计算新特征Fp,再利用递归特征消除方法[21]去除冗余特征,得到32维特征向量Fp,表示如下:
| $ F_p=\left[f_1, f_2, \cdots, f_i, \cdots, f_{32}\right]^{\mathrm{T}} \text { 。} $ |
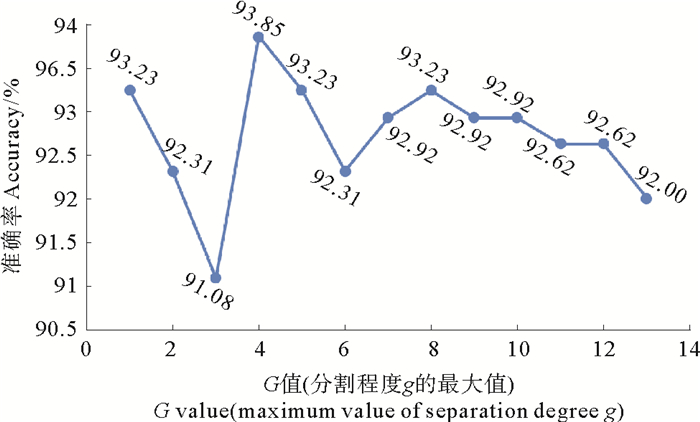
|
图 2 G值从1到13对应的准确率 Fig. 2 Accuracy corresponding to the G value from 1~13 |
本节将自然语言处理技术应用到生物信息学中,每个DNA序列视为一个“句子”,所有可能长度为的核苷酸片段序列(称为n-gram)视为“单词”。文献[19]利用FastText模型的子词信息计算特征向量时,使用高元字符8-gram作为“单词”来表示DNA序列,这极有可能忽略掉低元字符n-gram(n=1, 2, 3)的相关信息。利用低元字符1-gram, 2-gram表示DNA序列过于简单,经过测试3-gram得到的效果是最好的,所以本文使用低元字符3-gram作为“单词”来表示DNA序列。图 3展示了沿着DNA序列用大小为3,步长为1的窗口将DNA序列划分为一个个长度为3的片段序列(3-gram)的过程。因为DNA由4种核苷酸组成,所以共有64种3-gram。数据集中的每个DNA序列样本都可由3-gram表示。
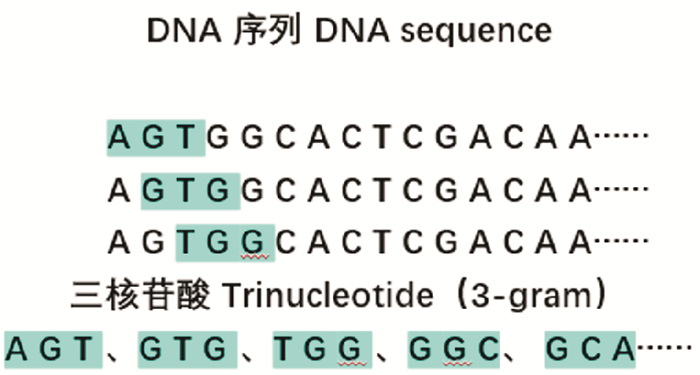
|
图 3 3-gram提取过程 Fig. 3 Extraction process of 3-gram |
由于计算机分类模型只能接收数值型输入,所以需要将3-gram转化成对应的特征向量。one-hot编码[22]是一种非常简单的词表示方式,但使用one-hot编码表示单词存在一定的缺陷,它的维数较高且无法体现不同单词之间的关系。为弥补这些缺陷,本文使用Word2Vec的skip-gram模型[22]将3-gram的one-hot编码映射到低维稠密空间得到新的特征向量,这个特征向量是低维的且相互之间有一定的关系,是3-gram的词向量。
如图 4所示,skip-gram模型是一种由输入层、隐含层和输出层组成的神经网络。计算3-gram的词向量时,将DNA序列任意位置的3-gram作为中心词输入,这个中心词的上下文单词(上下文距离为5)[23]作为输出。训练完整个模型后,得到一个维数是64×64的3-gram词向量矩阵
| $ \boldsymbol{W}=\left[w_1, w_2, \cdots, w_{64}\right]^{\mathrm{T}} 。$ | (8) |
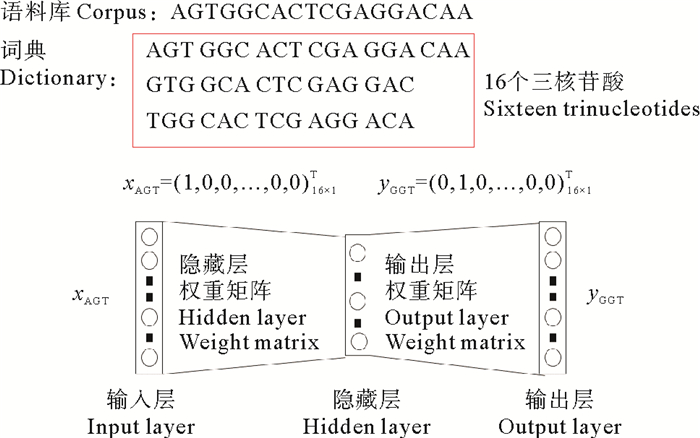
|
图 4 用skip-gram模型训练3-gram的简化表示 Fig. 4 Simplified representation of 3-gram is trained by skip-gram model |
式中wi=(v1, v2, ⋯, v64)(i=1, 2, ⋯, 64)是3-gram对应的词向量。
对于每个长度为L的DNA序列样本,按照图 3的方式会分割成L-2个3-gram,结合3-gram词向量和(10)式,得到了代表DNA序列的64维新特征向量,表示为:
| $ F_w=\left(b_1, b_2, \cdots, b_{64}\right)^{\mathrm{T}}=\frac{\sum\limits_{j=1}^{L-2} w_{j i}}{L}, i=1, 2, \cdots, 64 。$ | (9) |
式中wji表示DNA序列样本第j个位置上的3-gram所对应的词向量。
1.3 分类算法DNA重组位点识别研究的是将给定的DNA序列分配给热点还是冷点的分类问题。因此,选择一个合适的分类算法至关重要。SVM[24-25]因在生物问题上表现优异而常被用于各种生物问题,所以本文选择SVM作为分类算法。本文基于Scikit-learn包实现SVM分类器,使用GridSearchCV函数寻找最佳核函数和核函数相关参数,直接利用GridSearchCV的best_estimator_属性训练模型,保证模型的最佳性能。
1.4 预测评估为与其他现存方法保持一致,本文采用了五倍交叉验证。五倍交叉验证循环中加入参数优化过程, 以确保模型的最佳性。
除评估方法外,本文还使用了几个常用的评估指标。准确率(Accuracy,Acc)是所有分类正确的样本占全部样本的比例,是最常用的分类性能指标。敏感性(Sensitivity,Sen)又称为召回率,表示分类器预测正确的正样本占所有正样本的比例。特异性(Specificity, Spec)用于衡量分类器对负样本的识别能力。F1-measure是精确度和敏感度的调和平均(取值为[0, 1]),越接近1越好。受试者操作特性曲线图(Receiver operating characteristic curve,ROC)是以假阳性概率为横轴、真阳性概率为纵轴组成的坐标图,是最有价值的统计工具。ROC曲线下的面积(Area under curve, AUC)是衡量学习器性能优劣的一种性能指标,范围是[0, 1],越接近1说明分类器效果越好。
2 结果与讨论本节将讨论新特征的重要性,且将本文所提出的方法与现存方法进行比较。在基准数据集上,通过5倍交叉验证获取评估指标,具体细节在以下小节中描述。
2.1 新特征重要性分析为了更加全面地表征DNA序列信息,本文利用公式(6)、(7)与DNA特性相结合,得到新特征向量Fp(见公式(8)),将Fp与已有的特征Ff(公式(3))直接拼接得到
| $ F_f+F_p=\left(a_1, a_2, \cdots, a_{100}, f_1, f_2, \cdots, f_{32}\right), $ | (10) |
以此表征DNA序列信息识别重组位点。
由表 2可知,与只用特征向量Ff表征DNA序列的分类结果相比,组合特征向量Ff+Fp的Sen、Acc和MCC值分别提高了2.65%、0.55%和0.011 9,但Spec没有得到改善。
|
|
表 2 特征重要性分析结果比较 Table 2 Comparison of feature importance analysis results |
特征向量Ff只包含嵌入在高元字符8-gram的特定信息,低元字符(3-gram)的相关信息被忽略掉。为了获得3-gram相关信息,本文选择自然语言处理中的Word2Vec模型计算3-gram的词向量,再利用公式(10)计算DNA序列的平均词向量,得到了新特征向量Fw。为了证明特征向量Fw的重要性,将Fw与特征向量Ff+Fp进行拼接组合,得到最终的组合特征:
| $ F_f+F_p+F_w=\left(a_1, \cdots, a_{100}, f_1, \cdots, f_{32}, b_1, \cdots, b_{64}\right), $ | (11) |
以此表征DNA序列信息识别重组位点。
如表 2所示,组合特征Ff+Fp+Fw对应的Sen、Spec、Acc和MCC值分别为93.88%、95.08%、94.54%和0.890 2,相比只用Ff和Ff+Fp表征DNA序列识别重组位点,各指标都得到提升,这充分说明低元字符3-gram和DNA特性相关信息的特征是重要的,同时也说明本文提出的特征提取方法在识别重组位点方面的有效性。
2.2 与现存方法比较为了进一步评估所提出方法的有效性,将本文提出的方法与其他方法进行比较,为了比较的公平性,与那些使用相同数据集和交叉验证的方法进行比较。它们的性能结果在表 3中给出,最好的结果用粗体表示。
|
|
表 3 同一基准数据集上与其他现存方法比较 Table 3 Compared with other existing methods on the same benchmark dataset |
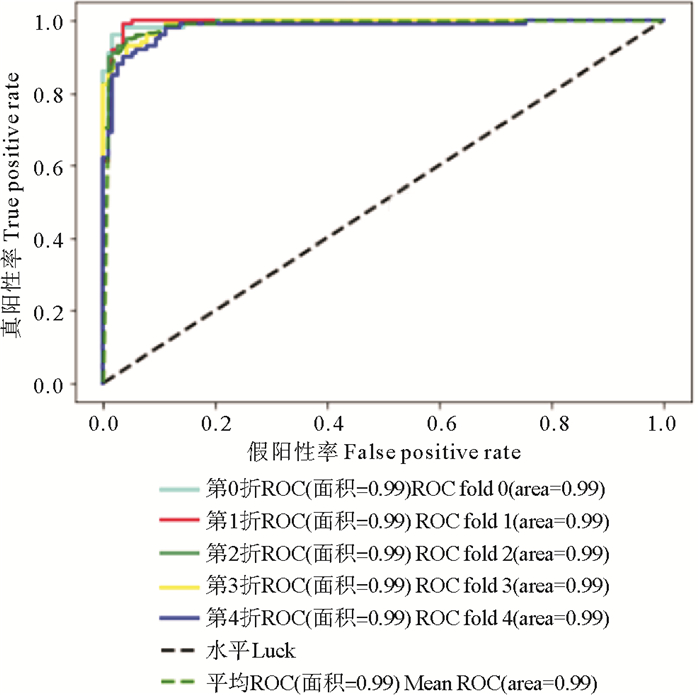
由表 3可知,本文提出的方法在识别重组位点方面获得了93.88%的Sen、95.08%的Spec、94.54%的Acc和0.890 2的MCC值,各指标都优于最新的Fast-Text-SVM[19]方法。AUC是十分重要的统计参数工具,图 5给出了不同折叠值下的ROC曲线分析,AUC均值为0.99, 这表明该模型的分类真实性。除此之外,93.99%的F1-measure值表明该预测模型没有过拟合。以上评估指标均表明本文提出的方法在识别重组位点方面的有效性和可靠性。
|
图 5 本文模型的ROC曲线 Fig. 5 The ROC curve of the model in this paper |
为了更加全面地表征DNA序列信a息,提高重组位点的分类准确率,本文提出了一个新的DNA序列特征提取方法来识别重组位点,将Word2Vec模型得到的低元字符相关信息新特征和基于DNA特性计算得到的新特征,与文献[19]的高元字符相关信息特征(FastText模型获取)进行组合,用组合特征表示DNA序列识别重组位点。通过将本文提出的方法与现存方法进行比较,验证了本文方法的有效性和优势。同时,研究结果也表明低元字符的信息和DNA特性不可忽略。本文提出的方法为研究生物序列信息提取的相关问题提供新的思路和启示。
| [1] |
Paul P, Nag D S, Chakraborty S. Recombination hotspots: Models and tools for detection[J]. DNA Repair, 2016, 40: 47-56. DOI:10.1016/j.dnarep.2016.02.005 (  0) 0) |
| [2] |
Jensen-Seaman M I, Furey T S, Payseur B A, et al. Comparative recombination rates in the rat, mouse, and human genomes[J]. Genome Research, 2004, 14: 528-538. DOI:10.1101/gr.1970304 (  0) 0) |
| [3] |
Dong C, Yuan Y, Zhang F, et al. Combining pseudo dinucleotide composition with the Z curve method to improve the accuracy of predicting DNA elements: A case study in recombination spots[J]. Molecular BioSystems, 2016, 12: 2893. DOI:10.1039/C6MB00374E (  0) 0) |
| [4] |
Gerton J L, DeRisi J, Shroff R, et al. Global mapping of meiotic recombination hotspots and coldspots in the yeast Saccharomyces cerevisiae[J]. Proceedings of the National Academy of Sciences, 2000, 97: 11383-11390. DOI:10.1073/pnas.97.21.11383 (  0) 0) |
| [5] |
Lefeuvre P, Lett J M, Varsani A, et al. Widely conserved recombination patterns among single-stranded DNA viruses[J]. Journal of Virology, 2009, 83: 2697-2707. DOI:10.1128/JVI.02152-08 (  0) 0) |
| [6] |
Sang F, Wu H, Wei J, et al. RF-DYMHC: Detecting the yeast meiotic recombination hotspots and coldspots by random forest model using gapped dinucleotide composition features[J]. Nucleic Acids Research, 2007, 35: 47-51. (  0) 0) |
| [7] |
Zhou T, Weng J, Sun X, et al. Support vector machine for classification of meiotic recombination hotspots and coldspots in Saccharomyces cerevisiae based on codon composition[J]. BMC Bioinformatics, 2006, 7: 223. DOI:10.1186/1471-2105-7-223 (  0) 0) |
| [8] |
Liu G, Liu J, Cui X, et al. Sequence-dependent prediction of recombination hotspots in Saccharomyces cerevisiae[J]. Journal of Theoretical Biology, 2012, 293: 49-54. DOI:10.1016/j.jtbi.2011.10.004 (  0) 0) |
| [9] |
Chou K C. Some remarks on protein attribute prediction and pseudo amino acid composition[J]. Journal of Theoretical Biology, 2011, 273: 236-247. DOI:10.1016/j.jtbi.2010.12.024 (  0) 0) |
| [10] |
Feng P M, Chen W, Lin H, et al. iRSpot-PseDNC: Identify recombination spots with pseudo dinucleotide composition[J]. Nucleic Acids Research, 2013, 41: 68. DOI:10.1093/nar/gks1450 (  0) 0) |
| [11] |
Qiu W R, Xiao X, Chou K C. iRSpot-TNCPseAAC: Identify recombination spots with trinucleotide composition and pseudo amino acid components[J]. International Journal of Molecular Sciences, 2014, 15: 1746. DOI:10.3390/ijms15021746 (  0) 0) |
| [12] |
Liu G, Xing Y, Cai L. Using weighted features to predict recombination hotspots in Saccharomyces cerevisiae[J]. Journal of Theoretical Biology, 2015, 382: 15-22. DOI:10.1016/j.jtbi.2015.06.030 (  0) 0) |
| [13] |
Long R, Wang S, Liu B, et al. iRSpot-EL: Identify recombination spots with an ensemble learning approach[J]. Bioinformatics, 2016, 33: 35-41. (  0) 0) |
| [14] |
Zhang L, Kong L. iRSpot-ADPM: Identify recombination spots by incorporating the associated dinucleotide product model into Chou's pseudo components[J]. Journal of Theoretical Biology, 2018, 441: 1-8. DOI:10.1016/j.jtbi.2017.12.025 (  0) 0) |
| [15] |
Yang H, Qiu W R, Liu G, et al. iRSpot-Pse6NC: Identifying recombination spots in Saccharomyces cerevisiae by incorporating hexamer composition into general PseKNC[J]. International Journal of Biological Sciences, 2018, 14: 883. DOI:10.7150/ijbs.24616 (  0) 0) |
| [16] |
Al Maruf M A, Shatabda S. iRSpot-SF: Prediction of recombination hotspots by incorporating sequence based features into Chou's Pseudo components[J]. Genomics, 2018, 111: 966-972. (  0) 0) |
| [17] |
Khan Z U, Ali F, Khan I A, et al. iRSpot-SPI: Deep learning-based recombination spots prediction by incorporating secondary sequence information coupled with physio-chemical properties via Chou's 5-step rule and pseudo components[J]. Chemometrics and Intelligent Laboratory Systems, 2019, 189: 169-180. DOI:10.1016/j.chemolab.2019.05.003 (  0) 0) |
| [18] |
Asgari E, Mofrad M R K. Continuous distributed representation of biological sequences for deep proteomics and genomics[J]. PLoS One, 2015, 10: e0141287. DOI:10.1371/journal.pone.0141287 (  0) 0) |
| [19] |
Do D T, Le N. A sequence-based approach for identifying recombination spots in saccharomyces cerevisiae by using hyper-parameter optimization in fasttext and support vector machine[J]. Chemometrics and Intelligent Laboratory Systems, 2019, 194: 103855. DOI:10.1016/j.chemolab.2019.103855 (  0) 0) |
| [20] |
Chen W, Lin H, Chou K C. Pseudo nucleotide composition or PseKNC: An effective formulation for analyzing genomic sequences[J]. Molecular Biosystems, 2015, 11: 2620-2634. DOI:10.1039/C5MB00155B (  0) 0) |
| [21] |
Zhang X, Xin L, Qian S, et al. Recursive SVM feature selection and sample classification for mass-spectrometry and microarray data[J]. BMC Bioinformatics, 2006, 7(1): 197. DOI:10.1186/1471-2105-7-197 (  0) 0) |
| [22] |
Hamid M N, Friedberg I. Identifying antimicrobial peptides using word embedding with deep recurrent neural networks[J]. Bioinformatics, 2019, 35: 2009-2016. DOI:10.1093/bioinformatics/bty937 (  0) 0) |
| [23] |
Mikolov T, Chen K, Corrado G, et al. Efficient estimation of word representations in vector space[J]. Computer Science, 2013, 1301: 3781. (  0) 0) |
| [24] |
Cortes C, Vapnik V. Support-vector networks[J]. Machine Learning, 1995, 20(3): 273-297. (  0) 0) |
| [25] |
Chang C C, Lin C J. LIBSVM: A library for support vector machines[J]. ACM Transactions on Intelligent Systems and Technology, 2011, 2: 27. (  0) 0) |
| [26] |
Zhang L, Kong L. iRSpot-PDI: Identification of recombination spots by incorporating dinucleotide property diversity information into Chou's pseudo components[J]. Genomics, 2019, 111(3): 457-464. DOI:10.1016/j.ygeno.2018.03.003 (  0) 0) |
 2023, Vol. 53
2023, Vol. 53


