基于弹性理论的反射波地震勘探技术在能源、资源勘探开发和环境调查等领域发挥了重要作用,但目前随着人们对深部能源勘探开发问题的日益重视和对地球深部地层结构和岩性等问题的持续关注,业界都对深部地层的地震勘探精度提出了更高要求。由于地下岩石普遍具有粘弹性质,常规基于弹性假设的地震勘探技术在解决深部地层的勘探问题时往往表现出不适应性,表现在:(1)对于深部地层,由于地震反射波的传播路径很长,介质粘滞性对地震波传播影响的累积效应增大,地震波的实际传播规律与弹性介质假设情况严重不符,基于弹性介质假设的地震资料处理与反演技术很难取得满意处理效果;(2)岩石粘滞性造成深部地层反射波的高频成分衰减严重,深部地层的地震反射波高频成分缺失,频带变窄,倍频程减小,分辨率降低;(3)岩石粘滞性造成深部地层的反射波能量减弱,信噪比降低,增加了成像难度;(4)地层粘滞性使得不同深度地层反射波的频谱不一致,导致部分处理流程的参数选择困难,同时将成像结果的垂向分辨率变成t0时的函数,导致地下浅、中、深层具有不同的分辨率,增加了解释和反演难度。
研究并利用基于粘弹假设的地震勘探理论和方法可以克服上述缺陷,更好地解决深部地层的精确勘探问题。所谓粘弹介质是指力学性质介于完全弹性和完全粘性之间的介质,这种介质在外力作用下会同时表现出弹性性质和粘性性质,故地震波在这种介质中传播时具有不同于弹性介质的传播机理,这一独特传播机理是研发基于粘弹假设的地震勘探技术的理论基础,因此研究粘弹介质中的地震波传播机理对于解决深部地层的精确勘探问题具有重要意义。
业界对粘弹理论的研究始于1945年的Stokes粘弹地震波动方程[1],该方程主要考虑了由质点内摩擦引起的地震波能量耗损,之后粘弹地震波传播理论得到了快速发展[2-11],目前已形成了Kelvin模型、Maxwell介质模型、标准线性介质和达朗贝尔模型等具有不同粘弹性质的连续介质力学模型,其中Kelvin模型是目前地震勘探领域应用最多的粘弹性介质模型。
上述模型对应的地震波方程的解析解或数值解是研究不同类型粘弹介质中地震波传播规律的重要基础,复杂模型条件下地震波方程解析解的求取极为困难,故业界往往采用波动方程的数值解来研究波传播机理或解决实际问题,粘弹介质中地震波方程的数值求解是粘弹地震理论与方法的重要研究内容。
目前,业界用于求取地震波方程数值解的算法主要包括反射率法[3-4]、有限元法[10]、虚谱法[6]、有限差分法[5, 8-9, 11]等,其中有限差分法由于具有计算速度快、精度高、易实现等优点而得到了广泛应用。本文内容属粘弹性波方程的有限差分数值求解范畴,首先基于交错网格技术[12-13]给出了基于Kelvin模型中的粘弹性波方程的高阶有限差分格式、稳定性条件和吸收边界条件。其次针对粘弹介质中纵横波的解耦问题,本文借鉴完全弹性介质中纵横波的解耦技术[14],从散度算子和旋度算子出发,通过理论分析给出了一种粘弹介质中纵横波的保幅分离算法,将粘弹介质中的矢量弹性波场分解为矢量纵波场和矢量横波场,再依据纵横波传播方向与偏振方向之间的关系,将三维矢量纵波与矢量横波合成为标量纵波与标量横波,以获取具有实际意义的纵、横波波场和单炮记录,实现了基于纵横波保幅分离的粘滞介质弹性波正演模拟。
1 粘弹介质中的弹性波方程及有限差分求解方法 1.1 三维粘弹介质中的弹性波方程三维Kelvin模型中的粘弹性波方程为:
| $ \left\{ \begin{array}{l} \rho \frac{{\partial {v_x}}}{{\partial t}} = \frac{{\partial {\sigma _{xx}}}}{{\partial x}} + \frac{{\partial {\sigma _{xy}}}}{{\partial v}} + \frac{{\partial {\sigma _{xz}}}}{{\partial z}}\\ \rho \frac{{\partial {v_y}}}{{\partial t}} = \frac{{\partial {\sigma _{yx}}}}{{\partial x}} + \frac{{\partial {\sigma _{yy}}}}{{\partial y}} + \frac{{\partial {\sigma _{yz}}}}{{\partial z}}\\ \rho \frac{{\partial {v_z}}}{{\partial t}} = \frac{{\partial {\sigma _{zx}}}}{{\partial x}} + \frac{{\partial {\sigma _{zy}}}}{{\partial y}} + \frac{{\partial {\sigma _{zz}}}}{{\partial z}}\\ \frac{{\partial {\sigma _{xx}}}}{{\partial t}} = \rho c_p^2\frac{{\partial {v_x}}}{{\partial x}} + \left( {\rho c_p^2 - 2\rho c_s^2} \right)\left( {\frac{{\partial {v_y}}}{{\partial y}} + \frac{{\partial {v_z}}}{{\partial z}}} \right) + \\ \;\;\;\;\;\frac{{\rho c_p^2}}{{{Q_p}\omega }}\frac{{{\partial ^2}{v_x}}}{{\partial x\partial t}} + \left( {\frac{{\rho c_p^2}}{{{Q_p}\omega }} - \frac{{2\rho c_s^2}}{{{Q_s}\omega }}} \right)\left( {\frac{{{\partial ^2}{v_y}}}{{\partial y\partial t}} + \frac{{{\partial ^2}{v_z}}}{{\partial z\partial t}}} \right)\\ \frac{{\partial {\sigma _{yy}}}}{{\partial t}} = \rho c_p^2\frac{{\partial {v_y}}}{{\partial y}} + \left( {\rho c_p^2 - 2\rho c_s^2} \right)\left( {\frac{{\partial {v_x}}}{{\partial x}} + \frac{{\partial {v_z}}}{{\partial z}}} \right) + \\ \;\;\;\;\;\frac{{\rho c_p^2}}{{{Q_p}\omega }}\frac{{{\partial ^2}{v_y}}}{{\partial y\partial t}} + \left( {\frac{{\rho c_p^2}}{{{Q_p}\omega }} - \frac{{2\rho c_s^2}}{{{Q_s}\omega }}} \right)\left( {\frac{{{\partial ^2}{v_x}}}{{\partial x\partial t}} + \frac{{{\partial ^2}{v_z}}}{{\partial z\partial t}}} \right)\\ \frac{{\partial {\sigma _{zz}}}}{{\partial t}} = \rho c_p^2\frac{{\partial {v_z}}}{{\partial z}} + \left( {\rho c_p^2 - 2\rho c_s^2} \right)\left( {\frac{{\partial {v_x}}}{{\partial x}} + \frac{{\partial {v_y}}}{{\partial y}}} \right) + \\ \;\;\;\;\;\frac{{\rho c_p^2}}{{{Q_p}\omega }}\frac{{{\partial ^2}{v_z}}}{{\partial z\partial t}} + \left( {\frac{{\rho c_p^2}}{{{Q_p}\omega }} - \frac{{2\rho c_s^2}}{{{Q_s}\omega }}} \right)\left( {\frac{{{\partial ^2}{v_x}}}{{\partial x\partial t}} + \frac{{{\partial ^2}{v_y}}}{{\partial y\partial t}}} \right)\\ \frac{{\partial {\sigma _{xy}}}}{{\partial t}} = \rho c_s^2\left( {\frac{{\partial {v_y}}}{{\partial x}} + \frac{{\partial {v_x}}}{{\partial y}}} \right) + \frac{{\rho c_s^2}}{{{Q_s}\omega }}\left( {\frac{{{\partial ^2}{v_y}}}{{\partial x\partial t}} + \frac{{{\partial ^2}{v_x}}}{{\partial y\partial t}}} \right)\\ \frac{{\partial {\sigma _{xz}}}}{{\partial t}} = \rho c_s^2\left( {\frac{{\partial {v_z}}}{{\partial x}} + \frac{{\partial {v_x}}}{{\partial z}}} \right) + \frac{{\rho c_s^2}}{{{Q_s}\omega }}\left( {\frac{{{\partial ^2}{v_z}}}{{\partial x\partial t}} + \frac{{{\partial ^2}{v_x}}}{{\partial y\partial t}}} \right)\\ \frac{{\partial {\sigma _{yz}}}}{{\partial t}} = \rho c_s^2\left( {\frac{{\partial {v_z}}}{{\partial y}} + \frac{{\partial {v_y}}}{{\partial z}}} \right) + \frac{{\rho c_s^2}}{{{Q_s}\omega }}\left( {\frac{{{\partial ^2}{v_z}}}{{\partial y\partial t}} + \frac{{{\partial ^2}{v_y}}}{{\partial z\partial t}}} \right) \end{array} \right.。$ | (1) |
其中:x, y, z为三个直角坐标;t为时间;ρ为密度;vx、vy、vz分别为x, y, z三个方向的质点震动速度分量;σxx, σyyσzz, σxy, σxz, σyz为应力分量;cp为纵波速度;cs为横波速度;Qp为纵波品质因子;Qs为横波品质因子;ω为圆频率。
1.2 三维粘弹介质中的弹性波方程的交错网格有限差分解法交错网格法[12-13]是指在常规网格中引入半网格点,在半网格点上进行空间导数的计算,把应力分量和速度分量定义在两套网格上。与常规网格相比,交错网格能够有效解决一阶弹性波方程速度分量和应力分量的耦合关系,在不增加计算量的前提下提高计算精度和稳定性。以式(1)中的σxx分量和vx分量为例,它在交错网格空间中的高阶有限差分格式如式(2)、(3)所示:其他分量的差分格式可用类似方法导出。
| $ \begin{array}{l} \left( {{\sigma _{xx}}} \right)_{i,j,k}^n = \left( {{\sigma _{xx}}} \right)_{i,j,k}^{n - 1} + \frac{{\Delta t{\rho _{i,j,k}}\left( {{c_p}} \right)_{i,j,k}^2}}{{\Delta x}} \times \\ \sum\limits_{m = 1}^N {{a_m}} \left[ {\left( {{v_x}} \right)_{i + \frac{{2m - 1}}{2},j,k}^{n - \frac{1}{2}} - \left( {{v_x}} \right)_{i - \frac{{2m - 1}}{2},j,k}^{n - \frac{1}{2}}} \right] + \\ \frac{{\Delta t{\rho _{i,j,k}}\left[ {\left( {{c_p}} \right)_{i,j,k}^2 - 2\left( {{c_s}} \right)_{i,j,k}^2} \right]}}{{\Delta y}}\sum\limits_{m = 1}^N {{a_m}} \left[ {\left( {{v_y}} \right)_{i,j + \frac{{2m - 1}}{2},k}^{n - \frac{1}{2}} - } \right.\\ \left. {\left( {{v_y}} \right)_{i,j - \frac{{2m - 1}}{2},k}^{n - \frac{1}{2}}} \right] + \\ \frac{{\Delta t{\rho _{i,j,k}}\left[ {\left( {{c_p}} \right)_{i,j,k}^2 - 2\left( {{c_s}} \right)_{i,j,k}^2} \right]}}{{\Delta z}}\sum\limits_{m = 1}^N {{a_m}} \left[ {\left( {{v_z}} \right)_{i,j,k + \frac{{2m - 1}}{2}}^{n - \frac{1}{2}} - } \right.\\ \left. {\left( {{v_z}} \right)_{i,j,k - \frac{{2m - 1}}{2}}^{n - \frac{1}{2}}} \right] + \\ \frac{{\Delta t{\rho _{i,j,k}}\left( {{c_p}} \right)_{i,j,k}^2}}{{{{\left( {{Q_p}} \right)}_{i,j,k}}\omega \Delta x}}\sum\limits_{m = 1}^N {{a_m}} \left[ {U_{i + \frac{{2m - 1}}{2},j,k}^{n - \frac{1}{2}} - U_{i - \frac{{2m - 1}}{2},j,k}^{n - \frac{1}{2}}} \right] + \\ \frac{{\Delta t{\rho _{i,j,k}}}}{{\omega \Delta y}}\left( {\frac{{\left( {{c_p}} \right)_{i,j,k}^2}}{{{{\left( {{Q_p}} \right)}_{i,j,k}}}} - \frac{{2\left( {{c_s}} \right)_{i,j,k}^2}}{{{{\left( {{Q_s}} \right)}_{i,j,k}}}}} \right)\sum\limits_{m = 1}^N {{a_m}} \left[ {V_{i,j + \frac{{2m - 1}}{2},k}^{n - \frac{1}{2}} - } \right.\\ \left. {V_{i,j + \frac{{2m - 1}}{2},k}^{n - \frac{1}{2}}} \right] + \\ \frac{{\Delta t{\rho _{i,j,k}}}}{{\omega \Delta z}}\left( {\frac{{\left( {{c_p}} \right)_{i,j,k}^2}}{{{{\left( {{Q_p}} \right)}_{i,j,k}}}} - \frac{{2\left( {{c_s}} \right)_{i,j,k}^2}}{{{{\left( {{Q_s}} \right)}_{i,j,k}}}}} \right)\sum\limits_{m = 1}^N {{a_m}} \left[ {W_{i,j,k + \frac{{2m - 1}}{2}}^{n - \frac{1}{2}} - } \right.\\ \left. {W_{i,j,k + \frac{{2m - 1}}{2}}^{n - \frac{1}{2}}} \right]。\end{array} $ | (2) |
| $ \begin{array}{l} \left( {{v_x}} \right)_{i + \frac{1}{2},j,k}^{n + \frac{1}{2}} = \left( {{v_x}} \right)_{i + \frac{1}{2},j,k}^{n - \frac{1}{2}} + \\ \frac{{\Delta t}}{{{\rho _{i + \frac{1}{2},j,k}}\Delta x}}\sum\limits_{m = 1}^N {{a_m}} \left[ {\left( {{\sigma _{xx}}} \right)_{i + m,j,k}^n - \left( {{\sigma _{xx}}} \right)_{i - m,j,k}^n} \right] + \\ \frac{{\Delta t}}{{{\rho _{i + \frac{1}{2},j,k}}\Delta y}}\sum\limits_{m = 1}^N {{a_m}} \left[ {\left( {{\sigma _{xy}}} \right)_{i + \frac{1}{2},j + \frac{{2m - 1}}{2},k}^n - \left( {{\sigma _{xy}}} \right)_{i + \frac{1}{2},j - \frac{{2m - 1}}{2},k}^n} \right] + \\ \frac{{\Delta t}}{{{\rho _{i + \frac{1}{2},j,k}}\Delta z}}\sum\limits_{m = 1}^N {{a_m}} \left[ {\left( {{\sigma _{xz}}} \right)_{i + \frac{1}{2},j,k + \frac{{2m - 1}}{2}}^n - \left( {{\sigma _{xz}}} \right)_{i + \frac{1}{2},j,k - \frac{{2m - 1}}{2}}^n} \right]。\end{array} $ | (3) |
其中:i、j、k分别为x、y、z三个方向的离散点序号;n为时间离散序号;Δx、Δy、Δz分别为x、y、z方向的空间步长;Δt为时间步长;am为交错网格差分系数[12];
| $ U = \frac{{\partial {v_x}}}{{\partial t}} = \frac{1}{\rho }\left( {\frac{{\partial {\sigma _{xx}}}}{{\partial x}} + \frac{{\partial {\sigma _{xy}}}}{{\partial y}} + \frac{{\partial {\sigma _{xz}}}}{{\partial z}}} \right)。$ | (4) |
差分计算方法为:
| $ \begin{array}{l} U_{i + \frac{1}{2},j,k}^{n + \frac{1}{2}} = \frac{{\Delta t}}{{{\rho _{i + \frac{1}{2},j,k}}\Delta x}}\sum\limits_{m = 1}^N {{a_m}} \left[ {\left( {{\sigma _{xx}}} \right)_{i + m,j,k}^n - } \right.\\ \left. {\left( {{\sigma _{xx}}} \right)_{i - m + 1,j,k}^n} \right] + \\ \frac{{\Delta t}}{{{\rho _{i + \frac{1}{2},j,k}}\Delta y}}\sum\limits_{m = 1}^N {{a_m}} \left[ {\left( {{\sigma _{xy}}} \right)_{i + \frac{1}{2},j + \frac{{2m - 1}}{2},k}^n - \left( {{\sigma _{xy}}} \right)_{i + \frac{1}{2},j - \frac{{2m - 1}}{2},k}^n} \right] + \\ \frac{{\Delta t}}{{{\rho _{i + \frac{1}{2},j,k}}\Delta z}}\sum\limits_{m = 1}^N {{a_m}} \left[ {\left( {{\sigma _{xz}}} \right)_{i + \frac{1}{2},j,k + \frac{{2m - 1}}{2}}^n - \left( {{\sigma _{xz}}} \right)_{i + \frac{1}{2},j,k - \frac{{2m - 1}}{2}}^n} \right]。\end{array} $ | (5) |
式(2)、(3)、(5)的稳定性条件为:
| $ \Delta t \cdot {c_{\max }}\sqrt {\frac{1}{{\Delta {x^2}}} + \frac{1}{{\Delta {y^2}}} + \frac{1}{{\Delta {z^2}}}} \le \frac{1}{{\sum\limits_{n = 1}^N {{a_m}} }}。$ | (6) |
其中cmax为模型中最大纵波速度。
1.3 吸收边界条件采用PML边界条件[15-16]解决式(1)求解过程中的截断边界问题。PML吸收边界的基本思想是在计算区域增加吸收层,在吸收层内设置衰减因子对波场进行衰减。对计算区域镶边后的三维空间如图 1所示。以vx分量为例,依据PML的分裂思路[15-16],可将其分解为x, y, z三个方向的分量vx_x,vx_y,vx_z,即:
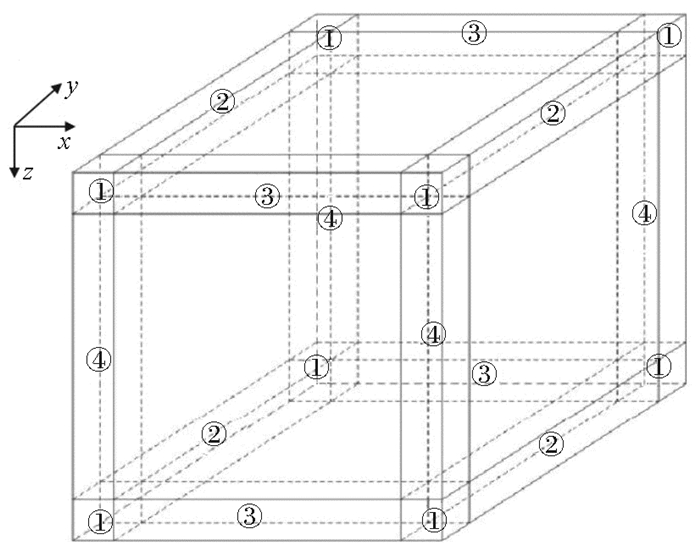
|
图 1 三维空间PML吸收边界示意图 Fig. 1 Three-dimensional PML absorption boundary diagram |
| $ {v_x} = {v_{x{\rm{\_}}x}} + {v_{x{\rm{\_}}y}} + {v_{x{\rm{\_}}z}}。$ | (7) |
各分量的吸收方程如下:
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial {v_{x{\rm{\_}}x}}}}{{\partial t}} + d\left( x \right){v_{x{\rm{\_}}x}} = \frac{1}{\rho }\frac{{\partial {\sigma _{xx}}}}{{\partial x}}}\\ {\frac{{\partial {v_{x{\rm{\_}}y}}}}{{\partial t}} + d\left( y \right){v_{x{\rm{\_}}y}} = \frac{1}{\rho }\frac{{\partial {\sigma _{xy}}}}{{\partial y}}}\\ {\frac{{\partial {v_{x{\rm{\_}}z}}}}{{\partial t}} + d\left( z \right){v_{x{\rm{\_}}z}} = \frac{1}{\rho }\frac{{\partial {\sigma _{xz}}}}{{\partial z}}} \end{array}} \right.。$ | (8) |
其中d(x)、d(y)、d(z)分别为x、y、z三个方向上的衰减因子,其取值详见文献[15]。
在不同的边界对不同的分量进行吸收即可压制截断边界的伪反射。仍以vx分量为例,在图 1所示的三维吸收边界示意图中,各个边界区域的衰减因子如下:
| $ \left\{ \begin{array}{l} d\left( x \right) \ne 0;d\left( y \right) \ne 0;d\left( z \right) \ne 0\;\;\;\;区域①\\ d\left( x \right) = 0;d\left( y \right) \ne 0;d\left( z \right) \ne 0\;\;\;\;区域②\\ d\left( x \right) \ne 0;d\left( y \right) = 0;d\left( z \right) \ne 0\;\;\;\;区域③\\ d\left( x \right) \ne 0;d\left( y \right) \ne 0;d\left( z \right) = 0\;\;\;\;区域④\\ d\left( x \right) \ne 0;d\left( y \right) = 0;d\left( z \right) = 0\;\;\;\;垂直于\;z\;轴的两个边界平面\\ d\left( x \right) = 0;d\left( y \right) \ne 0;d\left( z \right) = 0\;\;\;\;垂直于\;z\;轴的两个边界平面\\ d\left( x \right) = 0;d\left( y \right) = 0;d\left( z \right) \ne 0\;\;\;\;垂直于\;z\;轴的两个边界平面 \end{array} \right.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~。$ |
式(1)中vx、vy、vz的本质是质点的振动速度矢量v在直角坐标系三个坐标轴上的投影,由于纵波与横波均可引起这三个方向上的质点振动,因此vx、vy、vz分量都同时包含纵波与横波,两种波耦合在一起不便于分析纵横波的传播与衰减机理,因此有必要在粘弹介质弹性波方程正演的过程中采用适当方法对纵横波进行解耦,以得到合成纵波记录和横波记录。
各向同性介质中纵波是无旋场,横波是无散场,因此可通过求取弹性波场的散度与旋度得到纵波场与横波场,Aki和Richards以此为基础,利用v的散度和旋度算子实现了弹性介质中的纵横波分离[17],这种方法实现简单,计算量小,但会使波场的相位和振幅信息产生畸变[18-19],且分离后的波场在极性反转位置上无法与分离前混合波场各分量对应,因此基于散度和旋度算子的波场解耦方法是不保幅的。
由于本文研究的Kelvin模型仍属于各向同性介质范畴,因此弹性各向同性介质中基于散度与旋度算子的波场解耦方法同样无法解决Kelvin模型的纵横波保幅分离问题。本文的主要目标就是研究新的方法实现Kelvin粘弹模型的纵横波保幅分离。
假设Kelvin粘弹模型中的矢量波场v由vp和vs两个矢量场组成:
| $ \mathit{\boldsymbol{v}} = {\mathit{\boldsymbol{v}}_p} + {\mathit{\boldsymbol{v}}_s}。$ | (9) |
其中vp为由纵波引起的质点振动速度矢量;vs为由横波引起的振动速度矢量,这两个矢量在笛卡尔坐标系中的表达形式为vp=(vp_x, vp_y, vp_z),vs=(vs_x, vs_y, vs_z)。
对式(9)分别求散度和旋度可得:
| $ \left\{ {\begin{array}{*{20}{l}} {\nabla \cdot v = \nabla \cdot {v_p} + \nabla \cdot {v_s}}\\ {\nabla \times v = \nabla \times {v_p} + \nabla \times {v_s}} \end{array}} \right.。$ | (10) |
由于纵波为无旋场,横波为无散场,有:
| $ \left\{ {\begin{array}{*{20}{l}} {\nabla \times {v_p} = 0}\\ {\nabla \cdot {v_s} = 0} \end{array}} \right.。$ | (11) |
(7) 式可写为:
| $ \left\{ {\begin{array}{*{20}{l}} {\nabla \cdot v = \nabla \cdot {v_p}}\\ {\nabla \times v = \nabla \times {v_s}} \end{array}} \right.。$ | (12) |
将上式变换到波数域,有:
| $ \left\{ {\begin{array}{*{20}{l}} {K \cdot \tilde v = {K_p} \cdot {{\tilde v}_p}}\\ {K \times \tilde v = {K_s} \times {{\tilde v}_s}} \end{array}} \right.。$ | (13) |
其中:
纵横波的波数域单位传播矢量Kp、Ks与纵横波速度及圆频率ω之间满足以下关系:
| $ \left\{ {\begin{array}{*{20}{l}} {c_p^2\left( {\mathit{\boldsymbol{K}}_{p{\rm{\_}}x}^2 + \mathit{\boldsymbol{K}}_{p{\rm{\_}}y}^2 + \mathit{\boldsymbol{K}}_{p{\rm{\_}}z}^2} \right) = {\omega ^2}}\\ {c_s^2\left( {\mathit{\boldsymbol{K}}_{s{\rm{\_}}x}^2 + \mathit{\boldsymbol{K}}_{s{\rm{\_}}x}^2 + \mathit{\boldsymbol{K}}_{s{\rm{\_}}x}^2} \right) = {\omega ^2}} \end{array}} \right.。$ | (14) |
联立式(10)和式(11)可得:
| $ \left\{ {\begin{array}{*{20}{l}} {{\omega ^2}{{\tilde v}_p} = c_p^2{\mathit{\boldsymbol{K}}_p}\left( {\mathit{\boldsymbol{K}} \cdot \tilde v} \right)}\\ {{\omega ^2}{{\tilde v}_s} = - c_s^2{\mathit{\boldsymbol{K}}_p} \times \left( {\mathit{\boldsymbol{K}} \times \tilde v} \right)} \end{array}} \right.。$ | (15) |
对上式作傅里叶反变换,可得
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\partial ^2}{v_p}}}{{\partial {t^2}}} = c_p^2\nabla \left( {\nabla \cdot v} \right)}\\ {\frac{{{\partial ^2}{v_s}}}{{\partial {t^2}}} = - c_s^2\nabla \times \left( {\nabla \times v} \right)} \end{array}} \right.。$ | (16) |
上式即为各向同性粘弹介质中的纵横波保幅分离算子,它可以在时间空间域利用有限差分来实现,具体计算公式为:
| $ \left\{ {\begin{array}{*{20}{l}} {v_p^{n + 1} = 2v_p^n - v_p^{n - 1} + \Delta {t^2}c_p^2\nabla \left( {\nabla \cdot v} \right)}\\ {v_s^{n + 1} = 2v_s^n - v_s^{n - 1} - c_s^2\nabla \times \left( {\nabla \times v} \right)} \end{array}} \right.。$ | (17) |
和Aki等的方法[17]相比,本文方法的优势在于:不会引起纵横波振幅和相位畸变,且将纵波当作矢量进行处理,在物理意义和波场的极性反转位置上能与分离前混合波场各分量对应;和李振春等的方法[20]相比,本文方法的优势在于:首先利用地层中纵横波的传播速度对分离后的矢量波场进行振幅补偿,对补偿结果再沿时间方向进行积分使得分离结果更具保真性。
利用图 2a所示的水平层状模型验证本文算法的保幅性,两层介质的纵波速度分别为2 500、3 000 m/s,横波速度分别为1 443、1 764 m/s,密度分别为2 000、2 500 kg/m3,纵、横波品质因子为常数80,界面埋深400 m。波场模拟所用的参数为:震源为主频f0=35 Hz的雷克子波,震源置于地表,其水平位置为(500 m,250 m),空间网格大小5 m×5 m,时间步长0.5 ms。由于本文是在时间域对式(1)进行求解,故假定圆频率ω为常数,其值为2πf0。图 2b~2d为正演过程中记录t=350 ms时的三分量波场快照,由图可见,每个分量快照中都同时包含纵波与横波,纵横波耦合在一起,互为串扰,必须将之分解为相对独立的纵波分量和横波分量才便于分析粘弹介质中的纵横波传播规律。
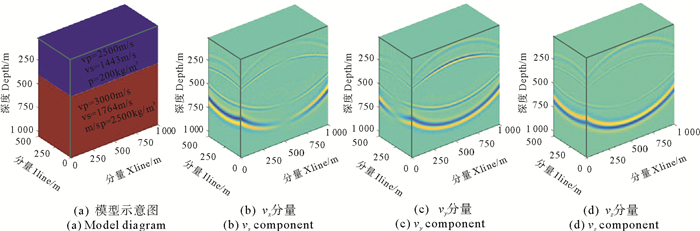
|
图 2 模型示意图及其三分量快照 Fig. 2 Model diagram and snapshot of three components |
在正演模拟过程中分别利用Aki等的方法[17]、李振春等的方法[20]和本文算法进行波场解耦。图 3、4和5分别为上述三种方法的纵横波解耦结果快照,由图可见,这三种方法都能在波场模拟过程中实现纵横波的解耦,其中Aki的方法[17]将弹性波场分解为标量纵波和矢量横波,后两种方法则将弹性波场分解为矢量纵波和矢量横波,由于标量可以看作一种特殊的矢量,因此解耦结果中的纵波无论是标量还是矢量,在理论上都是正确的。但图 3中矢量横波各个分量中的极性反转位置与原波场不一致,同时分离结果中横波的z分量(见图 3d)在inline方向的波场值为零,这与vz分量中的横波存在明显差异,这些现象说明散度算子和旋度算子对横波场具有改造作用,它无法得到地下真实的横波场,只能得到改造后的横波场。
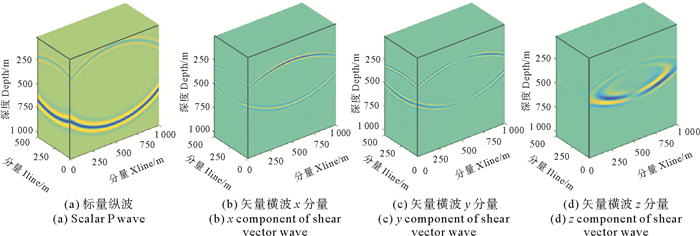
|
图 3 散度和旋度算子的波场解耦快照 Fig. 3 Decoupled wave field Snapshots of divergence and curl |
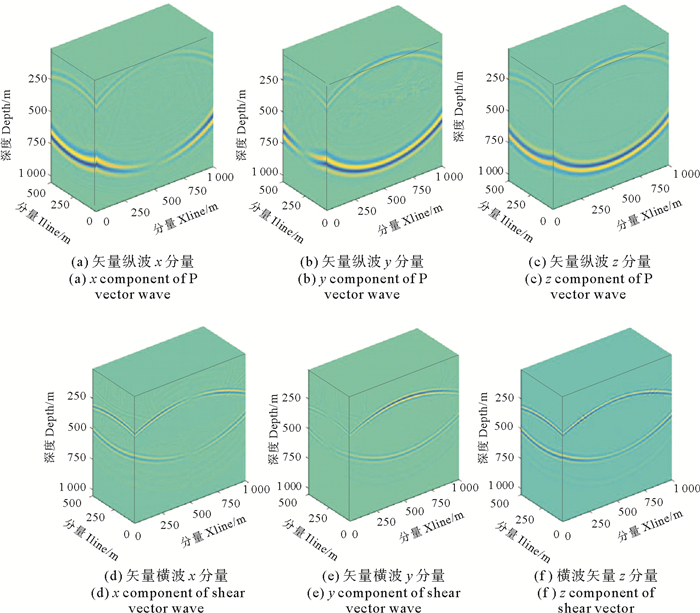
|
图 4 李振春等算法的波场解耦快照 Fig. 4 Decoupled wave field Snapshots of LiZhenchun et al |
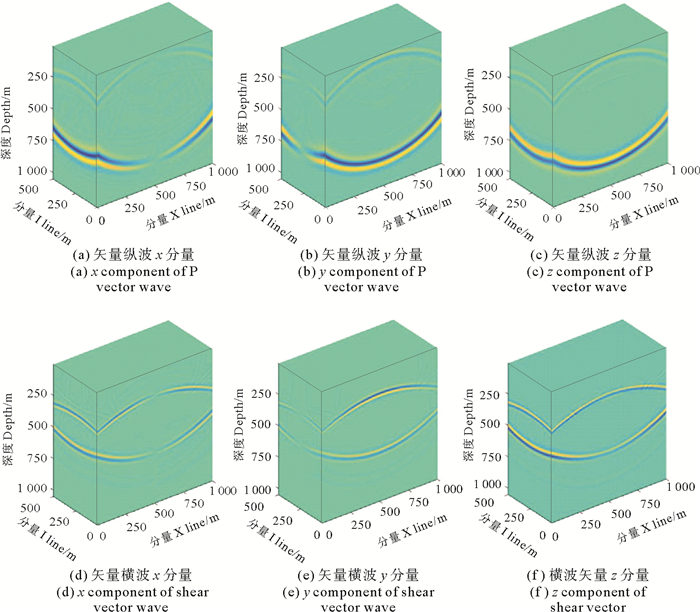
|
图 5 本文算法的波场解耦快照 Fig. 5 Decoupled wave field Snapshots in this paper |
图 4、图 5为采用后两种方法得到的纵横波分离快照,由图可见,这两种方法都能实现纵横波的完全解耦,且解耦前后纵、横波各分量的极性反转位置能够准确对应,这表明后两种方法的解耦精度高于散度和旋度算子。但对于纵波的三个分量,李振春等的方法[20]得到的结果与分离前的数据存在90°的相位差,而本文方法与原始数据之间不存在相位变化,说明本文算法的解耦精度高于第二种方法。
为证明本文算法的保幅优势,从不同方法分离前后的快照结果中选取一道数据进行比较,该道在地表的投影位置为:(650,50),图 6a为不同方法分离前后的纵波z分量显示,其中第一道数据为波场分离前的z分量混合波场,第二道为利用散度算子[17]得到的标量纵波,第三、第四道为分别利用李振春等[20]和本文算法得到的矢量纵波z分量,由图可见,本文算法得到的纵波z分量结果与原波场中的纵波的振幅和相位完全一致,而另外两种方法得到的结果的振幅比原波场小1~2个数量级,且存在90°相位差。图 6b为不同方法分离前后的横波x分量显示,其中第一道数据为场分离前的x分量混合波场,其余三道分别为利用旋度算子、李振春等的方法和本文算法得到的矢量横波的x分量,三种方法对横波的分量结果都不存在相位畸变,但前两种分离算法分离结果的振幅比原始数据小一个数量级,本文方法的分离结果则与分离前的横波完全一致。图 7为该位置处用不同方法得到的正演单道记录的比较,分析该图可以得到与图 6相同的结论,这表明本文给出的粘弹介质纵横波分离方法是保幅的。
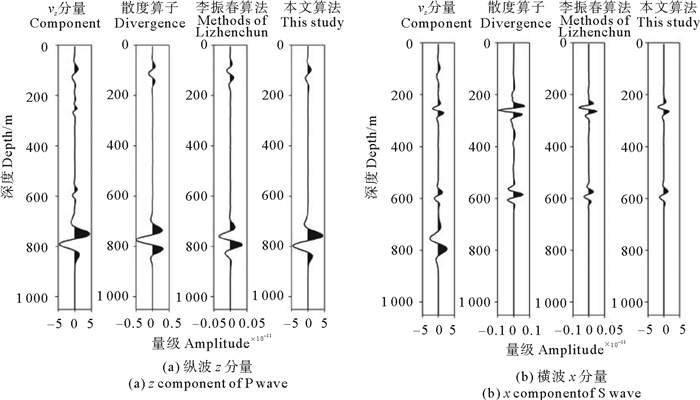
|
图 6 不同分离方法得到的波场快照比较 Fig. 6 The snapshot comparison of wave field obtained by different methods |
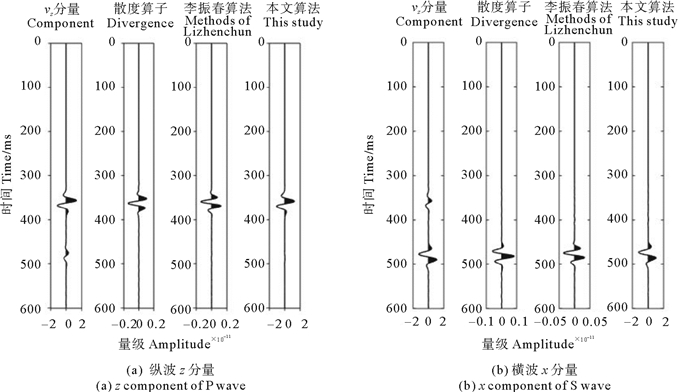
|
图 7 不同分离方法得到的合成记录单道比较 Fig. 7 Single channel comparison of synthetic records obtained by different methods |
本文的纵横波保幅解耦方法能为研究粘弹介质纵、横波的传播规律提供保真的数据,还能为基于点积互相关的弹性波逆时偏移成像[21]提供保真的矢量纵波和矢量横波数据。但在常规逆时偏移技术[22-23]中往往需要用标量的纵波与横波进行互相关成像,同时,工业界也倾向于利用更具明确地球物理意义的标量纵波与标量横波来解决地质问题,在这种情况下就需要对分离后的矢量纵波与矢量横波进行标量合成。
矢量波场的标量合成问题一般由振幅计算和极性确定两部分组成。对于标量波的振幅计算问题,不管是纵波还是横波,都可以通过求取矢量波场的模来完成,问题的难点在于如何确定标量化后的波场的极性。本文采用质点振动法求取标量横波的极性[24],对于标量纵波的极性问题,本文规定质点振动方向与z轴夹角小于90°时为负,反之为正,由此可以将纵波的极性求取问题转换为质点振动方向的求取问题,由于纵波的传播方向与质点的振动方向相同,因此可利用纵波的传播方向确定质点振动方向,进而确定标量纵波的极性。纵波的传播方向信息可利用坡印廷矢量得到,弹性波坡印廷矢量的求取方法已有多人做过研究[25-26],本文不赘述。图 8为利用上述原理对图 5所示的波场快照进行标量合成的结果,标量合成后的纵、横波场具有更为明确的物理意义且更便于实际应用。
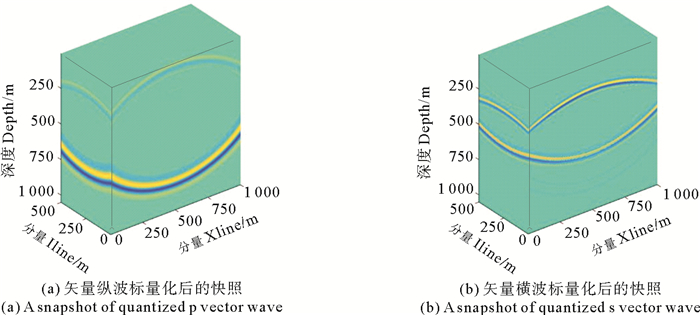
|
图 8 矢量纵、横波标量化后的快照 Fig. 8 Snapshots of the quantified compress and shear wave |
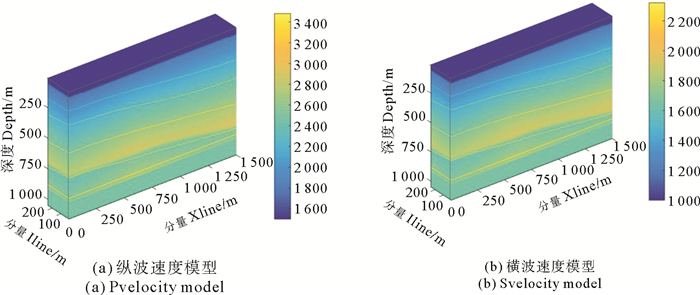
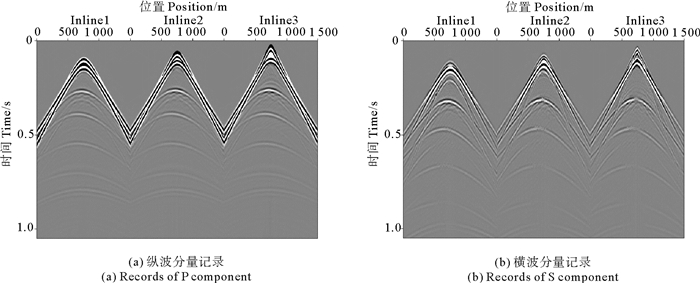
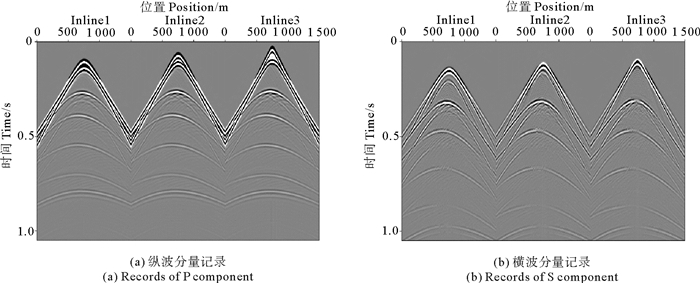
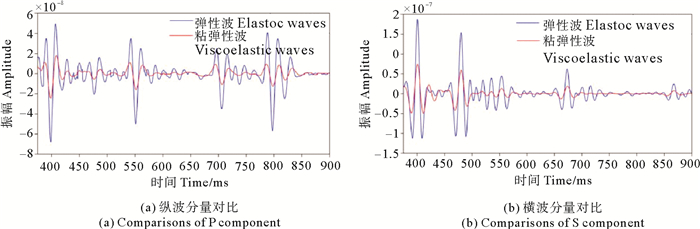
模型的纵横波速度如图 9所示,纵、横波品质因子均取常数80,正演所用的参数如下:模型大小为1 500 m×250 m×1 050 m,空间网格大小为5 m×5 m×5 m,采用间隔为0.35 ms,记录长度为1.05 s。采用Ricker子波作为震源,主频为35 Hz,震源位于(760 m,250 m, 0 m)处,三线接收,线距50 m,每条测线300道接收。图 10为基于本文算法的合成纵波记录和转换横波单炮记录,图 11为该模型完全弹性情况下的合成反射纵波记录和转换横波记录,对比图 10,11可以看出粘弹介质情况下,由于受到地层的粘滞吸收作用,反射纵波和转换横波的能量均弱于弹性情况,图 12为第1条线100道纵、横波分量中的375~900 ms时间段波场对比图,图中无论是纵波还是转换横波,介质完全弹性情况下的振幅明显高于粘弹情况,且随着时间的增大,这种差别也逐渐增大,其原因为:传播时间的增大往往意味着传播距离的增加,即传播的波长数增大,介质粘滞性的累积效果增加。
|
图 9 纵横波速度模型 Fig. 9 Compress and shear velocity model |
|
图 10 粘弹条件下的合成纵横波记录 Fig. 10 Synthetic compress and shear wave recording under viscoelastic condition |
|
图 11 完全弹性条件下的合成纵横波记录 Fig. 11 Synthetic compress and shear wave recording under fully elastic condition |
|
图 12 不同条件下第1条线100道地震记录对比 Fig. 12 Comparison of the 100th seismic recording of the first line under different conditions |
(1) 本文将标量纵波看作一种特殊的矢量,推导了三维粘滞弹性波的纵横波保幅解耦公式,给出了差分求解方法。本文算法的解耦结果能够实现与原三分量波场的对应,解耦结果可方便的用于波场分析,且具有很高的保幅性。
(2) 本文算法解耦后的纵、横波三分量数据可直接用于基于点积互相关的逆时偏移成像;纵、横波的标量合成结果可直接用于常规的弹性波逆时偏移成像。
(3) 本文基于纵横波保幅分离的粘弹介质弹性波正演模拟算法既可以获得常规三分量合成地震记录,也可以获得波场解耦后的纵波合成记录与转换横波合成记录,还可以获得三分量矢量纵波记录和矢量横波记录。
| [1] |
Stockes G G. On the theories of internal friction of fluids in motion and of the equilibrium and motion of elastic solids[J]. Trans Cambridge Philos Soc, 1845, 8(Part Ⅲ): 287-319.
(  0) 0) |
| [2] |
Emmerich H, Korn M. Incorporation of attenuation into time-domain computations of seismic wave fields[J]. Geophysics, 1987, 52(9): 1252-1264. DOI:10.1190/1.1442386
(  0) 0) |
| [3] |
Carcione J M. Viscoacoustic wave propagation simulation in the earth[J]. Geophysics, 1988, 53(6): 769-777. DOI:10.1190/1.1442512
(  0) 0) |
| [4] |
Carcione J M, Dan K, Kosloff R. Wave propagation simulation in a linear viscoacoustic medium[J]. Geophysical Journal International, 1988, 93(2): 393-401. DOI:10.1111/j.1365-246X.1988.tb02010.x
(  0) 0) |
| [5] |
Robertsson J O A, Blanch J O, Levander A, et al. 3-D viscoelastic finite-difference modeling[J]. Geophysics, 1994, 59(9): 1444-1456. DOI:10.1190/1.1443701
(  0) 0) |
| [6] |
刘财, 张智, 邵志刚, 等. 线性粘弹体中地震波场伪谱法模拟技术[J]. 地球物理学进展, 2005, 20(3): 640-644. Liu C, Zhang Z, Shao Z G. Pseudo spectral forward modeling of seismic wave in linear viscoelasic solid[J]. Progress in Geophysics, 2005, 20(3): 640-644. DOI:10.3969/j.issn.1004-2903.2005.03.010 (  0) 0) |
| [7] |
孙成禹, 印兴耀. 三参数常Q粘弹性模型构造方法研究[J]. 地震学报, 2007, 29(4): 348-357. Sun Y C, Yin X Y. Construction of constant Q viscoelastic model with three parameters[J]. Acta Seismologica Sinica, 2007, 29(4): 348-357. (  0) 0) |
| [8] |
孟凡顺, 郭海燕, 等. 复杂地质体粘滞弹性波正演模拟的有限差分法[J]. 青岛海洋大学学报(自然科学版), 2000, 30(2): 315-320. Meng F S, Guo H Y. Viscoelastic wave simulating in complex medium by finite difference method[J]. Journal of Ocean University of Qingdao, 2000, 30(2): 315-320. (  0) 0) |
| [9] |
王美霞.双相及粘弹性介质中波传播方程的保辛算法及其波场模拟[D].北京: 清华大学, 2012. Wang M X. Symplectic Stereo Modelling Method for Wave Equations in Two-Phase and Viscoelastic Media and Its Numerical Simulations[D]. Beijing: Tsinghua University, 2012. (  0) 0) |
| [10] |
张明, 王润秋. 有限元解三维弹性波方程的并行算法[J]. 计算数学, 1995, 2: 127-135. Zhang M, Wang R Q. a parallel algorithm with finite element for solving 3-D elastic wave equations[J]. Mathematica Numerica Sinica, 1995, 2: 127-135. (  0) 0) |
| [11] |
赵童鑫.粘弹性介质中的声波方程及其有限差分数值模拟[D].成都: 西南石油大学, 2016. Zhao T X. Acoustic Wave Equation in Viscoelastic Media and Finite Difference Numerical Simulation[D]. Chengdu: Southwest Petroleum University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10615-1016098454.htm (  0) 0) |
| [12] |
董良国, 马在田, 曹景忠. 一阶弹性波方程交错网格高阶差分解法稳定性研究[J]. 地球物理学报, 2000, 439(6): 43-864. Ma L G, Ma Z T, Cao J Z. A study on stability of the staggered grid high order difference method of first order elastic wave equation[J]. Chinese Journal of Geophysics, 2000, 439: 43-864. (  0) 0) |
| [13] |
Virieux J. P-SV wave propagation in heterogeneous media: Velocity-stress finite-difference method[J]. Geophysics, 1986, 51(4): 889-901. DOI:10.1190/1.1442147
(  0) 0) |
| [14] |
胡楠, 何兵寿. 三维各向同性介质矢量波场保幅分离方法[J]. 煤炭学报, 2017, 42(9): 2420-2426. Hu L, He B S. Amplitude-preserving separation method of 3D isotropic medium vector wave field[J]. Journal of the China Coal Society, 2017, 42(9): 2420-2426. (  0) 0) |
| [15] |
Berenger J P. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 1994, 114(2): 185-200. DOI:10.1006/jcph.1994.1159
(  0) 0) |
| [16] |
Weng C C, Weedon W H. A 3D perfectly matched medium from modified maxwell's equations with stretched coordinates[J]. Microwave & Optical Technology Letters, 1994, 7(13): 599-604.
(  0) 0) |
| [17] |
Aki K, Richards P G. Quantitative Seismology[M]. 2nd Ed. [s.l.]: W. H. Freeman, 1980: 5-43.
(  0) 0) |
| [18] |
Sun R, Chow J, Chen K J. Phase correction in separating P-and S-waves in elastic data[J]. Geophysics, 2001, 66(5): 1515-1518. DOI:10.1190/1.1487097
(  0) 0) |
| [19] |
Sun R, Mcmechan G A, Chuang H H. Amplitude balancing in separating P-and S-waves in 2D and 3D elastic seismic data[J]. Geophysics, 2011, 76(3): S103. DOI:10.1190/1.3555529
(  0) 0) |
| [20] |
李振春, 雍鹏, 黄建平, 等. 基于矢量波场分离弹性波逆时偏移成像[J]. 中国石油大学学报(自然科学版), 2016, 40(1): 42-48. Li Z C, Yong P, Huang J P. Elastic wave reverse time migration based on vector wave field separation[J]. Journal of China University of Petroleum(Edition of Natural Science), 2016, 40(1): 42-48. (  0) 0) |
| [21] |
王鹏飞, 何兵寿. 基于行波分离的三维弹性波矢量场点积互相关成像条件[J]. 石油地球物理勘探, 2017, 52(3): 477-483. Wang P F, He B S. Vector field dot product cross-correlation imaging based on 3D elastic wave separation[J]. OGP, 2017, 52(3): 477-483. (  0) 0) |
| [22] |
何兵寿, 张会星. 多分量波场的矢量法叠前深度偏移技术[J]. 石油地球物理勘探, 2006, 41(4): 368-374. He B S, Zhang H X. Vector prestack depth migration of multi-component wavefield[J]. OGP, 2006, 41(4): 368-374. (  0) 0) |
| [23] |
Chang W F. Elastic reverse-time migration[J]. Geophysics, 1987, 52(10): 1365-1375. DOI:10.1190/1.1442249
(  0) 0) |
| [24] |
Sun R, McMechan G, Hsiao H, et al. Separating P-and S-waves in prestack 3D elastic seismograms using divergence and curl[J]. Geophysics, 2004, 69(1): 286-297. DOI:10.1190/1.1649396
(  0) 0) |
| [25] |
Tang H G, He B S, Mou H B. P-and S-wave energy flux density vectors[J]. Geophysics, 2016, 81(6): T357-T368. DOI:10.1190/geo2016-0245.1
(  0) 0) |
| [26] |
Chen T, He B S. A normalized wave field separation cross-correlation imaging condition for reverse-time migration based on Poynting Vector[J]. Applied Geophysics, 2014, 11(2): 158-188. DOI:10.1007/s11770-014-0441-5
(  0) 0) |
 2020, Vol. 50
2020, Vol. 50


