2. 中国海洋大学海底科学与探测技术教育部重点实验室, 山东 青岛 266100;
3. 青岛海洋科学与技术试点国家实验室 海洋矿产资源评价与探测技术功能实验室,山东 青岛 266237;
4. 中国海洋大学工程学院, 山东 青岛 266100;
5. 中国海洋大学环境科学与工程学院, 山东 青岛 266100
中国海域辽阔,海洋资源丰富,海底地质构造类型齐全,随着对海洋的深入探索,各种水下探测技术不断进步,对于多物理场探测的要求不断提高,目前成熟的水下探测方式主要有声学、光学、和电磁探测等[1-6]。水下电磁探测具有精度高、稳定性好,受水文天气限制相对较小等优点,在特定场合具有不可替代的作用[1]。近年来,随着深远海探测的需要,我国极低频电磁信号探测技术作为一个新兴的方向,在水下电磁探测中得到快速发展,未来的极低频电磁探测在深海探测、深海开发方面将具有非常广泛的应用前景。然而,海水运动产生的感应电磁噪声与水下极低频电磁信号存在部分频率范围的重叠,这成为水下电磁探测信噪比降低的主要因素。为了提高探测质量,在进一步提高发射天线辐射效率和等效带宽的同时,压制海水运动感应电磁噪声,并提高水下电磁信号信噪比,则是一种可行的方案,且具重要的研究意义[7]。
魏文博等[8]、于彩霞等[9]、Chen Kai等[10]进行了海洋大地电磁法(Magnetotelluric,MT)中的海水运动感应电磁噪声压制研究,通过压制海浪感应电磁噪声提高了海洋MT数据质量;在有源信号探测方面,罗忠涛、常浩等人开展了水下电磁通信中的噪声压制相关研究,这些工作一般将噪声源简化为低频噪声或高斯白噪声[11-12],没有考虑海洋动力环境产生的影响。另外,因海流运动其振幅及周期特性随时间变化而变化,产生的海流感应电磁场为非平稳信号,常用的频域滤波或时域滤波方法不利于压制复杂的海洋环境噪声。小波分析方法因其具有多分辨率分析的特性和时频局部化的优势,适于处理非平稳信号,阈值去噪更适于处理有源信号中的非平稳噪声。本文在分析海流感应电磁噪声对电磁信号影响的基础上,合成包含MT信号、海流感应电磁噪声的极低频探测信号数据,通过小波阈值去噪方法压制实测数据中海流感应电磁噪声,提高资料信噪比,改善水下探测质量。
1 海流感应电磁场噪声压制方法按照海水运动的类型及频率特征,海水运动感应电磁场信号可简单分为海浪感应电磁场和海流感应电磁场。Fraser[13]、Andrew[14]、张自力等[15]、张宝强[16]研究表明风生海浪的感应电磁场其影响频带范围较窄,大多分布在0.03~0.15 Hz,海浪运动越强烈其感应电磁场频率范围越低[16],根据《中华人民共和国无线电频率划分规定》,极低频频率范围是3~30 Hz(Extremely Low Frequency,ELF),所以一般海况下的海浪运动对水下极低频信号影响较小。引起海洋表面波动的要素除了风浪还有地震、潮汐等多种要素,这些波动产生多种形式的海流运动,如潮流、风生环流、密度流、大洋环流分支等,其周期从0.01 s到百年尺度[17],其频率特征使其成为影响水下极低频电磁信号的重要因素,如潮流产生的感应电磁场其能量强弱及影响频率范围与涨落潮密切相关,涨潮与落潮期,潮流速度较大,引起的感应电磁场能量较强[10, 18],平潮期流速较小,感应电磁场能量较弱。
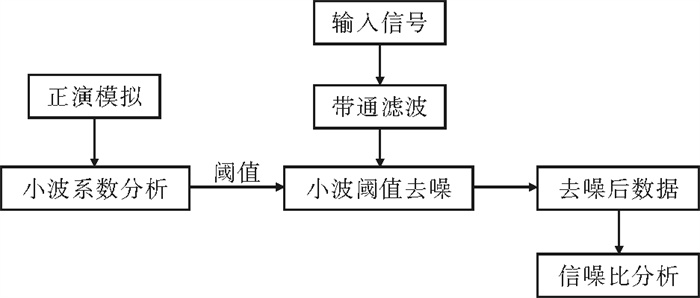
海水运动的复杂性导致了海水运动感应电磁场的复杂性,通过正演模拟可以有针对性地进行噪声和信号分析,基于正演模拟和小波系数分析确定阈值,考虑实际极低频电磁信号的频率范围,结合带通滤波和小波阈值去噪进行极低频电磁信号中的海流感应电磁噪声压制,以信噪比衡量噪声压制的效果,设计的处理流程如图 1所示。
|
图 1 去噪流程图 Fig. 1 Denoising flow chart |
结合正演模拟结果,根据小波系数密度分布确定阈值及小波基函数[19],对小波变换后的小波系数进行处理,设置阈值界定有效信号和噪声,将小于阈值的小波系数充零或收缩,大于阈值的小波系数保留,最后反变换就得到了去噪后的数据[20]。
采用的离散小波变换公式为:
| $ {W_f}\left( {j, k} \right) = {}_Rf\left( t \right)\frac{1}{{\sqrt {{a_0}^j} }}\overline {\psi \left( {\frac{t}{{{a_0}^j}} - k{\tau _0}} \right)} {\rm{d}}t。$ | (1) |
式中:K∈Z;a0为离散窗格; τ0为时移因子; Ψ代表小波基;
在小波基函数不变的情况下,某一分解层小波系数的大小与信号片段fi在频率域的振幅ai呈正相关Wi∝ai,即频率域振幅ai越大,对应小波系数Wi越大。
某一分解层小波系数的阈值量化处理过程可以表示为:
| $ {W_i}\left( j \right) = sign\left( {{W_i}\left( j \right)} \right) \cdot {F_T}\left( {{W_i}\left( j \right)} \right)。$ | (2) |
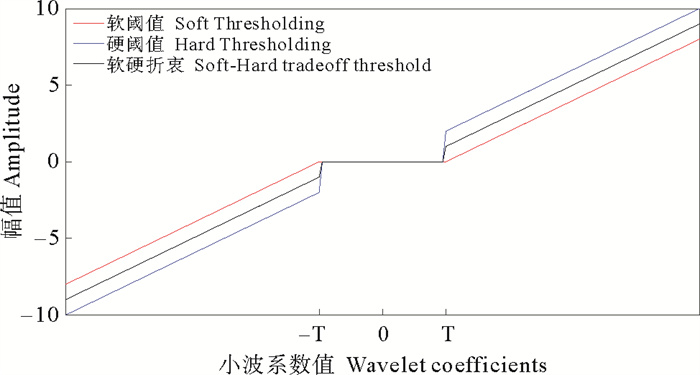
式中: Wi(j)是第j分解层的小波系数; Wi(j)是阈值量化后的小波系数; sign是符号函数; FT(Wi(j))是阈值函数; T是阈值。本文采用图 2所示的软硬折衷阈值函数。
|
图 2 常用阈值函数曲线 Fig. 2 Common threshold function curves |
根据Mallat算法和小波多尺度分解思想[21-22],分解层数与频率的对应关系为:
| $ Range\left( j \right) = \left( {\frac{{fs}}{{{2^{j + 1}}}}, \frac{{fs}}{{{2^j}}}} \right)。$ | (3) |
式中: fs为信号采样频率; Range(j)为第j层细节系数对应频率范围,所以分解层数可由目标信号的频率范围确定。
在此,为了分析去噪效果,设去噪前后信噪比SNR为:
| $ SNR = 10{\rm{lo}}{{\rm{g}}_{10}}\left( {\frac{{{E_{{\rm{signal}}}}}}{{{E_{{\rm{noise}}}}}}} \right)。$ | (4) |
其中: Esignal为信号能量; Enoise为一定带宽内背景噪声的平均能量。
2 合成数据实验 2.1 合成包含海流运动感应电磁场的数据为了进行合成数据实验,需要获得包含大地电磁信号的海流感应电磁场数据。首先,构建大地电磁模拟所需的地电模型,在此以胶州湾海域地质情况为例:胶州湾地区第四系地层厚度在0.5~30 m不等,主要为海相沉积淤泥及淤泥质地层、河流冲洪积形成粘性土地层及砂层。下部为白垩系沉积岩及青山群火山岩地层,埋深在20~65 m,湾口处为花岗岩,埋深在30~65 m[23-24],参考孙永福给出的海底土的电阻率[25],设置一维地电模型如图 3所示。基于该地电模型,利用构造系统函数法[26],获得大地电磁正演模拟数据水平分量(见图 4(a)、图 5(a)),结合实测数据情况,考虑海水运动对海洋磁场信号的影响较大[6],本文以磁场分量为例进行阐述。

|
( σ为电导率,h为层厚度。σ indicates conductivity, h indicates layer thickness. ) 图 3 正演模拟一维层状电导率模型 Fig. 3 1D layered conductivity model for forward modeling |
|
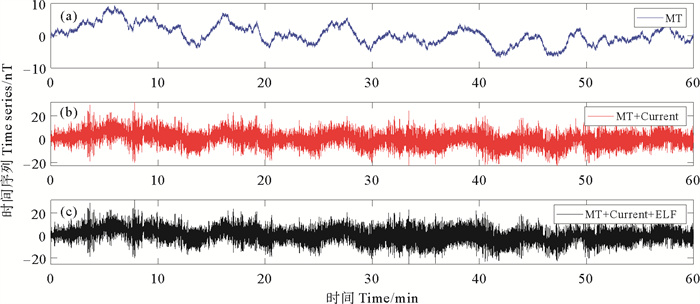
( (a)正演模拟的MT数据磁场水平分量Magnetic horizontal component of MT data from forward modeling;(b)引入海流感应磁场噪声的背景磁场数据Background magnetic field data with current induced magnetic noise;(c)加入极低频信号的合成数据Synthetic data with ELF signal. ) 图 4 合成数据时间序列 Fig. 4 Time series of the synthetic data |
|
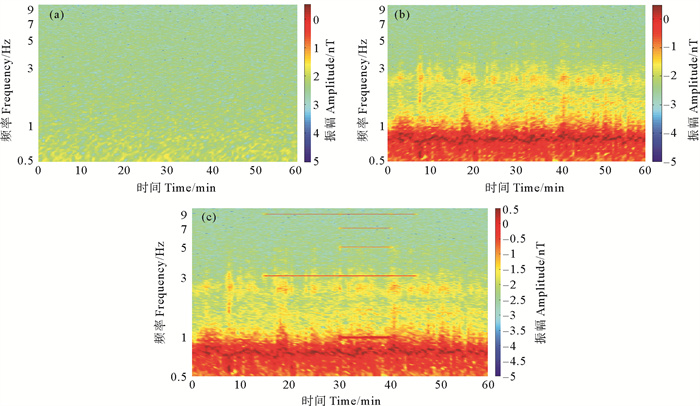
( (a)正演模拟的MT数据磁场水平分量Magnetic horizontal component of MT data from forward modeling;(b)引入海流感应磁场噪声的背景磁场数据Background magnetic field data with current induced magnetic noise;(c)加入极低频信号的合成数据时频图Synthetic data with ELF signal. 振幅取对数表示。The Amplitude is expressed in logarithm. ) 图 5 合成数据时频图 Fig. 5 Time-frequency spectrum of the synthetic data |
为了进一步引入海流感应电磁场的影响,本文根据该区域长期观测电磁数据分析结果,选取涨潮期连续观测1 h、受海水运动影响明显、频率范围为0.1~10 Hz左右的海洋电磁场数据磁场水平分量作为合成数据中的海流感应电磁场数据,进而可得到极低频电磁探测的背景场数据,如图 4(b)、图 5(b)所示。为了突出极低频段信号处理效果,在此设置时频图的频率显示范围为0.5~10 Hz。
在以上背景电磁场数据基础上加入模拟的极低频电磁信号,其中包括:发射频率为1 Hz的模拟源信号(时长10 min)和发射频率为3Hz的模拟源信号(时长30 min),信号时频图如图 4(c)、图 5(c)所示。由图 5(c)可见:由于作为模拟源信号的方波信号是奇谐信号,会产生奇数倍的谐波信号,即1和3 Hz的极低频信号分别产生了各自的谐频信号(3、5、7、9 Hz),这些信号均受到了海洋环境电磁场影响,其中1Hz基频信号所受影响较为严重。
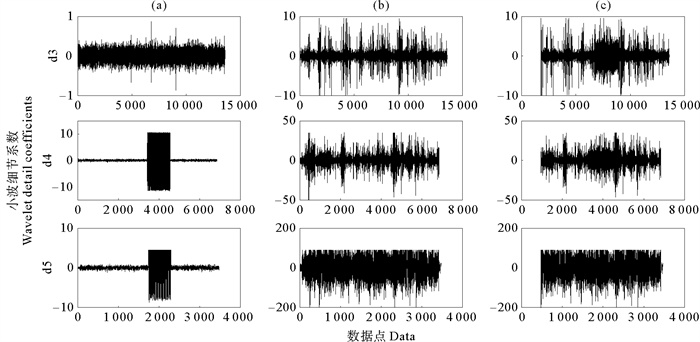
2.2 小波系数分析根据公式(3)确定分解层数为第3、4、5层;按照基于正演模拟确定小波阈值的思路[19],通过分别对包含有模拟MT信号与模拟极低频信号的数据、海流感应电磁场数据及由这些数据合成的数据进行小波系数分析,如图 6所示,可见:模拟源信号在MT资料背景中很容易被识别;而海流感应电磁噪声所对应的小波系数远大于MT数据和源信号所对应的小波系数,这表明MT信号和极低频信号均会被较强的海流噪声影响所淹没,那么数据处理的关键环节就集中于海流感应电磁噪声的压制。基于海流感应电磁噪声与MT数据和源信号之和在小波系数密度分布上的差别,进行噪声压制处理。
|
( (a)MT+极低频信号MT+ELF;(b)海流感应电磁场Current induced electromagnetic field;(c)包含前述数据的合成数据Synthetic data containing the above data. ) 图 6 模拟数据在目标分解层的小波系数 Fig. 6 Wavelet coefficients of simulated data at target decomposition level |
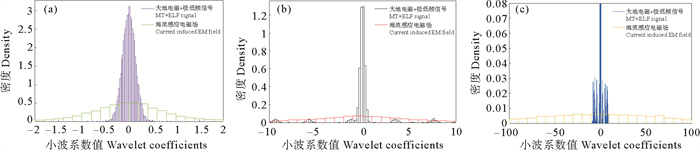
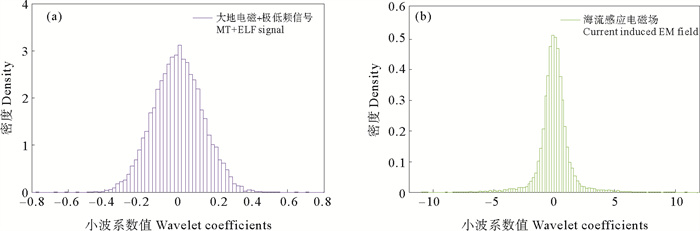
在小波系数分析结果(见图 6)基础上结合小波系数密度分布情况(见图 7),确定小波基函数及阈值:首先,以不同小波基对信号做小波变换,可得到源信号所代表的小波系数和背景信号所代表的小波系数,求取二者之比,在待选用的55个小波基中选取比值最大的小波基作为数据处理的小波基函数[16],在此选用‘dmey’小波基;然后,阈值的确定以合成数据实验中第3分解层为例(见图 8),阈值确定方法为:由于MT和极低频信号相对较弱,小波系数绝对值最大值为0.676 6,而同一分解层海流数据小波系数绝对值最大值为12.404 2;MT和极低频信号对应数据在第3层的小波系数密度分布中,大多数的小波系数绝对值都是在0.6以内,且阈值设置不应大于数据在相应分解层数小波系数最大值,综合图 6和图 8信息,确定第3层的阈值为0.6;同理确定第4、第5层阈值分别为1和2。
|
图 7 小波系数密度在(a)第3层;(b)第4层;(c)第5层的分布 Fig. 7 The density distribution of wavelet coefficients in (a) level 3, (b) level 4, (c) level 5 |
|
( (a)代表MT和极低频信号MT and ELF signal; (b)代表海流感应电磁场Current induced electromagnetic field. ) 图 8 第3层小波系数密度分布图 Fig. 8 The density distribution of wavelet coefficients in level 3 |
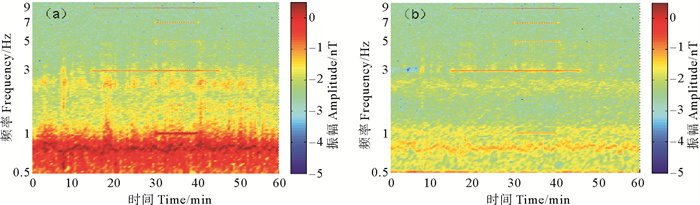
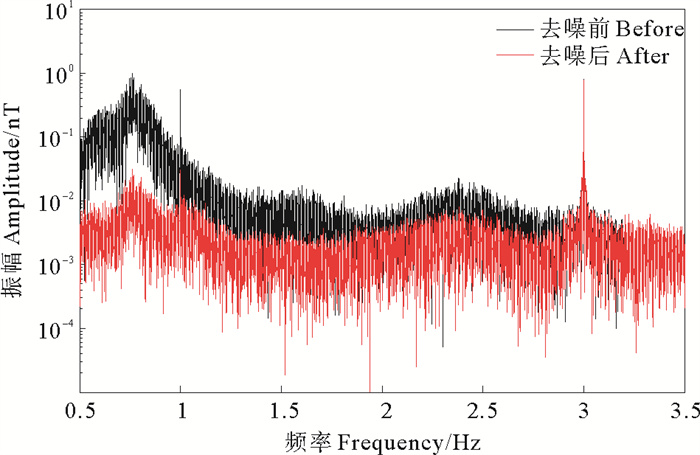
按照本文小波阈值去噪方法压制噪声,对包含1和3 Hz以及其倍频信号的合成数据进行处理,得到处理前后效果对比,如图 9和图 10所示,可见:3 Hz以下的海流感应电磁噪声得到明显压制,淹没于噪声的1 Hz频率的信号也被较好地识别,两种信号在时频域的识别能力均有所提高。表 1列出了去噪前后3和1 Hz频率的信号信噪比变化情况,3 Hz信号附近的噪声被压制,信噪比从21.81 dB提升到29.33 dB,淹没在海流感应电磁噪声中的1 Hz频率的信号得以显现,其信噪比也有所提升,从-5.00 dB提升到1.47 dB。
|
( (a)噪声压制前数据Data before noise suppression;(b)噪声压制后结果The result after noise suppression. 振幅取对数表示。The Amplitude is expressed in logarithm. ) 图 9 合成数据时频图 Fig. 9 Time-frequency spectra of the synthetic data |
|
图 10 噪声压制前后振幅谱 Fig. 10 Amplitude spectrum before and after noise suppression |
|
|
表 1 噪声压制前后信噪比(不同频率信号) Table 1 SNR before and after noise suppression (Different frequency signals) |
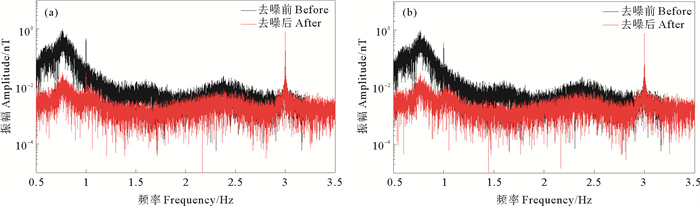
为进一步分析该方法的有效性,针对1 Hz的极低频信号,计算了两种更低信噪比条件下的噪声压制结果,处理前后振幅谱以及信噪比如图 11和表 2所示,可见:在较低信噪比条件下,该方法仍具备一定的噪声压制能力。
|
( (a)信噪比一6.46 dB SNR —6.46 dB; (b)信噪比—8.07 dB SNR —8.07 dB. ) 图 11 低信噪比合成数据噪声压制效果(极低频信号频率为1 Hz) Fig. 11 Noise suppression effect of low SNR synthetic data (ELF signal of 1 Hz) |
|
|
表 2 噪声压制前后信噪比(处理前信号的信噪比较低) Table 2 SNR before and after noise suppression (Low SNR before processing) |
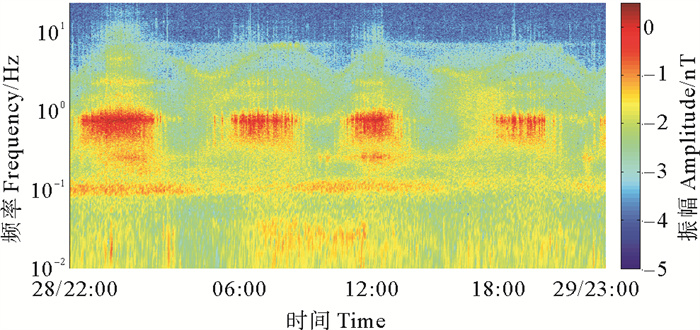
为验证该方法的有效性,在南黄海海域开展极低频电磁信号探测试验。首先,需要了解试验的背景环境,利用海底电磁场采集站(OBEM)开展5 d背景场观测试验,从试验数据中截取25 h数据,获得如图 12所示背景场时频图,可见:周期约为6 h的强能量干扰重复出现,这与试验区正规半日潮的潮流特征相吻合,判断其为海流运动引起的感应电磁场周期性的体现,其影响频率范围从0.01至几Hz,涨潮期接收到的电磁场信号比平潮期大1个数量级以上,足以影响水下极低频电磁信号的频率。
|
( 振幅取对数表示。The Amplitude is expressed in logarithm. ) 图 12 OBEM采集的25 h背景场(磁场)信号时频图 Fig. 12 Time-frequency spectrogram of 25 h background field (magnetic field) signal collected by OBEM |
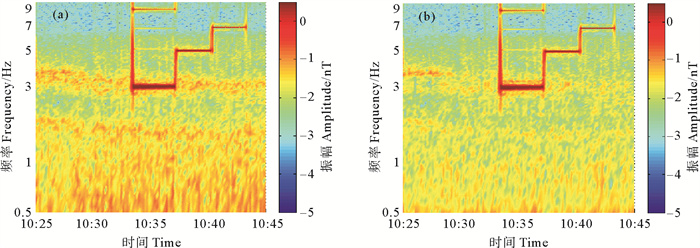
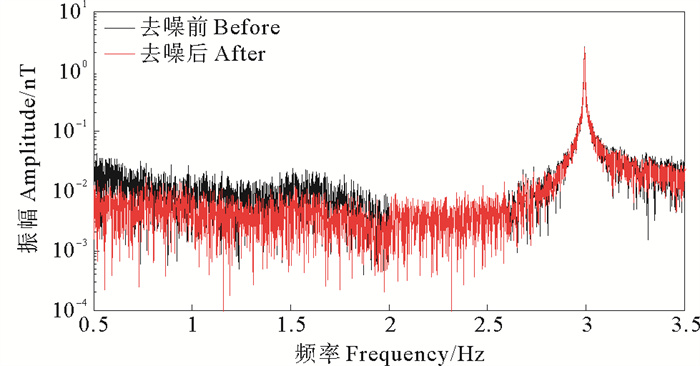
在此基础上开展水下极低频电磁信号探测试验,在海流流速开始增强的时段发射3、5和7 Hz三个频率的极低频电磁信号,各频率信号均稳定发射5 min,如图 13(a)所示。对于此实测数据,以不同小波基对信号做小波变换,可得到源信号所代表的小波系数和背景信号所代表的小波系数,求取二者之比,在待选用的55个小波基中选取比值最大的‘bior3.7’小波基作为此次海上试验数据处理的小波基函数。然后,根据公式(3)及小波系数分析方法,确定分解层数为第4、5层,阈值分别为0.8和2,得到噪声压制后结果,如图 13(b)所示,可见,影响极低频频段内的噪声已被明显压制,信号未受明显影响。利用振幅谱(见图 14)和公式(4)计算噪声压制前后信噪比,得到处理前信噪比约为16.05 dB, 处理后信噪比为20.11 dB,信噪比得到了较明显提升,同时极低频信号在时频域内的识别能力得到进一步提高。
|
( (a)噪声压制前数据Data before noise suppression;(b)噪声压制后结果The result after noise suppression. 振幅取对数表示。The Amplitude is expressed in logarithm. ) 图 13 实测数据时频图 Fig. 13 Time-frequency spectra of measured data |
|
图 14 噪声压制前后的振幅谱 Fig. 14 Amplitude spectrum before and after noise suppression |
在地磁场作用下海流运动产生的感应电磁场是极低频电磁探测中的重要噪声来源,其严重影响着极低频水下电磁探测信号的信噪比。本文将海流感应电磁场特征引入小波分析的阈值优化中,基于构造系统函数法获得MT信号,合成包含海流感应电磁噪声的极低频信号,并用于模型测试;通过合成数据试验和南黄海海域电磁信号探测试验先后对该方法进行了测试,结果表明该方法可有效压制海流感应电磁场噪声的影响,并提高了极低频探测信号的信噪比。
| [1] |
王毅凡, 周密, 宋志慧. 水下无线通信技术发展研究[J]. 通信技术, 2014, 47(6): 589-594. Wang Y F, Zhou M, Song Z H. Development of underwater wireless communication technology[J]. Communications Technology, 2014, 47(6): 589-594. DOI:10.3969/j.issn.1002-0802.2014.06.001 (  0) 0) |
| [2] |
李凯鹏, 刘芳华, 陈勇强, 等. 水下激光探测技术发展概述[C]. [s. l. ]: 2019年红外、遥感技术与应用研讨会暨交叉学科论坛论文集, 2019: 272-279. Li K P, Liu F H, Chen Y Q. Development of Underwater Laser Detection Technology: [C]. [s. l. ]: Symposium on Infrared and Remote Sensing Technology and Application and Interdisciplinary Forum in 2019, 2019: 272-279. (  0) 0) |
| [3] |
陈允锋, 刘伟. 非声探潜新技术浅析[J]. 光纤与电缆及其应用技术, 2016(6): 29-32. Chen Y F, Liu W. Brief analysis of new non-acoustic submarine detecting technologies[J]. Optical Fiber & Electric Cable and Their Application, 2016(6): 29-32. (  0) 0) |
| [4] |
卢俊, 张群飞, 史文涛. 水下探测通信一体化关键技术分析[J]. 水下无人系统学报, 2018, 26(5): 470-479. Lu J, Zhang Q F, Shi W T. Analysis on the key technology of integrated underwater detection and communication[J]. Journal of Unmanned Undersea Systems, 2018, 26(5): 470-479. (  0) 0) |
| [5] |
刘勇, 孙景芳. 0.1 Hz~30 kHz频段电波特性及应用研究[J]. 舰船科学技术, 2008, S1: 36-41. Liu Y, Sun J F. The characteristics and application research of 0.1 Hz~30 kHz radios[J]. Ship Science and Technology, 2008, S1: 36-41. (  0) 0) |
| [6] |
徐震寰, 李予国, 罗鸣. 船舶轴频电磁场信号的海底测量及其特性分析[J]. 哈尔滨工程大学学报, 2018, 39(4): 652-657. Xu Z H, Li Y G, Luo M. Seabed survey and property analysis of ship's shaft-rate electromagnetic signal[J]. Journal of Harbin Engineering University, 2018, 39(4): 652-657. (  0) 0) |
| [7] |
梁涓. 水下无线通信技术的现状与发展[J]. 中国新通信, 2009, 11(23): 67-71. Liang J. Current situation and development of underwater wireless communication[J]. China New Telecommunications, 2009, 11(23): 67-71. DOI:10.3969/j.issn.1673-4866.2009.23.017 (  0) 0) |
| [8] |
魏文博, 邓明, 温珍河, 等. 南黄海海底大地电磁测深试验研究[J]. 地球物理学报, 2009, 52(3): 740-749. Wei W B, Deng M, Wen Z H, et al. Experimental study of marine magnetotellurics in southern Huanghai[J]. Chinese Journal of Geophysics, 2009, 52(3): 740-749. (  0) 0) |
| [9] |
于彩霞, 魏文博, 景建恩, 等. 希尔伯特-黄变换在海底大地电磁测深数据处理中的应用[J]. 地球物理学进展, 2010, 25(3): 1046-1056. Yu C X, Wei W B, Jing J E, et al. Application of Hilbert—Huang transformation to marine magnetotelluric sounding data processing[J]. Progress in Geophysics, 2010, 25(3): 1046-1056. DOI:10.3969/j.issn.1004-2903.2010.03.045 (  0) 0) |
| [10] |
Chen K, Zhao Q, Deng M, et al. Seawater motion-induced electromagnetic noise reduction in marine magnetotelluric data using current meters[J]. Earth, Planets and Space, 2020, 72(1): 1-11. DOI:10.1186/s40623-019-1127-2
(  0) 0) |
| [11] |
罗忠涛, 卢鹏, 张杨勇, 等. 低频电磁噪声实验及通信处理分析[J]. 舰船科学技术, 2018, 40(5): 113-116. Luo Z T, Lu P, Zhang Y Y, et al. Experimental study of low frequency noise and analysis on communication processing algorithms[J]. Ship Science and Technology, 2018, 40(5): 113-116. DOI:10.3404/j.issn.1672-7649.2018.05.021 (  0) 0) |
| [12] |
常浩, 杨立波, 石宇轩, 等. 一种强噪声环境下的水声信号提取算法研究(英文)[J]. Journal of Measurement Science and Instrumentation, 2020, 11(3): 222-227. Chang H, Yang L B, Shi Y X, et al. Underwater acoustic signal extraction algorithm in a strong noise environment[J]. Journal of Measurement Science and Instrumentation, 2020, 11(3): 222-227. DOI:10.3969/j.issn.1674-8042.2020.03.004 (  0) 0) |
| [13] |
Fraser D C. The magnetic fields of ocean waves[J]. Geophysical Journal of the Royal Astronomical Society, 1966, 11(5): 507-517. DOI:10.1111/j.1365-246X.1966.tb03162.x
(  0) 0) |
| [14] |
Andrew R Ochadlick. Measurements of the magnetic fluctuations associated with ocean swell compared with Weaver's Theory[J]. Journal of Geophysical Research, 1989, 94(C11): 16237-16242. DOI:10.1029/JC094iC11p16237
(  0) 0) |
| [15] |
张自力, 魏文博, 李庚伟, 等. 海浪感应磁场的频谱特性[J]. 渤海大学学报(自然科学版), 2006(4): 354-357. Zhang Z L, Wei W B, Li G W, et al. Spectral character of magnetic field generated by ocean waves[J]. Journal of Bohai University (Natural Science Edition), 2006(4): 354-357. DOI:10.3969/j.issn.1673-0569.2006.04.016 (  0) 0) |
| [16] |
张宝强. 基于小波分析的海洋MT资料海浪感应电磁噪声压制方法研究[D]. 青岛: 中国海洋大学, 2018. Zhang B Q. Removal of Induced Electromagnetic Noise due to Ocean Waves in Marine MT Data by Using Wavelet Analysis Method[D]. Qingdao: Ocean University of China, 2018. (  0) 0) |
| [17] |
苏纪兰. 中国近海的环流动力机制研究[J]. 海洋学报(中文版), 2001(4): 1-16. Su J L. A review of circulation dynamics of the coastal oceans near China[J]. Acta Oceanologica Sinica, 2001(4): 1-16. DOI:10.3321/j.issn:0253-4193.2001.04.001 (  0) 0) |
| [18] |
朱心宇, 李予国. 有限水深海流感应电磁场数值模拟[J]. 中国海洋大学学报(自然科学版), 2020, 50(8): 109-114. Zhu X Y, LI Y G. Numrical simulation of electromagnetic field Induced by ocean current in finite water depth[J]. Periodical of Ocean University of China, 2020, 50(8): 109-114. (  0) 0) |
| [19] |
裴建新, 孙公毅. 基于MT正演模拟的小波阈值去噪方法[C]. 南京: SPG/SEG南京2020年国际地球物理会议论文集(中文), 2020: 1256-1259. Pei J X, Sun G Y. Wavelet Denoising Method Based on MT Simulation[C]. Nanjing: Proceedings of SPG / SEG Nanjing 2020 International Geophysical Conference (Chinese), 2020: 1256-1259 (  0) 0) |
| [20] |
Donoho D L, Johnstone I M. Ideal spatial adaptation by wavelet shrinkahe[J]. Biometrika, 1994, 81(3): 425-455. DOI:10.1093/biomet/81.3.425
(  0) 0) |
| [21] |
Mallat S G. Multiresolution approximations and wavelet orthonormal bases of L 2(R)[J]. Transactions of the American Mathematical Society, 1989, 315(1): 69.
(  0) 0) |
| [22] |
Mallat S G. A theory for multiresolution signal decomposition: The wavelet representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11(7): 674-693. DOI:10.1109/34.192463
(  0) 0) |
| [23] |
支鹏遥. 胶州湾地质构造特征及成因研究[D]. 青岛: 国家海洋局第一海洋研究所, 2008. Zhi P Y. The Geological and Structural Characteristics and Origin of the Jiaozhou Bay[D]. Qingdao: First Institute of Oceanography, SOA, 2008. (  0) 0) |
| [24] |
盛根来, 何瑞. 胶州湾沉积岩地层桩基参数确定的初步研究[C]. [s. l. ]: 2014全国工程勘察学术大会论文集, 2014: 21-24. Sheng G, He R. Preliminary Study on Determination of Pile Foundation Parameters in Jiaozhou Bay Sedimentary Str[C]. [s. l. ]: Proceedings of 2014 National Engineering Survey Conference, 2014: 21-24. (  0) 0) |
| [25] |
孙永福, 孙惠凤, 董立峰. 海底土的电阻率特征及其腐蚀性评价[J]. 海岸工程, 2005, 24(2): 48-53. SUN Y F, SUN H F, DONG L F. Seabed sediment resistivity characteristics and its corrosivity assessment[J]. Coastal Engineering, 2005, 24(2): 48-53. DOI:10.3969/j.issn.1002-3682.2005.02.008 (  0) 0) |
| [26] |
张宝强, 裴建新, 王启. 基于构造系统函数的大地电磁时间序列模拟方法[J]. 石油地球物理勘探, 2018, 53(2): 410-417. Zhang B Q, Pei J X, Wang Q. MT time series simulation based on constructed system function[J]. Oil Geophysical Prospecting, 2018, 53(2): 410-417. (  0) 0) |
2. The Key Laboratory of Submarine Geosciences and Prospecting Techniques, Ministry of Education, Ocean University of China, Qingdao 266100, China;
3. Laboratory for Marine Mineral Resources, Pilot National Laboratory for Marine Science and Technology (Qingdao), Qingdao 266237, China;
4. College of Engineering, Ocean University of China, Qingdao 266100, China;
5. College of Environmental Science and Engineering, Ocean University of China, Qingdao 266100, China
 2021, Vol. 51
2021, Vol. 51


