2. 中国海洋大学 海底科学与探测技术教育部重点实验室,山东 青岛 266100
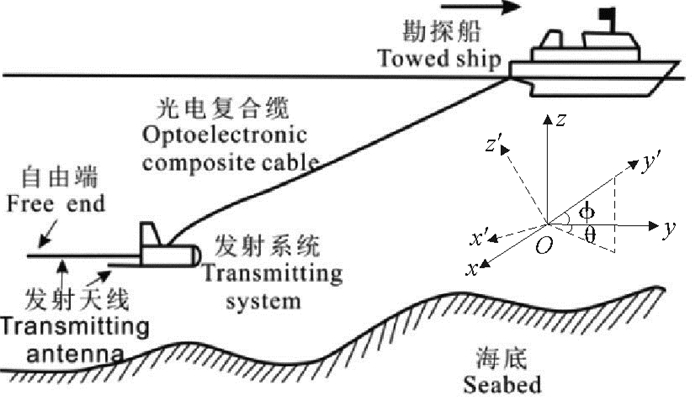
海洋可控源电磁法是一种新的海洋地球物理勘探方法,它在海洋油气资源勘探和天然气水合物调查中具有广阔的应用前景[1-2]。海洋可控源电磁勘探以海洋电磁拖曳系统为平台,该平台由勘探船、光电复合缆、拖体、发射天线等组成,如图 1所示。
|
图 1 海洋可控源电磁拖曳系统示意图 Fig. 1 Shematic illustration of the towed marine controlled-source electromagnetic system |
海洋电磁拖曳系统一般在深海海域工作,设计工作水深可达4 000 m。在海洋可控源电磁勘探时,通常勘探船经由光电复合拖缆缓慢地拖曳着拖体和发射天线在海底电磁采集站排列上方几十米处沿测线前行,并发射低频电磁信号。由于拖体的影响,使得其两侧的张力和姿态角不连续。本文为了便于分析,将忽略拖体的空间尺寸大小,将其看做质点,并称其为不连续点。实际上发射天线由两条导线组成,其长度分别为10和110 m,由于发射天线为中性浮力缆,故可将其等效为一条长为120 m的天线。
通过物理实验方法和数值仿真模拟,可以掌握拖曳系统的运动规律。虽然实验方法相比于仿真模拟可以提供更为准确的数据, 但是反复进行实验,势必会消耗大量的人力、物力和时间。而通过仿真模拟了解拖曳系统的运动特性及规律,可以节省大量的时间和资金[3-4]。
对拖缆的数值仿真模拟研究,早在上个世纪初期就已出现。目前拖曳系统的研究已成为现代海洋开发的重要课题之一,越来越多的学者和研究人员致力于这方面的研究工作。Ablow[5]和Sun[6]分析了拖曳系统的动态运动特征,王春杰[7]对横向流作用下海洋地震拖缆姿态进行了研究,王飞[8]对水下拖缆的定深控制问题进行了初步探讨。
前人的研究工作主要涉及浅水拖曳系统,其沉放深度一般不会超过300 m。而海洋可控源电磁拖曳系统,设计深度可达4 000 m。由于拖体沉放深度深、质量大,对光电复合缆和绞车的强度有着较高的要求。因而估计绞车所受的牵引张力,掌握绞车牵引张力随拖曳速度的变化规律,对工作方案的设计具有重要意义。
对于各种拖曳系统,水下拖缆在首尾两端的边界条件通常是确定的,因此拖曳系统的稳态问题可以转换为两点边值问题。目前,通常采用打靶法求解两点边值问题。但打靶法需要人为设置一个初始假定值,以便进行迭代求解,该方法误差较大且十分耗时。若初始猜测值设置不当,很有可能导致计算不收敛。
本文采用拖曳系统的稳态运动求解方法[9],首先把拖缆离散为一系列由节点相连、长度相等的弹性无摩擦微元,对离散的拖缆微元进行受力分析,得到受力平衡方程。以勘探船和自由端为边界条件,建立微分方程组并求解。
文中首先介绍拖曳系统模拟的基本理论,然后建立海洋拖曳系统模型,将模拟结果与王飞[10]的模拟结果进行对比;接着建立海洋可控源电磁拖曳系统模型,模拟不同缆长时拖体在海水中的位置,以及放缆时绞车所受的牵引张力,并将模拟结果与海试实测数据进行对比分析。
1 拖曳系统模拟理论在海上作业时,由于受到海水复杂多变运动的影响,勘探船会产生前后、左右、上下的晃动,使得勘探船的航速和航向难以保持稳定不变,而是在一定范围内波动。拖缆弯曲时会产生弯曲张力,并且拖缆的物性参数会随拖曳深度的变化而发生细微的改变。
为了简化计算,在拖曳系统仿真模拟时,常常假定勘探船航速保持稳定且航向不变,并且不考虑船体的晃动。将拖缆看成理想的均匀柔性圆柱状,其拉伸满足胡克定律,而且忽略拖缆形变时横截面积的变化,不考虑拖缆弯曲度的影响[11],并假定拖缆阻力系数等物性参数不随深度的改变而发生变化。
1.1 惯性坐标系与局部坐标系把拖缆离散为一系列由节点相连、长度相等的弹性无摩擦微元。为便于计算分析,建立两个直角坐标系,即惯性坐标系(x, y, z)与局部坐标系(x′, y′, z′)(见图 1)。惯性坐标系将勘探船看成原点,假定其行进方向为y方向。局部坐标系将微元的端点看成原点,其轴向为y′方向。假设l为拖缆微元距拖缆自由端的长度,L为拖缆总长度,0≤l≤L。θ和ϕ分别为拖缆微元在惯性坐标系下的偏移角和仰角,假定θ与y轴重合时为0°,顺时针半周为正,逆时针半周为负,取值范围为-180°<θ≤180°;ϕ与水平面重合时为0°,与z轴正方向夹角为正,与z轴负方向夹角为负,取值范围为-90°≤ϕ≤90°。惯性坐标系下的速度转换到局部坐标系下可以表示为
| $ \vec u = {\left| {{u_{x'}},{u_{y'}},{u_{z'}}} \right|^T} = {A^{ - 1}}\vec U。$ | (1) |
式中:
| $ A = \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{\sin \theta cos\phi }&{ - \sin \theta \sin \phi }\\ { - \sin \theta }&{\cos \theta \cos \phi }&{ - \cos \theta \sin \phi }\\ 0&{\sin \phi }&{ - \cos \phi } \end{array}} \right]。$ | (2) |
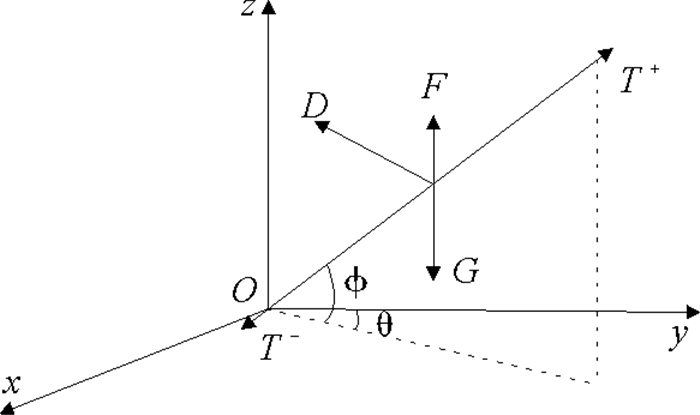
如图 2所示,在水中,单位长度拖缆微元受到重力
| $ \frac{{d\vec T}}{{dl}} + \vec F + \vec G + \vec D = 0。$ | (3) |
| $ G = mg,F = \rho \sigma g。$ | (4) |
|
图 2 拖缆微元受力分析 Fig. 2 A force analysis of the towline element |
式中:m为单位长度拖缆的质量;ρ为流体密度;σ为拖缆横截面积;g为重力加速度。
拖缆微元所受到的流体阻力可分为法向阻力Dn与切向阻力Dt,其计算式为:
| $ \begin{array}{l} {D_n} = - \frac{1}{2}\rho {S_n}{C_n}v_n^2 = - \frac{1}{2}\rho dl\left( {1 + \varepsilon } \right)d{C_n}v_n^2,\\ {D_t} = - \frac{1}{2}\rho {S_t}{C_t}v_t^2 = - \frac{1}{2}\pi \rho dl\left( {1 + \varepsilon } \right)d{C_t}v_t^2。\end{array} $ | (5) |
式中:Sn、St分别为拖缆微元法向和切向横截面积;Ct和Cn分别为拖缆在流体中的切向和法向阻力系数;d为拖缆微元的直径;vn和vt分别为拖缆微元法向速度和切向速度;ε为拖缆单位长度的形变量。
将
| $ \frac{{d\vec T}}{{dl}} = T\cos \phi \frac{{d\theta }}{{dl}}\vec x' + \frac{{dT}}{{dl}}\vec y' + T\frac{{d\phi }}{{dl}}\vec z'. $ | (6) |
把式(3)、(4)、(5)代入式(6),可得到局部坐标系(x′, y′, z′)下拖缆受力平衡方程[13]
| $ \begin{array}{l} T{\rm cos}\phi \frac{{d\theta }}{{dl}} = \frac{1}{2}\rho {\rm{ \mathsf{ π} }}d\sqrt {1 + \varepsilon } {C_n}{u_{x'}}\sqrt {u_{y'}^2 + u_{x'}^2} ,\\ \frac{{dT}}{{dl}}\omega \sin \phi + \frac{1}{2}\rho {\rm{ \mathsf{ π} }}d\sqrt {1 + \varepsilon } {C_t}{u_{y'}}\left| {{u_{y'}}} \right|,\\ T\frac{{d\phi }}{{dl}} = \omega \cos \phi + \frac{1}{2}\rho d\sqrt {1 + \varepsilon } {C_n}{u_{z'}}\sqrt {u_{y'}^2 + u_{z'}^2} 。\end{array} $ | (7) |
将拖缆均匀划分为很多小微元,当微元足够小时,可把每个微元的长度看成dl,从自由端出发,由(7)式可依次得到下一个微元所受到的张力、姿态角以及位置改变量。将局部坐标系下微元的改变量dl转换到惯性坐标系下。
| $ {\left[ {dx,dy,dz} \right]^{\rm{T}}} = \left( {1 + \varepsilon } \right)dlA{\left[ {0,1,0} \right]^{\rm{T}}}。$ | (8) |
式(7)和式(8)共同组成了拖缆系统的稳态运动控制方程,通过式(7)和式(8)可以得到所有微元在惯性坐标系下的坐标改变量,进而得到所有微元在惯性坐标系下的位置。
1.3 自由端参数的选取由于海洋可控源电磁拖曳系统一般在深海海域工作,因此可忽略表层海流的影响,即可以将其视为二维模型求解。在自由端(即l=0)处,拖缆张力以及仰角的变化率均为0。
由式(7),可知:
| $ \begin{array}{l} T\frac{{d\phi }}{{dl}} = \omega \cos \phi + \\ \frac{1}{2}\rho d\sqrt {1 + \varepsilon } {C_n}{u_{y'}}\sqrt {u_{y'}^2 + u_{z'}^2} 。\end{array} $ | (9) |
将T0=0,ux′=0,uz′=-|u|sinϕ0,ε=0代入(9)式,并整理得:
| $ \begin{array}{l} {\phi _0} = sign\left( \omega \right)\arccos \\ \;\;\;\;\;\;\;\left[ {\frac{{ - \left| \omega \right| + \sqrt {{{\left( {\rho d{C_n}{u_{z'}}{{\left| {\vec u} \right|}^2}} \right)}^2} + {\omega ^2}} }}{{\rho d{C_n}{u_{z'}}{{\left| {\vec u} \right|}^2}}}} \right]。\end{array} $ | (10) |
式中:sign(x)是符号函数。对于式(7),T0=0为奇点,为了方便计算,这里可简单地将其设置为一个小值,如令T0=0.1。
1.4 不连续点的处理将拖缆离散成一系列拖缆微元后,假设在惯性坐标系下,拖体位于节点i处,则节点i处受力平衡方程为:
| $ {{\vec F}_i} = {F_x}\vec i + {F_y}\vec j + {F_z}\vec k。$ | (11) |
该节点两侧的张力及姿态角分别用Ti-、Ti+、θi-、θi+、ϕi-、ϕi+表示,根据受力平衡条件,该节点两侧x、y、z三个方向的受力方程分别为:
| $ \begin{array}{l} T_i^ + \sin \phi _i^ + = T_i^ - \sin \phi _i^ - ,\\ T_i^ + \cos \theta _i^ + = T_i^ - \cos \theta _i^ - ,\\ T_i^ + \cos \theta _i^ + = T_i^ - \sin \theta _i^ - + {m_0}g。\end{array} $ | (12) |
式中:m0为拖体在水中的重量。根据式(12),如已知不连续点一侧的参量Ti-、θi-、ϕi-,则可得到另一侧的参量Ti+、θi+、ϕi+。
2 算法验证为了验证本文所述算法和程序的正确性, 计算海洋地震拖曳系统模型受力情况,并与前人结果进行对比。假定海洋地震拖曳系统可以分为两段,其上半段为与水面勘探船相连的引导缆,下半段为浮力与重力大致相等的尾绳, 其主要起到稳定作用。引导缆和尾绳的物理参数如表 1所示。
|
|
表 1 海洋地震拖曳系统模型参数 Table 1 Model parameters of the towed marine seismic system |
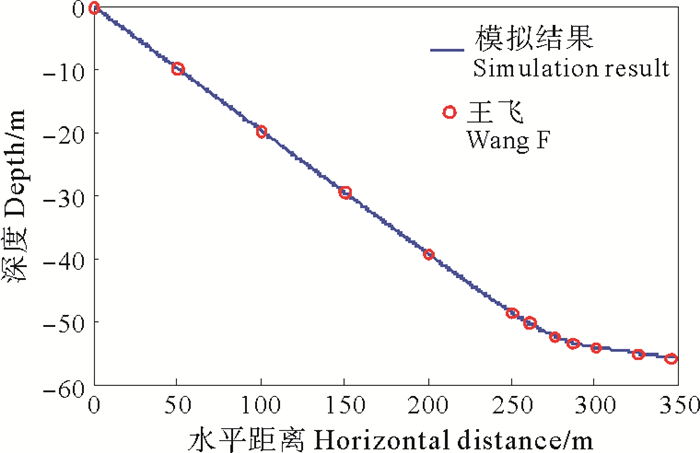
在模拟计算中, 为了获得高精度的模拟结果,需要将拖缆微元长度设置得尽可能小, 本文将其设置为0.5 m。假定拖曳速度为2 m/s。图 3中,实线为利用本文算法得到的拖缆下沉深度与离船水平距离关系曲线,红圈为王飞[10]的模拟结果,两者吻合得非常好。利用本文算法得到的拖缆末端深度和勘探船绞车牵引张力分别为-55.689 9 m和1.531 3 kN。对于相同的模型,王飞等[10]得到的拖缆末端深度和勘探船绞车牵引张力分别为-55.69 m和1.531 kN,可见两种模拟结果非常相近。
|
图 3 海洋地震拖曳系统模型模拟结果 Fig. 3 The numerical results for the towed marine seismic system |
根据实际的海洋可控源电磁拖曳系统建立模型,光电复合缆首端与勘探船相连,其末端与水下拖体相连,且拖体尾部连接有发射天线,可以起到稳定作用。发射天线为中性浮力缆,即在水中其重力与浮力相等。根据海试实测数据估计出光电复合缆、发射天线的阻力系数。拖体重约1.7 t,由于拖体的体积较大,故其阻力不可忽略。光电复合缆和发射天线的物理参数如表 2所示。
|
|
表 2 海洋可控源电磁拖曳系统模型参数 Table 2 Model parameters of the towed marine controlled-source electromagnetic system |
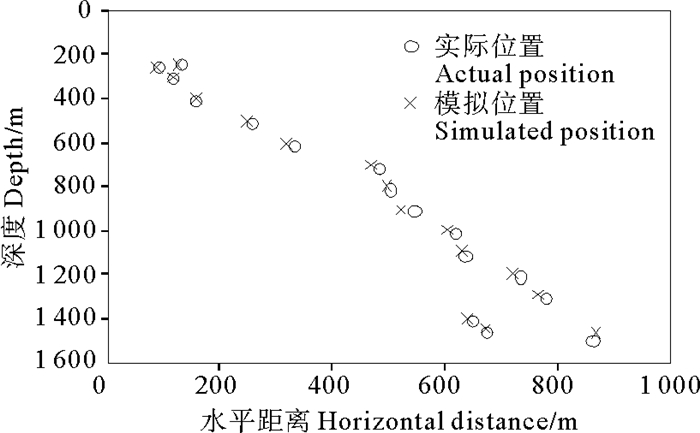
在实际海上作业时,拖体上安装有定位装置,于是从勘探船上可以实时监测到拖体的位置。根据光电复合缆的长度和拖曳速度,可以模拟拖体的位置,并与实测数据作对比,(见图 4)。从图中可以看出拖体位置的模拟结果与实际位置较为吻合,表明可以通过模拟来估计拖体的位置。由于在实际情况中,拖曳速度不是恒定不变的,而是在某一范围内不停地跳动,因而在模拟时基本选取最大速度与最小速度的平均值作为该时刻的拖曳速度。
|
图 4 拖体的实际位置与模拟位置 Fig. 4 Comparison of the observed locations of the towed fish with the simulated results |
海洋可控源电磁拖曳系统对光电复合缆和绞车的强度有着较高的要求,为了保障作业安全,避免拖缆崩断、绞车损坏等事故的发生,需要对绞车牵引张力进行评估,确保其在安全范围内。
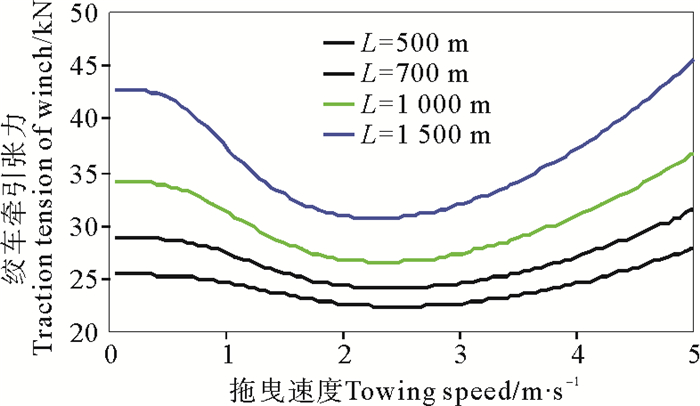
首先,讨论光电复合缆长度变化时时绞车所受牵引张力与勘探船航速的关系。为此,我们模拟了水中光电复合缆长度分别为500、700、1 000和1 500 m四种情况下,勘探船航速在0.01~5 m/s范围内变化时绞车的所受力情况(见图 5)。随着拖曳速度的增大,绞车的牵引张力先减小再增大,在拖曳速度为2.2~2.6 m/s时,牵引张力达到极小值,并且这种现象在光电复合缆长度越长时越明显。根据图 2受力情况可知,在拖曳速度不大时,拖缆微元与垂直方向的夹角比较小,拖曳速度的法向分量较大,法向阻力远大于切向阻力,法向阻力的垂直分量可以抵消部分拖缆微元的重力,随着拖曳速度的增大法向阻力的垂直分量逐渐增大,因而绞车牵引张力逐渐减小;随着拖曳速度的继续增大,拖缆微元与垂直方向的夹角逐渐增大,切向阻力逐渐变大,并且增速快于法向阻力,所以在拖曳速度增大到某一值后,随着拖曳速度的增大绞车的牵引张力逐渐增大。
|
图 5 4种不同缆长时绞车所受牵引张力与速度的变化规律 Fig. 5 The winch's tension versus the towed speeds for various towline lengths |
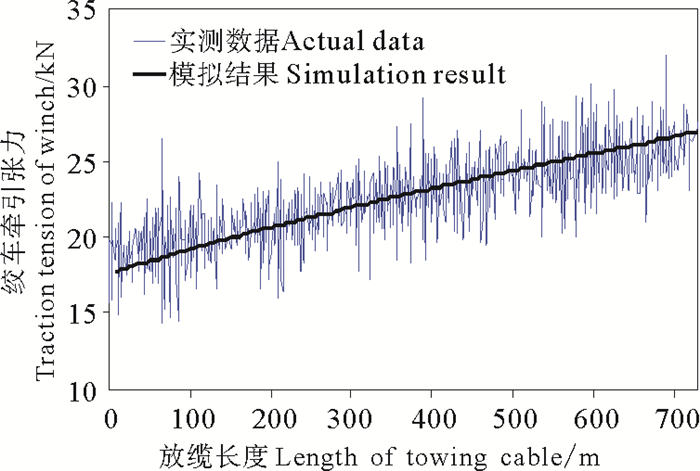
其次,讨论光电复合缆长度与绞车牵引张力的关系。为此,我们根据海洋可控源电磁拖曳系统布放过程中的航速、流速、放缆长度等,模拟了海洋可控源电磁拖曳系统布放过程中绞车所受张力大小,并与实测数据进行了对比。
在拖曳系统下放过程中,勘探船顶流航行,航速约为3节,缆长从0 m变化到730 m,放缆速度为12 m/min。图 5中红线为采用本文方法得到的模拟结果,蓝线为实测数据,两者变化趋势一致。由图 6可见,当勘探船航速一定时,水中光电复合缆越长,绞车所受张力越大,且绞车所受张力随着放缆长度的增长而线性增大。
|
图 6 光电复合缆沉放过程中绞车牵引张力模拟结果与实测数据对比 Fig. 6 Comparison of the observed winch's tension with the simulated results |
本文采用拖曳系统稳态运动求解方法实现了海洋可控源电磁拖曳系统运动仿真模拟,从而可以估算拖体在海水中的位置和绞车牵引张力。算例表明,当光电复合缆长度一定时,随着拖曳速度的增大,绞车牵引张力先减小再增大,光电复合缆长度越长这种现象越明显。
| [1] |
Zhdanov M S. Electromagnetic geophysics: Notes from the past and the road ahead[J]. Geophysics, 2010, 75(5): 557-560.
(  0) 0) |
| [2] |
Constable S. Ten years of marine csem for hydrocarbon exploration[J]. Geophysics, 2010, 75(5): 75A67-75A81. DOI:10.1190/1.3483451
(  0) 0) |
| [3] |
李志印, 吴家鸣. 水下拖曳系统水动力特性的计算流体力学分析[J]. 中国造船, 2007, 48(2): 9-19. Li Z Y, Wu J M. The Hydrodynamic behavior prediction of an underwater towed system with CFD method[J]. Shipbuilding Of China, 2007, 48(2): 9-19. DOI:10.3969/j.issn.1000-4882.2007.02.002 (  0) 0) |
| [4] |
张攀.拖曳系统运动仿真计算[D].武汉: 武汉理工大学, 2005. Zhang P. The Simulation of the Movement of Towed System[D]. Wuhan: Wuhan University of Technology, 2005. http://cdmd.cnki.com.cn/article/cdmd-10497-2005041463.htm (  0) 0) |
| [5] |
Ablow C M, Schechter S. Numerical simulation of undersea cable dynamics[J]. Ocean Engineering, 1983, 10(6): 443-457. DOI:10.1016/0029-8018(83)90046-X
(  0) 0) |
| [6] |
Sun Y, Leonard J W, Chiou R B. Simulation of unsteady oceanic cable deployment by direct inte- gration with suppression[J]. Ocean Engineering, 1994, 21(3): 243-256. DOI:10.1016/0029-8018(94)90001-9
(  0) 0) |
| [7] |
王春杰.横向流作用下海洋地震拖缆姿态控制研究[D].上海: 上海交通大学, 2011. Wang C J. Attitude Control of Marine Seismic Streamer Under Transverse Flow[D]. Shanghai: Shanghai Jiao Tong University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10248-1011267945.htm (  0) 0) |
| [8] |
王飞.海洋勘探拖曳系统运动仿真与控制技术研究[D].上海: 上海交通大学, 2007. Wang F. Simulation and Control Research of Marine Towed Seismic System[D]. Shanghai: Shanghai Jiao Tong University, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10248-2007053403.htm (  0) 0) |
| [9] |
Wang Fei, Huang Guoliang, Deng Deheng. Steady state analysis of towed marine[J]. Journal of Shanghai Jiaotong University, 2008, 13(2): 239. DOI:10.1007/s12204-008-0239-9
(  0) 0) |
| [10] |
王飞, 黄国樑, 邓德衡. 水下拖曳系统的稳态运动分析与设计[J]. 上海交通大学学报, 2008, 42(4): 679-684. Wang F, Huang G L, Deng D H. The design and steady-state simulation of underwater towed system[J]. Journal of Shanghai Jiaotong University, 2008, 42(4): 679-684. DOI:10.3321/j.issn:1006-2467.2008.04.035 (  0) 0) |
| [11] |
汪鸿振, 汪开军. 用有限元法求解水下拖缆振动特性[J]. 上海交通大学学报, 1999, 33(8): 1047-1050. Wang H Z, Wang K J. Solving for vibration behavior of towed underwater cables by FEM[J]. Journal of Shanghai Jiaotong University, 1999, 33(8): 1047-1050. DOI:10.3321/j.issn:1006-2467.1999.08.034 (  0) 0) |
| [12] |
Fei W, Huang G L, Deng D H. Dynamic response analysis of towed cable during deployment/retrieval[J]. Journal of Shanghai Jiaotong University, 2008, 13(2): 245-251. DOI:10.1007/s12204-008-0245-y
(  0) 0) |
| [13] |
苑志江, 金良安, 迟卫, 等. 海洋拖曳系统稳定姿态的影响因素研究[J]. 科学技术与工程, 2013, 13(5): 1127-1134. Yuan Z J, Jin L A, Chi W, et al. Influential factors on the steady state of underwater towed system[J]. Science Technology and Engineering, 2013, 13(5): 1127-1134. DOI:10.3969/j.issn.1671-1815.2013.05.002 (  0) 0) |
| [14] |
Huang S. Dynamic analysis of three-dimensional marine cables[J]. Ocean Engineering, 1994, 21(6): 587-605. DOI:10.1016/0029-8018(94)90008-6
(  0) 0) |
2. Ocean University of China, Key Lab of Submarine Geosciences and Prospecting Techniques of Ministry of Education, Qingdao 266100, China
 2018, Vol. 48
2018, Vol. 48


