矢量序列信号的瞬时频率分析具有重要的应用需求,诸如雷达海杂波分析、海洋声信号分析等。瞬时频率计算对噪声污染非常敏感,因此矢量序列噪声抑制是不可回避的第一步环节。但是,从噪声污染信号中提取信号,面临的是一个“病态”投影信号复原的挑战性问题。对于海杂波尤其如此。噪声污染又加上海面结构所导致的信号非线性和非平稳性,更加剧了信号分析的困难。
现代信号处理越来越依赖于概率和统计以解决信号处理中的挑战问题[1]。对于矢量形式的高斯噪声,人们认识到它的相位服从均匀分布(白色)而矢径服从高斯分布。借助信息熵的术语,均匀分布的信息熵最大,也意味着它的随机性最强,因此需要最为精细尺度的处理方法。而对于服从非均匀分布的矢径序列,有效的途径是处理算法的尺度能够依赖于数据的局部性尺度。
纵观近年来已有的分解处理方法,全变分TV(Total Variation)方法具有最为精细的时间变化分析性能。全变分降噪模型[2]自从提出之后,由于物理意义的明显和精细处理特点,在图像分解、复原、分割等多方面得到广泛应用,目前已经形成了一种信号和图像处理领域的艺术级别的流派。TV方法的数字化计算过程中有2个参数,调整因子和迭代次数,需要进行选择,文献[2]给出了这参数调整因子的计算公式。而后,诸多学者研究了对处理效果的影响、诸如图像的边缘保持特性等。文献[3]在超声信号降噪的TV应用中认为该参数计算的耗费太大,经验性的给出了该参数的选择范围。
1998年,Nudun Huang等[4]提出了适应于非平稳非线性信号的EMD(Empirical Mode Decomposition)分解方法。EMD将信号看作为“零均值快变震荡信号与慢变震荡信号的叠加”,其分解的主要特点是依据待分解数据的“局部尺度”,将原始信号分解为不同震荡频率的细节和內禀性模式IMFS。而后,通过Hilbert-Huang Spectrum计算信号的瞬时频率。文中也证明了利用分解量可以完全重构原始信号。但是,Nudun Huang的EMD方法仅仅适用于1D实数序列分解。
为了能够进行矢量序列分析,近年来逐步发展了RIEMD[5]、BEMD[6]等基于EMD的分解方法。BEMD认为当分析数据是两变量数据时,振动的表示是模糊的。他们以旋转表示两变量信号:“两变量信号=快速旋转信号叠加于慢速旋转信号”之上。文献[6]同时给出了包络均值的求取算法。文献[7]注意到,对于规定两个方向的情况RIEMD与BEMD是等价的。文献[8]应用BEMD研究了在认知雷达场景分析的应用。
根据噪声统计特性及TV和EMD分析方法的特点,本文提出由TV相位降噪和矢径EMD分解相组合的矢量序列降噪、分解方法。在相位降噪中,以最大信杂比为准则,优化选择迭代计算中的调整因子和迭代次数,以获得最大信杂比的降噪效果。在矢径EMD分解中,为了防止重构矢量的相位跳变,对分解增加了非负判定环节。最后,将经过降噪的相位序列和EMD分解的矢径序列,以采样时间(样点序号)为参考,一一对应组合,重构矢量。考虑到历史的传承性,我们将该种矢量分解方法称之为VEMD(Vector Empirical Mode Decomposition)方法。
1 矢量时间序列的分解 1.1 相位序列TV降噪任意一个矢量时间序列可以表示为
| $ Z(t)=a(t)\exp\{jφ(t)\}。$ | (1) |
其中:a(t)是矢量的矢径;φ(t)是矢量在时刻t的相位。
将噪声污染的相位序列φ(t)表达为
| $ φ=y+n。$ | (2) |
式中n为噪声。TV降噪模型为
| $ \arg {\min _s}({\smallint _\mathit{\Omega }}[\nabla \varphi + \frac{\lambda }{2}{\left( {\varphi - y} \right)^2}]){\rm{d}}x。$ | (3) |
式中Ω信号定义域,调整参数λ>0控制平滑量。(3)式中的第1项称为正则项,第2项称为保真项。(3)式最速下降法的Euler-Lagrange方程是
| $ \frac{{\partial \varphi }}{{\partial t}} = {\rm{div}}\left( {\frac{{\nabla \varphi }}{{\left| {\nabla \varphi } \right|}}} \right) + \lambda \left( {\varphi - y} \right)。$ | (4) |
但对于单变量信号,由
| $ {y^{n + 1}} = \varphi - \frac{1}{\lambda }y_{tt}^n。$ | (5) |
式中yttn为第n次迭代yn的二阶差分,初始化y0=φ,迭代过程结束后,以yn+1作为目标函数φDenoise。文献[9]中给出了yn迭代计算的MATLAB程序网址。
TV降噪的计算过程涉及调整因子和迭代次数的选择。以自适应方法选择将会导致大计算量耗费。最大信杂比是信号处理所追求的一般性准则。本文采用最大信杂比为准则的方法指导和迭代次数的选择。信杂比估计采用了经验性估计方法。假设信号频率低于噪声频率,将低频功率谱峰面积与背景杂波的功率谱面积之比作为估计的信杂比。
最大信杂比TV相位降噪及参数过程如下:首先设定λ和的初始数值及其变化步长;在每一次迭代计算之后,估计信杂比。最后,以最大信杂比下的调整因子和迭代次数作为参数,应用于TV降噪。一个实际过程的信杂比估计的图形如1所示。
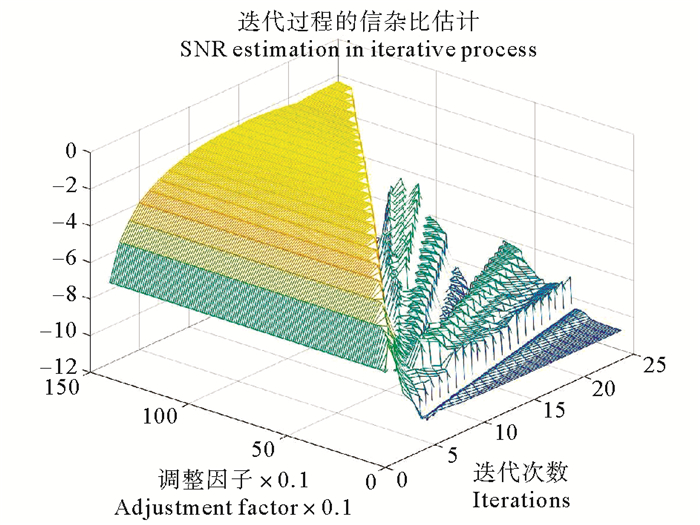
|
图 1 TV迭代过程参数变化的信杂比 Fig. 1 The SNR with the parameters adjusting in TV iteration processes |
考虑到矢量重构,关于矢径分解的一个重要约束是不能够改变原数值的符号(正/负)。因为改变一个矢量的正负,等价于矢量相位的变化。本文在原始EMD分解框架的基础上,增加一个IMF的判别环节,∀lmf(ti) < 0,则分解停止。
EMD分解框架:
记矢径序列为{x(i)}i=1N。
(1) 寻{x(i)}i=1N的局部极大值/极小值:使得局部极大和极小值的数量相等或最多差1。
(2) 求局部包络:在相邻的极大值之间(极小值之间同样处理),利用立方样条插值,形成极大值包络emax(和极小值包络emin)。
(3) 局部均值曲线:对每一个样点,均值曲线:
| $ Imf\left( i \right) = \frac{1}{2}[{e_{\max }}\left( i \right) + {e_{\min }}\left( i \right)]。$ | (6) |
(4) Imf非负判断:如果∀Imf(ti) < 0, 停止。
(5) 从信号中减均值,得到分解的细节Detail(i)=x(i)-Imf(i)。
经过上述过程,从原始信号得到第一层分解的Imf1和Detail1。
将Imf1作为新的待分解信号,重复(1)~(5),直到L层的ImfL。其中,(4)条为本文加入的约束条件。
1.3 矢量重构将VEMD分解的最后一层内禀性模式与降噪相位序列φDenoise一一对应,构成矢径、相位对,则称为重构的分解矢量序列,
| $ {z_{re}}\left( i \right) = \{ im{f_L}\left( i \right){{\rm{e}}^{j{\varphi _{Denoise}}\left( i \right)}}\} _{i = 1}^N。$ | (7) |
它保留了原始信号的最大能量并且满足TV相位保真性约束条件,因此将其看作为纯净信号的近似。
1.4 瞬时相位梯度与瞬时功率谱计算瞬时频率的计算在历史上是一个有争议的问题。概念上,瞬时频率定义为
对重构的,通过(8)式计算瞬时相位梯度。为了与瞬时频率对应,乘以因子
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;f({t_i}) = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\frac{{\Delta \varphi ({t_i})}}{{\Delta t}} = \\ \frac{1}{{2{\rm{ \mathsf{ π} }}}}[Angle({Z_{re}}({t_i})) - Angle({Z_{re}}({t_{i + 1}}))]。\end{array} $ | (8) |
为了计算瞬时功率谱,在(8)式的基础上,将
| $ \begin{array}{l} P({t_i}) = \frac{1}{2}[P({t_i}) + P({t_{i + 1}})] = \\ \frac{1}{2}[im{f^2}\left( i \right) + im{f^2}\left( {i + 1} \right)]。\end{array} $ | (9) |
赋给联合坐标,作为瞬时功率谱。
2 分解实验为了验证本文所提出方法的有效性,我们以人工产生的线性频率调制信号,线性+正弦频率调制的信号进行了分解噪声实验。实验过程如下:首先生成纯净的矢量时间序列信号Zpure(t),然后利用MATLAB功能函数,在信号上叠加信噪比为1dB的高斯白噪声(请注意这是信杂比较低的情况),然后利用本文的VEMD分解方法进行分解。为了表示的统一性,记矢径分解的最后一层为Imf(t)。将Imf(t)与经过TV降噪的相位序列一一对应组合,构成近似矢量Zre(t)=Imf(t)exp{jφDenoise(t)},计算瞬时频率。
实验用例1,线性频率调制信号Zpure(t)=3.0exp{j2π300(t2)/2},实验结果如图 2所示。
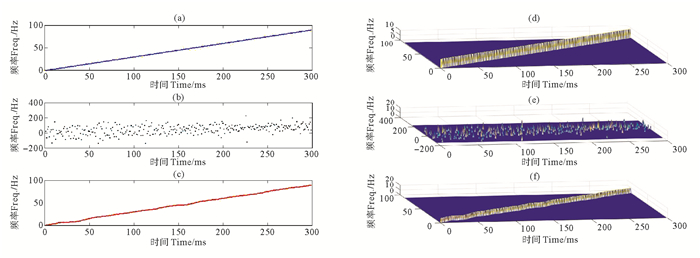
|
((a)纯净信号的瞬时频率;(b)噪声污染信号的瞬时频率;(c)本文方法降噪信号的瞬时频率;(d)纯净信号的瞬时功率;(e)噪声污染信号的瞬时功率;(f)本文方法降噪信号的瞬时功率。(a) Instantaneous frequency of the pure signal; (b) Instantaneous frequency of the noising signal; (c) The de-noising signal's instantaneous frequency by method this paper; (d) Instantaneous power of the pure signal; (e) Instantaneous power of the noising signal; (f) Instantaneous power of the de-noising signal by method this paper.) 图 2 分解降噪实验 Fig. 2 Experiment de-noising by decomposition |
实验用例2,线性频率调制+正弦频率调制信号,过程同实验用例1。
Z(t)=3exp{j2π300(t2)/2+j5sin(2π10t)}实验结果如图 3所示。
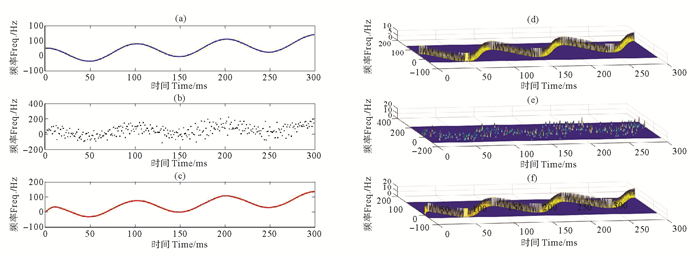
|
((a)纯净信号的瞬时频率;(b)噪声污染信号的瞬时频率;(c)本文方法降噪信号的瞬时频率;(d)纯净信号的瞬时功率;(e)噪声污染信号的瞬时功率;(f)本文方法降噪信号的瞬时功率。(a) Instantaneous frequency of the pure signal; (b) Instantaneous frequency of the noising signal; (c) The de-noising signal's instantaneous frequency by method this paper; (d) Instantaneous Power of the pure signal; (e) Instantaneous Power of the noising signal; (f) Instantaneous Power of the de-noising signal by method this paper.) 图 3 分解降噪实验 Fig. 3 Experiment de-noising bydecomposition |
由上述2个实验结果的可见,本文的方法可以有效抑制矢量高斯噪声。虽然在瞬时频率的初始和最后阶段有所形变,但是基本上保持了纯净信号的变化规律。
实验用例3,加拿大IPIX雷达数据这里采用的试验数据来自于加拿大McMaster大学的IPIX雷达数据库网站,其雷达数据包括了HH、HV、VH,VV四种极化方式,每一个数据文件含有14个距离门的回波信号,其中目标为一个直径1 m的球形密封器件,表面包裹了铝箔,以增强反射回波信号。
图 4是IPIX实测数据的降噪实验结果,使用了IPIX数据文件31#HV极化方式的1 500个样点,主要用以实验本文方法的有效性。由图 4可见,本文的分解降噪方法的确较为有效的抑制了噪声干扰。以此为基础,可进行降噪数据的分析,建模等研究。由于时间限制,这些研究工作有待后续进行。
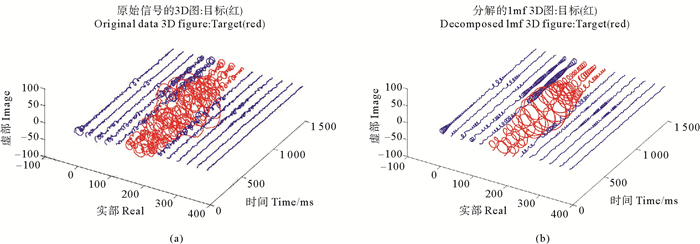
|
((a)为原始数据;(b)为本文方法的分解降噪结果。(a)Original data; (b)The result of proposed method.) 图 4 IPIX数据降噪实验 Fig. 4 The experiment of IPIX de-nosing data |
信号的统计特性是处理方法选择的重要依据。高斯噪声的相位服从均匀分布,意味着其具有最强的随机性。因此,本文利用细致的TV方法对矢量序列的相位进行降噪;又根据矢量的矢径序列一般服从非均匀分布特点,利用适用于非线性非平稳序列的EMD方法进行矢径分解;据此形成一种新的矢量序列分解、降噪方法。这种针对不同统计特性“分而治之”的信号处理方法,希望能够为读者提供一定的参考。以此为基础,后续将进行降噪之后的数据分析,建模等研究。
| [1] |
Pereyra M, Schniter P, Chouzenoux E, et al. A survey of stochastic simulation and optimization methods in signal processing[J]. IEEE Journal of Selected Topics in Signal Processing, 2016, 10(2): 224-241. DOI:10.1109/JSTSP.2015.2496908
(  0) 0) |
| [2] |
Rudin L I, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms[J]. Physica D: Nonlinear Phenomena, 1992, 60(1-4): 259-268. DOI:10.1016/0167-2789(92)90242-F
(  0) 0) |
| [3] |
Sinding K M, Drapaca C S, Tittmann B R. Digital signal processing methods for ultrasonic echoes[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2016, 63(8): 1172-1176. DOI:10.1109/TUFFC.2016.2557283
(  0) 0) |
| [4] |
Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[C].//Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. London: The Royal Society of London, 1998, 454(1971): 903-995.
(  0) 0) |
| [5] |
Altaf M U B, Gautama T, Tanaka T, et al. Rotation invariant complex empirical mode decomposition[C].//Acoustics, Speech and Signal Processing. Honolulu, Hawaii: ASSP 2007, IEEE International Conference, 2007: 1009-1012.
(  0) 0) |
| [6] |
Rilling G, Flandrin P, Goncalves P, et al. Bivariate empirical mode decomposition[J]. IEEE Signal Processing Letters, 2007, 14(12): 936-939. DOI:10.1109/LSP.2007.904710
(  0) 0) |
| [7] |
Looney D, Mandic D P. Multiscale image fusion using complex extensions of EMD[J]. IEEE Transactions on Signal Processing, 2009, 57(4): 1626-1630. DOI:10.1109/TSP.2008.2011836
(  0) 0) |
| [8] |
Güntürkün U. Bivariate empirical mode decomposition for cognitive radar scene analysis[J]. IEEE Signal Processing Letters, 2015, 22(5): 603-607. DOI:10.1109/LSP.2014.2365361
(  0) 0) |
| [9] |
Selesnick I. Total Variation Denoising (an MM Algorithm)[CP/OL].[2017-05-15]. http://cnx.org/content/m44934/1.4/
(  0) 0) |
 2019, Vol. 49
2019, Vol. 49


