中尺度涡是海洋中普遍存在而又十分重要的物理现象,其时间尺度从几天到几个月、空间尺度在几十至几百公里[1],主要特征是环流能够较长时间维持封闭状态,环流速度高达1~2 m/s。中尺度涡从大尺度背景环流中吸收能量而产生,其具有的动能在海洋运动能量谱中是一个显著的峰区[2],对温度、盐度及生物化学过程都有极其重要的影响;消失时又将能量耗散到小尺度中,同时又对小尺度过程产生极大的影响[3]。中尺度涡对温度、盐度及物质的输运作用不仅对海洋温盐结构和流速分布有直接影响[4-5],也会对局地海洋化学及生物环境产生重要影响[6-8]。此外,中尺度涡所造成的上升流,将下层海洋营养盐携带至真光层,也会促进海洋初级生产力的提高。中尺度涡虽然普遍存在于大洋中,但空间分布不均匀。卫星观测表明,在西北太平洋的各个海区都存在着大量的中尺度涡, 尤其在南海、黑潮及黑潮延伸体附近, 以及在北赤道流和黑潮延伸体之间的副热带逆流区, 中尺度涡活动异常活跃。受海洋大范围、长时间观测资料的限制,至今人们对海洋中尺度过程了解较少,对中尺度涡三维结构特征的研究亦未得到较为清晰且统一的认识。
Johannessen等利用NOAA卫星红外数据结合ADC(声学多普勒海流剖面仪)、CTD等观测资料,给出了挪威沿岸流中涡旋的流速、温跃层三维结构[9]。近几年,卫星高度计与Argo浮标观测系统的结合,使中尺度涡的研究有了质的飞跃。Chaigneau等研究了秘鲁智利沿岸的涡旋垂直结构,发现暖核要比冷核深,涡旋引起的温度异常大约为1℃[10];Liu等统计了副热带逆流区涡旋结构,发现冷涡暖涡的冷暖核深度相差不多,涡旋的影响深度可以达到1 000 m[11]。Yang等对西北副热带太平洋中尺度涡三维结构的研究发现,由于主温跃层内模态水的存在,涡致温度异常表现出一个双核垂直结构,在气旋涡图像中尤其显著,盐度异常由于垂直水团的分布表现出类三明治型结构,在反气旋涡图像中更加明显[12];Castelao研究了南大西洋海岸和墨西哥湾流区域中尺度涡的垂直结构,研究表明,由反气旋涡引起的温盐异常较气旋涡范围更大、深度更深[13];Yang等利用新版本的日分辨率卫星高度计资料与Argo浮标剖面数据研究了东南热带印度洋中尺度涡的垂直结构,通过涡旋合成分析发现,涡旋对温盐的影响主要在海洋上300 m层处[14];Dandapat和Chakraborty研究了孟加拉湾西部中尺度涡的三维特性,根据中尺度涡的正负极性对温跃层产生的不同影响进行分别研究:气旋涡一般在研究海域次表层处增强,温度异常型显示出反气旋涡和气旋涡都存在一个单核垂直结构且核分布在100 m深度处[15];Dong等利用ROMS模式数据对南加州海岸涡旋的垂直结构进行研究,发现大多数涡旋最大深度在50 m,大于50 m深的涡旋数量急剧减少,并且气旋涡比反气旋涡发展深度更大[16]。
之前的研究者大多选择温盐分布作为描述涡旋结构的指标,分析的是涡旋的局地特征,所以得到的涡旋三维结构也不尽相同。Zhang等则从涡旋的动力学结构出发,基于卫星高度计资料结合Argo资料,采用合成分析和归一化的方法以涡旋密度场及压强场的角度来研究中尺度涡,得到了全球范围内中尺度涡的三维统一结构。他们对不同深度的均一化压强序列进行分析,发现在不同深度上虽然振幅不同,但各个深度上压强异常序列变化存在一致性,即压强异常序列不随深度变化,进而得出中尺度涡压强异常场的水平结构和垂直结构是独立变化的。在数学表达式上可以表示为两个分离函数乘积的形式,其中水平统一结构为R(rn)=(1-rn2/4)·exp(-rn2/4),描述压强异常水平变化趋势;通过坐标变换得到在拉伸坐标下的中尺度涡垂直统一结构,表达式为Hn=sin(zn),描述不同深度压强异常变化的振幅[17-18]。
Zhang等通过观测资料得到了中尺度涡三维统一结构,但由于Argo对中尺度涡的观测不是同步的,且需要进行Argo剖面与最近涡旋中心区域配对处理,因此研究的结果受有意义的统计样本数据量影响。与观测资料相比,模式数据具有连续性好、分辨率高、准同步等优势,因此本文将利用HYCOM模式数据采用归一化和坐标变换的研究方法,分析中尺度涡的三维结构,并与观测结果进行比较。
1 数据和方法 1.1 数据HYCOM(Hybrid Coordinate Ocean Model)是近些年来主流的全球海洋环流模式,其水平网格采用Arakawa C网格和标准笛卡尔坐标系,垂向采用混合坐标(等密度坐标、δ坐标和z坐标)。其优点是可以在不同层结的海洋中使用相应垂向坐标:层化明显的开阔海洋中选用等密度坐标,在浅海或陆架区域的随地坐标中,混合层或层化不明显的海域则由等密度坐标平滑过渡到z坐标。因此HYCOM模式混合坐标系的应用较传统模式单一垂向坐标系更加接近真实海洋。HYCOM模式数据包含海表面高度(SSH)、温盐(TS)及流场(UV)数据,数据存放格式为NetCDF格式,空间分辨率为1/12(°)×1/12(°),时间分辨率为1天,垂直分辨率为从海表面5 m至底层5 000 m,共计40层(详细介绍见:http://hycom.org/)。本文选用2004—2008年共计5年的模式数据,用到的变量有海表面高度、温度和盐度,水平范围为10°N~30°N,120°E~160°E,垂向范围从0到26层(数据下载网址为:http://tds.hycom.org/thredds/GLBu0.08/expt_19.1.html)。
1.2 方法首先采用标准大气压下国际海水状态方程,通过温盐数据计算得到海水密度,再根据海表高度SSH和ρ0计算海表压强P0:
| $ {P_0} = g{\rho _0}{\rm{SSH, }} $ |
最后从海面向下积分得到压强场分布:
| $ p\left( {x, y, z, t} \right) = \int\limits_0^z {g\rho \left( {x, y, z', t} \right){\rm{d}}z' + {P_0}}。$ |
对涡旋的识别探测应用Okubo-Weiss参数法[19-20],该方法常被缩写为OW,是从中尺度涡旋的物理特性出发,通过海表面高度或温度场的信息来进行识别:将物理场信息参数化,当该参数超过设定阈值时就识别为中尺度涡。此方法能够揭示中尺度涡的物理本质,对尺度较小的中尺度涡识别更加准确,缺点是对阈值设定比较敏感,容易错误识别。
OW参数是通过流场中的拉伸、剪切以及相对涡度来定义的:
| $ W = S_s^2 + S_n^2-{\omega ^2}。$ |
其中Ss、Sn以及ω分别表示的是拉伸变形率,剪切变形率以及相对涡度。它们的计算方法为:
| $ {S_s} = \frac{{\partial v}}{{\partial x}} + \frac{{\partial u}}{{\partial y}}, {S_n} = \frac{{\partial u}}{{\partial x}}-\frac{{\partial v}}{{\partial y}}, \omega = \frac{{\partial v}}{{\partial x}}-\frac{{\partial u}}{{\partial y}}。$ |
在满足地转平衡条件下,水平无辐散流的OW参数可以简化为[21]:
| $ W = 4\left( {u_x^2 + {v_x}{u_y}} \right)。$ |
其中u和v表示海表面地转流速异常的水平速度分量。根据地转关系由SLA梯度计算得到:
| $ u =-g{f^{-1}}\frac{{\partial \left( {SLA} \right)}}{{\partial y}}, v = g{f^{-1}}\frac{{\partial \left( {SLA} \right)}}{{\partial x}}。$ |
式中:g为重力加速度;f为科氏力参数;∂x和∂y分别为向东以及向北的距离差。
2 结果与分析本文采用OW参数法对西北太平洋中尺度涡进行识别,在研究期间共追踪反气旋涡350个、气旋涡426个。虽然实际海洋中尺度涡形状各异,但为了研究方便,本文所研究的中尺度涡均为轴对称结构。因此在研究中尺度涡的三维结构时,采用圆心在涡心的柱坐标系更为方便。为了得到中尺度涡的统一结构,需要利用归一化的方法剔除涡旋的个体差异和地域差异。通过张正光[18]的分析可知,归一化的中尺度涡压强异常场具有独立的水平结构与垂直结构,可以表示为:
| $ {p_n}({r_n}, z) = R({r_n}) \cdot H\left( z \right)。$ |
其中:R(rn)为中尺度涡归一化压强异常场的径向结构函数,利用涡旋半径进行归一化rn=r/R0,R0为不同涡旋半径;H(z)是中尺度涡归一化压强异常场的垂向结构函数,将压强异常场与海表面处的值进行振幅归一化pn=p′/P0。式中:p′为压强异常值;P0为不同涡旋海表面中心处压强值。
2.1 中尺度涡统一水平结构在对所选区域内的中尺度涡进行探测识别时,首先利用HYCOM模式数据中海表面高度异常数据确定涡旋中心位置,找到局地SLA极大值(极小值)作为疑似涡旋中心;再利用OW参数判断该极值点是否真实,如果该极值点能够被W=-2×10-12s-2[22]的闭合等值线包围,则该点为真实的涡旋中心;涡旋的极性由极值的正负确定;确定了涡旋中心位置后,再根据W=-2×10-12s-2等值线包围的面积计算涡旋半径;最后对全部识别出的涡旋进行归一化:利用涡旋半径R0进行归一化,排除中尺度涡水平尺度差异造成的影响,得到合成后的径向坐标rn;再利用海表面涡心处压强P0归一化压强异常场p′,排除由涡旋振幅和极性因素带来的影响,得到合成后的纵坐标。
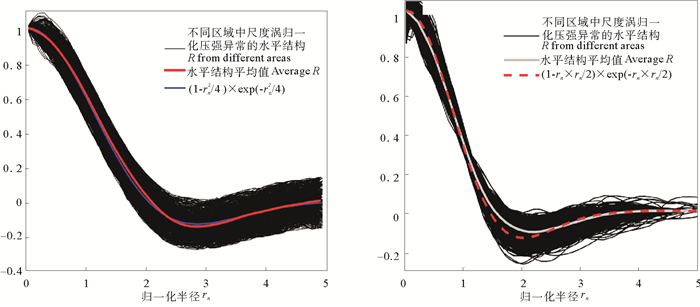
从图 1可以看出,在整体上二者得到的水平结构趋势较为一致:涡中心处压强异常最大,大致在1~2个涡旋归一化半径内压强异常骤减,而后缓慢增大。通过HYCOM数据识别出的中尺度涡,黑线集宽度更大,进行压强异常合成时得到的水平结构可以用解析函数R(rn)=(1-rn2/4)·(-rn2/4)表示,而张等通过观测数据得到的合成结果可以和解析函数R(rn)=(1-rn2/2)·(-rn2/2)很好的逼近。产生这种差异的原因可能是由于HYCOM模式数据的高分辨率导致在涡旋探测识别过程中,将小尺度、次中尺度等信号引进,导致随机扰动因子增多从而引起压强异常结构较观测数据有所偏离。并且在计算压强异常p′时,张等[17]扣除了多年逐季平均场,排除了季节信号的污染。而本文仅对5年数据进行分析,简单地扣除了5年逐月平均得到压强异常场p′,因此季节信号也可能对压强异常的统一水平结构带来影响。
|
(黑色实线为不同区域中尺度涡压强异常归一化水平结构,红色实线为平均值,蓝色实线为解析函数R(rn)=(1-rn2/4)·exp(-rn2/4)。Black curves represent horizontal structures of pressure anomalies with normalization in different areas; The red curve shows their average; The blue curve is an analytical function (1-rn2/4)×exp(-rn2/4.) 图 1 中尺度涡压强异常场统一水平结构HYCOM模式数据结果(左)和(右)文献[17]观测数据结果 Fig. 1 The universal horizontal structure of pressure anomalies based on HYCOM data (left) and observation data of reference[17] in mesoscale eddies (right) |
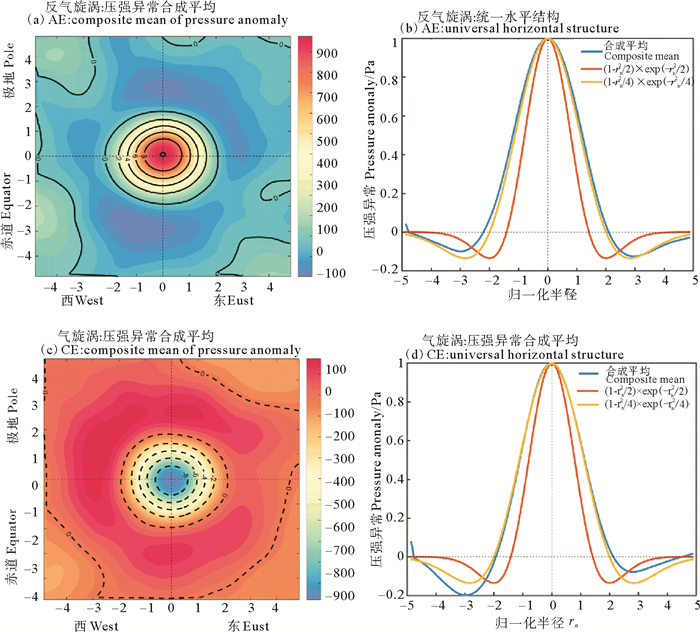
为了进一步研究产生这种差异的原因,本文对识别的涡旋进行了合成分析(合成区域定义为以涡旋中心为合成中心的5倍标准化半径范围内),得到图 2。从图 2((a)、(c))中可以看出,在西北太平洋暖、冷涡的合成空间分布特征相似,2倍标准化半径范围内涡旋具有良好的空间对称性,Wang等通过全球卫星SLA资料对中尺度涡进行识别,得到了在2倍标准化半径范围内超过50%的涡旋具有高斯型水平分布结构R(rn)=(1-rn2)·(-rn2)[23]。而在2倍标准化半径范围外,压强异常分布具有明显的区域差异性。另外,选取通过涡旋中心东西向的标准化压强异常得到图 2((c),(d)),可以看出合成平均的水平结构与解析函数R(rn)=(1-rn2/4)·(-rn2/4)更接近,在2倍标准化半径内几乎完全重合,并且暖涡拟合结果优于冷涡。因此,在水平方向不同剖面的选取也会对拟合结果产生影响,中尺度涡的空间区域差异性也可能是导致统一水平结构存在差异的原因。
|
图 2 (a) 暖涡、(c)冷涡的合成空间分布特征(阴影表示压强异常:单位:Pa,等值线为SSH;单位:cm)与(b)暖涡、(d)冷涡的统一水平结构 Fig. 2 Composite mean of pressure anomaly (colors; unit: Pa) with SSH (contours; unit: cm) inside (a) warm, (b) cold eddies and universal horizontal structure of (b) warm, (d) cold eddies |
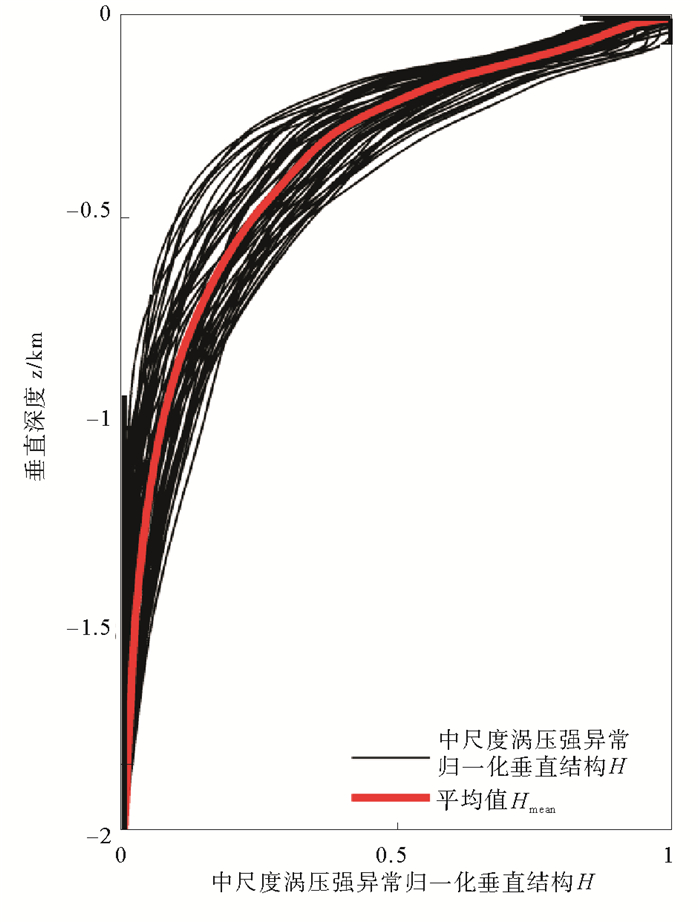
为了描述中尺度涡的垂直结构,首先利用海表面处涡心值对压强异常场进行归一化,得到图 2结构。从图 2中可以看出,在z坐标系下,压强异常p′在海表面涡中心处值最大,随深度z减小,2 000 m处减小至0。但是不同涡旋的压强异常垂直结构的振幅各不相同,因此在z坐标系下无法得到中尺度涡的统一垂直结构特征。
由于海洋背景层结存在区域差异以及科氏参数随纬度变化,压强异常的垂向结构必然会有所不同。为了得到统一的垂直结构,就需要将海洋的背景层结与局地的科氏参数带来的影响剔除掉。Flierl利用拉伸坐标系zs来处理连续层结旋转中涡旋的动力学问题[24],可以最大程度上减小背景层结与科氏参数的地域差别带来的影响:
| $ {z_s} = \int_0^z {\frac{N}{f}dz} 。$ |
其中浮力频率N(z)表示局地海洋背景层结,zs=0对应于海面。
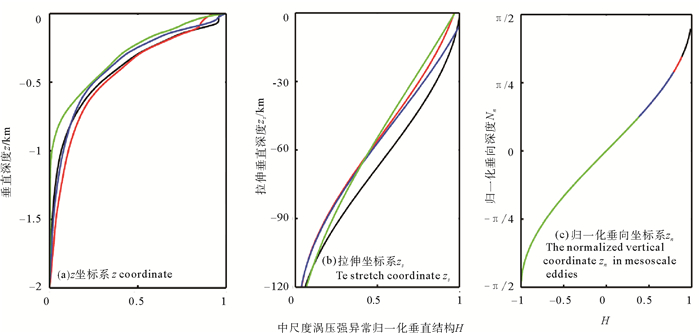
为了确定在拉伸坐标系下能够得到压强异常的统一垂直结构,先选取4个差别较大的涡旋,通过坐标变换将涡旋垂直结构投影到新的坐标系下。从图 3(b)中可以看出,在拉伸坐标系下,(a)中的4个中尺度涡垂直压强异常结构曲线可以近似看成正弦曲线,通过对(b)中H(zs)进行正弦函数拟合:
|
(黑色实线为不同区域中尺度涡压强异常归一化垂直结构,红色实线为平均值。Black curves represent vertical structures of pressure anomalies with normalization in different areas; The red curve shows their average.) 图 3 中尺度涡压强异常场垂直结构 Fig. 3 The vertical structure of pressure anomalies in mesoscale eddies |
| $ \begin{array}{l} H\left( {{z_s}} \right) = {H_0} \cdot \sin \left( {k \cdot {z_s} + {\theta _0}} \right) + {H_{ave}}, \\ \;\;\;\;\;\;\;\;\;\;\;{z_n} = k \cdot {z_s} + {\theta _0}, \\ H\left( {{z_n}} \right) = \frac{{H\left( {{z_s}} \right)-{H_{ave}}}}{{{H_0}}} = \sin \left( {{z_n}} \right)。\end{array} $ |
其中拟合正弦函数的各个常数振幅H0、均值Have、波数k和初位相θ0在拟合过程中即可确定,并且对不同的中尺度涡这些常数各不相同。将拟合后的4条H(zn)曲线绘制在zn坐标系下,(c)中的四条曲线具有很好的一致性,并且完全重合于正弦函数曲线。
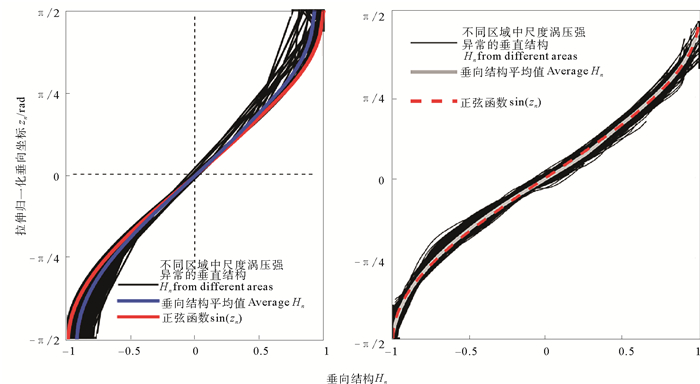
将上述方法——拉伸坐标变换与归一化应用到所选区域内所有中尺度涡上,得到归一化垂向结构(见图 4)。如图(5)所示,可以看出不同中尺度涡的垂直结构曲线与平均曲线的差距并不显著,并且通过HYCOM模式数据的得到的垂向结构与张等[17]利用观测数据得到的结果完全一致,这意味着经过坐标变换和归一化处理后的垂向压强异常场具有统一的结构特征,这一统一垂直结构可以被一个简单的正弦函数所代表:
|
图 4 中尺度涡统一的压强异常场垂直结构 Fig. 4 The vertical structure of pressure anomaliesin |
|
(黑色实线为不同区域中尺度涡压强异常归一化垂直结构,红色实线为平均值,蓝色实线为正弦函数H(zn)=sin(zn)。Black curves represent vertical structures of pressure anomalies with normalization in different areas; The red curve shows their average; The blue curve is an sine function sin(zn).) 图 5 中尺度涡压强异常场统一垂直结构HYCOM模式数据结果(左)和文献[17]观测数据结果(右) Fig. 5 The universal vertical structure of pressure anomalies based on HYCOM data(left) and observation data of Reference[17] in mesoscale eddies(right) |
| $ H({z_n}) = \sin ({z_n})。$ |
本文为了得到HYCOM模式数据下中尺度涡的统一结构,采用Zhang等[17]研究全球中尺度涡统一三维结构的思路和方法,利用两个假设条件:静力平衡条件和地转平衡条件,根据标准气压下海水状态方程计算密度剖面进而得到压强场分布;再利用OW参数法对中尺度涡进行探测识别。通过张等[17]的分析可知,归一化的中尺度涡压强异常场的水平结构与垂直结构分量相互独立,可以表示为:
| $ {p_n}({r_n}, z) = R({r_n})\cdot H\left( z \right)。$ |
其中R(rn)与H(z)分别是中尺度涡归一化压强异常场的径向结构函数与垂向结构函数,揭示了海洋中尺度涡重要的三维结构特征。
从中尺度涡水平结构R(rn)的对比中可以看出,与观测数据得到的结果相比,HYCOM模式数据得到的结构在一定程度上可以看出中尺度涡具有统一的水平结构特征,并且可以用解析函数R(rn)=(1-rn2/4)·exp(-rn2/4)来表示,表明了HYCOM模式数据具有一定的实用性及可行性。然而观测结果与解析函数R(rn)=(1-rn2/2)·exp(-rn2/2)较为接近,通过分析可知,产生这种差异的原因有:一是由于HYCOM模式数据比观测数据具有更高的分辨率,因此在涡旋探测识别过程中,会将小尺度、次中尺度等识别为中尺度信号,从而引进随机扰动因子导致二者的压强异常水平结构有所差异;二是在计算压强异常时,张等[17]扣除了多年逐季平均场,排除了季节信号的污染,而本文数据时间长度较短,且简单地扣除了逐月平均场,因此季节信号也可能是产生这种差异的原因;三是区域差异性,从合成平均的压强异常水平分布中可以看出,在2倍标准化半径内的涡旋具有较好的空间对称性,而在之外空间分布存在差异,因此在西北太平洋中尺度涡的统一水平结构也受区域差异的影响。
从中尺度涡垂直结构H(z)的对比中可以看出,当消除地球旋转及海洋层结产生的影响时,在拉伸坐标系下即可得到归一化的中尺度涡统一垂直结构,并且HYCOM模式数据得到的结构与观测数据的得到的结果完全一致,其统一的垂直结构可以用正弦函数来表示:H(zn)=sin(zn)。
本文通过HYCOM模式数据得到的中尺度涡统一水平结构与观测数据结果有所差异,这种差异是否为海洋存在的真实结构?未来的涡旋研究还需要对这种统一结构进行验证。并且本文并未对造成中尺度涡统一结构的动力学原因及过程进行解释,如为什么中尺度涡的统一结构能够被解析函数所描述?为什么采用拉伸坐标系后可以得到统一的垂向结构?这些问题需要进一步深入分析和讨论。
| [1] |
Chelton D B, Schlax M G, Samelson R M. Global observations of nonlinear mesoscale eddies[J]. Progress in Oceanography, 2011, 91(2): 167-216. DOI:10.1016/j.pocean.2011.01.002
(  0) 0) |
| [2] |
Ikeda M, Mysak L A, Emery W J. Observation and modeling of satellite-sensed meanders and eddies off Vancouver Island[J]. Journal of Physical Oceanography, 1984, 14(1): 3-21. DOI:10.1175/1520-0485(1984)014<0003:OAMOSS>2.0.CO;2
(  0) 0) |
| [3] |
Yang Q, Zhou L, Tian J, et al. The roles of Kuroshio intrusion and mesoscale eddy in upper mixing in the northern South China Sea[J]. Journal of Coastal Research, 2013, 30(1): 192-198.
(  0) 0) |
| [4] |
Roemmich D, Gilson J. Eddy transport of heat and thermocline waters in the North Pacific: A key to interannual/decadal climate variability?[J]. Journal of Physical Oceanography, 2001, 31(3): 675-687. DOI:10.1175/1520-0485(2001)031<0675:ETOHAT>2.0.CO;2
(  0) 0) |
| [5] |
Qiu B, Chen S. Eddy-induced heat transport in the subtropical North Pacific from Argo, TMI, and altimetry measurements[J]. Journal of Physical Oceanography, 2005, 35(4): 458-473. DOI:10.1175/JPO2696.1
(  0) 0) |
| [6] |
Klein P, Lapeyre G. The oceanic vertical pump induced by mesoscale and submesoscale turbulence[J]. Annual Review of Marine Science, 2009, 1: 351-375. DOI:10.1146/annurev.marine.010908.163704
(  0) 0) |
| [7] |
Frenger I. On Southern Ocean Eddies and Their Impacts on Biology and the Atmosphere[D]. Hamburg: Universitāt Hamburg, 2013. http://dx.doi.org/10.3929/ethz-a-009938120
(  0) 0) |
| [8] |
Kouketsu S, Kaneko H, Okunishi T, et al. Mesoscale eddy effects on temporal variability of surface chlorophyll a in the Kuroshio Extension[J]. Journal of Oceanography, 2016, 72(3): 439-451. DOI:10.1007/s10872-015-0286-4
(  0) 0) |
| [9] |
Johannessen J A, Sandven S, Lygre K, et al. Three-dimensional structure of mesoscale eddies in the Norwegian Coastal Current[J]. Journal of Physical Oceanography, 1989, 19(1): 3-19. DOI:10.1175/1520-0485(1989)019<0003:TDSOME>2.0.CO;2
(  0) 0) |
| [10] |
Chaigneau A, Le Texier M, Eldin G, et al. Vertical structure of mesoscale eddies in the eastern South Pacific Ocean: A composite analysis from altimetry and Argo profiling floats[J]. Journal of Geophysical Research: Oceans, 2011, 116(C11): C11025-C11040. DOI:10.1029/2011JC007134
(  0) 0) |
| [11] |
Liu Y, Dong C, Guan Y, et al. Eddy analysis in the subtropical zonal band of the North Pacific Ocean[J]. Deep Sea Research Part Ⅰ: Oceanographic Research Papers, 2012, 68: 54-67. DOI:10.1016/j.dsr.2012.06.001
(  0) 0) |
| [12] |
Yang G, Wang F, Li Y, et al. Mesoscale eddies in the northwestern subtropical Pacific Ocean: Statistical characteristics and three‐dimensional structures[J]. Journal of Geophysical Research: Oceans, 2013, 118(4): 1906-1925. DOI:10.1002/jgrc.20164
(  0) 0) |
| [13] |
Castelao R M. Mesoscale eddies in the South Atlantic Bight and the Gulf Stream recirculation region: vertical structure[J]. Journal of Geophysical Research: Oceans, 2014, 119(3): 2048-2065. DOI:10.1002/2014JC009796
(  0) 0) |
| [14] |
Yang G, Yu W, Yuan Y, et al. Characteristics, vertical structures, and heat/salt transports of mesoscale eddies in the southeastern tropical Indian Ocean[J]. Journal of Geophysical Research: Oceans, 2015, 120(10): 6733-6750. DOI:10.1002/2015JC011130
(  0) 0) |
| [15] |
Dandapat S, Chakraborty A. Mesoscale eddies in the Western Bay of Bengal as observed from satellite altimetry in 1993-2014: Statistical characteristics, variability and three-dimensional properties[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(11): 5044-5054. DOI:10.1109/JSTARS.2016.2585179
(  0) 0) |
| [16] |
Dong C, Lin X, Liu Y, et al. Three-dimensional oceanic eddy analysis in the Southern California Bight from a numerical product[J]. Journal of Geophysical Research: Oceans, 2012, 117(C7): 92-99.
(  0) 0) |
| [17] |
Zhang Z, Zhang Y, Wang W, et al. Universal structure of mesoscale eddies in the ocean[J]. Geophysical Research Letters, 2013, 40(14): 3677-3681. DOI:10.1002/grl.50736
(  0) 0) |
| [18] |
张正光. 中尺度涡[D]. 青岛: 中国海洋大学, 2014. Zhang Zhong-guang. Mesoscale Eddy[D]. Qingdao: Ocean Univeisity of China, 2014. (  0) 0) |
| [19] |
Okubo A. Horizontal dispersion of floatable particles in the vicinity of velocity singularities such as convergences[J]. Deep Sea Research and Oceanqraphic Abstracts, 1970, 17(3): 445-454. DOI:10.1016/0011-7471(70)90059-8
(  0) 0) |
| [20] |
Weiss J. The dynamics of enstrophy transfer in two-dimensional hydrodynamics[J]. Physica D: Nonlinear Phenomena, 1991, 48(2-3): 273-294. DOI:10.1016/0167-2789(91)90088-Q
(  0) 0) |
| [21] |
Isern-Fontanet J, García-Ladona E, Font J. Vortices of the Mediterranean Sea: An altimetric perspective[J]. Journal of Physical Oceanography, 2006, 36(1): 87-103. DOI:10.1175/JPO2826.1
(  0) 0) |
| [22] |
Chaigneau A, Eldin G, Dewitte B. Eddy activity in the four major upwelling systems from satellite altimetry (1992-2007)[J]. Progress in Oceanography, 2009, 83(1): 117-123.
(  0) 0) |
| [23] |
Wang Z, Qiuyang L I, Sun L, et al. The most typical shape of oceanic mesoscale eddies from global satellite sea level observations[J]. Frontiers of Earth Science, 2015, 9(2): 202-208. DOI:10.1007/s11707-014-0478-z
(  0) 0) |
| [24] |
Flierl G R. Isolated eddy models in geophysics[J]. Annual Review of Fluid Mechanics, 1987, 19(1): 493-530. DOI:10.1146/annurev.fl.19.010187.002425
(  0) 0) |
 2018, Vol. 48
2018, Vol. 48


