2. 中国工商银行青岛市分行,山东 青岛 266000;
3. 中国农业发展银行信阳市分行,河南 信阳 464000
2. Industrial and Commercial Bank of China Qingdao Branch, Qingdao 266000, China;
3. China Agricultural Development Bank Xinyang Branch, Xinyang 464000, China
能源为世界经济的发展提供了源源不断的动力,任何一个国家的经济的发展都离不开能源的贡献,当然也都饱受着能源市场的波动所带来的冲击。随着经济全球化以及金融自由化的发展,投资者可以在全球范围内投资,导致国际能源市场价格波动加剧,这不仅增加了能源市场上投资者的投资风险,而且也给世界经济的稳定发展带来了不良影响。而能源期货市场作为能源市场的重要组成部分,投资者能够利用它来规避能源现货市场价格波动所造成的风险。能源期货市场与能源现货市场不同,它具有明显的高杠杆性,这使能源期货市场面临着更大的风险,从而影响风险规避效果。因此,如何对能源期货市场风险进行精确的度量及有效的管理,成为能源投资者们所关心的热点问题之一。
国内外相关文献研究表明,多元GARCH模型为刻画多变量的波动与风险特征提供了一个有效的工具。[1]它能够对能源市场所具有的尖峰厚尾性、非对称性、波动集聚性等特性进行很好的描述。Bollerslev,Engle和Wooldridge首次提出VEC-GARCH模型,它是对多个金融市场的波动同时刻画的多变量GARCH模型,该模型估计出的方差-协方差是动态变化的,是时间序列,不再是常数,不足之处在于它不仅估计的参数较多,难以用经济学理论解释,而且还不能保证所估计出的协方差矩阵的正定性。[2]为了确保协方差矩阵的正定性,Engle和Kroner在VEC-GARCH模型的基础上提出了非对称BEKK-GARCH模型,国内外有许多学者利用该模型对能源市场的波动进行了刻画。[3]在国外,Bradley T. E.等分别利用单变量GARCH和BEKK-MGARCH模型对美国石油价格与股市之间的波动溢出效应进行实证分析,发现石油价格与股市之间不存在波动溢出效应;[4]在国内,张倩等利用BEKK-MGARCH模型对石油期货市场、美元汇率、石油现货市场之间是否存在波动溢出效应进行了检验,检验结果表明,石油期货市场对石油现货市场有单向波动溢出效应,石油期货价格的波动会影响石油现货价格,但石油现货价格的波动不会影响石油期货价格,石油现货市场对美元汇率存在单向波动溢出效应,石油现货市场的风险会传给美元汇率市场,石油期货市场与美元汇率市场存在双向波动溢出效应;[5]虽然BEKK-MGARCH模型能够确保协方差矩阵的正定性,但是估计出的许多参数都不显著,而且参数的经济意义不够明确。另外,Bollerslev还曾提出过一个常相关多元(Constant Conditional Correlation) GARCH模型,这个模型不仅估计方便,经济意义明确,而且还能保证协方差矩阵的正定性,但是它假设多种资产之间的相关性是不变的;[6]从资产相关性的角度出发,Bollerslev提出了动态条件相关系数(Dynamic Conditional Correlation),利用它构成的DCC-MGARCH模型克服了其他多元GARCH模型的缺陷,不仅具有良好的计算优势,可以用来估计大规模的相关系数矩阵,而且估计出的相关系数矩阵是动态的、时变的。[7]张秋利等运用基于多元t分布的DCC-MGARCH模型对CERs期货价格收益同能源期货价格收益之间的动态相依关系进行了实证分析,实证结果显示,CERs期货价格收益与能源期货价格收益之间存在正相关性,而且以动态条件相关系数测算时变套期保值比率明显低于组合收益的方差并提升了组合收益的均值,其套期保值绩效要优于条件相关系数。[8]公茂刚等利用VECM和DCC-MGARCH模型分析了国际能源价格与粮食价格间的关联性,结果表明,在价格水平方面,长期来看,国际能源价格对粮食价格具有显著正向影响,在价格波动方面,总体粮食价格波动与石油价格波动间存在显著正向相关关系。[9]蔡庆丰等在VECM-DCC-MGARCH的基础上,以GJR形式考虑变量非对称作用、用t分布来刻画股市数据的非正态特征,构建了VECM-GJR-DCC-MGARCH-t模型,并实证分析了沪深300股指期货与沪深300期现货的动态波动关系,结果表明,沪深300期现货市场波动之间存在较高的关联性,但相关性是时变的,在上涨行情中,两者的相关性会减弱。[10]
在金融市场与能源市场的风险度量方面,应用最为广泛的是在险价值法(Value-at-Risk),即VaR法,它是一种有效的工具。[11]该方法最早是在1994年由J.P摩根集团提出,用于估计一段时间内一定置信水平下投资组合可能面临的最大损失值,常用的计算VaR方法还有方差-协方差法、历史模拟法,以及蒙特卡洛模拟法。
综上所述,在能源市场上多变量GARCH模型的应用大多是集中在对不同能源市场以及能源市场与其他市场之间的波动溢出效应分析方面,对风险度量的应用还比较少;在模型应用方面,大多是采用单一分布。基于以上两点,本文以马科维茨投资组合理论为理论基础,分别运用基于正态分布、学生t分布,以及广义误差分布的BEKK-MGARCH和DCC-MGARCH模型对由三种能源期货产品组成的能源投资组合的风险进行度量,并分别计算出了在90%、95%和99%分位点出的VaR,而且还利用线性规划估计出在不同模型下能源期货投资组合的最优分配方案。
二、风险度量模型的建立风险度量模型的构建主要分为两步。第一步,对样本数据进行处理,并建立多元GARCH模型,对投资组合的波动进行描述;第二步,基于马科维茨投资组合理论,在给定限定条件下,对研究对象的VaR进行度量。
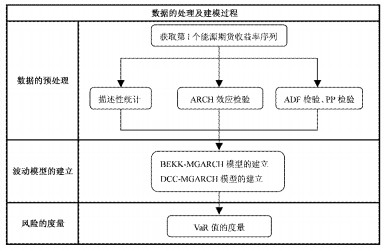
本文从收益率的角度对能源期货市场的风险进行评估,建模对象分别为原油、天燃气和热燃油期货的价格序列。通过建立基于BEKK-VaR和DCC-VaR的能源价格风险度量模型,预测在不同权重分配方案下的VaR值,选取在VaR最小时的最优分配方案,即按照此方案进行投资,所面临的风险最小,建模过程如图 1所示。
|
图 1 BEKK-VaR和DCC-VaR能源期货风险度量建模过程 |
通过样本数据,计算每一种能源期货价格序列的对数收益率ri, t,并对收益率序列进行ADF检验和PP检验以检验其是否平稳。
| $ {r_{i, t}} = 100 \times \left( {\ln \left( {{p_{i, t + 1}}} \right) - \ln \left( {{p_{i, t}}} \right)} \right) $ | (1) |
其中,pi, t表示第i中能源期货市场第t期的交易价格,ri, t表示第i中能源期货市场第t期的收益率。
为了更好地对n种能源期货组成的投资组合进行风险度量,考虑到能源期货市场之间具有相关性,建立多元回归模型,具体表达式如下:
| $ {r_{i, t}} = K + \sum\limits_{i = 1}^N {{L_i}{r_{i, t - 1}}} + {\varepsilon _{i, t}} $ | (2) |
对于多元回归模型,ri, t表示收益率,K表示常数项,Li表示回归系数,是一个1×n矩阵,εi, t表示残差序列。
(二) BEKK-MGARCH模型Bollerslev、Engle和Wooldridge在单变量广义条件异方差模型的基础上提出了指数加权移动平均模型,即VEC模型。该模型虽然可以对多个时间序列同时进行估计,却存在两个明显的不足:不能保证协方差矩阵的正定性,而且不能解释不同时间序列之间的动态相依性。因此,Engle和Kroner对其进行了改进并提出了非对称BEKK模型,它是多变量GARCH模型的一种,这种模型估计出的方差是时变的,不再是常数。常规BEKK模型的方程如下式表示:
| $ \sum {_i} = MM\mathit{' + }\sum\limits_{i = 1}^m {{A_i}} \left( {{\varepsilon _{t - i}}\varepsilon _{t - i}^\mathit{'}} \right)A\mathit{' + }\sum\limits_{j = 1}^s {{B_j}} \sum {_{t - j}} B\mathit{'} $ | (3) |
对于N元BEKK模型,∑t表示样本的方差矩阵,常数项矩阵M为下三角矩阵,系数项矩阵A、B都是n×n的矩阵,m, s均为非负整数。
在多元正态条件下的对数极大似然函数表达式为:
| $ \log L = - \frac{{TN}}{2}\log \left( {2\pi } \right) - \frac{1}{2}\sum\limits_{t = 1}^T {\left( {\log \left| {{H_t}} \right| + \varepsilon _t^\mathit{'}H_t^{ - 1}{\varepsilon _t}} \right)} $ | (4) |
其中,N为所估计的市场个数,T是样本个数。
(三) DCC-MGARCH模型Bollerslev在前人的基础上提出了CCC-MGARCH模型,该模型虽然具有计算方便、经济意义明确的优势,但是却存在一个明显的不足:假设多种资产之间的相关系数不变。从这个角度出发,Engle对CCC-MGARCH模型进行了进一步的改进,并提出不仅能克服其它多变量GARCH模型的缺点,而且相关系数也是时变的DCC-MAGRCH模型。该模型的具体形式为:
| $ \begin{array}{l} {H_t} = {D_t}{R_t}{D_t}\\ D_t^2 = diag\left\{ {{\omega _i}} \right\} + diag\left\{ {{k_i}} \right\} \otimes {u_{t - 1}}u_{t - 1}^\mathit{'}\\ \;\;\;\;\;\;\;\;{\rm{ + }}diag\left\{ {{\lambda _i}} \right\} \otimes D_{t - 1}^2\\ {u_t} = D_t^{ - 1}{\varepsilon _t}\\ {Q_t} = \left( {1 - \alpha - \beta } \right)\overline Q + \alpha \otimes {u_{t - 1}}u_{t - 1}^\mathit{'} + \beta \otimes {Q_{t - 1}}\\ {R_t} = diag{\left\{ {{Q_t}} \right\}^{ - 1/2}}{Q_t}diag{\left\{ {{Q_t}} \right\}^{ - 1/2}} \end{array} $ | (5) |
对于N元DCC-MGARCH模型,Hi是第t时期的条件协方差矩阵,Dt2是一个对角矩阵,对角线的元素为单变量GARCH模型估计出的条件方差,即Dt2=
DCC-MGARCH模型的估计过程一般分为两步:第一步,利用单变量GARCH模型对各个市场进行估计,得到方差参数及标准化的残差序列;第二步,利用第一步得到的标准化残差来估计出动态相关系数矩阵。
根据Engle的描述,DCC-MGARCH模型可以通过下面对数似然函数的极大化来对参数进行估计,对数似然函数的表达式为:
| $ \begin{array}{l} \log L = - \frac{1}{2}\sum\limits_{t = 1}^T {\left[ {N\log \left( {2II} \right) + 2\log \left( {\left| {{D_t}} \right|} \right) + } \right.} \\ \left. {\log \left( {\left| {{R_t}} \right|} \right)| + \varepsilon _t^\mathit{'}R_t^{ - 1}{\varepsilon _t}} \right] \end{array} $ | (6) |
在险价值是现今金融市场应用最为广泛的金融风险管理工具,它表示投资组合收益率的分布的百分位数。它是指在一定时期和置信水平下,投资者可能出现的最大损失值。在本文中,rt=100×ln(pt+1/pt),其中rt表示第t时期的对数收益率,pt表示第t时期的期货价格。在一定置信水平下,先对t+1期的收益率进行预测,进而对t+1期的VaRt+1/tp进行度量,方程如下:
| $ \Pr \left( {{r_{t + 1}} < VaR_{t + 1/t}^p} \right) = p $ | (7) |
在本文中,多种能源期货投资组合的VaR的计算采用如下方程:
| $ VaR_{t + 1}^p = \sum\limits_{i = 1}^n {{w_i}{r_{i, t + 1/t}}} + F_{\left( p \right)}^{ - 1}{\sigma _{t + 1/t, por}} $ | (8) |
其中,F(p)-1是假设分布在p百分位点的分位数,wi为第i种能源期货产品在总投资中所占的权重,σt+1/t, por为投资组合在第t+1期的条件标准差,计算方程如下:
| $ {\sigma _{t + 1/t, por}} = {\left( {\sum\limits_{i = 1}^n {w_i^2\sigma _{ii, t + 1}^2} + 2\sum\limits_{\mathop {i = 1}\limits_{j \ne i} }^m {{w_i}{w_j}{\rho _{ij, t + 1}}{\sigma _{ii, t + 1}}{\sigma _{jj, t + 1}}} } \right)^{1/2}} $ | (9) |
假定能源期货市场上存在M种可供交易的风险资产,所有风险资产的期望收益率与方差各不相等。在准许卖空的条件下,最优资产组合是下列数学规划问题的解:
令Fα(w, VaRα)=VaRt+1/t, porp,在置信水平为α的条件下,此时目标规划问题就转化为:
| $ \left\{ \begin{array}{l} \min {F_\alpha }\left( {w, {\mathit{V}_a}{R_\alpha }} \right)\\ s.t\sum\limits_{i = 1}^K {{w_i}} = 1\\ 0 < {w_i} < 1 \end{array} \right. $ | (10) |
利用matlab中的fmincon函数求出规划问题的解,即在给定预期收益情况下,投资组合中各金融产品所占的权重。
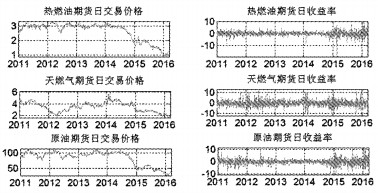
三、实证分析 (一) 数据说明本文选取美国纽约商品交易所的原油、天燃气、热燃油期货日交易价格,数据选取从2011年1月3日至2016年3月22日剔除不合条件的数据后共计1306组样本。三种能源期货的日交易价格与日收益率走势如图 2所示,数据来源于美国能源信息署。
|
图 2 三种能源期货日交易价格与日收益率序列走势图 |
从三种能源期货日交易价格与日收益率序列走势可以看出,热燃油期货与原油期货在样本选取期内的交易价格与收益率的走势比较相近;天燃气期货交易价格波动较为剧烈,收益率序列的波动也越来越明显。在热燃油期货期货市场上,从2011年至2014年初,交易价格维持在3美元附近,然而,从2014年至2016年交易价格有着明显的下降趋势,日收益率走势图也显示,在这段时期,收益率波动也比较剧烈,且在2015年至2016年表现出明显的波动集聚性。[14]天燃气期货日交易价格走势可以分为三个阶段:第一阶段,从2011年至2012年初,交易价格在不断下跌,此时的收益率序列波动并未明显增加;第二阶段,从2012年初到2014年初,日交易价格在震荡中上涨,收益率震荡加剧,在2012年中与2014年初振幅最大;第三阶段是从2014年初至2016年初,交易价格有着明显的下降趋势,在2015年前后有一段时间的平稳期,而此时的收益则表现出比较明显的波动集聚性。在原油期货市场上,在2011年至2014年中,交易价格一直维持在100美元附近,然而从2014年下半年开始,交易价格有着明显下降的趋势,收益率的波动幅度也相比之前也更大。
利用样本数据建立BEKK-VaR和DCC-VaR能源风险度量模型,研究三者组成的投资组合的风险,并通过预测在固定收益率条件下,不同权重的VaR值来确定最优投资方案。在建模之前要对样本数据进行描述性统计、平稳性检验及条件异方差效应检验,结果如表 1所示。
|
|
表 1 样本数据的描述性统计、平稳性检验及ARCH检验 |
由表 1第一部分可知,三种能源期货收益率的均值都小于0,表明若在样本选取期内持有这三种能源期货产品,则会产生一定的损失。因此,如何有效的降低损失,也就体现了本文在风险预测研究的重要性。从JB统计量的值可以看出,三组数椐都不服从正态性假设,而且,由Ljung-Box-Pierce检验的Q(20)的值也表明,这三种能源期货的收益率序列均存在序列自相关性,再者,各能源期货市场之间也存在相关性。
从第二部分的ADF检验和PP检验结果可以看出,三组收益率序列在99%的置信水平下都是平稳的,均可以对收益率序列建模;而且,在表中的第三部分中,分别对三个研究对象的条件异方差进行检验,在滞后10阶的条件异方差效应检验结果表明,在99%的置信水平下,无论是原油,还是天燃气或者热燃油期货市场均都存在明显的条件异方差性,因此可以构建GARCH类模型。
(二) 能源投资组合的风险度量结果分析为了能够对在不同条件下的VaR计算结果进行比较分析,本文以马科维茨投资组合理论为理论基础,分别运用BEKK模型和DCC模型基于不同分布条件下对由三种能源期货组成的投资组合的波动进行拟合,并利用组合VaR法分别计算出在90%、95%和99%分位点下的能源投资组合的在险价值。基于不同分布及分位点下的VaR度量结果如下表所示。
|
|
表 2 基于不同分布假设及不同分位点处的预测出的VaR值 |
由度量结果可以看出,利用基于不同分布的BEKK模型和DCC模型度量出的VaR值随着分位点的提高风险也在不断增加,在现实情况下,高收益也伴随这高风险,极端条件下的风险要大于一般情况下的风险,这与现实情况相符。在90%分位点处,BEKK-t模型和DCC-t模型计算出的VaR值最大,分别为1.4282和1.2498,而BEKK-ged模型和DCC-ged模型得出的VaR值均最小,分别为0.7439和0.8367,说明BEKK-ged模型和DCC-ged模型的度量效果分别优于在其他分布假设条件下的BEKK模型和DCC模型,从数值上看,BEKK-ged模型优于DCC-ged模型;在95%分位点处,对样本的度量结果中可以看出,BEKK-t模型和DCC-t模型计算出的VaR值仍是最大,分别为1.9086和1.6744,VaR值最小的分别为BEKK-ged模型和DCC-ged模型的,1.3216和1.4451,说明在95%分位点处,BEKK-ged模型和DCC-ged模型的度量效果分别优于在其他分布假设条件下的BEKK模型和DCC模型,从数值上看,BEKK-ged模型优于DCC-ged模型;然而,在99%分位点处,利用在正态分布假设条件下的BEKK-n模型和DCC-n模型计算出的VaR最小,分别为2.4350和2.1120,运用BEKK-t模型与DCC-ged模型预测的结果却是最大的,VaR值分别为3.1461和3.2988,说明在99%分位点处,BEKK-n模型和DCC-n模型预测效果要优于其他分布假设条件下的BEKK模型和DCC模型,而且,从度量效果上看,BEKK-n模型优于DCC-n模型。
从模型的估计结果看,在90%和95%分位点处,均是BEKK-ged模型和DCC-ged模型计算出的VaR值最小,BEKK-t模型和DCC-t模型得出的VaR值最大,说明BEKK-ged模型和DCC-ged模型的度量效果优良,BEKK-t模型和DCC-t模型度量最差;然而在99%分位点处,BEKK-ged模型和DCC-ged模型计算出的VaR最大,BEKK-n模型和DCC-n模型计算出的VaR值最小,说明BEKK-ged模型和DCC-ged模型的度量效果最差,BEKK-n模型和DCC-n模型度量效果优良。
|
|
表 3 基于不同分布假设条件下的BEKK-VaR法与DCC-VaR法在不同分位点处的权重 |
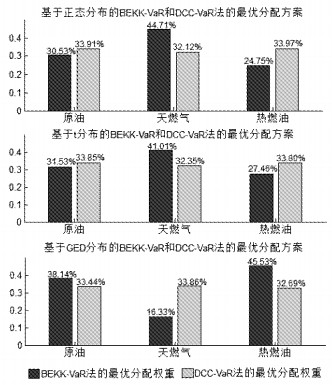
图 3给出了基于BEKK-VaR法和DCC-VaR法的最优分配方案具体数值。BEKK-VaR法计算结果表明,在能源期货投资组合中,原油期货所占比重为31.52%,天燃气期货所占比重为41.05%,热燃油期货所占比重为27.43%时风险最小;而在DCC-VaR法最优分配方案中,原油期货所占比例为33.91%,天燃气期货所占比重为32.12%,热燃油期货所占比重为33.97%时风险最小。从图 3中可以看出,利用BEKK-VaR法计算出的最优投资方案中天燃气期货所占比例最大,为41.05%,而利用DCC-VaR法计算出的最优投资方案中天燃气期货所占比例最小,为32.12%。从样本收益率的走势图(图 2)可以看出,天燃气期货市场收益率波动是最剧烈的,投资比重过大,会增加投资组合收益率的不确定性;同样的,由于热燃油期货市场收益率比较平稳,利用DCC-VaR法计算出的最优投资组合中的权重最大,能够有效的保障能源组合收益率不遭受过大冲击。
|
图 3 基于BEKK模型和DCC模型的各种能源期货所占权重最优分配方案对比图 |
本文基于不同分布假设条件,利用BEKK-MGARCH模型和DCC-MGARCH模型结合在险价值,对由美国纽约交易所的原油、天燃气及热燃油期货组成的能源期货投资组合VaR进行了度量分析,结果显示,在三个不同分位点上,基于正态分布与学生t分布的BEKK-VaR法比DCC-VaR法计算出的VaR值大;然而,无论是在90%、95%,还是99%分位点,基于广义误差分布的DCC-VaR法都比BEKK-VaR法计算出的VaR大。这表明,基于正态分布与学生t分布的DCC-VaR法要优于BEKK-VaR法;但是,基于广义误差分布的BEKK-VaR法比DCC-VaR法度量效果优良。
通过运用BEKK-MGARCH模型与DCC-MGARCH模型对各种能源期货在投资组合中所占权重的估计结果不同。运用BEKK-VaR法估计出的能源期货投资组合的最优权重分别为原油31.52%、天燃气41.05%、热燃油27.43;运用DCC-VaR法估计出的能源期货投资组合的最优权重分别为原油33.91%、天燃气32.12%、热燃油33.97。这是由于BEKK-MGARCH模型与DCC-MGARCH模型描述波动的方程不同所导致的。
在金融风险管理领域,投资组合的VaR值度量的准确性关键在于资产概率分布假设的设定以及模型的选取。以上结论有助于更加清晰地认识能源期货投资组合的风险特性,对如何选取能够真实反映金融资产波动的模型及准确预测由不同能源期货组成的投资组合的在险价值提供了一个可行的技术解决方案。
| [1] |
L. Bauwens, S. Laurent, J. V. K. Rombouts Multivarivate Garch M odels: A Survey[R].CORE discussion paper, 2003, (31).
(  0) 0) |
| [2] |
John W. S. Analysis of Financial Time Series: 3rd ed[M]. New Jersey: Hoboken, 2010: 143.
(  0) 0) |
| [3] |
Engles R. F., Kroner K.. Multivariate simultaneous generalized ARCH[J]. Econometric Theory, 1995, (11): 122-150.
(  0) 0) |
| [4] |
Bradley T. Ewinga, Farooq Malik, Volatility spillovers between oil prices and the stock market under structural breaks[J]. Global Finance Journal, 2016, (29): 12-23.
(  0) 0) |
| [5] |
张倩, 张歀慧. 基于MGARCH-BEKK模型的石油市场波动溢出效应研究[J]. 统计与决策, 2013, (13): 130-132. (  0) 0) |
| [6] |
Bollerslev T.. Modeling the Coherence in Short-Run Nominal Exchange Rates: A Multivariate Generalized ARCH Model[J]. Review of Economics and Statistics, 1990, 72(3): 498-505. DOI:10.2307/2109358
(  0) 0) |
| [7] |
Engle R.F. Dynamic Conditional Correlation: A Simple Class of Multivariate Generalized Auto regresive Conditional Heteroskedasticity Models[J]. Journal of Business and Economic Statistics, 2002, 20(3): 339-350. DOI:10.1198/073500102288618487
(  0) 0) |
| [8] |
张秋利, 杨超, 门明. 国际碳市场与能源市场动态相依关系研究与启示——基于DCC-MGARCH模型[J]. 经济评论, 2012, (5): 112-122. (  0) 0) |
| [9] |
公茂刚, 王学真. 国际粮食价格与能源价格的关联性——基于VECM和DCC-MGAERCH模型的实证分析[J]. 统计与信息论坛, 2014, 29(11): 37-44. DOI:10.3969/j.issn.1007-3116.2014.11.007 (  0) 0) |
| [10] |
蔡庆丰, 郭俊峰, 陈耀辉. 沪深300期现货市场动态波动关系研究:基于VECM-GJR-DCC-MGARCH-t模型的视角[J]. 系统管理学报, 2015, 24(2): 209-214. (  0) 0) |
| [11] |
Ahmed. G., Abdelwahed. T. Energy portfolio risk management using time-varying extreme value copula methods[J]. Economic Modelling, 2014, (38): 470-485.
(  0) 0) |
| [12] |
冯金余. 基于DCC—MVGARCH模型的证券组合VaR测度与拓展模型[J]. 统计与信息论坛, 2009, 24(2): 64-71. DOI:10.3969/j.issn.1007-3116.2009.02.013 (  0) 0) |
| [13] |
周德田, 郭景刚. 基于二元VAR-GARCH(1, 1)-BEKK模型的金融市场与石油市场的溢出效应研究[J]. 中国石油大学学报(自然科学版), 2014, 38(1): 177-185. DOI:10.3969/j.issn.1673-5005.2014.01.028 (  0) 0) |
| [14] |
任仙玲, 肖毓琨, 孙文岳. 国际能源市场与中国股市之间的波动溢出效应研究[J]. 中国海洋大学学报(社会科学版), 2017, (6): 65-71. DOI:10.3969/j.issn.1672-335X.2017.06.012 (  0) 0) |
 2019
2019 
