金融一体化、经济全球化趋势使各国或地区股票市场之间的联系更加密切。区域股票市场关联度的提高不仅促进了国际资本的流动,给投资者带来更加丰富的投资机会,也优化了资源在全球范围内的配置,促进全球经济的发展。但同时,股票市场间的高度关联也引发了一系列问题。其中最显著的便是风险能够更轻易地在各市场间流转,加剧风险在全球股票市场上蔓延。极端事件是指发生概率小、但影响较大的事件。它是造成财产、生命损害的直接原因,主要包括洪水、地震等自然灾害以及金融危机、战争暴乱等突发性事件。当某地区股票市场在极端事件的冲击下出现剧烈波动时,经过交叉传染,风险会传播至其他股票市场,导致其他股市发生波动,在极端情况下,还会爆发系统性金融风险,甚至会引起严重的金融危机,对世界经济造成巨大冲击。
近年来,国际经济环境动荡不安,中美贸易摩擦和乌克兰危机的发生在阻碍世界经济健康平稳发展的同时,也对全球股票市场造成巨大冲击,引发全球股市的波动。那么,在这两次极端事件发生期间,全球股市之间是否存在风险溢出效应呢?如果存在,各国或地区股市在风险溢出系统中扮演什么角色?两次极端事件发生期间的风险溢出效应有何差异?全球股市风险溢出网络结构又是怎样的?这些均是本文所要探讨的问题。有鉴于此,本文通过测算全球主要经济体股票市场的收益波动率溢出指数,构建风险溢出网络,从风险溢出方向及强度两个方面,挖掘全球股市在中美贸易摩擦和乌克兰危机时期的风险溢出特征。同时,本文还重点分析股市风险溢出效应在极端事件发生时期与平稳时期的差异,进一步探讨中美贸易摩擦及乌克兰危机对全球股市风险传染的影响。
本文的边际贡献可能在于:(1)对股市风险的总体溢出指数进行动态测算后,分时段构建风险溢出网络。一方面,可以展示股市风险溢出效应的动态变化趋势;另一方面,可以从空间维度去刻画风险溢出的渠道,探寻各股市在风险溢出网络中的影响力。(2)选取平稳时期作为中美贸易摩擦和乌克兰危机的比较对象,既能横向分析对比两次极端事件对股市风险溢出效应的影响,又可以纵向对比分析极端事件与正常状态下股市风险溢出效应的差异,以期对已有研究进行有益补充。
二、文献综述如何衡量金融市场间的风险溢出效应是金融风险领域一直关注的焦点问题,目前应用最为广泛的方法为Copula函数法和溢出指数法。Copula函数是一类将联合分布函数与它们各自的边缘分布函数连接在一起的函数,可以有效测量变量间的相依性。基于这种特性,不少学者利用Copula函数刻画变量间的相依结构,进而求得CoVAR, 以研究不同金融市场或不同市场主体间的风险溢出关系。[1][2][3]相较于传统的分位数回归方法,Copula函数方法可以测量非线性溢出关系, 但是其对时变风险非线性相关性的反映较弱,且无法直观体现风险传播方向。DY溢出指数法是在广义向量自回归框架下,采用方差分解预测误差方差,度量金融市场风险溢出效应的方法。[4][5]该方法最显著的特征是用矩阵形式反映总体风险溢出的大小及方向,可以更直观地体现金融市场风险溢出去向及风险接收来源。随着研究的深入,学者基于复杂网络理论,[6][7][8][9]根据DY溢出指数法结果进一步构建风险溢出网络,从空间维度对风险溢出效应进行分析。目前,这种方法广泛应用于外汇和股票等金融市场风险溢出效应问题研究。[10][11][12][13]然而,DY溢出指数法最大缺陷是要人为设置滚动窗口,这会带来信息缺失等问题。为弥补这一缺陷,Antonakanis和Gabauer提出了基于时变参数向量自回归模型(TVP-VAR)的溢出指数计算方法,在这一框架下,利用系数矩阵和协方差矩阵的时变特性,可以准确测度任一时点的风险溢出效应。[14]王伟强基于TVP-VAR模型测算了全球14个经济体的经济政策不确定性溢出指数,对比分析不同国家经济政策不确定性的溢出效应。[15]孟浩等将中国金融市场划分为货币、资本、大宗商品交易、外汇、黄金和房地产市场,通过构建TVP-VAR溢出指数对中国金融市场的溢出效应进行静态和动态研究。[16]郭娜等利用基于TVP-VAR模型的溢出指数法对中国股票市场与能源市场之间的风险溢出效应进行动态分析,发现极端事件的发生导致股市崩盘时,股票市场与能源市场之间的风险溢出水平会显著提升。[17]
目前,现有文献已证实国际股票市场之间存在显著的风险溢出效应,[18][19]但对不同极端事件下股市间风险溢出效应的对比研究较少。因此,本文选取中美贸易摩擦和乌克兰危机作为事件背景展开研究,深入剖析两次极端事件冲击下国际股市间风险溢出效应的异同之处,并通过与平稳时期的对比研究,进一步突出极端事件对国际股市间风险溢出效应的影响,以期为中国防范金融风险与应对极端事件挑战提供相应的参考依据。
三、模型构建Antonakakis和Gabauer基于时变参数向量自回归(TVP-VAR),结合DY法构建出新的时变溢出指数。[14]该方法在分析市场间风险溢出关系时无须人为设置滚动窗口,不会造成信息损失等情况,很好地克服了DY溢出指数法的缺陷。
P阶的TVP-VAR的表现形式为:
| $ y_t=a_0+A_1 y_{t-1}+\cdots+A_p y_{t-p}+\varepsilon_t $ | (1) |
其中,yt表示为N个股票市场的对数收益率,a0为截距向量,A1⋯Ap表示为系数矩阵,εt为误差列向量,各分量之间是独立同分布的。
令βt=vec(a0', A1'⋯Ap'),xt=I⊗(1, yt-1', ⋯yt-p'),假设系数βt服从随机游走过程,则:
| $ y_t=\beta_t x_t+\varepsilon_t $ | (2) |
| $ \beta_t=\beta_{t-1}+\delta_t $ | (3) |
其中,δt~N(0, Ω)。确定TVP-VAR模型的表现形式后,运用蒙特卡洛模拟法对时变参数进行估计。
方差贡献度的定义为,当变量yi受到外部冲击时,变量yi的h步预测方差中可以由yj进行解释的比例dij(h)。
方差贡献度主要刻画的是变量所受自身和系统中其他变量影响大小的程度。度量溢出指数的关键环节就是预测方差贡献度,预测公式为:
| $ d_{i j}(h)=\frac{\sigma_{i i}^{-1} \sum\limits_{h=0}^H\left(e_i^{\prime} A_h \sum e_j\right)^2}{\sum\limits_{h=0}^H\left(e_i^{\prime} A_h \sum A_h^{\prime} e_j\right)^2} $ | (4) |
其中,Σ表示误差向量εt的协方差矩阵,σii表示εt的标准差,ej表示第j个元素是1的单位向量,i, j=1⋯N, i≠j。方差分解矩阵Dij(h)是由不同市场的方差贡献度堆叠形成的,即:
| $ D_{i j}(h)=\left[\begin{array}{ccc} d_{11} & \cdots & d_{1 N} \\ \vdots & \ddots & \vdots \\ d_{N 1} & \cdots & d_{N N} \end{array}\right] $ | (5) |
Dij(h)并非对称矩阵。其中,除对角元素之外的其他元素代表对其他市场的溢出强度,对角元素则代表对自身的溢出强度。根据上述定义,方差分解矩阵Dij(h)第k行中除对角元素的其他元素相加即可得到市场k接收其他市场风险外溢的程度;第k列中除对角元素的其他元素相加即可得到市场k对其他市场的风险外溢程度。
用Ck←.H表示市场k接收其他股票市场的定向溢入效应(对应实证结果分析部分表 3中的From项),即:
| $ C_{k \leftarrow .}^H=\sum\limits_{\substack{j=1 \\ j \neq k}}^N d_{k j} $ | (6) |
用C.←kH表示市场k对其他股票市场的定向溢出效应(对应实证结果分析部分表 3中的To项),即:
| $ C_{. \leftarrow k}^H=\sum\limits_{\substack{i=1 \\ i \neq k}}^N d_{i k} $ | (7) |
用CkH表示市场k的风险净溢出效应,即:
| $ C_k^H=C_{. \leftarrow k}^H-C_{k \leftarrow.}^H $ | (8) |
用CH表示各国或地区股票市场的风险总溢出效应,即:
| $ C^H=\frac{1}{N} \sum\limits_{\substack{i, j=1 \\ i \neq j}}^N d_{i j} $ | (9) |
本文将溢出效应分为动态研究和静态研究,动态研究计算的是每一时点上的溢出指数大小和方向,可以反映溢出指数的变化趋势。而静态研究则是动态溢出指数加总后的平均值,反映平均溢出效应大小,不能反映变化趋势。
四、实证分析 (一) 数据来源本文选择13个经济较为活跃的国家或地区的股票市场作为研究对象,其中包括两个北美洲国家(美国、加拿大),五个欧洲国家(法国、英国、德国、意大利、俄罗斯),五个亚洲国家或地区(中国、中国香港、韩国、日本、新加坡)以及一个大洋洲国家(澳大利亚),将这些国家或地区的主要股票指数收益率作为样本数据展开研究,样本区间为2016年1月4日-2023年3月31日。表 1为选取的股票指数,所有股指的价格数据均来源于wind数据库。
|
|
表 1 股票指数 |
表 2是股指对数收益率的描述性统计结果。由表 2可知,除中国上证综指的对数收益率平均值小于0外,其他股指收益率均大于0,美国S&P500指数和法国CAC40指数收益率的均值最大。从收益波动情况来看,各股指收益率均存在不同程度波动。其中,俄罗斯RTS指数收益率的标准差最大,收益波动最剧烈;新加坡STI指数收益率的标准差最小,收益波动程度最弱。此外,除中国香港恒生指数收益率右偏外,其他数据序列均左偏,且峰度均大于3,具有显著的“尖峰厚尾”特征。经检验,13个股票指数的对数收益率均为平稳序列,满足GARCH模型建模条件,因此,利用GARCH(1,1)模型提取股指波动率来代表股市风险,并以此进行实证研究。
|
|
表 2 股指收益率的描述性统计 |
静态风险溢出指数是每一时点上的溢出指数加总后所求得的平均值,由AIC准则确定的TVP-VAR模型滞后阶数为4,本文设定广义方差分解的预测步长为10,表 3为全样本时期的静态溢出指数结果。值得注意的是,风险溢出指数矩阵并非对称矩阵,矩阵对角元素表示的是各股市对自身溢出强度的大小,除对角元素外的行数据表示某股市接收其他股市风险溢入强度(From值), 除对角元素外的列数据表示某股市对其他股市的风险溢出强度(To值)。NET值则为To值减去From值后的净值,可以用来确认各股市在风险溢出系统中所扮演的角色,即当NET值大于0时为风险净溢出者,当NET值小于0时为风险净接收者。
|
|
表 3 静态溢出指数结果 |
根据表 3结果可知,股票市场之间存在显著的风险溢出效应。具体来看:(1)同属区域股市间的风险溢出水平较高,“地理集聚效应”显著,[20]如中国香港恒生指数对同属亚洲区域其他股市的总风险溢出值大于欧美股市。同时,接收来自亚洲区域股市的风险溢入强度也大于欧美股市。美国股市对加拿大股市风险溢出强度(15.9%)最大的同时,接收来自加拿大股市的风险溢入强度(17.2%)也最大。(2)从To值和From值序列看,法国股市在整个股市风险溢出系统中表现“活跃”,在风险溢出总值(112.8%)最大的同时,风险溢入总值(79.5%)也最大。其中,法国股市对德国(18%)、意大利(16.9%)及英国(15.6%)股市的风险溢出强度最大,接收来自这些股市的风险溢入强度也最大,分别为17%、14.3%、13.8%。中国股市的风险溢出总值(32%)及风险溢入总值(52.3%)最低。从影响范围来看,中国股市对中国香港等亚洲地区股市的风险冲击最大,而亚洲地区股市在中国股市接收风险溢入比例中的占比也较高。(3)从风险溢出净值看,除俄罗斯外,其他欧美地区股市的NET值大于0,在系统中扮演风险净溢出者的角色,而俄罗斯股市、澳大利亚股市及亚洲地区股市的NET值小于0,说明这些股市是系统中的风险接收者,股市具有“脆弱性”,容易遭受来自欧美股市的风险冲击。
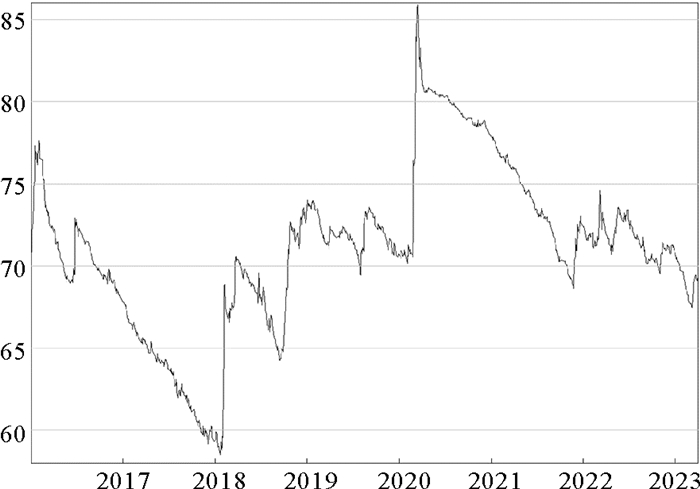
(四) 动态风险溢出分析本文对股市风险的总体溢出指数进行动态刻画,进一步挖掘股市间风险溢出效应在不同时点上的变化,图 1为2016年1月4日—2023年3月31日股票市场风险的总体溢出指数时变图。
|
图 1 风险的总体溢出指数时变图 |
由图 1可以发现,股市风险的总体溢出指数具有显著的时变特征,大致可以分为四个阶段。第一阶段:2016年1月—2017年12月。在此阶段,股市风险的溢出指数曲线总体呈现下降趋势,并未出现大幅波动,只在2016年年初及2016年年中出现小幅上升。第二阶段:2018年1月—2019年12月。在此阶段,中美贸易摩擦持续发酵,股市风险总溢出指数经历了两次较为显著的增长,分别为2018年年初及2018年下半年。2018年3月,美国前总统特朗普签署总统备忘录,宣布对从中国进口的商品加征25%的关税,正式挑起中美贸易摩擦。在中美贸易摩擦的冲击下,股市风险的总溢出指数曲线在短时间内直线上升,系统性风险快速积累,达到峰值后,呈现缓慢的波动下降趋势。2018年9月,美国对华第二轮加征关税,宣布对2000亿商品加征10%的关税,股市总溢出指数再次呈现跳跃式增长趋势,由65%左右迅速提升至70%以上,随后保持小幅波动状态。第三阶段:2020年1月—2021年12月。2020年初,欧盟签署英国脱欧协议,英国正式脱欧,加之中美贸易摩擦尚未完全结束,股市收益的不确定性进一步增大,恐慌情绪加剧风险蔓延,导致总溢出指数迅速攀升至85%以上,随后呈现下降趋势,直至2021年末,风险溢出总值降到70%以下。第四阶段:2022年1月—2023年3月。此阶段是乌克兰危机爆发时期,股市风险总溢出指数一直呈现小幅波动状态,未出现跳跃式增长或大幅下跌趋势。
本文发现,股市风险总溢出指数的增长与消减存在显著的非对称性特征。具体来看,2018年年初及2018年下半年,股市风险总溢出指数在中美贸易摩擦的冲击下迅速增长,达到峰值后,总溢出指数没有快速下降至原水平,而是呈现缓慢下降或是小幅波动状态。而在2020年初,受到中美贸易摩擦的持续性影响,并在英国脱欧的冲击下,股市风险总溢出指数快速攀升,达到更高峰值后,历经两年时间才缓慢下降至快速攀升前的水平。这说明中美贸易摩擦和英国脱欧对股市风险溢出的影响具有持久性,即股票市场系统性风险在极端事件冲击下快速积累,而这一风险溢出需要历经很长时间才能完全消减。此外,股票市场风险总溢出指数对不同极端事件冲击的敏感程度存在差异。对比中美贸易摩擦和乌克兰危机时期的总溢出指数曲线变化趋势可以发现,中美贸易摩擦时期出现较为显著的直线增长趋势,而乌克兰危机时期并无显著的增长或下降趋势。这说明相较于乌克兰危机,中美贸易摩擦对股市间风险溢出效应的影响较大。
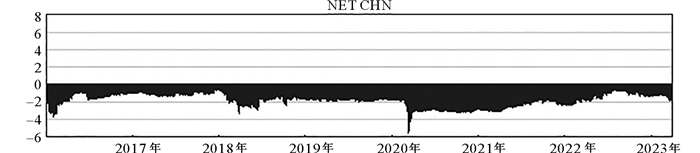
(五) 中国股市的方向性溢出指数为进一步探究中国股市风险净溢出效应以及与其他股市之间的风险溢出效应的变化,本文分别对中国股市在全样本时段上的风险净溢出指数、与其他股市之间的方向性溢出指数进行动态刻画,图 2是中国股市风险净溢出指数动态结果。
|
图 2 中国股市风险净溢出指数 |
由图 2可知,中国股市在整个样本时段上的净溢出指数均为负值,是股市风险溢出系统的净接收者,而非风险输出者,容易遭受其他股市的波动冲击。具体而言,在2018年和2020年初,中国股市分别在中美贸易摩擦和英国正式脱欧的冲击下,风险净溢出指数出现显著下降趋势,这意味着中国股市在这两个时间节点上的风险净溢入强度增大。总体来看,中国股市在2018—2019年中美贸易摩擦时期的风险净溢入强度显著高于2022—2023年乌克兰危机时期,风险溢出净值在-2%左右上下浮动。
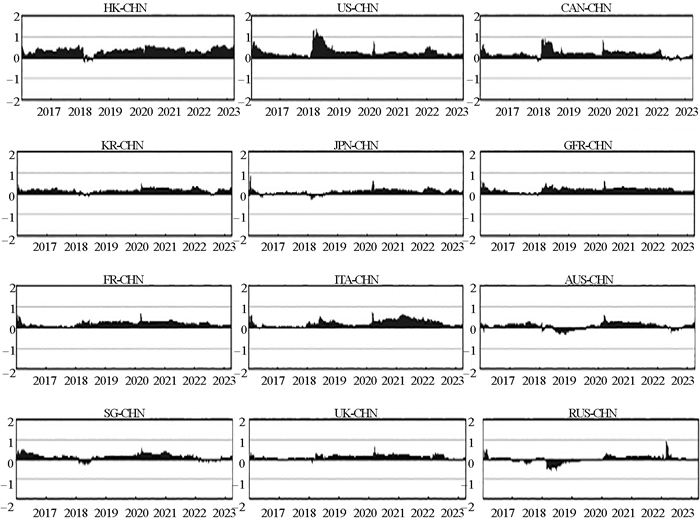
图 3为中国股市与其他股市在整个样本时段内的方向性溢出指数结果,当溢出指数为正值时,说明其他股市对中国股市存在正向风险溢出效应;当溢出指数为负值时,则说明中国股市对其他股市存在正向风险溢出效应。由图 3可知,在2016—2017年无重大极端事件发生时期,除俄罗斯股市外,中国与其他股市之间的方向性溢出指数几乎均为正值,说明其他股市在此阶段对中国股市存在正向风险溢出效应,中国股市在此阶段容易遭受其他股市的波动冲击。在2018—2019年中美贸易摩擦时期,中国股市与其他股市间的风险溢出效应发生变化。从风险溢出强度层面看,中国股市与美国、加拿大、德国、法国、意大利及英国股市之间的方向性溢出指数在中美贸易摩擦开始之初显著增长。这表明,在中美贸易摩擦的冲击下,中国股市对除俄罗斯股市外的其他欧美股市形成更大的风险接收敞口,这些股市对中国股市的波动冲击强度增大。从风险溢出方向层面看,在中美贸易摩擦开始之初,中国股市对亚洲地区其他股市(中国香港、韩国、日本、新加坡)存在短暂的正向风险溢出后,方向性溢出指数由负值变为正值,中国股市转变为风险接收者,接收其他亚洲地区股市的风险净溢入。在2022—2023年乌克兰危机时期,中国股市与加拿大、新加坡及澳大利亚股市之间的溢出指数除存在显著的正负方向变化外,与其他股市之间的风险溢出方向几乎未发生变化,中国股市接收其他股市的风险净溢入。其中,俄罗斯股市在乌克兰危机开始之初对中国股市的风险溢出效应显著增强,但随即下降至较低水平。
|
图 3 中国股市与其他股市间的方向性溢出指数 |
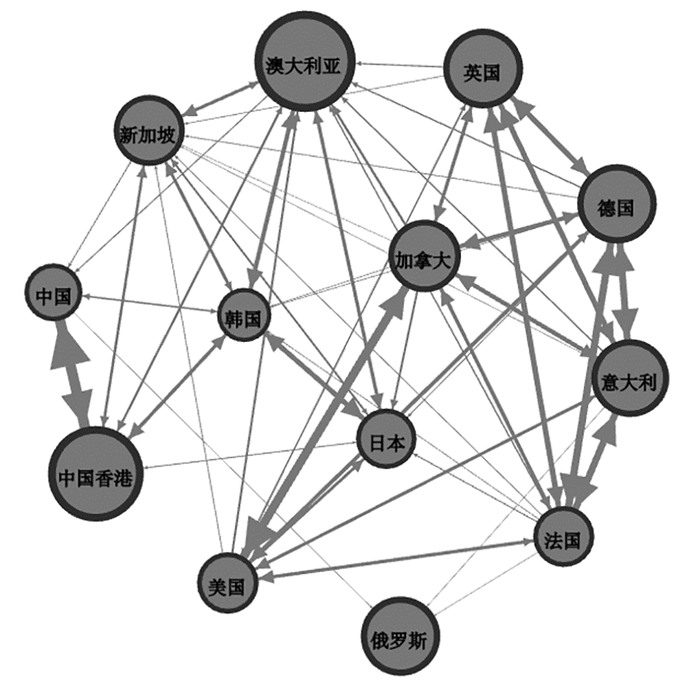
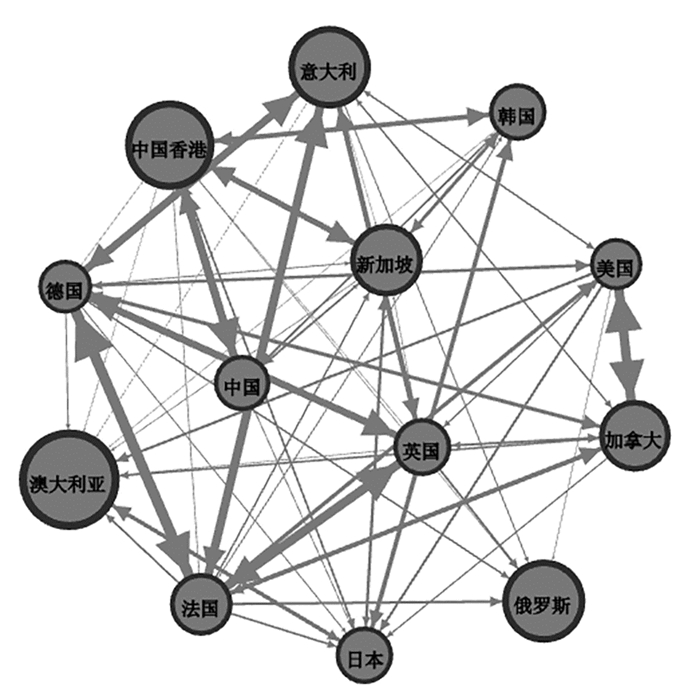
本文将2016年1月4日—2017年12月28日定义为平稳时期,将2018年3月8日—2019年12月30日定义为中美贸易摩擦时期,将2022年3月1日—2023年3月31日定义为乌克兰危机时期,并借鉴Demrier et al.的做法,[21]基于复杂网络理论,采用阈值法构建三个时期的风险溢出网络,从空间维度表示股市间的风险溢出效应。本文选择股票市场风险溢出值(To值)在各阶段的中间值作为阈值,既保证网络节点全部连接、不会形成局部独立网络,又可以对风险溢出信息进行最大限度筛选,进而实现有效建网。图 4、图 5、图 6分别是股票市场在平稳时期、中美贸易摩擦时期及乌克兰危机时期的风险溢出网络结果,箭头指向表示风险溢出方向,连边粗细反映风险溢出强度大小。即:连边越粗,风险溢出强度越大;连边越细,风险溢出强度越小。
|
图 4 平稳时期风险溢出网络图 |
|
图 5 中美贸易摩擦时期风险溢出网络图 |
|
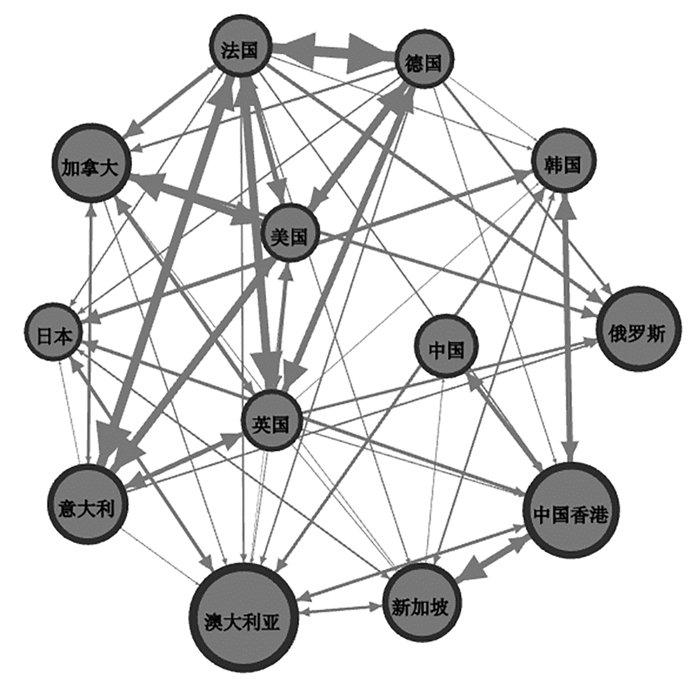
图 6 乌克兰危机时期风险溢出网络结果 |
本文利用平均路径长度与平均聚类系数两大拓扑指标对整体风险溢出网络特征进行描述。其中,平均路径长度代表网络节点距离的平均值,平均聚类系数则是衡量网络连接紧密度的指标。当平均路径长度越小,而平均聚类系数越大时,网络连接越紧密,风险在网络中的流转速率越高;反之,当平均路径长度越大,而当平均聚类系数越小时,网络连接越稀疏,风险在网络中的流转速率越低。
表 4为风险溢出网络的拓扑指标结果。由表 4可知,相较于平稳时期,风险溢出网络在中美贸易摩擦时期和乌克兰危机时期的平均聚类系数较大,平均路径长度小,这说明在两次极端事件的冲击下,各国或地区股市之间的风险连接更为紧密,推动了股市风险的蔓延,风险流转速率提高。此外,相较于乌克兰危机时期,风险溢出网络在中美贸易摩擦时期的平均聚类系数更大,平均路径长度更小,这也证明了中美贸易摩擦对全球股市风险溢出效应的影响大于乌克兰危机,股市间的风险联系紧密度在中美贸易摩擦时期更大。
|
|
表 4 风险溢出网络的拓扑指标结果 |
本文利用入度和出度指标来进行节点拓扑特征分析。入度指的是由其他节点出发,指向某节点连边个数的总和。出度是指由节点出发,指向其他节点连边个数的总和。在前文风险溢出静态分析中,From值和To值是在完全信息的基础上,对各股票市场风险接收或溢出强度进行分析,而复杂网络节点的入度和出度偏重于描述各股市接收风险溢入范围大小或对其他股市风险溢出范围大小。入度越大,说明有更多节点的风险可以传送至该节点,风险来源范围更广。而出度越大,说明该节点的风险可以传送至更多节点,风险溢出渠道增多,溢出范围更大。表 5是网络节点拓扑特征结果。
|
|
表 5 网络节点拓扑特征结果 |
根据表 5测算结果可知,除俄罗斯股市外,其他欧美地区股市在三个阶段的出度排名较高,入度排名较低,是主要的风险输出者。而除中国股市外,其他亚洲地区股市及澳大利亚股市的出度排名较低,入度排名较高,是主要的风险输入者。中国股市在三个阶段的出度及入度均较低,风险对外输送渠道少,潜在的风险来源范围也较小,对风险传播的贡献度低。具体来看,在平稳时期,法国股市的出度为10,在网络中的风险对外输送渠道最多,风险溢出范围大,覆盖面广。从风险溢出网络结果中可以看出,接收法国股市风险溢入强度最大的国家分别是德国、意大利、英国、加拿大以及美国,这些国家均与法国存在密切的经贸往来,并且均属于欧美地区。新加坡股市在平稳时期的入度排名最高,股市较为“脆弱”,潜在风险来源范围大,直接接收11个股市的风险溢入。其中,澳大利亚、韩国及中国香港对其风险溢出强度最大。中国股市在此阶段的出度及入度均为4,同属亚洲区域的中国香港、韩国以及新加坡股市与中国股市存在双向风险溢出关系。由上述分析可以发现,平稳时期的股市风险溢出渠道主要为地域、经贸等宏观渠道。
在中美贸易摩擦时期,法国股市的出度排名最高,风险直接溢出范围覆盖11个股市,在风险溢出网络中的影响力最大。英国及德国股市的出度也较高,排名紧跟法国股市之后,位列第二。它们对彼此的风险溢出强度最大的同时,对同属欧洲区域的意大利、俄罗斯股市以及与其存在密切经贸往来的加拿大、美国股市的风险传染效应也较为显著。在此阶段,澳大利亚股市入度为10,排名最高,潜在的风险来源范围最大。中国股市与其他股市之间的风险溢入及溢出关系呈现出明显的地域特征。中国香港、韩国以及新加坡股市成为中国股市风险对外输送渠道的同时,又与日本股市一同成为中国股市的风险溢入来源。
在乌克兰危机时期,法国、德国及英国仍然是主要的股市风险溢出国,在网络中的风险溢出渠道最多,股市影响力最大。澳大利亚股市入度排名最高,是最大的风险输入国,中国香港、韩国及日本股市对其风险溢出强度最大。相较于前两个阶段,中国股市在此阶段的出度及入度均有所降低。中国股市与中国香港股市之间存在双向风险溢出关系的同时,直接接收来自新加坡股市的风险溢入。通过以上分析可以发现,无论在平稳时期还是两次极端事件发生时期,股市之间的风险传染渠道与地理距离、经贸往来有绝对关系。
五、研究结论与政策建议 (一) 研究结论首先,本文采用基于TVP-VAR模型的溢出指数法,构建多维股市风险的溢出指数矩阵,从静态角度识别各国或地区股市在风险溢出系统中的角色与地位。其后,对股市风险溢出指数进行动态刻画,掌握国际股票市场间风险溢出效应的时变特征,深入探究中国股市在整个样本时段内的风险溢出净效应及与其他股市之间的风险溢出效应。最后,构建平稳时期、中美贸易摩擦时期及乌克兰危机时期的风险溢出网络,对比分析股市间风险溢出效应在不同时期的差异。得到结论如下:(1)股票市场风险溢出效应存在区域“抱团”现象,同属区域股票市场间的风险溢出强度较大;(2)除俄罗斯外,其他欧美地区股市是风险净溢出者,俄罗斯、澳大利亚及亚洲地区股市为风险净接收者;(3)相较于乌克兰危机,中美贸易摩擦对股市风险溢出效应的影响更大,总体溢出指数呈现出显著的跳跃式上升趋势,同时,中美贸易摩擦时期风险溢出网络的平均聚类系数大于乌克兰危机时期和平稳时期,网络连接更紧密,风险流转效率更高;(4)中国股市在中美贸易摩擦时期的风险溢入净值大于乌克兰危机时期,遭受其他股市的风险冲击更大。
(二) 政策建议本文针对以上研究结论提出以下政策建议:
第一,在全球产业链深度融合、信息技术高度发达的今天,各国股票指数间的联系日益密切,股市风险外溢程度高,传播范围广。在这种背景下,当发生极端事件时,任何一个国家都不能独善其身,各国应密切合作,巩固全球风险监管机制,制定统一的风险防范准则,及时平抑风险的过度外溢。另外,股市风险存在显著的“邻居效应”,这意味着同区域间股票指数的风险溢出强度更大,因此位于同一区域内的国家或地区应协力建立区域风险监管机制及风险隔离制度。
第二,当前全球经济环境动荡,极端事件频发,由此带来的恐慌情绪及经济政策不确定性仍是资本市场的一大威胁。一方面,各国需要遏制国内极端事件的发展蔓延,尽量降低风险因素对金融资本市场的负面打击;另一方面,各国应团结起来,秉持命运共同体理念,一同维护国际经济的稳定,降低极端事件发生概率,为全球金融市场的健康发展创造良好环境。
第三,在极端风险事件冲击下,股票市场风险溢出总值可能会出现明显的上升趋势,此时,系统性风险快速积累,风险外溢强度高。这就要求监管技术部门构建一套高效、完整的风险监测办法,建立合规的风险预警机制,定期对国内外股票市场进行风险追踪检测和预测分析,在危机初露端倪时及时预警,以便采取有效应对措施。
第四,政府危机干预是确保股票市场健康平稳发展的重要措施。当极端事件发生时,政府可以通过制定合理的财政政策和货币政策,对股指收益走势加以引导,减少投资者恐慌情绪。同时,由高层官员在公开场合就股市情况进行表态,声明政府将尽最大努力稳定股市基本面,尽量降低股市大幅下跌的可能性,从而稳定股市参与者的预期。此外,应尽快降准降息,向市场提供充足流动性,为实体经济发展提供支撑。
| [1] |
周爱民, 韩菲. 股票市场和外汇市场间风险溢出效应研究——基于GARCH-时变Copula-CoVaR模型的分析[J]. 国际金融研究, 2017, (11): 54-64. (  0) 0) |
| [2] |
任英华, 赵婉茹, 罗良清. 基于Copula函数的股票市场风险溢出网络特征研究[J]. 统计与信息论坛, 2020, 35(8): 53-63. (  0) 0) |
| [3] |
淳伟德, 朱航聪. 我国股指期货与现货市场风险溢出效应研究——基于混频时变Copula-CoVaR模型[J]. 会计之友, 2022, (3): 9-15. (  0) 0) |
| [4] |
Diebold F X, Yilmaz K. Better to give than to receive: Predictive directional measurement of volatilityspillovers[J]. International Journal of Forecasting, 2012, 28(1): 57-66. DOI:10.1016/j.ijforecast.2011.02.006
(  0) 0) |
| [5] |
Diebold F X, Yilmaz K. On the network topology of variance decompositions: Measuring the connectedness of financial firms[J]. Journal of Econometrics, 2014, 182(1): 119-134. DOI:10.1016/j.jeconom.2014.04.012
(  0) 0) |
| [6] |
Erdös P. Graph theory and probability[J]. Canadian Journal of Mathematics, 1959, 11: 34-38. DOI:10.4153/CJM-1959-003-9
(  0) 0) |
| [7] |
Watts D J, Strogatz S H. Collective dynamics of 'small-world'networks[J]. Nature, 1998, 393(6684): 440-442. DOI:10.1038/30918
(  0) 0) |
| [8] |
Barabási A L, Albert R. Emergence of scaling in random networks[J]. Science, 1999, 286(5439): 509-512. DOI:10.1126/science.286.5439.509
(  0) 0) |
| [9] |
Mantegna R N. Hierarchical structure in financialmarkets[J]. The European Physical Journal B-Condensed Matter and Complex Systems, 1999, 11(1): 193-197. DOI:10.1007/s100510050929
(  0) 0) |
| [10] |
蔡源, 崔婕. "一带一路"沿线国家股市风险溢出效应——基于突发事件的实证检验[J]. 统计学报, 2022, 3(6): 74-92. (  0) 0) |
| [11] |
梁琪, 李政, 郝项超. 中国股票市场国际化研究: 基于信息溢出的视角[J]. 经济研究, 2015, 50(4): 150-164. (  0) 0) |
| [12] |
王智勇, 郭靖波. 人民币汇率市场动态传导效应研究——基于信息溢出的视角[J]. 云南财经大学学报, 2021, 37(3): 55-66. (  0) 0) |
| [13] |
赵艳平, 秦力宸, 黄友星. 全球外汇市场压力的风险溢出效应研究: 基于溢出指数和网络拓扑分析[J]. 世界经济研究, 2020, (8): 3-16. (  0) 0) |
| [14] |
Antonakakis N, Gabauer D. Refined measures of dynamic connectedness based on TVP-VAR[R]. MPRA Paper, No. 78282, 2017.
(  0) 0) |
| [15] |
王伟强. 经济政策不确定性的跨国溢出效应研究[J]. 郑州大学学报(哲学社会科学版), 2021, 54(5): 56-63. (  0) 0) |
| [16] |
孟浩, 张蕾, 程烨. 中国金融市场风险溢出效应研究[J]. 统计与信息论坛, 2021, 36(11): 63-75. (  0) 0) |
| [17] |
郭娜, 张骏. 中国能源市场与股票市场的波动溢出效应研究——基于TVP-VAR-DY模型的实证研究[J]. 西南民族大学学报(人文社会科学版), 2022, 43(5): 122-133. (  0) 0) |
| [18] |
刘晓星, 段斌, 谢福座. 股票市场风险溢出效应研究: 基于EVT-Copula-CoVaR模型的分析[J]. 世界经济, 2011, 399(11): 145-159. (  0) 0) |
| [19] |
刘海云, 吕龙. 全球股票市场系统性风险溢出研究——基于ΔCoVaR和社会网络方法的分析[J]. 国际金融研究, 2018, (6): 22-33. (  0) 0) |
| [20] |
沈悦, 李朝前, 赵欣悦, 等. 重大风险事件下全球股票市场风险传染效应研究[J]. 国际经贸探索, 2023, 39(4): 82-99. (  0) 0) |
| [21] |
Demirer M, Diebold F X, Liu L, et al. Estimating global bank network connectedness[J]. Journal of Applied Econometrics, 2018, 33(1): 1-15.
(  0) 0) |
 2023
2023 
