分数阶微分方程被视为非线性微分方程的替代模型,作为有效的数学建模工具之一,在对物理学、生物学、信号处理、控制理论、系统识别等科学领域的非线性现象进行数学建模的过程中发挥了重要作用。[1-3]此外,分数阶微分方程还被用于社会科学领域,如气候、金融和经济学[4],是研究的热点内容之一。越来越多的研究者致力于寻找分数阶微分方程的解析解或精确解,并提出了一些有效的求解方法,如分数阶Adomian分解法[5]、变分迭代法[6]、有限差分法[7]、首次积分法[8]、分数阶子方程法[9-11]、指数函数法[12-13]、(G′/G)-展开法[14-15]等。
Li和He[16-17]提出了一个分数阶复变换,可将分数阶偏微分方程转化为常微分方程,使求解过程变得简单。最近,分数阶复变换已经被用于处理具有修正Riemann-Liouville导数[18]的分数阶微分方程向整数阶微分方程的转换,转化后的方程可以通过符号计算系统Maple来求解。本文将分数阶复变换与(G′/G)-展开法[19]相结合,得到了如下时空分数阶Cahn-Hilliard方程[4, 20]新的精确解
| $ D_{t}^{\alpha }u-\eta D_{x}^{\beta }u-6u{{\left( D_{x}^{\beta }u \right)}^{2}}-\left( 3{{u}^{2}}-1 \right)D_{x}^{2\beta }u+D_{x}^{4\beta }u=0, 0 < \alpha, \beta \le 1, $ | (1) |
其中:u=u(x, t),η为任意非0常数。
1. 分数阶微积分定义分数阶微积分研究提出了许多种定义,目前最常使用的3种是:Caputo定义、Grünwald-Letnikov定义[21-22]和Riemann-Liouville定义。
定义1(Caputo分数阶导数定义[21]) 对于正实数α, 令n-1<α≤n,函数f(x)为定义在区间[a, b]上的可积函数, 则f(x)的α阶Caputo分数阶导数为
| $ _{a}^{c}D_{x}^{\alpha }f\left( x \right)=\frac{1}{\mathit{\Gamma }\left( n-\alpha \right)}\int_{\alpha }^{x}{\frac{f^\left( n \right)\left( \xi \right)}{{{\left( x-\xi \right)}^{\alpha-n+1}}}d\xi, } $ | (2) |
其中:Γ(x-α)是伽玛函数, 其广义定义为
| $ \mathit{\Gamma }\left( x \right)\int_{0}^{\infty }{{{e}^{-y}}{{y}^{x-1}}dy, } $ | (3) |
且满足Γ(x+1)=xΓ(x), 则当n∈N时,有Γ(n)=(n-1)!。
定义2(Riemann-Liouville分数阶导数定义[21-22]) 对于正实数α和a,令n-1≤α<n,函数f(x)为定义在区间[a, b]上的可积函数,则f(x)的α阶Riemalnn-Liouville分数阶导数为
| $ _{a}D_{x}^{\alpha }f\left( x \right)=\frac{1}{\mathit{\Gamma }\left( n-\alpha \right)}\frac{{{d}^{n}}}{d{{x}^{n}}}\left( \int_{a}^{x}{\frac{f\left( \tau \right)}{{{\left( x-\tau \right)}^{\alpha-n+1}}}d\tau } \right)。 $ | (4) |
Jumarie修正的Riemann-Liouville分数阶导数为[18, 23-24]
| $ D_{x}^{\alpha }f\left( x \right)=\left\{ \begin{align} &\frac{1}{\mathit{\Gamma }\left( 1-\alpha \right)}\frac{d}{dx}\int_{a}^{x}{{{\left( x-\xi \right)}^{-\alpha }}\left( f\left( \xi \right)-f\left( 0 \right) \right)d\xi, 0 < \alpha < 1, } \\ &{{\left( {{f}^{\left( n \right)}}\left( x \right) \right)}^{\alpha-n}}, n\le \alpha < n+1, n\ge 1, \\ \end{align} \right. $ | (5) |
且具有如下性质[24]
| $ \ \begin{array}{c} d^{\alpha}x\left( t \right) =\varGamma \left( 1+\alpha \right) dx\left( t \right), \\ f^{\left( \alpha \right)}\left[x\left( t \right) \right] =\frac{df}{dx}x^{\left( \alpha \right)}\left( t \right), \\ D_{x}^{\alpha}x^{\beta}=\frac{\varGamma \left( 1+\beta \right)}{\varGamma \left( 1+\beta -\alpha \right)}x^{\beta -\alpha}。\\ \end{array} $ | (6) |
Jumarie修正的Riemann-Liouville分数阶导数具有Riemann-Liouville分数阶导数和Caputo分数阶导数二者的优点,可成功应用于分数阶拉普拉斯问题[25]、概率演算[26]、多变量的分数阶变分法[27]、分数阶变分迭代方法[28]和自然边界条件的分数阶变分法[29]等。
2. (G′/G)-展开法概述给定时空分数阶偏微分方程
| $ P\left( u, \ D_{t}^{\alpha}u, \ D_{x}^{\beta}u, \ D_{t}^{2\alpha}u, \ D_{x}^{2\beta}u, \ ... \right) =0, \ \ 0 < \alpha, \beta \le 1, $ | (7) |
其中:u=u(x, t)是一个关于自变量x, t的未知函数,
步骤1:文献[16]中,Li和He提到的一个分数阶复变换可将分数阶偏微分方程转化为常微分方程。该分数阶复变换为:
| $ u\left( x, t \right) =U\left( \xi \right), \ \xi =\frac{Kx^{\beta}}{\varGamma \left( \beta +1 \right)}+\frac{Lt^{\alpha}}{\varGamma \left( \alpha +1 \right)}, $ | (8) |
其中:K, L为任意非0常数,当α=β=1时,ξ=Kx+Lt为行波变换。
将(8) 式代入(7) 式可得如下常微分方程
| $ Q\left( U, \ U', \ U'', \ U''', \ ... \right) =0, $ | (9) |
其中:
步骤2:设常微分方程(9) 的解可表示为关于(G′/G)的多项式
| $ U\left( \xi \right) = \sum\limits_{i = - n}^n {{a_i}{{\left( {\frac{{G'}}{G}} \right)}^i}} , $ | (10) |
其中:G=G(ξ)满足如下二阶非线性常微分方程
| $ G''G=\lambda G'^2+\mu GG'+\omega G^2。 $ | (11) |
这里a-n, …, an, λ, μ, ω均为待定常数。
直接求解方程(11) 可得以下3种形式的解
| $ \frac{G'\left( \xi \right)}{G\left( \xi \right)}=\left\{ \begin{array}{l} \frac{\sqrt{\mu ^2+4\, \omega-4\, \lambda \, \omega}}{2\left( 1-\lambda \right)}\left( \frac{C_1\sinh\left( \frac{\sqrt{\mu ^2+4\, \omega-4\, \lambda \, \omega}}{2}\xi \right) +C_2\cosh\left( \frac{\sqrt{\mu ^2+4\, \omega-4\, \lambda \, \omega}}{2}\xi \right)}{C_1\cosh\left( \frac{\sqrt{\mu ^2+4\, \omega -4\, \lambda \, \omega}}{2}\xi \right) +C_2\sinh\left( \frac{\sqrt{\mu ^2+4\, \omega -4\, \lambda \, \omega}}{2}\xi \right)} \right) +\\ \frac{\mu}{2\left( 1-\lambda \right)}, \left( \mu ^2-4\left( \lambda -1 \right) \omega >0, \ \lambda \ne 1 \right), \\ \frac{\sqrt{4\, \lambda \, \omega -4\, \omega -\mu ^2}}{2\left( 1-\lambda \right)}\left( \frac{-C_1\sin \left( \frac{\sqrt{4\, \lambda \, \omega -4\, \omega -\mu ^2}}{2}\xi \right) +C_2\cos \left( \frac{\sqrt{4\, \lambda \, \omega -4\, \omega -\mu ^2}}{2}\xi \right)}{C_1\cos \left( \frac{\sqrt{4\, \lambda \, \omega -4\, \omega -\mu ^2}}{2}\xi \right) +C_2\sin \left( \frac{\sqrt{4\, \lambda \, \omega -4\, \omega -\mu ^2}}{2}\xi \right)} \right) +\\ \frac{\mu}{2\left( 1-\lambda \right)}, \left( \mu ^2-4\left( \lambda -1 \right) \omega <0, \ \lambda \ne 1 \right), \\ \frac{1}{1-\lambda}\left( \frac{C_1}{C_1\xi +C_2}+\frac{\mu}{2} \right), \ \left( \mu ^2-4\left( \lambda -1 \right) \omega =0, \ \lambda \ne 1 \right), \\ \end{array} \right. $ | (12) |
其中:C1, C2为任意常数。
步骤3:(10) 式中的正整数n是由(9) 式中线性最高阶导数项和非线性项通过齐次平衡原理[30]来确定的。此处假设U(ξ)的阶数为Deg[U(ξ)]=n,则其他表达式的阶数为
| $ D\left( \frac{d^qU}{d\xi ^q} \right) =n+q, \ \ \ \ \ D\left[U^p\left( \frac{d^qU}{d\xi ^q} \right) ^s \right] =pn+s\left( n+q \right), $ | (13) |
由此即可确定(10) 式中n的值。
步骤4:将(10) 式代入(9) 式,运用关于(G′/G)的二阶常微分方程(11) 来合并(G′/G)的相同幂次项,并令(G′/G)的各次幂的系数为0, 得到一个关于未知数a-n, …, an, K, L, λ, μ, ω的非线性代数方程组。
步骤5:求解上述代数方程组,将所得结果代入(10) 式,并利用(11) 式在不同情况下的通解,即可获得方程(7) 的多个不同类型的精确解。
3. 时空分数阶Cahn-Hilliard方程的精确解结合Jumarie修正的Riemann-Liouville分数阶导数,对方程(1) 作分数阶复变换(8),可得如下常微分方程
| $ LU'-\eta KU'-6K^2U\left( U' \right) ^2-3K^2U^2U''+K^2U''+K^4U''''=0, $ | (14) |
其中:′=d/dξ, η, K, L是任意非0常数。
对(14) 式关于行波变量ξ积分一次,取积分常数为0得
| $ LU-\eta KU-3K^2U^2U'+K^2U'+K^4U'''=0。 $ | (15) |
对方程(15) 应用齐次平衡原理,即平衡线性最高阶导数项U3U′和非线性项U2U′, 有3n+1=n+3,从而n=1。将n=1代入(10) 式,可知方程(1) 的解具有如下形式
| $ U\left( \xi \right) =a_0+a_1\left( \frac{G'}{G} \right) +a_{-1}\left( \frac{G'}{G} \right) ^{-1}。 $ | (16) |
将(16) 式代入常微分方程(15) 可得关于(G′/G)的各阶幂次项,合并(G′/G)相同的幂次项,并令各次幂项的系数为0, 得到如下非线性代数方程组
| $ \left\{ \begin{array}{l} 3\, K^2a_{-1}^{3}\omega -6\, K^4a_{-1}\omega ^3=0, \\ -12\, K^4a_{-1}\mu \, \omega ^2+3\, K^2a_{-1}^{3}\mu +6\, K^2a_{-1}^{2}a_0\omega =0, \\ 8\, K^4a_{-1}\omega ^2+6\, K^2a_{-1}^{2}a_0\mu +3\, K^2a_{-1}a_{0}^{2}\omega +3\, K^2a_{-1}^{2}a_1\omega +3\, K^2a_{-1}^{3}\lambda -K^2a_{-1}\omega -\\ 8\, K^4a_{-1}\lambda \, \omega ^2-3\, K^2a_{-1}^{3}-7\, K^4a_{-1}\mu ^2\omega =0, \\ 6\, K^2a_{-1}^{2}a_0\lambda -6\, K^2a_{-1}^{2}a_0+8\, K^4a_{-1}\mu \, \omega -\eta \, Ka_{-1}+3\, K^2a_{-1}a_{0}^{2}\mu +3\, K^2a_{-1}^{2}a_1\mu +\\ La_{-1}-8\, K^4a_{-1}\lambda \, \mu \, \omega -K^2a_{-1}\mu -K^4a_{-1}\mu ^3=0, \\ 3\, K^2a_{-1}^{2}a_1\lambda -3\, K^2a_{-1}a_{0}^{2}+K^4a_{-1}\mu ^2-K^4a_{-1}\lambda \, \mu ^2+K^4a_1\mu ^2\omega -3\, K^2a_1a_{0}^{2}\omega -\\ 2\, K^4a_{-1}\omega +2\, K^4a_1\lambda \, \omega ^2-\eta \, Ka_0+4\, K^4a_{-1}\lambda \, \omega\\ +3\, K^2a_{-1}a_{0}^{2}\lambda -2\, K^4a_{-1}\lambda ^2\omega +K^2a_{-1}-3\, K^2a_{-1}a_{1}^{2}\omega -2\, K^4a_1\omega ^2+La_0-\\ 3\, K^2a_{-1}^{2}a_1+K^2a_1\omega -K^2a_{-1}\lambda =0, \\ -\eta \, Ka_1-6\, K^2a_{1}^{2}a_0\omega +K^4a_1\mu ^3+La_1-8\, K^4a_1\mu \, \omega +8\, K^4a_1\lambda \, \mu \, \omega -\\ 3\, K^2a_1a_{0}^{2}\mu -3\, K^2a_{-1}a_{1}^{2}\mu +K^2a_1\mu =0, \\ -3\, K^2a_{-1}a_{1}^{2}\lambda -K^2a_1+3\, K^2a_{-1}a_{1}^{2}-3\, K^2a_{1}^{3}\omega \\ -16\, K^4a_1\lambda \, \omega +8\, K^4a_1\lambda ^2\omega -3\, K^2a_1a_{0}^{2}\lambda\\ +3\, K^2a_1a_{0}^{2}-6\, K^2a_{1}^{2}a_0\mu +7\, K^4a_1\lambda \, \mu ^2+K^2a_1\lambda -7\, K^4a_1\mu ^2+8\, K^4a_1\omega =0, \\ 12\, K^4a_1\mu +12\, K^4a_1\lambda ^2\mu -3\, K^2a_{1}^{3}\mu +6\, K^2a_{1}^{2}a_0-6\, K^2a_{1}^{2}a_0\lambda -24\, K^4a_1\lambda \, \mu =0, \\ 3\, K^2a_{1}^{3}-18\, K^4a_1\lambda ^2+18\, K^4a_1\lambda -3\, K^2a_{1}^{3}\lambda +6\, K^4a_1\lambda ^3-6\, K^4a_1=0。\\ \end{array} \right. $ | (17) |
利用符号计算系统Maple求解方程组(17),获得3组解:
第一组解:
| $ \begin{array}{l} K=\pm \sqrt{\frac{2}{\mu ^2-8\omega +8\lambda \omega}}, \ \ L=\pm \eta \sqrt{\frac{2}{\mu ^2-8\omega +8\lambda \omega}}, \ \ a_0=\pm \frac{\mu}{\sqrt{\mu ^2-8\omega +8\lambda \omega}}, \ \\\ a_1=\pm \frac{2\left( \lambda-1 \right)}{\sqrt{\mu ^2-8\omega +8\lambda \omega}}, \ \ a_{-1}=\pm \frac{2\omega}{\sqrt{\mu ^2-8\omega +8\lambda \omega}}。\\ \end{array} $ | (18) |
其中:λ≠1,μ,ω,η为任意非0常数。
将(18) 式代入(16) 式可得
| $ U\left( \xi \right) =\pm \frac{\mu}{\sqrt{\mu ^2-8\omega +8\lambda \omega}}\pm \frac{2\left( \lambda-1 \right) \left( \frac{G'}{G} \right)}{\sqrt{\mu ^2-8\omega +8\lambda \omega}}\pm \frac{2\omega \left( \frac{G'}{G} \right) ^{-1}}{\sqrt{\mu ^2-8\omega +8\lambda \omega}}。 $ | (19) |
将(12) 式代入(19) 式,可在不同的参数约束条件下,获得方程(1) 不同形式的精确解。
情形1-1 当μ2-4(λ-1)ω>0,λ≠1时,可得双曲函数解
| $ \begin{array}{l} u\left( x, t \right) =\pm \frac{\mu}{\sqrt{\mu ^2-8\omega +8\lambda \omega}}\pm\\ \, \, \frac{2\left( \lambda-1 \right)}{\sqrt{\mu ^2-8\omega +8\lambda \omega}} \left( \frac{\sqrt{\mu ^2+4\, \omega-4\, \lambda \, \omega}}{2\left( 1-\lambda \right)}\left( \frac{C_1\sinh\left( \frac{\sqrt{\mu ^2+4\, \omega-4\, \lambda \, \omega}}{2}\xi \right) +C_2\cosh\left( \frac{\sqrt{\mu ^2+4\, \omega -4\, \lambda \, \omega}}{2}\xi \right)}{C_1\cosh\left( \frac{\sqrt{\mu ^2+4\, \omega -4\, \lambda \, \omega}}{2}\xi \right) +C_2\sinh\left( \frac{\sqrt{\mu ^2+4\, \omega -4\, \lambda \, \omega}}{2}\xi \right)} \right) +\frac{\mu}{2\left( 1-\lambda \right)} \right) \pm\\ \, \, \frac{2\omega}{\sqrt{\mu ^2-8\omega +8\lambda \omega}}\left( \frac{\sqrt{\mu ^2+4\, \omega -4\, \lambda \, \omega}}{2\left( 1-\lambda \right)}\left( \frac{C_1\sinh\left( \frac{\sqrt{\mu ^2+4\, \omega -4\, \lambda \, \omega}}{2}\xi \right) +C_2\cosh\left( \frac{\sqrt{\mu ^2+4\, \omega -4\, \lambda \, \omega}}{2}\xi \right)}{C_1\cosh\left( \frac{\sqrt{\mu ^2+4\, \omega -4\, \lambda \, \omega}}{2}\xi \right) +C_2\sinh\left( \frac{\sqrt{\mu ^2+4\, \omega -4\, \lambda \, \omega}}{2}\xi \right)} \right) +\frac{\mu}{2\left( 1-\lambda \right)} \right) ^{-1}。 \\ \end{array} $ | (20) |
其中:
对于(20) 式,考虑以下两种特殊情况,可得其如下形式的孤立波解。
情形1-1-1 当C1≠0, C2=0时,孤立波解为
| $ \begin{array}{l} u\left( x, t \right) =\pm \frac{\mu}{\sqrt{\mu ^2-8\omega +8\lambda \omega}}\pm\\ \, \, \, \, \, \, \frac{2\left( \lambda-1 \right)}{\sqrt{\mu ^2-8\omega +8\lambda \omega}}\left( \frac{\sqrt{\mu ^2+4\, \omega-4\, \lambda \, \omega}}{2\left( 1-\lambda \right)}\tanh\left( \frac{\sqrt{\mu ^2+4\omega-4\lambda \omega}}{2}\xi \right) +\frac{\mu}{2\left( 1-\lambda \right)} \right) \pm\\ \, \, \, \, \, \, \frac{2\omega}{\sqrt{\mu ^2-8\omega +8\lambda \omega}}\left( \frac{\sqrt{\mu ^2+4\, \omega -4\, \lambda \, \omega}}{2\left( 1-\lambda \right)}\tanh\left( \frac{\sqrt{\mu ^2+4\omega -4\lambda \omega}}{2}\xi \right) +\frac{\mu}{2\left( 1-\lambda \right)} \right) ^{-1}。\\ \end{array} $ | (21) |
情形1-1-2 当C1=0, C2≠0时,孤立波解为
| $ \begin{array}{l} u\left( x, t \right) =\pm \frac{\mu}{\sqrt{\mu ^2-8\omega +8\lambda \omega}}\pm\\ \, \, \, \, \, \, \frac{2\left( \lambda-1 \right)}{\sqrt{\mu ^2-8\omega +8\lambda \omega}}\left( \frac{\sqrt{\mu ^2+4\, \omega-4\, \lambda \, \omega}}{2\left( 1-\lambda \right)}\coth\left( \frac{\sqrt{\mu ^2+4\omega-4\lambda \omega}}{2}\xi \right) +\frac{\mu}{2\left( 1-\lambda \right)} \right) \pm\\ \, \, \, \, \, \, \frac{2\omega}{\sqrt{\mu ^2-8\omega +8\lambda \omega}}\left( \frac{\sqrt{\mu ^2+4\, \omega -4\, \lambda \, \omega}}{2\left( 1-\lambda \right)}\coth\left( \frac{\sqrt{\mu ^2+4\omega -4\lambda \omega}}{2}\xi \right) +\frac{\mu}{2\left( 1-\lambda \right)} \right) ^{-1}。\\ \end{array} $ | (22) |
若将(21) 式中的常数分别取值为:α=0.9, β=0.23, λ=3, μ=5, ω=2, η=10,则图 1为孤立波解(21) 的三维图,其中:

|
图 1 时空分数阶Cahn-Hilliard方程精确解(21) 的三维图 |
情形1-2 当μ2-4(λ-1)ω<0, λ≠1时,可得三角函数解
| $ \begin{array}{l} u\left( x, t \right) =\pm \frac{\mu}{\sqrt{\mu ^2-8\omega +8\lambda \omega}}\pm\\ \, \, \, \, \, \frac{2\left( \lambda-1 \right)}{\sqrt{\mu ^2-8\omega +8\lambda \omega}}\left( \frac{\sqrt{4\, \lambda \, \omega-4\, \omega-\mu ^2}}{2\left( 1-\lambda \right)}\left( \frac{-C_1\sin \left( \frac{\sqrt{4\, \lambda \, \omega -4\, \omega -\mu ^2}}{2}\xi \right) +C_2\cos \left( \frac{\sqrt{4\, \lambda \, \omega -4\, \omega -\mu ^2}}{2}\xi \right)}{C_1\cos \left( \frac{\sqrt{4\, \lambda \, \omega -4\, \omega -\mu ^2}}{2}\xi \right) +C_2\sin \left( \frac{\sqrt{4\, \lambda \, \omega -4\, \omega -\mu ^2}}{2}\xi \right)} \right) +\frac{\mu}{2\left( 1-\lambda \right)} \right) \pm\\ \, \, \, \, \frac{2\omega}{\sqrt{\mu ^2-8\omega +8\lambda \omega}}\left( \frac{\sqrt{4\, \lambda \, \omega -4\, \omega -\mu ^2}}{2\left( 1-\lambda \right)}\left( \frac{-C_1\sin \left( \frac{\sqrt{4\, \lambda \, \omega -4\, \omega -\mu ^2}}{2}\xi \right) +C_2\cos \left( \frac{\sqrt{4\, \lambda \, \omega -4\, \omega -\mu ^2}}{2}\xi \right)}{C_1\cos \left( \frac{\sqrt{4\, \lambda \, \omega -4\, \omega -\mu ^2}}{2}\xi \right) +C_2\sin \left( \frac{\sqrt{4\, \lambda \, \omega -4\, \omega -\mu ^2}}{2}\xi \right)} \right) +\frac{\mu}{2\left( 1-\lambda \right)} \right) ^{-1}。 \\ \end{array} $ | (23) |
其中:
若将(23) 式中的常数分别取值为:α=0.504 6,β=0.006,λ=3,μ=2,ω=5,η=2,C1=C2=1,则图 2为精确解(23) 的三维图,其中:

|
图 2 时空分数阶Cahn-Hilliard方程精确解(23) 的三维图 |
情形1-3 当μ2-4(λ-1)ω=0, λ≠1,即
| $ \begin{array}{l} u\left( x, t \right) =\pm \frac{\mu}{\sqrt{\mu ^2-8\omega +8\lambda \omega}}\pm \frac{2\left( \lambda-1 \right)}{\sqrt{\mu ^2-8\omega +8\lambda \omega}}\left( \frac{1}{1-\lambda}\left( \frac{C_1}{C_1\xi +C_2}+\frac{\mu}{2} \right) \right) \pm\\ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \frac{2\omega}{\sqrt{\mu ^2-8\omega +8\lambda \omega}}\left( \frac{1}{1-\lambda}\left( \frac{C_1}{C_1\xi +C_2}+\frac{\mu}{2} \right) \right) ^{-1}。\\ \end{array} $ | (24) |
其中:
将
| $ u\left( x, t \right) =\pm \frac{\sqrt{3}}{3}\pm \frac{2\sqrt{3}\left( \lambda-1 \right)}{3\mu}\left( \frac{1}{1-\lambda}\left( \frac{C_1}{C_1\xi +C_2}+\frac{\mu}{2} \right) \right) \pm \\ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \frac{2\sqrt{3}\left( \lambda-1 \right)}{3\mu}\left( \frac{1}{1-\lambda}\left( \frac{C_1}{C_1\xi +C_2}+\frac{\mu}{2} \right) \right) ^{-1}。 $ | (25) |
其中:
若将(25) 式中的常数分别取值为:α=0.8,β=0.02,λ=3,μ=5,η=2,C1=0.001, C2=5,则图 3为精确解(25) 的三维图,其中:

|
图 3 时空分数阶Cahn-Hilliard方程精确解(25) 的三维图 |
第二组解:
| $ \, \, \, \, \, \, K=\pm \sqrt{\frac{2}{\mu ^2+4\omega-4\lambda \omega}}, \ \ L=\pm \eta \sqrt{\frac{2}{\mu ^2+4\omega-4\lambda \omega}}, \\ a_0=\pm \frac{\mu}{\sqrt{\mu ^2+4\omega-4\lambda \omega}}, \ \ a_1=\pm \frac{2\left( \lambda -1 \right)}{\sqrt{\mu ^2+4\omega -4\lambda \omega}}, \ \ a_{-1}=0。 $ | (26) |
其中:λ≠1, μ, ω, η为任意非0常数。
将(26) 式代入(16) 式可得
| $ U\left( \xi \right) =\pm \frac{\mu}{\sqrt{\mu ^2+4\omega-4\lambda \omega}}\pm \frac{2\left( \lambda-1 \right) \left( \frac{G'}{G} \right)}{\sqrt{\mu ^2+4\omega-4\lambda \omega}}。 $ | (27) |
将(12) 式代入(27) 式,可在不同的参数约束条件下,获得方程(1) 如下不同形式的精确解。
情形2-1 当μ2-4(λ-1)ω>0, λ≠1时,可得双曲函数解
| $ u\left( x, t \right) =\pm \frac{\mu}{\sqrt{\mu ^2+4\omega-4\lambda \omega}}\pm \frac{2\left( \lambda-1 \right)}{\sqrt{\mu ^2+4\omega-4\lambda \omega}}\\ \, \, \, \, \, \, \, \, \, \, \, \, \, \left( \frac{\sqrt{\mu ^2+4\, \omega -4\, \lambda \, \omega}}{2\left( 1-\lambda \right)}\left( \frac{C_1\sinh\left( \frac{\sqrt{\mu ^2+4\, \omega -4\, \lambda \, \omega}}{2}\xi \right) +C_2\cosh\left( \frac{\sqrt{\mu ^2+4\, \omega -4\, \lambda \, \omega}}{2}\xi \right)}{C_1\cosh\left( \frac{\sqrt{\mu ^2+4\, \omega -4\, \lambda \, \omega}}{2}\xi \right) +C_2\sinh\left( \frac{\sqrt{\mu ^2+4\, \omega -4\, \lambda \, \omega}}{2}\xi \right)} \right) +\frac{\mu}{2\left( 1-\lambda \right)} \right) 。 $ | (28) |
其中:
对于(28) 式,考虑以下两种特殊情况,便可获得其如下形式的孤立波解。
情形2-1-1 当C1≠0,C2=0时,孤立波解为
| $ u\left( x, t \right) =\pm \frac{\mu}{\sqrt{\mu ^2+4\omega-4\lambda \omega}}\pm \\ \, \, \, \, \, \, \, \, \, \, \, \, \frac{2\left( \lambda-1 \right)}{\sqrt{\mu ^2+4\omega-4\lambda \omega}}\left( \frac{\sqrt{\mu ^2+4\, \omega -4\, \lambda \, \omega}}{2\left( 1-\lambda \right)}\tanh\left( \frac{\sqrt{\mu ^2+4\omega -4\lambda \omega}}{2}\xi \right) +\frac{\mu}{2\left( 1-\lambda \right)} \right) 。 $ | (29) |
情形2-1-2 当C1=0,C2≠0时,孤立波解为
| $ u\left( x, t \right) =\pm \frac{\mu}{\sqrt{\mu ^2+4\omega-4\lambda \omega}}\pm \\ \, \, \, \, \, \, \, \, \, \, \, \, \frac{2\left( \lambda-1 \right)}{\sqrt{\mu ^2+4\omega-4\lambda \omega}}\left( \frac{\sqrt{\mu ^2+4\, \omega -4\, \lambda \, \omega}}{2\left( 1-\lambda \right)}\coth\left( \frac{\sqrt{\mu ^2+4\omega -4\lambda \omega}}{2}\xi \right) +\frac{\mu}{2\left( 1-\lambda \right)} \right) 。 $ | (30) |
若将(29) 式中的常数分别取值为:α=0.9,β=0.01,λ=3,μ=5,ω=1,η=6,则图 4所示为孤立波解(29) 的三维图,其中:

|
图 4 时空分数阶Cahn-Hilliard方程精确解(29) 的三维图 |
情形2-2 当μ2-4(λ-1)ω<0, λ≠1时,可得三角函数解
| $ u\left( x, t \right) =\pm \frac{\mu}{\sqrt{\mu ^2+4\omega-4\lambda \omega}}\pm \\ \, \, \, \, \, \, \, \, \frac{2\left( \lambda-1 \right)}{\sqrt{\mu ^2+4\omega-4\lambda \omega}}\left( \frac{\sqrt{4\, \lambda \, \omega -4\, \omega -\mu ^2}}{2\left( 1-\lambda \right)}\left( \frac{-C_1\sin \left( \frac{\sqrt{4\, \lambda \, \omega -4\, \omega -\mu ^2}}{2}\xi \right) +C_2\cos \left( \frac{\sqrt{4\, \lambda \, \omega -4\, \omega -\mu ^2}}{2}\xi \right)}{C_1\cos \left( \frac{\sqrt{4\, \lambda \, \omega -4\, \omega -\mu ^2}}{2}\xi \right) +C_2\sin \left( \frac{\sqrt{4\, \lambda \, \omega -4\, \omega -\mu ^2}}{2}\xi \right)} \right) +\frac{\mu}{2\left( 1-\lambda \right)} \right) 。 $ | (31) |
其中:
若将(31) 式中的常数分别取值为:α=0.9,β=0.8,λ=3,μ=2,ω=5,η=28,C1=C2=1,则图 5所示为精确解(31) 的三维图,其中:
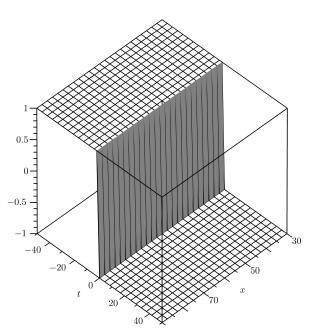
|
图 5 时空分数阶Cahn-Hilliard方程精确解(31) 的三维图 |
第三组解:
| $ K=\pm \sqrt{\frac{2}{\mu ^2+4\omega-4\lambda \omega}}, \, \, \, \, \ L=\pm \eta \sqrt{\frac{2}{\mu ^2+4\omega-4\lambda \omega}}, \\ a_0=\pm \frac{\mu}{\sqrt{\mu ^2+4\omega-4\lambda \omega}}, \, \, \ \text{ }a_1=0, \, \, \ \text{a}_{-1}=\pm \frac{2\omega}{\sqrt{\mu ^2+4\omega -4\lambda \omega}}。 $ | (32) |
其中:λ≠1, μ, ω, η为任意非0常数。
将(32) 式代入(16) 式可得
| $ U\left( \xi \right) =\pm \frac{\mu}{\sqrt{\mu ^2+4\omega-4\lambda \omega}}\pm \frac{2\omega \left( \frac{G'}{G} \right) ^{-1}}{\sqrt{\mu ^2+4\omega-4\lambda \omega}}。 $ | (33) |
将(12) 式代入(33) 式,可在不同的参数约束条件下,获得方程(1) 不同形式的精确解。
情形3-1 当μ2-4(λ-1)ω>0, λ≠1时,可得双曲函数解
| $ u\left( x, t \right) =\pm \frac{\mu}{\sqrt{\mu ^2+4\omega-4\lambda \omega}}\pm\\ \, \, \, \, \frac{2\omega}{\sqrt{\mu ^2+4\omega-4\lambda \omega}}\left( \frac{\sqrt{\mu ^2+4\, \omega-4\, \lambda \, \omega}}{2\left( 1-\lambda \right)}\left( \frac{C_1\sinh\left( \frac{\sqrt{\mu ^2+4\, \omega -4\, \lambda \, \omega}}{2}\xi \right) +C_2\cosh\left( \frac{\sqrt{\mu ^2+4\, \omega -4\, \lambda \, \omega}}{2}\xi \right)}{C_1\cosh\left( \frac{\sqrt{\mu ^2+4\, \omega -4\, \lambda \, \omega}}{2}\xi \right) +C_2\sinh\left( \frac{\sqrt{\mu ^2+4\, \omega -4\, \lambda \, \omega}}{2}\xi \right)} \right) +\frac{\mu}{2\left( 1-\lambda \right)} \right) ^{-1}。 $ | (34) |
其中:
对于(34) 式,考虑以下两种特殊情况,便可获得其如下形式的孤立波解。
情形3-1-1 当C1≠0,C2=0时,孤立波解为
| $ u\left( x, t \right) =\pm \frac{\mu}{\sqrt{\mu ^2+4\omega-4\lambda \omega}}\pm \\ \, \, \, \, \, \, \, \, \, \, \frac{2\omega}{\sqrt{\mu ^2+4\omega-4\lambda \omega}}\left( \frac{\sqrt{\mu ^2+4\, \omega-4\, \lambda \, \omega}}{2\left( 1-\lambda \right)}\tanh\left( \frac{\sqrt{\mu ^2+4\omega -4\lambda \omega}}{2}\xi \right) +\frac{\mu}{2\left( 1-\lambda \right)} \right) ^{-1}。 $ | (35) |
情形3-1-2 当C1=0,C2≠0时,孤立波解为
| $ u\left( x, t \right) =\pm \frac{\mu}{\sqrt{\mu ^2+4\omega-4\lambda \omega}}\pm \\ \, \, \, \, \, \, \, \, \, \, \frac{2\omega}{\sqrt{\mu ^2+4\omega-4\lambda \omega}}\left( \frac{\sqrt{\mu ^2+4\, \omega-4\, \lambda \, \omega}}{2\left( 1-\lambda \right)}\coth\left( \frac{\sqrt{\mu ^2+4\omega -4\lambda \omega}}{2}\xi \right) +\frac{\mu}{2\left( 1-\lambda \right)} \right) ^{-1}。 $ | (36) |
若将(35) 式中的常数分别取值为:α=0.8,β=0.1,λ=3,μ=5,ω=2,η=6,则图 6所示为孤立波解(35) 的三维图,其中:

|
图 6 时空分数阶Cahn-Hilliard方程精确解(35) 的三维图 |
情形3-2 当μ2-4(λ-1)ω<0, λ≠1时,可得三角函数解
| $ u\left( x, t \right) =\pm \frac{\mu}{\sqrt{\mu ^2+4\omega-4\lambda \omega}}\pm \\ \, \, \, \, \, \frac{2\omega}{\sqrt{\mu ^2+4\omega-4\lambda \omega}}\left( \frac{\sqrt{4\, \lambda \, \omega-4\, \omega -\mu ^2}}{2\left( 1-\lambda \right)}\left( \frac{-C_1\sin \left( \frac{\sqrt{4\, \lambda \, \omega -4\, \omega -\mu ^2}}{2}\xi \right) +C_2\cos \left( \frac{\sqrt{4\, \lambda \, \omega -4\, \omega -\mu ^2}}{2}\xi \right)}{C_1\cos \left( \frac{\sqrt{4\, \lambda \, \omega -4\, \omega -\mu ^2}}{2}\xi \right) +C_2\sin \left( \frac{\sqrt{4\, \lambda \, \omega -4\, \omega -\mu ^2}}{2}\xi \right)} \right) +\frac{\mu}{2\left( 1-\lambda \right)} \right) ^{-1}。 $ | (37) |
其中:
若将(37) 式中的常数分别取值为:α=0.8,β=0.6,λ=3,μ=2,ω=5,η=2,C1=2.1, C2=0.1,则图 7所示为孤立波解(37) 的三维图,其中:

|
图 7 时空分数阶Cahn-Hilliard方程精确解(37) 的三维图 |
本文利用分数阶复变换和Jumarie修正的Riemann-Liouville分数阶导数,结合齐次平衡原理,通过(G′/G)-展开法研究了时空分数阶Cahn-Hilliard方程的精确解,获得了该方程含有多参数的新双曲函数、三角函数和有理函数等不同形式的精确解,且当双曲函数解中部分参数取特殊值时即可获得其孤立波解,从而丰富了时空分数阶Cahn-Hilliard方程的解系,并给出了其中孤立波解、周期波解和行波解的三维图。
| [1] | Miller K S, Ross B. An Introduction to the Fractional Calculus and Fractional Differential Equations[M]. New York: John Wiley and Sons, 1993: 384. |
| [2] | Kilbas A A, Srivastava H M, Trujillo J J. Theory and Applications of Fractional Differential Equations[M]. Oxford: Elsevier Science and Technology, 2006: 540. |
| [3] | Podlubny I. Fractional Differential Equations[M]. San Diego: Academic Press, 1999: 340. |
| [4] | Bekir A, Güner Ö, Cevikel A C. Fractional Complex Transform and exp-Function Methods for Fractional Differential Equations[J]. Abstract and Applied Analysis, 2013(1): 1–8. |
| [5] | 牛红玲, 郝玲, 余志先, 等. Adomian分解法求解非线性分数阶积分微分方程[J]. 辽宁工程技术大学学报(自然科学版), 2013, 32(1): 132–135. |
| [6] | 王文华. 分数阶微分方程的变分迭代解法[D]. 长沙: 长沙理工大学硕士学位论文, 2010: 1-32. |
| [7] | Cui M. Compact finite difference method for the fractional diffusion equation[J]. Journal of Computational Physics, 2009, 228(20): 7792–7804. DOI:10.1016/j.jcp.2009.07.021 |
| [8] | Lu B. The first integral method for some time fractional differential equations[J]. Journal of Mathematical Analysis and Applications, 2012, 395(2): 684–693. DOI:10.1016/j.jmaa.2012.05.066 |
| [9] | Zhang S, Zhang H Q. Fractional sub-equation method and its applications to nonlinear fractional PDEs[J]. Physics Letters A, 2011, 375(7): 1069–1073. DOI:10.1016/j.physleta.2011.01.029 |
| [10] | Alzaidy J F.The Fractional Sub-Equation Method and Exact Analytical Solutions for Some Nonlinear Fractional PDEs[J].2013, (1):14-19. |
| [11] | Tang B, He Y, Wei L, et al. A generalized fractional sub-equation method for fractional differential equations with variable coefficients[J]. Physics Letters A, 2012, 376(38-39): 2588–2590. DOI:10.1016/j.physleta.2012.07.018 |
| [12] | Zhang S, Zong Q A, Liu D, et al. A Generalized Exp-Function Method for Fractional Riccati Differential Equations[J]. Communications in Fractional Calculus, 2010(1): 48–51. |
| [13] | Zheng B. Exp-Function Method for Solving Fractional Partial Differential Equations[J]. The Scientific World Journal, 2013(3-4): 465723. |
| [14] | 尹君毅. 扩展的(G'/G)-展开法和Zakharov方程组的新精确解[J]. 物理学报, 2013, 62(20): 1–5. |
| [15] | Yao Ruoxia, Wang Wei, Chen Tinghua. New Solutions of Three Nonlinear Space-and Time-Fractional Partial Differential Equations in Mathematical Physics[J]. Communications in Theoretical Physics, 2014, 62(5): 689–696. DOI:10.1088/0253-6102/62/5/10 |
| [16] | Li Z B, He J H. Application of the Fractional Complex Transform to Fractional Differential Equations[J]. Mathematical and Computational Applications, 2011, 15(5): 97–137. |
| [17] | Li Z B, Zhu W H, He J H. Exact solutions of time-fractional heat conduction equation by the fractional complex transform[J]. Thermal Science, 2012, 16(2): 335–338. DOI:10.2298/TSCI110503069L |
| [18] | Jumarie G. Modified Riemann-Liouville derivative and fractional Taylor series of nondifferentiable functions further results[J]. Computers and Mathematics with Applications, 2006, 51(9-10): 1367–1376. DOI:10.1016/j.camwa.2006.02.001 |
| [19] | Wang Mingliang, Li Xiangzheng, Zhang Jinliang. The (G′/G)-expansion method and traveling wave solutions of nonlinear evolution equations in mathematical physics[J]. Physics Letters A, 2008, 21(4): 417–423. |
| [20] | Dahmani Z, Benbachir M. Solutions of the Cahn-Hilliard Equation with Time-and Space-Fractional Derivatives[J]. nt.j.nonlinear Sci, 2009, 8(1): 19–26. |
| [21] | 胡桐春, 钱德亮, 李常品. 分数阶微分方程的比较定理[J]. 应用数学与计算数学学报, 2009, 23(1): 97–103. |
| [22] | 林孔容. 关于分数阶导数的几种不同定义的分析与比较[J]. 闽江学院学报, 2003, 24(5): 3–6. |
| [23] | Atangana A, Secer A. A Note on Fractional Order Derivatives and Table of Fractional Derivatives of Some Special Functions[J]. Abstract and Applied Analysis, 2013(4): 215–222. |
| [24] | Liu Wenjun, Chen Kewang. The functional variable method for finding exact solutions of some nonlinear time-fractional differential equations[J]. Indian Academy of Sciences, 2013, 81(3): 377–384. |
| [25] | Jumarie G. Table of some basic fractional calculus formulae derived from a modified Riemann-Liouville derivative for non-differentiable functions[J]. Applied Mathematics Letters, 2009, 22(3): 378–385. DOI:10.1016/j.aml.2008.06.003 |
| [26] | Jumarie G. New stochastic fractional models for Malthusian growth, the Poissonian birth process and optimal management of populations[J]. Mathematical and Computer Modelling, 2006, 44(3-4): 231–254. DOI:10.1016/j.mcm.2005.10.003 |
| [27] | Almeida R, Malinowska A B, Torres D F M. A fractional calculus of variations for multiple integrals with application to vibrating string[J]. Journal of Mathematical Physics, 2010, 51(3): 10375. |
| [28] | Wu G C, Lee EWM. Fractional variational iteration method and its application[J]. Physics Letters A, 2010, 374(25): 2506–2509. DOI:10.1016/j.physleta.2010.04.034 |
| [29] | Wu Guocheng. A fractional characteristic method for solving fractional partial differential equations[J]. Applied Mathematics Letters, 2011, 24(1): 1046–1050. |
| [30] | 王明亮, 李志斌, 周宇斌. 齐次平衡原则及其应用[J]. 兰州大学学报(自然科学版), 1999, 35(3): 8–16. |
 2017, Vol. 32
2017, Vol. 32