0 引言

波动率在衍生品定价、资产配置和风险管理等方面起到重要的作用，波动率的典型建模方法是Engle和Bollerslev提出的GARCH类模型^[1-2]以及Taylor提出的随机波动率模型(Stochastic Volatility, SV)^[3]。然而这两类模型都是基于收益率的建模方法即利用收益率的绝对值或者平方作为波动率的代理变量，进而得到真实波动率的估计。由于收益率数据仅仅是利用了某一交易时段的收盘价信息，并不能完全反映时段内价格变动的信息，为弥补这一缺陷，学术界利用日内价格信息构建波动率模型，典型的是Parkinson等提出基于价格极差(Range，定义为某一时间段内最高价与最低价之差)的波动率^[4]，随后Garman和Klass在此基础上进一步引入开盘价和收盘价信息来构建波动率^[5]。为反映极差的动态特征，一些研究开始基于极差来对波动率建模如Alizadeh等提出了基于极差的SV模型^[6]，Chou提出条件极差波动模型^[7]，上述研究均证明了基于极差的波动率建模方法的有效性。

波动率过程通常具有长记忆性，如Andersen等研究发现股票和外汇市场的已实现波动率RV具有长记忆性特征^[8-9]；施红俊等利用GPH法对沪深A股指数以及上证180和深证成指部分样本股进行长记忆性检验，得出沪深两市的波动率序列均具有高度显著的长记忆特征^[10]；谢赤和岳汉奇运用经典R/S、V/S及小波方差分析，发现人民币兑美元汇率的波动率存在显著长记忆性特征^[11]。另一方面，对于期货市场波动率的特征研究相对较少，Areal和Taylor分析5分钟FSTE100股指期货的已实现波动率，发现已实现波动率具有持续的正自相关，显示出长记忆特征^[12]；Chen等分析多种期货合约的波动率持续性特征，其选取的波动率测度有GARCH波动率和已实现波动率，研究结论发现已实现波动率的持续性要强于GARCH波动率^[13]；庞淑娟等采用GPH方法检验中国期货市场的5种期货产品波动率的长记忆特征^[14]。

沪深300股指期货作为我国首个金融期货品种，其上市交易推动一直以来较为滞后的金融衍生品市场的发展。随着沪深300股指期货的推出，对于沪深300股指期货的研究日益增多，但这些研究更多是集中于期货市场的价格发现功能，对于极差波动率方面的研究还未涉及，本文拟弥补这一空白，分析沪深300股指期货极差波动率的相应统计特征。特别的以往基于R/S，修正R/S和V/S方法对真实长记忆过程和谬误长记忆过程缺乏检验效力，而Qu基于频域提出的检验方法，通过蒙特卡洛模拟发现有着最高的检验效力^[15]，因此本文利用Qu的检验方法，检验股指期货极差波动率的长记忆特征。

1 极差波动率与长记忆分析 1.1 基于极差的波动率模型

Parkinson在对数价格服从随机游走过程且波动率动态为分段线性过程条件下，给出经典的极差波动率估计量，其表达式为：

$ {S_t} = {R_t}/\sqrt {4{\rm{log}}\left( 2 \right)} 。 $

(1)

其中：R_t=$\mathop {{\rm{max}}}\limits_\tau {p_\tau } - \mathop {{\rm{min}}}\limits_\tau {p_\tau }$, t-1 < τ≤t，p_τ=log (P_τ)表示资产价格对数。

Parkinson指出极差利用了日内价格的变动信息而不仅仅是收盘时点的信息，可以显著提高波动率估计的效率，同时证明基于极差的波动率估计量效率要高于基于收益率的波动率估计量，前者的方差近似为后者的1/5，因此具有更小的置信区间。除了估计量精度的优势外，Alizadeh等进一步指出，对数极差波动率具有近似正态分布，从而避免了收益率尖峰厚尾分布带来的估计困难且对微观市场噪音稳健；另外，金融市场报价信息中通常都包含了日内交易的最高价和最低价，使得基于极差的波动率建模方法具有广泛的适用性。

1.2 极差波动率的长记忆性检验

长记忆性(long memory)指的是时间序列自相关的持续性，即自相关系数以非常缓慢的双曲线比率衰减，也就是说时间序列存在着一定的自相关性，历史的波动会对未来产生影响，从经济学的角度看，长记忆过程表明外在冲击的影响在长期内会消失，但是调整过程会很缓慢。对于长记忆性的时域检验方法有R/S分析、修正R/S分析和V/S分析，随着长记忆性研究方法的深入与发展，基于频域视角来检验长记忆性特征的统计量也不断涌现，如Qu通过比较长记忆性和谬误长期记忆性序列的谱域(spectral domain)性质，构建区分长记忆性和谬误长记忆性的检验统计量。其构建检验统计量的思路是利用局部Whittle似然函数：

$ Q\left( {G,d} \right) = \frac{1}{M}\sum\limits_{j = 1}^m {\left\{ {{\rm{log}}G\lambda _j^{ - 2d} + \frac{{I({\lambda _j})}}{{G\lambda _j^{ - 2d}}}} \right\}} 。 $

(2)

其中：I(λ_j)=(2πn)^-1| $\sum\nolimits_{t = 1}^n {{x_t}exp(i{\lambda _j}t)} $|²是序列在频率λ_j=2πj/n，j=1, 2，…, m，m < n/2上的周期图(下同)。关于G最小化Q(G, d)得到轮廓似然函数(profiled likelihood function)：

$ R\left( d \right) = {\rm{log}}G\left( d \right) - 2{m^{ - 1}}d\sum\limits_{j = 1}^m {{\rm{log}}{\lambda _j}} 。 $

(3)

其中：G(d)=m^-1$\sum\nolimits_{j = 1}^n {\lambda _j^{2d}I({\lambda _j})} $。

求R(d)关于d的导数：

$ \frac{{\partial R\left( d \right)}}{{\partial d}} = \frac{{2{G_0}}}{{\sqrt m G\left( d \right)}}\left\{ {{m^{ - 1/2}}\sum\nolimits_{j = 1}^m {{v_j}\left( {\frac{{I({\lambda _j})}}{{{G_0}\lambda _j^{ - 2d}}} - 1} \right)} } \right\}。 $

(4)

其中：v_j=logλ_j-(1/m) $\sum\nolimits_{j = 1}^n {\log {\lambda _j}} $，G₀为G的真实值。

在序列是长期记忆过程且d=d₀时，Qu证明部分和过程m^-1/2$\sum\nolimits_{j = 1}^{\left[ {mr} \right]} {{v_j}} $(I_x(λ_j)λ_j^2d₀/G₀-1)满足泛函中心极限定理且为一致O_p(1)，同时如果序列不是长期记忆过程，则上述部分和过程不具有零均值且发散。基于上述过程，Qu给出其长期记忆性检验统计量

$ W = \mathop {sup}\limits_{r \in [\varepsilon ,1]} {\left( {\sum\nolimits_{j = 1}^m {v_{j = 1}^2} } \right)^{ - 1/2}}\left| {\sum\nolimits_{j = 1}^{\left[ {mr} \right]} {{v_j}\left( {\frac{{I\left( {{w_j}} \right)}}{{G\left( {\hat d} \right)\lambda _j^{ - 2\hat d}}} - 1} \right)} } \right|。 $

(5)

其中：${\hat d}$为使用带宽m得到参数d的局部Whittle估计值，ε为修剪参数。m应满足m/n^0.5→ ∞来达到较高的势且m应小于n^0.8以避免估计d时导致的偏差，在原假设成立和合适的条件下，Qu给出检验统计量W的极限分布为：

$ \mathop {sup}\limits_{r \in [\varepsilon ,1]} \left| {\int_0^r {(1 + {\rm{log}}s)} dW\left( s \right) - W\left( 1 \right)\int_0^r {(1 + {\rm{log}}s)} ds - \Phi \left( r \right)\int_0^r {(1 + {\rm{log}}s)} dW\left( s \right)} \right|。 $

(6)

其中：Φ(r)=$\int_0^r {{{\left( {1 + \log s} \right)}^2}ds} $，W(r)为定义在[0, 1]区间上的维纳过程，由于W的渐近分布与参数无关，Qu通过模拟方法给出检验统计量W的临界值。

1.3 长记忆性参数估计

除对序列是否是长记忆过程进行检验外，长记忆过程研究中需要解决的另一个问题是对分整阶数(fractional integrated order)即长记忆参数进行估计，基于频域的半参数方法将参数和非参数方法相结合，一方面降低参数方法中的正态性要求，一方面在估计参数时提出相应假设条件，改进非参数方法稳健性差的问题。常用的半参数估计法有Geweke和Porter-Hudak所提出的GPH估计量^[16]以及Robinson所提出的局部Whittle估计量^[17]。GPH的长记忆参数估计量采用如下的谱回归(spectrum regression)或对数周期图回归(log periodogram)：

$ {\rm{ln}}I({\lambda _j}) = c - d{\rm{ln}}\left\{ {4si{n^2}({\lambda _j}/2)} \right\} + {\varepsilon _j},j = 1,2, \ldots ,m。 $

(7)

对式(7)利用OLS法进行估计，可得到长记忆参数d的一致估计$ {{\hat d}_{GPH}}$。GPH估计具有简便性，使该方法在实证研究方面广泛应用，Geweke and Porter-Hudak给出$ {{\hat d}_{GPH}}$的极限分布：

$ \sqrt m ({{\hat d}_{GPH}} - d) \Rightarrow N(0,{\pi ^2}/24)。 $

(8)

Robinson提出一种高斯半参数估计法(也称为局部Whittle方法)，与GPH方法相比，该估计量的假设条件相对较弱，但更加渐近有效，且具有渐近正态性和一致性等特点。Robinson通过最大化式(3)得到长记忆参数的局部Whittle估计量并给出该估计量的极限分布：

$ \sqrt m ({{\hat d}_{LW}} - d) \Rightarrow N(0,1/4){\rm{.}} $

(9)

由于1/4 < π²/24，因此对于相同的频率m，局部Whittle估计量在渐近意义上较GPH估计量更为有效。

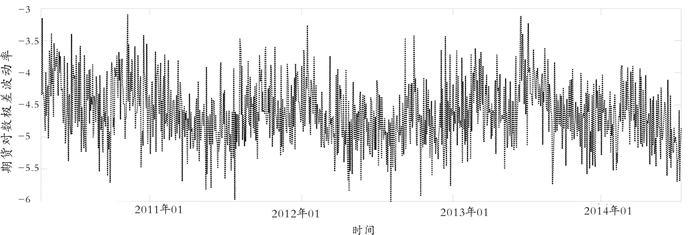
2 实证分析

选取沪深300股指和其对应的期货主力合约“当月合约”构成的当月连续指数的日数据，包括日最高价和最低价，样本期共计1 028个交易日，数据来源于Wind数据库。通过式(1)构建沪深300期货的极差波动率，对极差波动率序列取自然对数，图 1给出了期货对数极差波动率的时序图。

对对数极差波动率的统计特征分析，采用了如下统计量：均值(Mean)、标准差(S. D)、偏度(Skewness)、峰度(Kurtosis)、Jarque-Bera统计量、Ljung-Box Q统计量、ADF统计量，表 1给出了具体的统计结果。

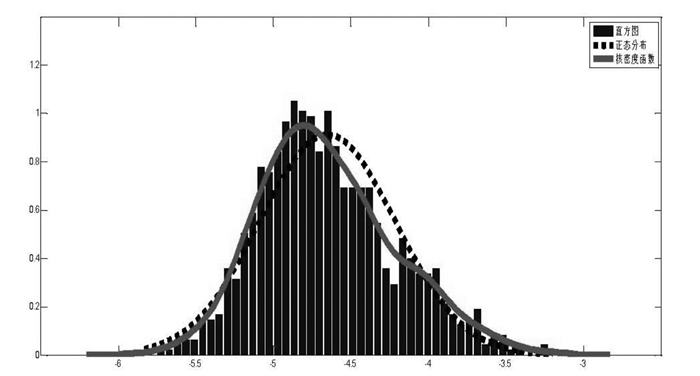
第一，从表 1的统计分析结果可以看出，对数极差波动率的偏度系数0.193，稍大于0，而峰度系数为2.919，相较于正态分布的0和3稍有差异，分布呈现左偏形态，但JB正态性检验在5%显著性水平上拒绝正态分布的原假设，图 2给出对数极差波动率的直方图和相应核密度图以及以表 1中均值和标准差得到的正态分布图，由图 2中可看到，首先，在尾部区域核密度函数与正态分布函数基本重合，而在中间区域两者之间具有一定差异；其次，由Ljung-Box Q统计量对自相关的检验结果可知，在较长的时间范围内(100期以内)都显著拒绝自相关系数为零的原假设，自相关系数显示出缓慢衰减，具有长记忆特征；最后，以AIC信息准则确定最优检验滞后阶数的ADF单位根检验结果可知，显著拒绝存在单位根的原假设，因此，可以认为对数极差波动率都是平稳时间序列，可以直接进行下一步的工作--对长记忆性进行检验。

第二，进行长记性分析。Perron和Qu指出均值受到结构变化或平滑趋势影响的短记忆过程同样显示出缓慢衰减的自相关函数，满足长记忆过程的特征^[18]，这样的短记忆过程通常称为伪长记忆过程，因此观察到给定时间序列具有长记忆特征并不意味着其就是由长记忆过程产生的。为进一步确认σ_{t, F}是否为长记忆过程，采用Qu的长记忆检验统计量进行检验，Qu通过模拟研究发现在带宽m=[n^0.7]时，检验统计量可以在显著性和势之间达到很好的权衡，为进行比较我们也给出其他带宽下的检验结果，结果见表 2。从表 2中，可以看到在不同修剪参数ε下，所计算得到检验统计量值稍有不同，通过与不同显著性水平下的临界值进行比较，在不同带宽下检验统计量均未超过10%显著性水平下的临界值，因此不能拒绝原假设，从而接受期货极差波动率为长记忆过程的结论，为随后进行长记忆性参数估计奠定基础。

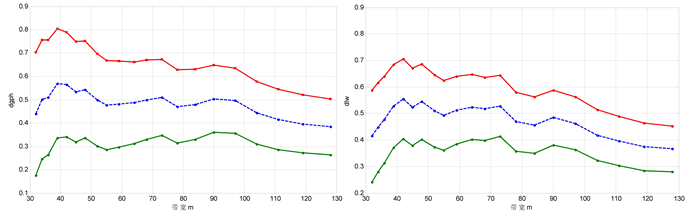
利用半参数方法估计长记忆参数d，需要确定带宽m的大小，大量研究表明，带宽的选择对于d的估计非常重要，在实践中常常取带宽[n^0.5]≤m≤n/2，为更好地把握GPH和LW估计的特征，我们选取带宽m=[n^α]，其中：α取值为0.5到0.8，间隔0.02，图 3给出对数极差波动率的长记忆参数d的GPH估计和局部Whittle估计结果和相应95%渐近置信区间，表 3为部分带宽下d的估计结果。

由表 3和图 3中可看到，不同带宽参数下GPH和局部Whittle估计的结果十分相近，GPH和局部Whittle估计在不同带宽下的平均值分别为0.469和0.447，两者差异不大，这些估计类似于Andersen等分析汇率和Areal和Taylor分析FSTE100期货的结果，而GPH估计具有明显较大的置信区间且这些置信区间均不包含0，因此，根据GPH的检验方法也进一步印证极差波动率为长记忆过程。

3 结语

传统基于收益率的波动率模型由于仅利用收盘价信息而忽略区间内的价格变动，损失大量信息，导致估计效率低下，而以极差构建波动率，更多利用日内价格信息，相较于基于收益的方法更为有效，而相较于已实现波动率，可以避免微观噪声等影响。基于沪深300股指期货上市4年内的日内最高价和最低价，采用极差波动率方法分析股指期货波动的相应性质。不同于以往对于长记忆性的分析，本文采用Qu创新的检验方法对股指期货极差波动率的长记忆性进行检验，得到其为真实长记忆过程，因此，外生突发事件会对股市的影响具有长期性。通过半参数估计方法得到其记忆参数接近典型值0.4，未来可进一步通过长记忆模型对极差波动率进行建模，进行波动率预测的工作。