b. 渭南师范学院 数理学院,陕西 渭南 714099
b. School of Mathematics and Physics,Weinan Normal University,Weinan 714099,China
MATLAB是由美国Mathworks公司发布的主要面对科学计算、可视化以及交互程序设计的高科技计算环境。它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于实用的视窗环境中,提供可靠丰富的矩阵运算、数据处理、图形绘制、图像处理等功能,为科学研究、工程设计以及必须进行有效数值计算的众多课题提供了一种全面的解决方案,并在很大程度上摆脱了传统非交互式程序设计语言的编辑模式,代表了当今国际科学计算软件的先进水平。[1]MATLAB软件的基本特点是:第一,有较强的数值计算功能和作图功能,也有很强的符号计算功能;第二,图形窗口式操作直观简洁,方便理解;[2]第三,用简单的指令就可以完成大量烦琐的计算过程和作图功能。编程语法简单,程序设计方便,正是因其具有这样的特点,所以在求解复杂的力学问题时应用MATLAB就易得出准确直观的物理结果。[3]
力学问题就是建立和求解力学体系的运动微分方程,找出力学体系的运动规律,但有时在力学和物理学中会遇到这样一些微分方程,它们无法求出或者很难求出解析解。[4]此时利用MATLAB不仅可以由力学体系的运动方程求出其运动规律,而且还能绘制出其运动曲线,使力学体系的运动规律可视化,同时也能使我们更加容易且深入地认识其运动特征。[5]
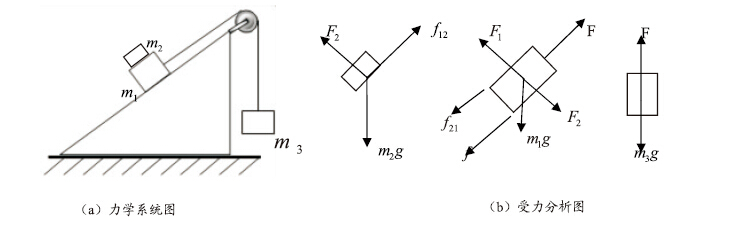
1 用MATLAB软件来解决力学问题中的实例 1.1 求解线性方程组的问题在如图 1(a)的力学系统中,已知m1=1.0 kg,m2=2.0 kg,m3=3.5 kg,物体1与斜面之间的摩擦系数μ1=0.1,物体1与物体2之间的摩擦系数μ2=0.8,不计绳和滑轮的质量及摩擦。求作用在m1与m2上的正压力F1、F2,绳子的张力F以及3个质块的加速度α1、α2、α3。
|
图 1 力学系统图和受力分析图 |
分析如下:
在对m1、m2、m3分别作受力分析的基础上列出方程组:
| $\left\{ \begin{matrix} {{F}_{1}}-{{F}_{2}}={{m}_{1}}g\cos \alpha , \\ -{{\mu }_{1}}{{F}_{1}}-{{\mu }_{2}}{{F}_{2}}+F-{{m}_{1}}{{\alpha }_{1}}={{m}_{1}}g\sin \alpha , \\ {{F}_{2}}={{m}_{2}}\text{g}\cos \alpha , \\ {{\mu }_{2}}{{F}_{2}}-{{m}_{2}}{{\alpha }_{2}}={{m}_{2}}\text{gsin}\alpha \\ -F-{{m}_{1}}{{\alpha }_{1}}=-{{m}_{3}}\text{g}\text{。} \\ \end{matrix} \right.$ | (1) |
求解该方程组的5个未知数应该不成问题,但联解5个方程在演算上却相当烦琐,而MATLAB解这样的线性方程组非常简单。如果把方程组按线性代数的形式写出来就是:
| $A\centerdot x=b$ | (2) |
其中:
| $A\text{=}\left[ \begin{matrix} 1 & -1 & 0 & 0 & 0 \\ -{{\mu }_{1}} & -{{\mu }_{2}} & 1 & -{{m}_{1}} & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & {{\mu }_{2}} & 0 & 0 & -{{m}_{2}} \\ 0 & 0 & 1 & -{{m}_{1}} & 0 \\ \end{matrix} \right],x=\left[ \begin{matrix} {{F}_{1}} \\ {{F}_{2}} \\ F \\ {{a}_{1}} \\ {{a}_{2}} \\ \end{matrix} \right],b=\left[ \begin{matrix} {{m}_{1}}g\cos \alpha \\ {{m}_{1}}g\sin \alpha \\ {{m}_{2}}g\cos \alpha \\ {{m}_{2}}g\sin \alpha \\ -{{m}_{3}}g \\ \end{matrix} \right].$ | (3) |
A是由方程组中每个未知数的系数组成的矩阵,x是未知数组成的向量,b则是由各方程中的常数项组成的向量。解这样的线性方程组是线性代数的基本问题,其解是:
| $x={{A}^{-1}}\centerdot b。$ | (4) |
据此可编写程序:
clear
m1=1;m2=2;m3=3.5;μl=0.1;μ2=0.8;g=9.8;
alfa=30*pi/180;
A=[1,-1,0,0,0;-μl,-μ2,1,-m1,0;0,1,0,0,0;0,μ2,0,0,-m2;0,0,1,-m1,0];
b=[m1*g*cos(alfa);m1*g*sin(alfa);m2*g*cos(alfa);m2*g*sin(alfa);-m3*g];
x=A\b;
执行结果如下:
F1=25.461 1 N,F2=16.974 1 N,F=23.975 3 N;
a1=2.949 9 m/s2,a2=1.889 6 m/s2,a3=a1=2.949 9 m/s2。
对于求解物理问题的数学结果,再回过头来作一番物理分析,是解题的一个重要步骤。它需要我们从物理意义和物理实体的角度对数学结果作出判断,摒弃那些明显不合理的解,明确所得结果的物理思想、适用范围,并由数学解检查所列方程是否正确。
1.2 势能曲线问题一质量为1 kg的物体,在保守力的作用下,沿ox轴正方向运动(x>0),与该保守力相应的势能是
分析如下:
根据
保守力与势能的关系为:
令
x=[0.27:0.01:6];
a=1;b=2;
Ep=a./(x.^2)-b./x;
plot(x,Ep,‘b’,[0, 6],[0, 0],‘k’,[0,6],[-0.5,-0.5],‘r:’);
grid;
xlabel(‘x/m’);
ylabei(‘Ep/J’);
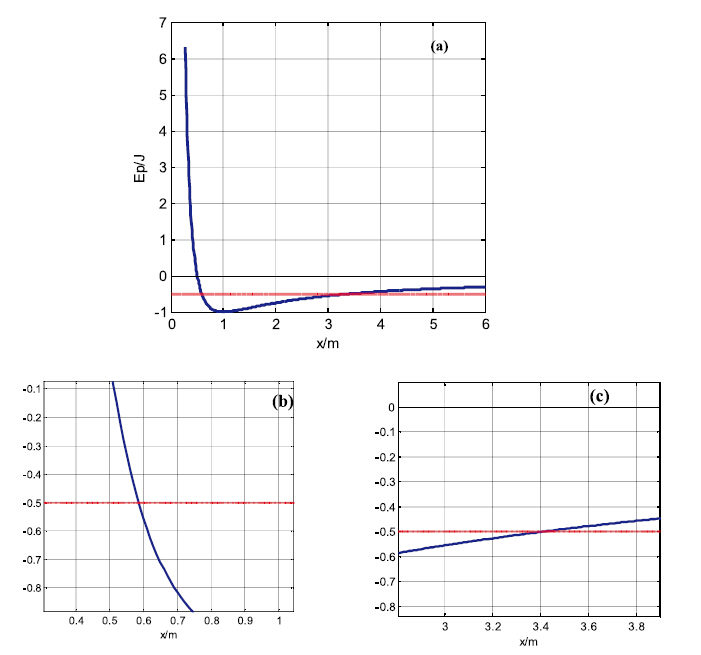
程序执行结果如图 2所示。从图 2(a)中可看出在x=1 m处,势能最小,这就是平衡位置,与一般作法完全一致。
|
图 2 物体的势能曲线图和交点放大图 (a)势能曲线图;(b)放大曲线左边交点;(c)放大曲线右边交点 |
为了求出总能量E=-0.5 J保持不变的物体的运动范围,我们已在曲线图上画出了一条比较粗的虚线,它与势能曲线的两个交点所指示的x值就是总能量E=-0.5 J保持不变的物体的运动区间,为x∈(0.586,3.414)。但有时从交点很难直接读出x的数值,这时可以利用MATLAB为我们提供的强大的图形放大功能获取x的精细数值。从放大图中我们就能很清晰准确地读出曲线左边的交点位置在x=0.586 m处(见图 2(b)),曲线右边的交点位置在x=3.414 m处(见图 2(c))。
势能曲线和E=-0.5 J的直线在x1=0.586 m与x2=3.414 m处相交,这两点即表明物体在E=-0.5 J的总能量不变时的运动范围。同样,利用传统做法,令Ep(x)=E,也可以求出物体动能为0的位置,但计算过于烦琐。也就是,令
通过比较,我们看到利用MATLAB软件绘制的图像具有直观性和可视性,直接就能得到精确的量值关系和平衡位置及物体在保持平衡时的范围,进而能够求得物体动能为0的位置。
1.3 最小值问题碰撞问题包含单质点和多质点的弹性碰撞和非弹性碰撞,而涉及的典型碰撞问题有静摩擦、行星运动、离子散射、斜抛运动、强迫振动等,[7]如利用MATLAB解决炮弹射击问题:在距离我军前方阵地1 000 m处有一高50 m的山丘,山上建有敌方一座碉堡,求我方大炮在什么角度下以最小速度发射炮弹就能摧毁敌方的这座碉堡。[6]
分析如下:
抛体运动轨迹方程为:
| $y=x\tan \theta -\frac{g{{x}^{2}}}{2v_{0}^{2}{{\cos }^{2}}\theta }.$ | (5) |
由此可解出发射速度v0与发射角度θ的关系为:
| ${{v}_{0}}=x\sqrt{\frac{g}{2}}\frac{1}{\cos \theta \sqrt{x\tan \theta -y}}.$ | (6) |
由式(6) 不难分析出,当tanθ=y/x及θ=π/2时,v0都将接近无穷大,在这中间必有一个极小值的角度。令
| $\frac{d{{v}_{0}}}{\partial \theta }=0,$ |
将目标位置x=1 000,y=50代入方程求解,原则上可以求出目标炮弹的最小速度,但由此产生的超越方程难以得出解析解。为此,我们应用MATLAB软件试解此题。
程序如下:
clear
L=1000;g=9.8;h=50;
beta=atan(h/L);
v0=[];alfa=[];
for a=beta:0.1:70;
alfa=[alfa a];
sita=pi*a/180;
A=L*sqrt(g/2);
v=A/((cos(sita))*sqrt(L*tan(sita)-h));
v0=[v0 v];
end
subplot(2,2,1);
plot(alfa,v0);
axis([20 70 100 140]);
xlabel(‘发射角度’);
ylabel(‘发射速度/(m/s)’);
[v0,n]=min(v0);
angle=(n-1)*0.1+20;
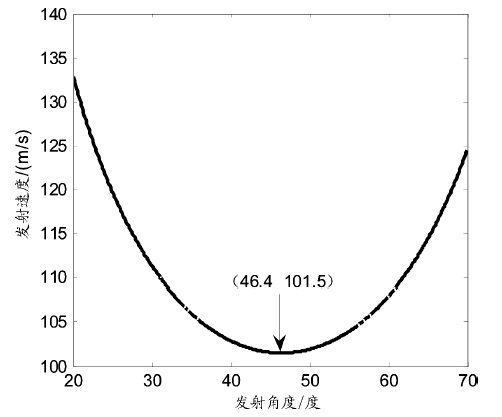
程序执行结果如图 3所示:
|
图 3 炮弹的初速度与发射角度的关系曲线 |
从图 3可以看出我方大炮在46.4度角时以最小速度101.5 m/s发射炮弹就能摧毁敌军的碉堡。
如果我们用解析的方法求出这个最小速度值的角度θ,不仅计算麻烦而且还容易出错。比如按以下方法求解,就容易出错:
求解最小速度值的条件是式(6) 对θ的一阶导数等于0,即
| $\frac{d{{v}_{0}}}{d\theta }=x\sqrt{\frac{g}{2}}\frac{(x{{\cos }^{2}}\theta -x{{\sin }^{2}}\theta +2y\cos \theta \sin \theta )}{{{(xsin\theta \cos \theta -y\cos 2\theta )}^{-3/2}}}=0.$ | (7) |
令分子等于0,并由三角公式cos2-sin2θ=cos2θ,2sinθcosθ=sin2θ得
| $x{{\cos }^{2}}\theta -x{{\sin }^{2}}\theta +2y\cos \theta \sin \theta =x\cos 2\theta +ysin2\theta =0,$ |
则
| $\tan 2\theta =-\frac{x}{y}=\frac{1000}{50}=-20.$ | (8) |
查表知:2θ=-87.14°,于是很容易得出θ=-43.57°的错误结果。
显然,发射角为负是没有意义的。
正确解法:
| $\tan 2\theta =\frac{2\tan \theta }{1-{{\tan }^{2}}\theta }=-\frac{x}{y}.$ | (9) |
由这个关于tanθ的二次方程解得:
| $\tan \theta =\frac{y+\sqrt{{{x}^{2}}+{{y}^{2}}}}{x},$ | (10) |
所以
| $\theta =\arctan \frac{50+\sqrt{{{1000}^{2}}+{{50}^{2}}}}{1000}={{46.4}^{\circ }}.$ | (11) |
这个结果与直接从式(6) 的计算机数值解的结果一致,由此可见,计算机的数值解既避免了复杂的运算,也避免了可能出现的问题。
2 结语以上三个应用实例,通过与常用办法求解作比较,我们发现:常规的解物理方程只能是某特定情况下的一个数值点或几个数值点,而MATLAB数值解是以图形的方式展示出来的各种情况下的结果,可以看出整个物理过程,大大加深了对物理知识的理解。这样既使我们容易理解,同时也能把计算机技术与解决理论和实际问题相结合。[8]
本文通过对力学问题求解过程中解线性方程组和超越方程时引入MATLAB软件,说明了MATLAB软件的基本功能,经过对这两种求解过程的比较,展现了MATLAB软件在解题中的直观性和实用性,极大地简化了解题过程,也能使复杂的解变得简明直观,加深了我们对物理内容的理解。同时利用MATLAB工具还可以灵活自主、快速直观、简单方便地修改分析数据,处理分析结果,提高我们对物理过程的理解。
| [1] | 王清, 龚长青. MATLAB在"理论力学"教学中的应用[J]. 中国电力教育, 2011(9): 200–203. |
| [2] | 梁兰菊. MATLAB在力学教程中的应用[J]. 长春师范学院学报(自然科学版), 2008(4): 120–123. |
| [3] | 钟季康, 鲍鸿吉. 大学物理习题计算机解法[M]. 北京: 机械工业出版社, 2008. |
| [4] | 熊万杰. MATLAB用于大学物理教学[J]. 物理通报, 2004(2): 88–92. |
| [5] | 王锋, 李秀芬, 王小荣, 等. MATLAB在求解质点动力学问题中的应用[J]. 内江科技, 2008, 29(6): 83–84. |
| [6] | 张丽, 王相和, 白晶. MATLAB软件在力学教学中的应用[J]. 产业与科技论坛, 2011, 10(9): 148–150. |
| [7] | 黄宁宁. MATLAB在理论力学教学中的应用[J]. 江西科技师范学院学报, 2004(4): 88–91. |
| [8] | 闫琴, 李斌. 有阻尼斜抛物体运动的分析[J]. 石河子大学学报(自然科学版), 2004, 22(6): 522–524. |
 2016, Vol. 31
2016, Vol. 31