随着信息技术和网络技术的飞速发展,各种各样的数字图像在网络上越来越多地进行传输。其中,有很多的图像信息非常重要,它们小到有可能涉及个人的隐私, 大到可能涉及国家的安全,其价值无法衡量。 另外,由于网络的普及,使得任何人都有可能接触到其中的部分信息,因此在网络上传输数字图像的安全性便尤为重要,从而对数字图像进行加密或隐藏就成了重要的研究课题。
图像具有表达直观、所含信息量大等特点,因而图像信息在存储和传输过程中的安全问题就显得非常重要。 近年来,为了解决数字图像的安全问题,典型的手段有信息隐藏与伪装技术[1-4],其中有几个重要课题: (1) 数字图像的加密技术; (2) 数字图像的分存技术; (3) 数字图像的隐藏技术; (4) 数字图像的水印技术。 其中, 加密技术中最主要的是数字图像的置乱技术。 已有的数字图像的置乱技术主要有基于Arnold变换的、FASS 曲线的、Gray 码变换的、Conway“游戏”的、仿射模变换的、基于三角函数的等等。[5-10]
混沌系统具有许多重要特性, 例如对初始条件和系统参数的极端敏感性、拓扑传递性、周期点的稠密性、伪随机性等等。混沌现象是在确定性的非线性系统中不需要附加任何随机因素便可以出现的一种内在随机性, 因此其伪随机行为能够准确再生。这些特性与密码学中要求的扩散、混合和随机特性相吻合, 因此在加密算法中混沌有着广泛的应用。
本文提出了一种基于非线性混沌序列的数字图像加密算法, 数字实验表明, 该方法思想简单易于实现, 加密效果较好, 抗攻击性较强, 安全性较好。
1、基本原理 (1.1) 一维Logistic混沌映射分析由一维Logistic混沌映射生成混沌序列,Logistic混沌映射可以表示为:
| ${{a}_{n+1}}=F({{a}_{n}})=\lambda {{a}_{n}}(1{{a}_{n}}),\text{ }\lambda \in \left( 0,4 \right)\text{ },\text{ }n=1,2,\ldots $ | (1) |
其中:初值a0和参数λ都可以用来作为密钥。
通过试验可以发现, 参数λ可以分为三部分, 通过如下条件进行试验:a0=0.2, 当λ∈(0,3) 时经过若干次迭代的结果没有混沌现象;当λ∈(3,3.569 946 …)时系统出现周期性;当3.569 946 …≤λ≤4时,Logistic映射的输入和输出都分布在区间(0,1) 上, 且工作处于混沌状态, 即此时由初值a0在Logistic混沌映射的作用下所产生的序列ak;k=0,1,2,…具有非周期的、不收敛并对初始值非常敏感的性质。由以上分析可以看出, 当λ∈(0,3.569 946 …)时Logistic映射所得的点集中在某些值上, 不能应用于加密, 因此应用Logistic映射的加密系统密钥空间比较小且安全性比较脆弱。
(1.2) 非线性混沌系统的设计为了克服上述缺点, 利用非线性函数设计出一种新的混沌算法。为了提高安全性, 最好使用非线性函数去改变密钥空间的连续性, 因此利用幂函数(1-x)β和正切函数tanx替代线性函数。非线性混沌系统可以定义为[3]
| ${{a}_{n+1}}=\lambda \text{tan}(\alpha {{a}_{n}}){{(1{{a}_{n}})}^{\beta }}$ | (2) |
其中:an∈(0,1) ,n=1,2,…, λ=cot
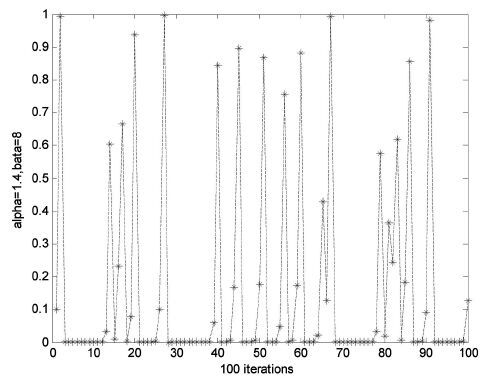
当α∈(0,1.4],β∈[5,43]或α∈(1.4,1.5],β∈[9,38]或α∈(1.5,1.57],β∈[3,15]时该系统处于混沌状态。
|
图 1 非线性混沌序列的分布图 |
首先,利用公式(2) 生成混沌图像,并对原始图像和此混沌图像进行二维离散小波变换[11-14];
其次,对由小波变换所得的低频和高频信息分别进行线性插值;
最后,利用二维离散小波逆变换重构图像, 从而得到加密图像。
这里加密的密钥可以选取为: 生成混沌矩阵的初始值、线性插值时的融合参数, 以及迭代次数等等。
(1.4) 加密算法Step1:输入加密密钥迭代次数times、混沌序列的初始值α,β和融合参数t;
Step2:输入原始图像, 大小为M×N;
Step3:利用公式(2) 获得M×N的一维混沌序列, 并将其转换为M×N的矩阵, 生成混沌矩阵, 通过排序变换将每一行的N个值由小到大排序, 生成b1,
| $CI={{\left[ {{G}_{1}}{{G}_{2}}\ldots {{G}_{M}} \right]}^{T}}$ |
Step4:对原始图像SI和混沌图像CI分别进行二维离散小波变换, 分别得到原始图像SI的小波变换系数SLLC,SLHC,SHLC,SHHC和混沌图像CI的小波变换系数CLLC,CLHC, CHLC,CHHC;
Step5:对Step4中所得的SI的小波变换系数和CI的小波变换系数通过融合系数t利用公式(3) 进行融合, 得到融合图像。
| $MI=tSI+\left( 1-t \right)CI;$ | (3) |
Step6:利用二维离散小波逆变换对Step5所得的融合结果进行重构, 得到加密图像EI;
Step7:返回Step3直到迭代结束。
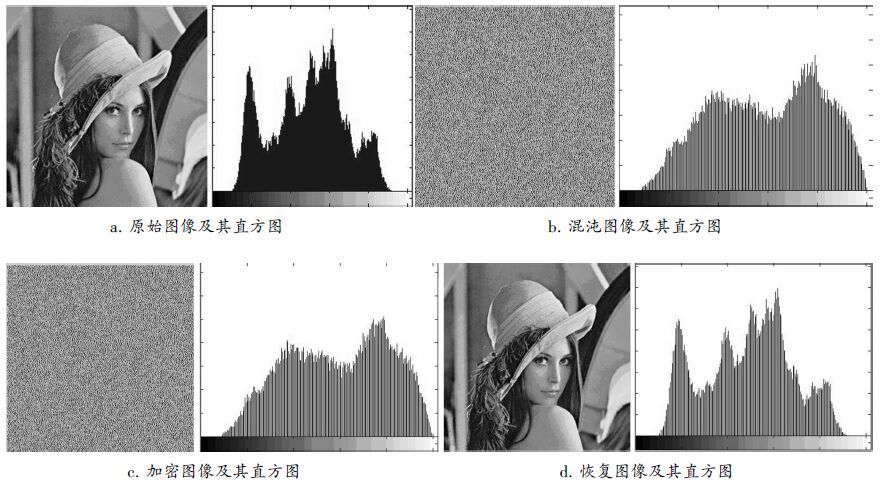
2、试验结果与分析 (2.1) 加密和恢复实例图 2是基于本文算法给出的数字图像加密和恢复的实例。其中,选取Lena图(256×256) 为原始图像, 迭代次数times=3, 混沌序列的初始值分别取α=1.4,β=8,融合参数t=0.1;对原始图像Lena图和生成的混沌图像CI应用Daubecchies小波变换(db1) 。图 2a表示原始图像及其直方图,图 2b表示Step3生成的混沌图像及其直方图,图 2c表示加密后的图像及其直方图,图 2d表示恢复图像及其直方图。
由图 2可以看出该算法具有较好的加密和恢复效果。
|
图 2 数字图像加密和恢复实例 |
传统的客观评价方法用恢复图像偏离原始图像的误差来衡量恢复图像的质量, 最常用的有均方根误差RMSE(Root Mean Squared Error)和峰值信噪比PSNR(Peak Signal to Noise Ratio)[15]。
均方根误差RMSE的表达式为
| $RMSE=\sqrt{\frac{\sum\limits_{i=1}^{M}{\sum\limits_{j=1}^{N}{{{\left[ {{F}^{\prime }}\left( i,j \right)-F\left( i,j \right) \right]}^{2}}}}}{M*N}}$ | (4) |
其中:Fi,j表示原始图像的(i,j)位置处像素灰度值、Fi,j′表示恢复图像的像素值, 1≤i≤M, 1≤j≤N。
均方根误差RMSE越小, 便说明两幅图像越相像。
峰值信噪比PSNR的表达式为
| $PSNR=10*\lg \left[ \frac{M*N*{{255}^{2}}}{\sum\limits_{i=1}^{M}{\sum\limits_{j=1}^{N}{{{\left[ {{F}^{\prime }}\left( i,j \right)-F\left( i,j \right) \right]}^{2}}}}} \right]$ | (5) |
峰值信噪比PSNR越大, 说明图像的保真度越好, 两幅图像越相似。
峰值信噪比PSNR本质上与均方根误差RMSE相同, 其关系表达式为
| $PSNR=10*\text{lg}\frac{{{255}^{2}}}{RMS{{E}^{2}}}$ | (6) |
利用本文算法恢复图像与原始秘密图像的峰值信噪比PSNR为279.17, 由此可知, 两幅图像的保真度较好, 两幅图像非常像;RMSE为均方根误差2.805e-12, 从而可以得出算法的恢复效果较好。
(2.3) 噪声攻击数字图像在网络传输的过程中, 经常会受到各种各样的攻击,如受到某种干扰而含有各种噪声。图 3a对秘密图像添加了密度为0.5%的高斯噪声后的恢复图像; 图 3b为对秘密图像添加了1%的高斯噪声后的恢复图像;图 3c为对秘密图像添加了0.5%的椒盐噪声后的恢复图像; 图 3d为对秘密图像添加了1%椒盐噪声后的恢复图像。
从图 3可以看出, 该算法对高斯噪声和乘性椒盐噪声具有较好的稳健性。

|
图 3 对秘密图像分别添加高斯噪声和椒盐噪声后的恢复图像 |
本文给出了一种基于非线性混沌图像的数字图像加密算法, 该算法思想简单, 易于编程, 具有较好的安全性, 且恢复图像质量较高。另外, 可以利用不同的混沌系统生成混沌图像, 且融合参数t可以利用混沌序列, 以增加密钥空间。
| [1] | Kumsawat P, Attkitmongcol K, Srikaew A, et al. Wavelet-based image watermarking using the genetic algorithm[J].Knowledge-based intelligent information and engineering systems 8th International Conference, KES2004. Proceedings (Lecture Notes in Artificial Intelligence), 2004,(3):643-649. |
| [2] | Bao P,Ma Xiaohu. Image adaptive watermarking using wavelet domain singular value decomposition[J].IEEE Trans.on Circuits and Systems for Video Technology, 2005,15(1):96-102. |
| [3] | Haojiang Gao, Yisheng Zhang, Shuyun Liang, et al. A new chaotic algorithm for image encryption[J]. Chaos, Solitons and Fractals, 2006, 29: 393–399. DOI:10.1016/j.chaos.2005.08.110 |
| [4] | Zhang Lin-hua, Liao Xiao-feng, Wang Xue-bing. An image encryption approach based on chaotic maps[J]. Chaos, Solitons and Fractals, 2005, 24(3): 759–765. DOI:10.1016/j.chaos.2004.09.035 |
| [5] | 黄丽芳. 基于混沌系统的新型DNA混合图像加密算法研究[J]. 九江学院学报(自然科学版), 2016, 31(1): 77–79. |
| [6] | 乐鸿辉, 李涛, 石磊. 应用Henon超混沌系统改进的图像加密[J]. 计算机应用, 2011, 31(7): 1909–1916. |
| [7] | 翟依依, 王光义. 基于Tent混沌序列的数字图像加密方法[J]. 现代电子技术, 2014, 37(12): 73–77. |
| [8] | 刘乐鹏, 张雪锋. 基于混沌和位运算的图像加密算法[J]. 计算机应用, 2013, 33(4): 1070–1073. |
| [9] | 王雅庆, 周尚波. 基于分数阶陈氏混沌系统的图像加密算法[J]. 计算机应用, 2013, 33(4): 1043–1046. |
| [10] | 丁玮, 闫伟齐, 齐东旭. 基于Arnold变换的数字图像置乱技术[J]. 计算机辅助设计与图形学学报, 2001, 13(4): 338–341. |
| [11] | Barni M, Bartolini F, Cappellini V, et al. A DCT-domain System for robust Image Watermarking[J]. Signal Processing, 1998, 66(3): 352–357. |
| [12] | Kunder D, Hatzinkos D. A Robust Digital Image Watermarking Method Using Wavelet-based Fusion[J]. In international Conference on Image rocessing, 1997(3): 544–547. |
| [13] | 徐晨, 赵瑞珍, 甘小冰. 小波分析应用算法[M]. 北京: 科学出版社, 2004. |
| [14] | 葛哲学, 沙威. 小波分析理论与MATLABR2007实现[M]. 北京: 电子工业出版社, 2007. |
| [15] | 孙兆林. MATLAB 6.X图像处理[M].北京:清华大学出版社,2002.192-197. |
 2016, Vol. 31
2016, Vol. 31