渭南师范学院学报 2016, Vol. 31 Issue (19): 14-18  
0

引用本文

雷前召, 张宁宁. 规则形状均匀带电平面之中心垂轴电场差异性研究[J]. 渭南师范学院学报, 2016, 31(19): 14-18.
LEI Qian-zhao, ZHANG Ning-ning. Research on the Differences between the Electric Fields of the Vertical Shafts to the Regular-shaped Uniformly Charged Planes Centers[J]. Journal of Weinan Normal University, 2016, 31(19): 14-18.

基金项目

陕西省教育厅专项科研计划项目：泾渭流域对流层波导的超短波传播影响研究（15JK1242）；陕西省扶持学科数学学科基金资助项目：贝塞尔函数在电磁波传播与散射中的应用（201606）

作者简介

雷前召(1967-), 男, 河南信阳人, 渭南师范学院数理学院副教授, 西安电子科技大学博士研究生, 主要从事复杂介质中的光、波传播研究

文章历史

收稿日期：2016-08-11
Contents              Abstract              Full text              Figures/Tables              PDF
规则形状均匀带电平面之中心垂轴电场差异性研究
雷前召 , 张宁宁     
渭南师范学院 数理学院，陕西 渭南 714099
收稿日期：2016-08-11
基金项目：陕西省教育厅专项科研计划项目：泾渭流域对流层波导的超短波传播影响研究（15JK1242）；陕西省扶持学科数学学科基金资助项目：贝塞尔函数在电磁波传播与散射中的应用（201606）
作者简介：雷前召(1967-), 男, 河南信阳人, 渭南师范学院数理学院副教授, 西安电子科技大学博士研究生, 主要从事复杂介质中的光、波传播研究
摘要: 对均匀带电圆盘和正多边形面盘、圆环和正多边形环以及含圆孔、正多边形的无限大平面中心垂轴的电场分布进行了计算，并对所得解析结果进行了对比。通过模拟，得到圆盘、圆环均匀带电平面中心垂轴电场分布图，尤其是不同环面宽度的中心垂轴场强分布；对模拟结果进行了分析及总结。正多边形的面盘、环的模拟结果具有相同的结论。通过对比，加深了对各种规则形状带电平面中心垂轴电场差异性的认识。
关键词: 规则形状    中心垂轴    电场差异性    
Research on the Differences between the Electric Fields of the Vertical Shafts to the Regular-shaped Uniformly Charged Planes Centers
LEI Qian-zhao, ZHANG Ning-ning     
School of Mathematics and Physics, Weinan Normal University, Weinan 714099, China
Abstract: First the electric fields at the vertical shafts of the regular-shaped uniformly charged planes centers were calculated, the regular-shaped planes covering the circular and regular polygon plates, the circle and regular polygon rings and infinite plane with circular hole or regular polygon; the obtained analytical results were compared. Then the uniformly charged disc, the annulus center vertical axial electric field distributions were simulated; especially so were done the electric field intensity distributions at the ring central vertical axes under different ring width; similarly it could get the simulation results of the regular polygon plate, ring. Finally, the simulation results were analyzed and the differences between the electric fields of vertical shafts to various shapes charged planes centers were summarized. By contrast, a deep understanding about these differences was obvious.
Key words: regular shape    vertical shaft    electric fields difference    

带电体的电场分布研究、带电体的场强计算方法较多[1-9]，其中规则形状带电平面中心垂轴电场强度分布研究，比如对圆线圈、圆盘、圆柱面等中心轴线上的电场强度的计算[1-7]，一般局限于对场强分布公式进行推导，或对某一形状带电体电场进行较深入探讨；而对各种有规则形状带电平面轴线的电场分布的比较研究较少，对这些电场分布的一些共同特性研究不够深入。而这些研究仅依靠简单形状均匀带电体的电场强度计算方法--高斯定理、电势梯度和场强积分等，往往得不到理想结果，因此，开展本研究尚有必要。

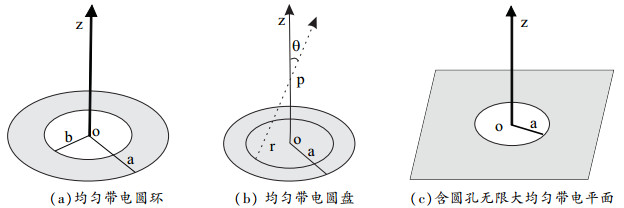
1 均匀带电圆盘、圆环、有圆孔无限大平面中心垂轴电场 1.1 电场分布计算

均匀带电圆盘、圆环及含圆孔平面如图 1所示，电荷面密度为σ。圆环内外半径分别是b和a，圆盘半径为a，带孔平面所含圆孔半径为a。则利用连续电荷积分法可以计算图 1的(a)(b)(c)各分图对应的中心垂轴电场[10-11]，分别为：

$\begin{array}{l} \vec E = {{\vec e}_z}\frac{{\sigma z}}{{2{\varepsilon _0}}}(\frac{1}{{\sqrt {{b^2} + {z^2}} }} - \frac{1}{{\sqrt {{a^2} + {z^2}} }}){\mathop{\rm sgn}} \left( z \right),\\ \vec E = {{\vec e}_z}\frac{\sigma }{{2{\varepsilon _0}}}\left[ {1 - \frac{z}{{\sqrt {{a^2} + {z^2}} }}} \right]{\mathop{\rm sgn}} \left( z \right),\\ \vec E = {{\vec e}_z}\frac{{\sigma z}}{{2{\varepsilon _0}\sqrt {{a^2} + {z^2}} }}{\mathop{\rm sgn}} \left( z \right)。 \end{array}$ (1)

其中：符号函数${\mathop{\rm sgn}} \left( z \right) = \left\{ {\begin{array}{*{20}{l}} {1\;\;\;\;\;z > 0,}\\ {0\;\;\;\;z = 0,}\\ { - 1\;\;\;\;z < 0。} \end{array}} \right.$

图 1 均匀带电圆盘、圆环及含圆孔平面
1.2 均匀带电圆环、圆盘中心轴线电场分布模拟及分析

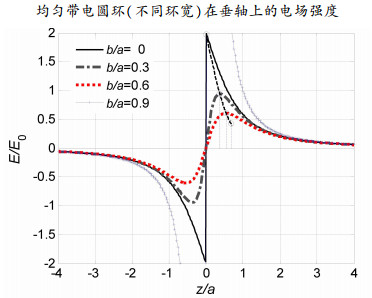
由前面推导所得圆盘、圆环轴线电场分布公式(1)，假设均匀带电圆环外半径为a、内半径为b，带电量为Q，模拟所得结果如图 2所示。

图 2 均匀带电圆环(不同环宽)中心垂轴上的电场分布

模拟结果分析：

圆盘电荷在z=0附近点产生的场强最大，此电场强度等同于“无限大”带电平面的场强。但由于圆盘两边场强方向不同，电场强度在z=0点不连续，在圆盘中点场强为0。

模拟图显示，当距离增加时，电场强度值持续减小。而当中心垂轴距盘心距离|z| > 3a时，其电场强度近似于盘心同等电量的点电荷产生的场强，且距离越远近似程度越高。

当均匀带电圆环面外环半径不变，逐渐减小内环半径b，向圆盘演变的过程中，环中心的场强均为0；除中心z=0点外，中心垂轴各点可导，且不论圆环宽度如何，每一环宽的圆环轴线场强分布都有一个极值点。

不同环宽的圆环轴线场强的极值点分布在一条曲线上，极值点对应的场强随圆环面宽度的增加(b值减小)而增加，且逐渐向中心点靠近。当b=0，圆环最终变成圆盘，场强的极值达到最大，极值点即盘中心。

2 均匀带电正多边形盘、环以及含正多边形孔的无限大平面之中心垂轴电场 2.1 电场分布计算

边长为a，均匀带电线密度为λ的线段，其中垂轴上距线段中点为r处的场强为[12]

$\vec E = \frac{1}{{4\pi {\varepsilon _0}}}\frac{{\lambda a}}{{r\sqrt {{r^2} + \frac{{{a^2}}}{4}} }}{\vec e_r}。$ (2)

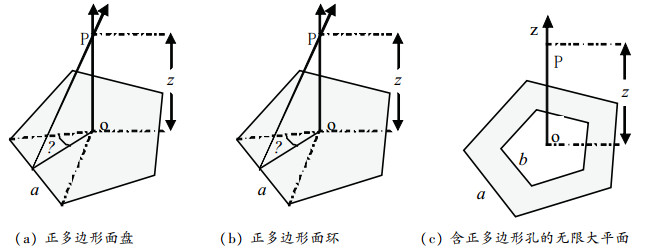
据此，容易推导正n边形面盘中心垂轴的电场强度。如图 3(a)所示，边长为a，均匀带电面密度为σ，正n边形面盘中心垂轴上任意点P (距盘中心点为z)的场强[13]为

$\vec E = {{\vec e}_z}\frac{{n\sigma }}{{2\pi {\varepsilon _0}}}\arctan \frac{{\cot \alpha \sqrt {1 + \frac{{{a^2}{{\csc }^2}\alpha }}{{4{z^2}}}} - \cot \alpha }}{{1 + {{\cot }^2}\alpha \sqrt {1 + \frac{{{a^2}{{\csc }^2}\alpha }}{{4{z^2}}}} }}{\mathop{\rm sgn}} \left( z \right)。$ (3)
图 3 均匀带电正多边形盘、环以及含正多边形孔的无限大平面

同样均匀带电面密度为σ，同轴正n边形面环，如图 3(b)所示，其环的内、外边长分别为b、a，则其中心垂轴任意点P (距离环心为z)的电场强度为

$\begin{array}{l} \vec E = {{\vec e}_z}\frac{{n\sigma }}{{2\pi {\varepsilon _0}}}\arctan \frac{{\left[ {\cot \alpha \sqrt {1 + \frac{{{a^2}{{\csc }^2}\alpha }}{{4{z^2}}}} - \cot \alpha } \right]}}{{1 + {{\cot }^2}\alpha \sqrt {1 + \frac{{{a^2}{{\csc }^2}\alpha }}{{4{z^2}}}} }}{\mathop{\rm sgn}} \left( z \right) - \\ {{\vec e}_z}\frac{{n\sigma }}{{2\pi {\varepsilon _0}}}\arctan \frac{{\left[ {\cot \alpha \sqrt {1 + \frac{{{b^2}{{\csc }^2}\alpha }}{{4{z^2}}}} - \cot \alpha } \right]}}{{\left( {1 + {{\cot }^2}\alpha \sqrt {1 + \frac{{{b^2}{{\csc }^2}\alpha }}{{4{z^2}}}} } \right)}}{\mathop{\rm sgn}} \left( z \right)。 \end{array}$ (4)

由反三角函数两角差公式，式(4)进一步推导为

$\begin{array}{l} \vec E = {{\vec e}_z}{\mathop{\rm sgn}} \left( z \right)\frac{{n\sigma }}{{2\pi {\varepsilon _0}}}\\ \arctan \frac{{\cot \alpha \sqrt {1 + \frac{{{a^2}{{\csc }^2}\alpha }}{{4{z^2}}}} - \cot \alpha \sqrt {1 + \frac{{{b^2}{{\csc }^2}\alpha }}{{4{z^2}}}} - {{\cot }^3}\alpha \sqrt {1 + \frac{{{b^2}{{\csc }^2}\alpha }}{{4{z^2}}}} + {{\cot }^3}\alpha \sqrt {1 + \frac{{{a^2}{{\csc }^2}\alpha }}{{4{z^2}}}} }}{{\left[ {1 + {{\cot }^2}\alpha \sqrt {1 + \frac{{{a^2}{{\csc }^2}\alpha }}{{4{z^2}}}} } \right]\left[ {1 + {{\cot }^2}\alpha \sqrt {1 + \frac{{{b^2}{{\csc }^2}\alpha }}{{4{z^2}}}} } \right] + {{\cot }^2}\alpha \left[ {\sqrt {1 + \frac{{{a^2}{{\csc }^2}\alpha }}{{4{z^2}}}} - 1} \right]\left[ {\sqrt {1 + \frac{{{b^2}{{\csc }^2}\alpha }}{{4{z^2}}}} - 1} \right]}},\\ \vec E = {{\vec e}_z}\frac{{n\sigma }}{{2\pi {\varepsilon _0}}}\arctan \frac{{\cot \alpha \left[ {\sqrt {1 + \frac{{{a^2}{{\csc }^2}\alpha }}{{4{z^2}}}} - \sqrt {1 + \frac{{{b^2}{{\csc }^2}\alpha }}{{4{z^2}}}} } \right]}}{{1 + {{\cot }^2}\alpha \sqrt {1 + \frac{{{b^2}{{\csc }^2}\alpha }}{{4{z^2}}}} \sqrt {1 + \frac{{{b^2}{{\csc }^2}\alpha }}{{4{z^2}}}} }}{\mathop{\rm sgn}} \left( z \right)。 \end{array}$ (5)

含正多边形孔的无限大平面，如图 3(c)所示，中心垂轴任一P点电场

$\vec E = {{\vec e}_z}\frac{\sigma }{{2{\varepsilon _0}}}{\mathop{\rm sgn}} \left( z \right) - {{\vec e}_z}\frac{{n\sigma }}{{2\pi {\varepsilon _0}}}\arctan \frac{{\left[ {\cot \alpha \sqrt {1 + \frac{{{a^2}{{\csc }^2}\alpha }}{{4{z^2}}}} - \cot \alpha } \right]}}{{1 + {{\cot }^2}\alpha \sqrt {1 + \frac{{{a^2}{{\csc }^2}\alpha }}{{4{z^2}}}} }}{\mathop{\rm sgn}} \left( z \right)。$ (6)
2.2 均匀带电正多边形环、盘中心垂轴电场分布特性

前面式(3)(5)和(6)分别为均匀带电正多边形盘、环和有正多边形孔的无限大平面中心垂轴电场分布公式，和式(1)对比，似乎差异很大，但这只是表面现象。

可以证明[14]，当n→∞时，式(5)(6)(7)就由正n边形过渡到对应的圆形带电情形。正n边形盘、环中心垂轴电场分布模拟结果完全类似于均匀带电圆盘、圆环，其电场分布特性也和均匀带电圆盘、圆环相似。不仅如此，对相同面积、相同电荷密度的正多边形盘来说，其边数n的变化对盘中心垂轴同一点场强的大小几乎没有影响，甚至和相同面积、相同电荷密度的圆环中心垂轴同一点场强非常接近。

设正四边形边长为a，具有相同面积的圆半径为r，则有${r^2} = \frac{1}{\pi }{a^2}$。由正多边形面盘中心垂轴电场公式(3)和圆盘中心垂轴电场公式(1)，且为简化起见，只考虑z=z0=2a的情形，则有

${{\vec E}_{正三边形}} = {{\vec e}_z}\frac{{3\sigma }}{{2\pi {\varepsilon _0}}}\arctan \frac{1}{{\sqrt 3 }}\frac{{\left[ {\sqrt {1 + \frac{{4{a^2}}}{{3\sqrt 3 {z^2}}}} - 1} \right]}}{{1 + \frac{1}{3}\sqrt {1 + \frac{{4{a^2}}}{{3\sqrt 3 {z^2}}}} }} = 0.0188\frac{\sigma }{{{\varepsilon _0}}}{{\vec e}_z},$ (7)
${{\vec E}_{圆盘}}\left( {{z_0}} \right) = {{\vec e}_z}\frac{\sigma }{{2{\varepsilon _0}}}\left[ {1 - \frac{z}{{\sqrt {{r^2} + {z^2}} }}} \right] = {{\vec e}_z}\frac{\sigma }{{2{\varepsilon _0}}}\left[ {1 - \frac{1}{{\sqrt {1 + \frac{{{a^2}}}{{\pi {z_0}^2}}} }}} \right] = 0.0187\frac{\sigma }{{{\varepsilon _0}}}{{\vec e}_z}。$ (8)

可以看出${{\vec E}_{正三边形面盘}}\left( {{z_0}} \right)$非常接近${{\vec E}_{圆盘}}\left( {{z_0}} \right)$，而当n取4、6等有限数值时，则其面盘轴线上z0点电场强度和三边形完全一样为0.0188$\frac{\sigma }{{{\varepsilon _0}}}$；z选取轴上不同点同样是这个结果。只是对正n边形环而言，n的变化对场强有一点影响，且具有规律性，n越大中心垂轴同一点场强越小[15]。

3 结语

利用泰勒级数展式可以计算带电圆盘在空间任意点的电场分布，但如果选取泰勒级数的一级近似，精度不高，而如果利用高阶近似，则计算大为复杂。对规则形状均匀带电平面垂轴上任意点场强进行深入分析，通过对比研究，不仅能够帮助我们熟悉轴线上电场分布规律，也有助于了解近轴区域电场分布大致情况，在此基础上再根据需要决定是否对其电场分布区域做普遍性研究。

参考文献
[1] 周海英, 陈浩, 张晓炜. 均匀带电薄圆盘的电场[J]. 大学物理, 2005, 24(11): 31–34.
[2] 江俊勤. 也谈均匀带电细圆环的电场分布[J]. 大学物理, 2007, 26(11): 39–42.
[3] 贾秀敏. 再论带电细圆环与导体球壳系统的场分布[J]. 浙江大学学报(理学版), 2011, 38(2): 182–184.
[4] 贾秀敏. 有限长均匀带电圆柱壳的电场[J]. 浙江大学学报(理学版), 2014, 41(5): 528–530.
[5] 曹玉娟, 董慎行. 数值积分求解均匀带电圆环平面上的电场分布[J]. 物理与工程, 2005, 15(3): 12–14.
[6] 樊雅平, 黄生学. 均匀带电正三角形线圈的电场[J]. 贺州学院学报, 2008, 24(3): 113–117.
[7] 樊雅平, 黄生学. 均匀带电正方形线圈的空间电场分布[J]. 河池学院学报, 2009, 29(5): 29–32.
[8] 阳喜元, 蔡新华, 吴丹. 微元法研究均匀带电体的电场分布[J]. 广西物理, 2008, 29(3): 34–37.
[9] 魏生贤, 陈光学, 陶昌. 填补法与高斯定理结合解决非对称静电场问题[J]. 曲靖师范学院学报, 2013, 32(3): 23–26.
[10] 郑金. 探究几种均匀带电体的场强及最大值[J]. 物理通报, 2014(12): 57–59.
[11] 窦春升, 杨志怀, 王参军. 大学物理[M]. 西安: 陕西科学技术出版社, 2010.
[12] 赵凯华, 陈熙谋. 电磁学[M]. 北京: 高等教育出版社, 2011.
[13] 李成金, 赵勋杰. 正多边形带电框、带电面轴线上的场强分布[J]. 物理与工程, 2006, 16(5): 25–27.
[14] 王嘉乐. 利用多边形逼近圆环的思想计算有限长均匀带电的偏轴圆筒在空间任意一点的电场[J]. 大学物理, 2013, 32(1): 38–41.
[15] 方嵩林, 范双菲, 傅芸, 等. 浅论正多边形带电环盘筒柱的场强[J]. 物理通报, 2012(12): 24–26.